Development of a Binary Classification Model to Assess Safety in Transportation Systems Using GMDH-Type Neural Network Algorithm
Abstract
1. Introduction
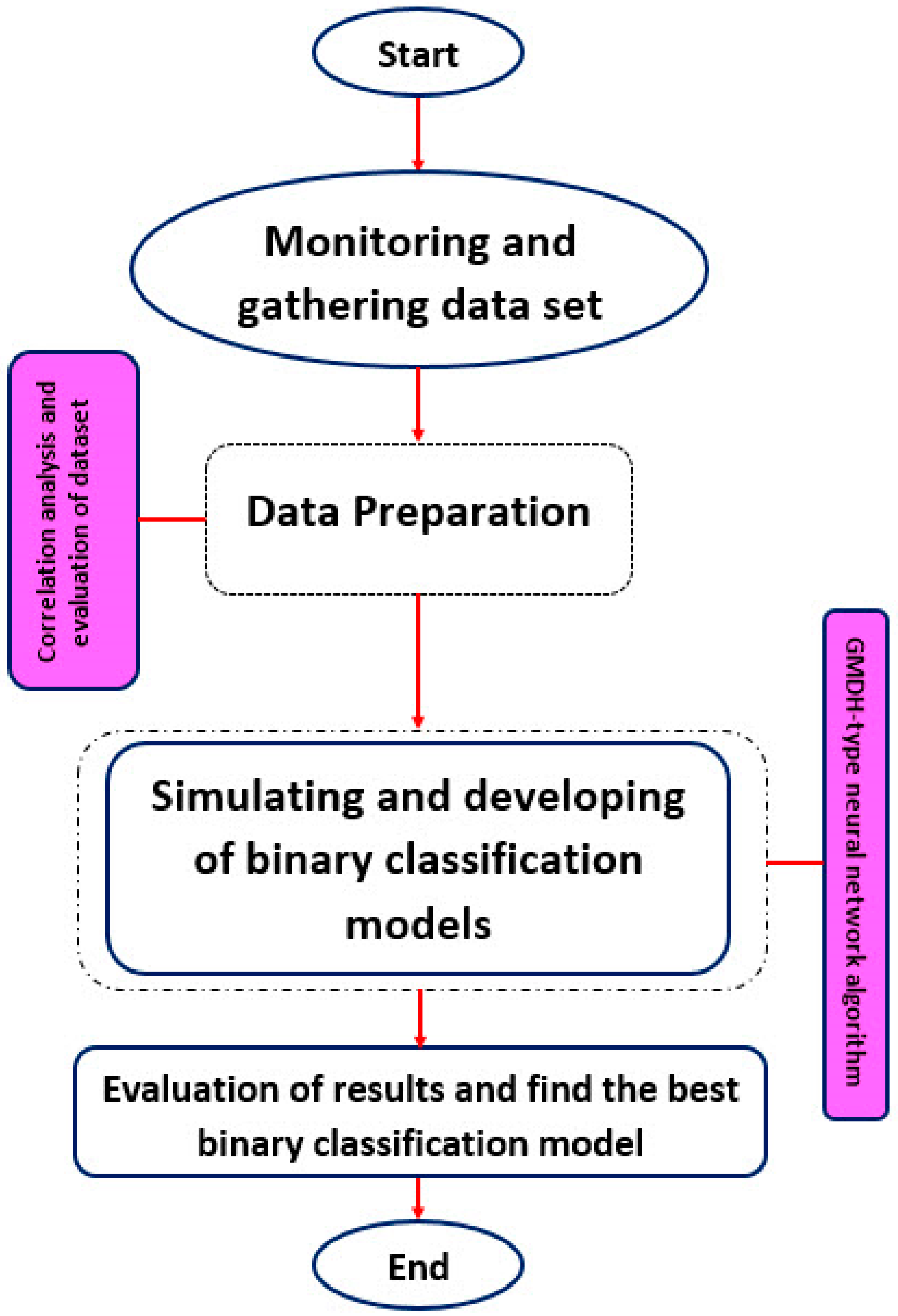
2. Methods
2.1. Group Method of Data Handling (GMDH) Type of Neural Network
2.2. Correlation Analysis
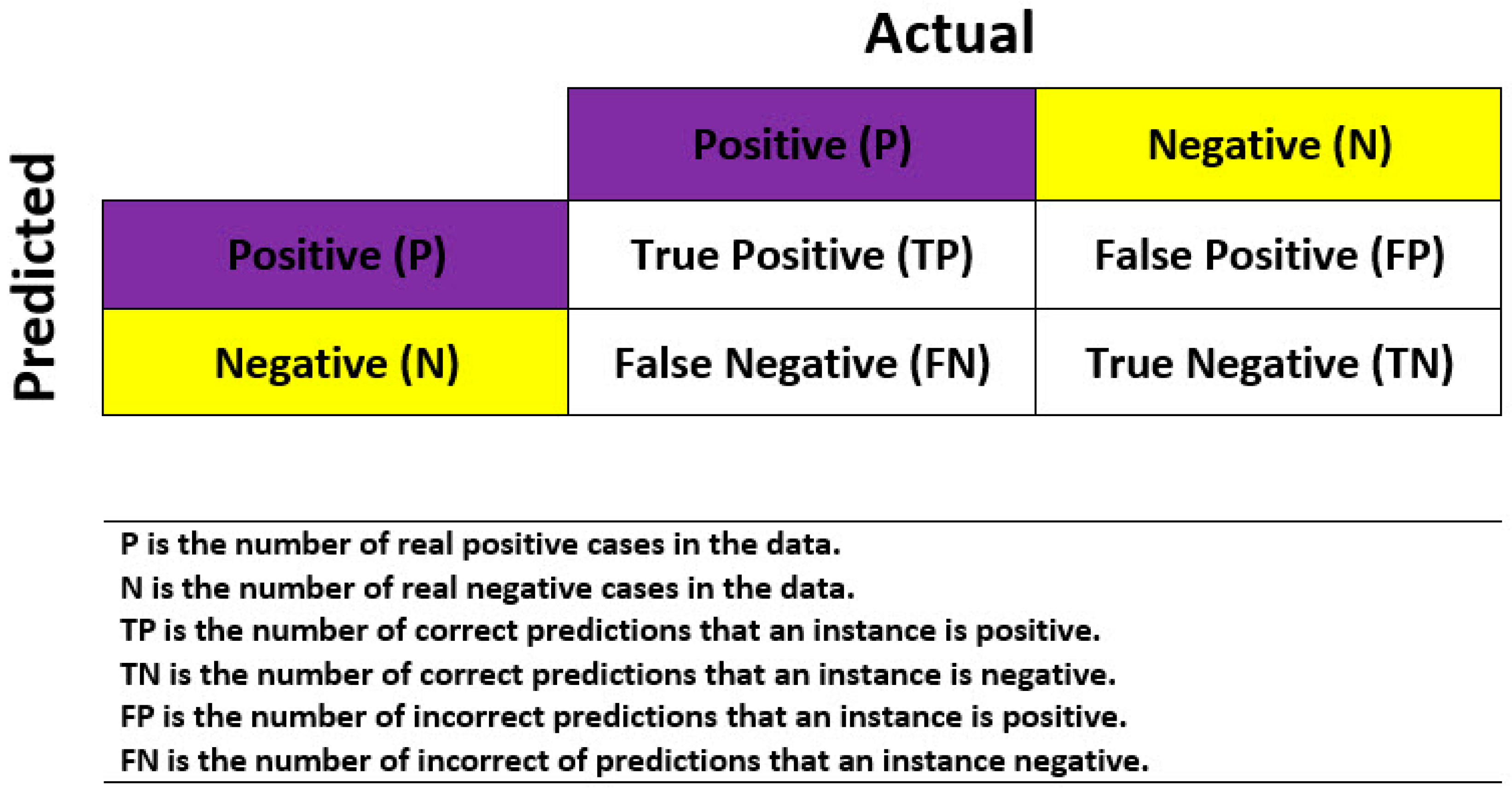
2.3. Binary Modeling
3. Case Study
3.1. Data Collection and Preparation
- -
- Road accidents: those that occur in a road open to public traffic, as a result of which, one or more people were injured or killed and in which at least one vehicle was involved;
- -
- Dead: people who died instantly (within 24 h) or those who died from the second to the thirtieth day, starting with that of the accident included;
- -
- Injured: people who suffered injuries as a result of the accident. Given the difficulty of defining objective criteria on the level of severity of the injuries suffered, there is no distinction between serious or light injuries.
3.2. Correlation Analysis
3.3. Binary Modeling
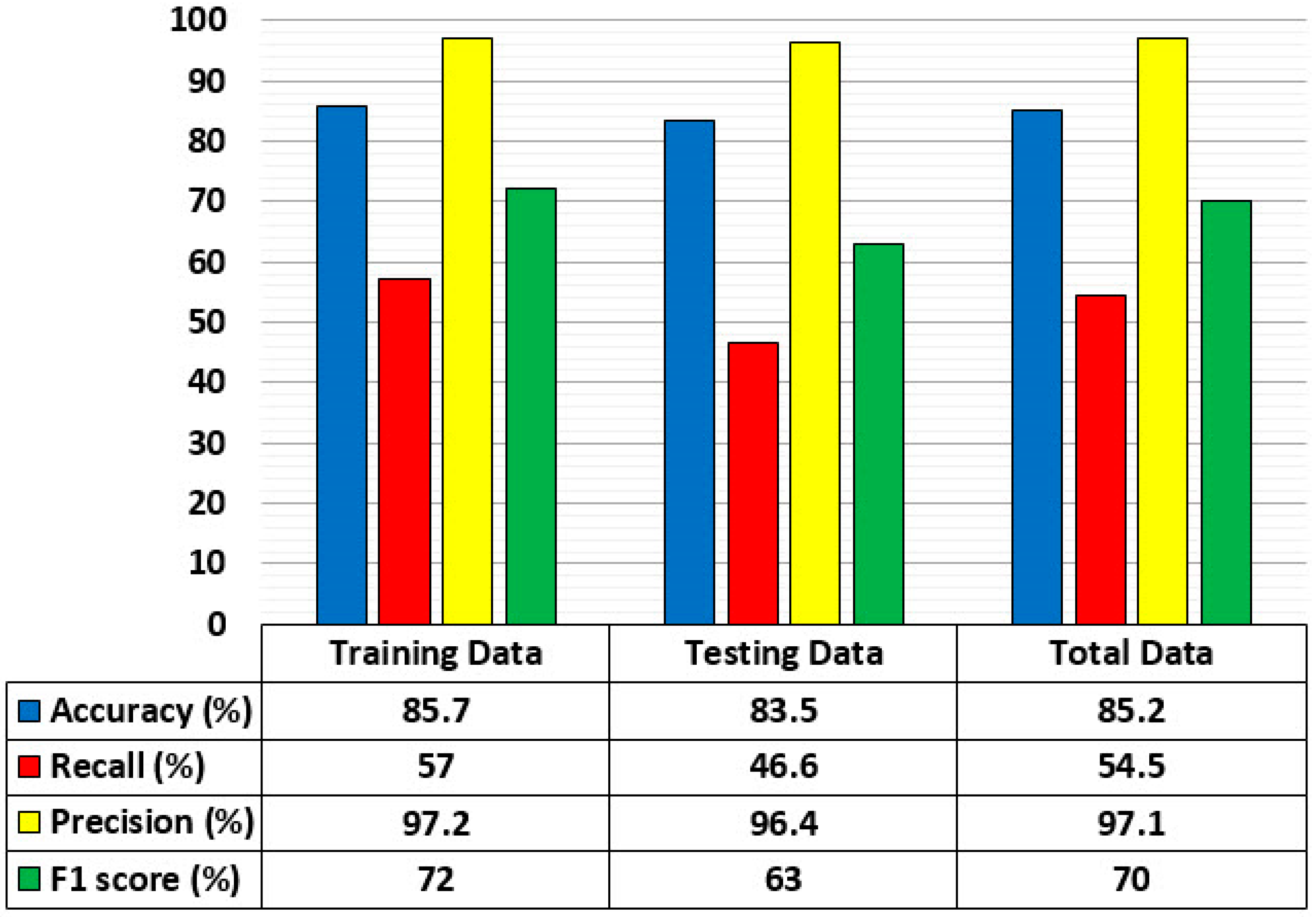
4. Results and Discussion
- -
- The correlation analysis showed that input data including Daylight, Weekday, Type of accident, Location, Speed limit and Average speed were correctly considered for the binary classification;
- -
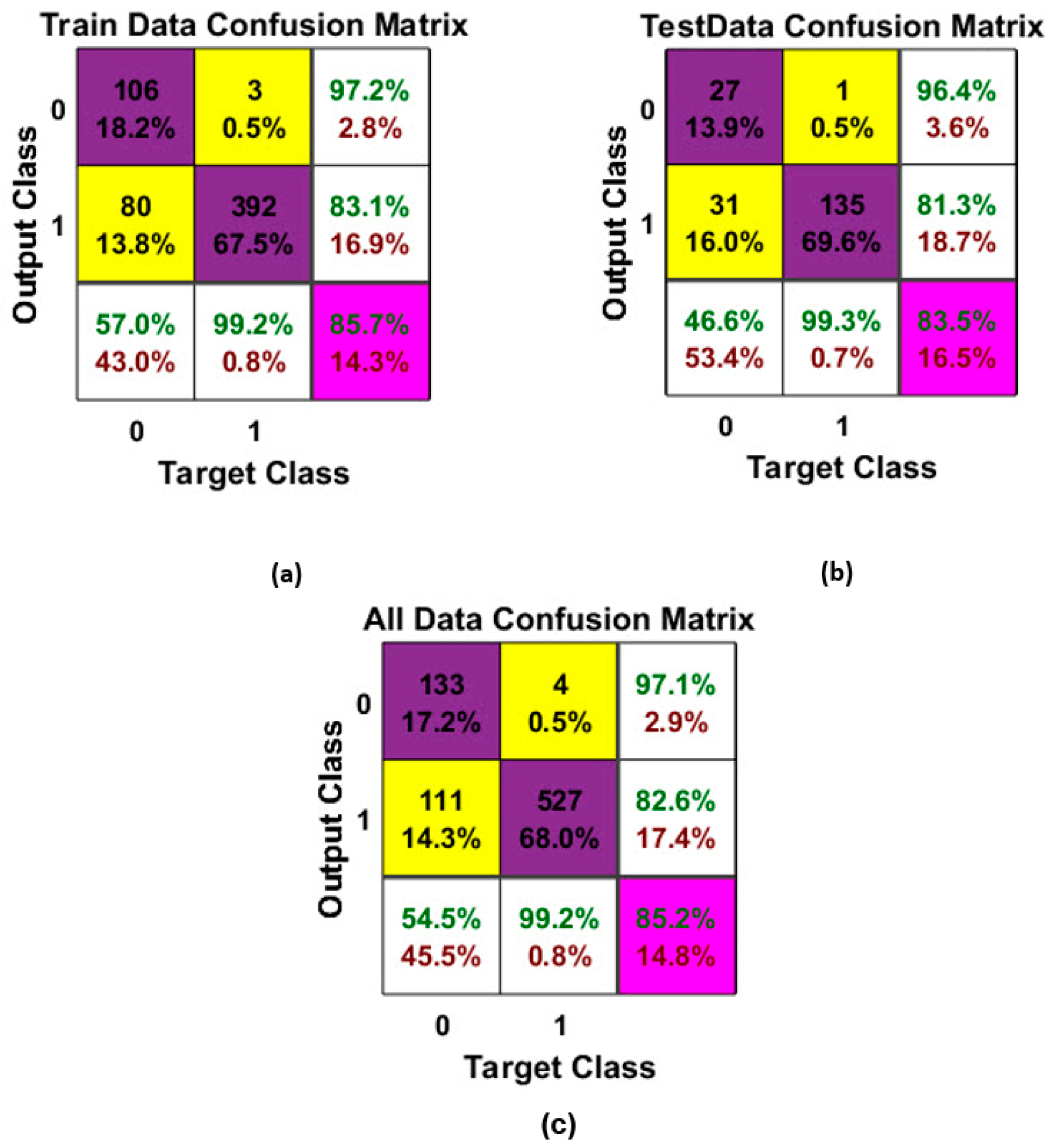
- Figure 6, Figure 7, Figure 8 and Figure 9 depict that the GMDH algorithm has a high capability to train and develop the model, which can correctly predict 661 data of the first and second classes from 775 data (total). Additionally, on the basis of the acquired results of confusion matrices, the results were assessed by the other three performance indexes and they indicated that the proposed model can provide higher performance capacity in evaluation of safety in transportation system;
- -
- Consequently, it can be concluded that the proposed binary classification model based on the GMDH algorithm was a reliable and alternative model instead of the classical model with a high appropriate acceptable degree to predict the number of vehicles involved in an accident, which may lead transportation engineers toward a greater accuracy and robustness of design and planning of roads by eventually investigating opportune countermeasures to reduce the safety risk;
- -
- It is worth mentioning that the binary classification model presented in this study is a model developed for the road network of the Cosenza area, which requires a more in-depth analysis to be transferred to other contexts;
- -
- In spite of the fact that the developed model was a reliable system model for evaluation of safety in transportation systems of this case study, it does not have capability for investigation of safety in transportation systems with incomplete data.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mannering, F.L.; Bhat, C.R.; Shankar, V.; Abdel-Aty, M. Big data, traditional data and the tradeoffs between prediction and causality in highway-safety analysis. Anal. Methods Accid. Res. 2020, 25, 100113. [Google Scholar] [CrossRef]
- Mannering, F.L. Temporal instability and the analysis of highway accident data. Anal. Methods Accid. Res. 2018, 17, 1–13. [Google Scholar] [CrossRef]
- Imprialou, M.; Quddus, M. Crash data quality for road safety research: Current state and future directions. Accid. Anal. Prev. 2019, 130, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Schlögl, M.; Stütz, R. Methodological considerations with data uncertainty in road safety analysis. Accid. Anal. Prev. 2019, 130, 136–150. [Google Scholar] [CrossRef]
- Gomes, S.V. The influence of the infrastructure characteristics in urban road accidents occurrence. Accid. Anal. Prev. 2013, 60, 289–297. [Google Scholar] [CrossRef]
- Theofilatos, A.; Yannis, G. A review of the effect of traffic and weather characteristics on road safety. Accid. Anal. Prev. 2014, 72, 244–256. [Google Scholar] [CrossRef]
- Papadimitriou, E.; Filtness, A.; Theofilatos, A.; Ziakopoulos, A.; Quigley, C.; Yannis, G. Review and ranking of crash risk factors related to the road infrastructure. Accid. Anal. Prev. 2019, 125, 85–97. [Google Scholar] [CrossRef]
- Hossain, M.; Abdel-Aty, M.; Quddus, M.; Muromachi, Y.; Sadeek, S.N. Real-time crash prediction models: State-of-the-art, design pathways and ubiquitous requirements. Accid. Anal. Prev. 2019, 124, 66–84. [Google Scholar] [CrossRef]
- Ziakopoulos, A.; Yannis, G. A review of spatial approaches in road safety. Accid. Anal. Prev. 2020, 135, 105323. [Google Scholar] [CrossRef]
- Elvik, R.; Vaa, T.; Hoye, A.; Sorensen, M. (Eds.) The Handbook of Road Safety Measures; Emerald Group Publishing: West Yorkshire, UK, 2009. [Google Scholar]
- Vaiana, R.; Iuele, T.; Gallelli, V.; Rogano, D. Demanded versus assumed friction along horizontal curves: An on-the-road experimental investigation. J. Transp. Saf. Secur. 2017, 10, 318–344. [Google Scholar] [CrossRef]
- Lee, J.; Abdel-Aty, M.; De Blasiis, M.R.; Wang, X.; Mattei, I. International transferability of macro-level safety performance functions: A case study of the United States and Italy. Transp. Saf. Environ. 2019, 1, 68–78. [Google Scholar] [CrossRef]
- Greibe, P. Accident prediction models for urban roads. Accid. Anal. Prev. 2003, 35, 273–285. [Google Scholar] [CrossRef]
- Saeed, T.U.; Hall, T.; Baroud, H.; Volovski, M.J. Analyzing road crash frequencies with uncorrelated and correlated random-parameters count models: An empirical assessment of multilane highways. Anal. Methods Accid. Res. 2019, 23, 100101. [Google Scholar] [CrossRef]
- Singleton, M.; Qin, H.; Luan, J. Factors Associated with Higher Levels of Injury Severity in Occupants of Motor Vehicles That Were Severely Damaged in Traffic Crashes in Kentucky, 2000-2001. Traffic Inj. Prev. 2004, 5, 144–150. [Google Scholar] [CrossRef]
- Dissanayake, S.; Lu, J.J. Factors influential in making an injury severity difference to older drivers involved in fixed object-passenger car crashes. Accid. Anal. Prev. 2002, 34, 609–618. [Google Scholar] [CrossRef]
- Hanrahan, R.B.; Layde, P.M.; Zhu, S.; Guse, C.E.; Hargarten, S.W. The Association of Driver Age with Traffic Injury Severity in Wisconsin. Traffic Inj. Prev. 2009, 10, 361–367. [Google Scholar] [CrossRef] [PubMed]
- Kwon, O.H.; Rhee, W.; Yoon, Y. Application of classification algorithms for analysis of road safety risk factor dependencies. Accid. Anal. Prev. 2015, 75, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Cafiso, S.; D’Agostino, C. Assessing the stochastic variability of the Benefit-Cost ratio in roadway safety management. Accid. Anal. Prev. 2016, 93, 189–197. [Google Scholar] [CrossRef] [PubMed]
- Han, C.; Huang, H.; Lee, J.; Wang, J. Investigating varying effect of road-level factors on crash frequency across regions: A Bayesian hierarchical random parameter modeling approach. Anal. Methods Accid. Res. 2018, 20, 81–91. [Google Scholar] [CrossRef]
- Briz-Redón, Á.; Martínez, F.; Montes, F. Spatial analysis of traffic accidents near and between road intersections in a directed linear network. Accid. Anal. Prev. 2019, 132, 105252. [Google Scholar] [CrossRef]
- Khattak, A.J.; Kantor, P.; Council, F.M. Role of Adverse Weather in Key Crash Types on Limited-Access: Roadways Implications for Advanced Weather Systems. Transp. Res. Rec. J. Transp. Res. Board 1998, 1621, 10–19. [Google Scholar] [CrossRef]
- Kockelman, K.M.; Kweon, Y.-J. Driver injury severity: An application of ordered probit models. Accid. Anal. Prev. 2002, 34, 313–321. [Google Scholar] [CrossRef]
- Kaplan, S.; Prato, C.G. Risk factors associated with bus accident severity in the United States: A generalized ordered logit model. J. Saf. Res. 2012, 43, 171–180. [Google Scholar] [CrossRef]
- Mohamed, M.G.; Saunier, N.; Miranda-Moreno, L.; Ukkusuri, S.V. A clustering regression approach: A comprehensive injury severity analysis of pedestrian–vehicle crashes in New York, US and Montreal, Canada. Saf. Sci. 2013, 54, 27–37. [Google Scholar] [CrossRef]
- Rivière, C.; Lauret, P.; Ramsamy, J.M.; Page, Y. A Bayesian Neural Network approach to estimating the Energy Equivalent Speed. Accid. Anal. Prev. 2006, 38, 248–259. [Google Scholar] [CrossRef]
- Huang, H.; Chin, H.; Haque, M. Empirical Evaluation of Alternative Approaches in Identifying Crash Hot Spots. Transp. Res. Rec. J. Transp. Res. Board 2009, 2103, 32–41. [Google Scholar] [CrossRef]
- De Oña, J.; López, G.; Mujalli, R.; Calvo-Poyo, F. Analysis of traffic accidents on rural highways using Latent Class Clustering and Bayesian Networks. Accid. Anal. Prev. 2013, 51, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Huang, H. Bayesian spatial joint modeling of traffic crashes on an urban road network. Accid. Anal. Prev. 2014, 67, 105–112. [Google Scholar] [CrossRef] [PubMed]
- Shi, Q.; Abdel-Aty, M.; Lee, J. A Bayesian ridge regression analysis of congestion’s impact on urban expressway safety. Accid. Anal. Prev. 2016, 88, 124–137. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Chang, F.; Zhou, H.; Lee, J. Modeling unobserved heterogeneity for zonal crash frequencies: A Bayesian multivariate random-parameters model with mixture components for spatially correlated data. Anal. Methods Accid. Res. 2019, 24, 100105. [Google Scholar] [CrossRef]
- Oviedo-Trespalacios, O.; Afghari, A.P.; Haque, M. A hierarchical Bayesian multivariate ordered model of distracted drivers’ decision to initiate risk-compensating behaviour. Anal. Methods Accid. Res. 2020, 26, 100121. [Google Scholar] [CrossRef]
- Lee, C.; Abdel-Aty, M. Presence of passengers: Does it increase or reduce driver’s crash potential? Accid. Anal. Prev. 2008, 40, 1703–1712. [Google Scholar] [CrossRef] [PubMed]
- Shankar, V.; Mannering, F.L.; Barfield, W. Statistical analysis of accident severity on rural freeways. Accid. Anal. Prev. 1996, 28, 391–401. [Google Scholar] [CrossRef]
- Shankar, V.; Mannering, F.L. An exploratory multinomial logit analysis of single-vehicle motorcycle accident severity. J. Saf. Res. 1996, 27, 183–194. [Google Scholar] [CrossRef]
- Hu, S.-R.; Li, C.-S.; Lee, C.-K. Investigation of key factors for accident severity at railroad grade crossings by using a logit model. Saf. Sci. 2010, 48, 186–194. [Google Scholar] [CrossRef]
- Hu, W.; Donnell, E. Severity models of cross-median and rollover crashes on rural divided highways in Pennsylvania. J. Saf. Res. 2011, 42, 375–382. [Google Scholar] [CrossRef]
- Dimitriou, L.; Stylianou, K.; Abdel-Aty, M. Assessing rear-end crash potential in urban locations based on vehicle-by-vehicle interactions, geometric characteristics and operational conditions. Accid. Anal. Prev. 2018, 118, 221–235. [Google Scholar] [CrossRef]
- Hamed, M.M.; Al-Eideh, B.M. An exploratory analysis of traffic accidents and vehicle ownership decisions using a random parameters logit model with heterogeneity in means. Anal. Methods Accid. Res. 2020, 25, 100116. [Google Scholar] [CrossRef]
- Eluru, N.; Bhat, C.R. A joint econometric analysis of seat belt use and crash-related injury severity. Accid. Anal. Prev. 2007, 39, 1037–1049. [Google Scholar] [CrossRef]
- Milton, J.C.; Shankar, V.N.; Mannering, F.L. Highway accident severities and the mixed logit model: An exploratory empirical analysis. Accid. Anal. Prev. 2008, 40, 260–266. [Google Scholar] [CrossRef]
- Malyshkina, N.V.; Mannering, F.L. Empirical assessment of the impact of highway design exceptions on the frequency and severity of vehicle accidents. Accid. Anal. Prev. 2010, 42, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Christoforou, Z.; Cohen, S.; Karlaftis, M.G. Vehicle occupant injury severity on highways: An empirical investigation. Accid. Anal. Prev. 2010, 42, 1606–1620. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Siddiqui, C.; Abdel-Aty, M. Indexing crash worthiness and crash aggressivity by vehicle type. Accid. Anal. Prev. 2011, 43, 1364–1370. [Google Scholar] [CrossRef] [PubMed]
- Ye, F.; Lord, D. Comparing three commonly used crash severity models on sample size requirements: Multinomial logit, ordered probit and mixed logit models. Anal. Methods Accid. Res. 2014, 1, 72–85. [Google Scholar] [CrossRef]
- Mannering, F.L.; Shankar, V.N.; Bhat, C.R. Unobserved heterogeneity and the statistical analysis of highway accident data. Anal. Methods Accid. Res. 2016, 11, 1–16. [Google Scholar] [CrossRef]
- Harrell, F.E. Regression Modeling Strategies: With Applications to Linear Models, Logistic and Ordinal Regression, and Survival Analysis; Springer Series in Statistics; Springer: New York, NY, USA, 2015; pp. 1–11. [Google Scholar]
- Cohen, J.; Cohen, P.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 2nd ed.; Lawrence Erlbaum Associates, Inc.: Mahwah, NJ, USA, 2003. [Google Scholar]
- Tabachnick, B.G.; Fidell, L.S. Using Multivariate Statistics, 6th ed.; Pearson: Boston, MA, USA, 2012. [Google Scholar]
- Siddiqui, C.; Abdel-Aty, M.; Huang, H. Aggregate nonparametric safety analysis of traffic zones. Accid. Anal. Prev. 2012, 45, 317–325. [Google Scholar] [CrossRef]
- Chang, L.-Y.; Wang, H.-W. Analysis of traffic injury severity: An application of non-parametric classification tree techniques. Accid. Anal. Prev. 2006, 38, 1019–1027. [Google Scholar] [CrossRef]
- Yan, X.; Radwan, E. Analyses of Rear-End Crashes Based on Classification Tree Models. Traffic Inj. Prev. 2006, 7, 276–282. [Google Scholar] [CrossRef]
- Pande, A.; Abdel-Aty, M. Assessment of freeway traffic parameters leading to lane-change related collisions. Accid. Anal. Prev. 2006, 38, 936–948. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, G.; Yang, J.; Milton, J.C.; Alcántara, A. “Dely” An explanatory analysis of driver injury severity in rear-end crashes using a decision table/Naïve Bayes (DTNB) hybrid classifier. Accid. Anal. Prev. 2016, 90, 95–107. [Google Scholar] [CrossRef]
- Li, Z.; Liu, P.; Wang, W.; Xu, C. Using support vector machine models for crash injury severity analysis. Accid. Anal. Prev. 2012, 45, 478–486. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Abdel-Aty, M. Analyzing crash injury severity for a mountainous freeway incorporating real-time traffic and weather data. Saf. Sci. 2014, 63, 50–56. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, G.; Qian, Z.; Tarefder, R.A.; Tian, Z. Investigating driver injury severity patterns in rollover crashes using support vector machine models. Accid. Anal. Prev. 2016, 90, 128–139. [Google Scholar] [CrossRef] [PubMed]
- Gu, X.; Li, T.; Wang, Y.; Zhang, L.; Wang, Y.; Yao, J. Traffic fatalities prediction using support vector machine with hybrid particle swarm optimization. J. Algorithms Comput. Technol. 2017, 12, 20–29. [Google Scholar] [CrossRef]
- Wang, J.; Liu, B.; Fu, T.; Liu, S.; Stipancic, J. Modeling when and where a secondary accident occurs. Accid. Anal. Prev. 2019, 130, 160–166. [Google Scholar] [CrossRef]
- Abdelwahab, H.T.; Abdel-Aty, M.A. Development of Artificial Neural Network Models to Predict Driver Injury Severity in Traffic Accidents at Signalized Intersections. Transp. Res. Rec. J. Transp. Res. Board 2001, 1746, 6–13. [Google Scholar] [CrossRef]
- Lu, J.; Chen, S.; Wang, W.; Van Zuylen, H.J. A hybrid model of partial least squares and neural network for traffic incident detection. Expert Syst. Appl. 2012, 39, 4775–4784. [Google Scholar] [CrossRef]
- Ali, G.A.; Tayfour, A. Characteristics and Prediction of Traffic Accident Casualties In Sudan Using Statistical Modeling and Artificial Neural Networks. Int. J. Transp. Sci. Technol. 2012, 1, 305–317. [Google Scholar] [CrossRef]
- Deka, L.; Quddus, M. Network-level accident-mapping: Distance based pattern matching using artificial neural network. Accid. Anal. Prev. 2014, 65, 105–113. [Google Scholar] [CrossRef]
- Mussone, L.; Bassani, M.; Masci, P. Analysis of factors affecting the severity of crashes in urban road intersections. Accid. Anal. Prev. 2017, 103, 112–122. [Google Scholar] [CrossRef]
- Huang, H.; Han, C.; Xu, G.; Jiang, M.; Wong, S.; Haque, M. Incorporating safety reliability into route choice model: Heterogeneous crash risk aversions. Anal. Methods Accid. Res. 2020, 25, 100112. [Google Scholar] [CrossRef]
- Li, Y.; Ma, D.; Zhu, M.; Zeng, Z.; Wang, Y. Identification of significant factors in fatal-injury highway crashes using genetic algorithm and neural network. Accid. Anal. Prev. 2018, 111, 354–363. [Google Scholar] [CrossRef] [PubMed]
- Amiri, A.M.; Sadri, A.; Nadimi, N.; Shams, M. A comparison between Artificial Neural Network and Hybrid Intelligent Genetic Algorithm in predicting the severity of fixed object crashes among elderly drivers. Accid. Anal. Prev. 2020, 138, 105468. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Q.; Huang, H. A stable and optimized neural network model for crash injury severity prediction. Accid. Anal. Prev. 2014, 73, 351–358. [Google Scholar] [CrossRef] [PubMed]
- Delen, D.; Sharda, R.; Bessonov, M. Identifying significant predictors of injury severity in traffic accidents using a series of artificial neural networks. Accid. Anal. Prev. 2006, 38, 434–444. [Google Scholar] [CrossRef]
- Wang, J.; Luo, T.; Fu, T. Crash prediction based on traffic platoon characteristics using floating car trajectory data and the machine learning approach. Accid. Anal. Prev. 2019, 133, 105320. [Google Scholar] [CrossRef]
- Liu, J.; Boyle, L.N.; Banerjee, A.G. Predicting interstate motor carrier crash rate level using classification models. Accid. Anal. Prev. 2018, 120, 211–218. [Google Scholar] [CrossRef]
- Formosa, N.; Quddus, M.; Ison, S.; Abdel-Aty, M.; Yuan, J. Predicting real-time traffic conflicts using deep learning. Accid. Anal. Prev. 2020, 136, 105429. [Google Scholar] [CrossRef]
- Iranitalab, A.; Khattak, A.J. Comparison of four statistical and machine learning methods for crash severity prediction. Accid. Anal. Prev. 2017, 108, 27–36. [Google Scholar] [CrossRef]
- Tang, J.; Zheng, L.; Han, C.; Yin, W.; Zhang, Y.; Zou, Y.; Huang, H. Statistical and machine-learning methods for clearance time prediction of road incidents: A methodology review. Anal. Methods Accid. Res. 2020, 27, 100123. [Google Scholar] [CrossRef]
- Huang, T.; Wang, S.; Sharma, A. Highway crash detection and risk estimation using deep learning. Accid. Anal. Prev. 2020, 135, 105392. [Google Scholar] [CrossRef] [PubMed]
- Xie, K.; Yang, D.; Ozbay, K.; Yang, H. Use of real-world connected vehicle data in identifying high-risk locations based on a new surrogate safety measure. Accid. Anal. Prev. 2019, 125, 311–319. [Google Scholar] [CrossRef] [PubMed]
- Geem, Z.W.; Chung, S.Y.; Kim, J.-H. Improved Optimization for Wastewater Treatment and Reuse System Using Computational Intelligence. Complexity 2018, 2018, 1–8. [Google Scholar] [CrossRef]
- Park, S.H.; Jang, Y.-H.; Geem, Z.W.; Lee, S.-H. CityGML-Based Road Information Model for Route Optimization of Snow-Removal Vehicle. ISPRS Int. J. Geo-Inf. 2019, 8, 588. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Ataei, M.; Khalokakaei, R.; Mikaeil, R.; Haghshenas, S.S. Investigating the role of coolant and lubricant fluids on the performance of cutting disks (case study: Hard rocks). Rudarsko-Geološko-Naftni zbornik 2019, 34, 13–25. [Google Scholar] [CrossRef]
- Dormishi, A.; Ataei, M.; Mikaeil, R.; Khalokakaei, R.; Haghshenas, S.S. Evaluation of gang saws’ performance in the carbonate rock cutting process using feasibility of intelligent approaches. Eng. Sci. Technol. Int. J. 2019, 22, 990–1000. [Google Scholar] [CrossRef]
- Mikaeil, R.; Haghshenas, S.S.; Sedaghati, Z. Geotechnical risk evaluation of tunneling projects using optimization techniques (case study: The second part of Emamzade Hashem tunnel). Nat. Hazards 2019, 97, 1099–1113. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Behnood, A.; Arashpour, M. Predicting the compressive strength of normal and High-Performance Concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Constr. Build. Mater. 2020, 232, 117266. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. Polynomial Theory of Complex Systems. IEEE Trans. Syst. Man. Cybern. 1971, 1, 364–378. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. Self-Organizing Methods in Modelling and Clustering: GMDH Type Algorithms; Systems Analysis and Simulation I; Springer: New York, NY, USA, 1988; pp. 86–88. ISBN 978-0-387-97091-2. [Google Scholar]
- Fiorini Morosini, A.; Haghshenas, S.S.; Haghshenas, S.S.; Geem, Z.W. Development of a Binary Model for Evaluating Water Distribution Systems by a Pressure Driven Analysis (PDA) Approach. Appl. Sci. 2020, 10, 3029. [Google Scholar] [CrossRef]
- Sezavar, R.; Shafabakhsh, G.; Mirabdolazimi, S. New model of moisture susceptibility of nano silica-modified asphalt concrete using GMDH algorithm. Constr. Build. Mater. 2019, 211, 528–538. [Google Scholar] [CrossRef]
- Dag, O.; Karabulut, E.; Alpar, R. GMDH2: Binary Classification via GMDH-Type Neural Network Algorithms—R Package and Web-Based Tool. Int. J. Comput. Intell. Syst. 2019, 12, 649. [Google Scholar] [CrossRef]
- Dag, O.; Kasikci, M.; Karabulut, E.; Alpar, R. Diverse classifiers ensemble based on GMDH-type neural network algorithm for binary classification. Commun. Stat.-Simul. Comput. 2019, 1–17. [Google Scholar] [CrossRef]
- Mikaeil, R.; Haghshenas, S.S.; Ozcelik, Y.; Gharehgheshlagh, H.H. Performance Evaluation of Adaptive Neuro-Fuzzy Inference System and Group Method of Data Handling-Type Neural Network for Estimating Wear Rate of Diamond Wire Saw. Geotech. Geol. Eng. 2018, 36, 3779–3791. [Google Scholar] [CrossRef]
- Feng, X.; Li, S.; Yuan, C.; Zeng, P.; Sun, Y. Prediction of Slope Stability using Naive Bayes Classifier. KSCE J. Civ. Eng. 2018, 22, 941–950. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Ataei, M.; Khalokakaei, R.; Mikaeil, R.; Haghshenas, S.S. Study of the effect of the cooling and lubricant fluid on the cutting performance of dimension stone through artificial intelligence models. Eng. Sci. Technol. Int. J. 2020, 23, 71–81. [Google Scholar] [CrossRef]
- Noori, A.M.; Mikaeil, R.; Mokhtarian, M.; Haghshenas, S.S.; Foroughi, M. Feasibility of Intelligent Models for Prediction of Utilization Factor of TBM. Geotech. Geol. Eng. 2020, 38, 3125–3143. [Google Scholar] [CrossRef]
- Pirouz, B.; Haghshenas, S.S.; Haghshenas, S.S.; Piro, P. Investigating a Serious Challenge in the Sustainable Development Process: Analysis of Confirmed cases of COVID-19 (New Type of Coronavirus) Through a Binary Classification Using Artificial Intelligence and Regression Analysis. Sustainability 2020, 12, 2427. [Google Scholar] [CrossRef]
- Salemi, A.; Mikaeil, R.; Haghshenas, S.S. Integration of Finite Difference Method and Genetic Algorithm to Seismic analysis of Circular Shallow Tunnels (Case Study: Tabriz Urban Railway Tunnels). KSCE J. Civ. Eng. 2017, 22, 1978–1990. [Google Scholar] [CrossRef]
- Aryafar, A.; Mikaeil, R.; Haghshenas, S.S.; Haghshenas, S.S. Application of metaheuristic algorithms to optimal clustering of sawing machine vibration. Measurement 2018, 124, 20–31. [Google Scholar] [CrossRef]
- Mikaeil, R.; Haghshenas, S.S.; Hoseinie, S.H. Rock Penetrability Classification Using Artificial Bee Colony (ABC) Algorithm and Self-Organizing Map. Geotech. Geol. Eng. 2017, 36, 1309–1318. [Google Scholar] [CrossRef]
- Mohammadi, D.; Mikaeil, R.; Abdollahi-Sharif, J. Implementation of an optimized binary classification by GMDH-type neural network algorithm for predicting the blast produced ground vibration. Expert Syst. 2020, e12563. [Google Scholar] [CrossRef]
- ACI-ISTAT. Localizzazione Incidenti Stradali. Available online: http://www.aci.it/laci/studi-e-ricerche/dati-e-statistiche/incidentalita.html (accessed on 10 January 2020).
- Dutta, N.; Fontaine, M.D. Improving freeway segment crash prediction models by including disaggregate speed data from different sources. Accid. Anal. Prev. 2019, 132, 105253. [Google Scholar] [CrossRef] [PubMed]
- Looney, C.G. Advances in feedforward neural networks: Demystifying knowledge acquiring black boxes. IEEE Trans. Knowl. Data Eng. 1996, 8, 211–226. [Google Scholar] [CrossRef]
- Zorlu, K.; Gokceoglu, C.; Ocakoglu, F.; Nefeslioglu, H.; Acikalin, S. Prediction of uniaxial compressive strength of sandstones using petrography-based models. Eng. Geol. 2008, 96, 141–158. [Google Scholar] [CrossRef]
- Faradonbeh, R.S.; Haghshenas, S.S.; Taheri, A.; Mikaeil, R. Application of self-organizing map and fuzzy c-mean techniques for rockburst clustering in deep underground projects. Neural Comput. Appl. 2019, 32, 8545–8559. [Google Scholar] [CrossRef]




| Data Field Type | Data Field | Description |
|---|---|---|
| Human characteristic | Driver gender | Male or female |
| Vehicle characteristic | Vehicle type | Car, motorcycle, truck and other |
| Road environment | Road type | National rural road, provincial rural road, national and provincial rural road in urban context, urban road |
| Geometric element | Straight, curve, crossroad, signalized intersection, traffic light | |
| Other environment | Date | Date of the accident |
| Light conditions | Daylight and nighttime | |
| Day of the week | Weekday and weekend | |
| Location environment | Macro area location | Urban and rural |
| Accident characteristic | Number of vehicles | Number of vehicles involved |
| Accident nature | Way out, collision with an accidental obstacle, side collision, front-side collision, rear-end collision, head-on collision, pedestrian collision, impact with parked vehicle, impact with stopped vehicle, fall from vehicle, sudden braking | |
| Accident severity | Injuries and deaths |
| Daylight | Type of Accident | Weekday | Location | Speed Limit | Average Speed | |
|---|---|---|---|---|---|---|
| Daylight | 1 | |||||
| Type of accident | −0.03 | 1 | ||||
| Weekday | −0.12 | −0.01 | 1 | |||
| Location | 0.05 | −0.16 | 0.01 | 1 | ||
| Speed Limit | 0.01 | −0.21 | 0.01 | 0.29 | 1 | |
| Average Speed | 0.01 | −0.15 | 0.03 | 0.16 | 0.85 | 1 |
| Model No. | SP | MNL | MNNL | Accuracy of Training (%) | Accuracy of Testing (%) |
|---|---|---|---|---|---|
| 1 | 0.6 | 5 | 5 | 81.2 | 76.2 |
| 2 | 0.6 | 5 | 10 | 80.6 | 76.8 |
| 3 | 0.6 | 5 | 20 | 81.9 | 78.9 |
| 4 | 0.6 | 5 | 30 | 81.1 | 77.8 |
| 5 | 0.6 | 10 | 5 | 81.6 | 76.8 |
| 6 | 0.6 | 10 | 10 | 81.4 | 77.5 |
| 7 | 0.6 | 10 | 20 | 82.6 | 80.9 |
| 8 | 0.6 | 10 | 30 | 82.8 | 77.8 |
| 9 | 0.6 | 15 | 5 | 81.4 | 81.2 |
| 10 | 0.6 | 15 | 10 | 82.8 | 82 |
| 11 | 0.6 | 15 | 20 | 82.6 | 78.5 |
| 12 | 0.6 | 15 | 30 | 81.6 | 80.9 |
| 13 | 0.6 | 20 | 5 | 80.4 | 80.2 |
| 14 | 0.6 | 20 | 10 | 82.5 | 81.9 |
| 15 | 0.6 | 20 | 20 | 81.1 | 79.9 |
| 16 | 0.6 | 20 | 30 | 85.7 | 83.5 |
| 17 | 0.6 | 30 | 5 | 81.6 | 80.9 |
| 18 | 0.6 | 30 | 10 | 79.4 | 78.8 |
| 19 | 0.6 | 30 | 20 | 81.1 | 75.3 |
| 20 | 0.6 | 30 | 30 | 83.5 | 80.9 |
| Model No. | SP | MNL | MNNL | Ranking for Accuracy of Training | Ranking for Accuracy of Testing | Total Rank |
|---|---|---|---|---|---|---|
| 1 | 0.6 | 5 | 5 | 12 | 10 | 22 |
| 2 | 0.6 | 5 | 10 | 10 | 11 | 21 |
| 3 | 0.6 | 5 | 20 | 15 | 16 | 31 |
| 4 | 0.6 | 5 | 30 | 11 | 13 | 24 |
| 5 | 0.6 | 10 | 5 | 14 | 11 | 25 |
| 6 | 0.6 | 10 | 10 | 13 | 12 | 25 |
| 7 | 0.6 | 10 | 20 | 17 | 18 | 35 |
| 8 | 0.6 | 10 | 30 | 18 | 13 | 31 |
| 9 | 0.6 | 15 | 5 | 13 | 12 | 25 |
| 10 | 0.6 | 15 | 10 | 18 | 13 | 31 |
| 11 | 0.6 | 15 | 20 | 17 | 14 | 31 |
| 12 | 0.6 | 15 | 30 | 14 | 18 | 32 |
| 13 | 0.6 | 20 | 5 | 9 | 17 | 26 |
| 14 | 0.6 | 20 | 10 | 16 | 19 | 35 |
| 15 | 0.6 | 20 | 20 | 11 | 16 | 27 |
| 16 | 0.6 | 20 | 30 | 20 | 20 | 40 |
| 17 | 0.6 | 30 | 5 | 14 | 18 | 32 |
| 18 | 0.6 | 30 | 10 | 8 | 15 | 23 |
| 19 | 0.6 | 30 | 20 | 11 | 9 | 20 |
| 20 | 0.6 | 30 | 30 | 19 | 18 | 37 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guido, G.; Haghshenas, S.S.; Haghshenas, S.S.; Vitale, A.; Gallelli, V.; Astarita, V. Development of a Binary Classification Model to Assess Safety in Transportation Systems Using GMDH-Type Neural Network Algorithm. Sustainability 2020, 12, 6735. https://doi.org/10.3390/su12176735
Guido G, Haghshenas SS, Haghshenas SS, Vitale A, Gallelli V, Astarita V. Development of a Binary Classification Model to Assess Safety in Transportation Systems Using GMDH-Type Neural Network Algorithm. Sustainability. 2020; 12(17):6735. https://doi.org/10.3390/su12176735
Chicago/Turabian StyleGuido, Giuseppe, Sina Shaffiee Haghshenas, Sami Shaffiee Haghshenas, Alessandro Vitale, Vincenzo Gallelli, and Vittorio Astarita. 2020. "Development of a Binary Classification Model to Assess Safety in Transportation Systems Using GMDH-Type Neural Network Algorithm" Sustainability 12, no. 17: 6735. https://doi.org/10.3390/su12176735
APA StyleGuido, G., Haghshenas, S. S., Haghshenas, S. S., Vitale, A., Gallelli, V., & Astarita, V. (2020). Development of a Binary Classification Model to Assess Safety in Transportation Systems Using GMDH-Type Neural Network Algorithm. Sustainability, 12(17), 6735. https://doi.org/10.3390/su12176735










