Safe and Ecological Speed Control for Heavy-Duty Vehicles on Long–Steep Downhill and Sharp-Curved Roads

Abstract

To contribute to the development of sustainable transport that is safe, eco-friendly, and efficient, this research proposed a safe and ecological speed control system for heavy-duty vehicles on long–steep downhill and sharp-curved roads under a partially connected vehicles environment consisting of connected heavy-duty vehicles (CHDVs) and conventional human-driven vehicles. This system prioritizes braking and lateral motion safety before improving fuel efficiency and ensuring traffic mobility at optimal status, and optimizes the speed trajectories of CHDVs to control the entire traffic. Speed optimization is modelled as an optimal control problem and solved by the iterative Pontryagin’s maximum principle algorithm. The simulation-based evaluation shows that the proposed system effectively reduces the peak temperature of the brake drums, the lateral slip angle of the vehicle wheels, and the lateral load transfer rate of the vehicle body; all these measurements of effectiveness are limited to safe ranges. A detailed investigation reveals that the proposed system reduces fuel consumption by up to 15.49% and inhibits the adverse effects on throughput. All benefits increase with the market penetration rate (MPR) of CHDVs and the traffic congestion level and reach significant levels under low MPRs of CHDVs. This indicates that the proposed system has good robustness for the impedance from conventional vehicles and could be implemented in the near future.

1. Introduction

Due to the limitations of topography and geological structures, there are often some road sections with poor alignments on mountain highways, such as long–steep downhill and sharp-curved roads [1]. Heavy-duty vehicles, which have a high weight and high center of gravity, are prone to brake failure [2] and rollover accidents [3] on these dangerous road sections. Many governments and researchers have focused on the avoidance of brake fade on downhill roads [4] and improvements in vehicle lateral stability on curved roads [5]. A variety of approaches for safety enhancement, including the optimization of alignment design and the speed limit of downhill and curved roads [6], the development of high-temperature-resistant brake materials [7], and the improvement of vehicle structure design [8], have been proposed and achieved certain results. Auxiliary braking and active safety technology, such as engine braking [9] and electronic stability control [10], are being gradually applied to heavy-duty vehicles.

Traditional brake fade prevention has mainly focused on the longitudinal length and gradient of downhill roads. In the 1990s, Limpert first proposed a temperature prediction model of vehicle brake drums using heat transfer theory [11]. Based on this pioneering work, the Federal Highway Administration (FHWA) developed the Grade Severity Rating System, which includes a temperature prediction model of brake drums [12]. This model includes various infrastructure and vehicle factors, such as the length and gradient of downhill roads and the weight and velocity of vehicles, and the field application indicates that it effectively estimates the brake temperature of heavy-duty vehicles during the while process of downhill. Due to the remarkable performance of this model, it was then introduced into the Vehicle Dynamics Analysis Non-Linear (VDANL) module of the Interactive Highway Safety Design Model developed by FHWA [13]. The University of Michigan’s Transportation research Institute further examined the thermal energy and heat transfer of brake drums to calibrate and refine the parameters of Limpert’s model [14]. However, most of these studies assume that vehicles tend to maintain a constant speed and do not use any auxiliary braking systems [15], which does not completely conform the complex traffic environment in the real world with vehicle interactions and frequent speed oscillation, and the complex traffic composition that includes vehicles with engine braking systems. Most vehicle braking controllers developed using these models has two drawbacks: first, it fails to provide time-varying advisory speed for vehicles, and is unable to precisely control the vehicle speed; second, it can only adjust the braking profile of the drum brake and not effectively utilize the auxiliary braking systems [16]. Later, Seykens proposed a dynamic engine brake model for control purposes, which can predict the engine brake torque based on the engine speed. This model enables the vehicle braking controller to exactly obtain the braking force provided by the vehicle engine and can accordingly optimize the braking profile of the drum brake [17]. Some other studies introduced a retarder into the braking controller [18]. The controllers developed based on this kind of auxiliary braking models can effectively reduce the thermal energy generated by the drum brake to avoid brake fade [19]. At present, there are still few studies about speed control and guidance for vehicles running on downhill roads based on the temperature rise models of brake drums for time-varying vehicle speed.

The lateral stability enhancement of vehicles on curved roads is an important function of the active safety system [20]. Recent studies can be divided into two categories: yaw stability [21] and roll stability [22]. Most studies on yaw stability control aim at minimizing the sideslip angle of vehicle wheels by controlling the wheel torque distribution [23] and steering angle [21,24]. Feed forward and feedback control [25], model predictive control [26], adaptive control [27], etc., have been widely used to ensure that heavy-duty vehicles operate at the desired yaw rate. These controllers are suitable for vehicles on roads with low friction coefficients. As the friction coefficient of road surface increasing, roll stability became another research hotspot [28]. To accurately predict the roll motion of vehicle bodies, some multiple degrees-of-freedom vehicle dynamics models were proposed to replace the typical bicycle model, which is unable to describe large variations in lateral acceleration [29,30]. On this basis, two different rollover prevention modes have been proposed. One mode involves reducing the steering angle of the front wheel to avoid dangerous roll maneuvers [28,31]. The other mode involves reducing the longitudinal speed of the vehicle to decrease its lateral acceleration [32]. These two modes essentially lower the risk of rollover by decreasing the yaw moment of the vehicle. Thus, some studies focused on a combination of yaw and roll stability and optimized the yaw motion input, braking force, and traction force distribution to prevent sideslip maneuvers and rollover on roads with different friction coefficients [33].

In the last decade, the rapid development of connected vehicle technology has provided brand new strategies for vehicle control. Many existing studies have attempted to utilize the information obtained through V2X communication to prevent traffic accidents such as vehicle collision and pedestrian crashes, but ignored the crashes of out-of-control vehicles [34]. Besides safety, ecology is a new research focus in the field of intelligent vehicle control, especially for heavy-duty vehicles with high fuel consumption and emissions [35]. Recent studies can also be divided into two categories: eco-driving on a freeway [36,37,38] and eco-approach at a signalized intersection [39,40]. The eco-driving on freeway is essentially a cooperative adaptive cruise control that reduces the speed oscillation of vehicles in platoon to decrease the accelerating and decelerating maneuvers with a high fuel consumption [37,38]. The eco-approach at signalized intersection involves a controller that smooths the vehicle speed trajectory to decelerate in advance and avoid idling maneuvers at the stop bar of the intersection [41,42]. These two ecological control strategies primarily improve the fuel efficiency of the vehicle by optimizing its kinematics state, instead of adjusting its dynamic state like active safety control. The difference between these two techniques is manifested in the traffic mobility of controlled road sections. The eco-driving can cluster vehicles into fast marching platoons to ensure that the throughput of the freeway remains at a good level [37,38]. The eco-approach makes vehicles slowly approach and enter the intersection, and thereby has significant adverse effects on the throughput of intersections [43]. This drawback leads to that the corresponding controllers cannot be implemented under moderate and high congestion levels. To solve this problem, some of the latest studies have proposed a new eco-approach strategy that prioritizes mobility over improving fuel efficiency [43,44,45]. The corresponding controllers force vehicles to accelerate before reaching the stop bar and drive through the intersection at the tightest headway and legal speed limit. The throughput of the intersection can thus be ensured to be optimum [46,47]. Apart from directly controlling the kinematics state of vehicles, some other eco-driving systems utilize the information on vehicles’ kinematics state and road infrastructure to evaluate the instantaneous fuel consumption of vehicles, and according to improve the driving style of human drivers [48,49]. These systems can be generally applied on freeways and at intersections, and significantly reduce the fuel consumption, while cannot achieve an optimum status of fuel efficiency. However, these studies about ecology speed control mainly focused on the vehicles on straight roads or urban networks with multiple intersections. This ideal of ecology control has not been introduced into the speed control on downhill and curved roads.

Sustainable transport should be safe, eco-friendly, and efficient [50], but few studies take these three important performance indexes into overall consideration. Some recent studies only adopted vehicle safety as a constraint to optimize fuel efficiency and traffic mobility. Safety, fuel efficiency, and traffic mobility cannot simultaneously be at good levels [46,47]. Moreover, most controllers proposed in these studies were designed on the basis of accurate information on the surrounding vehicles, and can only be implemented in fully connected vehicles environment [37,38,39,40,41,42]. The poor robustness of these controller to traffic randomness leads to no feasibility of implementation in the near future [43]. Then, some more practical controllers were developed, which release speed information using traditional roadside speed limits [51]. These controllers macroscopically optimize the movement of entire traffic consisting of connected vehicles and human-driven vehicles, allowing them to be readily implemented in the real world [52]. Most of these traditional controllers prefer to adopt low speed limits to ensure driving safety, and leads to significant adverse effects on the throughput on the roads [53]. This phenomenon can further cause traffic congestion under high saturation conditions. So how to solve the contradiction between the practicability of control system and traffic mobility will be the future research focus.

To overcome the drawbacks summarized above, this study takes into account safety, ecology and efficiency, and proposes a speed control system for heavy-duty vehicles on long–steep downhill and sharp-curved roads from the perspective of microcosmic control. The control objective is enhancing safety and improving fuel efficiency for heavy-duty vehicles, while ensuring that the adverse effects on the traffic mobility on these high-risk roads remain minimal. This control system contains a brake drum temperature rise model with the consideration of engine braking, and a lateral stability model based on vehicle dynamics model, which can provide accurate time-varying information on braking system and vehicle for enhancing the control effect. To guarantee the implementation feasibility in the near future, this study designs a prediction method for obtaining the information on human-driven vehicles and, thereby, this control system can sense the surrounding traffic of controlled vehicles and be functional in a partially connected vehicles environment.

The rest of the paper is organized as follows: In Section 2, “Control Structure”, a detailed description and highlights of the proposed speed control system are provided. In Section 3, ”Mathematical Formulation”, the problem formulation of the speed control system are presented; in Section 3.1, “Optimal Controller for Connected Heavy-Duty Vehicles”, the formulation of the optimal control problem is described in detailed in Section 3.1.1, Section 3.1.2, Section 3.1.3, Section 3.1.4 and Section 3.1.5, and its associated solution is introduced in Section 3.1.6 and Section 3.1.7; the controller formulated in this subsection is used to control the longitudinal motions of connected heavy-duty vehicles to achieve the expected control objective; in Section 3.2, “Predictor for Conventional Human-Driven Vehicles”, the formulation of the predict method improved from a microscopic car-following model is presented, this predictor providing the kinematics information of conventional human-driven vehicles to the optimal controller for connected heavy-duty vehicles as constraints for optimization. In Section 4, “Simulation and Evaluation”, the simulation platform and set-up are described in Section 4.1, all simulation results are presented in Section 4.2 and the evaluation results are divided into four parts according to the expected control objective, including brake stability, lateral stability, fuel economy and mobility. In Section 5, “Conclusions and Future Research”, the conclusions of this study and the valuable research directions for future studies are summarized.

2. Control Structure

The goal of the proposed speed controller is to enhance driving safety and improve fuel efficiency for heavy-duty vehicles running on long–steep downhill and sharp-curved roads by optimizing their longitudinal speed, while minimizing the adverse effects on traffic mobility. There are four highlights of this optimal controller:

Braking stability and lateral stability: Heavy-duty vehicles, especially those that lack an auxiliary brake, have much higher risks of brake fade, sideslip, and rollover than light-duty vehicles due to their greater mass and higher center of gravity. To enhance the driving safety of heavy-duty vehicles, the proposed controller guarantees the braking effect and lateral motion function at their optimum levels. This design aims at avoiding the activation of active safety control such as electronic stability control (ESC) and electronic stability program (ESP), which can further enhance the driving safety of heavy-duty vehicles. In other words, this controller can help heavy-duty vehicles maintain both braking stability and lateral stability when driving on high-risk roads, such as long–steep downhill and sharp-curved roads.

Driving safety priority: The proposed controller provides the safest and smoothest speed advisories for heavy-duty vehicles to achieve braking stability and lateral stability. The controller puts driving safety a higher priority than other performance indicators. It enforces the running costs of the controlled vehicle to enhance its driving safety. This design ensures that the generation rate of brake thermal energy, the yaw rate of the whole vehicle, and the lateral load transfer of the vehicle body are all at a lower level. Therefore, the proposed controller enables the braking system to avoid thermal decay to provide continuous and stable braking force and helps vehicles avoid yaw and roll instability to travel under a stable and controllable state. This is an active safety controller that can prevent high-risk maneuvers in advance.

Ecology and mobility: The proposed controller further improve fuel efficiency and maintains traffic mobility at an optimum level on the basis of enhancing driving safety. From an energy transformation and vehicle dynamics perspective, the generation rate of the brake’s thermal energy, the yaw rate of the whole vehicle, and the lateral load transfer of the vehicle body have close correlations with vehicle longitudinal speed and acceleration. Thus, by enhancing driving safety, the speed and acceleration of the controlled vehicle can be optimized. In other words, the proposed controller forces heavy-duty vehicles to decelerate at a low deceleration rate and maintain an appropriate speed while approaching and driving on long–steep downhill and sharp-curved roads. This strategy also helps improve the fuel efficiency of heavy-duty vehicles. To obtain good ecological performance, this controller introduces fuel consumption into the running costs. This design ensures that the most ecological one of all safe speed advisories are provided to the controlled vehicle.

In addition, the proposed controller enforces the terminal condition to optimize traffic mobility. It ensures that each controlled vehicle passes through the ends of high-risk roads at an expected time point to reduce the travel time unless blocked by a preceding vehicle. From a macro perspective, the controller optimizes the throughput on high-risk roads by increasing the traffic density and space mean speed.

To ensure the priority of driving safety, the proposed controller gives much higher weight to safety costs than ecology and mobility costs. This design also guarantees that the controller will apply to scenarios with different congestion levels by adjusting the weight of the mobility cost.

Partially connected vehicles’ environment: The proposed controller aims at being functional under mixed traffic conditions consisting of two types of vehicles. One type is connected vehicles, which load the proposed controller and communication device, exchange information with both the other connected vehicles and road infrastructure via V2X technology, and run according to the optimal speed profile generated by the controller. The other is unconnected vehicles, known as “conventional” human-driven vehicles, in which no optimal speed controller or communication devices are installed. This controller can indirectly control unconnected vehicles by utilizing car-following behaviors and thereby improve the driving safety of entire traffic on high-risk roads.

The architecture of the proposed speed control system for heavy-duty vehicles is presented in Figure 1. The equipment comprising the control system includes the following.

(1)

Road condition sensors and communication devices installed along both high-risk roads and their approaching sections. Road condition sensors monitor the friction coefficient of road surface in real-time by infrared spectral analysis technology, which is free from dependence on information of weather and temperature around the sensors. Communication devices provide information on road design and surface conditions for connected heavy-duty vehicles (CHDVs) named “Roadside units”. List format hanging 0.75.

(2)

Communication devices installed on CHDVs to enable communication between multiple vehicles or between vehicles and roadside units called “Vehicle-loaded units”.

(3)

Sensors installed on CHDVs to obtain the state of their preceding unconnected vehicles.

The approaching section provides enough room for CHDVs to adjust their speed before entering the high-risk roads. The control structure of the proposed control system is shown in Figure 2. When a CHDV arrives at the entrance point of the control area, the control system is activated by the roadside signal received by the vehicle-loaded communication device. At that moment, this CHDV attempts to establish a communication connection with the preceding vehicles. Only the connected vehicle can respond to the request. If the nearest preceding vehicle is a connected one, its speed profile and spatial-temporal trajectory are transmitted to this CHDV. Hence, module 1, “Optimal controller for connected heavy-duty vehicles”, is activated directly. Otherwise, if the nearest preceding vehicle is a human-driven one, its instantaneous speed and location are detected by the vehicle-load sensors installed on the CHDV. In this case, module 2, “Predictor for conventional human-driven vehicles”, will be activated first. Then, the predicted speed profile and spatial-temporal trajectory are input into the optimal controller, and module 1 will be subsequently activated. All the aforementioned modules are installed on each CHDV, and their details are as follows.

Module 1: Optimal controller for connected heavy-duty vehicles. This module is activated when the CHDV reaches the entrance point of the control area. The module first collects the initial speed and entrance time of the CHDV along with the speed profile and spatial-temporal trajectory of the nearest preceding vehicle. Then, it calculates the expected terminal time at the exit point that can guarantee a short travel time for the CHDV. The optimal controller utilizes the expected terminal time and the expected terminal speed to optimize the future speed profile of the CHDV. To fully use the gravity force to accelerate the CHDV before it reaches the exit point, and optimize the speed profile of the CHDV in the acceleration process, the expected terminal speed is set to be equal to the initial speed that is close to its desired speed before entering the control area. This strategy could effectively reduce the waste of gravitational potential energy and avoid the aggressive and conservative acceleration maneuvers to further improve the fuel efficiency of the CHDV. The terminal speed of the CHDV could be adjusted according to the actual traffic conditions in the future implementation. Finally, the optimized speed profile is output to the electronic control unit as the speed advisory and transmitted to the connected vehicles behind it for future use.

Module 2: Predictor for conventional human-driven vehicles. This module is activated when the CHDV reaches the entrance point and is unable to communicate with its nearest preceding vehicle. The module obtains the instantaneous speed and location of the nearest preceding vehicle. Then, it makes a prediction of the future kinematics state of the preceding human-driven vehicle by using a microscopic car-following model called the “Intelligent Driver Model” (IDM) [54]. The IDM car-following model could more accurately describe the dynamics of the location and speed of single vehicle compared to low order methods, and does not show contradictory properties such as negative speed or vehicles sharing the same space.

Module 3: Electronic Control Unit. This module receives the optimal speed profile from Module 1 and adjusts the vehicle speed accordingly by controlling the power and braking systems.

3. Mathematical Formulation

This section details the formulations of Module 1 and Module 2 for the aforementioned control system. The optimal controller for CHDVs is formulated as an optimal control problem. The predictor for conventional human-driven vehicles is constructed based on the IDM car-following model. The optimal controller and predictor have certain assumptions, as follows:

(1)

The optimal speed profile is adopted by the CHDV as the desired speed and can be overruled by the car-following behavior to guarantee safety.

(2)

The desired speed of conventional human-driven vehicles equals the 85th percentile speed of all heavy-duty vehicles that have safely driven through the high-risk roads; all the human-driven vehicles run at the desired speed unless impeded by the preceding vehicle.

(3)

The friction coefficient of road surface is accurately monitored by road condition sensors, and the measured values are not affected by traffic flow on the road. The wind speed equals 0 km/h.

The detailed formulations of these two modules are introduced in the following sections. All indices and parameters are shown in Appendix A.

3.1. Optimal Controller for Connected Heavy-Duty Vehicles

The objective of this module is to enhance driving safety and improve the fuel efficiency for CHDVs while maintaining an optimal mobility status for high-risk roads. As shown in Figure 2, this module is triggered when a CHDV attempts to communicate with roadside units. The inputs include the initial speed and time of the CHDV at the entrance point, the speed and trajectory profile of its preceding vehicle, and information on road traffic and infrastructure. The optimal control problem is constructed based on Pontryagin’s Minimum Principle (PMP). To guarantee timely speed control, this problem is solved using a numerical PMP algorithm, which can greatly reduce the computational burden [43,46].

3.1.1. State Explanation

The system state vector $\mathit{x}\left(t\right)$ of a CHDV can be defined as follows:

$$\mathit{x}\left(t\right)={\left[x_1\left(t\right),x_2\left(t\right)\right]}^T$$

(1)

The state dynamics is:

$$\dot{\mathit{x}}\left(t\right)=f\left(\mathit{x}\left(t\right),\mathit{u}\left(t\right)\right)={\left[x_2\left(t\right),u\left(t\right)\right]}^T$$

(2)

The control input is the acceleration of the vehicle, $\mathit{u}\left(t\right)=u\left(t\right)$.

3.1.2. Cost Function

The cost function is formulated as follows:

$$J=\phi \left(\mathit{x}\left(t_{l+L}\right)\right)+{\displaystyle {\int }_{t_0}^{t_{l+L}}L\left(\mathit{x}\left(t\right),u\left(t\right)\right)}dt$$

(3)

$$t_{l+L}=max\left(t_{l+L}^p+t_h,t_{l+L}^e\right)$$

(4)

$$t_{l+L}^e=\frac{l+L-\left(\frac{{v_{85\%}}^2-x_2{\left(t_0\right)}^2}{2\underset{\_}{u}}+\frac{x_2{\left(t_0\right)}^2-{v_{85\%}}^2}{2g\left(sin\alpha -\mu \cdot cos\alpha \right)}\right)}{v_{85\%}}+\frac{v_{85\%}-x_2\left(t_0\right)}{\underset{\_}{u}}+\frac{x_2\left(t_0\right)-v_{85\%}}{g\left(sin\alpha -\mu \cdot cos\alpha \right)}$$

(5)

where $\phi \left(\mathit{x}\left(t_{l+L}\right)\right)$ is the terminal cost, and ${\displaystyle {\int }_{t_0}^{t_{l+L}}L\left(\mathit{x}\left(t\right),u\left(t\right)\right)}dt$ is the running cost. The terminal cost is formulated as

$$\phi \left(\mathit{x}\left(t_{l+L}\right)\right)=w_1{\left(x_1\left(t_{l+L}\right)-l-L\right)}^2+w_2{\left(x_2\left(t_{l+L}\right)-x_2\left(t_0\right)\right)}^2,w_1\in {\mathbf{R}}^{+},w_2\in {\mathbf{R}}^{+}$$

(6)

The terminal cost ensures a constraint on the final state of the CHDV, which forces the CHDV to depart the bottom of the downhill sections or the ends of the curved sections at the expected speed. To reduce the speed adjustment maneuvers of the CHDVs after exiting the control area to maximize their fuel efficiency and mobility, the terminal speed of each CHDV is set to be equal to its initial speed at location 0, which can be considered the desired speed of vehicles running on flat and straight sections.

The running cost is formulated as

$$\begin{array}{lll}L\left(\mathit{x}\left(t\right),u\left(t\right)\right)& =& w_3\cdot \chi \left(p_{nt}\left(t\right)\right)\stackrel{{Cost}_{Thermal-energy}}{\overbrace{\left(p_{nt}\left(t\right)\right)}}+w_4\cdot \stackrel{Cos{t}_{Slip-motion}}{\overbrace{{\left(\varpi \left(t\right)-{\varpi }_d\left(t\right)\right)}^2}}+w_5\cdot \stackrel{Cos{t}_{Roll-motion}}{\overbrace{r_{llt}{\left(t\right)}^2}}+\dots \\ & & w_6\cdot \underset{Cos{t}_{Fuel}}{\underbrace{r_f\left(t\right)/x_2\left(t\right)}}+\frac{1}{2}\underset{Cos{t}_{Comfort}}{\underbrace{u{\left(t\right)}^2}},w_3\in {\mathbf{R}}^{+},w_4\in {\mathbf{R}}^{+},w_5\in {\mathbf{R}}^{+},w_6\in {\mathbf{R}}^{+}\end{array}$$

(7)

3.1.3. Conditions and Constraints

The initial conditions are as follows:

$$x_1\left(t_0\right)=0,x_2\left(t_0\right)=v_0$$

(8)

To solve the optimal control problem, the cost function should satisfy the following constraints.

Speed constraint: For consideration of safety and legality, speed is designed to be adjusted in a reasonable range. The maximum speed is the legal speed limit of the downhill or curved section, and the minimum speed is greater than or equal to 0 km/h, which means that the CHDV can stop in the emergency lane and cool its brake drums if no safe speed profile can be provided by the optimal controller. This constraint can be expressed as

$$V=\left\{x_2|0\le x_2\left(t\right)\le v_{lim},\forall t\in \left[t_0,t_{l+L}\right]\right\}$$

(9)

Acceleration constraint: All acceleration solutions output from the optimal controller should be feasible under the given conditions of the maximum traction and brake power. To ensure safety, the minimum acceleration can be overruled to prevent possible collisions caused by the lane-changing and overtaking maneuvers of the surrounding vehicles. This means that the CHDVs can decelerate much faster than the minimum acceleration when a risk to vehicle safety appears. This constraint can be specified as

$$U=\left\{u|\underset{\_}{u}\le u\left(t\right)\le \overline{u},\forall t\in \left[t_0,t_{l+L}\right]\right\}$$

(10)

Jerk constraint: Jerk is the rate at which acceleration of the vehicle changes with respect to time. To avoid vehicle passengers from losing control over their bodies and becoming injured, jerk should be limited within a reasonable range. This constraint can be formulated as

$$K=\left\{k|\underset{\_}{k}\le k\left(t\right)\le \overline{k},\forall t\in \left[t_0,t_{l+L}\right]\right\}$$

(11)

Temperature constraint: To ensure that the braking system is in good working condition, the temperature of each brake drum should be constrained to avoid brake fade caused by a buildup of heat in the braking surfaces. This constraint can be expressed as

$$\Gamma =\left\{T_{tb}^i|T_{tb}^i\left(t\right)\le {\overline{T}}_{tb},\forall t\in \left[t_0,t_{l+L}\right]\right\}$$

(12)

Yaw constraint: When a heavy-duty vehicle is running on a sharp-curved road, an excessive yaw rate can cause tail flick or even a loss of control. To avoid these dangerous sideslip maneuvers, the following constraint of the yaw rate should be satisfied:

$$W=\left\{\varpi |\varpi \left(t\right)\le \overline{\varpi },\forall t\in \left[t_0,t_{l+L}\right]\right\}$$

(13)

Roll constraint: Lateral load transfer occurs while cornering and involves a shift of mass across the wheels due to centrifugal force and lateral acceleration. The vertical forces on the outer tires increase at the expense of the inner tires, which can cause a roll-over accident. To guarantee safety, the constraint of the lateral load transfer ratio should be formulated as

$$R_{llt}=\left\{r_{llt}|{\underset{\_}{r}}_{llt}\le r_{llt}\left(t\right)\le {\overline{r}}_{llt},\forall t\in \left[t_0,t_{l+L}\right]\right\}$$

(14)

3.1.4. Brake Drum Temperature Rise Model

(1) Energy Conversion of the Whole Vehicle

While running on long–steep downhill roads, heavy-duty vehicles tend to accelerate due to the effect of gravity. Thus, frequent and continuous braking is necessary for maintaining the vehicle speed within a reasonable and safe range. Some non-brake forces also resist the motion of heavy-duty vehicles, including rolling resistance and aerodynamic drag. The rotational kinetic energy of the vehicle’s rotating parts is not considered in this research. Therefore, the gravitational potential energy of the whole vehicle is converted into its kinetic energy and then ultimately to thermal energy of brake drums, air, tires and road surface. The thermal energy generated by the brake drums of heavy-duty vehicles during the whole downhill process can be modeled as follows:

$$E_T\left(t\right)=E_f\left(t\right)-E_{eb}\left(t\right)-E_{rr}\left(t\right)-E_{ad}\left(t\right),\forall t\in \left[t_0,t_{l+L}\right]$$

(15)

$$E_f\left(t\right)=E_k\left(t_0\right)+E_g\left(t_0\right)-\left(E_k\left(t\right)+E_g\left(t\right)\right)=\frac{1}{2}m\left(x_2{\left(t_0\right)}^2-x_2{\left(t\right)}^2\right)+\chi \left(t-t_l\right)mg\left(x_1\left(t\right)-l\right)sin\alpha$$

(16)

$$\chi \left(t-t_l\right)=\{\begin{array}{ll}0,& \forall t\in \left[t_0,t_l\right)\\ 1,& \forall t\in \left[t_l,t_{l+L}\right]\end{array}$$

(17)

where $\chi \left(t-t_l\right)$ is a Heaviside function of time.

(2) Effect of Engine Braking

According to an engine brake model extended from the TNO’s dynamic engine model “DYNAMO”, the normalized engine brake torque under a steady state is linearly related to the engine speed [17]. The formula of this relationship can be simplified as

$$B_t\left(t\right)=q_1\cdot v_e\left(t\right)+q_2$$

(18)

During the process of engine braking, vehicles usually downshift into and maintain a lower gear to achieve high brake torque. In the steady state of engine braking in a certain gear, the vehicle speed is proportional to the engine speed. Thus, the energy of engine braking can be formulated as follows:

$$E_{eb}\left(t\right)={\displaystyle \underset{t_0}{\overset{t}{\int }}\frac{B_t\left(\tau \right)}{R_w}{x}_2\left(\tau \right)\cdot d\tau }={\displaystyle \underset{t_0}{\overset{t}{\int }}\frac{q_1\cdot r_{ev}\cdot x_2\left(\tau \right)+q_2}{R_w}{x}_2\left(\tau \right)\cdot d\tau }$$

(19)

(3) Effect of Rolling Resistance

Rolling resistance is a force resisting the motion when the tires roll on the road surface. Rolling resistance is mainly caused by non-plastic effects. A part of the energy needed for deformation of the tires or roadbed cannot be recovered when the pressure is removed. The thermal energy generated by rolling resistance between the tires and the road surface can be formulated as follows [16]:

$$E_{rr}\left(t\right)={\displaystyle \sum _{i=1}^I{e}_{rr}^i\left(t\right)},\forall t\in \left[t_0,t_{l+L}\right]$$

(20)

$$e_{rr}^i\left(t\right)=F_{rr}^i\left(t\right)\cdot s=\chi \left(t_l-t\right)C_{rr}{\eta }_i{x}_1\left(t\right)+\chi \left(t-t_l\right)\left(C_{rr}{\eta }_{i}cos\alpha \cdot \left(x_1\left(t\right)-l\right)+C_{rr}{\eta }_{i}l\right)$$

(21)

$${\displaystyle \sum _{i=1}^I{\eta }_i}=mg$$

(22)

(4) Effect of Aerodynamic Drag

Aerodynamic drag is a force acting opposite to the relative motion of a vehicle moving with respect to the surrounding air and depends on the properties of the air along with the size, shape, and speed of the heavy-duty vehicle. The thermal energy generated by aerodynamic drag is [16]

$$E_{ad}\left(t\right)={\displaystyle \underset{\tau =t_0}{\overset{t}{\int }}{F}_{ad}\left(\tau \right)x_2\left(\tau \right)\cdot d\tau }={\displaystyle \underset{\tau =t_0}{\overset{t}{\int }}\frac{1}{2}{C}_{ad}A\rho v_r{\left(\tau \right)}^2{x}_2\left(\tau \right)\cdot d\tau },\forall t\in \left[t_0,t_{l+L}\right]$$

(23)

In this research, the wind speed is assumed to be 0, therefore $v_r\left(\tau \right)=x_2\left(\tau \right)$.

The thermal energy generation rate of the drum-brakes of the heavy-duty vehicle is deduced as follows:

$$\begin{array}{ccc}{p}_{tp}\left(t\right)\hfill & =\hfill & \frac{\partial E_T\left(t\right)}{\partial t}=\frac{\partial \left(E_f\left(t\right)-E_{eb}\left(t\right)-E_{rr}\left(t\right)-E_{ad}\left(t\right)\right)}{\partial t}\hfill \\ & =\hfill & \{\begin{array}{cc}-m{x}_2\left(t\right)u\left(t\right)-\frac{q_1{r}_{ev}{x}_2\left(t\right)+q_2}{R_w}{x}_2\left(t\right)-{\displaystyle \sum _{i=1}^I{C}_{rr}{\eta }_i{x}_2\left(t\right)}-\frac{1}{2}{C}_{ad}A\rho x_2{\left(t\right)}^3\hfill & ,\forall t\in \left[t_0,t_l\right)\hfill \\ -m{x}_2\left(t\right)u\left(t\right)+mg{x}_2\left(t\right)sin\alpha -\frac{q_1{r}_{ev}{x}_2\left(t\right)+q_2}{R_w}{x}_2\left(t\right)-\dots \hfill \\ {\displaystyle \sum _{i=1}^I}{C}_{rr}{\eta }_{i}cos\alpha \cdot x_2\left(t\right)-\frac{1}{2}{C}_{ad}A\rho x_2{\left(t\right)}^3& ,\forall t\in \left[t_l,t_{l+L}\right]\hfill \end{array}\end{array}$$

(24)

(5) Effect of Heat Transfer

In the braking process, a portion of thermal energy is dissipated into ambient energy by heat transfer, including convective and radiative heat transfer. No thermal conduction is considered in this research. The thermal energy dissipated by the convective heat transfer of the brake drum k is

$$E_{ct}^i\left(t\right)={\displaystyle \underset{\tau =t_0}{\overset{t}{\int }}{A}_d^i{h}_c\left(T_{eb}^i\left(\tau \right)-T_{ab}^i\left(\tau \right)\right)}\cdot d\tau ,\forall t\in \left[t_0,t_{l+L}\right]$$

(25)

$$h_c=0.92+\beta x_2\left(\tau \right)\cdot exp\left(-\frac{x_2\left(\tau \right)}{328}\right)$$

(26)

According to the Stefan–Boltzmann Law, the thermal energy dissipated by the radiative heat transfer of the brake drum i can be formulated as follows:

$$E_{rt}^i\left(t\right)={\displaystyle \underset{\tau =t_0}{\overset{t}{\int }}{A}_d^i\epsilon \sigma \left(T_{tb}^i{\left(\tau \right)}^4-T_{ta}^i{\left(\tau \right)}^4\right)}\cdot d\tau ,\forall t\in \left[t_0,t_{l+L}\right]$$

(27)

The temperature of brake drum i can be formulated as follows:

$$T_{tb}^i\left(t\right)=T_{tb}^i\left(t_0\right)+\frac{{\zeta }_i{E}_T\left(t\right)-E_{ct}^i\left(t\right)-E_{rt}^i\left(t\right)}{C_{sh}{m}_d^i}$$

(28)

The thermal energy dissipation rate of the drum-brakes of the heavy-duty vehicle is

$$\begin{array}{ll}{p}_{td}\left(t\right)=\frac{\partial \left({\displaystyle \sum _{i=1}^I{E}_{ct}^i\left(t\right)}+{\displaystyle \sum _{i=1}^I{E}_{rt}^i\left(t\right)}\right)}{\partial t}=& {\displaystyle \sum _{i=1}^I{A}_d^i\left(0.92+\beta x_2\left(t\right)exp\left(-\frac{x_2\left(t\right)}{328}\right)\right)\left(T_{eb}^i\left(t\right)-T_{ab}^i\left(t\right)\right)}+\dots \\ & {\displaystyle \sum _{i=1}^I{A}_d^i\epsilon \sigma \left(T_{tb}^i{\left(t\right)}^4-T_{ta}^i{\left(t\right)}^4\right)},\forall t\in \left[t_0,t_{l+L}\right]\end{array}$$

(29)

The net thermal energy of the drum-brakes of the heavy-duty vehicle can be calculated as:

$$p_{nt}\left(t\right)=p_{tp}\left(t\right)-p_{td}\left(t\right)$$

(30)

3.1.5. Lateral Stability Model

While running on sharp-curved roads, the centripetal forces from the tires act on the road surface towards the center of the curve, and the inertial force acts horizontally through the center of mass away from the center of the curve, as shown in Figure 3. These two opposite forces make the vehicle sideslip or roll towards the outside of the curve. An excessive sideslip angle and roll angle may lead to losing control of the vehicle or even result in a rollover accident for heavy-duty vehicles with a high center of gravity.

(1) Yaw Motion Model

When heavy-duty vehicles drive on sharp-curved roads at a high speed or yaw rate, their tires may be not able to provide enough centripetal force for the vehicle, thereby causing the vehicle to slip towards the outside of the curve. According to the motion rules of the vehicle cornering process, the yaw rate has a significantly positive correlation with the speed. Thus, the optimal controller proposed in this study attempts to maintain the yaw rate of the CHDV at a moderate level, which can reduce the risk of an uncontrollable sideslip while producing few adverse effects on fuel efficiency and traffic mobility.

As previously mentioned, vehicle longitudinal acceleration is the control input of the proposed optimal controller. Hence, only the longitudinal kinematics information of CHDV are provided for calculating the optimization cost. The vehicle yaw rate is approximately formulated as

$$\varpi \left(t\right)\approx \frac{x_{2,x}\left(t\right)}{R_c\left(x_1\left(t\right)\right)}$$

(31)

The reference value of the yaw rate is selected as the desired yaw rate, which is the steady-state yaw rate of the 3 degrees-of-freedom vehicle dynamics model [28] shown in Figure 3a. The desired yaw rate of the CHDV can be calculated as follows:

$${\varpi }_d\left(t\right)=\{\begin{array}{cc}0\hfill & ,\forall t\in \left[t_0,t_l\right)\hfill \\ \underset{Ya{w}_{horizontal road}}{\underbrace{\delta x_{2,x}{\left(t\right)}^3{\left(\left(1-\frac{m\left(D_{gf}{S}_f-D_{gr}{S}_r\right)x_{2,x}{\left(t\right)}^2}{2S_f{S}_r{\left(D_{gf}+D_{gr}\right)}^2}\right)\left(D_{gf}+D_{gr}\right)R_c\left(x_1\left(t\right)\right)\right)}^{-1}}}+\dots \hfill \\ \underset{{Yaw}_{bankangle}}{\underbrace{g\cdot sin\theta {\left(x_{2,x}\left(t\right)+\frac{2S_f{S}_r{\left(D_{gf}+D_{gr}\right)}^2}{m\left(D_{gf}{S}_f+D_{gr}{S}_r\right)x_{2,x}\left(t\right)}\right)}^{-1}}}& ,\forall t\in \left[t_l,t_{l+L}\right]\hfill \end{array}$$

(32)

(2) Roll Motion Model

Besides excessive sideslip, heavy-duty vehicles also face a high risk of rollover accidents while driving on sharp-curved roads. The combined action of the centripetal force from the tires and the horizontal inertial force at the center of mass makes a certain load of the inner wheels transfer to the outer wheels, as shown in Figure 3b. The vehicle will then roll over towards the outside of the curve when this combined force is enough to overcome the force of gravity. The vertical load of each wheel can be calculated as follows:

$$F_z^{fl}\left(t\right)=\frac{m\left(g{D}_{gr}cos\alpha \cdot cos\theta -g{h}_{g}sin\alpha -u_x\left(t\right)h_g\right)}{2\left(D_{gf}+D_{gr}\right)}+\frac{m\left(gcos\alpha sin\theta D_{gr}{h}_g-u_y\left(t\right)D_{gr}{h}_g\right)}{\left(D_{gf}+D_{gr}\right)D_{tw}}-\frac{S_f\varphi \left(t\right)}{D_{tw}}$$

(33)

$$F_z^{rl}\left(t\right)=\frac{m\left(g{D}_{gf}cos\alpha \cdot cos\theta +g{h}_{g}sin\alpha +u_x\left(t\right)h_g\right)}{2\left(D_{gf}+D_{gr}\right)}+\frac{m\left(gcos\alpha sin\theta D_{gf}{h}_g-u_y\left(t\right)D_{gf}{h}_g\right)}{\left(D_{gf}+D_{gr}\right)D_{tw}}-\frac{S_r\varphi \left(t\right)}{D_{tw}}$$

(34)

$$F_z^{fr}\left(t\right)=\frac{m\left(g{D}_{gr}cos\alpha \cdot cos\theta -g{h}_{g}sin\alpha -u_x\left(t\right)h_g\right)}{2\left(D_{gf}+D_{gr}\right)}+\frac{m\left(u_y\left(t\right)D_{gr}{h}_g-gcos\alpha sin\theta D_{gr}{h}_g\right)}{\left(D_{gf}+D_{gr}\right)D_{tw}}+\frac{S_f\varphi \left(t\right)}{D_{tw}}$$

(35)

$$F_z^{rr}\left(t\right)=\frac{m\left(g{D}_{gf}cos\alpha \cdot cos\theta +g{h}_{g}sin\alpha +u_x\left(t\right)h_g\right)}{2\left(D_{gf}+D_{gr}\right)}+\frac{m\left(u_y\left(t\right)D_{gf}{h}_g-gcos\alpha sin\theta D_{gf}{h}_g\right)}{\left(D_{gf}+D_{gr}\right)D_{tw}}+\frac{S_r\varphi \left(t\right)}{D_{tw}}$$

(36)

In rollover prevention research, the lateral load transfer ratio is a common performance index to define the safety area [55]. The real-time lateral load transfer ratio is

$$\begin{array}{lll}{r}_{llt}\left(t\right)& =& \frac{F_z^{fl}\left(t\right)+F_z^{rl}\left(t\right)-\left(F_z^{fr}\left(t\right)+F_z^{rr}\left(t\right)\right)}{F_z^{fl}\left(t\right)+F_z^{rl}\left(t\right)+F_z^{fr}\left(t\right)+F_z^{rr}\left(t\right)}\\ & =& \{\begin{array}{ll}0\hfill & ,\forall t\in \left[t_0,t_l\right)\hfill \\ \frac{2\left(mgcos\alpha \cdot sin\theta h_g-m{u}_y\left(t\right)h_g-\left(S_f+S_r\right)\varphi \left(t\right)\right)}{mg{D}_{tw}cos\alpha \cdot cos\theta }& ,\forall t\in \left[t_l,t_{l+L}\right]\hfill \end{array}\end{array}$$

(37)

In a steady-state case, the relationship between lateral acceleration and road curvature can be approximately expressed as

$$u_y\left(t\right)={\dot{x}}_{2,y}\left(t\right)+\frac{x_{2,x}{\left(t\right)}^2}{R_c\left(x_1\left(t\right)\right)}\approx \frac{\partial R_c\left(x_1\left(t\right)\right)}{\partial t}+\frac{x_{2,x}{\left(t\right)}^2}{R_c\left(x_1\left(t\right)\right)}$$

(38)

The roll angle is approximated as a linear function of the lateral acceleration of the vehicle:

$$\varphi \left(t\right)\approx c_1\cdot u_y\left(t\right)+c_2$$

(39)

3.1.6. Solution Based on Pontryagin’s Minimum Principle

The PMP approach is adopted in this research to solve the aforementioned optimal control problem of the maximum-safety speed trajectory of heavy-duty vehicles. The Hamiltonian function is defined as follows:

$$\mathcal{\mathscr{H}}\left(\mathit{x}\left(t\right),\mathit{u}\left(t\right),\mathbf{\lambda }\left(t\right),t\right)=L\left(\mathit{x}\left(t\right),\mathit{u}\left(t\right),t\right)+\mathbf{\lambda }{\left(t\right)}^T\cdot f\left(\mathit{x}\left(t\right),\mathit{u}\left(t\right),t\right)$$

(40)

where $\mathbf{\lambda }\left(t\right)$ denotes the so-called co-state of the state $\mathit{x}\left(t\right)$. The PMP requires that the optimal state trajectory ${\mathit{x}}^{*}\left(t\right)$, optimal control ${\mathit{u}}^{*}\left(t\right)$, and corresponding co-state ${\mathbf{\lambda }}^{*}\left(t\right)$ minimize the Hamiltonian $\mathcal{\mathscr{H}}$. The necessary conditions for the optimal control ${\mathit{u}}^{*}\left(t\right)$ can be derived as

$$\mathcal{\mathscr{H}}\left({\mathit{x}}^{*}\left(t\right),{\mathit{u}}^{*}\left(t\right),{\mathbf{\lambda }}^{*}\left(t\right),t\right)\le \mathcal{\mathscr{H}}\left({\mathit{x}}^{*}\left(t\right),\mathit{u}\left(t\right),{\mathbf{\lambda }}^{*}\left(t\right),t\right),\forall \mathit{u}\left(t\right)\in \mathcal{U},t\in \left[t_{0,}{t}_{l+L}\right]$$

(41)

where $\mathcal{U}$ is the permissible set of control input $\mathit{u}\left(t\right)$. This necessary condition can also be expressed as

$$0=\frac{\partial \mathcal{\mathscr{H}}\left(\mathit{x}\left(t\right),\mathit{u}\left(t\right),\mathbf{\lambda }\left(t\right),t\right)}{\partial \mathit{u}\left(t\right)}$$

(42)

$$\dot{\mathbf{\lambda }}\left(t\right)=-\frac{\partial \mathcal{\mathscr{H}}\left(\mathit{x}\left(t\right),\mathit{u}\left(t\right),\mathbf{\lambda }\left(t\right),t\right)}{\partial \mathit{x}\left(t\right)}$$

(43)

$$\dot{\mathit{x}}\left(t\right)=-\frac{\partial \mathcal{\mathscr{H}}\left(\mathit{x}\left(t\right),\mathit{u}\left(t\right),\mathbf{\lambda }\left(t\right),t\right)}{\partial \mathbf{\lambda }\left(t\right)}$$

(44)

Equations (42) and (43) are used to solve the optimal control ${\mathit{u}}^{*}\left(t\right)$, and Equation (44) is the same as that for state dynamics.

$$\mathcal{\mathscr{H}}={\lambda }_1\left(t\right)x_2\left(t\right)+{\lambda }_{2}u\left(t\right)+w_3\chi \left(p_{nt}\left(t\right)\right)\left(p_{nt}\left(t\right)\right)+w_4\varpi {\left(t\right)}^2+w_5{r}_{llt}{\left(t\right)}^2+w_6{r}_f\left(t\right)/x_2\left(t\right)+\frac{1}{2}u{\left(t\right)}^2$$

(45)

The instantaneous fuel consumption rate $r_f\left(t\right)$ can be calculated by utilizing the fuel consumption and emission model developed by Akcelik [56]:

$$r_f\left(t\right)={\displaystyle \sum _{j=0}^3{\psi }_j{x}_2{\left(t\right)}^j}+{\varsigma }_1{x}_2\left(t\right)u\left(t\right)+{\varsigma }_2{x}_2\left(t\right)u{\left(t\right)}^2\chi \left(u\left(t\right)\right),\forall t\in \left[t_0,t_{l+L}\right]$$

(46)

$$\chi \left(u\left(t\right)\right)=\{\begin{array}{l}1,\forall u\left(t\right)\ge 0\\ 0,\forall u\left(t\right)<0\end{array}$$

(47)

where $w_3$, $w_4$, and $w_5$ are the weighting factors for the brake safety, yaw stability, and roll stability of the vehicle, respectively. $w_6$ is the weighting factor for the fuel efficiency of the power system.

In this research, the optimal controller achieves its desired goals by controlling the longitudinal motion of a heavy-duty vehicle. Therefore, in the process of formulating the Hamiltonian function, $x_{2,x}\left(t\right){=x}_2\left(t\right)$ is substituted into in the cost of yaw stability and roll stability.

According to Equations (45) and (42), the control law is determined as follows:

$$0=\frac{\partial \mathcal{\mathscr{H}}}{\partial \mathit{u}\left(t\right)}\Rightarrow u\left(t\right)=\{\begin{array}{ll}{w}_{3}m{x}_2\left(t\right)-{\lambda }_2\left(t\right)-w_6{\varsigma }_1\hfill & ,\forall P_{nt}\left(t\right)\in \left[0,+\infty \right),t\in \left[t_0,t_{l+L}\right]\hfill \\ -{\lambda }_2\left(t\right)-w_6{\varsigma }_1\hfill & ,\forall P_{nt}\left(t\right)\in \left(-\infty ,0\right),u\left(t\right)\in \left[\underset{\_}{u},0\right),t\in \left[t_0,t_{l+L}\right]\hfill \\ \left(-{\lambda }_2\left(t\right)-w_6{\varsigma }_1\right)/\left(2w_6{\varsigma }_2{x}_2\left(t\right)+1\right)\hfill & ,\forall P_{nt}\left(t\right)\in \left(-\infty ,0\right),u\left(t\right)\in \left[0,\overline{u}\right],t\in \left[t_0,t_{l+L}\right]\hfill \end{array}$$

(48)

Similarly, Equation (41) provides

$${\dot{\lambda }}_1\left(t\right)=-\frac{\partial \mathcal{\mathscr{H}}}{\partial x_1\left(t\right)}=0\Rightarrow {\lambda }_1\left(t\right)=C$$

(49)

where $C$ is a constant to be solved.

$$\begin{array}{lll}{\dot{\lambda }}_2\left(t\right)=-\frac{\partial \mathcal{\mathscr{H}}}{\partial x_2\left(t\right)}=& -& {\lambda }_1\left(t\right)-w_3\chi \left(p_{nt}\left(t\right)\right)\frac{\partial \left(p_{nt}\left(t\right)\right)}{\partial x_2\left(t\right)}-2w_4\left(\varpi \left(t\right)-{\varpi }_d\left(t\right)\right)\frac{\partial \left(\varpi \left(t\right)-{\varpi }_d\left(t\right)\right)}{\partial x_2\left(t\right)}-\dots \\ & & 2w_5{r}_{llt}\left(t\right)\frac{\partial \left(r_{llt}\left(t\right)\right)}{\partial x_2\left(t\right)}-w_6\frac{\partial \left(r_f\left(t\right)/x_2\left(t\right)\right)}{\partial x_2\left(t\right)}\end{array}$$

(50)

$$\frac{\partial \left(p_{nt}\left(t\right)\right)}{\partial x_2\left(t\right)}=\{\begin{array}{c}-mu\left(t\right)-\frac{2q_1{r}_{ev}{x}_2\left(t\right)+q_2}{R_w}-{\displaystyle \sum _{i=1}^I{C}_{rr}{\eta }_i}-\frac{3}{2}{C}_{ad}A\rho x_2{\left(t\right)}^2-\dots \hfill \\ {\displaystyle \sum _{i=1}^I}{A}_d^i\beta \left(T_{eb}^i\left(t\right)-T_{ab}^i\left(t\right)\right)\left(1-\frac{x_2\left(t\right)}{328}\right)exp\left(-\frac{x_2\left(t\right)}{328}\right)& ,\forall t\in \left[t_0,t_l\right)\hfill \\ -mu\left(t\right)+mgsin\alpha -\frac{2q_1{r}_{ev}{x}_2\left(t\right)+q_2}{R_w}-{\displaystyle \sum _{i=1}^I}{C}_{rr}{\eta }_i-\frac{3}{2}{C}_{ad}A\rho x_2{\left(t\right)}^2-\dots \hfill \\ {\displaystyle \sum _{i=1}^I}{A}_d^i\beta \left(T_{eb}^i\left(t\right)-T_{ab}^i\left(t\right)\right)\left(1-\frac{x_2\left(t\right)}{328}\right)exp\left(-\frac{x_2\left(t\right)}{328}\right)& ,\forall t\in \left[t_l,t_{l+L}\right]\hfill \end{array}$$

(51)

$$\frac{\partial \left(\varpi \left(t\right)-{\varpi }_d\left(t\right)\right)}{\partial x_2\left(t\right)}=\{\begin{array}{ll}0\hfill & ,\forall t\in \left[t_0,t_l\right)\hfill \\ \frac{1}{R_c\left(x_1\left(t\right)\right)}-\dots \hfill \\ \frac{\delta S_f{S}_r\left(D_{gf}+D_{gr}\right)\left(12S_f{S}_r{\left(D_{gf}+D_{gr}\right)}^2{x}_2{\left(t\right)}^2-2m\left(D_{gf}{S}_f-D_{gr}{S}_r\right)x_2{\left(t\right)}^4\right)}{{\left(2S_f{S}_r{\left(D_{gf}+D_{gr}\right)}^2-m\left(D_{gf}{S}_f-D_{gr}{S}_r\right)x_2{\left(t\right)}^2\right)}^2{R}_c\left(x_1\left(t\right)\right)}+\dots \hfill \\ \frac{gsin\theta }{{\left(x_2\left(t\right)+\frac{2S_f{S}_r{\left(D_{gf}+D_{gr}\right)}^2}{m\left(D_{gf}{S}_f+D_{gr}{S}_r\right)x_2\left(t\right)}\right)}^2}\left(1-\frac{2S_f{S}_r{\left(D_{gf}+D_{gr}\right)}^2}{m\left(D_{gf}{S}_f+D_{gr}{S}_r\right)x_2{\left(t\right)}^2}\right)\hfill & ,\forall t\in \left[t_l,t_{l+L}\right]\end{array}$$

(52)

$$\frac{\partial \left(r_{llt}\left(t\right)\right)}{\partial x_2\left(t\right)}=\{\begin{array}{ll}0\hfill & ,\forall t\in \left[t_0,t_l\right)\hfill \\ -\frac{4x_2\left(t\right)\left(m{h}_g+c_1\left(S_f+S_r\right)\right)}{mg{D}_{tw}cos\alpha \cdot cos\theta \cdot R_c\left(x_1\left(t\right)\right)}& ,\forall t\in \left[t_l,t_{l+L}\right]\hfill \end{array}$$

(53)

$$\frac{\partial \left(r_f\left(t\right)/x_2\left(t\right)\right)}{\partial x_2\left(t\right)}=-{\psi }_0{x}_2{\left(t\right)}^{-2}+{\psi }_2+2{\psi }_3{x}_2\left(t\right),\forall t\in \left[t_0,t_{l+L}\right]$$

(54)

As described before, the desired final state $\phi \left(\mathit{x}\left(t_{l+L}\right)\right)$ of the CHDV should be enforced to ensure that the optimal controller has a minimally adverse effect on traffic mobility [43]. For this, the following terminal condition for $\mathbf{\lambda }\left(t\right)$ needs to be met:

$$\mathbf{\lambda }\left(t_{l+L}\right)=\frac{\partial \phi \left(\mathit{x}\left(t_{l+L}\right)\right)}{\partial \mathit{x}}\Rightarrow \{\begin{array}{l}{\lambda }_1\left(t_{l+L}\right)=2w_1\left(x_1\left(t_{l+L}\right)-l-L\right)\\ {\lambda }_2\left(t_{l+L}\right)=2w_2\left(x_2\left(t_{l+L}\right)-x_2\left(t_0\right)\right)\end{array}$$

(55)

3.1.7. Iterative PMP Algorithm to Solve the Optimal Control

A numerical solution is introduced to solve the aforementioned optimal control problem [37,43]. This solution iteratively finds the state $\mathit{x}\left(t\right)$ forwards in time and, subsequently, the co-state $\mathbf{\lambda }\left(t\right)$ backwards in time. This procedure is briefly described in the following:

• Step 1: Initialize the co-state ${\mathsf{\Lambda }}^{\left(0\right)}\left(t\right)=0$, $\forall t\in \left[t_{0,}{t}_{l+L}\right]$.
• Step 2: Start the iterative solving process with the iteration number $n=1$.
• Step 3: Solve Equation (43) forward in time subject to the initial conditions and constraints for state ${\mathit{x}}^{\left(n\right)}\left(t\right)$ using co-state ${\mathsf{\Lambda }}^{\left(n-1\right)}\left(t\right)$. The downhill gradient and curve radius are updated according to the vehicle’s actual position.
• Step 4: Solve Equation (42) backwards in time for co-state ${\mathbf{\lambda }}^{\left(n\right)}\left(t\right)$ with ${\mathit{x}}^{\left(n\right)}\left(t\right)$.
• Step 5: Update the co-state ${\mathsf{\Lambda }}^{\left(n\right)}\left(t\right)$ with the weight factor $\gamma$ that can smooth the co-state updating process, ${\mathsf{\Lambda }}^{\left(n\right)}\left(t\right)=\left(1-\gamma \right)\cdot {\mathsf{\Lambda }}^{\left(n-1\right)}\left(t\right)+\gamma \cdot {\lambda }^{\left(n\right)}\left(t\right)$.
• Step 6: If the error $\xi =\Vert {\mathsf{\Lambda }}^{\left(t\right)}\left(t\right)-{\mathbf{\lambda }}^{\left(t\right)}\left(t\right)\Vert <\overline{\xi }$, then stop the iteration; otherwise, set $n=n+1$ and loop back to step 3. $\overline{\xi }$ is the pre-set error threshold.

3.2. Predictor for Conventional Human-Driven Vehicles

The objective of this module is to predict the speed profiles and spatial-temporal trajectories of conventional human-driven vehicles. As shown in Figure 2, this module is triggered when a CHDV reaches the entrance point and is unable to communicate with the preceding vehicle. The inputs include the initial speed and the location of the conventional human-driven vehicle along with the information of road traffic and infrastructure. This predictor is improved from the IDM microscopic car-following model [54]. The formulations of the IDM car-following model are

$$u\left(t\right)=\overline{u}\left[1-{\left(\frac{x_2\left(t\right)}{v_d}\right)}^{\vartheta }-{\left(\frac{\Delta x_1^{*}\left(x_2\left(t\right),\Delta x_2\left(t\right)\right)}{\Delta x_1\left(t\right)}\right)}^2\right],\forall t\in \left[t_0,\infty \right)$$

(56)

$$\Delta x_1^{*}\left(x_2\left(t\right),\Delta x_2\left(t\right)\right)=D_{mdn}+max\left(x_2\left(t\right)\cdot t_s+\frac{x_2\left(t\right)\cdot \Delta x_2\left(t\right)}{2\sqrt{\overline{u}\cdot u_d}},0\right)$$

(57)

$$\Delta x_1\left(t\right)=x_1^p\left(t\right)-x_1\left(t\right),\Delta x_2\left(t\right)=x_2\left(t\right)-x_2^p\left(t\right)$$

(58)

This model needs information on the current speed of the predicted conventional vehicle, the distance to the vehicle in front, and the speed difference between these two vehicles. However, the vehicle-loaded sensors of the CHDV can only obtain the kinematics information for a predicted conventional vehicle that is the nearest preceding conventional vehicle to the CHDV. This study borrowed a method called “Virtual Preceding Vehicle” as a solution to this problem, which sets a virtual vehicle running at a given speed in front of the predicted conventional vehicle [43,46]. The objective of this method is to help the predictor compute the most common kinematics state for the predicted conventional vehicle. The details are expressed as follows:

(1)

When the predicted conventional vehicle is driving on the approach sections connected to high-risk roads, it will prefer to gradually decelerate to a desired speed before entering said high-risk roads. The desired speed of the predicted vehicle equals its initial speed at the entrance point, $v_d=x_2\left(t_0\right)$. The speed and location of its virtual preceding vehicle are

$$x_1^p\left(t\right)=l+v_{85\%}\cdot t_h,x_2^p\left(t\right)=v_{85\%},\forall t\in \left[t_0,t_l\right)$$

(59)

(2)

When both the predicted conventional vehicle and its virtual preceding vehicle are traveling on high-risk roads, the predicted vehicle will maintain a stable net distance from the virtual preceding vehicle. The desired speed of the predicted vehicle is the 85th percentile speed of all heavy-duty vehicles, $v_d=v_{85\%}$. The speed and location of its virtual preceding vehicle are

$$x_1^p\left(t\right)=l+v_{85\%}\cdot \left(t-t_l+t_h\right),x_2^p\left(t\right)=v_{85\%},\forall t\in \left[t_l,t_{l+L}-t_h\right)$$

(60)

(3)

When the predicted conventional vehicle is driving on high-risk roads, and its virtual preceding vehicle is traveling on the departure section, the predicted vehicle will gradually increase speed until leaving the high-risk roads. The desired speed of the predicted vehicle remains equal to the 85th percentile speed of all heavy-duty vehicles. The speed and location of the virtual preceding vehicle can be calculated as

$$x_2^p\left(t\right)=\{\begin{array}{ll}{v}_{85\%}+\frac{1}{2}{k}_d^p\cdot {\left(t-t_{l+L}+t_h\right)}^2\hfill & ,\forall t\in \left[t_{l+L}-t_h,t_{l+L}-t_h+\overline{u}/k_d^p\right)\hfill \\ v_{85\%}+\overline{u}\left(t-t_{l+L}+t_h\right)-\frac{{\overline{u}}^2}{2k_d^p}\hfill & ,\forall t\in \left[t_{l+L}-t_h+\overline{u}/k_d^p,t_{l+L}\right]\hfill \end{array}$$

(61)

$$x_1^p\left(t\right)=\{\begin{array}{cc}l+L+v_{85\%}\cdot \left(t-t_{l+L}+t_h\right)+\frac{k_d^p}{6}{\left(t-t_{l+L}+t_h\right)}^3& ,\forall t\in \left[t_{l+L}-t_h,t_{l+L}-t_h+\overline{u}/k_d^p\right)\hfill \\ l+L+\left(v_{85\%}-\frac{{\overline{u}}^2}{2k_d^p}\right)\left(t-t_{l+L}+t_h\right)+\dots \hfill \\ \frac{\overline{u}}{2}{\left(t-t_{l+L}+t_h\right)}^2+\frac{{\overline{u}}^3}{6{\left(k_d^p\right)}^2}& ,\forall t\in \left[t_{l+L}-t_h+\overline{u}/k_d^p,t_{l+L}\right]\hfill \end{array}$$

(62)

Then, the speed profile and spatial-temporal trajectory of the predicted vehicle can be calculated as follows:

$$x_2\left(t\right)={\displaystyle \underset{\tau =t_0}{\overset{t}{\int }}u\left(\tau \right)}\cdot d\tau$$

(63)

$$x_1\left(t\right)={\displaystyle \underset{\tau =t_0}{\overset{t}{\int }}{x}_2\left(\tau \right)}\cdot d\tau$$

(64)

4. Simulation and Evaluation

4.1. Simulation Platform and Scenarios

The proposed speed control system is next evaluated through a co-simulation of vehicle dynamics and kinematics. The test roads are shown in Figure 4. Mixed traffic is generated on the roads. Consequently, this speed control system only focuses on the longitudinal motion of the vehicles, with no lane-changing or overtaking maneuvers allowed for any CHDV.

An integrated simulation platform was developed using MATLAB/Simulink (MathWorks, Natick, MA, USA), VISSIM (PTV Group, Karlsruhe, Germany), and TruckSim (MSC, Ann Arbor, MI, USA). The workflow of this simulation platform and the function of each software are detailed as follows:

(1)

MATLAB/Simulink is the master control program and is responsible for optimizing the speed profiles of the CHDVs, predicting the speed profiles of the conventional human-driven vehicles, and communicating between TruckSim and VISSIM. The optimal controller for CHDVs and the predictor for conventional human-driven vehicles of the proposed speed control system are only implemented in MATLAB/Simulink. The input of the optimal controller and predictor are information on acceleration, speed and location of CHDVs and conventional human-driven vehicles transmitted from VISSIM.

(2)

VISSIM establishes the test roads and conducts a microscopic traffic simulation on high-risk roads using its own microscopic car-following model called “Wiedemann 74”. To ensure the realness of the simulation results output from VISSIM, the Wiedemann 74 car-following model is calibrated according to the Highway Capacity Manual 2010, the base saturation flow rate of single lane equals 1830 veh/h. The Wiedemann 74 car-following model could simulate complex vehicle interactions realistically on a microscopic level, and thereby verify the accuracy of predictor in module 2 improved from IDM car-following model. The optimal speed advisory transmitted from MATLAB/Simulink is written to the corresponding CHDV as the “Desired Speed”. Then, the motion profiles of the CHDVs and conventional human-driven vehicles generated in VISSIM are sent to the optimal controller and predictor in MATLAB/Simulink, and are transmitted to TruckSim as the control input for the vehicles through MATLAB/Simulink.

(3)

TruckSim constructs a dynamics model of heavy-duty vehicles and configures the CHDVs or conventional human-driven vehicles to run according to the corresponding speed profiles obtained from VISSIM. To ensure the realness of the simulation results output from VISSIM, the dynamics model of heavy-duty vehicles is calibrated by field test data of a heavy-duty vehicle called “Sinotruk HOWO”.

The proposed speed controller for heavy-duty vehicles is evaluated according to two factors: traffic-related factors, including the congestion level and market penetration rate (MPR) of controlled vehicles, and infrastructure-related factors, including the downhill gradient and curve radius. The measurements of effectiveness (MOEs) are the temperature of the brake drum, the yaw rate, lateral load transfer ratio and fuel consumption of the vehicle, and the throughput of high-risk roads. To calculate the fuel consumption of the vehicle more accurately, the evaluation adopts a well-accepted microscopic fuel consumption and emissions model called “VT-Micro” instead of the simple fuel consumption model used in the cost function [57]. The main attributes in the simulation are shown in

Table 1. Main attributes set in the simulation.

Category	Parameters	Value
Simulation platform	Length of approach section (m)	120
	Gradient of downhill road (%)	2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6
	Radius of curved road (m)	40, 45, 50, 55, 60, 65, 70
	Congestion level	0.3, 0.8
	MPR of connected vehicles	20, 30, 40, 50, 60, 70, 80
	Warming time of VISSIM (s)	120
Optimal controller for connected heavy-duty vehicles	Legal speed limit (km/h)	50
	Maximum acceleration (m/s2)	3.5
	Minimum acceleration (m/s2)	−4
	Maximum jerk (m/s2)	10
	Minimum jerk (m/s2)	0
	Pre-set headway (s)	5
	Weighting factors ($w_1,w_2,w_3,w_4,w_5,w_6$)	(1,10,100,100,100,1)
Predictor for conventional human-driven vehicles	Acceleration exponent	4
	Minimum desired net distance (m)	7
	Desired speed (km/h)	50
	Minimum speed (km/h)	0
	Safe time headway (s)	5
	Desired deceleration (m/s2)	−2.0

.

Two kinds of scenarios are simulated in this research: controlled scenarios and baseline scenarios. Each controlled scenario includes mixed traffic consisting of conventional human-driven vehicles and CHDVs. All heavy-duty vehicles have the same size, kinematics, and dynamics characteristics. The baseline scenario does not involve V2X communication, which means that all heavy-duty vehicles are operated by human beings with no assistance, including CHDVs and conventional human-driven vehicles. Each scenario is repeatedly simulated at least 30 times with various vehicle arrivals to eliminate the interference of benefits generated under certain traffic generation patterns and thereby ensure that the differences in the controlled and baseline scenarios are statistically significant. The before-and-after MOEs of the brake drum temperature, fuel consumption of the vehicle, and the throughput of the test roads are tested by a two-tailed paired t-test at a significance level of 0.05.

4.2. Simulation Results

The simulation results are illustrated in this section. All the results verify that the proposed speed control system achieves the expected control objectives. It effectively enhances driving safety and improves fuel efficiency for heavy-duty vehicles running on long–steep downhill and sharp-curved roads while minimizing adverse effects on traffic mobility.

4.2.1. Brake Stability

Figure 5a shows the brake thermal benefits of CHDVs under various levels of downhill gradients and MPRs of CHDVs. The proposed speed control system effectively decreases the brake temperature of the CHDVs when driving on downhill roads with different gradients. The thermal benefits of the braking system increase with the downhill gradient and reach their peak value when the gradient equals 3.5%. As shown in Figure 6, the temperature curves of the CHDVs in the controlled scenarios are much smoother than those in the baseline scenarios. The proposed control system effectively utilizes engine braking and reduces harsh braking maneuvers that would cause a sharp increase in brake temperature, thereby limiting the brake temperature below the maximum working temperature of 300 °C during the whole downhill process.

Figure 5b shows the brake thermal benefits of human-driven, heavy-duty vehicles (HD2V). Significant benefits can be observed under various downhill gradients and MPR levels, with a similar change trend to the brake thermal benefits of CHDVs. The peak benefit appears at a 4% gradient. This occurs because the CHDVs have effective impacts on the following HD2Vs through car-following behavior, just like the state-of-the-art eco-approach system under partially connected and automated vehicles environment [43]. The proposed speed control system can “indirectly” control the HD2Vs by optimizing the speed profiles of CHDVs. Since the HD2Vs can only achieve approximately optimal speed profiles, their brake thermal benefits are much lower than those of CHDVs.

In addition, the brake’s thermal benefits show a growing trend with the MPR of CHDVs. Significant thermal benefits can be generated as long as CHDVs are present. The upward trend levels off when the MPR of CHDVs reach 50%. This phenomenon could be because CHDVs have greater effects on following HD2Vs at a higher MPR level of CHDVs. The following HD2Vs have more similar speed trajectories to the preceding CHDVs as the MPR increases. In other words, the proposed speed control system can more effectively control the entire traffic under higher MPRs of CHDVs and are less affected by the stochastic human driving behaviors of conventional vehicles.

4.2.2. Lateral Stability

Figure 7 shows the lateral slip angles (LSAs) of CHDV wheels while cornering on sharp-curved roads with various radii. Here, the friction coefficient between the tires and road surface equals 0.4. On the left, the LSA curves, called “uncontrolled”, are taken from the simulation of CHDVs in the baseline scenarios without any assisting control. On the right, the LSA curves, called “controlled”, are collected from the simulation with the CHDVs running at the advised speed optimized by the proposed speed control system. The comparison between the uncontrolled and controlled LSA curves indicates that the proposed speed control system effectively reduces the lateral slip of all four wheels. The peak LSAs of the vehicle wheels in the controlled scenarios are limited below the maximum safe LSA of 2 deg/s. This performance can greatly decrease the understeer at the front wheels and the oversteer at the rear wheels. The proposed speed control system improves the yaw stability of the CHDVs and prevents these vehicles from becoming out of control on curved roads.

Figure 8 shows the lateral load transfer rate (LLTR) of CHDV wheels while cornering on sharp-curved roads with various radii; the friction coefficient between the tires and road surface equals 0.7. Overall, the LLTRs of all vehicle wheels in the controlled scenarios are much lower than those in the corresponding baseline scenarios. The LLTR of each wheel is in a safe range from −0.6 to 0.6. The proposed speed controller enhances the roll stability of CHDVs and prevents them from experiencing rollover accidents. However, compared with the vehicles in the baseline scenarios, the vehicles in the controlled scenarios spend more travel time driving through curved roads. This will have a certain adverse effect on the throughput of the curved roads under high traffic congestion levels. The reason for this phenomenon is that the roll stability is given a much higher weight than other factors in the cost function to ensure the priority of safety. This can be avoided by adjusting the weights of traffic mobility in the running cost function as described later in Section 4.2.4.

Figure 9 and Figure 10, respectively, show the LSAs and the LLTR of HD2V wheels in the controlled scenarios. Similar to the simulation results of the vehicles running on long–steep downhill roads, the proposed speed control system can “indirectly” inhibit the lateral slip and lateral roll motions of HD2Vs by optimizing the speed profiles of their preceding CHDVs. Comparing the simulation results under various congestion levels, the HD2V generates more similar lateral slip angle and load transfer rate curves to the CHDV under high congestion levels. This indicates that the proposed speed control system has a better control effect on the lateral stability of HD2Vs.

4.2.3. Fuel Economy

Figure 11, Figure 12 and Figure 13 show the average fuel consumption benefits of the vehicles running on long–steep downhill and sharp-curved roads. Significant fuel consumption benefits can be observed in various scenarios. These benefits first increase rapidly and then decrease gradually as the downhill gradient and curve radius increase. The peak benefits usually appear at a 4% downhill gradient and a 55-m curve radius. An excessively large downhill gradient and curve radius, respectively, lead to a frequent use of drum-brakes and minor changes in longitudinal speed, which means less difference between the optimized and baseline speed profiles.

Notably, the fuel consumption benefits on downhill roads are much lower than those on curved roads. This is because the engine braking used in the downhill process consumes little fuel in the baseline and controlled scenarios. The proposed speed control system can slightly decrease fuel consumption by increasing the usage of engine braking. Fuel savings primarily occur during the deceleration process on the approach sections and during the acceleration process on the departure sections, which can effectively optimize the usage of drum braking and engine power to reduce vehicle fuel consumption.

Moreover, the fuel consumption benefits increase with the MPR of CHDVs and reach a higher level when the MPR is greater than 40%. Due to the better “indirect” control effect of the proposed speed control system on HD2Vs, the fuel consumption benefits under high congestion levels are much greater than those under low congestion levels.

4.2.4. Mobility

Figure 14, Figure 15 and Figure 16 present the throughput of long–steep downhill and sharp-curved roads. No significant throughput benefits can be obtained for the downhill and curved road scenarios under a low congestion level. Some positive throughput benefits (the red area in Figure 14) are observed in the scenarios of downhill roads under low gradient levels. Significant negative throughput benefits (the blue areas in Figure 15 and Figure 16) were generated when the proposed speed control system was implemented on curved roads under high congestion levels and ranged up to 4.97%. This occurs because the CHDV slightly lowers its speed to prevent excessive sideslip and rollover, which significantly increases the travel time on the curved roads, as shown in the simulation results presented in Section 4.2.2.

However, this adverse effect is inevitable; thus, the most feasible strategy is to minimize it. Some existing control methods that attempt to enhance vehicle safety or reduce fuel consumption and emissions by substantially reducing vehicle speed can increase this adverse effect by up to 8.24% [43] or even more [53], such as some eco-driving controllers developed for individual vehicles without consideration of following traffic [43,58] and safety controllers with excessively low speed limits less than 40 km/h [53]. Compared with these methods, the proposed control system effectively inhibits the reduction of traffic mobility and balances safety enhancement, fuel efficiency improvement, and mobility optimization. In other words, the proposed control is nearly a “win-win” system that enhances safety and improves fuel efficiency while maintaining traffic mobility at an optimum level. This system also has strong robustness against the stochastic human driving behavior to be implemented in the real world in the near future.

5. Conclusions and Future Research

This research proposed a safe and ecological speed control system for long–steep downhill and sharp-curved roads under a partially connected vehicles environment. This speed control system effectively integrates the functions of existing speed controllers and overcomes their shortcomings, including (i) improving the thermal stability of brakes, the lateral slip and the roll stability, and the fuel efficiency while ensuring traffic mobility remains at a good level; (ii) being robust against random human-driven behavior to function in partially connected vehicles environment which means that this system is ready for implementation in the near future.

The evaluation results of the proposed speed control system showed the following:

(1)

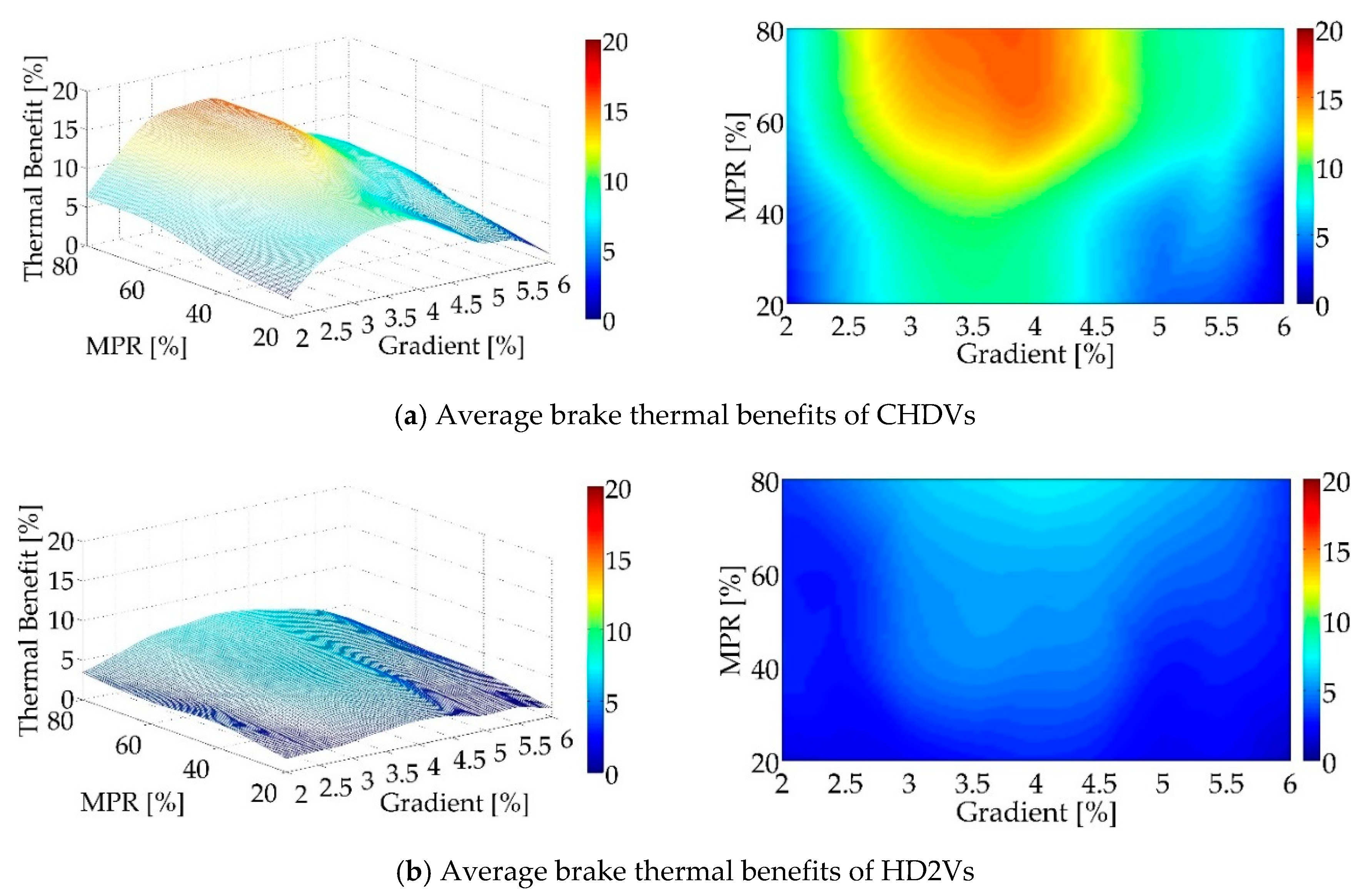
The brake thermal benefits of CHDVs range from 1.07% to 15.50%, and their brake drums maintain a safe temperature. The brake thermal benefits of HD2Vs range from 1.06% to 7.22%. These variations are caused by the MPR of CHDVs and the downhill gradient. The optimal gradient is 3.5%.

(2)

The lateral slip angles and the lateral load transfer rates of heavy-duty vehicles in controlled scenarios, including CHDVs and HD2Vs, are much lower than those in the baseline scenarios. The lateral slip angles and the lateral load transfer rates of the CHDVs in the controlled scenarios are within a safe range. The inhibition effect on the lateral slip angle and the lateral load transfer rate of the HD2Vs increase with the congestion level of road traffic.

(3)

The fuel consumption benefits range from 2.08% to 8.15% when the heavy-duty vehicles are driving on downhill roads and range from 1.34% to 15.49% on curved roads. These variations are caused by the MPR of CHDVs, the curve radius, and the congestion level. The benefits increase as the MPR of CHDVs and the congestion level increase.

(4)

Significant negative impacts on throughput by up to 4.97% were observed on curved roads, but this adverse effect of the proposed control system is at least 3.27% lower than that of most similar controllers without the consideration of all traffic and the stochastic driving behaviors of human-driven vehicles.

(5)

The brake thermal benefits, fuel consumption benefits, and control effects on the lateral slip and load transfer show increasing trends with the MPR of CHDVs. Significant benefits can be obtained as long as there are few CHDVs. Thus, the proposed speed control system has great feasibility for future implementation in the real world.

(6)

The fuel consumption benefits, control effects on lateral slip, and load transfer under high congestion levels are much greater that those under low congestion levels. The proposed control system offers better control over the entire traffic flow under high congestion levels.

(7)

The optimal downhill gradient for the proposed speed controller is 2.5~4.5%, and the optimal curve radius is 50~70 m. All benefits and control effects are at high levels under these conditions.

This research focused only on straight heavy-duty vehicles with all their axles attached to a single frame. The proposed speed control system is not applicable to vehicles with more complex dynamics characteristics. Future research could focus on semi-trailer trucks or tank trucks, which are the main tools for cargo transportation, and conducting a field test on the speed control systems to confirm their effectiveness in real contexts. Moreover, more advanced controllers for continuous multiple curved roads without sufficient approach room for vehicle speed adjustments should also be explored; these controllers would be more practical in road networks.