Sustainable Method Using Filtering Techniques for a Fermentation Process State Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Defining the System Structure of the Process
- (a)
- to use P, the product concentration, as the output variable (the concentration of ethylic alcohol);
- (b)
- or to use the released carbon dioxide concentration as the output variable.
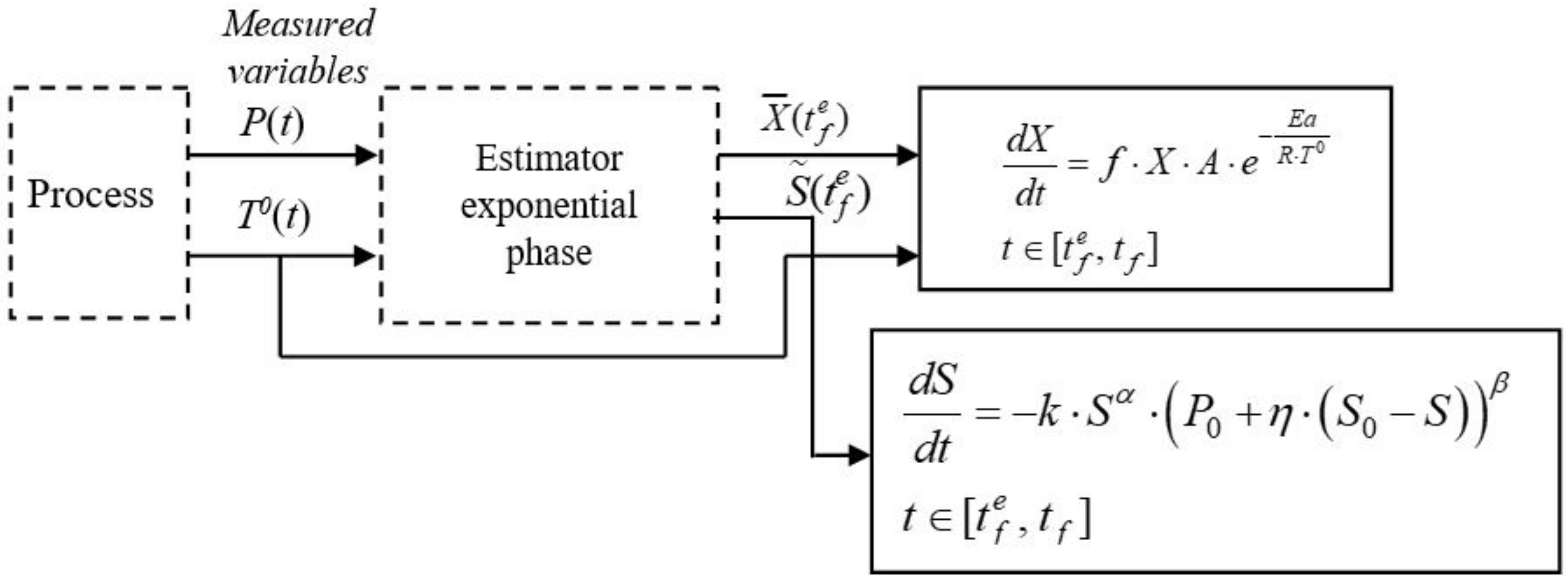
2.2. Developing the Extended Observer for State Estimation of the Exponential Growth Phase
2.3. Developing the EKF for State Estimation of the Exponential Growing Phase
2.3.1. First Variant of the EKF
2.3.2. Second Variant of the EKF
2.4. The State Estimation of the Decay Phase
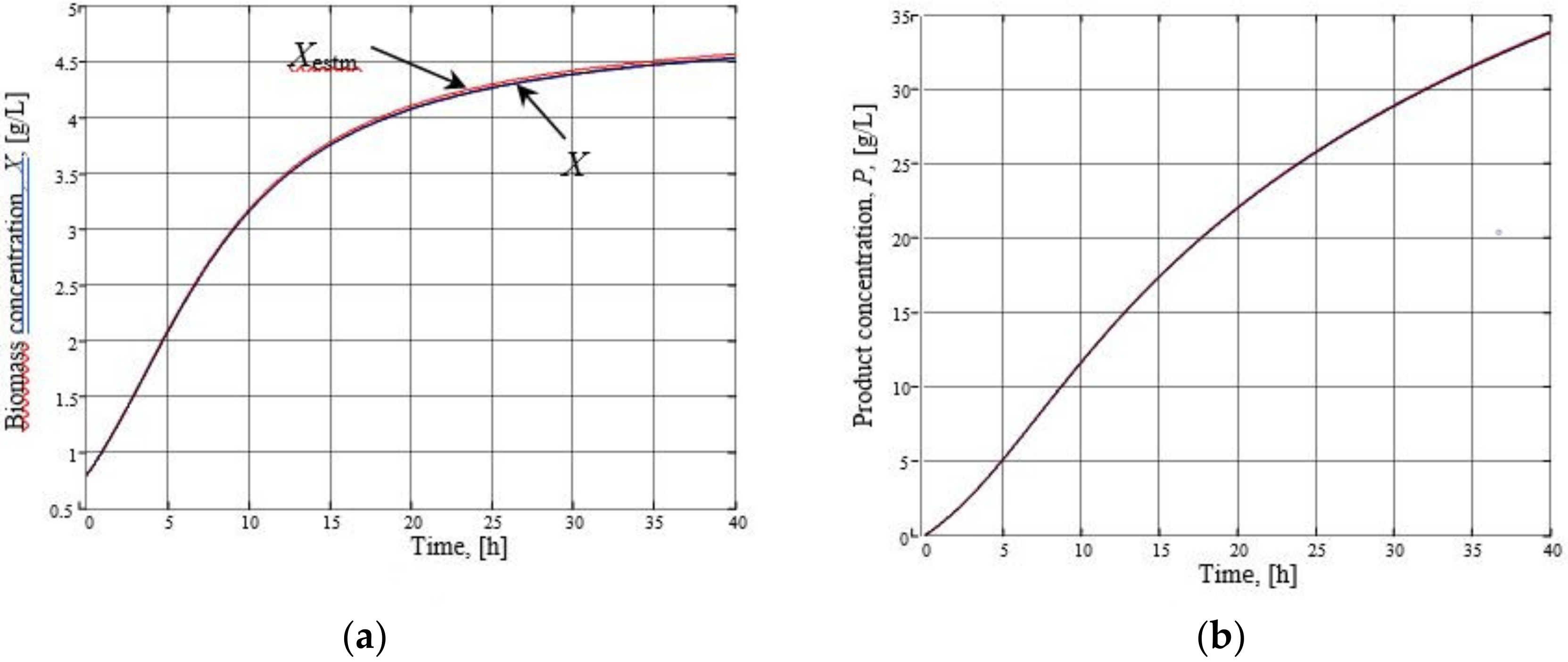
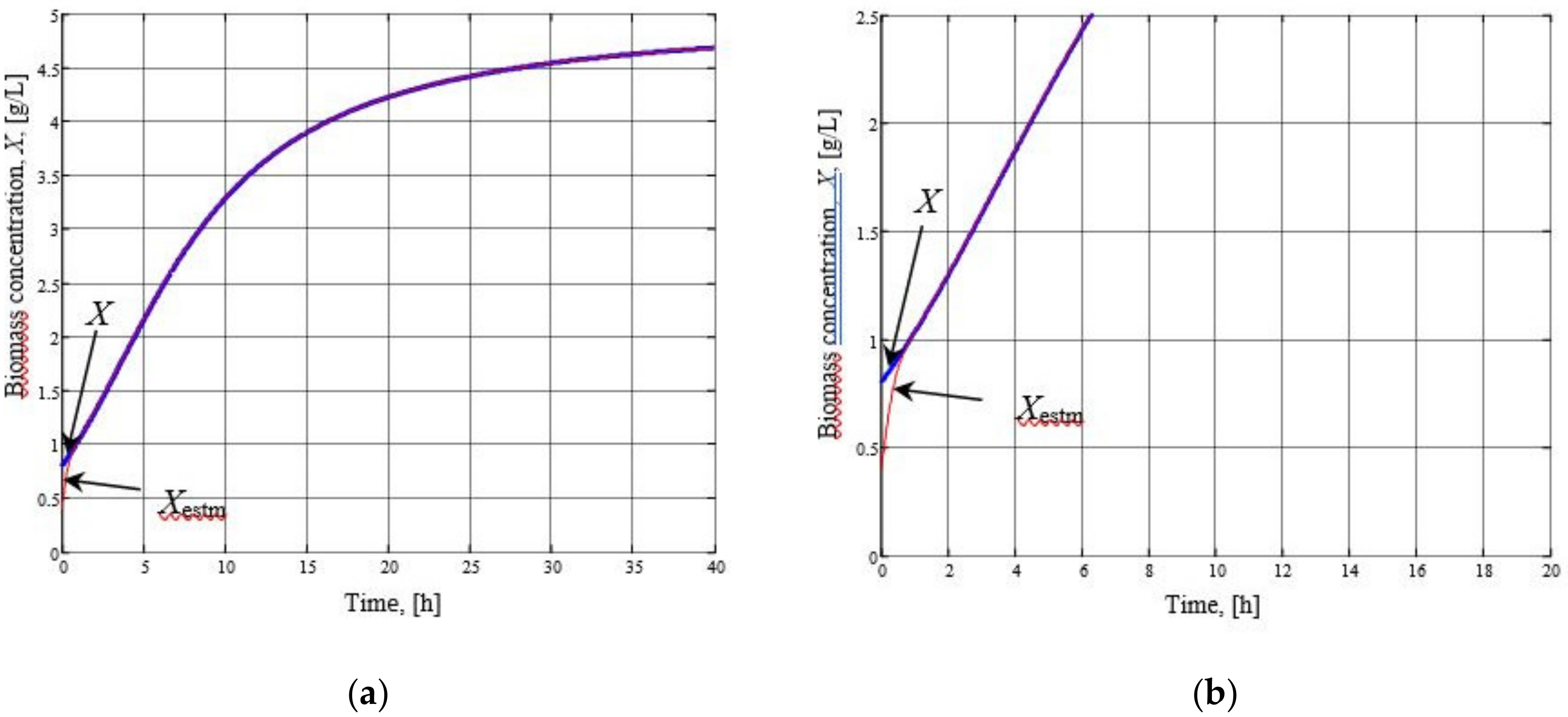
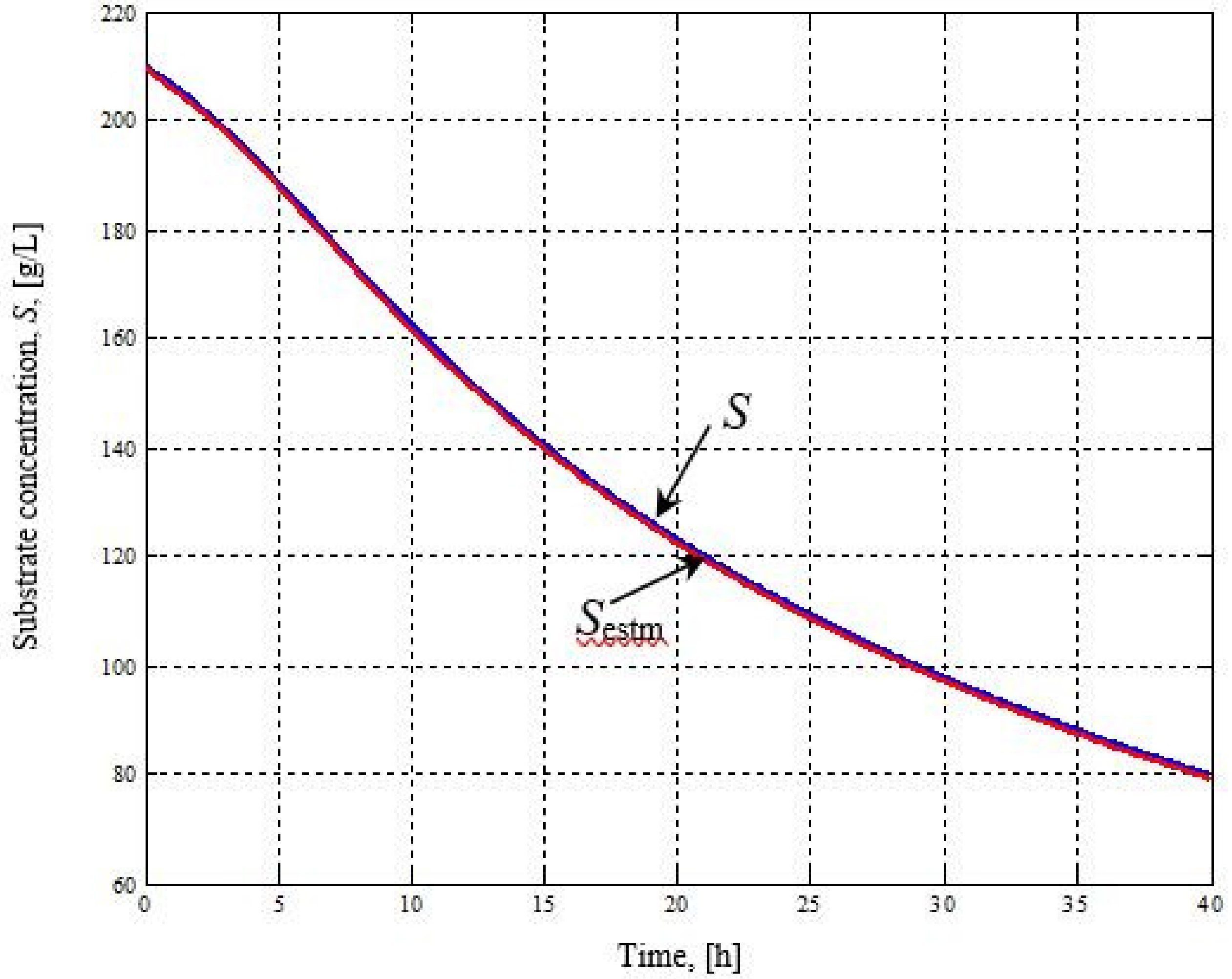
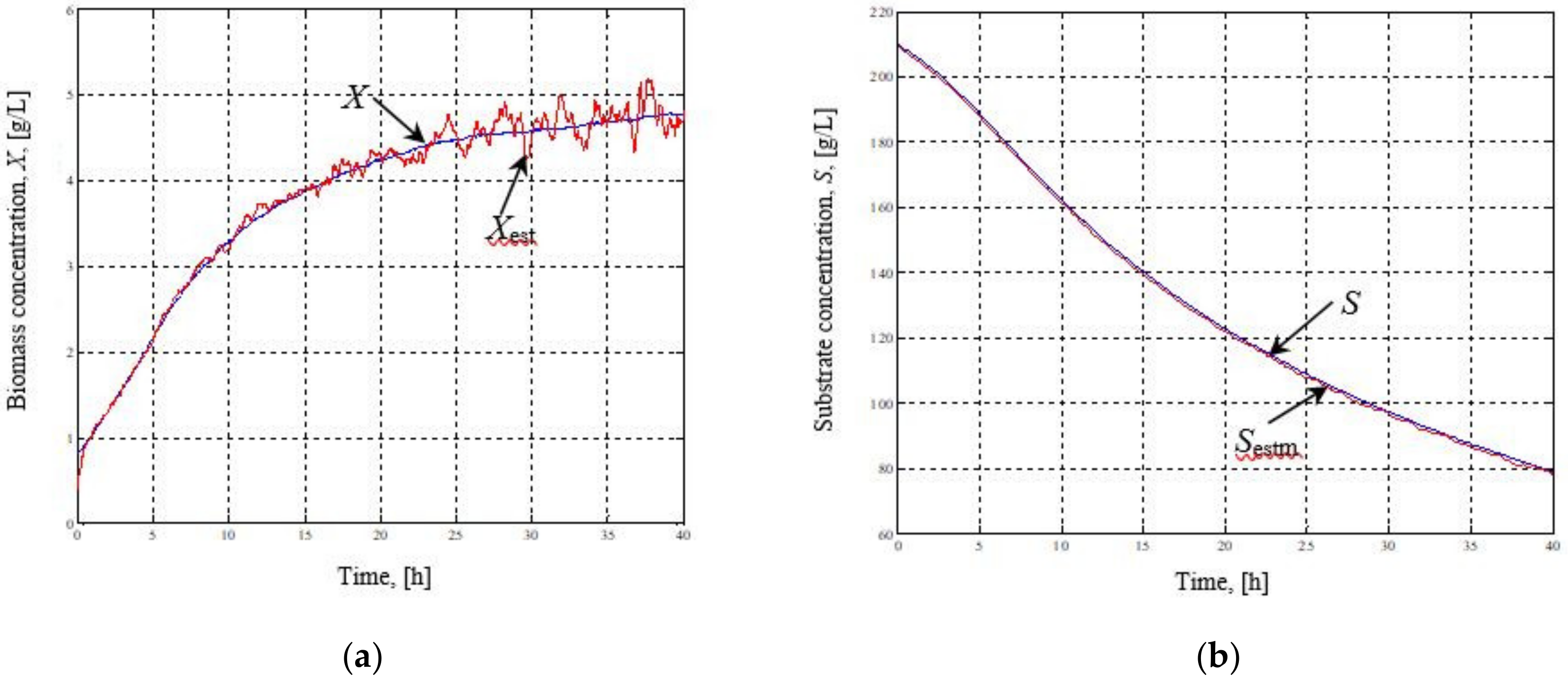
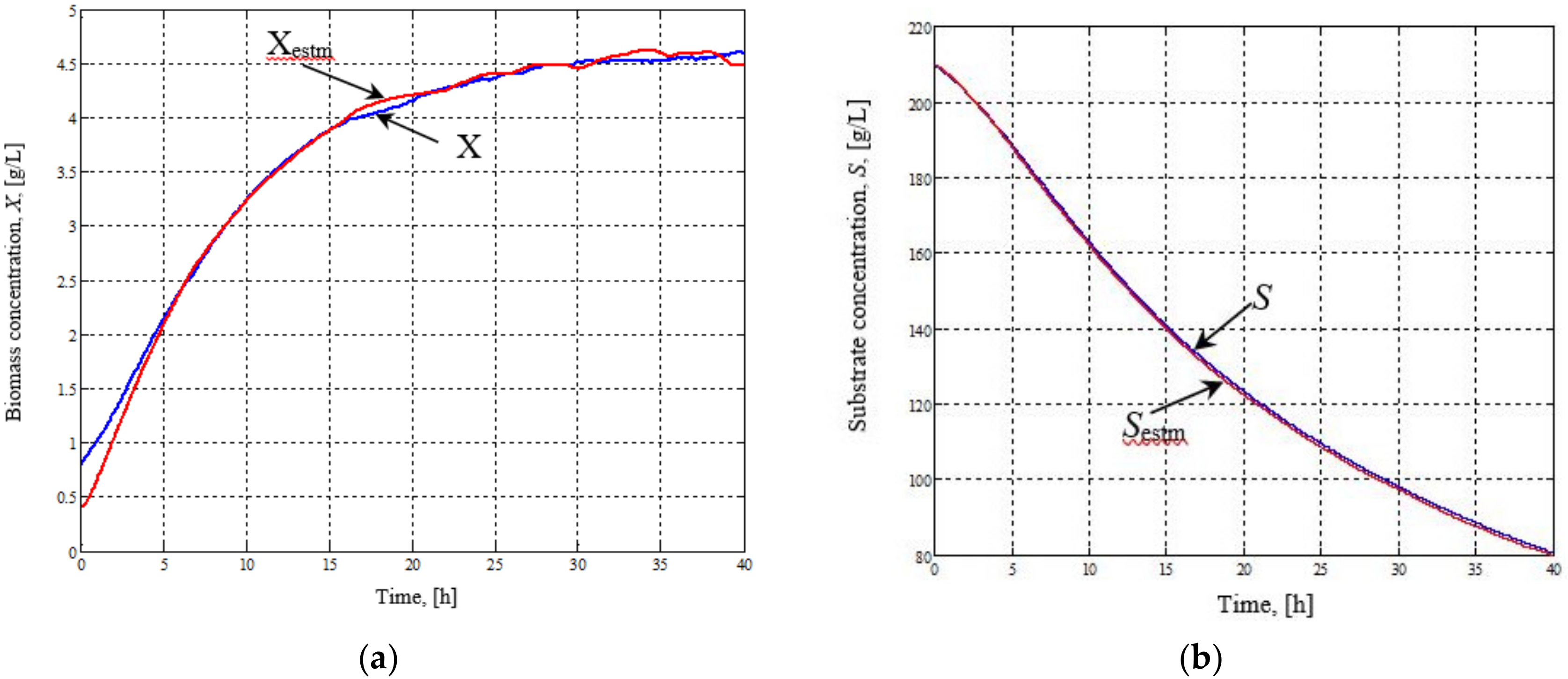
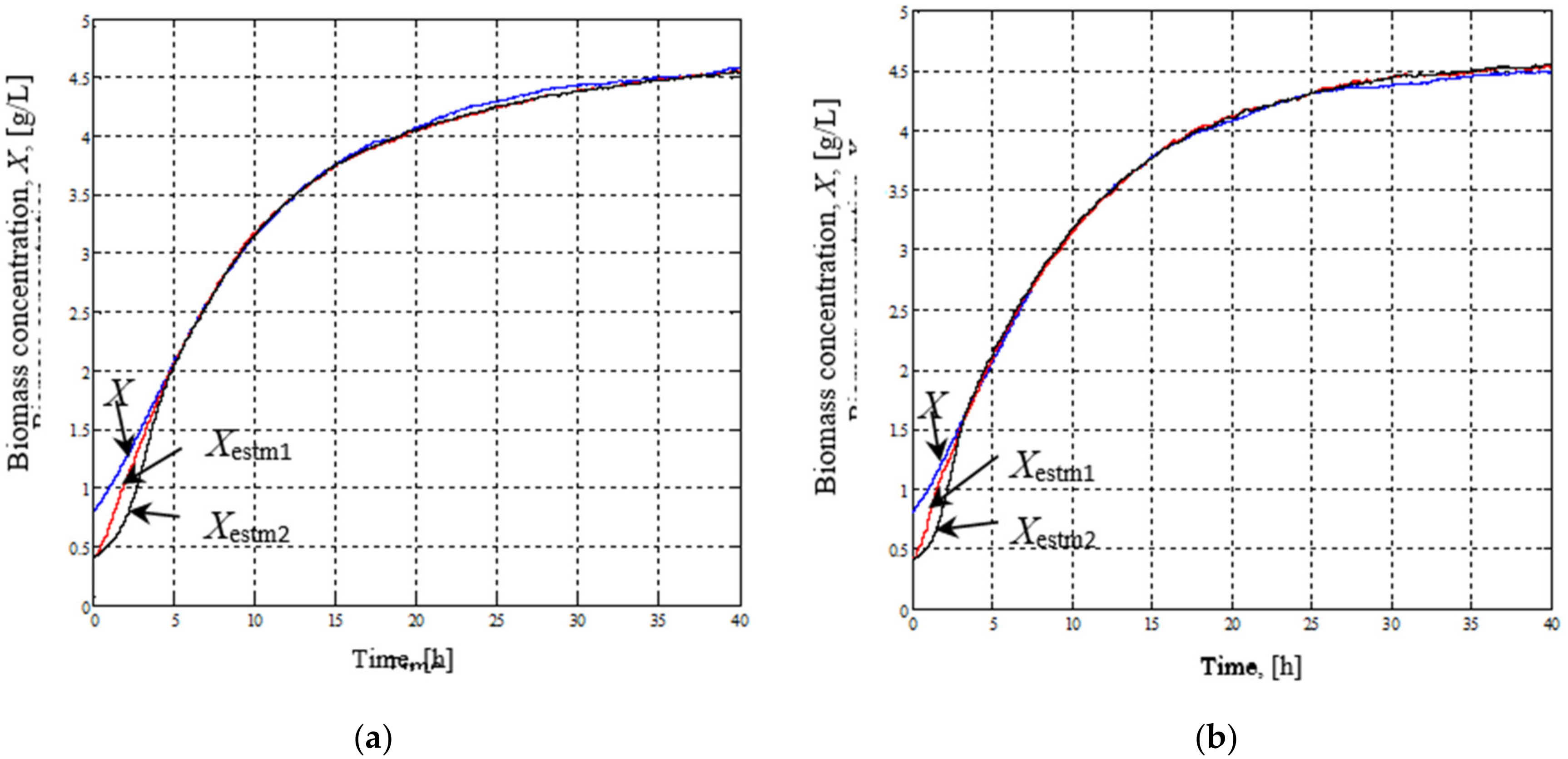
3. Results and Discussion
4. Conclusions
Funding
Conflicts of Interest
References
- Genc, M.; Genc, S.; Goksungur, Y. Exergy analysis of wine production: Red wine production process as a case study. Appl. Therm. Eng. 2017, 117, 511–521. [Google Scholar] [CrossRef]
- Schenka, C.; Schulzb, V.; Roschc, A.; von Wallbrunn, C. Less cooling energy in wine fermentation—A casestudy in mathematical modeling, simulation and optimization. Food Bioprod. Process. 2017, 103, 131–138. [Google Scholar] [CrossRef]
- Merli, R.; Preziosi, M.; Acampora, A. Sustainability experiences in the wine sector: Towards the development of an international indicators system. J. Clean. Prod. 2018, 172, 3791–3805. [Google Scholar] [CrossRef]
- Grumezescu, A.M.; Holban, A.M. Fermented Beverages; Woodhead Publishing: Sawston, UK, 2019. [Google Scholar]
- Mozell, M.R.; Thach, L. The impact of climate change on the global wine industry: Challenges & Solutions. Wine Econ. Policy 2014, 3, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Calicioglu, O.; Flammini, A.; Bracco, S.; Bellù, L.; Sims, R. The future challenges of food and agriculture: An integrated analysis of trends and solutions. Sustainability 2019, 11, 222. [Google Scholar] [CrossRef] [Green Version]
- Galati, M.; Galati, A.; Crescimanno, M.; Tinervia, S. The integration of quality and safety concerns in the wine industry: The role of third-party voluntary certifications. J. Clean. Prod. 2016, 112, 267–274. [Google Scholar] [CrossRef]
- Gilinsky, A.; Newton, S.K.; Vega, R.F. Sustainability in the Global Wine Industry: Concepts and Cases. Agric. Agric. Sci. Procedia 2016, 8, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Jose de Assis, A.; Filho, R.M. Soft sensors development for on-line bioreactor state estimation. Comp. Chem. Eng. 2000, 24, 1099–1103. [Google Scholar] [CrossRef]
- Marcin Błazejowski, M.; Kwiatkowski, J.; Gazda, J. Sources of economic growth: A global perspective. Sustainability 2019, 11, 275. [Google Scholar] [CrossRef] [Green Version]
- Şipoş, A. Current State and Perspective in the Models Applicable to Oenology. In Grapes and Wines—Advances in Production, Processing, Analysis and Valorization; Jordão, A.M., Cosme, F., Eds.; InTechOpen: Rijeka, Croatia, 2018; pp. 143–169. [Google Scholar] [CrossRef] [Green Version]
- Farza, M.; Hammouri, H.; Othman, S.; Busawon, K. Nonlinear observers for parameter estimation in bioprocesses. Chem. Eng. Sci. 1997, 52, 4251–4267. [Google Scholar] [CrossRef]
- Harms, P.; Kostov, Y.; Rao, G. Bioprocess monitoring. Curr. Opin. Biotechnol. 2002, 13, 124–127. [Google Scholar] [CrossRef]
- Kress-Rogers, E.; Brimelow, C.J.B. Instrumental measurements and sensory parameters. In Instrumentation and Sensors for the Food Industry, 2nd ed.; Woodhead Publishing Series in Food Science; Technology and Nutrition: Sawston, UK, 2001; pp. 31–60. [Google Scholar] [CrossRef]
- Ferreira, L.S.; De Souza, M.B., Jr.; Trierweiler, J.O.; Broxtermann, O.; Folly, R.O.M.; Hitzmann, B. Aspects concerning the use of biosensors for process control: Experimental and simulation investigations. Comp. Chem. Eng. 2003, 27, 1165–1173. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Chantzis, D.; Doukas, C.; Papacharalampopoulos, A.; Chryssolouris, G. Monitoring and Control of Manufacturing Processes: A Review. In Proceedings of the (CIRP CMMO) Procedia CIRP, 14th CIRP Conference on Modelling of Machining Operations, Turin, Italy, 13–14 June 2013; Volume 8, pp. 421–425. [Google Scholar]
- Ljung, L. Asymptotic behavior of the extended Kalman filter as a parameter estimator for linear systems. IEEE Trans. Autom. Control 1979, 24, 36–50. [Google Scholar] [CrossRef] [Green Version]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Proceedings of the SPIE 3068 Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 28 July 1997. [Google Scholar] [CrossRef]
- Barbu, M. Conducerea Automată a Proceselor Biotehnologice; Editura Galati University Press: Galati, Romania, 2009; pp. 134–140. [Google Scholar]
- Athanasopoulou, L.; Papacharalampopoulos, A.; Stavropoulos, P. Context awareness system in the use phase of a smart mobility platform: A vision system for a light-weight approach. Proc. CIRP 2020, 88, 560–564. [Google Scholar] [CrossRef]
- Sipos, A.; Agachi, P.S.; Meyer, X.M.; Strehaiano, P. Batch fermentation process: Modeling and direct sensitivity analysis. Acta Aliment Hung 2010, 39, 222–233. [Google Scholar] [CrossRef] [Green Version]

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sipos, A. Sustainable Method Using Filtering Techniques for a Fermentation Process State Estimation. Sustainability 2020, 12, 7105. https://doi.org/10.3390/su12177105
Sipos A. Sustainable Method Using Filtering Techniques for a Fermentation Process State Estimation. Sustainability. 2020; 12(17):7105. https://doi.org/10.3390/su12177105
Chicago/Turabian StyleSipos, Anca. 2020. "Sustainable Method Using Filtering Techniques for a Fermentation Process State Estimation" Sustainability 12, no. 17: 7105. https://doi.org/10.3390/su12177105
APA StyleSipos, A. (2020). Sustainable Method Using Filtering Techniques for a Fermentation Process State Estimation. Sustainability, 12(17), 7105. https://doi.org/10.3390/su12177105




