Fuzzy Approach for the Decision on Disposable or Returnable Packaging
Abstract
:1. Introduction
2. Materials (Fuzzy Signatures)
Aggregation of Fuzzy Signatures
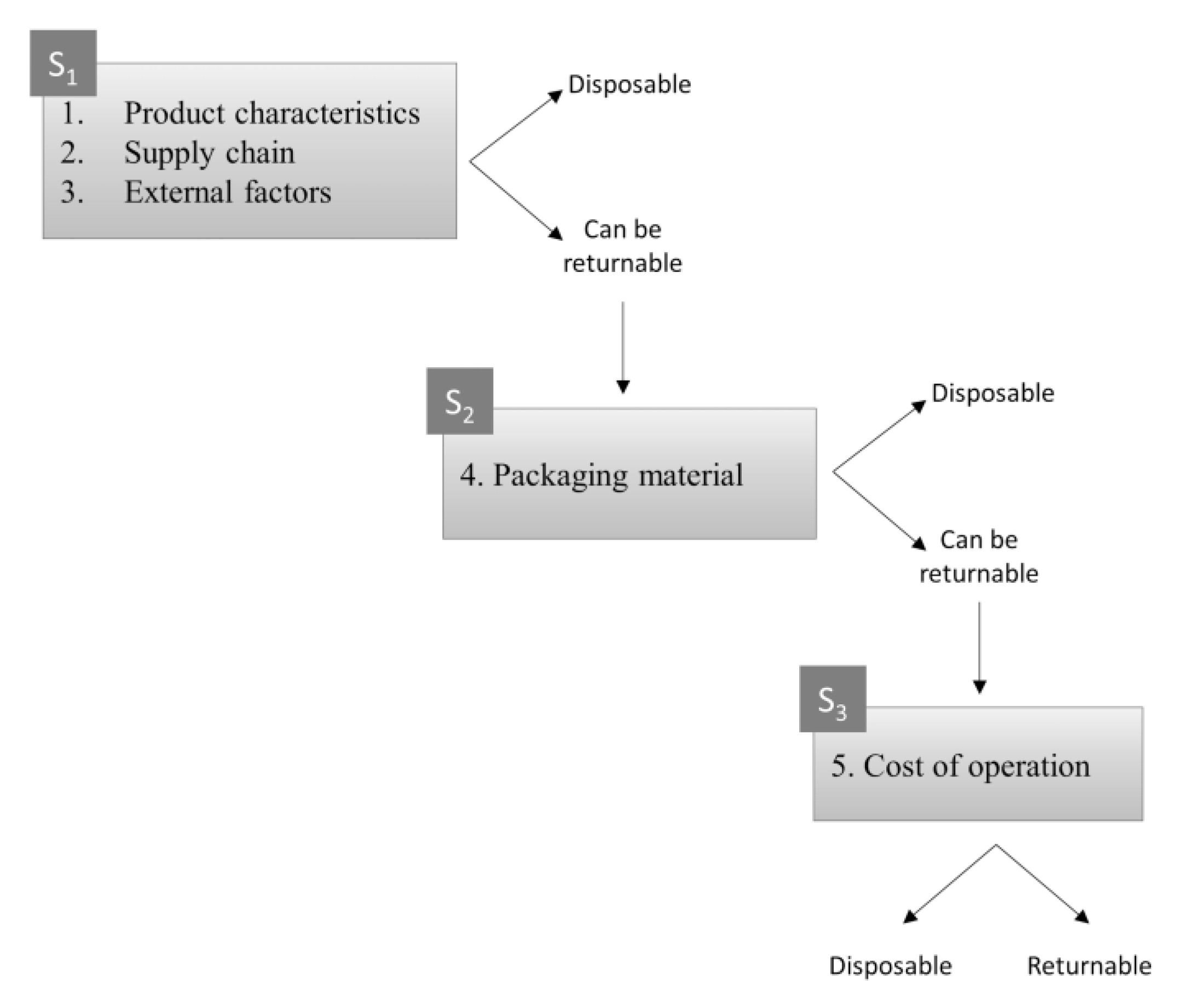
3. Methods (Framework for Packaging Decision)
- Characteristics of the product to be packaged;
- Characteristics of the supply chain; and,
- External factors.
- 4.
- Characteristics of the packaging material and device.
- 5.
- Operation cost of given packaging system.
| R: | S1: | ifµS1 ≥ 0.5 then check S2 else one-way |
| S2: | ifµS1 ≥ 0.5 and µS2 ≥ 0.5 then check S3 else one-way | |
| S3: | ifµS1 ≥ 0.5 and µS2 ≥ 0.5 and µS3 ≥ 0.5 then returnable else one-way. |
3.1. Aggregation Operators
3.2. Main Aspects and the Weights
3.3. Product Characteristics
3.4. Supply Chain (Logistics) Characteristics
3.5. External Factors
3.6. Packaging Material and Device
3.7. Cost of Operation
4. Algorithm of Program
- It must be an aggregation if the line is not beginning with a hyphen. This is a root node. Only one root node is permitted. The line starts with “a”—the letter followed by the identity number of the node, an under-score character, and the aggregation type (in this case AWA), respectively. Naturally, the weight parameter is only permitted when the node has an AWA-type parent.
- Every other line must begin with hyphens. At the root node, there are no hyphens. When a line actually begins with n number of hyphens, its child should start with n+1 number of hyphens. Characters following the hyphens:
- ○
- Aggregation is “a” with the identity number for the given node, underscore, AWA, space character, “weight_”, and a float number.
- ○
- Fuzzy membership function is “u” (like μ) with the identity number for the node, coordinates, the “question” to answer the function, and the weight parameter (in case of AWA aggregation). Coordinates for instance are:
- 0H328.56 → x = 328.56, y = 0.00
- 1H328.56 → x = 328.56, y = 1.00
- FH328.56 → x = 328.56, y = 0.50
- ⁃
- a0_AWA
- ⁃
- -a1_AWA weight_3.0
- ⁃
- --u11 0H50.0 1H25000.0 ?20000.0 weight_9.0
- ⁃
- --u12 0H0.0 1H300.0 ?120.0 weight_9.0
- ⁃
- --a13_AWA weight_7.0
- ⁃
- ---u131 0H0.0 1H2.0 0H10.0 ?1.2 weight_4.0
- ⁃
- ---u132 0H0.0 1H1.0 0H10.0 ?2.2 weight_1.0
- ⁃
- ---u133 0H0.0 1H1000.0 1H2000.0 0H3000.0 ?500.0 weight_1.0
5. Results and Discussion
5.1. Case Study 1
5.2. Case Study 2
5.3. Limitations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Not Important | Very Important | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. Product characteristics | 1 | 2 | X | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1.1 Batch size | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | X | 10 | ||
| 1.2 Turnover | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | X | 10 | ||
| 1.3 Geometrical characteristics | 1 | 2 | 3 | 4 | 5 | 6 | X | 8 | 9 | 10 | ||
| 1.3.1 Shape | 1 | 2 | 3 | X | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1.3.2 Size | X | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1.3.3 Weight | X | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1.4 Sensitivity | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1.4.1 Physical | 1 | 2 | 3 | 4 | 5 | X | 7 | 8 | 9 | 10 | ||
| 1.4.1.1 Mechanical | 1 | 2 | 3 | 4 | 5 | X | 7 | 8 | 9 | 10 | ||
| 1.4.1.2 Climate | 1 | 2 | 3 | X | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1.4.2 Biological | 1 | 2 | X | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1.4.3 Chemical | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1.5 Value | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 2. Supply chain characteristics | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | X | 10 | ||
| 2.1 Transportation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 2.1.1 Distance | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 2.1.2 Volume | 1 | 2 | 3 | 4 | 5 | 6 | X | 8 | 9 | 10 | ||
| 2.1.3 Environmental impacts | 1 | 2 | 3 | 4 | X | 6 | 7 | 8 | 9 | 10 | ||
| 2.1.3.1 Temperature | 1 | 2 | 3 | X | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 2.1.3.2 Vibration | 1 | 2 | X | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 2.1.3.3 Humidity | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 2.1.4 Infrastructure | 1 | 2 | X | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 2.1.5 Modality | X | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 2.2 IT support | 1 | 2 | 3 | 4 | 5 | 6 | X | 8 | 9 | 10 | ||
| 2.3 Material handling | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 2.3.1 Transshipment | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 2.3.2 FTL/LTL | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 3. External factors | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 3.1 Cooperation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 3.2 Regulations | 1 | 2 | X | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 3.2.1 Environmental | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 3.2.2 Health | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 3.2.3 Benefits | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 3.2.4 Standards | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 3.3 Legal | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 3.4 Environmental effects | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 3.4.1 Production related | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | ||
| 3.4.1.1 Raw material | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | X | ||
| 3.4.1.2 Energy | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 3.4.2 CO2 emission | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 3.4.3 Pool size | 1 | 2 | 3 | 4 | 5 | 6 | X | 8 | 9 | 10 | ||
| 3.4.5 Vehicle utilization | 1 | 2 | 3 | 4 | X | 6 | 7 | 8 | 9 | 10 | ||
| 4. Packaging material | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 4.1 Used material | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | X | 10 | ||
| 4.1.1 Robustness | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 4.1.2 Availability | 1 | 2 | 3 | 4 | 5 | 6 | X | 8 | 9 | 10 | ||
| 4.1.3 Recyclability | 1 | 2 | 3 | X | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 4.1.4 Reusability | 1 | 2 | 3 | X | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 4.1.5 Tare weight | 1 | X | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 4.2 Packaging fill rate | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 4.3 Number of uses | 1 | 2 | 3 | 4 | 5 | 6 | X | 8 | 9 | 10 | ||
| 4.4 Collapsibility | 1 | 2 | 3 | 4 | 5 | 6 | X | 8 | 9 | 10 | ||
| 5. Cost of operation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | X | 9 | 10 | ||
| 5.1 Packaging material | 1 | 2 | 3 | 4 | X | 6 | 7 | 8 | 9 | 10 | ||
| 5.2 Disposal | 1 | 2 | 3 | 4 | X | 6 | 7 | 8 | 9 | 10 | ||
| 5.3 Capital asset | 1 | 2 | 3 | 4 | X | 6 | 7 | 8 | 9 | 10 | ||
| 5.4 Cleaning and maintenance | 1 | 2 | 3 | 4 | X | 6 | 7 | 8 | 9 | 10 | ||
| 5.5 Storage | 1 | 2 | 3 | 4 | X | 6 | 7 | 8 | 9 | 10 | ||
| 5.6 Administration | 1 | 2 | 3 | 4 | X | 6 | 7 | 8 | 9 | 10 | ||
Appendix B
| Type of Membership Function for Component | Wooden Crate | PET Bottle | ||
|---|---|---|---|---|
| Membership Value | Calculated Value by Aggregation | Membership Value | Calculated Value by Aggregation | |
| Product characteristics (a1121) | 0.656461 | 0.454869 | ||
| Batch size (µ11211), Trapezoidal | 0.799599 | 1 | ||
| Turnover (µ11212), Trapezoidal | 0.4 | 0.2 | ||
| Geometrical characteristics (a11213) | 0.627778 | 0.00116717 | ||
| Shape (µ112131), Triangular | 0.6 | 0.001 | ||
| Size (µ112132), Triangular | 0.866667 | 0.003 | ||
| Weight (µ112133), Trapezoidal | 0.5 | 0.000003 | ||
| Sensitivity (a11214) | 0.923273 | 0.191515 | ||
| Physical (a112141) | 0.922667 | 0.351111 | ||
| Mechanical (µ1121411), Trapezoidal | 0.977778 | 0.518519 | ||
| Climate (µ1121412), Triangular | 0.84 | 0.1 | ||
| Biological (µ112142), Triangular | 0.9 | 0 | ||
| Chemical (µ112143), Triangular | 0.96 | 0 | ||
| Value (µ11215), Trapezoidal | 1 | 0 | ||
| Supply chain characteristics (a1122) | 0.587906 | 0.579394 | ||
| Transportation (a11221) | 0.3093 | 0.82407 | ||
| Distance (µ112211), Triangular | 0.1 | 0.98 | ||
| Volume (µ112212), Trapezoidal | 0.1 | 0.9 | ||
| Environmental impacts (a112213) | 0.724638 | 0.327536 | ||
| Temperature (µ1122131), Trapezoidal | 0.630435 | 0.586957 | ||
| Vibration (µ1122132), Triangular | 0.8 | 0.2 | ||
| Humidity (µ1122133), Triangular | 0.8 | 0 | ||
| Infrastructure (µ112214), Triangular | 0.6 | 1 | ||
| Modality (µ112215), Trapezoidal | 0.5 | 1 | ||
| IT support (µ11222), Triangular | 0.8 | 0.4 | ||
| Material handling (a11223) | 0.96 | 0.228571 | ||
| Transshipment (µ112231), Trapezoidal | 1 | 0.285714 | ||
| FTL/LTL (µ112232), Triangular | 0.8 | 0 | ||
| External factors (a1123) | 0.632284 | 0.347161 | ||
| Cooperation (µ11231), Triangular | 0.6 | 0.2 | ||
| Regulations (a11232) | 0.575 | 0.533333 | ||
| Environmental (µ112321), Triangular | 0.8 | 0.6 | ||
| Health (µ112322), Triangular | 0.5 | 0.333333 | ||
| Benefits (µ112323), Triangular | 0.6 | 0.4 | ||
| Standards (µ112324), Triangular | 0.4 | 0.8 | ||
| Legal (µ11233), Triangular | 0.575 | 0.4 | ||
| Environmental effects (a11234) | 0.87963 | 0.603704 | ||
| Production related (a112341) | 0.888889 | 0.511111 | ||
| Raw material (µ1123411), Triangular | 0.8 | 0.6 | ||
| Energy (µ1123412), Triangular | 1 | 0.4 | ||
| CO2 emission (µ112342), Trapezoidal | 1 | 1 | ||
| Pool size (µ112343), Trapezoidal | 1 | 0.285714 | ||
| Vehicle utilized. (µ112344), Triangular | 0.5 | 0.6 | ||
| Packaging material (a111) | 0.842069 | 0.481103 | ||
| Used material (a1111) | 0.69 | 0.344 | ||
| Robustness (µ11111), Triangular | 1 | 0.8 | ||
| Availability (µ11112), Trapezoidal | 0.75 | 0 | ||
| Recyclability (µ11113), Triangular | 0.6 | 0 | ||
| Reusability (µ11114), Triangular | 0.25 | 0.5 | ||
| Tare weight (µ11115), Trapezoidal | 0.3 | 0.1 | ||
| Packaging fill rate (µ1112), Triangular | 0.7 | 0.9 | ||
| Number of uses (µ1113), Trapezoidal | 1 | 0.7 | ||
| Collapsibility (µ1114), Trapezoidal | 1 | 0 | ||
| Cost of operation (a12) | 0.533333 | - | ||
| Packaging material (µ121), Triangular | 0.6 | - | ||
| Disposal (µ122), Triangular | 0.8 | - | ||
| Capital asset (µ123), Triangular | 0.2 | - | ||
| Cleaning and maintenance (µ124), Triangular | 0.6 | - | ||
| Storage (µ125), Triangular | 0.6 | - | ||
| Administration (µ126), Triangular | 0.4 | - | ||
Appendix C
| Input | Membership Function/Aggregation | Membership Value | Weights |
|---|---|---|---|
| µ112211 µ112212 a112213 µ112214 µ112215 | AWA | a11221 = 0.3093 | 8 |
| x112211 = 9000 |  | µ112211 = 0.1 | 8 |
| x112212 = 10 |  | µ112212 = 0.1 | 7 |
| µ1122131 µ1122132 µ1122133 | AWA | a112213 = 0.724638 | 5 |
| x1122131 = 40 | 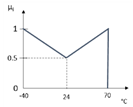 | µ1122131 = 0.630435 | 4 |
| x1122132 = 8 | 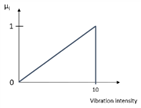 | µ1122132 = 0.8 | 3 |
| x1122133 = 80 | 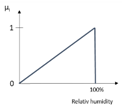 | µ1122133 = 0.8 | 2 |
| x112214 = 3 |  | µ112214 = 0.6 | 3 |
| x112215 = 4 | 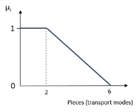 | µ112215 = 0.5 | 1 |
References
- Stock, J.R.; Lambert, D.M. Strategic Logistics Management; McGraw-Hill Higher Education: New York, NY, USA, 2001. [Google Scholar]
- Smith, A.D. Green Supply Chain Management and consumer sensitivity to greener and leaner options in the automotive industry. Int. J. Logist. Syst. Manag. 2012, 12, 1–31. [Google Scholar] [CrossRef]
- Na, B.; Sim, M.K.; Lee, W.J. Optimal Purchase Decision of Reusable Packaging in the Automotive Industry. Sustainability 2019, 11, 6579. [Google Scholar] [CrossRef] [Green Version]
- Böröcz, P.; Földesi, P. The application of the game theory onto the analysis of the decision theory of logistic packagings. Acta Tech. Jaurinensis 2008, 1, 259–268. Available online: https://acta.sze.hu/index.php/acta/article/view/119 (accessed on 21 October 2019).
- Dubiel, M. Costing Structure of Reusable Packaging Systems. Packag. Technol. Sci. 1996, 9, 237–254. [Google Scholar] [CrossRef]
- Yam, K.L. The Wiley Encyclopedia of Packaging Technology; John Wiley & Sons: New York, NY, USA, 2010; pp. 387–389. [Google Scholar] [CrossRef]
- European Parliament and the Council of the European Union. Directive (EU) 2018/852 of the European Parliament and of the Council of 30 May 2018 Amending Directive 94/62/EC on Packaging and Packaging Waste (Text with EEA Relevance). 2018. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32018L0852&from=EN (accessed on 17 August 2020).
- Nordin, N.; Selke, S. Social aspect of sustainable packaging. Packag. Technol. Sci. 2010, 23, 317–326. [Google Scholar] [CrossRef]
- Pålsson, H.; Finnsgård, C.; Wänström, C. Selection of packaging systems in supply chains from a sustainability perspective–the case of Volvo. Packag. Technol. Sci. 2013, 26, 289–310. [Google Scholar] [CrossRef]
- Sonneveld, K. The Role of Life Cycle Assessment as a Decision Support Tool for Packaging. Packag. Technol. Sci. 2000, 13, 55–61. [Google Scholar] [CrossRef]
- Early, C.; Kidman, T.; Menvielle, M.; Geyer, R.; McMullan, R. Informing packaging design decisions at Toyota motor sales using life cycle assessment and costing. J. Ind. Ecol. 2009, 13, 592–606. [Google Scholar] [CrossRef]
- Carrano, A.L.; Pazour, J.A.; Roy, D.; Thorn, B.K. Selection of pallet management strategies based on carbon emissions impact. Int. J. Prod. Econ. 2015, 164, 258–270. [Google Scholar] [CrossRef]
- Wohner, B.; Gabriel, V.H.; Krenn, B.; Krauter, V.; Tacker, M. Environmental and economic assessment of food-packaging systems with a focus on food waste. Case study on tomato ketchup. Sci. Total Environ. 2020, 738, 139846. [Google Scholar] [CrossRef]
- Niero, M.; Kalbar, P. Coupling material circularity indicators and life cycle based indicators: A proposal to advance the assessment of circular economy strategies at the product level. Resour. Conserv. Recycl. 2019, 140, 305–312. [Google Scholar] [CrossRef]
- Witt, C.E. Reusable distribution packaging saves money. Mater. Handl. Eng. 1993, 48, 14. [Google Scholar]
- Turki, S.; Didukh, S.; Sauvey, C.; Rezg, N. Optimization and Analysis of a Manufacturing–Remanufacturing–Transport–Warehousing System within a Closed-Loop Supply Chain. Sustainability 2017, 9, 561. [Google Scholar] [CrossRef] [Green Version]
- Grimes-Casey, H.G.; Seager, T.P.; Theis, T.L.; Powers, S.E. A game theory framework for cooperative management of refillable and disposable bottle life-cycles. J. Clean. Prod. 2007, 5, 1618–1627. [Google Scholar] [CrossRef]
- Mollenkopf, D.; Closs, D.; Twede, D.; Lee, S.; Burgess, G. Assessing the viability of reusable packaging: A relative cost approach. J. Bus. Logist. 2005, 26, 169–197. [Google Scholar] [CrossRef]
- Guo, D.; He, Y.; Wu, Y.; Xu, Q. Analysis of Supply Chain under Different Subsidy Policies of the Government. Sustainability 2016, 8, 1290. [Google Scholar] [CrossRef] [Green Version]
- Menesatti, P.; Canali, E.; Sperandio, G.; Burchi, G.; Devlin, G.; Costa, C. Cost and waste comparison of reusable and disposable shipping containers for cut flowers. Packag. Technol. Sci. 2012, 25, 203–215. [Google Scholar] [CrossRef]
- Braglia, M.; Frosolini, M.; Montanari, R. Fuzzy logic controller in a packaging plant. Packag. Technol. Sci. 2003, 16, 21–35. [Google Scholar] [CrossRef]
- Braglia, M. Designing a belt conveyor controller in a bottling plant using fuzzy logic and genetic algorithms. Packag. Technol. Sci. 2002, 14, 231–248. [Google Scholar] [CrossRef]
- Kang, Y.; Li, J. Green Rationality Evaluation of Degradable Packaging Based on LCA and Fuzzy AHP. In Proceedings of the IEEE 17Th International Conference on Industrial Engineering and Engineering Management, Xiamen, China, 29–31 October 2010; pp. 329–332. [Google Scholar] [CrossRef]
- Lozano-Olvera, G.; Ojeda-Benitez, S.; Castro, J.R.; Bravo-Zanoguera, M.; Rodriguez-Diaz, A. Identification of waste packaging profiles using fuzzy logic. Resour. Conserv. Recycl. 2008, 52, 1022–1030. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Kóczy, L.T.; Tikk, D. Fuzzy Systems; Typotex: Budapest, Hungary, 2001. [Google Scholar]
- Tamás, K.; Kóczy, L.T. Inference in fuzzy signature based models. Acta Tech. Jaurinensis 2008, 1, 573–594. [Google Scholar]
- Dubois, D.; Prade, H. Possibility Theory, Probability Theory and Multiple-valued Logics: A Clarification. Ann. Math. Artif. Intell. 2001, 32, 35–66. [Google Scholar] [CrossRef]
- Hwang, C.L.; Lai, Y.J.; Liu, T.Y. A new approach for multiple objective decision making. Comput. Oper. Res. 1993, 20, 889–899. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Zakarevicius, A.; Antucheviciene, J. Evaluation of Ranking Accuracy in Multi-Criteria Decisions. Informatica 2006, 17, 601–618. [Google Scholar] [CrossRef]
- Gogen, J.A. L-fuzzy Sets. J. Math. Anal. Appl. 1967, 18, 145–174. [Google Scholar] [CrossRef] [Green Version]
- Karnik, N.N.; Mendel, J.M. Operations on Type-2 Fuzzy Sets. Fuzzy Sets Syst. 2001, 122, 327–348. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Kóczy, L.T. Vectorial I-fuzzy set. In Approximate Reasoning in Decision Analysis; Gupta, M.M., Sanchez, E., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands; Oxford: New York, NY, USA, 1982; pp. 151–156. [Google Scholar]
- Kóczy, L.T.; Vámos, T.; Biró, G. Fuzzy signatures. In Proceedings of the Eurofuse-SIC’99, Budapest, Hungary, 25–28 May 1999. [Google Scholar]
- Kóczy, L.; Purvinis, O.; Susniene, D. Some considerations on data mining from questionnaires by constructing fuzzy signatures based on factor analysis. J. Intell. Fuzzy Syst. 2019, 36, 3739–3749. [Google Scholar] [CrossRef]
- Mendis, B.S.U.; Gedeon, T.D.; Kóczy, L.T. Investigation of aggregation in fuzzy signatures. In Proceedings of the 3rd International Conference on Computational Intelligence, Robotics and Autonomous Systems, Singapore, Singapore, 14 December 2005; Volume 406. [Google Scholar]
- Gedeon, T.D.; Wong, K.W.; Tikk, D. Constructing Hierarchical Fuzzy Rule Bases for Classification. In Proceedings of the 10th IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2001), Melbourne, Victoria, Australia, 2–5 December 2001; pp. 1388–1391. [Google Scholar]



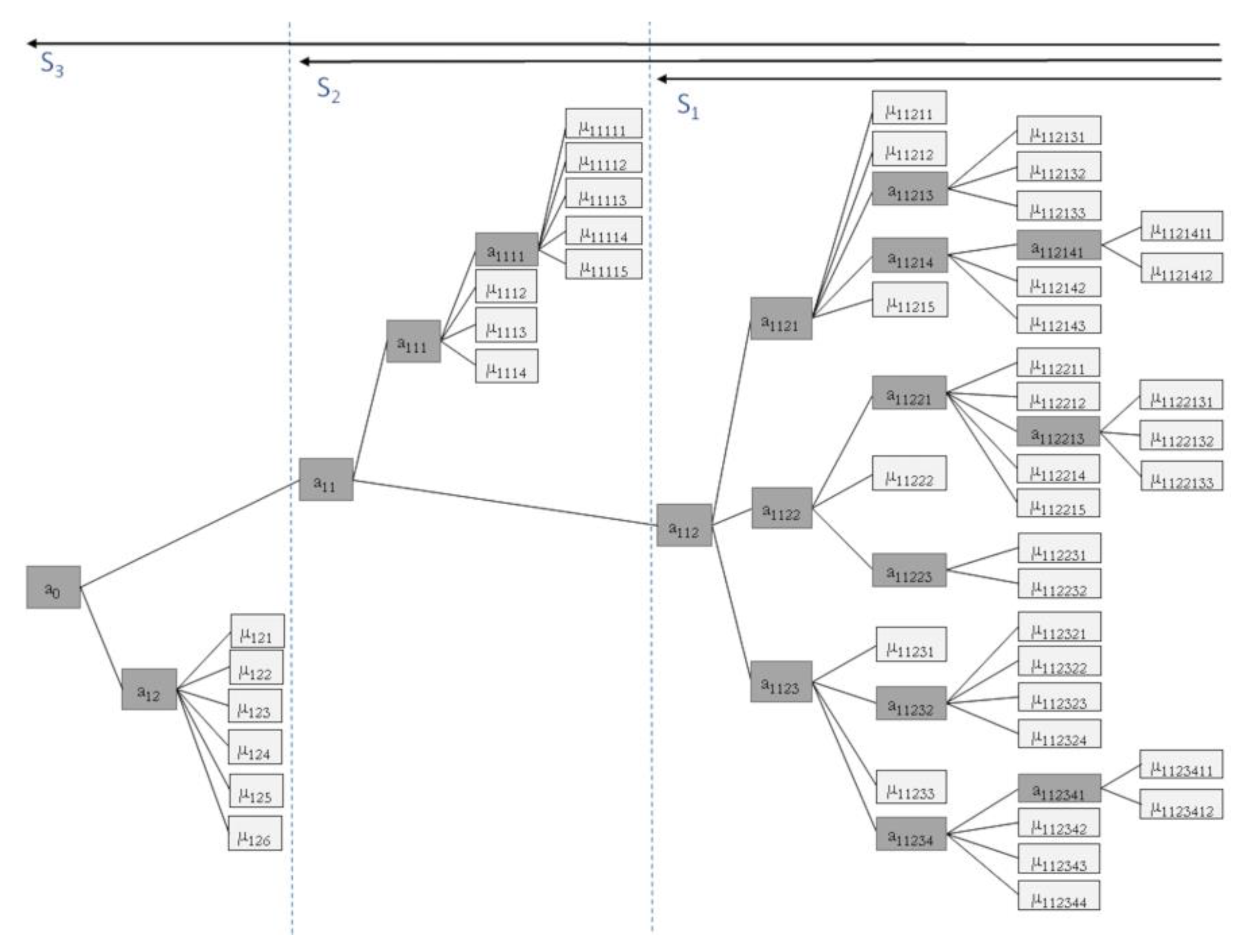



| ID (ai, µi) | Feature | Weight (wi) |
|---|---|---|
| 0 | S3 root | - |
| 12 | Cost of operation | 8 |
| 11 | S2 root | 4 |
| 111 | Packaging material | 8 |
| 112 | S1 root | 4 |
| 1121 | Product characteristics | 3 |
| 1122 | Supply chain | 9 |
| 1123 | External factors | 2 |
| ID (ai, µi) | Feature | Weight (wi) |
|---|---|---|
| 11211 | Batch size | 9 |
| 11212 | Turnover | 9 |
| 11213 | Geometrical characteristic | 7 |
| 112131 | Shape | 4 |
| 112132 | Size | 1 |
| 112133 | Weight | 1 |
| 11214 | Sensitivity | 2 |
| 112141 | Physical | 6 |
| 1121411 | Mechanical | 6 |
| 1121412 | Climate | 4 |
| 112142 | Biological | 3 |
| 112143 | Chemical | 2 |
| 11215 | Value | 2 |
| ID (ai, µi) | Feature | Weight (wi) |
|---|---|---|
| 11221 | Transportation | 8 |
| 112211 | Distance | 8 |
| 112212 | Volume | 7 |
| 112213 | Impacts | 5 |
| 1122131 | Temperature | 4 |
| 1122132 | Vibration | 3 |
| 1122133 | Humidity | 2 |
| 112214 | Infrastructure | 3 |
| 112215 | Modality | 1 |
| 11222 | IT support | 7 |
| 11223 | Material handling | 2 |
| 112231 | Transshipment | 8 |
| 112232 | FTL/LTL | 2 |
| ID (ai, µi) | Feature | Weight (wi) |
|---|---|---|
| 11231 | Cooperation | 8 |
| 11232 | Regulations | 3 |
| 112321 | Environmental | 2 |
| 112322 | Health | 2 |
| 112323 | Benefits | 2 |
| 112324 | Standards | 2 |
| 11233 | Legal | 2 |
| 11234 | Environmental effects | 2 |
| 112341 | Production related | 10 |
| 1123411 | Raw material | 10 |
| 1123412 | Energy | 8 |
| 112342 | CO2 emission | 8 |
| 112343 | Pool size | 7 |
| 112345 | Vehicle utilization | 5 |
| ID (ai, µi) | Feature | Weight (wi) |
|---|---|---|
| 1111 | Used material | 9 |
| 11111 | Robustness | 8 |
| 11112 | Availability | 7 |
| 11113 | Recyclability | 4 |
| 11114 | Reusability | 4 |
| 11115 | Tare weight | 2 |
| 1112 | Packaging fill rate | 8 |
| 1113 | Number of uses | 7 |
| 1114 | Collapsibility | 7 |
| ID (ai, µi) | Feature | Weight (wi) |
|---|---|---|
| 121 | Packaging material | 5 |
| 122 | Disposal | 5 |
| 123 | Capital asset | 5 |
| 124 | Cleaning, maintenance | 5 |
| 125 | Storage | 5 |
| 126 | Administration | 5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vöröskői, K.; Földesi, P.; Kóczy, L.T.; Böröcz, P. Fuzzy Approach for the Decision on Disposable or Returnable Packaging. Sustainability 2020, 12, 7304. https://doi.org/10.3390/su12187304
Vöröskői K, Földesi P, Kóczy LT, Böröcz P. Fuzzy Approach for the Decision on Disposable or Returnable Packaging. Sustainability. 2020; 12(18):7304. https://doi.org/10.3390/su12187304
Chicago/Turabian StyleVöröskői, Kata, Péter Földesi, László T. Kóczy, and Péter Böröcz. 2020. "Fuzzy Approach for the Decision on Disposable or Returnable Packaging" Sustainability 12, no. 18: 7304. https://doi.org/10.3390/su12187304
APA StyleVöröskői, K., Földesi, P., Kóczy, L. T., & Böröcz, P. (2020). Fuzzy Approach for the Decision on Disposable or Returnable Packaging. Sustainability, 12(18), 7304. https://doi.org/10.3390/su12187304







