Identification of Factors Affecting the Performance of Rural Road Projects in Colombia
Abstract
1. Introduction
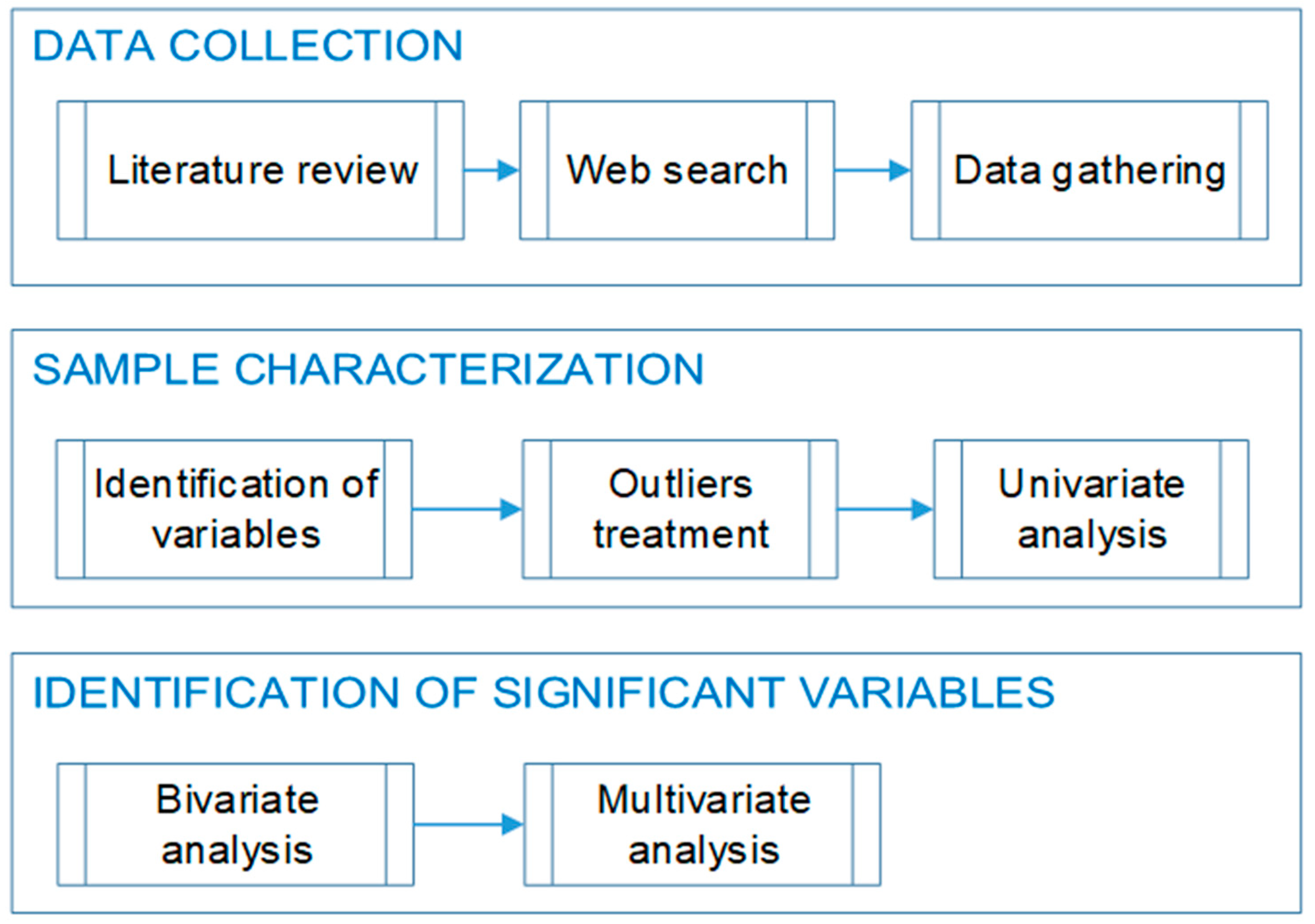
2. Research Methods and Data Collection
3. Results
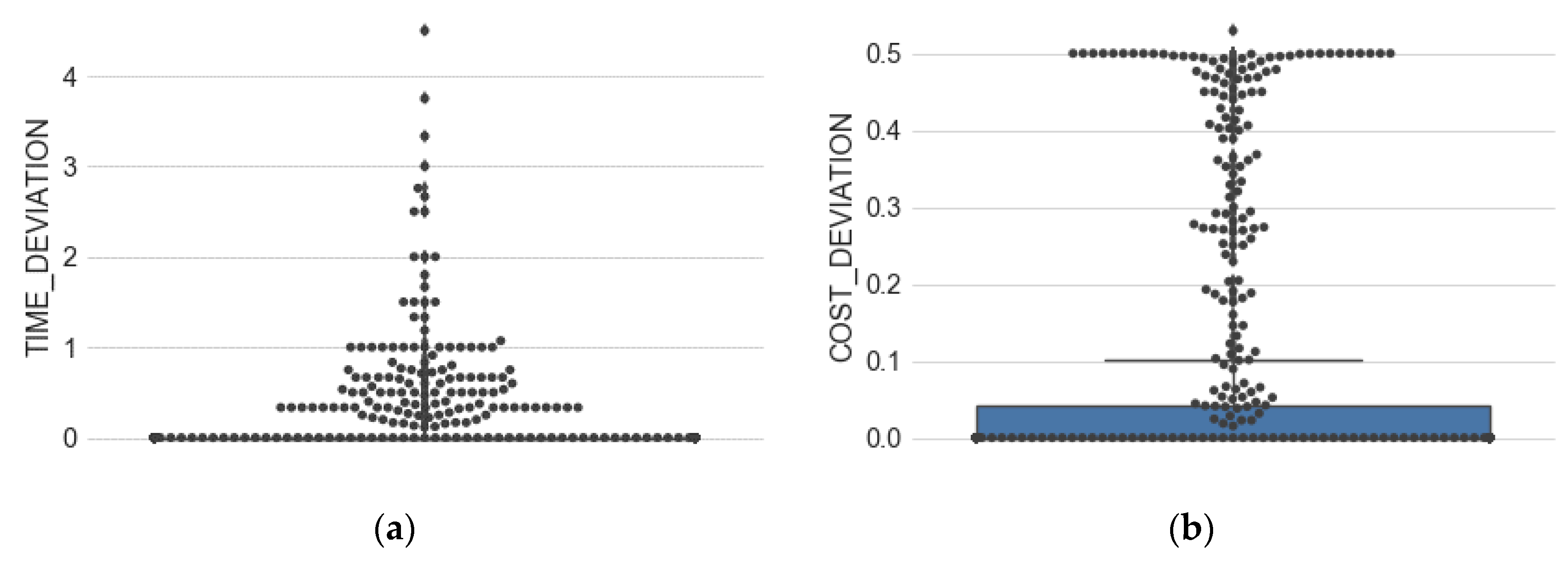
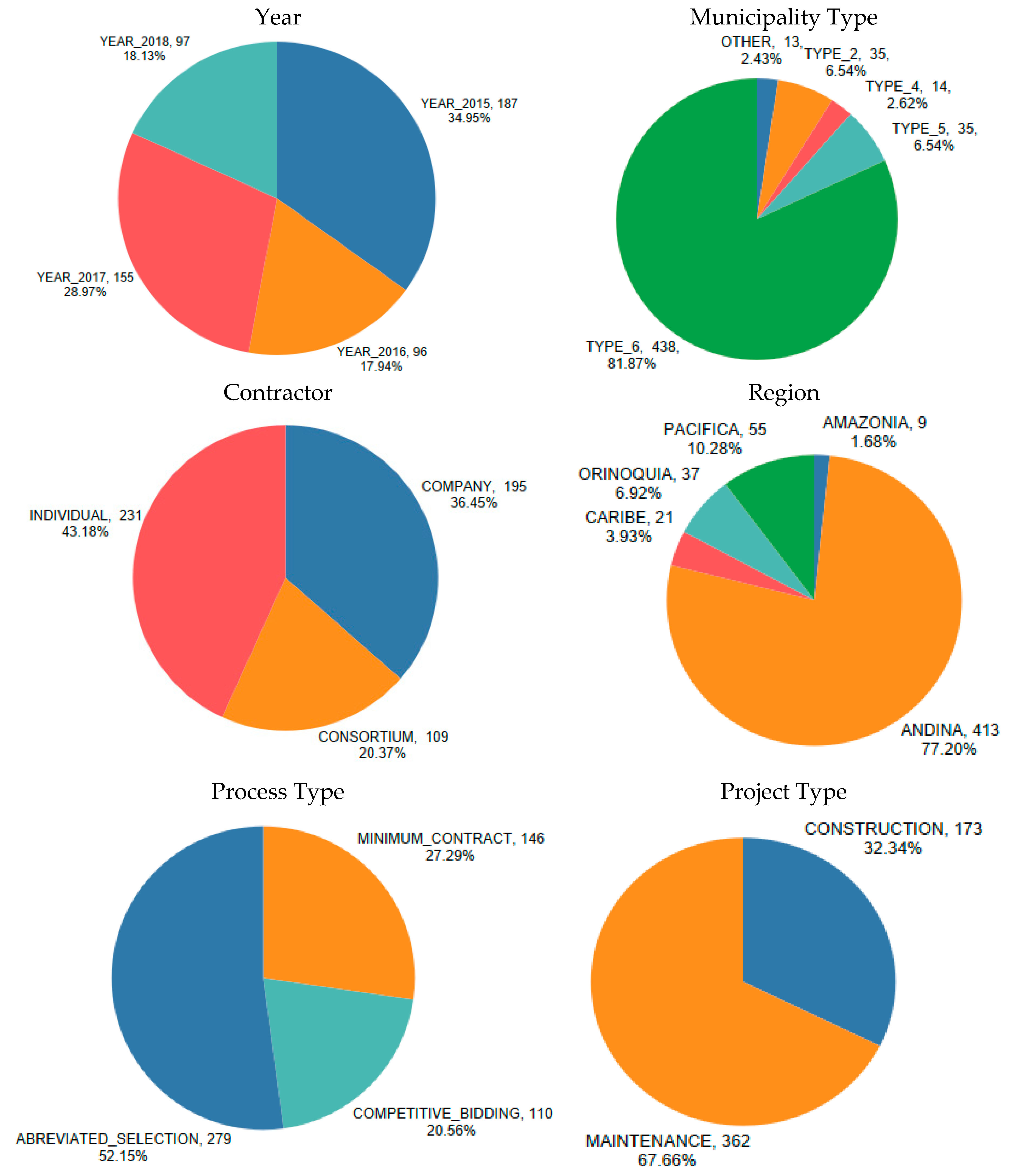
3.1. Univariate Analysis
3.2. Identification of Significant Variables through Bivariate Analysis
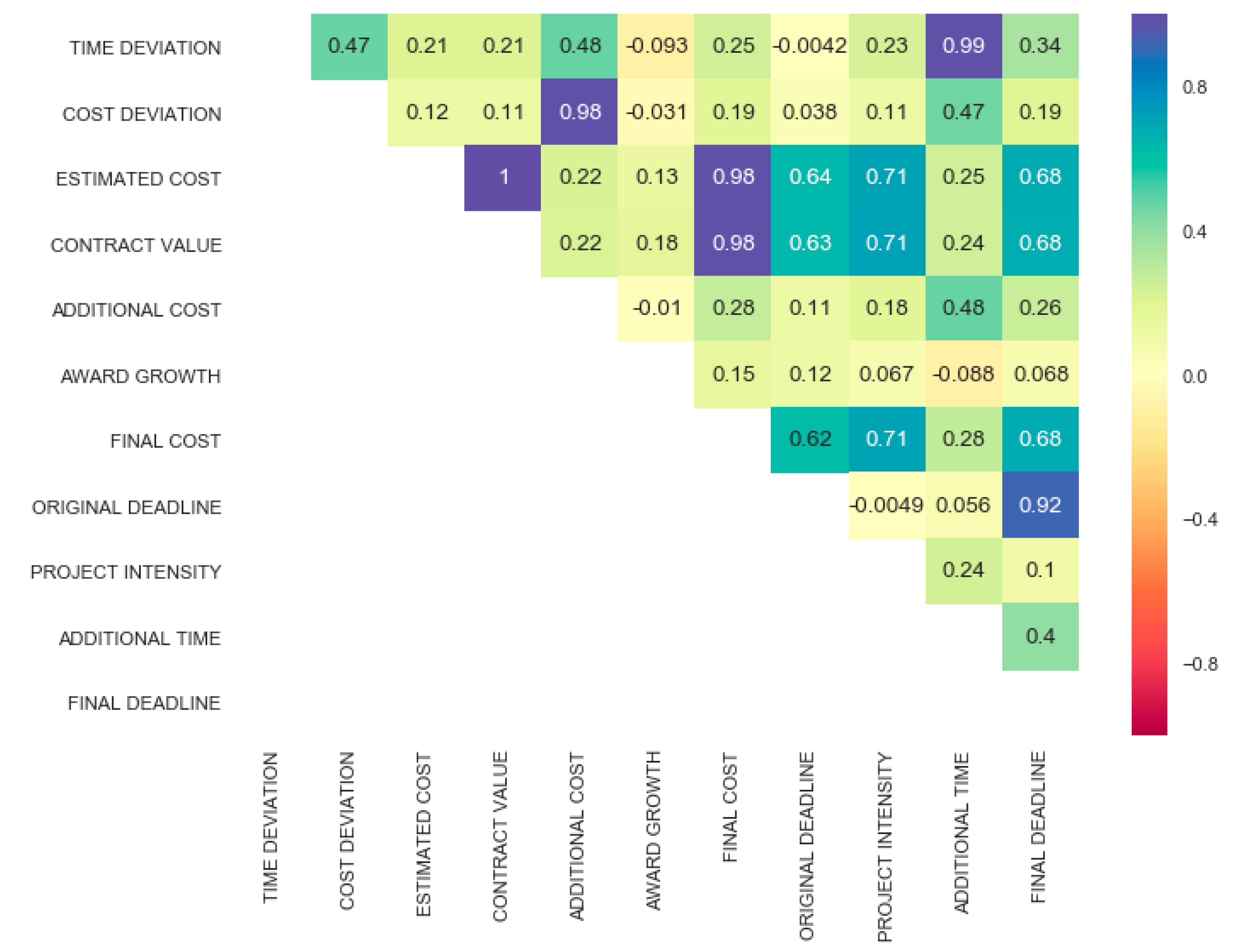
3.2.1. Matrix Correlation
3.2.2. Time Deviation
3.2.3. Cost Deviation
3.3. Identification of Significant Variables through Multivariate Analysis
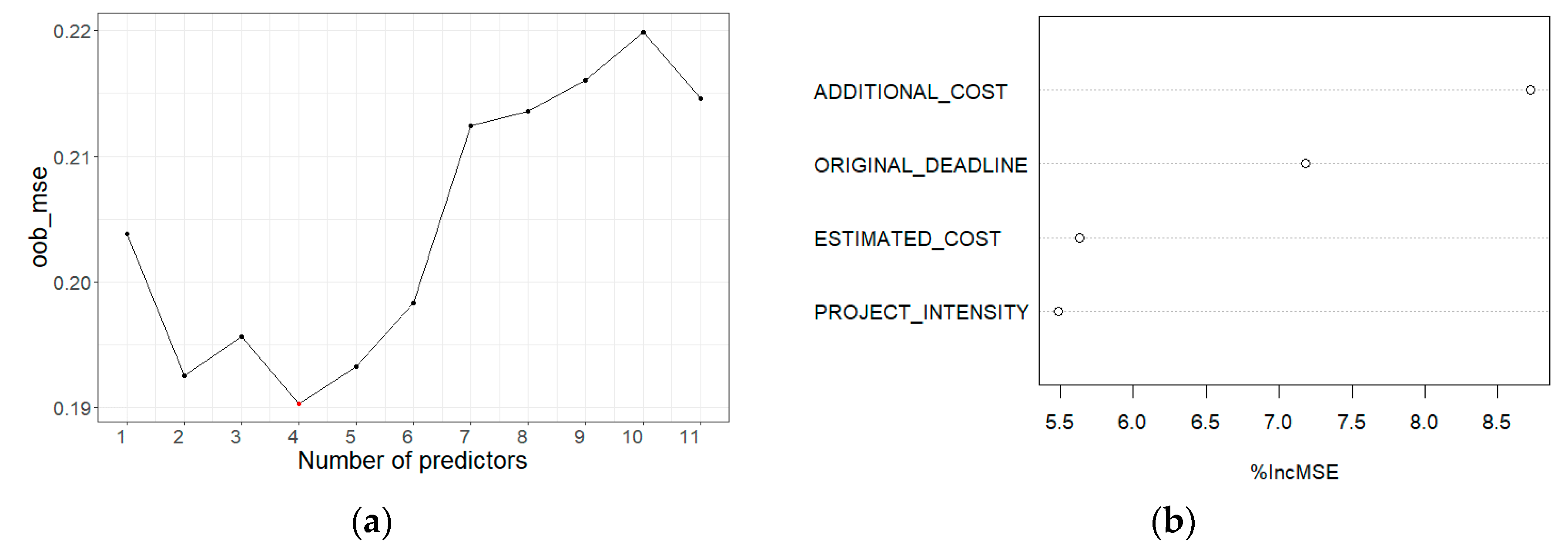
3.3.1. Time Deviation
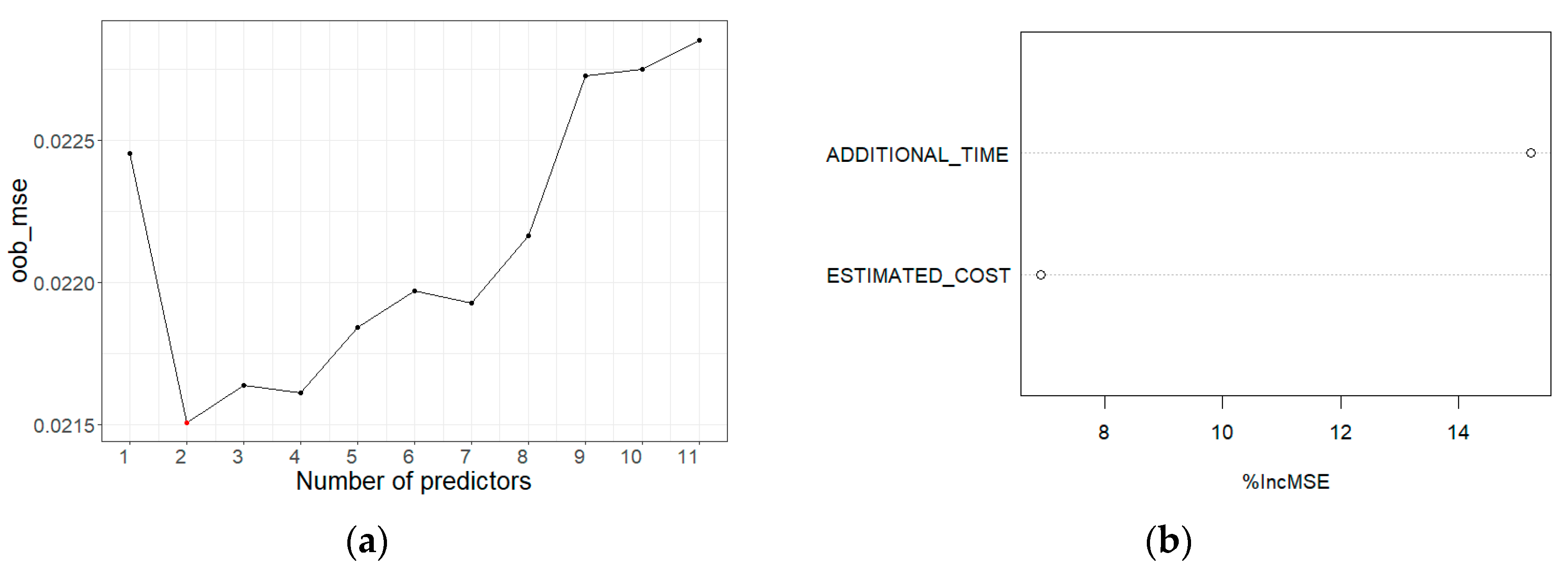
3.3.2. Cost Deviation
4. Discussion
5. Limitations of the Research
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mihai, F.-C.; Iatu, C. Sustainable Rural Development under Agenda 2030. In Sustainability Assessment at the 21st Century; IntechOpen: London, UK, 2020. [Google Scholar]
- Cook, J.; Huizenga, C.; Petts, R.; Visser, C.; Yiu, A. The Contribution of Rural Transport to Achieve the Sustainable Development Goals: Research Community for Access Partnership (ReCAP). Partnership on Sustainable, Low Carbon Transportation; Oxford, UK, 2017. Available online: http://www.slocat.net/wp-content/uploads/legacy/u15/contribution_of_rural_transport_to_the_sustainable_development_goals_paper_final.pdf (accessed on 6 June 2017).
- Burrow, M.P.N.; Evdorides, H.; Ghataora, G.S.; Petts, R.; Snaith, M.S. The Evidence for Rural Road Technology in Low-Income Countries. Proc. Inst. Civ. Eng. Transp. 2016, 169, 366–377. [Google Scholar] [CrossRef]
- Muzira, S.; de Díaz, D.H.; Mota, B.F.J. Rethinking Rural Road Infrastructure Delivery. Transp. Res. Rec. J. Transp. Res. Board 2015, 2474, 195–202. [Google Scholar] [CrossRef]
- Fundación Paz y Reconciliación. FUNDACION PAZ Y RECONCILIACION. Available online: https://pares.com.co/2016/07/28/las-vias-terciarias-del-postconflicto/ (accessed on 6 June 2017).
- Frimpong, Y.; Oluwoye, J.; Crawford, L. Causes of Delay and Cost Overruns in Construction of Groundwater Projects in a Developing Countries; Ghana as a Case Study. Int. J. Proj. Manag. 2003, 21, 321–326. [Google Scholar] [CrossRef]
- Flyvbjerg, B.; Skamris holm, M.K.; Buhl, S.L. How Common and How Large Are Cost Overruns in Transport Infrastructure Projects? Transp. Rev. 2003, 23, 71–88. [Google Scholar] [CrossRef]
- Kumaraswamy, M.M.; Chan, D.W.M. Contributors to Construction Delays. Constr. Manag. Econ. 1998, 16, 17–29. [Google Scholar] [CrossRef]
- Iyer, K.C.; Jha, K.N. Critical Factors Affecting Schedule Performance: Evidence from Indian Construction Projects. J. Constr. Eng. Manag. 2006, 132, 871–881. [Google Scholar] [CrossRef]
- Flyvbjerg, B.; Holm, M.S.; Buhl, S. Underestimating Costs in Public Works Projects: Error or Lie? J. Am. Plan. Assoc. 2002, 68, 279–295. [Google Scholar] [CrossRef]
- Shane, J.S.; Molenaar, K.R.; Anderson, S.; Schexnayder, C. Construction Project Cost Escalation Factors. J. Manag. Eng. 2009, 25, 221–229. [Google Scholar] [CrossRef]
- Gómez-Cabrera, A.; Ponz-Tienda, J.L.; Pellicer, E.; Sanz, A. Factors Generating Schedule Delays and Cost Overruns in Construction Projects. In Proceedings of the VIII Encuentro Latinoamericano de Gestión Y Economía de la Construcción, Londrina, Brasil, 23–25 October 2019. [Google Scholar]
- Kaliba, C.; Muya, M.; Mumba, K. Cost Escalation and Schedule Delays in Road Construction Projects in Zambia. Int. J. Proj. Manag. 2009, 27, 522–531. [Google Scholar] [CrossRef]
- Mahamid, I.; Bruland, A.; Dmaidi, N. Causes of Delay in Road Construction Projects. J. Manag. Eng. 2012, 28, 300–310. [Google Scholar] [CrossRef]
- Kamanga, M.; Steyn, W. Causes of Delay in Road Construction Projects in Malawi. J. S. Afr. Inst. Civ. Eng. 2013, 55, 79–85. [Google Scholar]
- Santoso, D.S.; Soeng, S. Analyzing Delays of Road Construction Projects in Cambodia: Causes and Effects. J. Manag. Eng. 2016, 32, 05016020. [Google Scholar] [CrossRef]
- Yang, J.-B.; Ou, S.-F. Using Structural Equation Modeling to Analyze Relationships among Key Causes of Delay in Construction. Can. J. Civ. Eng. 2008, 35, 321–332. [Google Scholar] [CrossRef]
- Bhargava, A.; Anastasopoulos, P.C.; Labi, S.; Sinha, K.C.; Mannering, F.L. Three-Stage Least-Squares Analysis of Time and Cost Overruns in Construction Contracts. J. Constr. Eng. Manag. 2010, 136, 1207–1218. [Google Scholar] [CrossRef]
- Huo, T.; Ren, H.; Cai, W.; Shen, G.Q.; Liu, B.; Zhu, M.; Wu, H. Measurement and Dependence Analysis of Cost Overruns in Megatransport Infrastructure Projects: Case Study in Hong Kong. J. Constr. Eng. Manag. 2018, 144, 05018001. [Google Scholar] [CrossRef]
- Federal Highway Administration. Alternative Contracting Method Performance in US Highway Construction; Federal Highway Administration: Washington, DC, USA, 2018.
- Congreso de la República. Ley 1150 de 2007; Congreso de la República: Bogotá, Colombia, 2007.
- Gransberg, D.; Villarreal Buitrago, M. Construction Project Performance Metrics. In AACE International Transactions; EBSCO Publishing: Ipswich, MA, USA, 2002; p. CSC.02. [Google Scholar]
- Westland, J. The Project Management Life Cycle: A Complete Step-by-Step Methodology for Initiating, Planning, Executing & Closing a Project Successfully; Kogan Page Publishers: London, UK, 2007. [Google Scholar]
- Flyvberg, B.; Skamris, H.; Buhl, S. What Causes Cost Overrun in Transport Infrastructure Projects? Transp. Rev. 2004, 24, 3–18. [Google Scholar] [CrossRef]
- Odeck, J. Cost Overruns in Road Construction—What Are Their Sizes and Determinants? Transp. Policy 2004, 11, 43–53. [Google Scholar] [CrossRef]
- Cantarelli, C.C.; Molin, E.J.E.; Van Wee, B.; Flyvbjerg, B. Characteristics of Cost Overruns for Dutch Transport Infrastructure Projects and the Importance of the Decision to Build and Project Phases. Transp. Policy 2012, 22, 49–56. [Google Scholar] [CrossRef]
- Larose, D.; Larose, C.D. Data Mining and Predictive Analytics. In Data Mining and Predictive Analysis; Wiley: Hoboken, NJ, USA, 2015; pp. 31–48. [Google Scholar]
- Alvarado, J.; Obagi, J.J. Fundamentos de Inferencia Estadística; Editorial Pontificia Universidad Javeriana: Bogotá D.C., Colombia, 2008. [Google Scholar]
- Hauke, J.; Kossowski, T. Comparison of Values of Pearson’s and Spearman’s Correlation Coefficients on the Same Sets of Data. Quaest. Geogr. 2011, 30, 87–93. [Google Scholar] [CrossRef]
- de Winter, J.C.F.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman Correlation Coefficients across Distributions and Sample Sizes: A Tutorial Using Simulations and Empirical Data. Psychol. Methods 2016, 21, 273–290. [Google Scholar] [CrossRef]
- Gatignon, H. Statistical Analysis of Management Data; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Goos, P.; Meintrup, D. Statistics with JMP; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Kotsiantis, S.; Kanellopoulos, D. Discretization Techniques: A Recent Survey. GESTS Int. Trans. Comput. Sci. Eng. 2006, 32, 47–58. [Google Scholar]
- Mooi, E.; Sarstedt, M. A Concise Guide to Market Research: The Process, Data, and Methods Using IBM SPSS Statistics; Springer: Berlin, Germany, 2011; ISBN 9783642125416. [Google Scholar]
- Auret, L.; Aldrich, C. Interpretation of Nonlinear Relationships between Process Variables by Use of Random Forests. Miner. Eng. 2012, 35, 27–42. [Google Scholar] [CrossRef]
- Chakure, A. Random Forest Regression-Towards Data Science. Available online: https://towardsdatascience.com/random-forest-and-its-implementation-71824ced454f (accessed on 3 April 2020).
- Grömping, U. Variable Importance Assessment in Regression: Linear Regression versus Random Forest Linked. Am. Stat. 2009, 63, 308–319. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest? In Machine Learning and Data Mining in Pattern Recognition; Elsevier: Amsterdam, The Netherlands, 2012; Volume 7376 LNAI, pp. 154–168. [Google Scholar] [CrossRef]
- Congreso Republica Colombia, Ley 80 De 1993; Bogotá, Colombia; 1993. Available online: http://www.suin-juriscol.gov.co/viewDocument.asp?ruta=Leyes/1790106 (accessed on 3 April 2020).
- Bohórquez, J.; Mejía, G. Relationship Between Cost Overruns and Complexity in Engineering Projects: A Mixed Approach. In Proceedings of the Viii Encuentro Latinoamericano de Gestión Y Economía de la Construcción, Londrina, Brasil, 23–25 October 2019. [Google Scholar]
- Vallejo-Borda, J.A.; Gutierrez-Bucheli, L.A.; Pellicer, E.; Ponz-Tienda, J.L. Behavior in Terms of Delays and Cost Overrun of the Construction of Public Infrastructure In. Sibragec Elagec 2015, 2015, 66–73. [Google Scholar] [CrossRef]
- Park, Y.I.; Papadopoulou, T.C. Causes of Cost Overruns in Transport Infrastructure Projects in Asia: Their Significance and Relationship with Project Size. Built Environ. Proj. Asset Manag. 2012, 2, 195–216. [Google Scholar] [CrossRef]
- Assaf, S.A.; Al-Khalil, M.; Al-Hazmi, M.; Odeh, A.M.; Battaineh, H.T.; Elinwa, A.U.; Joshua, M.; Gündüz, M.; Nielsen, Y.; Özdemir, M.; et al. Causes of Delay in Construction Projects in the Oil and Gas Industry in the Gulf Cooperation Council Countries: A Case Study. Int. J. Proj. Manag. 2006, 31, 171–181. [Google Scholar] [CrossRef]
- Bagaya, O.; Song, J. Empirical Study of Factors Influencing Schedule Delays of Public Construction Projects in Burkina Faso. J. Manag. Eng. 2016, 32, 05016014. [Google Scholar] [CrossRef]
- Batool, A.; Abbas, F. Reasons for Delay in Selected Hydro-Power Projects in Khyber Pakhtunkhwa (KPK), Pakistan. Renew. Sustain. Energy Rev. 2017, 73, 196–204. [Google Scholar] [CrossRef]
- Lo, T.Y.; Fung, I.W.; Tung, K.C. Construction Delays in Hong Kong Civil Engineering Projects. J. Constr. Eng. Manag. 2006, 132, 636–649. [Google Scholar] [CrossRef]
- Kaka, A.; Price, A.D.F. Relationship between Value and Duration of Construction Projects. Constr. Manag. Econ. 1991, 9, 383–400. [Google Scholar] [CrossRef]
- Kumaraswamy, M.M.; Chan, D.W.M. Determinants of Construction Duration. Constr. Manag. Econ. 1995, 13, 209–217. [Google Scholar] [CrossRef]
- Chan, A.P.C. Time-Cost Relationship of Public Sector Projects in Malaysia. Int. J. Proj. Manag. 2001, 19, 223–229. [Google Scholar] [CrossRef]
- Anastasopoulos, P.C.; Labi, S.; Bhargava, A.; Mannering, F.L. Empirical Assessment of the Likelihood and Duration of Highway Project Time Delays. J. Constr. Eng. Manag. 2012, 138, 390–398. [Google Scholar] [CrossRef]


| Phase | Variable (Type) | Description | Unit/Values | Source |
|---|---|---|---|---|
| Project initiation | Project type (Categorical) | The main project object. | Construction or Maintenance | [7,18,19] |
| Owner (Categorical) | The entity, or stakeholder, responsible for contracting the project. | Municipality or Other | [24] | |
| Geographic Location (Categorical) | Colombian regions where the project takes place. | Amazonia, Andina, Caribe, Orinoquia, or Pacifica | [10,25] | |
| Municipality Type (Categorical) | Class stated by Colombian law. (According to their number of inhabitants and income). | Type 1 to 6, 1 being the highest category | ||
| Period (Categorical) | The period of project execution, in this case, it was established in years. | Years: 2015, 2016, 2017, or 2018 | [10,25] | |
| Estimated Cost (Budget) (Numerical) | Budgeted construction cost, determined at the time of procurement by the owner. | Minimum salaries | [7,19,25,26] | |
| Original Deadline (Numerical) | The project planned duration, determined at the time of procurement by the owner. | Days | [18,24,25] | |
| Project Intensity (Numerical) | The ratio between the estimated cost and the original deadline. | Minimum salaries/days | [20] | |
| Project planning | Contract Value (Numerical) | The contract awarded amount. | Minimum salaries | [18,20] |
| Award Growth (Numerical) | The ratio between the difference of contract value and the estimated cost. | Percentage (%) | [20] | |
| Process Type (Categorical) | Modality chosen for the contractor procurement and selection. | Competitive Bidding, Abbreviated Selection, Minimum Contract | ||
| Contractor (Categorical) | Stakeholder responsible for executing the project. | Individual, Consortium, or Companies | ||
| Project execution and closure | Additional Cost (Numerical) | The difference between the contract value and the final contract cost. | Minimum salaries | [20,26] |
| Additional Time (Numerical) | Difference between the original deadline and the final contract deadline. | Days | [20] | |
| Final Cost (Numerical) | Final contract cost. | Minimum salaries | [26] | |
| Final Deadline (Numerical) | Final contract deadline. | Days | [25] |
| Variable | Min | Max | Mean | Median | Standard Deviation |
|---|---|---|---|---|---|
| Time deviation | 0.00 | 4.50 | 0.19 | 0.00 | 0.50 |
| Cost deviation | 0.00 | 0.53 | 0.08 | 0.00 | 0.16 |
| Variable | Min | Max | Mean | Median | Standard Deviation |
|---|---|---|---|---|---|
| Time deviation | 0.00 | 4.50 | 0.53 | 0.33 | 0.72 |
| Cost deviation | 0.00 | 0.53 | 0.24 | 0.25 | 0.20 |
| Variable (Unit) | Min | Max | Mean | Median | Standard Deviation |
|---|---|---|---|---|---|
| Estimated Cost (* MS) | 25.60 | 2420.45 | 258.84 | 126.31 | 387.20 |
| Contract Value (* MS) | 19.69 | 2415.74 | 257.35 | 126.31 | 385.88 |
| Additional Cost (* MS) | 0.00 | 828.98 | 21.40 | 0.00 | 71.80 |
| Final Cost (* MS) | 21.44 | 3244.72 | 278.75 | 128.57 | 419.06 |
| Original Deadline (Days) | 5.00 | 240.00 | 63.18 | 60.00 | 38.38 |
| Additional Time (Days) | 0.00 | 196.00 | 9.28 | 0.00 | 22.50 |
| Final Deadline (Days) | 5.00 | 361.00 | 72.46 | 60.00 | 47.11 |
| Project Intensity (* MS/Day) | 0.23 | 69.16 | 4.05 | 2.24 | 5.79 |
| Award Growth (%) | −0.29 | 0.00 | −0.01 | 0.00 | 0.03 |
| Phase | Variable | Spearman′s Rho | p-Value |
|---|---|---|---|
| Project initiation | Project intensity | 0.23 | <<0.01 |
| Estimated cost | 0.21 | <<0.01 | |
| Project planning | Award growth | −0.09 | 0.00 |
| Project execution and closure | Additional cost | 0.48 | <<0.01 |
| Phase | Variable | New Categories | Min | Max | Mean |
|---|---|---|---|---|---|
| Project initiation | Year | 2016 | 0.00 | 4.50 | 0.37 |
| Other | 0.00 | 3.00 | 0.15 | ||
| Region | Other | 0.00 | 4.50 | 0.20 | |
| Pacifica | 0.00 | 1.50 | 0.05 | ||
| Municipality type | Other | 0.00 | 3.00 | 0.35 | |
| Type 6 | 0.00 | 4.50 | 0.15 | ||
| Project planning | Process type | Competitive bidding | 0.00 | 3.00 | 0.28 |
| No competitive bidding | 0.00 | 4.50 | 0.16 |
| Phase | Variable | Spearman′s Rho | p-Value |
|---|---|---|---|
| Project initiation | Project intensity | 0.11 | 0.01 |
| Estimated cost | 0.12 | 0.00 | |
| Project execution and closure | Additional time | 0.47 | <<0.01 |
| Phase | Variable | New Categories | Min | Max | Mean |
|---|---|---|---|---|---|
| Project initiation | Year | 2016 | 0.00 | 0.53 | 0.16 |
| Other | 0.00 | 0.50 | 0.07 | ||
| Municipality type | Other | 0.00 | 0.53 | 0.14 | |
| Type 6 | 0.00 | 0.50 | 0.07 | ||
| Project planning | Process type | Competitive bidding | 0.00 | 0.53 | 0.09 |
| No competitive bidding | 0.00 | 0.50 | 0.08 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gómez-Cabrera, A.; Sanz-Benlloch, A.; Montalban-Domingo, L.; Ponz-Tienda, J.L.; Pellicer, E. Identification of Factors Affecting the Performance of Rural Road Projects in Colombia. Sustainability 2020, 12, 7377. https://doi.org/10.3390/su12187377
Gómez-Cabrera A, Sanz-Benlloch A, Montalban-Domingo L, Ponz-Tienda JL, Pellicer E. Identification of Factors Affecting the Performance of Rural Road Projects in Colombia. Sustainability. 2020; 12(18):7377. https://doi.org/10.3390/su12187377
Chicago/Turabian StyleGómez-Cabrera, Adriana, Amalia Sanz-Benlloch, Laura Montalban-Domingo, Jose Luis Ponz-Tienda, and Eugenio Pellicer. 2020. "Identification of Factors Affecting the Performance of Rural Road Projects in Colombia" Sustainability 12, no. 18: 7377. https://doi.org/10.3390/su12187377
APA StyleGómez-Cabrera, A., Sanz-Benlloch, A., Montalban-Domingo, L., Ponz-Tienda, J. L., & Pellicer, E. (2020). Identification of Factors Affecting the Performance of Rural Road Projects in Colombia. Sustainability, 12(18), 7377. https://doi.org/10.3390/su12187377







