Flexible Assignment of Loading Bays for Efficient Vehicle Routing in Urban Last Mile Delivery
Abstract
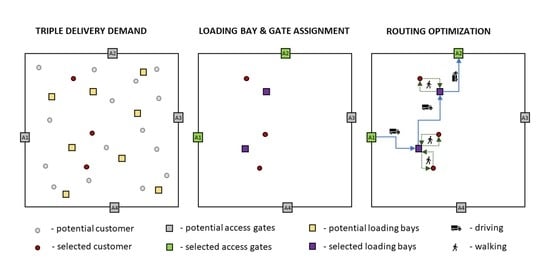
:1. Introduction
2. Materials and Methods
2.1. Model Characteristics and Functions
2.2. Clustering Procedure for Solving Facility Location Problem
- -
- = number of customers
- -
- = number of clusters
- -
- = -th data point (each data point corresponds with location of a particular customer)
- -
- = center of cluster
- -
- = degree of membership of customer to cluster
- -
- = parameter of fuzziness
- Randomly initialize the cluster membership values, .
- Calculate the cluster centers:
- Update according to the following:
- Calculate the objective function, .
- Repeat steps 2–4 until improves by less than a specified minimum threshold or until after a specified maximum number of iterations.
2.3. Vehicle Routing and Loading Bay Assignment Procedure
2.4. Potential Solutions/Outcomes
3. Simulation Results
3.1. Results—Driving Distances
| Max | Min | Avg | Max | Min | Avg | ||
|---|---|---|---|---|---|---|---|
| HD4 [m] | 2.011 | 451 | 1.494 | HD25 [m] | 2.652 | 472 | 1.592 |
| SD4 [m] | 897 | 451 | 624 | SD25 [m] | 1.743 | 237 | 1.044 |
| Difference [m] | −1.114 | 0 | −870 | Difference [m] | −909 | −235 | −548 |
| Difference [%] | −55.4% | 0,0% | −58.2% | Difference [%] | −34.3% | −49.8% | −34.4% |
| HD9 [m] | 2.584 | 566 | 1.499 | HD49 [m] | 2.627 | 818 | 1.577 |
| SD9 [m] | 1.400 | 256 | 809 | SD49 [m] | 1.889 | 451 | 1.213 |
| Difference [m] | −1.184 | −310 | −690 | Difference [m] | −738 | −367 | −363 |
| Difference [%] | −45.8% | −54.7% | −46.1% | Difference [%] | −28.1% | −44.9% | −23.1% |
| HD16 [m] | 2.854 | 429 | 1.695 | HD81 [m] | 2.530 | 590 | 1.617 |
| SD16 [m] | 1.772 | 237 | 1.106 | SD81 [m] | 2.062 | 211 | 1.320 |
| Difference [m] | −1.081 | −193 | −589 | Difference [m] | −468 | −379 | −297 |
| Difference [%] | −37.9% | −44.9% | −34.8% | Difference [%] | −18.5% | −64.3% | −18.4% |
3.2. Results—Walking Distances



| Max | Min | Avg | Max | Min | Avg | ||
|---|---|---|---|---|---|---|---|
| HW4 [m] | 2.430 | 445 | 1.501 | HW25 [m] | 1.129 | 73 | 539 |
| SW4 [m] | 4.945 | 1.266 | 2.955 | SW25 [m] | 2.099 | 320 | 1.103 |
| Difference [m] | 2.514 | 822 | 1.454 | Difference [m] | 970 | 247 | 563 |
| Difference [%] | 103.5% | 184.8% | 96.8% | Difference [%] | 85.9% | 337.3% | 104.4% |
| HW9 [m] | 1.726 | 369 | 963 | HW49 [m] | 816 | 40 | 358 |
| SW9 [m] | 3.154 | 605 | 1.870 | SW49 [m] | 1.282 | 56 | 724 |
| Difference [m] | 1.428 | 236 | 907 | Difference [m] | 466 | 16 | 366 |
| Difference [%] | 82.8% | 63.8% | 94.1% | Difference [%] | 57.0% | 41.2% | 102.4% |
| HW16 [m] | 1.207 | 94 | 703 | HW81 [m] | 783 | 27 | 284 |
| SW16 [m] | 2.318 | 320 | 1.392 | SW81 [m] | 1.246 | 109 | 577 |
| Difference [m] | 1.111 | 227 | 689 | Difference [m] | 463 | 82 | 293 |
| Difference [%] | 92.1% | 241.9% | 98.0% | Difference [%] | 59.2% | 310.9% | 103.5% |
3.3. Comparison Between Driving and Walking Distances

- The total length of average driving and walking distances decreases with the increase in the number of loading bays.
- The driving distance covered in the hard optimization approach does not show significant deviations with regard to the increase in the number of loading bays.
- Increasing the number of loading bays on the other hand shortens the length of walking distances.
| Sum | Avg | Ratio | Sum | Avg | Ratio | ||
|---|---|---|---|---|---|---|---|
| HD4 [m] | 497.666 | 1.494 | 49.9% | HD25 [m] | 530.015 | 1.592 | 74.7% |
| HW4 [m] | 499.841 | 1.501 | 50.1% | HW25 [m] | 179.647 | 539 | 25.3% |
| Total | 997.507 | 2.996 | Total | 709.662 | 2.131 | ||
| HD9 [m] | 499.203 | 1.499 | 60.9% | HD49 [m] | 525.021 | 1.577 | 81.5% |
| HW9 [m] | 320.762 | 963 | 39.1% | HW49 [m] | 119.205 | 358 | 18.5% |
| Total | 819.966 | 2.462 | Total | 644.225 | 1.935 | ||
| HD16 [m] | 564.286 | 1.695 | 70.7% | HD81 [m] | 538.377 | 1.617 | 85.1% |
| HW16 [m] | 234.146 | 703 | 29.3% | HW81 [m] | 94.408 | 284 | 14.9% |
| Total | 798.432 | 2.398 | Total | 632.785 | 1.900 |
- Ratio between driving and walking distances is changing with increasing the number of loading bays starting from approximately 50:50 when = 4, 60:40 when = 9, 70:30 when = 16, 57:25 when = 25, 82:18 when = 49, and 85:15 when = 81.
- Considering average walking distances (one way direction and divide with three customers), loading bays should cover 250 m in case of = 4, 160 m in case = 9, 116 m in case = 16, 90 mm in case = 25, 60 m in case = 49, 48 m in case = 81.

- The total distance (traveling and walking) decreases with the increase in the number of loading bays (similar to what we noticed with the hard optimization approach).
- The ratio between the length of the driving and walking distances is significantly different in this case; with the increase in the number of loading bays, there is a pronounced trend of increasing the length of driving distances and decreasing the length of walking (except for = 16, the length of driving distance is slightly longer than for = 49).
| Sum | Avg | Ratio | Sum | Avg | Ratio | ||
|---|---|---|---|---|---|---|---|
| SD4 | 207.827 | 624 | 29.4% | SD25 | 347.544 | 1.044 | 48.6% |
| SW4 | 499.841 | 1.501 | 70.6% | SW25 | 367.153 | 1.103 | 51.4% |
| Total | 707.667 | 2.125 | Total | 714.697 | 2.146 | ||
| SD9 | 269.288 | 809 | 30.2% | SD49 | 525.021 | 1.213 | 62.6% |
| SW9 | 622.666 | 1.870 | 69.8% | SW49 | 241.228 | 724 | 37.4% |
| Total | 891.953 | 2.679 | Total | 766.249 | 1.938 | ||
| SD16 | 368.194 | 1.106 | 44.3% | SD81 | 538.377 | 1.320 | 69.6% |
| SW16 | 463.655 | 1.392 | 55.7% | SW81 | 192.130 | 577 | 30.4% |
| Total | 831.849 | 2.498 | Total | 730.507 | 1.897 |
- The share of walking part of triple delivery is large (approximately 70%) by small number of loading bays ( = 4 and = 9).
- Ratio between driving and walking distances is improving with increasing the number of loading bays; approximately 44:56 when = 16, 49:51 when = 25, 63:37 when = 49, and 70:30 when = 81.
- Considering average walking distances (one way direction and divide with three customers), loading bays should cover 250 m in case of = 4, 312 m in case = 9, 232 m in case = 16, 184 m in case = 25, 120 m in case = 49, 96 m in case = 81.
4. Discussion
- The modelled city corresponds to idealized orthogonal urban area with different densities of loading bays;
- Locations of customers and access gates are generated randomly, following the uniform density (simulated by LHS procedure);
- Vehicles can enter and exit the urban area only at specific locations (access gates) and the distances between them (outside the studied area) are considered irrelevant;
- Simulations are restricted on up to three shipments per delivery (triple delivery);
- All deliveries from loading bays to customers are made individually even if one loading bay is selected for several customers.
Author Contributions
Funding
Conflicts of Interest
References
- Fiore, G.M. Space for Cities: Satellite Applications Enhancing Quality of Life in Urban Areas. In Studies in Space Policy; Springer: Cham, Switzerland, 2020; Volume 22, pp. 251–263. [Google Scholar]
- Harris, S.; Weinzettel, J.; Bigano, A.; Källmén, A. Low carbon cities in 2050? GHG emissions of European cities using production-based and consumption-based emission accounting methods. J. Clean. Prod. 2020, 248, 119206. [Google Scholar] [CrossRef]
- Olsson, J.; Hellström, D.; Pålsson, H. Framework of last mile logistics research: A systematic review of the literature. Sustainability 2019, 11, 7131. [Google Scholar] [CrossRef] [Green Version]
- Lindholm, M.; Behrends, S. Challenges in urban freight transport planning—A review in the Baltic Sea Region. J. Transp. Geogr. 2012, 22. [Google Scholar] [CrossRef]
- Rose, W.J.; Mollenkopf, D.A.; Autry, C.W.; Bell, J.E. Exploring urban institutional pressures on logistics service providers. Int. J. Phys. Distrib. Logist. Manag. 2016, 46, 153–176. [Google Scholar] [CrossRef]
- Lim, S.F.W.T.; Jin, X.; Srai, J.S. Consumer-driven e-commerce: A literature review, design framework, and research agenda on last-mile logistics models. Int. J. Phys. Distrib. Logist. Manag. 2018, 48, 308–332. [Google Scholar] [CrossRef] [Green Version]
- Kin, B.; Ambra, T.; Verlinde, S.; Macharis, C. Tackling Fragmented Last Mile Deliveries to Nanostores by Utilizing Spare Transportation Capacity—A Simulation Study. Sustainability 2018, 10, 653. [Google Scholar] [CrossRef] [Green Version]
- Iwan, S. Adaptative Approach to Implementing Good Practices to Support Environmentally Friendly Urban Freight Transport Management. Procedia Soc. Behav. Sci. 2014, 151, 70–86. [Google Scholar] [CrossRef] [Green Version]
- Lindholm, M. Urban freight transport from a local authority perspective—a literature review. Eur. Transp. Trasp. Eur. 2013, 54, 1–3. [Google Scholar]
- Letnik, T.; Marksel, M.; Luppino, G.; Bardi, A.; Božičnik, S. Review of policies and measures for sustainable and energy efficient urban transport. Energy 2018, 163, 245–257. [Google Scholar] [CrossRef]
- Comi, A. A modelling framework to forecast urban goods flows. Res. Transp. Econ. 2020, 80, 100827. [Google Scholar] [CrossRef]
- Simoni, M.D.; Bujanovic, P.; Boyles, S.D.; Kutanoglu, E. Urban consolidation solutions for parcel delivery considering location, fleet and route choice. Case Stud. Transp. Policy 2017, 6, 112–124. [Google Scholar] [CrossRef]
- Letnik, T.; Mencinger, M.; Bozicnik, S. Dynamic Management of Urban Last-Mile Deliveries. City Logist. 2 2018, 23–37. [Google Scholar] [CrossRef]
- Aljohani, K.; Thompson, R.G. An examination of last mile delivery practices of freight carriers servicing business receivers in inner-city areas. Sustainability 2020, 12, 2837. [Google Scholar] [CrossRef] [Green Version]
- Cherrett, T.; Allen, J.; McLeod, F.; Maynard, S.; Hickford, A.; Browne, M. Understanding urban freight activity–key issues for freight planning. J. Transp. Geogr. 2012, 24, 22–32. [Google Scholar] [CrossRef] [Green Version]
- Dezi, G.; Dondi, G.; Sangiorgi, C. Urban freight transport in Bologna: Planning commercial vehicle loading/unloading zones. Procedia Soc. Behav. Sci. 2010, 2, 5990–6001. [Google Scholar] [CrossRef] [Green Version]
- Ezquerro, S.; Moura, J.L.; Alonso, B. Illegal Use of Loading Bays and Its Impact on the Use of Public Space. Sustainability 2020, 12, 5915. [Google Scholar] [CrossRef]
- Aiura, N.; Taniguchi, E. Planning On-Street Loading-Unloading Spaces Considering the Behaviour of Pickup-Delivery Vehicles and Parking Enforcement. J. East. Asia Soc. Transp. Stud. 2005, 6, 2963–2974. [Google Scholar]
- Bányai, T. Real-time decision making in first mile and last mile logistics: How smart scheduling affects energy efficiency of hyperconnected supply chain solutions. Energies 2018, 11, 1833. [Google Scholar] [CrossRef] [Green Version]
- Browne, M.; Allen, J.; Nemoto, T.; Patier, D.; Visser, J. Reducing Social and Environmental Impacts of Urban Freight Transport: A Review of Some Major Cities. Procedia Soc. Behav. Sci. 2012, 39, 19–33. [Google Scholar] [CrossRef]
- Chloupek, A. i-Ladezone: Intelligent monitoring of loading bays in Vienna. Available online: http://www.bestfact.net/wp-content/uploads/2016/01/CL1_031_QuickInfo_iLadezonen-16Dec2015.pdf (accessed on 8 September 2020).
- Patier, D.; David, B.; Chalon, R.; Deslandres, V. A New Concept for Urban Logistics Delivery Area Booking. Procedia Soc. Behav. Sci. 2014, 125, 99–110. [Google Scholar] [CrossRef]
- McLeod, F.; Cherrett, T. Loading bay booking and control for urban freight. Int. J. Logist. Res. Appl. 2011, 14, 385–397. [Google Scholar] [CrossRef] [Green Version]
- Boussier, J.; Cucu, T.; Ion, L.; Breuil, D. Simulation of goods delivery process. Int. J. Phys. Distrib. Logist. Manag. 2011, 41, 913–930. [Google Scholar] [CrossRef]
- DynaLOAD: A simulation framework for planning, managing and controlling urban delivery bays. Transp. Res. Procedia 2017, 22, 335–344. [CrossRef] [Green Version]
- Oliveira, B.; Ramos, A.G.; De Sousa, J.P. A classification of two-tier distribution systems based on mobile depots. Transp. Res. Procedia 2020, 47, 115–122. [Google Scholar] [CrossRef]
- Prodhon, C.; Prins, C. A survey of recent research on location-routing problems. Eur. J. Oper. Res. 2014, 238, 1–17. [Google Scholar] [CrossRef]
- Crainic, T.G.; Ricciardi, N.; Storchi, G. Models for Evaluating and Planning City Logistics Systems. Transp. Sci. 2009, 43, 432–454. [Google Scholar] [CrossRef] [Green Version]
- Hemmelmayr, V.C.; Cordeau, J.-F.; Crainic, T.G. An adaptive large neighborhood search heuristic for Two-Echelon Vehicle Routing Problems arising in city logistics. Comput. Oper. Res. 2012, 39, 3215–3228. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Russo, F.; Comi, A. A Model For Simulating Urban Goods Transport and Logistics: The integrated Choice of ho.re.ca. Activity Decision-Making and Final Business Consumers. Procedia Soc. Behav. Sci. 2013, 80, 717–728. [Google Scholar] [CrossRef]
- Oskarbski, J.; Kaszubowski, D. Applying a Mesoscopic Transport Model to Analyse the Effects of Urban Freight Regulatory Measures on Transport Emissions—An Assessment. Sustainability 2018, 10, 2515. [Google Scholar] [CrossRef] [Green Version]
- Comi, A.; Schiraldi, M.M.; Buttarazzi, B. Smart urban freight transport: Tools for planning and optimising delivery operations. Simul. Model. Pract. Theory 2018, 88, 48–61. [Google Scholar] [CrossRef]
- Zhang, L.; Thompson, R.G. Understanding the benefits and limitations of occupancy information systems for couriers. Transp. Res. Part C Emerg. Technol. 2019, 105, 520–535. [Google Scholar] [CrossRef]
- McLeod, F.N.; Cherrett, T.J.; Bektas, T.; Allen, J.; Martinez-Sykora, A.; Lamas-Fernandez, C.; Bates, O.; Cheliotis, K.; Friday, A.; Piecyk, M.; et al. Quantifying environmental and financial benefits of using porters and cycle couriers for last-mile parcel delivery. Transp. Res. Part D Transp. Environ. 2020, 82, 102311. [Google Scholar] [CrossRef]
- Nguyê˜n, T.B.T.; Bektaş, T.; Cherrett, T.J.; McLeod, F.N.; Allen, J.; Bates, O.; Piotrowska, M.; Piecyk, M.; Friday, A.; Wise, S. Optimising parcel deliveries in London using dual-mode routing. J. Oper. Res. Soc. 2019, 70, 998–1010. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S. Improved formulations and an Adaptive Large Neighborhood Search heuristic for the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 123–147. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part B Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S.; Larsen, A. Integrated Berth Allocation and Quay Crane Assignment Problem: Set partitioning models and computational results. Transp. Res. Part E Logist. Transp. Rev. 2015, 81, 75–97. [Google Scholar] [CrossRef] [Green Version]
- Csiszár, C.; Csonka, B.; Földes, D.; Wirth, E.; Lovas, T. Urban public charging station locating method for electric vehicles based on land use approach. J. Transp. Geogr. 2019, 74, 173–180. [Google Scholar] [CrossRef]
- Rathore, P.; Sarmah, S.P.; Singh, A. Location–allocation of bins in urban solid waste management: A case study of Bilaspur city, India. Environ. Dev. Sustain. 2020, 22, 3309–3331. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Boysen, N. Optimizing the changing locations of mobile parcel lockers in last-mile distribution. Eur. J. Oper. Res. 2020, 285, 1077–1094. [Google Scholar] [CrossRef]
- Letnik, T.; Peruš, I.; Božičnik, S.; Mencinger, M. On fundamental principles of the optimal number and location of loading bays in urban areas. Transport 2019, 34, 722–740. [Google Scholar] [CrossRef] [Green Version]
- Husslage, B.G.M.; Rennen, G.; van Dam, E.R.; den Hertog, D. Space-filling Latin hypercube designs for computer experiments. Optim. Eng. 2011, 12, 611–630. [Google Scholar] [CrossRef] [Green Version]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer: Boston, MA, USA, 1981. [Google Scholar]
- Muñuzuri, J.; Cortés, P.; Onieva, L.; Guadix, J. Estimation of Daily Vehicle Flows for Urban Freight Deliveries. J. Urban Plan. Dev. 2012, 138, 43–52. [Google Scholar] [CrossRef]
- Holguín-veras, J.; Sánchez-díaz, I. Freight Demand Management and the Potential of Receiver-Led Consolidation programs. Transp. Res. Part A Policy Pr. 2016, 84, 109–130. [Google Scholar] [CrossRef]
- Letnik, T.; Farina, A.; Mencinger, M.; Lupi, M.; Bozicnik, S. Dynamic Management of Loading Bays for Energy Efficient Urban Freight Deliveries. Energy 2018, 159, 916–928. [Google Scholar] [CrossRef]










© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Letnik, T.; Mencinger, M.; Peruš, I. Flexible Assignment of Loading Bays for Efficient Vehicle Routing in Urban Last Mile Delivery. Sustainability 2020, 12, 7500. https://doi.org/10.3390/su12187500
Letnik T, Mencinger M, Peruš I. Flexible Assignment of Loading Bays for Efficient Vehicle Routing in Urban Last Mile Delivery. Sustainability. 2020; 12(18):7500. https://doi.org/10.3390/su12187500
Chicago/Turabian StyleLetnik, Tomislav, Matej Mencinger, and Iztok Peruš. 2020. "Flexible Assignment of Loading Bays for Efficient Vehicle Routing in Urban Last Mile Delivery" Sustainability 12, no. 18: 7500. https://doi.org/10.3390/su12187500