Peripheralization Risk Mitigation: A Decision Support Model to Evaluate Urban Regeneration Programs Effectiveness

Abstract

The term peripheralization indicates a process that can generate social, physical, and environmental degradation in urban areas. In the light of the new urban geography and the socio-economic trends taking place globally, there is a risk that the typical decay of a peripheral condition may affect city in their entirety, regardless of spatial proximity to its centre. Then, regeneration interventions should be targeted primarily at areas with a significant peripheralization risk, understood as a combination of potential degradation factors. Consequently, the decision-makers’ choice of the best design alternative should be informed by the knowledge of pre-existing vulnerability levels, and oriented towards the solution that maximizes their reduction. This is possible when the planning of interventions in the most vulnerable areas, through Urban Regeneration Programs, is able to take into account the results of the project alternatives economic evaluation. Such an approach constitutes the main novelty of the study. So, the aim of the work is to provide a decision support model for the evaluation of urban regeneration interventions effectiveness in areas of high peripheralization risk. To this end, the contribution defines a set of mitigation indicators and the assessment of the most effective design alternative through analytic hierarchy process (AHP). The proposed model was applied to an area of Marcianise Municipality, in Campania Region (Italy).

1. Introduction

Since the 1990s, in developed countries, including Italy, there has been a phase of experimentation with tools to combat the degradation of urban areas supported by public funding, known as the season of ‘complex programmes’. On an urban scale, the latter are urban planning instruments implementing the general municipal plan, aimed at countering the physical and functional degradation of urban neighbourhoods, also facing social degradation. To this end, these programs provide for a plurality of project actions and involve multiple subjects, which is why they are called complexes [1].

Over the years, the European Commission has repeatedly funded urban decay reduction initiatives, from complex programmes to the latest urban regeneration programmes. Areas targeted by these programmes have often been urban peripheries, which in Europe and Italy, they are generally associated with degraded areas [2]. Nevertheless, as cities continue to grow worldwide, urban areas result in a series of challenges varying from natural resources consumption, or ‘spatial peripheralization’, to the development of social and economic imbalances and physical and environmental degradation, in a process of ‘a-spatial peripheralization’ [3,4,5,6,7,8,9,10]. Some aspects of such process can be assimilated to the topic of urban poverty [11] or to the deprivation issue, developed in the European context [12,13]. The issues of reducing land take and urban poverty, through regeneration of deprived areas, are central: In the most recent European Union recommendations [14,15] and in the New Urban Agenda, adopted by the United Nations on the basis of the 2030 Agenda for Sustainable Development, which recognizes urban planning as playing a key role in the definition and programming of mitigation actions [16].

The analysis of the main international experiences highlights how the regeneration of deprived areas falls within the so-called ‘area-based’ contrast policies; that is, aimed at specific geographical areas in disadvantaged conditions.

To identify these areas, many European countries make use of scientific criteria, often considering composite indices, useful for measuring the degree of deprivation or urban poverty. Even if there is no agreement on the set of basic indicators for the construction of these indices [17], in general, this approach has shown that the most deprived areas are not necessarily urban peripheries—as traditionally understood in their geographic and spatial sense—but may also affect central parts of the city.

In the areas subject to intervention, as in the Italian case of complex programs, the planned project actions are both ‘hard measures’, i.e., physical–structural transformations of the neighborhoods or part of them (e.g., demolition, new infrastructure, housing regeneration, etc.), and ‘soft measures’, such as the promotion of social capital (e.g., favoring employment and inclusion of the population).

Urban renewal or regeneration programs in Europe have also been the subject of criticism, especially in relation to the phenomenon of gentrification, i.e., the expulsion of the original inhabitants from the neighborhood undergoing transformation, with the consequent increase in the irregular development of the entire city [18].

According to the most recent vision of the European Union, it is necessary to pursue a unitary approach to urban regeneration to ensure effective interventions. In the panorama of good practices in the EU, it emerges that an effective strategy is to start from actions on parts of cities that are placed, however, always in a dynamic relationship with the entire urban organism, of which they are an integral part, in order to overcome the risk of fragmentation and dispersion of interventions [15,19]. In this sense, the importance of urban planning is better understood in defining appropriate counter actions.

In Italy, where national legislation for urban regeneration is still lacking, there are generally no scientific criteria for the identification of intervention areas, which is usually left to the municipal authorities, on the occasion of sporadic calls for public funding [20,21]. As a result, urban regeneration interventions translate into operations mainly driven by convenience in real estate transformations. To counter this phenomenon, the technical literature proposes the use of multi-criteria evaluations of project proposals, capable of rationalizing choices driven by conflicting objectives, with the aim of maximizing public benefits. Among the various techniques, the use of the analytical hierarchy process (AHP) is frequent [22,23,24,25,26,27,28,29]. In fact, compared to other models, the AHP allows the choice of the best design alternative by considering a greater number of criteria [30], a circumstance frequently found in the analysis of a complex urban program.

However, in light of the new urban geography, urban regeneration interventions must be targeted primarily at areas that have a significant coexistence of degradation factors [31,32]. Consequently, the decision-makers choice of the best design alternative must be informed by the knowledge of pre-existing vulnerability levels and oriented towards the solution that maximizes their reduction [33,34,35,36,37,38,39]. This is possible by integrating the phase of interventions planning in the most vulnerable areas with that of the multi-criteria evaluation of the most effective project. This integration is the basis of this work.

This contribution is part of a wider research project, which proposes a methodology for the localization of areas subject to urban regeneration through the analysis of peripheralization risk. According to this approach, priority areas are those with the greatest aggregated vulnerability, due to the combination of social, building, and urban vulnerabilities. Vulnerability is measured with reference to a composite index, constructed from quantitative indicators, describing the potential degradation factors in the social, building, and urban domains of the city [40].

The objective of this paper is to provide a decision support model for evaluating the effectiveness of urban regeneration programs in areas with a high peripheralization risk. To this end, the following Section 2 proposes a set of indicators for the mitigation of the social, building, and urban vulnerability. Section 3 shows the model for the analysis of design alternatives. The model is defined with the aim of selecting the investment best able to pursue the peripheralization risk mitigation objectives. At this point, the protocol is tested with reference to a case study. In particular, the problematic issues of the investigation area are presented in Section 4, while Section 5 reports the implementation of the calculation algorithms. The results of the application are discussed in Section 6, which is followed by the conclusions of the study with specific indications on research prospects (Section 7).

2. Mitigation Indicators of Social, Building, and Urban Vulnerability

This work proposes a set of mitigation indicators as a useful tool to assess the ability of project actions to reduce vulnerability in social, building, and urban domains and, therefore, to mitigate peripheralization risk. Those mitigation indicators are selected by reference to vulnerability indicators already established for the location of priority urban areas, for which regeneration programs are targeted.

The vulnerability indicators were chosen as part of the research project in which the work is framed, taking into account those proposed: In the technical-scientific literature, to identify degraded urban areas, with regards to the ‘spatial aspects’ of peripheralization processes; in international reports and guidelines, to measure urban sustainability, with regards to the ‘a-spatial aspects’. In general, the criterion that guided the choice of the final set, consisting of 19 vulnerability indicators, was the identification of the critical factors on which it is possible to act through urban and territorial planning. Furthermore, the quality and availability of the data necessary for their measurement at the census section level, the unit chosen for mapping, was taken into account, such that the method was also transferable to geographical contexts other than the Italian one. In fact, the sources of the data necessary to measure these indicators are census data and other data that can be obtained from ordinary urban planning tools, as already documented in a previous contribution by the authors, to which reference should be made for further information [40].

Specifically, vulnerability indicators reveal the potential aptitude for degradation with regards to: The population, for the social dimension; the buildings, for the building domain; and the urban fabric, for the urban domain. More precisely, the indicators proposed to quantify social vulnerability measure the population tendency to live in a condition of socio-economic hardship: Unemployment rate; failure to reach minimum levels of education; and incidence of older people. These indicators relate to several sub-domains, defined factors of social vulnerability: Employment; education, and culture; and composition of the demographic structure.

Building vulnerability indicators refer, instead, to the quality of the building-housing stock. In particular, they measure the state of conservation and technological obsolescence of buildings.

Lastly, indicators for urban domain measure the fragmentation of urban fabric and the composition of the latter, with reference to non-permeable areas. Other indicators selected for this domain are the lack of services and the presence of urban criticalities, such as underutilized, disused, or abandoned areas and solid waste accumulation zones.

The combination of the abovementioned basic indicators, for each domain, makes it possible to obtain composite indices, representing respectively social, building, and urban vulnerability.

By further composing the latter, it is possible to explicate a single synthetic index of aggregated vulnerability.

The spatialization of the obtained indices, on a certain territory, allows to map both single vulnerabilities and both aggregated vulnerabilities, according to different intensity levels.

In addition, intersected with the exposure map, the aggregated vulnerability map leads to the identification of areas most at risk, to which priority actions should be addressed [40].

That said, in this paper, for the three considered domains, mitigation indicators are selected in order to quantitatively measure the vulnerability factors reduction, pursued by an urban regeneration program. The choice is made with specific reference to the previously defined vulnerability indicators but selecting those on which it is possible to act through a regeneration program, therefore the total number of mitigation indicators is reduced to 10, as better specified below.

With respect to the social domain, the proposed mitigation indicators quantify actions aimed at improving the following:

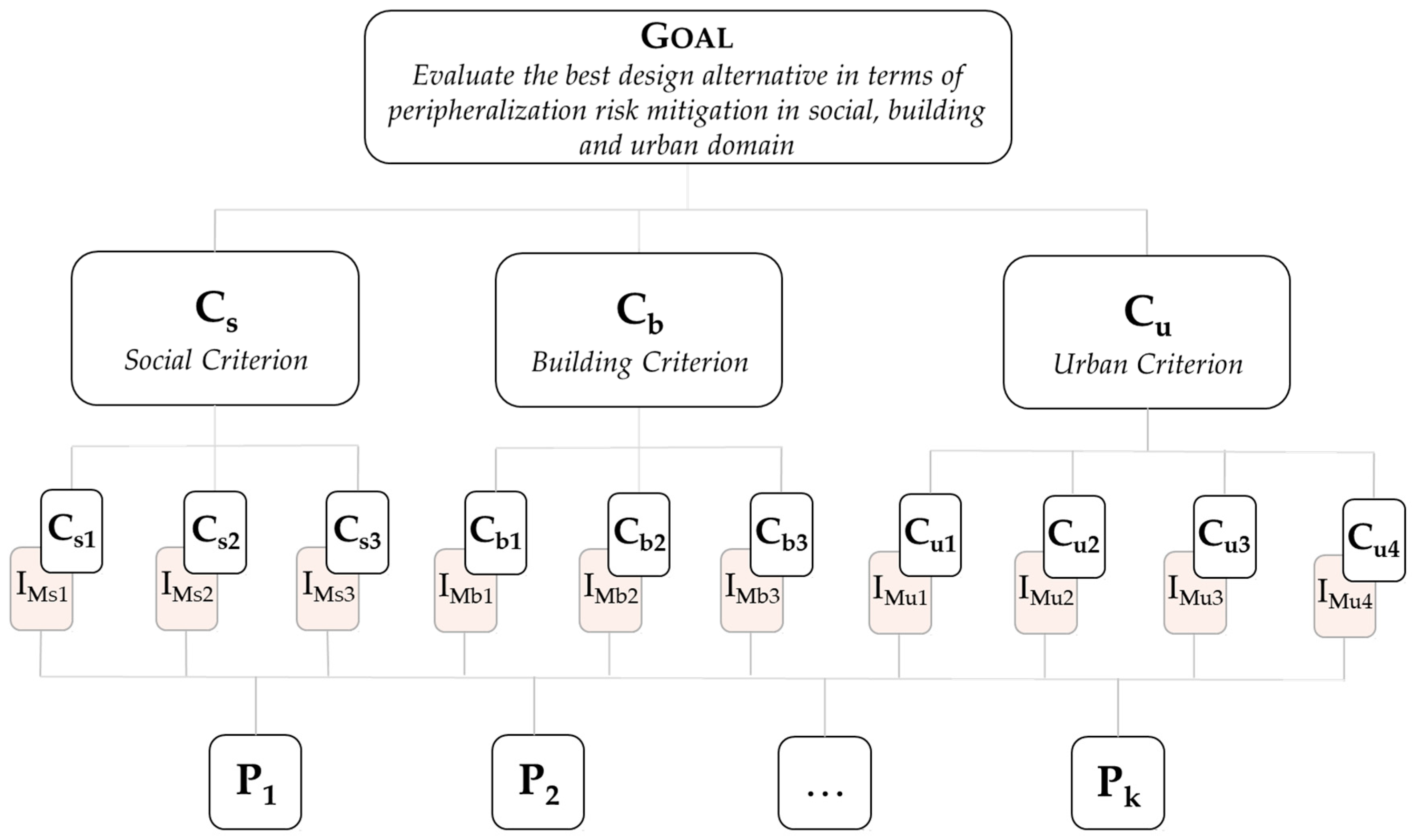
• Employment, in terms of number of new employees (I_Ms1);
• Education, as the number of new graduates in the first-grade secondary school (I_Ms2);
• Demographic structure, as capacity of the physical-functional organization to attract young families (I_Ms3).

The last action can be expressed with a qualitative judgment, which is associated with a proportional value on a scale from 1 to 7. It is the only qualitative indicator out of the total of those proposed.

With regard to the building domain, indicators measure the interventions that determine an improvement of buildings state of conservation and their technological obsolescence, in terms of:

• Number of buildings with historical, architectural, or artistic value subject to restoration (I_Mb1);
• Number of residential buildings subject to maintenance interventions (I_Mb2);
• Improper housing recovered and/or subject to health and hygiene improvements (I_Mb3).

For the urban domain, indicators measure actions aimed to:

• The reduction of urban fabric fragmentation (I_Mu1);
• The increase in permeable green spaces (I_Mu2);
• The improvement of the supply of services for population (I_Mu3);
• The recovery of abandoned and/or degraded areas, such as areas with waste accumulation and potentially contaminated sites (I_Mu4).

The novel dataset of the defined mitigation indicators is presented in

Table 1. Mitigations indicators, unit of measurement, and definition.

	Mitigation Indicator		U.M.	Definition
Social Domain	IMs1	New employees	n.	Number of new employees in the age group corresponding to the workforce
	IMs2	New graduates at secondary school cycle (middle school)	n.	Population of 15 years and over who will obtain a middle school diploma per year
	IMs3	Ability to attract young families	Qualitative judgement (value)	Ability to attract young families of city physical-functional structure: 1, very shoddy: the setting up of young families is strongly discouraged; 2, shoddy: the structure discourages the settlement of young families; 3, very low: the structure has no significant effect on the attraction of young families; 4, low: the city structure is suitable for the settlement of young families; 5, medium: the city structure is particularly suitable for the settlement of young families; 6, medium high: the setting up of young families is encouraged; 7, high: the setting up of young families is strongly encouraged.
Building Domain	IMb1	Recovered buildings of historical, architectural or artistic value	n.	Number of buildings with historical, architectural or artistic value subject to restoration.
	IMb2	Recovered residential buildings in bad and mediocre conservation state	n.	Number of residential buildings subject to extraordinary maintenance or renovation
	IMb3	Improper housing recovered	n.	Number of improper housing subject to health and hygiene improvements.
Urban Domain	IMu1	Edge Density	m/ha	Ratio between total sum of perimeters of the polygons of built up areas and the total surface of investigated area.
	IMu2	Increment of permeable areas	m2	Surface for additional permeable areas.
	IMu3	Increase in urban planning standards	m2	Surface provided for additional urban planning standards.
	IMu4	Recovered urban critical areas	m2	Surface of enclosed recovered spaces: abandoned production areas; areas with newly built artifacts that have not been used; undeveloped areas devoid of specific use or abandoned; areas with waste accumulation.

.

The necessary data to quantify the aforementioned mitigation indicators can be obtained by analyzing the urban regeneration programs under the decision-maker’s examination

3. An Innovative Model for the Optimal Selection of Design Alternatives for Vulnerability Mitigation

Once the mitigation indicators have been defined, the procedure is divided into the phases of the AHP method: Structure the problem hierarchically; build the decision matrix; compare judgements; and summarize priorities [41].

The hierarchy definition is a fundamental phase for modeling a complex problem [42]. In the proposed methodology, the dominance hierarchy consists of three levels (Figure 1).

At the highest level there is the goal, which in this case is to evaluate the best design alternative in terms of peripheralization risk mitigation in the social, building, and urban domains. At the second level there are the criteria (C_i), which correspond to the vulnerability domains: The social criterion (C_s); the building criterion (C_b); and the urban criterion (C_u). At the third level, there are the sub-criteria, corresponding to mitigation indicators (C_ij = I_Mij), in which there are three for the social criterion (C_s1 = I_Ms1, C_s2 = I_Ms2, C_s3 = I_Ms3), three for the building criterion (C_b1 = I_Mb1, C_b2 = I_Mb2, C_b3 = I_Mb3), and four for the urban criterion (C_u1 = I_Mu1, C_u2 = I_Mu2, C_u3 = I_Mu3, C_u4 = I_Mu4). The 10 overall sub-criteria are measurable for each k-th design alternative among which the decision maker is called to choose, in order to mitigate vulnerability component of risk for the study area.

The quantitative values of mitigation indicators for each design alternative are at the terminal level of the hierarchy and constitute the lines of the decision matrix. The comparison between the judgments has the aim of measuring the relative importance of criteria and sub-criteria with respect to the general objective. For this purpose, with reference to the decision matrix, this phase is divided into further sub-phases: Pairwise comparison of the design alternatives with respect to each sub-criterion; pairwise comparison of sub-criteria; pairwise comparison of criteria; and synthesis of priorities.

In the calculation of the orders, each proposal has a priority equal to:

PP_k: ∑ wP_kij × wC_ij × WC_i

(1)

where

• PP_k = priority of the k-th project proposal
• wP_kij = normalized vector of sub-criteria for each project proposal
• wC_ij = normalized vector of sub-criteria for each domain
• WC_i = normalized vector of criteria
• (with k = 1, …, n; i = s, b, u; j = 1, …, 4)

The last phase consists of choosing the best design alternative on the basis of the evaluation carried out (Figure 2).

4. Study Area and Project Alternatives

The case study concerns an area of Marcianise Municipality, belonging to the Caserta conurbation in Campania Region (Italy), which is located close to the Metropolitan Area of Naples.

It is a conurbation of 16 municipalities resulting from the merger, which began after the war, of the neighboring municipalities to the city of Caserta, the capital of the same name province. The Caserta conurbation is considered one of the most complex territories in Italy, because of lack of employment, urban disorder, and significant environmental pollution, due to existing production activities and the often illegal disposal of municipal solid waste [43].

The intervention area is located in an urban continuum, bordering Municipalities of San Marco Evangelista and Capodrise. It is delimited to the east by the motorway axis, Naples-Rome route, and by an industrial agglomeration, while, on the remaining three sides, it is connected to the surrounding urban fabric by road axes (Figure 3).

The area in question, with a surface of approximately 50 ha, is the largest of the three, which were identified as priorities for intervention in Marcianise Municipality, by the analysis of peripheralization risk conducted as part of the research project in which this contribution is framed (Figure 4).

The analysis of the most recent municipal urban planning instrumentation shows that the study area is subject to a complex program, in particular an Urban Recovery Program (PRU), due to the conditions of overall degradation by which it is affected. This circumstance validated the high peripheralization risk, already demonstrated through the analysis carried out for the Marcianise Municipality [40]. Therefore, among the three areas found to be at risk R3 and R4, the aforementioned area is selected as a case study in this work, being already destined for an urban regeneration intervention by policy makers, called upon to choose between different design alternatives.

From the analysis of the cognitive framework of the area targeted for the PRU, made available by the Marcianise Municipality [44], it emerges that there is significant social degradation due to the lack of employment and the lack of attractiveness for the younger generations. This confirms the high social vulnerability resulting from the previously carried out risk analysis.

With reference to the urban domain, the cognitive framework confirms the high vulnerability. In fact, the area under examination is characterized by a mainly residential consolidated urban fabric, with some unbuilt enclosed lots in a state of neglect and decay. The fabric is fragmented at the edges and made up of large, completely waterproof surfaces that generate heat islands. Furthermore, there are several disused public areas and structures in conditions of evident degradation. The study area also includes urban planning standards, which, however, are not sufficient according to current legislation. The structure of the study area results from the implementation of an economic and popular building plan, foreseen by the General Town Plan pursuant to the law of 18 April 1962, n. 167.

As a consequence, a high percentage of public residential buildings (IACP) can be noted, which are in a fairly good state of conservation, as are the other private buildings in the study area. This circumstance confirms the low degree of building vulnerability, resulting from the risk analysis carried out.

The three urban regeneration project proposals under consideration by the decision maker are: The PRU, corresponding to the P₁ project proposal (Figure 5); two subsequent modifications of the same PRU, corresponding to P₂ and P₃ project proposals, respectively in Figure 6 and Figure 7.

The examination of the three project proposals shows that each of them presents a plurality of interventions, but it is possible to identify specific guiding principles. P₁ proposal pays particular attention to the de-sealing of completely impervious surfaces. P₂ proposal gives emphasis to social animation, making the study area highly attractive to young families thanks to the creation of jobs and greater reception in schools. P₃ proposal emphasizes the increase in services of collective interest.

5. Application of the Model

The application of the model to the study area requires a careful analysis of the interventions foreseen in each of the three project proposals to be examined by the decision maker. This operation allows to determine the value of the mitigation indicators for each of the three design alternatives, so as to construct the decision matrix. From the latter, the matrices useful for the comparison between sub-criteria and criteria with respect to the general objective are extrapolated.

In this way, the vectors wP_kij, wC_ij, WC_i are defined, in order to apply the formula (1) and obtain the priority of each proposal. The individual phases mentioned above are clarified in detail in the following paragraphs.

5.1. Construction of the Decision Matrix

The values of mitigation indicators, for each design alternative, constitute the lines of the decision matrix, while the columns refer to the value of a single sub-criterion for each of the three P_k proposals (with k = 1, 2, 3).

For the implementation of the model it is necessary to derive a scalarized matrix. For this purpose, the sub-criteria values expressed according to a qualitative assessment can be replaced with the relative values obtained through a judgment scale. This is the case of C_s3 sub-criterion, which is low for P₁ proposal, high for P₂ proposal, and medium-high for P₃ proposal. The corresponding scores are 3, 7, and 6 (

Table 2. Scalarized decision matrix for the case study.

	Cs1 [n.]	Cs2 [n.]	Cs3 [value]	Cb1 [n.]	Cb2 [n.]	Cb3 [n.]	Cu1 [m/ha]	Cu2 [m2]	Cu3 [m2]	Cu4 [m2]
P1	33	0	3	0	0	5	0.0337	13,366.7	16,164.9	7059.52
P2	62	50	7	1	41	3	0.0333	5549.5	27,501.8	7059.52
P3	37	0	6	1	41	5	0.0334	11,565.0	36,852.8	7059.52

).

5.2. Pairwise Comparison of the Design Alternatives

We now proceed to the pairwise comparison of P_k design alternatives with respect to each sub-criterion. Hence, for the 10 sub-criteria, there are 10 comparison matrices. The latter are 3×3 matrices, in which the P_i appear, both in line and in column, while the a_ij elements represent the dominance coefficients. Thus, the values of individual columns are obtained from the scalarized decision matrix: An example, for the values of the C_s1 subcriterion, is in

Table 3. Values of criterion C_s1 for each design alternative.

	P1	P2	P3
Cs1	33	62	37

. We then proceed to the comparison between the different alternatives using the Saaty semantic scale (

Table 4. Semantic scale of Saaty.

Intensity	1	3	5	7	9	2-4-6-8
Judgement of Importance	Equal	Moderate	High	Very High	Extreme	Intermediate levels

).

After positioning the two compared values on this scale, if they are in the same band, the dominance coefficient a_ij of each value with respect to the other is 1; if there is one band, a_ij is 3 for the highest value, it is reciprocal for the lowest value; if there are two bands, the coefficient has a value of 5 for the highest value, 1/5 for the lowest value, and so on. The intermediate coefficients express intermediate situations.

The main diagonal of the matrix is obviously identical, and the property of coefficients reciprocity applies. As an example, Figure 8 shows the comparison between P₁ and P₂.

In the same way, the comparison matrix for the C_s1 sub-criterion is developed (

Table 5. Pairwise comparison matrix of the alternatives for C_s1 sub-criterion.

	P1	P2	P3
P1	1	1/6	1
P2	6	1	5
P3	1	1/5	1

).

Each matrix can be normalized using the simplified Fishburn method: Each cell must be divided by the sum of the corresponding column values [45]. The arithmetic mean of each line is then calculated. By repeating this operation for each of the 10 matrices, the wP_kij vector is composed (

Table 6. Pairwise comparison matrix of the alternatives for the C_s1 sub-criterion and wP_kij vector.

	P1	P2	P3	wPkij
P1	0.125	0.122	0.143	0.130
P2	0.750	0.732	0.714	0.732
P3	0.125	0.146	0.143	0.138

).

At this point, the consistency of the matrix is checked. It is verified in all cases since the consistency ratio is less than 5, which is the limit of the rank 3 matrices [46].

5.3. Pairwise Comparison of Sub-Criteria

The pairwise comparison of sub-criteria belonging to the same domain aims to establish their mutual importance. Therefore, three matrices are built, one for each criterion or domain. In the matrices for the pairwise comparison of sub-criteria, the dominance coefficients are assumed equal to 1. As in the previous comparison, applying the Fishburn method and carrying out the arithmetic mean for each line, the wC_ij vector is composed.

Table 7. Normalized matrix for pairwise comparison of C_s sub-criteria to obtain wC_ij vector.

	Cs1	Cs2	Cs3	wCij
Cs1	0.333	0.333	0.333	0.333
Cs2	0.333	0.333	0.333	0.333
Cs3	0.333	0.333	0.333	0.333

shows the example relating to the social criterion. It should be noted that, for the latter, three sub-criteria have been defined (C_s1, C_s2, C_s3), to which it was chosen to attribute equal importance. Therefore, the normalized matrix presents values that are all equal to 1/3. This also applies to the building criterion, for the same logic. For the urban criterion, according to a similar reasoning, the normalized matrix has values that are all equal to 1/4. In this case, it is verified that the consistency ratio is lower than 5 for the rank 3 matrices (social and building domains) and less than 9 for the rank 4 matrix (urban domain).

5.4. Pairwise Comparison of Criteria

The pairwise comparison of criteria aims at establishing the importance of one domain over the other. Two different scenarios are proposed, in order to reduce the evaluation subjectivity.

In scenario 0, all criteria are of equal importance. After building the pairwise comparison matrix of criteria with the same procedure previously seen, we proceed similarly with the normalization and calculation of the arithmetic mean of each line, composing the WC_i vector (

Table 8. Normalized matrix for pairwise comparison of criteria and WC_i vector–Scenario 0.

	Cs	Cb	Cu	WCi
Cs	0.33	0.33	0.33	0.33
Cb	0.33	0.33	0.33	0.33
Cu	0.33	0.33	0.33	0.33

). Even in this case, since there are three criteria (C_s, C_b, C_u) and in Scenario 0, they have the same importance, the matrix corresponding to this scenario has values that are all equal to 1/3. As it is a matrix of rank 3, it is verified that the consistency ratio is less than 5.

Therefore, Scenario 1 is proposed, in which different importance is attributed to the social, building, and urban criteria, depending on the pre-existing vulnerability level in the corresponding social, building, and urban domains. The vulnerability level is that resulting from the peripheralization risk analysis. Vulnerability maps, for each domain, return different vulnerability classes: Low-medium-high-very high. The higher the vulnerability of a specific domain is, the more important the actions addressed to that particular domain are. Low, medium, high, and very high values can be converted into proportional scalar values. Specifically, the scalars 1, 2, 3, and 4 correspond respectively to the low, medium, high, and very high values. Then, we proceed with the comparison in pairs between vulnerability classes, with the ultimate aim to establish the relative importance of the elements according to the scale in Figure 9. This figure allows you to divide the four intervals 1 (low), 2 (medium), 3 (high), and 4 (very high) into the 5 typical Saaty value ranges 0–0.8–1.6–2.4–3.2–4 returned in the lower part of the figure. In this way, it is possible to obtain a support matrix for the decision maker (

Table 9. Matrix for assigning weights to the criteria.

	Low	Medium	High	Very High
Low	1.000	0.333	0.167	0.111
Medium	3.000	1.000	0.333	0.167
High	6.000	3.000	1.000	0.333
Very High	9.000	6.000	3.000	1.000

).

The analysis of vulnerability maps for the case study shows the presence of potential social and urban degradation, while the building vulnerability is low (Figure 4).

Thus, in Scenario 1, the social criterion is high, the building criterion is low, and the urban criterion is high.

Table 10. Pairwise comparison matrix of criteria—Scenario 1.

	Cs (High)	Cb (Low)	Cu (High)
Cs (High)	1	6	1
Cb (Low)	0.167	1	0.167
Cu (High)	1	6	1

represents the comparison matrix between criteria.

Like Scenario 0, we proceed by normalizing the matrix and averaging. Then, the WC_i vector is composed (with i = s, b, u), obtaining the final matrix in

Table 11. Normalized matrix for pairwise comparison of criteria and WC_i vector—Scenario 1.

	Cs	Cb	Cu	WCi
Cs	0.462	0.462	0.462	0.46
Cb	0.077	0.077	0.077	0.07
Cu	0.462	0.462	0.462	0.46

, whose consistency is also verified.

5.5. Summary of Priorities

In order to evaluate priority of one project proposal over the other, the principle of hierarchical composition is used. The formula (1) already defined for the calculation of PP_k is applied, determining the importance of each element of the hierarchy in relation to the objective. Finally, with reference to the proposed scenarios, the related summary matrices are obtained (

Table 12. Final synthesis matrix—Scenario 0.

	CS (social)			Ce (Building)			Cu (Urban)				Priority
Wci	0.333			0.333			0.333
	CS1	CS2	CS3	Ce1	Ce2	Ce3	Cu1	Cu2	Cu3	Cu4
wCij	0.333	0.333	0.333	0.333	0.333	0.333	0.250	0.250	0.250	0.250
wP1	0.130	0.091	0.074	0.053	0.053	0.455	0.333	0.591	0.080	0.333	0.200
wP2	0.732	0.818	0.643	0.474	0.474	0.091	0.333	0.075	0.265	0.333	0.403
wP3	0.138	0.091	0.283	0.474	0.474	0.455	0.333	0.334	0.656	0.333	0.313

and

Table 13. Final synthesis matrix—Scenario 1.

	CS (social)			Ce (Building)			Cu (Urban)				Priority
Wci	0.4615			0.0769			0.4615
	CS1	CS2	CS3	Ce1	Ce2	Ce3	Cu1	Cu2	Cu3	Cu4
wCij	0.333	0.333	0.333	0.333	0.333	0.333	0.250	0.250	0.250	0.250
wP1	0.130	0.091	0.074	0.053	0.053	0.455	0.333	0.591	0.080	0.333	0.205
wP2	0.732	0.818	0.643	0.474	0.474	0.091	0.333	0.075	0.265	0.333	0.425
wP3	0.138	0.091	0.283	0.474	0.474	0.455	0.333	0.334	0.656	0.333	0.253

). By observing these matrices, it can be noticed that all values are equal, except the row corresponding to the WC_i vector and the priority column. The values are the same because the sub-criteria have been given equal importance, therefore equal weight, both in the comparison between project proposals in relation to each sub-criterion, both in the comparison between the sub-criteria. Instead, the values of the WC_i vector change because in Scenario 0 the same importance is attributed to the criteria, while in Scenario 1, the criteria are weighted according to the pre-existing vulnerability level. Consequently, the values in the priority column are also different.

6. Results and Discussion

Scenario 0 highlights how the best design alternative is P₂: P₂ alternative is of 0.09 priority over P₃, while P₂ is twice the distance from the P₁ alternative (Figure 10).

In Scenario 1, the most effective project proposal is still P₂ alternative. However, compared to Scenario 0, there is a greater dominance of P₂ proposal over P₃ proposal. On the other hand, the difference between P₁ and P₂ remains almost unchanged (Figure 11).

So, the analysis returns the same hierarchical order, only with more marked distances in Scenario 1 compared to Scenario 0. This is because Scenario 1 maximizes the reduction of pre-existing vulnerability levels. In fact, P₂ design alternative poses greater attention to the resolution of social and urban problems, where there are higher levels of vulnerability for the area in question.

The P₂ and P₃ proposals are quite similar to each other in terms of the number of interventions, almost double compared to those of the P₁ proposal, in which the redevelopment of the IACP buildings is not foreseen, and not even some services for the community, present instead in the others two proposals.

However, when less importance is given to the building criterion (Scenario 1), it emerges that the P₂ proposal ensures a more effective reduction of the pre-existing vulnerability levels for the area in question.

The mitigation indicators and the hierarchical model here described are proposed specifically to allow comparison between alternative projects in order to mitigate the social, building, and urban critical issues of an intra-city area. By measuring these indicators and applying the proposed model, it is possible to quantify the real extent of the interventions in relation to risk mitigation. This allows for an easier decision, especially when the design alternatives seem similar.

With respect to the multicriteria methods already used in the technical literature to evaluate urban regeneration programs, described in Section 1, the main novelty of the work is the approach pursued, based on the integration between the localization phase of the interventions and the evaluation phase of the most effective project. Such an approach, on the one hand, allows to operate where it is a priority; on the other, it makes the decision an intelligent process, which is informed of the pre-existing vulnerability levels. This allows the decision maker to select the design alternative that minimizes the actual vulnerability of an urban area, giving greater emphasis to the truly necessary interventions. In this way, in addition to effectively mitigating the risk, it is possible to optimize the economic resources to be invested in the implementation of the project actions.

However, it should be clarified that the proposed methodology presupposes the prior identification of priority areas of regeneration interventions, which coincide with those with the highest peripheralization risk. Given that a high risk level depends on a significant aggregated vulnerability, the methodology used to estimate the latter is fundamental. This is particularly true as there is no agreement in the international scientific community both on the most suitable set of vulnerability indicators and on the methods of combining them. In the broader research project into which the work is framed, a set of indicators has already been proposed with reference to the three social, building, and urban domains, and a method of combining them based on fuzzy logic is carried out to manage the uncertainty related to the vulnerability assessment [40].

Despite this, quantitative knowledge of the fragility of urban areas in the social, building, and urban dimensions is fundamental for building truly effective mitigation scenarios, contemporary challenges of Urban Intelligence, and Urban Knowledge.

Furthermore, this knowledge allows to reduce the subjectivity of the multicriteria evaluation model implemented according to the AHP logic.

It is also interesting to note that urban regeneration interventions can also have negative effects over time, in particular in relation to the aforementioned phenomenon of gentrification. The proposed support model for decision makers in choosing the most effective design alternative is specifically aimed at selecting the urban regeneration program that maximizes the reduction of pre-existing vulnerability levels. However, another factor to be taken into account in the decision may be to what extent the interventions produce negative effects, such as the expulsion of the original inhabitants due to the increase in property value. Several strategies are proposed in the technical literature and in practice to mitigate the displacement phenomenon, including avoiding the demolition and privatization of public housing buildings; initiating awareness campaigns regarding speculative interventions; establishing anti-eviction zones [47]; and providing for specific anti-displacement programs, including private initiatives [48,49]. In the case study, none of the project proposals being examined by the decision maker envisages the demolition or privatization of the IACP buildings, for which redevelopment with public funds is also planned in the proposals P₂ and P₃. This feature can certainly help to ensure a certain social mix in the study area and to mitigate the gentrification resulting from the implementation of the interventions. Although, the pursuit of the latter objective is not expressly declared by the municipality of Marcianise.

7. Conclusions

The research proposes a decision support tool based on the AHP method to evaluate the effectiveness of urban regeneration interventions envisaged in areas where the levels of peripheralization risk are significant. Specifically, the effectiveness of the interventions in terms of mitigation of the pre-existing vulnerability is assessed, in the social, building, and urban dimensions.

For this purpose, a set of mitigation indicators is defined, with reference to each vulnerability factor considered for the location of priority areas of intervention. Mitigation indicators are selected in order to analytically estimate the benefits that the projects are capable of generating, in terms of lowering vulnerability indicators values.

Once the values of the mitigation indicators have been clarified, the study proposes a multi-criteria model for the choice between possible urban regeneration interventions. The model is based on hierarchical analysis algorithms, which allow the management of a significant number of indicators. The proposed model has the advantage of determining the design solution that maximizes the reduction of pre-existing vulnerability levels. Furthermore, the best solution selected is the ideal alternative with which to compare different proposed solutions.

The application of the proposed method to the case study demonstrates that design alternatives apparently similar in number and type of interventions may have different effectiveness in relation to the reduction of social, building, and urban vulnerability.

The selection of the mitigation indicators set is carried out in order to build a complete, non-redundant, and coherent set, so as to favor consistency in the subsequent hierarchical analysis. Furthermore, the indicators set is generalized for an urban regeneration intervention and can also be used for monitoring the improvement effects produced by the same intervention on the individual vulnerability factors.

Research developments lie in the integration, in the proposed analysis scheme, of specific indicators measuring mitigation of other potential degradation factors, such as those relating to energy poverty and environmental justice [50,51,52], which certainly can contribute to determining peripheral conditions.

In addition, further investigations of the work may concern how to take into account, in the decision-making process, the extent to which the interventions are able to mitigate any negative effects produced by the interventions themselves over time, such as the phenomenon of gentrification. This aspect is of fundamental importance to discourage the creation of peripheral conditions determined by factors of social vulnerability in other parts of the city.