Design of Rotor Blades for Vertical Axis Wind Turbine with Wind Flow Modifier for Low Wind Profile Areas
Abstract
1. Introduction
- To design a WFM-based VAWT for low wind profile urban areas.
- To investigate the characteristics of the proposed model against conventional wind turbine models.
- To examine the lift–drag coefficient, lift–drag forces, torque, power coefficient, and power of the WFM-VAWT model at various turbine speeds.
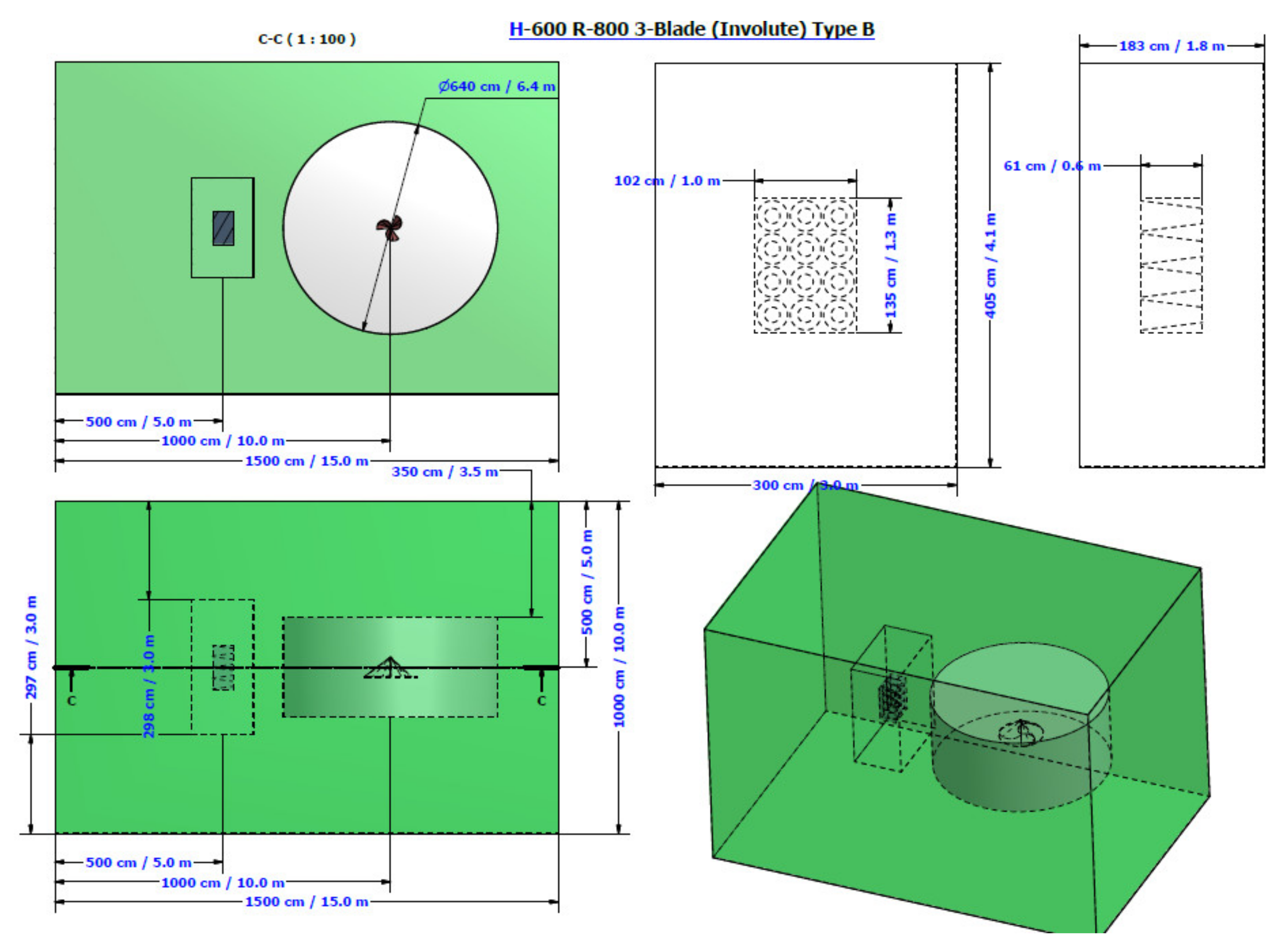
2. Proposed Rotor Model Geometry
- Case 1
- H-type Rotor with C-blade
- Case 2
- Involute blade type rotor
- Case 3
- Involute rotor with a wind flow modifier
2.1. Case 1: H-Type Rotor with C-Blade
2.2. Case 2: Involute Blade (Lift Force) Type Rotor
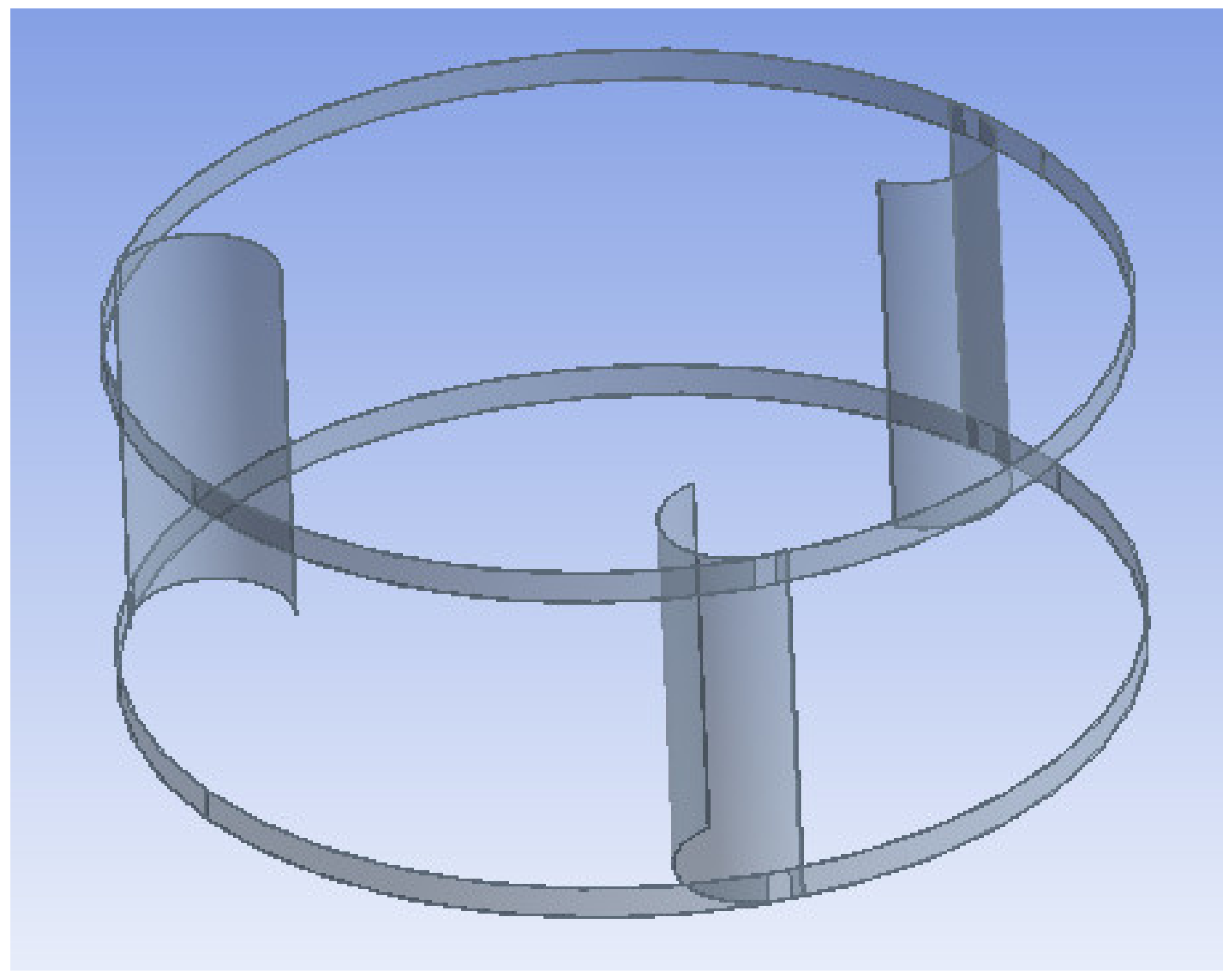
2.3. Case 3: Involute-Type Rotor with WFM
3. Numerical Solution Methods
3.1. General Governing Equations
3.2. Selection of Turbulence Model
3.3. Wind Turbine Governing Equations
4. Computational Arrangement for the Simulation
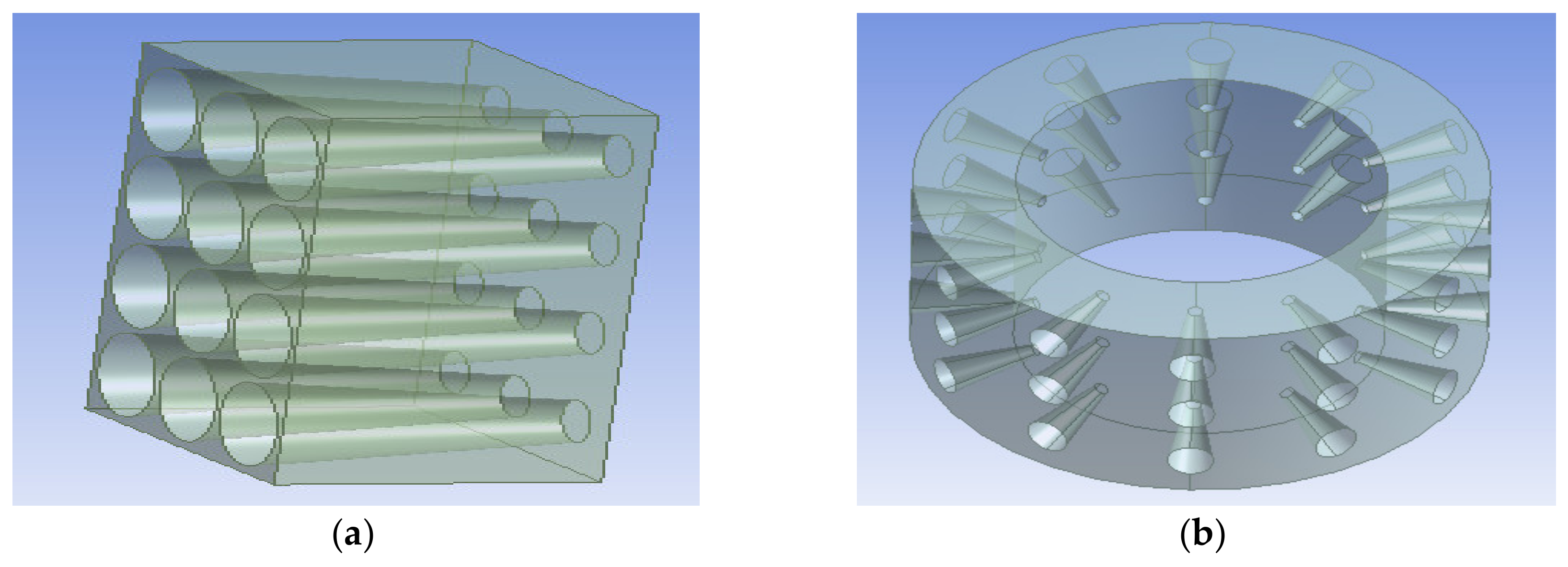
4.1. Computational Domain
4.2. Computational Meshing
4.3. Computational Solution Setup
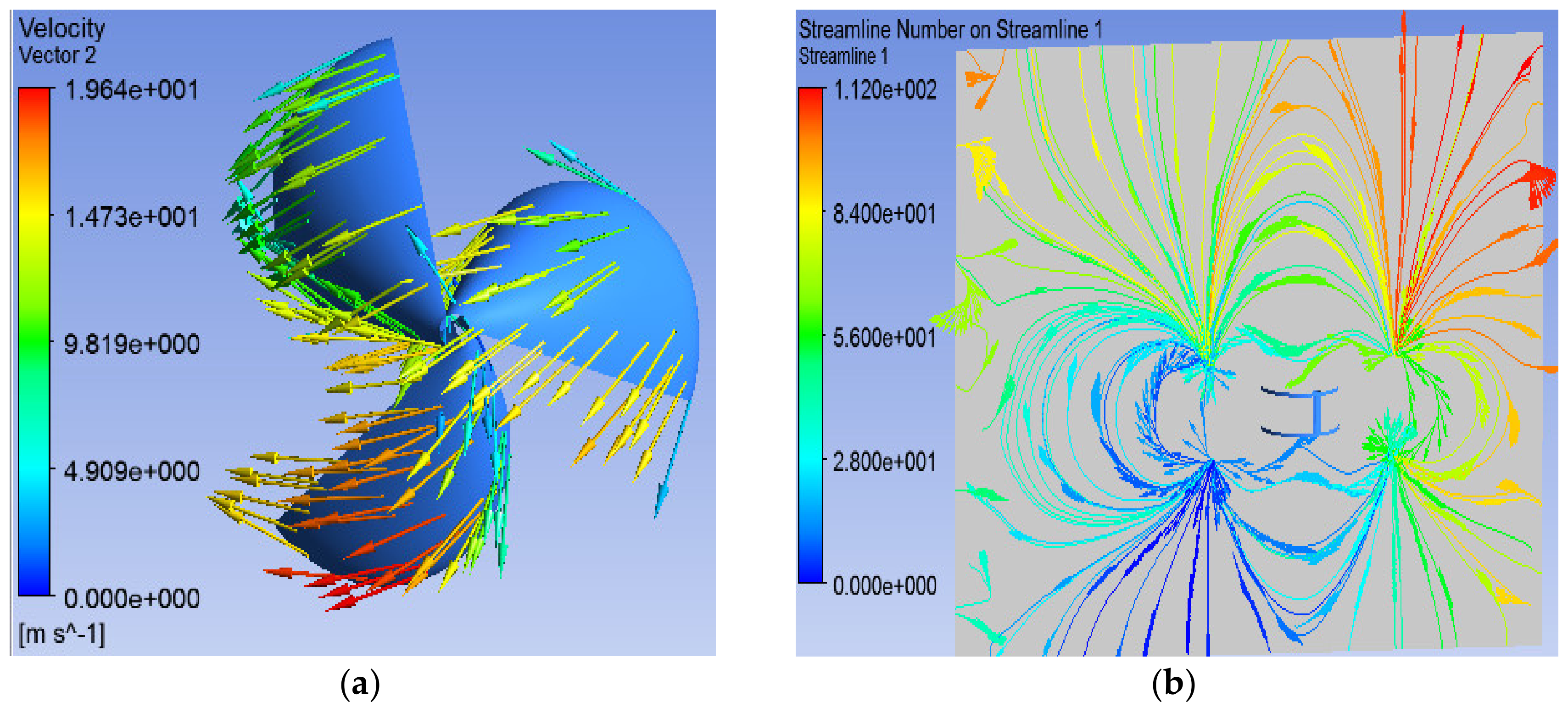
5. Simulation Results
5.1. Case 1: C-Shaped H-Type
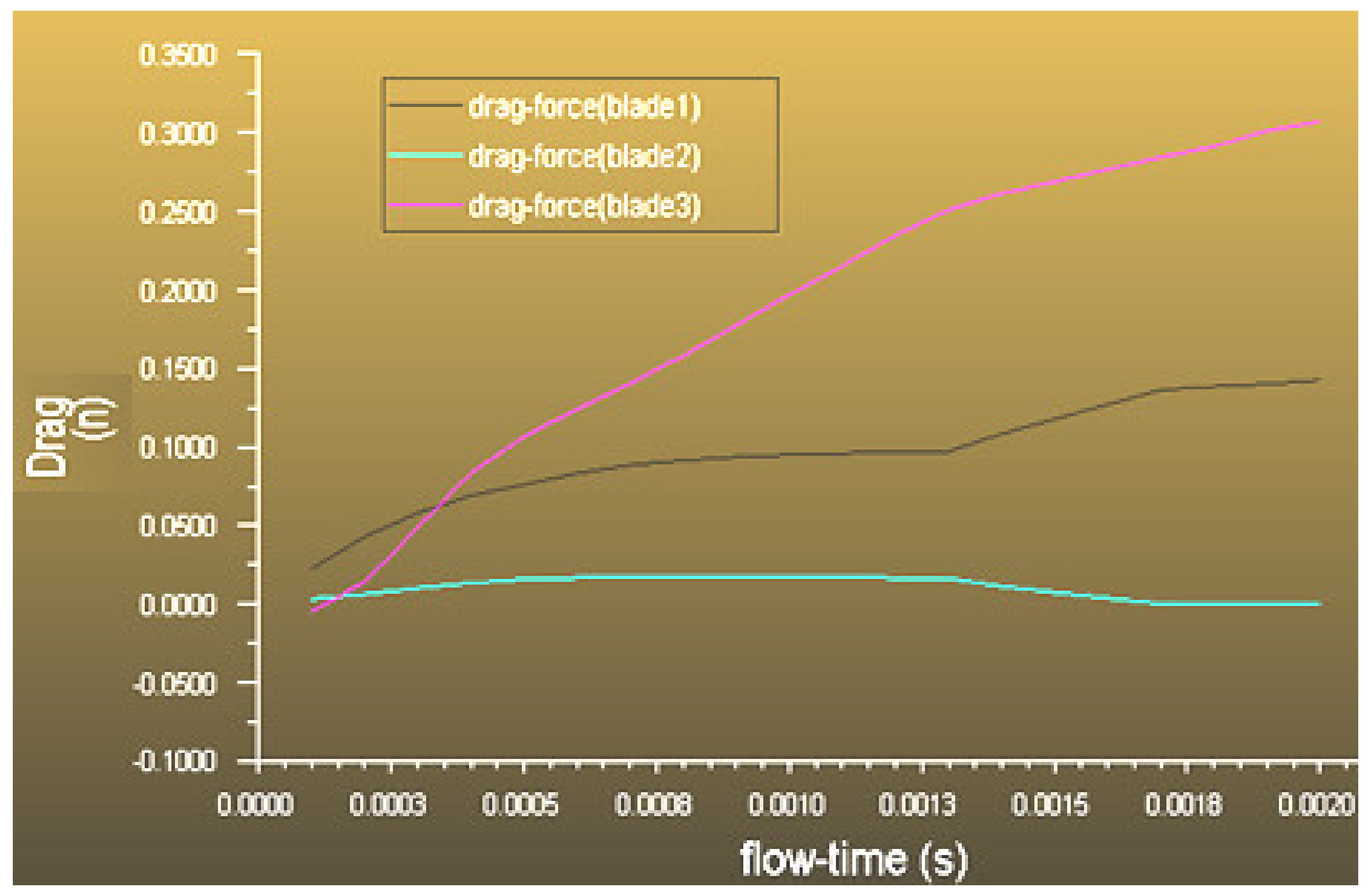
5.1.1. Individual Blade Performance
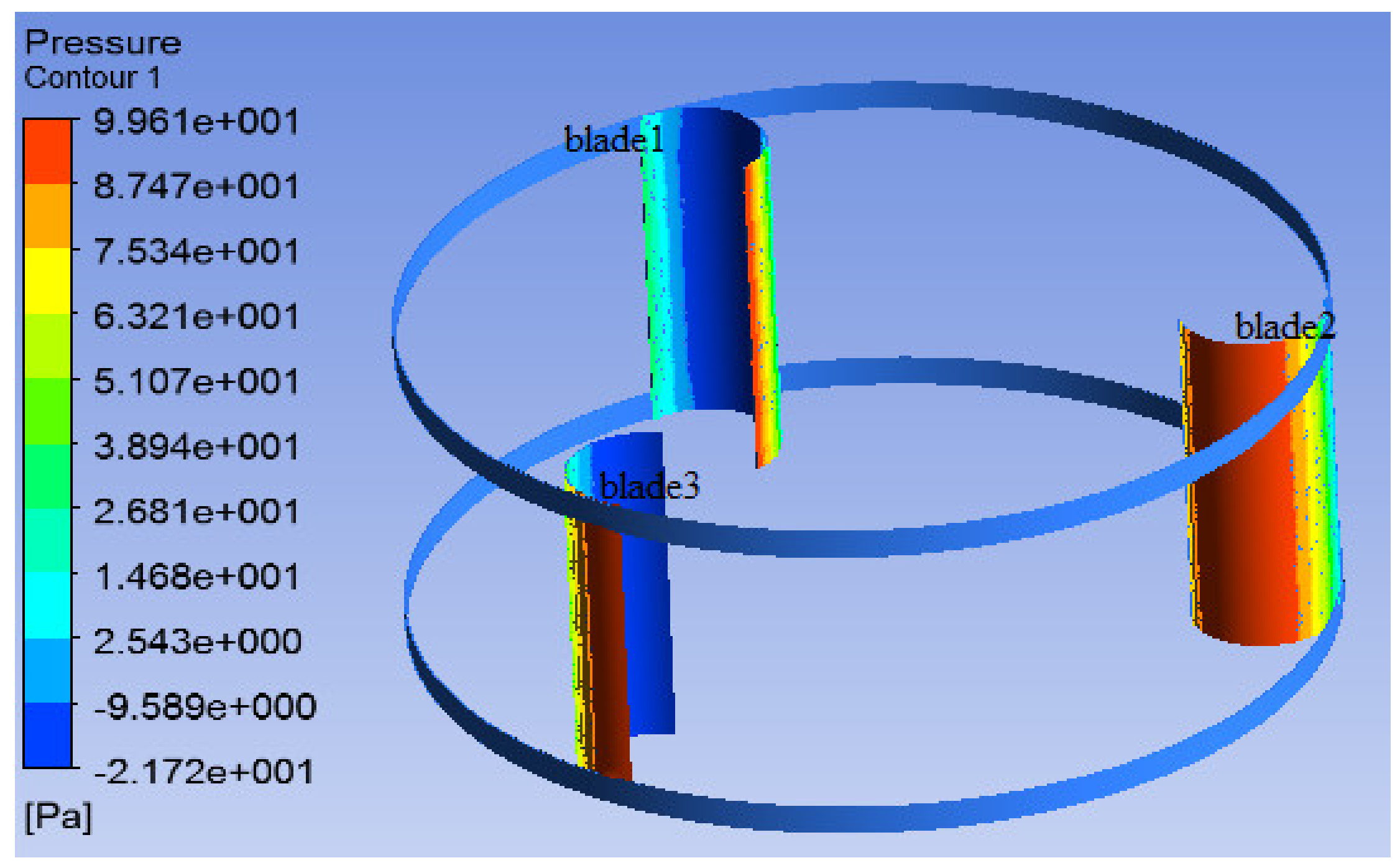
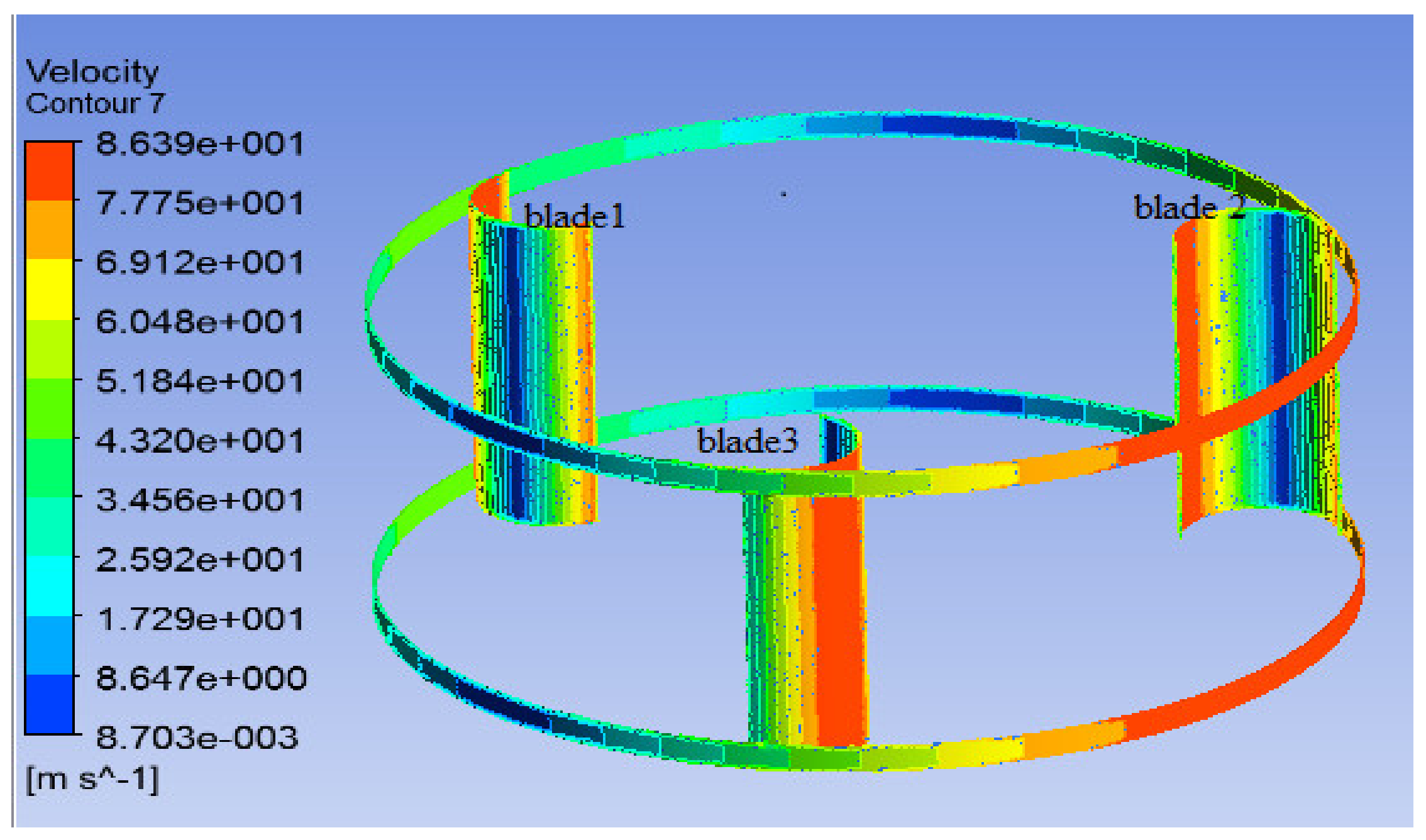
5.1.2. Rotor Performance
5.2. Case 2: Involute Type
5.2.1. Individual Blade Performance
5.2.2. Rotor Performance
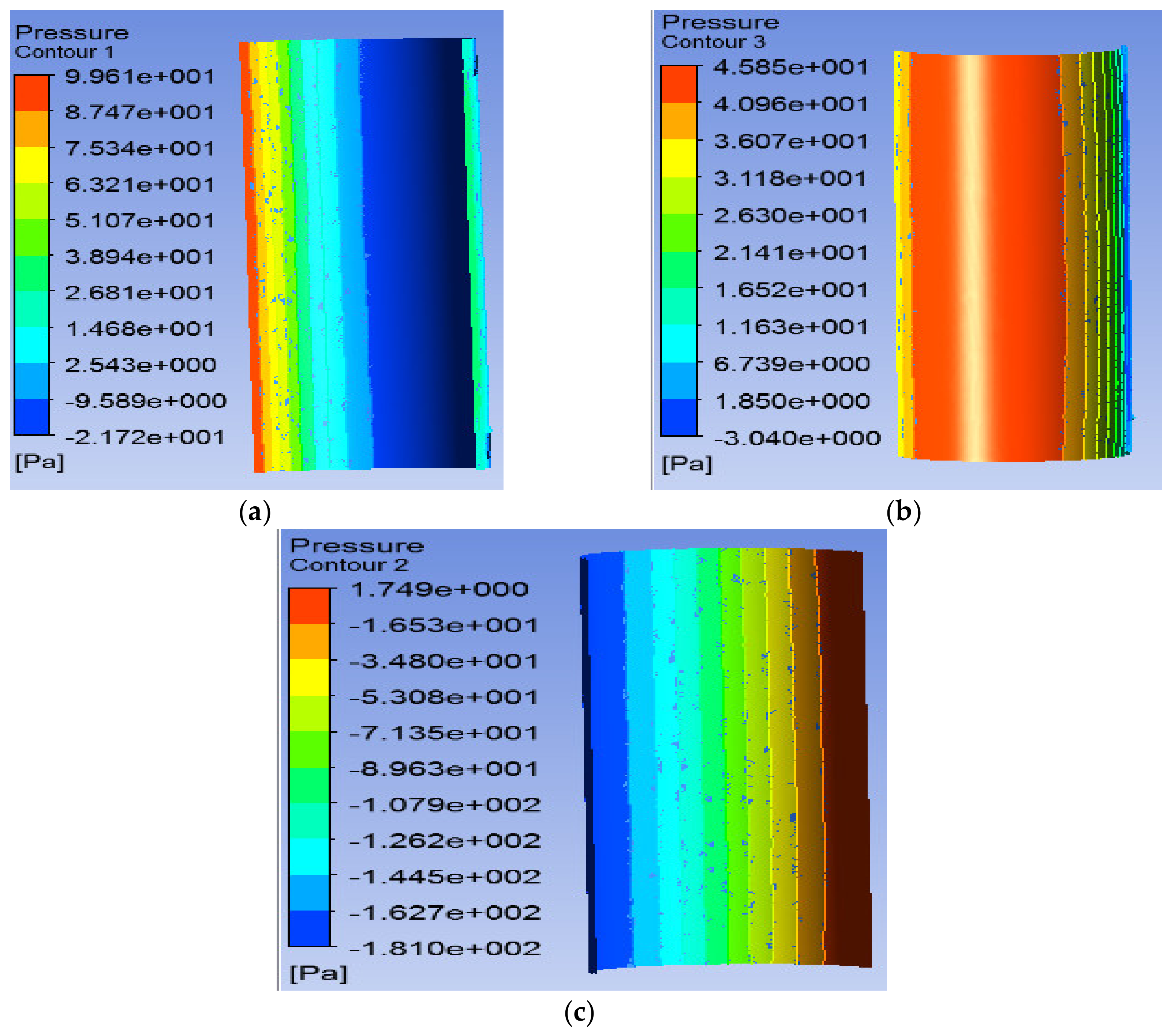
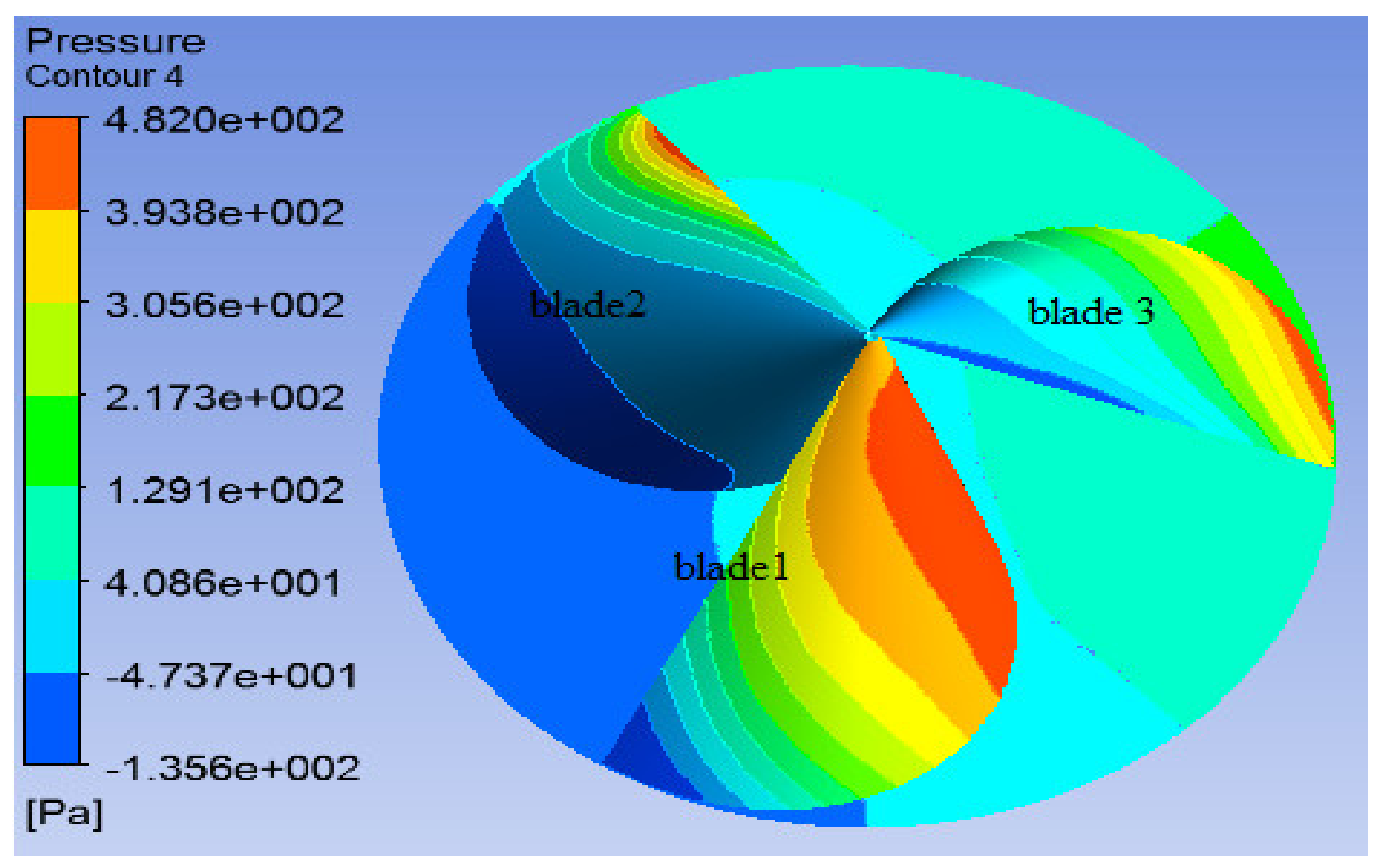
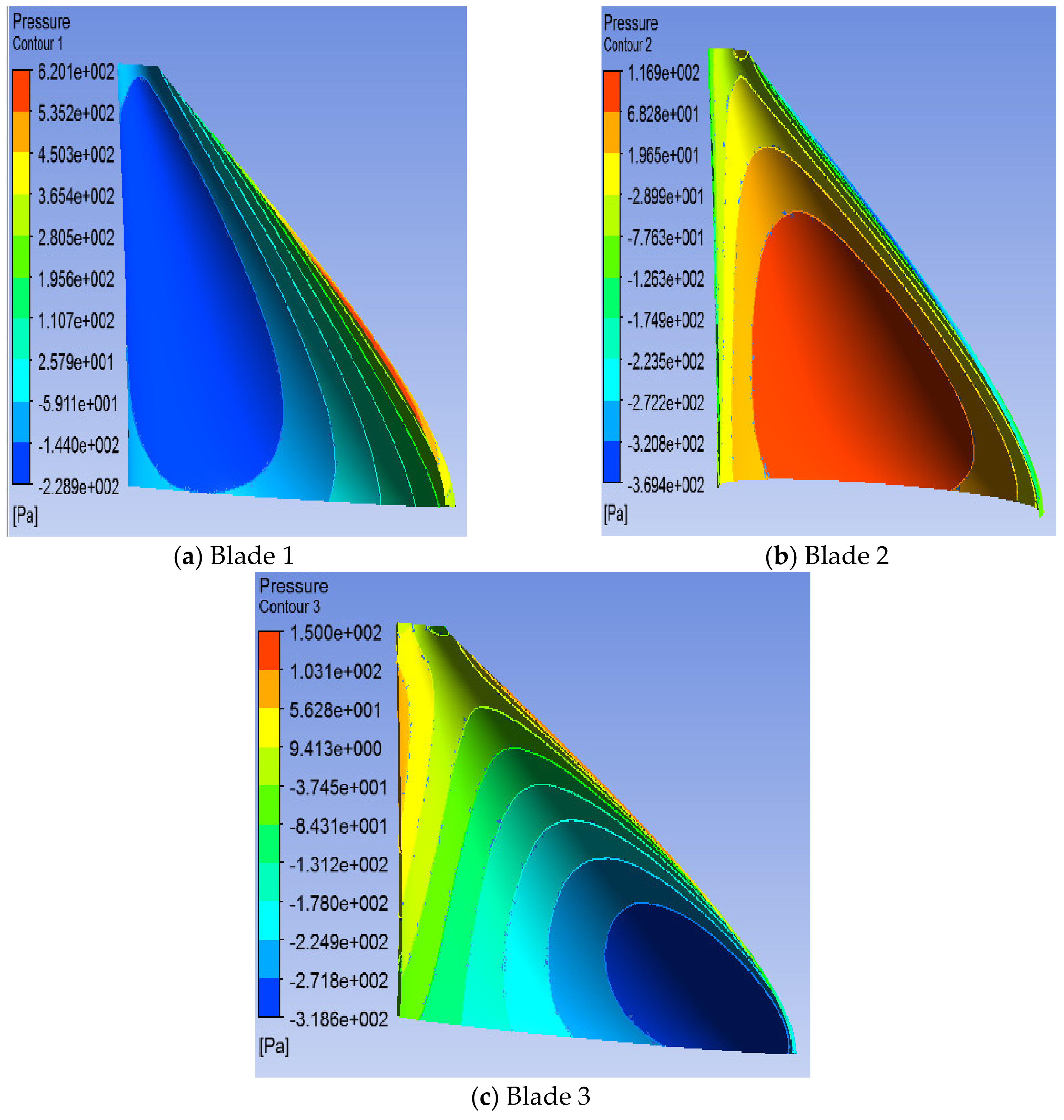
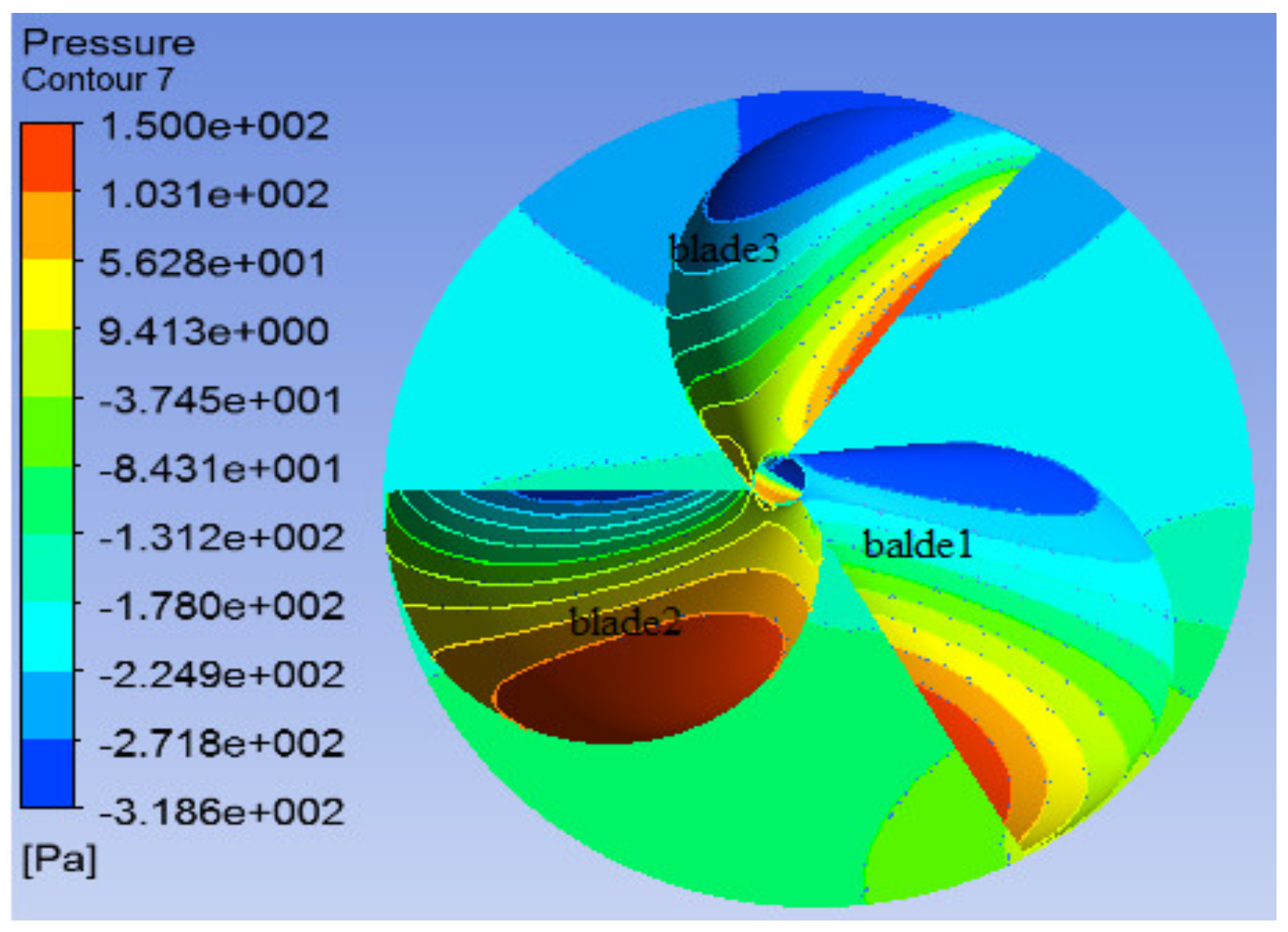
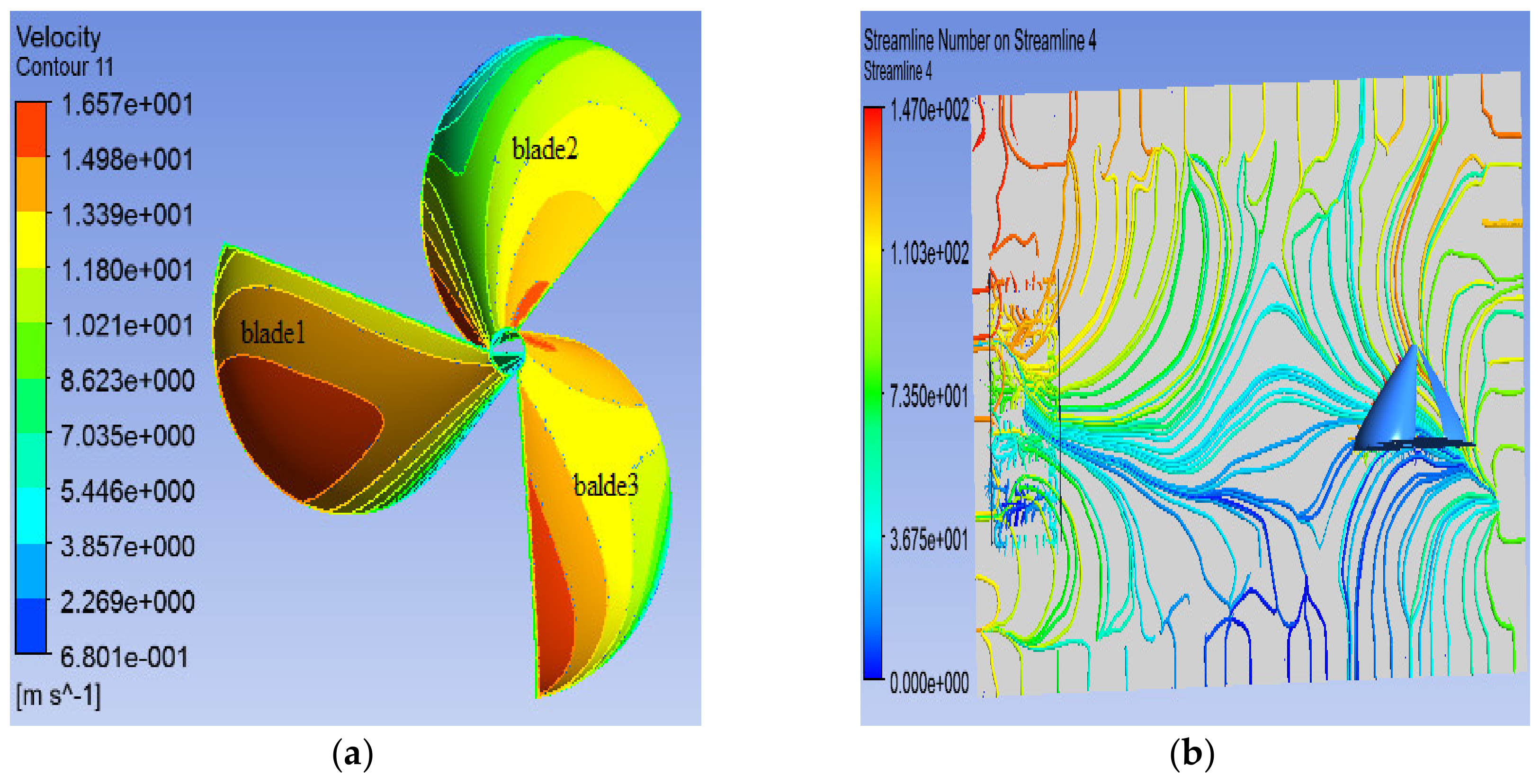
5.3. Case 3: Involute-Type Rotor with WFM
5.3.1. Individual Blade Performance
5.3.2. Rotor Performance
6. Discussions on Electrical and Mechanical Features
6.1. Mechanical Characteristics
6.2. Electrical Characteristics
7. Conclusions
- The lift—drag coefficient displays a greater value of about 19 at 60 rpm and 30 during 250 rpm, which is comparatively superior to other configurations.
- The addition of WFM effectively increases the aerodynamic forces of the wind turbine for all kinds of wind velocity.
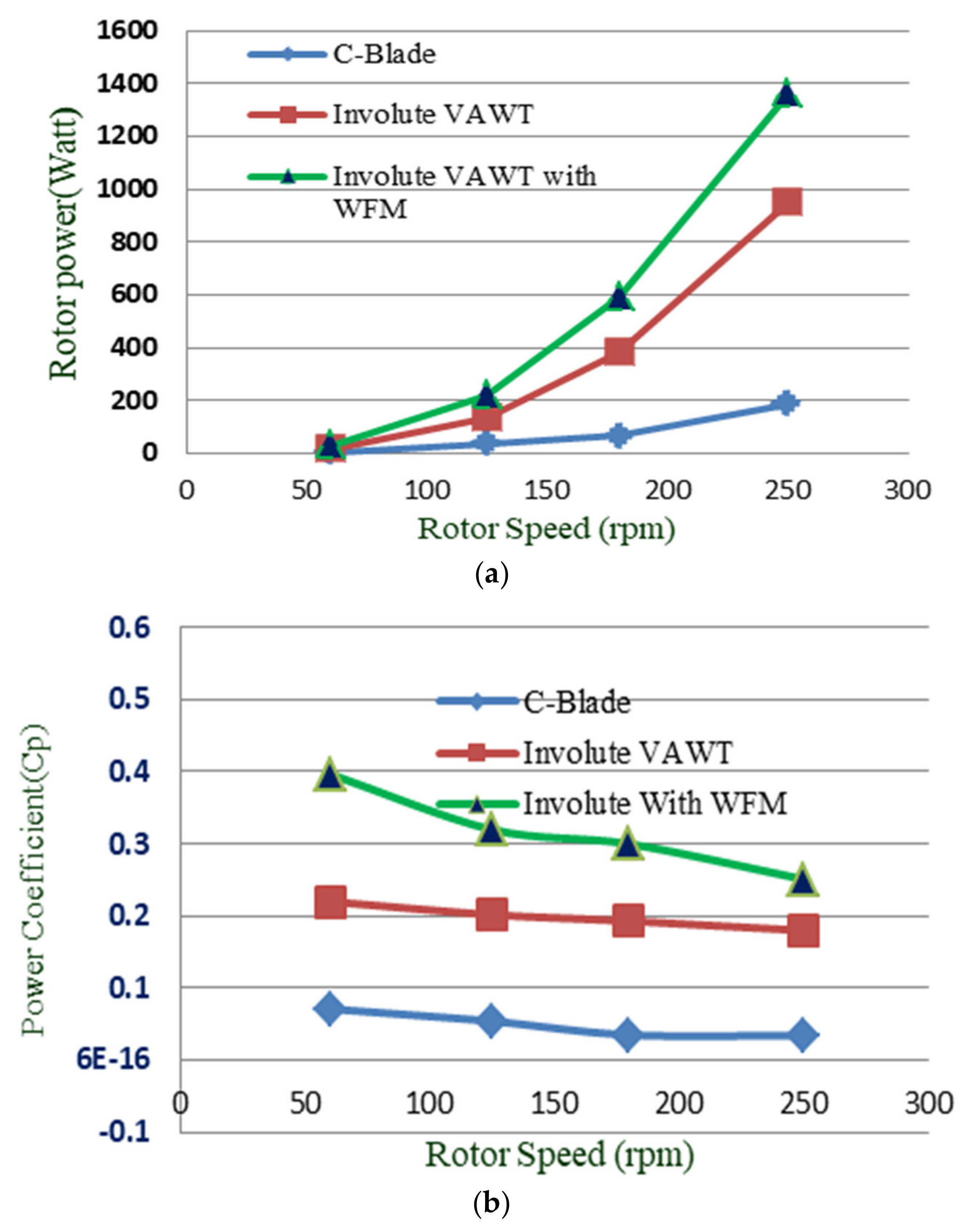
- The WFM model with an involute rotor generates a maximum of 1361 watts during the wind velocity of 250 rpm.
- The power coefficient of this model is significantly enhanced up to approximately 0.397, even at low wind velocity.
Author Contributions
Funding
Conflicts of Interest
References
- Blakers, A.; Stocks, M.; Lu, B.; Cheng, C.; Stocks, R. Pathway to 100% Renewable Electricity. IEEE J. Photovoltaics 2019, 9, 1828–1833. [Google Scholar] [CrossRef]
- Krishnamoorthy, R.; Udhayakumar, K.; Kannadasan, R.; Elavarasan, R.M.; Mihet-Popa, L. An Assessment of Onshore and Offshore Wind Energy Potential in India Using Moth Flame Optimization. Energies 2020, 13, 3063. [Google Scholar]
- Madurai Elavarasan, R.; Selvamanohar, L.; Raju, K.; Vijayaraghavan, R.R.; Subburaj, R.; Nurunnabi, M.; Khan, I.; Afridhis, S.; Hariharan, A.; Pugazhendhi, R.; et al. A Holistic Review of the Present and Future Drivers of the Renewable Energy Mix in Maharashtra, State of India. Sustainability 2020, 12, 6596. [Google Scholar] [CrossRef]
- Patnaik, K.; Samantaray, B. A Study of Wind Energy Potential in India. Bachelor’s Thesis, Department of Electrical Engineering, National Institute of Technology, Rourkela, India, 2010. [Google Scholar]
- Lakshmanan, N.; Gomathinayagam, S.; Harikrishna, P.; Abraham, A.; Ganapathi, S.C. Basic wind speed map of India with long-term hourly wind data. Curr. Sci. 2009, 96, 911–922. [Google Scholar]
- Majdi Nasab, N.; Kilby, J.; Bakhtiaryfard, L. The Potential for Integration of Wind and Tidal Power in New Zealand. Sustainability 2020, 12, 1807. [Google Scholar] [CrossRef]
- Zuo, H.; Bi, K.; Hao, H. A state-of-the-art review on the vibration mitigation of wind turbines. Renew. Sustain. Energy Rev. 2020, 121, 109710. [Google Scholar] [CrossRef]
- Pustina, L.; Lugni, C.; Bernardini, G.; Serafini, J.; Gennaretti, M. Control of power generated by a floating offshore wind turbine perturbed by sea waves. Renew. Sustain. Energy Rev. 2020, 132, 109984. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Ouakad, H.M.; Sahin, A.Z.; Bahaidarah, H.M.S. Vertical axis wind turbine aerodynamics: Summary and review of momentum models. J. Energy Resour. Technol. 2019, 141, 050801. [Google Scholar] [CrossRef]
- Deng, W.; Yu, Y.; Liu, L.; Guo, Y.; Zhao, H. Research on the dynamical responses of H-type floating VAWT considering the rigid-flexible coupling effect. J. Sound Vib. 2020, 469, 115162. [Google Scholar] [CrossRef]
- Kumar, R.; Raahemifar, K.; Fung, A.S. A critical review of vertical axis wind turbines for urban applications. Renew. Sustain. Energy Rev. 2018, 89, 281–291. [Google Scholar] [CrossRef]
- Wang, K.; Zou, L.; Wang, A.; Zhao, P.; Jiang, Y. Wind Tunnel Study on Wake Instability of Twin H-Rotor Vertical-Axis Turbines. Energies 2020, 13, 4310. [Google Scholar] [CrossRef]
- Viqueira-Moreira, M.; Ferrer, E. Insights into the Aeroacoustic Noise Generation for Vertical Axis Turbines in Close Proximity. Energies 2020, 13, 4148. [Google Scholar] [CrossRef]
- Niranjana, S.J. Power Generation by Vertical Axis Wind Turbine. Int. J. Emerg. Res. Manag. Technol. 2015, 7, 1–7. [Google Scholar]
- Naseem, A.; Uddin, E.; Ali, Z.; Aslam, J.; Shah, S.R.; Sajid, M.; Zaidi, A.A.; Javed, A.; Younis, M.Y. Effect of vortices on power output of vertical axis wind turbine (VAWT). Sustain. Energy Technol. Assess. 2020, 37, 100586. [Google Scholar] [CrossRef]
- Li, Z.; Han, R.; Gao, P.; Wang, C. Analysis and implementation of a drag-type vertical-axis wind turbine for small distributed wind energy systems. Adv. Mech. Eng. 2019, 11, 1–16. [Google Scholar] [CrossRef]
- Sobczak, K.; Obidowski, D.; Reorowicz, P.; Marchewka, E. Numerical Investigations of the Savonius Turbine with Deformable Blades. Energies 2020, 13, 3717. [Google Scholar] [CrossRef]
- Mauri, M.; Bayati, I.; Belloli, M. Design and realisation of a high-performance active pitch-controlled H-Darrieus VAWT for urban installations; CP651. In Proceedings of the 3rd Renewable Power Generation Conference (RPG 2014), Naples, Italy, 24–25 September 2014. [Google Scholar]
- Su, H.; Dou, B.; Qu, T.; Zeng, P.; Lei, L. Experimental investigation of a novel vertical axis wind turbine with pitching and self-starting function. Energy Convers. Manag. 2020, 217, 113012. [Google Scholar] [CrossRef]
- Kavade, R.K.; Ghanegaonkar, P. Design and Analysis of Vertical Axis Wind Turbine for Household Application. J. Clean Energy Technol. 2017, 5, 353–358. [Google Scholar] [CrossRef]
- Tirkey, A.; Sarthi, Y.; Patel, K.; Sharma, R.; Sen, P.K. Study on the effect of blade profile, number of blade. Int. J. Sci. Eng. Technol. Res. 2014, 3, 3183–3187. [Google Scholar]
- Mohanasundaram, A.; Valsalal, P. Analysis and design of vertical axis wind turbine for a low wind profile urban areas. J. Electr. Eng. 2019, 20, 363–375. [Google Scholar]
- Yi, M.; Jianjun, Q.; Yan, L. Airfoil Design for Vertical Axis Wind Turbine Operating at Variable Tip Speed Ratios. Open Mech. Eng. J. 2018, 9, 1007–1016. [Google Scholar] [CrossRef]
- Biadgo, A.M.; Simonović, A.; Komarov, D.; Stupar, S. Numerical and analytical investigation of vertical axis wind turbine. FME Trans. 2013, 41, 49–58. [Google Scholar]
- Suffer, K.H.; Quadir, G.A.; Ismail, K.A.; Ryspek, U. CFD analysis of three and four blades movable vanes type vertical axis wind turbine having movable vanes. Int. J. Smart Grid Clean Energy 2016, 5, 259–263. [Google Scholar] [CrossRef]
- Franchina, N.; Kouaissah, O.; Persico, G.; Savini, M. Three-Dimensional CFD Simulation and Experimental Assessment of the Performance of a H-Shape Vertical-Axis Wind Turbine at Design and Off-Design Conditions. Int. J. Turbomach. Propuls. Power 2019, 4, 30. [Google Scholar] [CrossRef]
- Alaimo, A.; Esposito, A.; Messineo, A.; Orlando, C.; Tumino, D. 3D CFD Analysis of a Vertical Axis Wind Turbine. Energies 2015, 8, 3013–3033. [Google Scholar] [CrossRef]
- D’souza, A.G.; Concessao, J.I.; Quadros, J. Study of Aerofoil Design Parameters for Low Speed Wind Tunnel. J. Mech. Eng. Autom. 2015, 5, 47–54. [Google Scholar]
- Zhu, H.T.; Hao, W.X.; Li, C.; Ding, Q.W. Impact of Solidity on Aerodynamic Performance of Building Augmented Vertical Axis Wind Turbine. Reneng Dongli Gongcheng J. Eng. Therm. Energy Power 2018, 33, 114–121. [Google Scholar]
- Sun, X.; Zheng, Z.; Huang, D.; Chen, Y.; Cao, Y.; Wu, G. Research on the aerodynamic characteristics of a lift drag hybrid vertical axis wind turbine. Adv. Mech. Eng. 2016, 8, 1687814016629349. [Google Scholar] [CrossRef]
- Rezaeiha, A.; Kalkman, I.; Blocken, B. Effect of pitch angle on power performance and aerodynamics of a vertical axis wind turbine. Appl. Energy 2017, 197, 132–150. [Google Scholar] [CrossRef]
- Mendoza, V.; Goude, A. Wake Flow Simulation of a Vertical Axis Wind Turbine Under the Influence of Wind Shear. J. Phys. Conf. Ser. 2017, 854, 12031. [Google Scholar] [CrossRef]
- Reitz, A.R.; Yan, C.R.; Ogle, J.; Seel, P. Computational Modeling of Wind Turbine Wake Interactions. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 2012. [Google Scholar]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. Towards optimal aerodynamic design of vertical axis wind turbines: Impact of solidity and number of blades. Energy 2018, 165, 1129–1148. [Google Scholar] [CrossRef]
- Turbulence Models in ANSYS® Fluent CFD. Available online: https://davis68.github.io/me498cf-fa16/resources/flec06/handout-turbulence.pdf (accessed on 28 August 2020).
- Muiruri, P.I.; Motsamai, O.S. Three Dimensional CFD Simulations of A Wind Turbine Blade Section; Validation. J. Eng. Sci. Technol. Rev. 2018, 11, 138–145. [Google Scholar] [CrossRef]
- Liang, Y.B.; Zhang, L.X.; Li, E.X.; Zhang, F.Y. Blade pitch control of straight-bladed vertical axis wind turbine. J. Cent. South Univ. 2016, 23, 1106–1114. [Google Scholar] [CrossRef]
- Mohamed, M.; Ali, A.; Hafiz, A. CFD analysis for H-rotor Darrieus turbine as a low speed wind energy converter. Int. J. Eng. Sci. Technol. 2014, 18, 1–13. [Google Scholar] [CrossRef]
- Prasad, D.; Ratkovich, N.R.; Kirkegaard, P.H.; Nielsen, S.R. Design of rotor blade for vertical axis wind turbine using double aerofoil. In Proceedings of the International Conference on Wind Energy: Materials, Engineering, and Policies (WEMEP 2012), Hydrabad, India, 22–23 November 2012. [Google Scholar]
- Pujol, T.; Massaguer, A.; Massaguer, E.; Montoro, L.; Comamala, M. Net Power Coefficient of Vertical and Horizontal Wind Turbines with Crossflow Runners. Energies 2018, 11, 110. [Google Scholar] [CrossRef]
- Kao, J.-H.; Tseng, P.-Y. Application of computational fluid dynamics (CFD) simulation in a vertical axis wind turbine (VAWT) system. IOP Conf. Series: Earth Environ. Sci. 2018, 114, 12002. [Google Scholar] [CrossRef]
- Reddy, K.; Dagamoori, K.; Sruthi, A.P.; Apurva, S.N.; Naidu, N.M.L. A Brief Research, Study, Design and Analysis on Wind turbine. J. Mod. Eng. Res. 2015, 5, 26. [Google Scholar]
- Jain, P.; Abhishek, A. Analysis and prediction of Vertical cycloidal Rotor Wind Turbine with variable amplitude pitching. In Proceedings of the ARF 2015—4th Asian-Australian Rotorcraft Forum, Bengaluru, India, 16–18 November 2015; pp. 5–7. [Google Scholar]
- Rathod, V.K.; Kamdi, S.Y. Design of PVC Bladed Horizontal Axis Wind Turbine for Low Wind Speed Region. J. Eng. Res. Appl. 2014, 4, 139–143. [Google Scholar]
- Geem, Z.W.; Hong, J. Improved Formulation for the Optimization of Wind Turbine Placement in a Wind Farm. Math. Probl. Eng. 2013, 2013, 481364. [Google Scholar] [CrossRef]
- Geem, Z.W. Size Optimization for a Hybrid Photovoltaic-Wind Energy System. Int. J. Electr. Power Energy Syst. 2012, 42, 448–451. [Google Scholar] [CrossRef]













| Parameters | Unit | Values |
|---|---|---|
| Height (H) | (m) | 0.6 |
| Radius (r) | (m) | 0.8 |
| Swept Area (S) | (m2) | 0.96 |
| Arc Radius (C) | (m) | 0.13 |
| Turbine Surface Area | (m2) | 2.548 |
| Blade Surface Area | (m2) | 0.477 |
| Rotor Volume | (m3) | 0.0042 |
| Dimension | Unit | Values |
|---|---|---|
| Height (H) | (m) | 0.6 |
| Radius (r) | (m) | 0.8 |
| Swept Area (S) | (m2) | 0.96 |
| Blade Curvature | (per mm) | 0.0024 |
| Max Curvature | (per m) | 1.799 |
| Turbine Surface Area | (m2) | 4.034 |
| Blade Surface Area | (m2) | 1.135 |
| Rotor Volume | (m3) | 0.0115 |
| Type of Rotor | Nodes | Elements | Cells in Mesh | Skewness |
|---|---|---|---|---|
| C-shaped | 93,555 | 405,679 | Tetrahedral | 0.6 |
| Involute | 940,201 | 437,894 | Tetrahedral | 0.7 |
| Involute & WFM | 256,895 | 1,147,223 | Tetrahedral | 0.7 |
| Blade No | Lift | Drag |
|---|---|---|
| 1 | −0.1225 | 0.0216 |
| 2 | −0.2728 | −0.0067 |
| 3 | −0.1570 | −0.0524 |
| Net rate | −0.5524 | −0.0375 |
| Blade No | Lift | Drag |
|---|---|---|
| 1 | 0.3308 | 0.0543 |
| 2 | 0.3247 | 0.0318 |
| 3 | 0.2280 | −0.0413 |
| Net rate | 0.8836 | 0.0448 |
| Factors | Units | Case 1 (H-Type Rotor with C-Blade) | Case 2 (Involute Blade Type Rotor) | Case 3 (Involute Rotor with a Wind Flow Modifier) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RPM | 60 | 125 | 180 | 250 | 60 | 125 | 180 | 250 | 60 | 125 | 180 | 250 | |
| rad/s | 6.23 | 13.08 | 18.84 | 26.17 | 6.23 | 13.08 | 18.84 | 26.17 | 6.23 | 13.08 | 18.84 | 26.17 | |
| Lift–coefficient () | - | −0.094 | −0.013 | −0.566 | −0.041 | 0.553 | 1.84 | 3.903 | 5.432 | 0.733 | 2.638 | 4.507 | 7.452 |
| Drag–coefficient () | - | 0.205 | 0.411 | 1.445 | 0.105 | 0.038 | 0.179 | 0.368 | 0.691 | −0.039 | −0.143 | −0.233 | −0.237 |
| Drag to Lift Ratio () | - | 2.181 | 2.361 | 2.553 | 2.521 | 14.02 | 10.27 | 10.60 | 7.861 | 18.60 | 18.44 | 19.343 | 31.44 |
| Lift Force () | N | −0.232 | −0.789 | −1.392 | −2.509 | 1.353 | 4.5 | 7.999 | 13.310 | 1.803 | 6.48 | 11.088 | 18.33 |
| Drag Force () | N | 0.505 | 1.863 | 3.554 | 6.325 | 0.092 | 0.438 | 3.265 | 1.693 | −0.09 | −0.35 | −0.57 | −0.58 |
| Torque on Blade 1 () | Nm | 0.814 | 3.09 | 5.215 | 9.67 | 0.631 | 2.034 | 3.437 | 5.430 | 1.98 | 7.369 | 12.2 | 19.39 |
| Torque on Blade 2 () | Nm | 0.159 | 1.081 | 0.626 | 1.928 | 1.994 | 6.461 | 12.137 | 20.365 | 1.72 | 5.925 | 10.739 | 18.464 |
| Torque on Blade 3 () | Nm | 0.169 | 0.746 | 1.01 | 0.521 | 1.059 | 3.747 | 6.25 | 10.523 | 1.09 | 4.015 | 6.621 | 11.001 |
| Torque on Turbine () | Nm | 0.839 | 2.768 | 3.57 | 7.22 | 2.623 | 10.45 | 20.385 | 36.351 | 4.71 | 16.77 | 31.146 | 52.02 |
| Turbine Power () | W | 5.23 | 36.4 | 67.25 | 188.9 | 16.34 | 136.6 | 384.1 | 951.31 | 29.35 | 219.3 | 592 | 1361.4 |
| Power Coefficient () | - | 0.071 | 0.054 | 0.035 | 0.034 | 0.22 | 0.202 | 0.193 | 0.18 | 0.397 | 0.32 | 0.3 | 0.29 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anthony, M.; Prasad, V.; Raju, K.; Alsharif, M.H.; Geem, Z.W.; Hong, J. Design of Rotor Blades for Vertical Axis Wind Turbine with Wind Flow Modifier for Low Wind Profile Areas. Sustainability 2020, 12, 8050. https://doi.org/10.3390/su12198050
Anthony M, Prasad V, Raju K, Alsharif MH, Geem ZW, Hong J. Design of Rotor Blades for Vertical Axis Wind Turbine with Wind Flow Modifier for Low Wind Profile Areas. Sustainability. 2020; 12(19):8050. https://doi.org/10.3390/su12198050
Chicago/Turabian StyleAnthony, Mohanasundaram, Valsalal Prasad, Kannadasan Raju, Mohammed H. Alsharif, Zong Woo Geem, and Junhee Hong. 2020. "Design of Rotor Blades for Vertical Axis Wind Turbine with Wind Flow Modifier for Low Wind Profile Areas" Sustainability 12, no. 19: 8050. https://doi.org/10.3390/su12198050
APA StyleAnthony, M., Prasad, V., Raju, K., Alsharif, M. H., Geem, Z. W., & Hong, J. (2020). Design of Rotor Blades for Vertical Axis Wind Turbine with Wind Flow Modifier for Low Wind Profile Areas. Sustainability, 12(19), 8050. https://doi.org/10.3390/su12198050









