Enhanced Circular Chain Control for Parallel Operation of Inverters in UPS Systems

Abstract

In this paper, a current sharing method based on the circular chain control (3C) method is proposed for controlling parallel inverters of unequal ratings in uninterruptible power supply (UPS) applications. Due to its circular structure, 3C is one of the most convenient methods which can be used in UPS as well as microgrid systems. However, the conventional 3C control strategy is only applicable to inverters of equal power ratings. The proposed method not only retains the circular structure of the 3C method, but also provides adaptability for the parallel operation of inverters with different power ratings. Moreover, this method adds hot-swap capability to the parallel inverter. A two-loop control structure is used to control the inverters. For proper current sharing, currents of inverters are conveyed in a circular structure with appropriate gains through control links. Simulation and experimental results for linear and nonlinear loads verify the effectiveness of the proposed strategy.

1. Introduction

By setting inverters in a parallel configuration, the uninterruptible power supply (UPS) system’s reliability, as well as redundancy, is improved [1,2]. This configuration also brings better thermal management besides size reduction. However, the challenges of such a configuration should also be considered by the designer to protect the equipment against possible damages. If the parallel inverters are of the same power rating, the load current must be equally shared between them. However, if their ratings are different, the load current should be shared in proportion with each inverter’s power rating [3]. To avoid circulating current, the output voltages of the parallel inverters should be synchronized in terms of amplitude and phase, and obviously, the frequency of the output voltages should be the same [4]. In addition, voltage limits of the dc-link capacitors have to be considered in case input rectifiers are unidirectional, which may face excessive voltages due to active power absorption by some inverters because of circulating currents [3,5].

Considering the mentioned challenges, it is essential to apply proper control schemes to corroborate convenient operation of parallel inverter systems [6,7]. There are two types of control schemes based on how the inverters communicate with each other [8,9]. If there is no information exchange between parallel inverters, the control scheme is called wireless load-sharing control [10] where the “droop” control method has been applied to ensure parallel operation of inverters by changing the voltage amplitude and frequency of each inverter [11,12]. The variation of each parameter (voltage and frequency) alters active and reactive power supplied by the inverters in the droop control method; load sharing is not accurately performed, and the control system transient response behaviour is slow. Furthermore, this method is not capable of proper harmonic current sharing in the nonlinear loading condition [13].

Many research works have been presented to address the drawbacks of droop control [14]. In [15], reactive power distribution is enhanced by altering the voltage bias of the typical droop control by activating a series of successive events via a low-bandwidth communication network. The accuracy of power-sharing is improved in [16] by feeding the output reactive power data to the output voltage reference of each unit. The low bandwidth which is mandatory in such a control scheme may jeopardize the stability of the system. In [17], three individual regulators are applied to control different parameters (voltage, active, and reactive power). The sporadic communication network to exchange data is a drawback of this control method in which each controller is responsible for its proximate and local voltage magnitude and frequency. The design of such a control system is not simple. In [18], a dc-link voltage protection controller is embedded into the droop control scheme to address the dc-link overvoltage issue due to power backfeeding in a parallel UPS system wherein obtained results verified the performance of the controller. In [19], a self-adjusting reactive power-voltage (Q−V) droop control was proposed to improve the reactive power sharing amongst parallel inverters and load voltage regulation by coupling the nominal voltage calculation with the system frequency. Reference [20] proposed a novel autonomous control scheme based on a virtual impedance concept for equal load current sharing between parallel inverters with LCL filters in UPS system. The control is achieved without exchanging information, but feeder parameters must be known and an advanced phase-locked loop (PLL) is required for unbalanced or nonlinear loads. In total, there has been an improvement in traditional droop method applying the aforementioned control methods, but the tradeoff between power-sharing, the complexity of the system, and regulation of frequency, voltage, and phase are still vivid [14].

In terms of intercommunication between the parallel UPS systems, active load-sharing (ALS) based control methods such as: average load sharing method [21], centralized control [22], master-slave control technique [23] and circular chain control (3C) are discussed in the literature. Centralized control method needs synchronous signals and current sharing modules in which the PLL block synchronizes the voltage phase angle and frequency [9]. Equal current sharing in centralized control is obtained by monitoring the total load and tracking the average current. Each module requires an individual controller to track voltage reference, and that’s an obstacle for system expansion. This issue is addressed in [24] where an instantaneous average current sharing method is proposed. The three parameters to control (voltage, frequency, and current) are regulated based on the average control of each module. The current sharing communication bus is responsible for providing an average reference current for each inverter [25]. If a line impedance varies, a gain scheduler is applied to enhance the power-sharing [26]. In the master/slave control method, voltage regulation is performed by the master converter and the slave one is responsible for equal current distribution by tracking the output current of the master converter [27,28]. The PLL block is avoided in this method as the slave units communicate with the master units. The reliability of such a system is endangered if the master module faces a failure [29]. In 3C control method, the circular chain connection is used for current sharing, wherein the current of inverter k is sent to inverter k + 1 as the current sharing reference, and the current of the last inverter is returned to the first inverter. Therefore, the inverters in this configuration track the current of its prior inverter to achieve equal current distribution [30,31]. The 3C control method responds to load change with suitable performance and realized voltage regulation along with a proper power-sharing [28]. This method has been introduced by [22] as the best method for UPS applications because of its special way of communication.

In the present paper, an enhanced 3C method with extra capabilities is proposed for multi-inverter systems with a focus on UPS applications. This method, unlike the conventional 3C, is able to share current with the desired ratio between inverters, and it has hot-swap capability. The output current and voltage of each inverter are regulated by an outer voltage loop and an inner current loop which can readily achieve a fast dynamic response. Therefore, amplitude, frequency, and phase can be synchronized, and proper current sharing among inverters can be achieved in proportion to the module power ratings. A proportional controller is used in the inner current loop and the proportional multi-resonant controller is designed as the outer voltage loop for proper operation of each module. Hot-swap capability is the main feature of the enhanced 3C method wherein numbers of active inverters as well as the turning-on and turning-off of them do not affect (1) the load feeding with standard voltage, (2) accurate load current sharing between inverters based on their ratings in both transient and steady-state conditions.

This paper is organized into six sections. Section two surveys the control method of a single-phase inverter. The 3C and enhanced 3C methods are presented in section three. Simulation and experimental results are provided in sections four and five, respectively, and section six summarizes the paper.

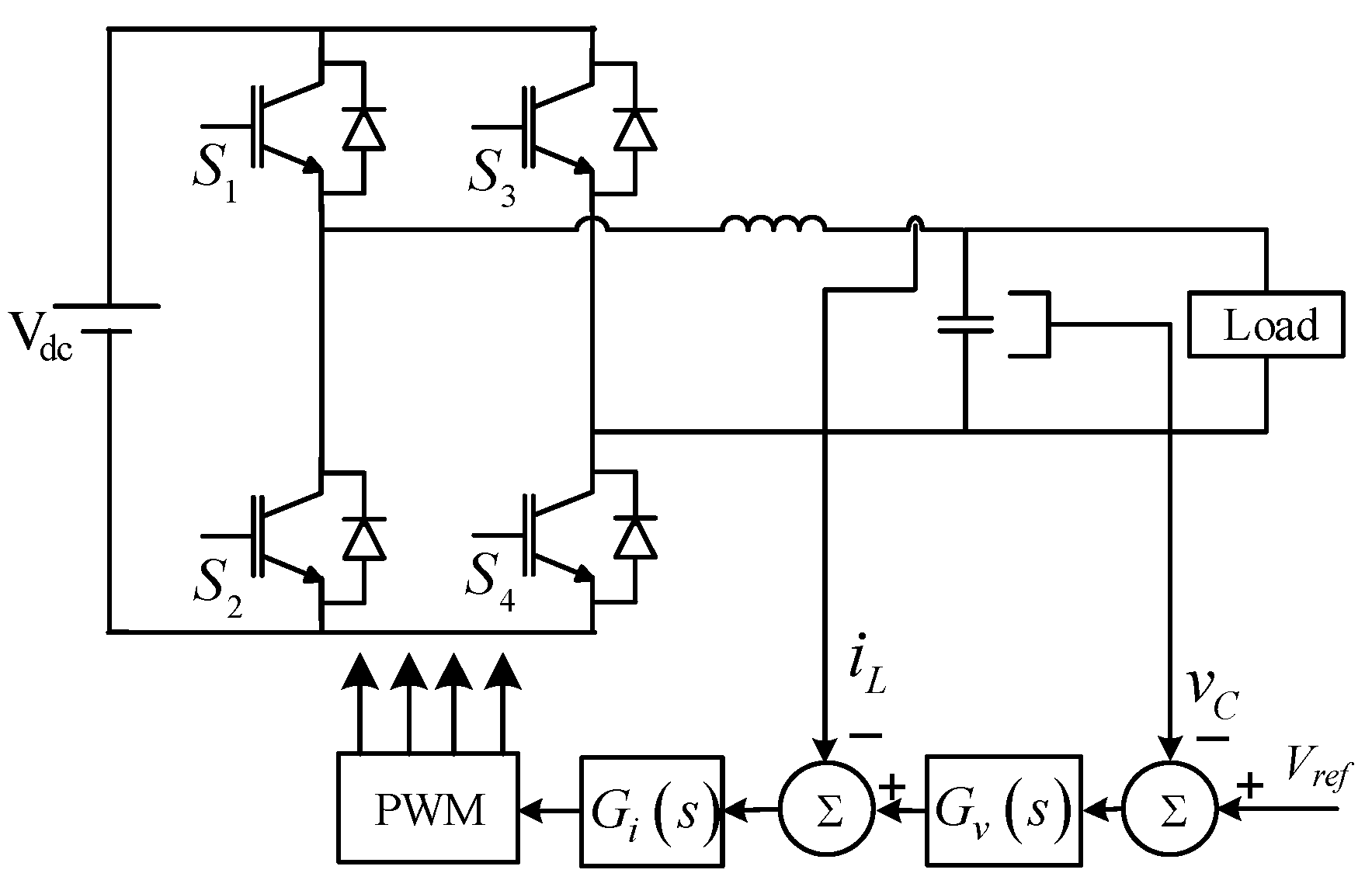
2. Single-Phase Inverter Control

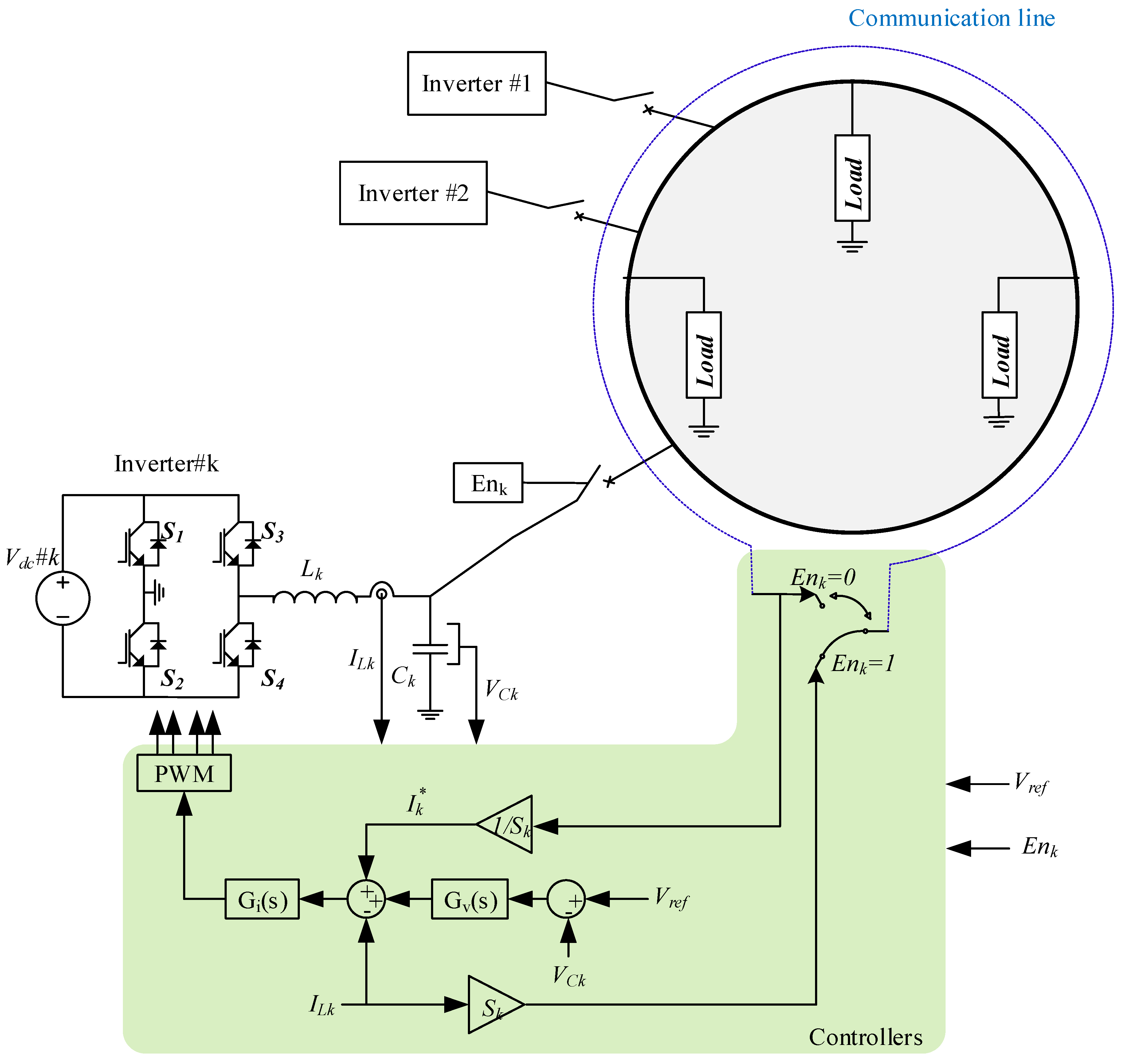
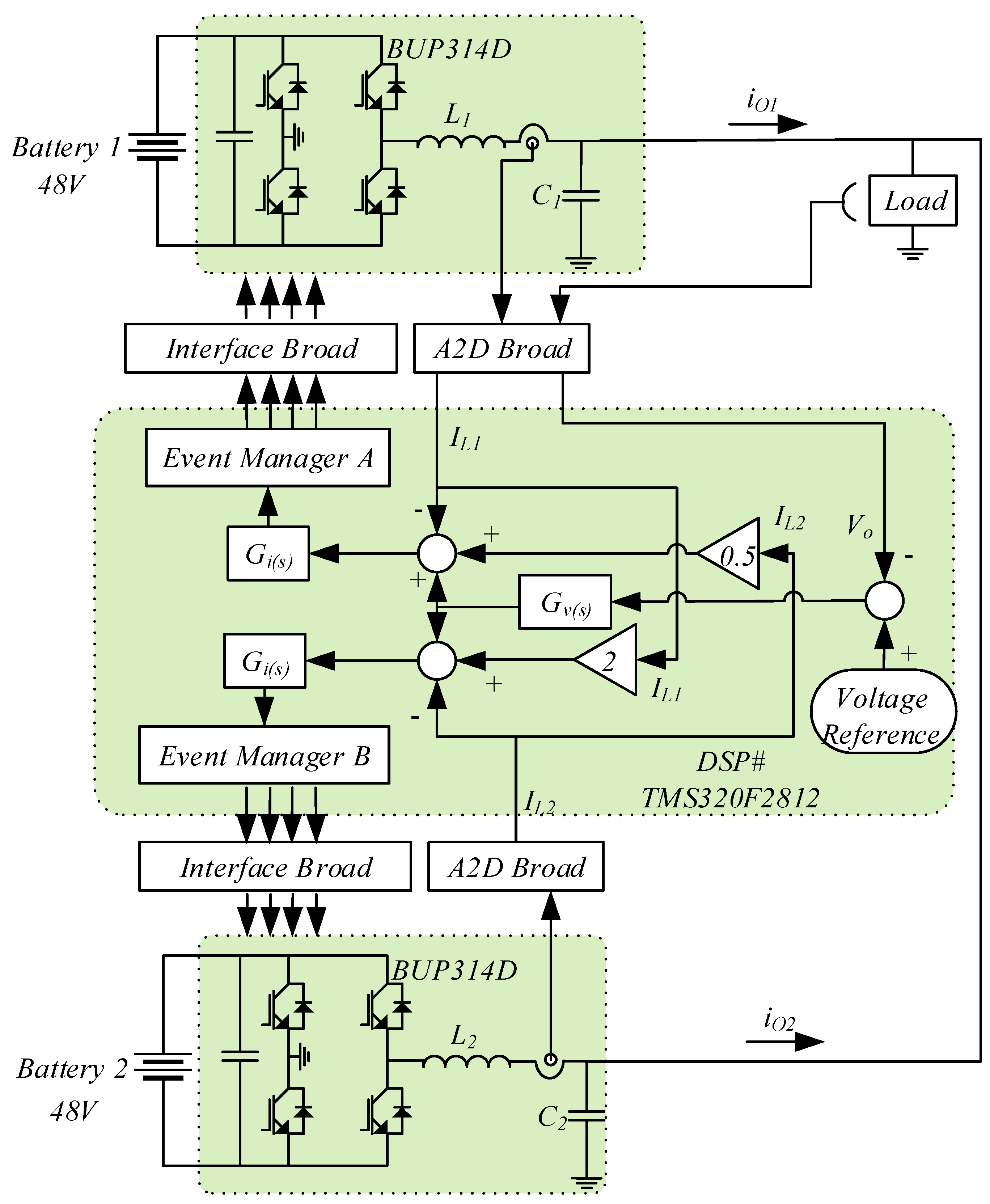
2.1. General Structure

A system configuration consisting of a single-phase inverter bridge with an LC filter is illustrated in Figure 1. Two regulators have been applied to control the output voltage and the inductor current. The overall two-loop control scheme aims to accomplish low steady-state error and fast transient response with sufficient stability margin. The block diagram of the inverter model with the two-loop control scheme is depicted in Figure 2. A proportional controller, G_i(s), has been used in the inner current loop for better resonance damping and power circuit protection. The voltage controller, G_v(s), tracks the voltage reference with fast transient response and minimum steady-state error [21].

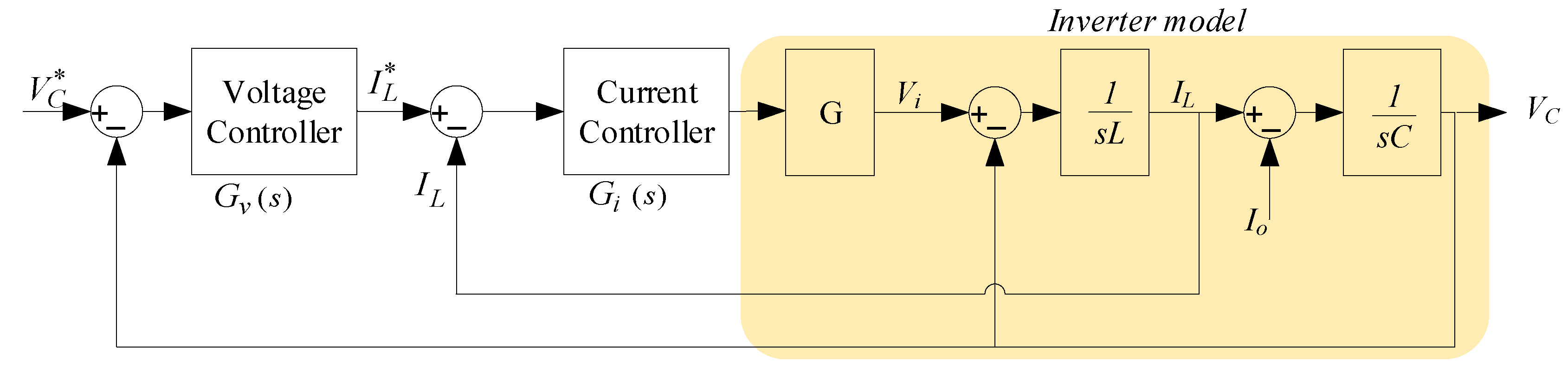
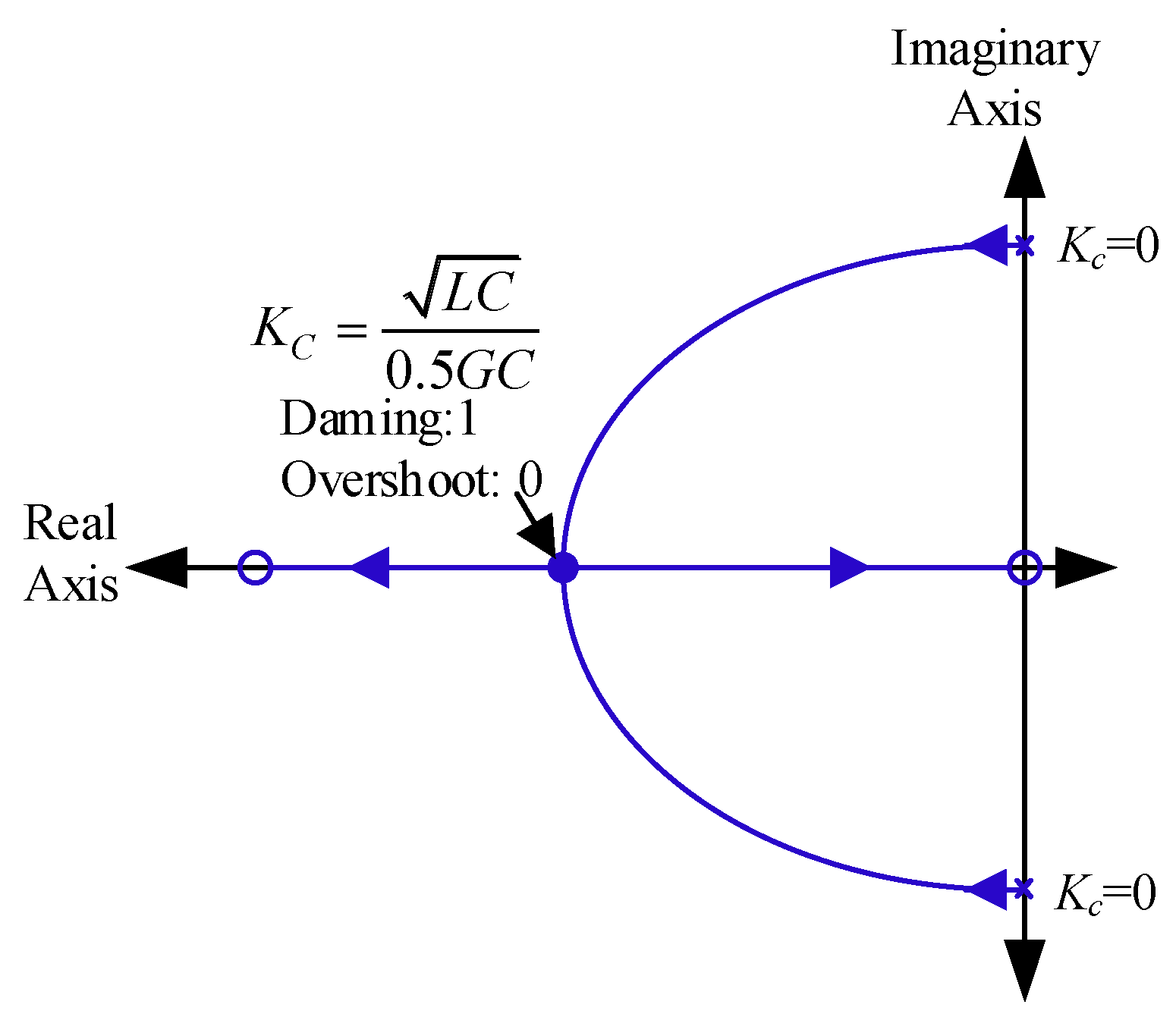
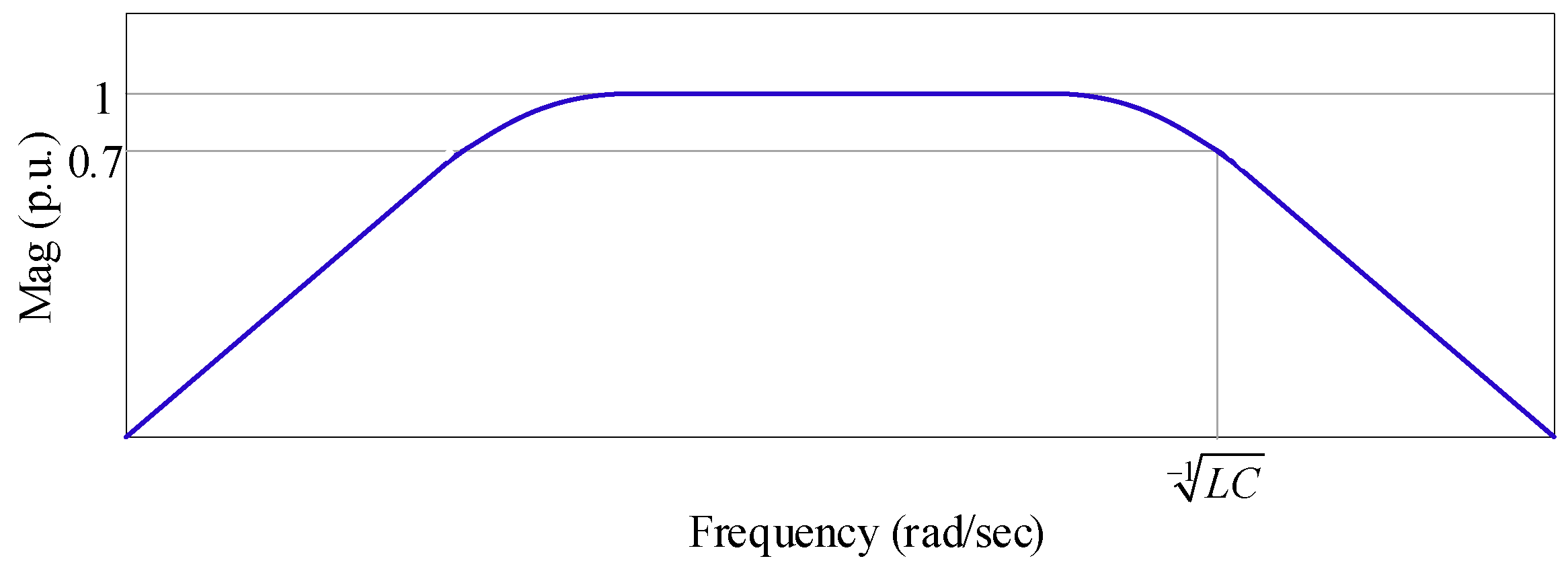
2.2. Inner Current Loop

There are choices to be considered as the control parameter in the internal current loop such as filter capacitor current, load current, and filter inductor current. Controlling the current flowing through filter inductor leads to better performance in resonant oscillation suppression [32]. Figure 3 depicts the internal current controller, where the plant transfer function (TF) is represented by I_L(s)/V_i(s) if I_o is overlooked and V_i represents the output voltage of the converter. The following equation describes the TF of the plant:

$$\frac{I_L\left(s\right)}{V_i\left(s\right)}=\frac{sC}{1+s^{2}LC}$$

(1)

The above system is exposed to resonant oscillation. The closed-loop TF of the internal current loop is derived as below:

$$\frac{I_L\left(s\right)}{I_L^{*}\left(s\right)}=\frac{s{K}_{c}GC}{1+s{K}_{c}GC+s^{2}LC}$$

(2)

where K_c and G are the current controller coefficient and the inverter gain, respectively. To address the resonance issue, K_c, which represents the gain of the current controller, should be increased. Figure 4 shows the root locus of the inner loop for examining how the roots of the system change with variation of K_c. It is evident that if K_c is chosen bigger than $\frac{\sqrt{LC}}{0.5GC}$, the inner control will not face resonance and works as an overdamped or a critically damped second-order system [33].

The multi-loop control design requires an approximation of closed-loop TF of the inner loop. The approximation in (3) is not wrong since the inner current loop with designed current behaves like a first-order system as demonstrated in Figure 5 [34].

$$\frac{I_L\left(s\right)}{I_L^{*}\left(s\right)}\approx \frac{sC}{1+0.5s{K}_{c}GC}$$

(3)

.

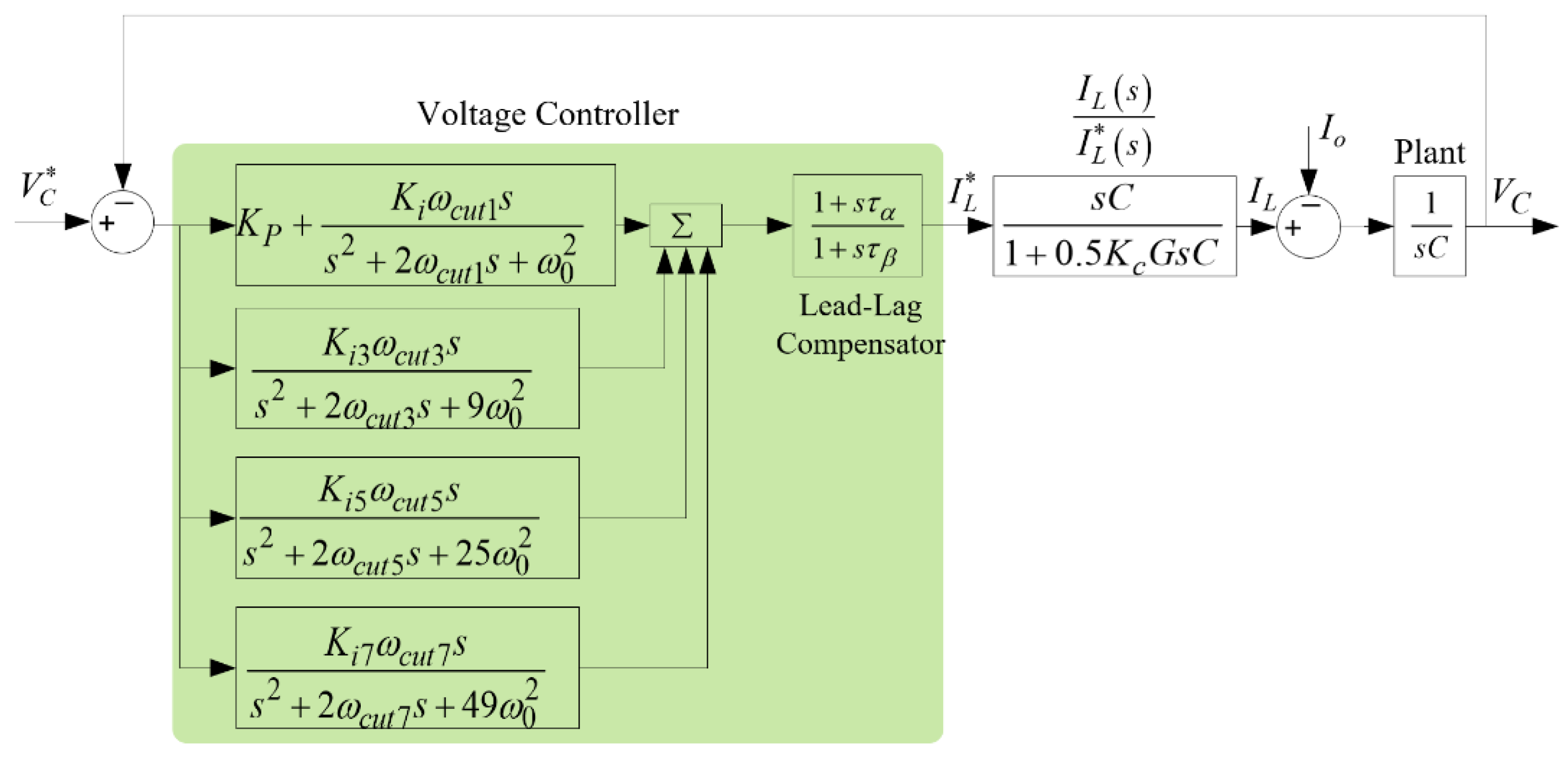
2.3. External Voltage Loop

After designing the current controller, the voltage controller Gv(s) must be designed such that all kinds of loads are fed with a fixed sinusoidal voltage. When the load is nonlinear, e.g., rectifier load, the output voltage contains harmonics. Hence, the limitation of voltage distortion in supplying the nonlinear load becomes a challenging issue, which has motivated the development of a variety of different control methods [33].

The multi-loop control consisting of the inner current and outer voltage loops is demonstrated in Figure 6, in which the PR controller plus a lead-lag compensator are used as a voltage controller Gv(s). Due to the implementation limits, a non-ideal form of PR controller has been used [35], wherein ω_cut is the cut-off frequency in the PR controller. The reference signal for inductor current control is the result of voltage control. Voltage control is essential due to the presence of undesired odd-order harmonic contents. Therefore, the main odd harmonics (i.e., 3rd, 5th, and 7th) are suppressed by the multi-resonant controller. Compared to many other methods such as sliding-mode control [36], deadbeat [37], feedback linearization method [38], the effectiveness of this controller is not limited by switching frequency.

The proposed voltage controller is described as follows.

$$G_v\left(s\right)=\left(K_p+{\displaystyle \sum _{i=1,3,5,7}^{}\frac{K_i{\omega }_{cut,i}s}{s^2+2{\omega }_{cut,i}s+{\left(i\times {\omega }_0\right)}^2}}\right)\left(\frac{1+s{\tau }_{\alpha }}{1+s{\tau }_{\beta }}\right)$$

(4)

In the above equation, if the voltage controller is assumed as three parts, the first part represents the proportional controller coefficient (K_p) and the second part is responsible for suppressing the resonance of the intended order (i = 1, 3, 5 and 7). So, i represents the harmonic order in K_i (resonance gain), ω_cut,i and i × ω₀. The lead-leg compensator is used to improve system stability by modifying the system phase response.

In the following, the design criterium of the voltage controller is investigated by Bode diagram. Figure 7 shows the Bode diagram of the open-loop TF of the voltage loop with different values of resonant gain. If K_i (i = 3, 5 and 7) is increased, then the magnitude of the Bode diagram will be a value more than 40 dB at the tuned frequencies and the control design requirements for steady-state errors less than 1% are fulfilled [39].

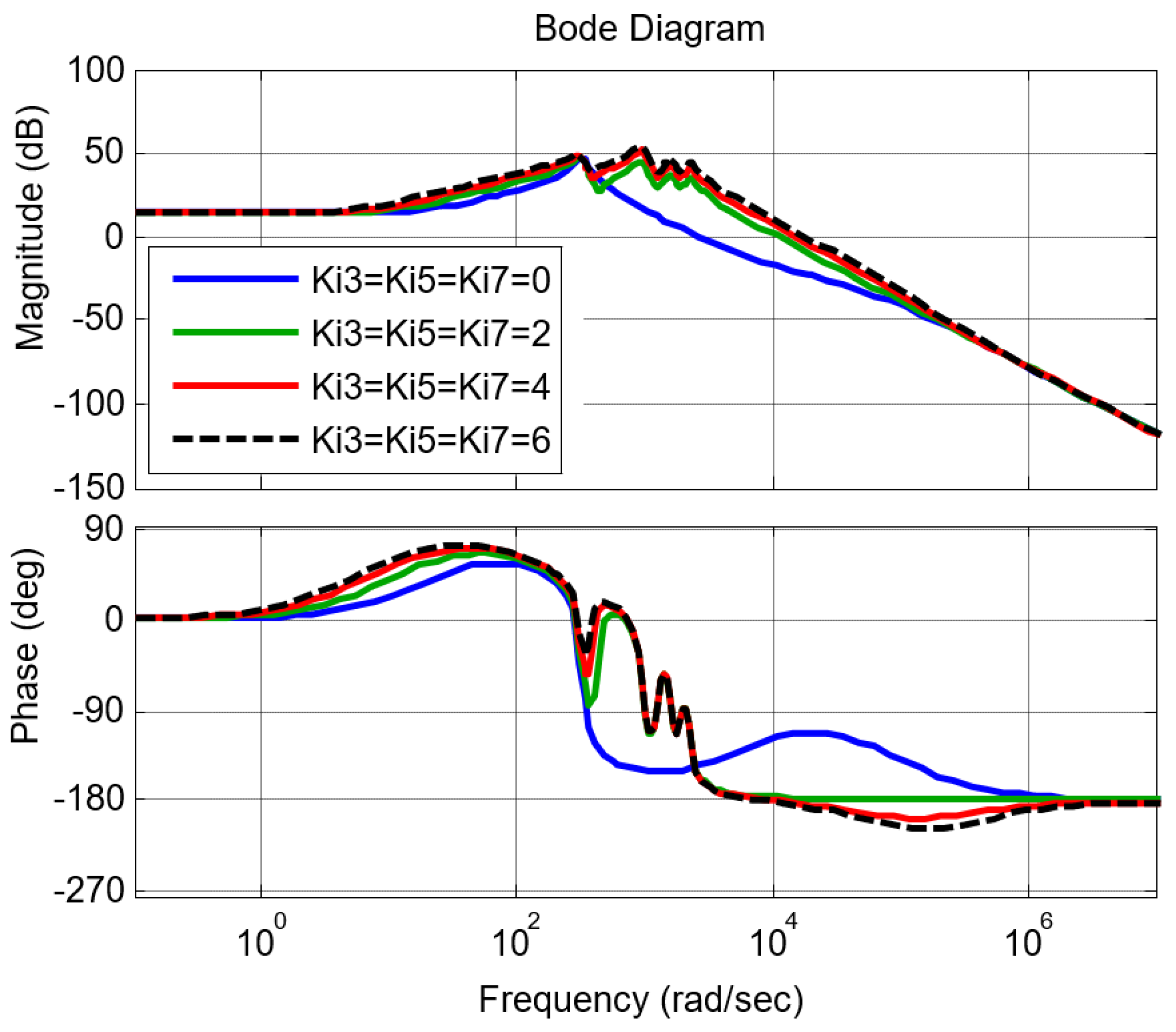
3. Enhanced Circular Chain Controller

The 3C method is presented in Figure 8 where V_ref is the sinusoidal reference voltage which is used for synchronizing inverters with each other. For parallel operation and equal current sharing, the measured inductor currents are conveyed among the inverters as the communicating signal. In order to share the load current, the reference current of each inverter is obtained by the inductor current of the previous inverter. The reference current of the first inverter is equal to the last inverter inductor current. This can be formulated as follows [40]:

$$\begin{array}{c}{I}_1^{*}=I_{Ln},\\ I_k^{*}=I_{L_{k-1}};k=2,\dots ,n\end{array}$$

(5)

The conventional 3C method is only applicable to parallel inverters with equal power ratings. In this section, this method is modified in a way that suits a system with unequal power rating inverters. The block diagram of the enhanced 3C is shown in Figure 9 wherein (1) the load current can be easily shared between inverters by adding some gains to 3C loop, (2) Connecting and disconnecting inverters do not distort the load voltage, and ratios of current sharing between inverters are kept correct (Hot-swap capability). Signal En_k is determined by the user to activate and deactivate inverter k.

To divide the load current unequally between the inverters, gain blocks are used on the routes of conveyed reference currents. This method is formalized as follow:

$$\begin{array}{l}{I}_1^{*}=S_1.\frac{I_{Ln}}{S_n},\\ I_k^{*}=S_k.\frac{I_{L_{k-1}}}{S_{k-1}},k=2,\dots ,n\end{array}$$

(6)

In (6), S_k is the nominal power of kth inverter.

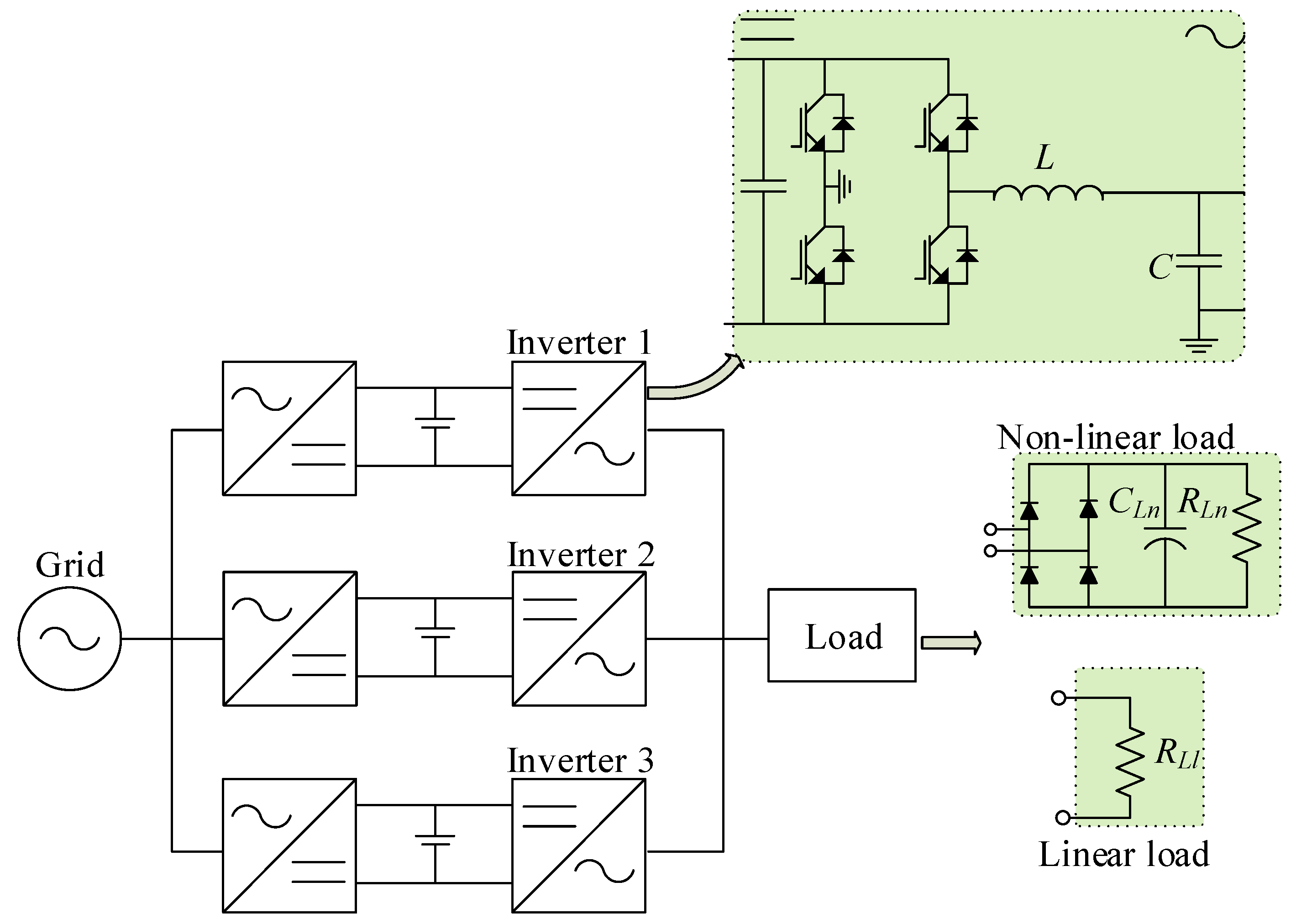
4. Simulation Results

To confirm the proposed control method, a UPS system including three inverters with different power ratings and parameters is simulated (see Figure 10). It assumes that the nominal powers of the second and the third inverters are two and three times higher than the first inverter. Inverter parameters are summarized in

Table 1. Specifications of simulations.

Parameter	Symbol	Value
Load voltage	VO	110 V, 50 HZ
Inverter power rating	S1, S2, S3	500 VA, 1000 VA, 1500 VA
DC source voltage	Vdc1, Vdc2, Vdc3	300 V
Inductor of LC filter	L1, L2, L3	1.35 mH, 0.9 mH, 0.45 mH
Capacitor of LC filter	C1, C2, C3	40 uF, 60 uF, 120 uF
Switching frequency	fs	20 kHz
Linear load resistance	RLl	6.05 Ω
Nonlinear load (diode bridge)	RLn, CLn	RLn = 12.1 Ω, CLn = 2000 uF

wherein the inductor and capacitor of LC filters are selected based on DC link voltage, switching frequency, and acceptable current ripple for the inverters [41].

Simulation results of supplying linear loads and nonlinear loads by three inverters are shown in Figure 11 and Figure 12, respectively. In these simulations, Inverter 2 is off from t = 0.1 s until t = 0.14 s. Results show that the load current is divided between three inverters before t = 0.1 s, then it is supplied by two inverters between t = 0.1 s and t = 0.14 s, and finally, three inverters provide the load current.

It is evident that the load current is shared between inverters based on their power rating; moreover, turning on and off an inverter does not affect the quality of load voltage (hot-swap capability). The harmonic spectrum of load voltage for supplying nonlinear is shown in Figure 13. The steady-state error for voltage tracking is around 0.66% and total harmonic distortion (THD) of voltage is around 0.36% which meets UPS standards [42].

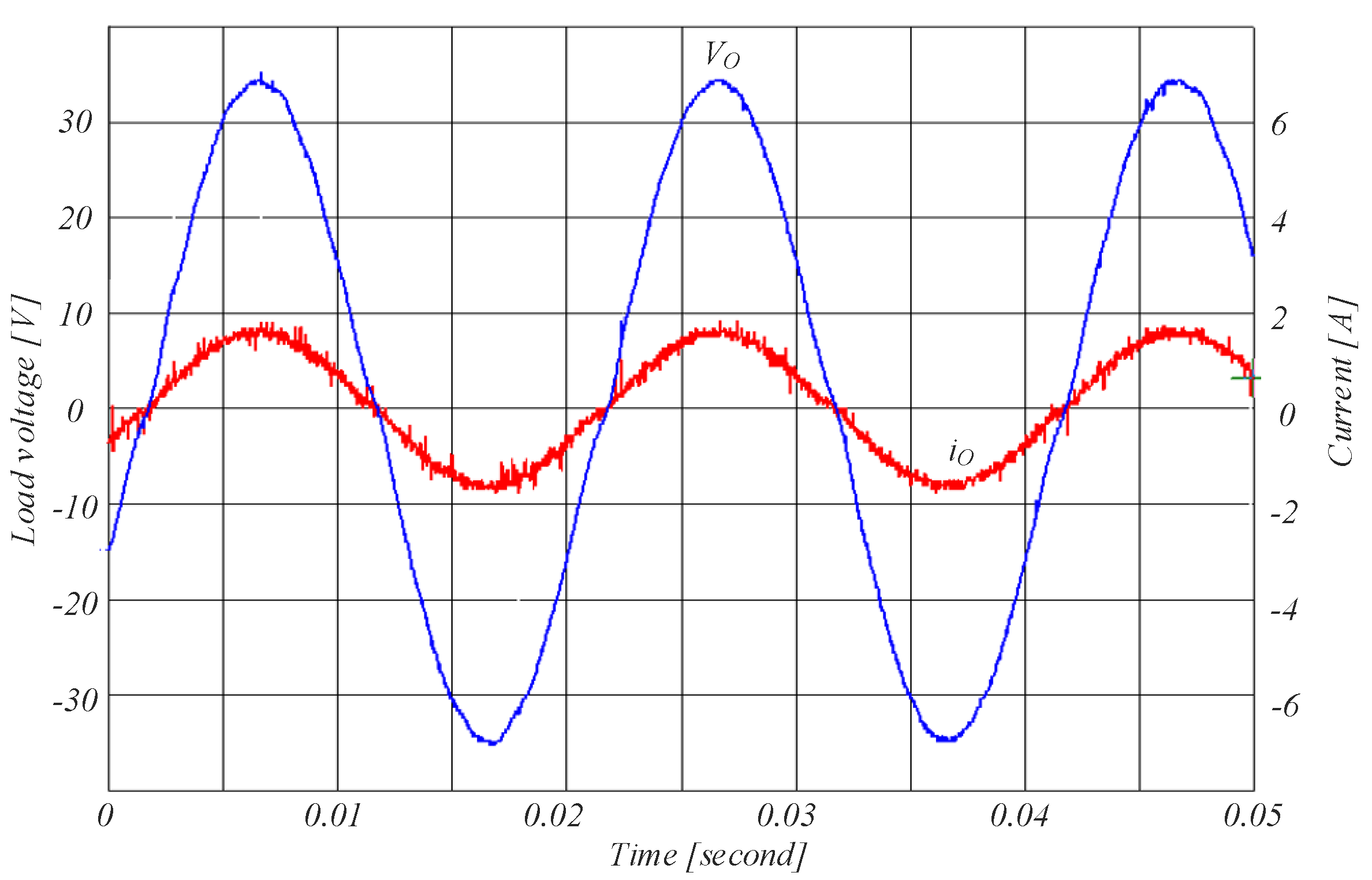
5. Experimental Results

To better demonstrate the effectiveness of the proposed control system, an experimental implementation is accomplished with parameters summarized in

Table 2. Specifications of experimental setup.

Parameter	Symbol	Value
Load voltage	VO	33 V, 50 HZ
Inverter power rating	S1, S2	50 VA, 100 VA
DC source voltage	Vdc1, Vdc2	48 V
Inductor of LC filter	L1, L2	4.2 mH
Capacitor of LC filter	C1, C2	10 uF
Switching frequency	fs	6 kHz
Linear load resistance	RLl	22 Ω
Nonlinear load (diode bridge)	RLn, CLn	RLn = 22 Ω, CLn = 500 uF

. Figure 14 shows the experimental set. TMS320F2812 DSP is used for controlling the inverters, which are of a bridge type made of four BUP314D switches. An LC filter is employed to provide sinusoidal output waveforms. Inductance current and capacitor voltage are measured through sensors connected to the DSP. The actual ratings of the inverters are the same (100 VA); however, in order to demonstrate the performance of the controller, it is assumed that the rating of Inverter 2 is two times of that of Inverter 1.

Figure 15 shows the load voltage and current waveforms. Inverter 1 and Inverter 2 currents, supplying linear and nonlinear loads, are shown in Figure 16 and Figure 17, respectively. It can be concluded from the results that the proposed structure properly provides a proper sharing of the load current between inverters.

6. Discussion

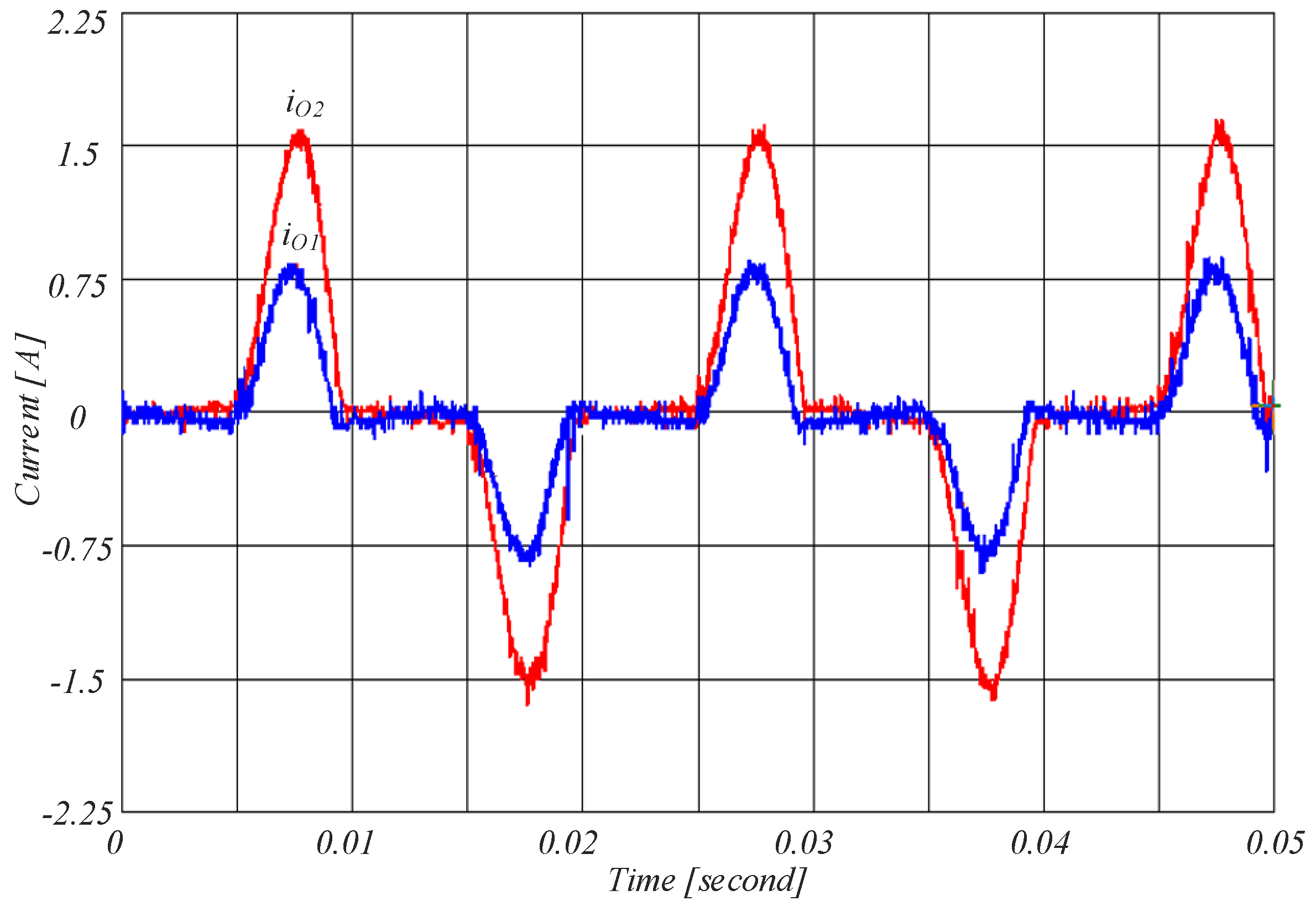
• The behaviour of the parallel inverters with unequal power ratings can be quickly deduced from the results presented above: this system allows correct sharing of load current among inverters while maintaining load voltage at its nominal value.
• The results presented above show that the linear and nonlinear load currents are shared with the desired ratio between inverters. It is also important to consider that the inductor and capacitor of LC filter is designed based on the inverter rating; therefore, parameters of LC filters of unequally rated inverters are different as listed in Table 1. The accuracy of conventional current sharing methods depends on the LC filter parameters while the accuracy of the proposed scheme is acceptable regardless of the system parameters uncertainties in transient and steady-state conditions.
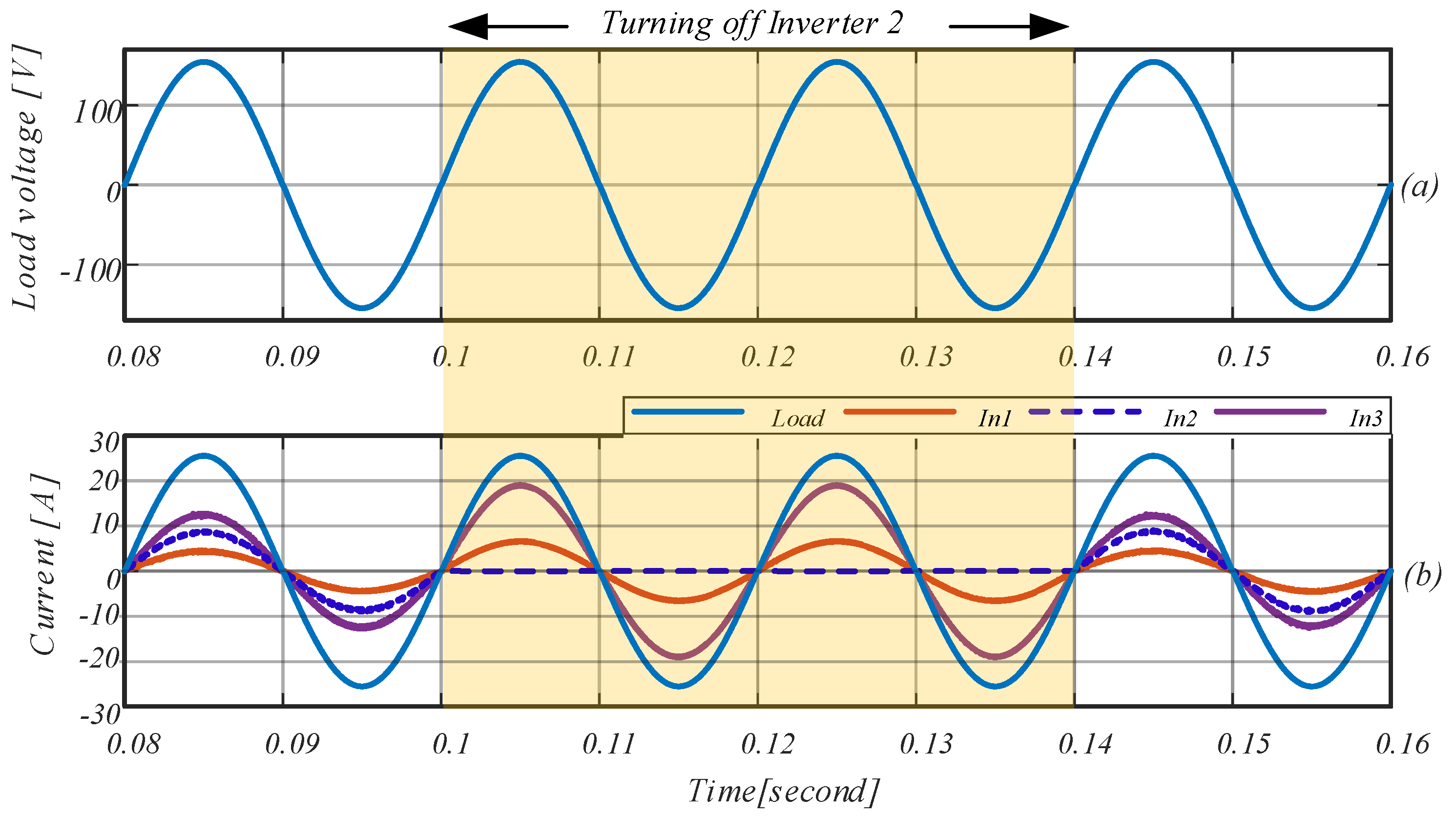
• An important aspect to be considered is the hot-swap capability of the system. Consider the case presented between t = 0.1 s and t = 0.14 s in Figure 11 and Figure 12. In this case, the number of inverters reduce from three to two and then, Inverter 2 is reconnected. The behaviour of the system is excellent; the load voltage and current sharing are not affected by turn-on and turn-off of inverters.
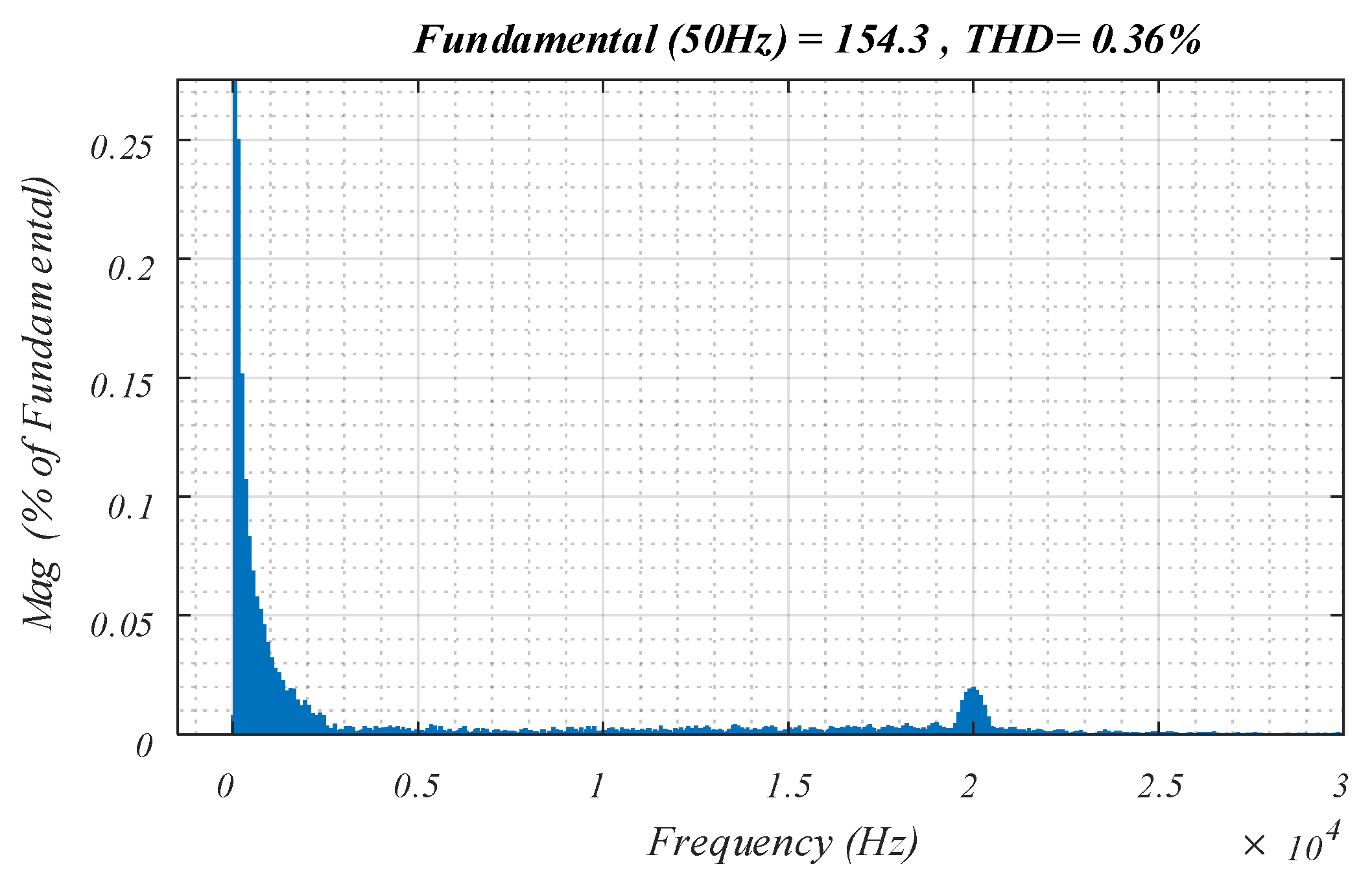
• A low harmonic distortion can be achieved at the output of parallel inverter because of the proposed control scheme: the inverter with the proposed PR controller at odd harmonic orders, as voltage controller, can generate a near sinusoidal voltage waveform that will exhibit a low harmonic distortion for linear and nonlinear loads. The harmonic spectrum of the load voltage is shown in Figure 13 for the nonlinear load (the worst case). The THD of the load voltage is less than 0.4% and all harmonic components are smaller than 0.25%.

7. Conclusions

The circular chain control method was used for controlling parallel inverters of unequal ratings. Due to its circular structure, the 3C method is convenient to be used in uninterruptible power supplies in industrial power systems and microgrids. Nevertheless, the conventional 3C control strategy is only applicable to inverters of equal power ratings. This method is modified here in a way that makes it suitable for applications of inverters with unequal power ratings. For proper current sharing regardless of the number of involved inverters and their working modes (off and on modes), measured currents are conveyed in a circular structure through communication links with appropriate gains, which are proportional to inverters’ power ratings. Since there is no need to change the parameters of preinstalled controller, the proposed system provides hot-swap capability, high modularity, and simple the power expansion. The internal controller of each inverter consists of an inner current loop and an outer voltage loop that are designed for proper current sharing and voltage regulation. A simulation study has been accomplished for a system of three unequally rated inverters in different operation conditions and loads. Experimental implementation was also carried out for a set of two inverters with different power ratings. The obtained results verified the proper performance of the proposed control scheme wherein linear and nonlinear load currents were shared with desired ratio among inverters and the load was supplied with a high-quality voltage.