MAS-Based Evacuation Simulation of an Urban Community during an Urban Rainstorm Disaster in China
Abstract
:1. Introduction
2. Research Method
2.1. Simulation Methods
2.2. MAS Modeling
2.3. Interaction Rules
| E = E-at; |
| if (crowd density>1){ |
| E = E-k*crowd_density; |
| } |
| if (wading the waterlogging point){ |
| E = E-E(risk); |
| } |
| if (crowd density>1){ |
| calculate speed in crowds; |
| calculate information volume; |
| calculate the energy consumed at waterlogging points; |
| } |
| while (survivor >0){ |
| Ei = wj+Ek-E; |
| once when Ei<0 |
| calculate the number of dead pedestrians |
| } |
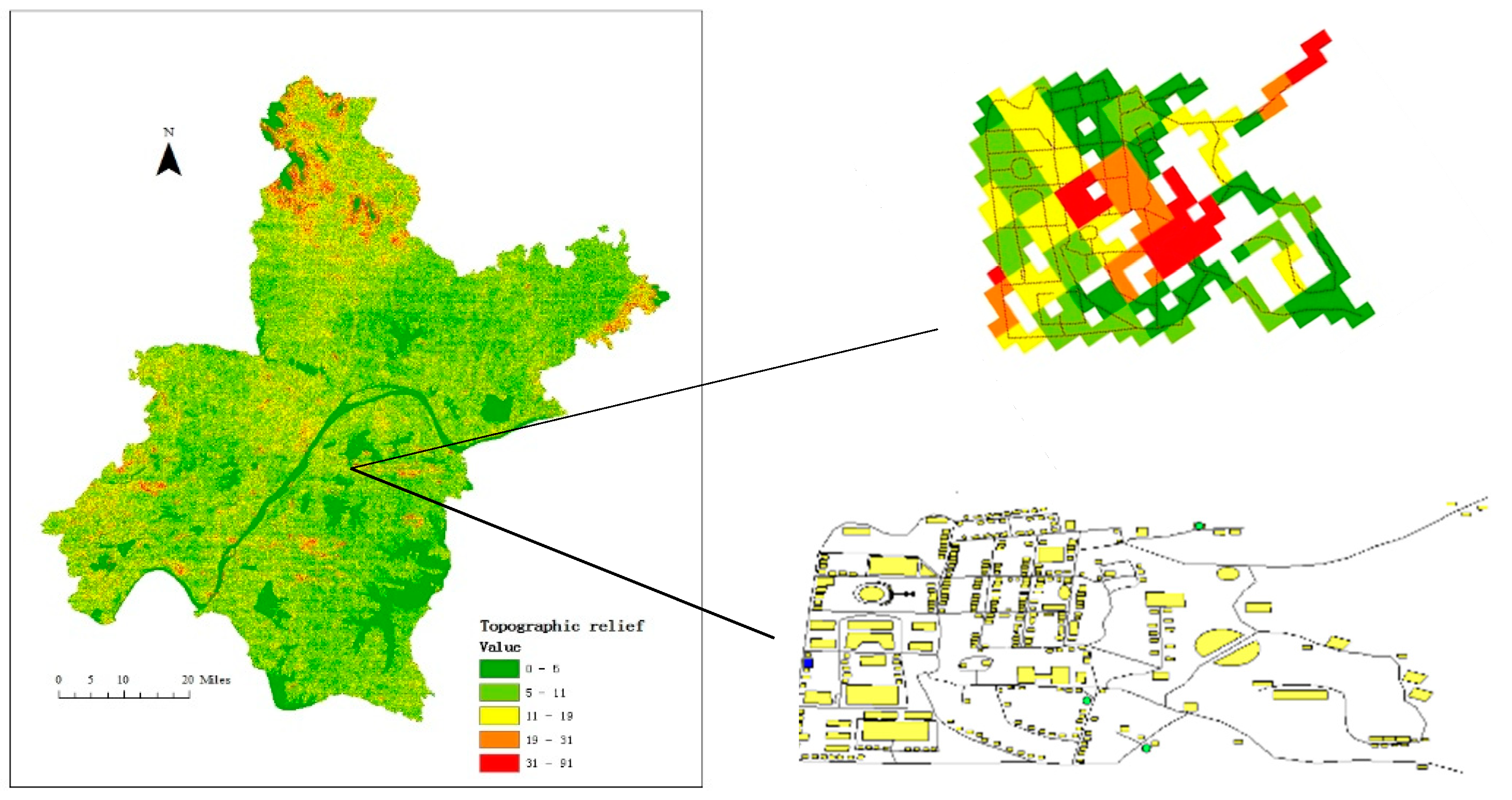
2.4. Simulation Scenarios
3. Result and Discussion
3.1. Crowds Survival Analysis
3.2. Crowds Cluster Analysis
3.3. Analysis of Sustainable Rescue after Entering Shelters
4. Conclusions and Recommendations
4.1. Conclusions
4.2. Recommendations
4.3. Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, X.; Yang, K.; Peng, S.; Xu, Q.; Meng, C. The study of urban rainstorm waterlogging scenario simulation based on GIS and SWMM model—Take the example of Kunming Dongfeng East Road catchment area. In Proceedings of the International Conference on Geoinformatics, Kaifeng, China, 20–22 June 2013; pp. 1–5. [Google Scholar]
- Han, B.; Wang, R.; Tao, Y.; Gao, H. Urban population agglomeration in view of complex ecological niche: A case study on Chinese prefecture cities. Ecol. Indic. 2014, 47, 128–136. [Google Scholar] [CrossRef]
- Su, B.; Huang, H.; Li, Y. Integrated simulation method for waterlogging and traffic congestion under urban rainstorms. Nat. Hazards 2016, 81, 23–40. [Google Scholar] [CrossRef]
- Chen, P.; Zhang, J.; Zhang, L.; Sun, Y. Evaluation of resident evacuations in urban rainstorm waterlogging disasters based on scenario simulation: Daoli district (Harbin, China) as an example. Int. J. Environ. Res. Public Health 2014, 11, 9964–9980. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, P.; Zhang, J.; Sun, Y.; Liu, X. Wargame simulation theory and evaluation method for emergency evacuation of residents from urban waterlogging disaster area. Int. J. Environ. Res. Public Health 2016, 13, 1260. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.; Zhao, F.; Tan, L. Whether a large disaster could change public concern and risk perception: A case study of the 7/21 extraordinary rainstorm disaster in Beijing in 2012. Nat. Hazards 2015, 78, 555–567. [Google Scholar] [CrossRef]
- Pan, Y.; Shao, Z.; Cheng, T.; Wang, Z.; Zhang, Z. Influence Analysis of Waterlogging Based on Deep Learning Model in Wuhan. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Wuhan, China, 18–22 September 2017; Volume XLII-2/W7. [Google Scholar]
- Zhang, W.; Wang, X.; Liu, Y.; Zhang, T. Simulation of Rainstorm Waterlogging Based on SWMM and Visualization Module Research. In Proceedings of the 2016 International Conference on Smart City and Systems Engineering (ICSCSE), Hunan, China, 25–26 November 2016. [Google Scholar]
- Huang, J.; Wang, S.; Deng, S.; Yang, X.; Zhou, Q. Numerical study on the impact of Gongji Road Rain Pump on the waterlogging in Huinan, Pudong District. J. Geosci. Environ. Prot. 2014, 2, 52–58. [Google Scholar] [CrossRef]
- Yu, D.P.; Coulthard, T.J. Evaluating the importance of catchment hydrological parameters for urban surface water flood modelling using a simple hydro-inundation model. J. Hydrol. 2015, 524, 385–400. [Google Scholar] [CrossRef] [Green Version]
- Jamieson, S.; Lhomme, J.; Gouldby, B. A highly efficient 2d flood modelling with sub-element topography. Water Manag. 2012, 165, 581–595. [Google Scholar]
- Yu, H.; Huang, G.; Wu, C. Application of the stormwater management model to a piedmont city: A case study of Jinan city, China. Water Sci. Technol. 2014, 70, 858. [Google Scholar] [CrossRef]
- Zhu, D.; Zhou, N.; Jiang, S. Research overview of runoff model for urban rainwater. J. Water Resour. Water Eng. 2011, 22, 132–137. (In Chinese) [Google Scholar]
- Bisht, D.; Chatterjee, C.; Kalakoti, S.; Upadhyay, P.; Sahoo, M.; Panda, A. Modeling urban floods and drainage using SWMM and MIKE urban: A case study. Nat. Hazards 2016, 84, 749–776. [Google Scholar] [CrossRef]
- Dawson, R.J.; Peppe, R.; Wang, M. An agent-based model for risk based flood incident management. Nat. Hazards 2011, 59, 167–189. [Google Scholar] [CrossRef]
- Whitehead, J.C.; Edwards, B.; van Willigen, M.; Maiolo, J.R.; Wilson, K.; Smith, K.T. Heading for higher ground: Factors affecting real and hypothetical hurricane evacuation behavior. Environ. Hazards 2001, 2, 133–142. [Google Scholar] [CrossRef]
- Drabek, T.E. Human System Responses to Disaster, Post-Impact Emergency Actions Human System Responses to Disaster; Springer: Berlin/Heidelberg, Germany, 1988; pp. 132–199. [Google Scholar]
- Senkbeil, J.C.; Rockman, M.S.; Mason, J.B. Shelter seeking plans of tuscaloosa residents for a future tornado event. Weather Clim. Soc. 2012, 4, 159–171. [Google Scholar] [CrossRef] [Green Version]
- Whyte, A. Survey of Households Evacuated during the Mississauga Chlorine Gas Emergency, Emergency Planning Project. Toronto, Canada, 10–16 November 1979; Institute for Environmental Studies, University of Toronto: Toronto, ON, Canada, 1980. [Google Scholar]
- Komatsu, N.; Sasabe, M.; Kawahara, J.; Kasahara, S. Automatic evacuation guiding scheme based on implicit interactions between evacuees and their mobile nodes. GeoInformatica 2018, 22, 127–141. [Google Scholar] [CrossRef]
- Murakami, Y.; Ishida, T.; Kawasoe, T.; Hishiyama, R. Scenario Description for Multi-Agent Simulation. Proc. Int. Conf. Auton. Agents 2003, 2, 369–376. [Google Scholar]
- Treuille, A.; Cooper, S.; Popović, Z. Continuum crowds. ACM Trans. Graphics 2006, 25, 1160–1168. [Google Scholar] [CrossRef]
- Hoogendoorn, S.P.; Daamen, W.; Duives, D.C.; Van Wageningen-Kessels, F.L.M. Optimal crowd evacuation. In Proceedings of the 93rd Annual Meeting Transportation Research Board, Washington, DC, USA, 12–16 January 2014; pp. 1–19. [Google Scholar]
- Guo, R.Y.; Huang, H.J.; Wong, S.C. Collection, spillback, and dissipation in pedestrian evacuation: A network-based method. Transp. Res. Part B Methodol. 2011, 45, 490–506. [Google Scholar] [CrossRef] [Green Version]
- Roger, L.H. A continuum theory for the flow of pedestrians. Transp. Res. Part B 2002, 36, 507–535. [Google Scholar]
- Henderson, L.F. The statistics of crowd fluids. Nature 1971, 229, 381–383. [Google Scholar] [CrossRef]
- Helbing, D. A fluid dynamic model for the movementof pedestrians. Complex. Syst. 1992, 6, 391–415. [Google Scholar]
- Roger, L.H. The flow of large crowds of pedestrians. Math. Comput. Simul. 2000, 53, 367–370. [Google Scholar]
- Burstedde, C.; Klauck, K.; Schadschneider, A.; Zittartz, J. Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Physica A 2001, 295, 507–525. [Google Scholar] [CrossRef] [Green Version]
- Kirchner, A.; Namazi, A.; Nishinari, K.; Schadschneider, A. Extended floor field CA model for evacuation dynamics. IEICE Trans. Inf. Syst. D 2003, 87, 726–732. [Google Scholar]
- Lee, J.Y.S.; Lam, W.H.K.; Wong, S.C. Pedestrian simulation model for Hong Kong underground stations. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Oakland, CA, USA, 25–29 August 2001; pp. 554–558. [Google Scholar]
- Masuda, H.; Kikuchi, S.; Arai, T. Performance Analysis of Retail Store Layout Using Agent-Based Simulation. J. Jpn. Ind. Manag. Assoc. 2009, 60, 128–144. [Google Scholar]
- Pelechano, N.; Badler, N.I. Modeling crowd and trained leader behavior during building evacuation. IEEE Comput. Graph. Appl. 2006, 26, 80–86. [Google Scholar] [CrossRef] [Green Version]
- Cuena, J.; Ossowski, S. 11 Distributed Models for Decision Support. In Multiagent Systems: A Modern Approach to Distributed Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1999; pp. 459–504. [Google Scholar]
- Chen, X.; Meaker, J.W.; Zhan, F.B. Agent-based modeling and analysis of hurricane evacuation procedures for the Florida Keys. Nat. Hazards 2006, 38, 321–338. [Google Scholar] [CrossRef]
- Aldewereld, H.; Tranier, J.; Dignum, F.; Dignum, V. Collaborative Agents—Research and Development; Agent-Based Crisis Management; Springer: Berlin/Heidelberg, Germany, 2011; pp. 31–43. [Google Scholar]
- Cheng, Y.; Zheng, X. Emergence of cooperation during an emergency evacuation. Appl. Math. Comput. 2018, 320, 485–494. [Google Scholar] [CrossRef]
- Bode, N.W.F.; KemlohWagoum, A.U.; Codling, E.A. Information use by humans during dynamic route choice in virtual crowd evacuations. R. Soc. Open Sci. 2015, 2. [Google Scholar] [CrossRef] [Green Version]
- Wong, S.K.; Wang, Y.S.; Tang, P.K.; Tsai, T.Y. Optimized evacuation route based on crowd simulation. Comput. Vis. Media 2017, 3, 243–261. [Google Scholar] [CrossRef] [Green Version]
- Pan, X.; Han, C.S.; Dauber, K.; Law, K.H. A multi-agent based framework for the simulation of human and social behaviors during emergency evacuations. AI Soc. 2007, 22, 113–132. [Google Scholar] [CrossRef]
- Bode, N.W.F.; Codling, E.A. Human exit route choice in virtual crowd evacuations. Anim. Behav. 2013, 86, 347–358. [Google Scholar] [CrossRef]
- Shen, Y.; Liu, S.; Fang, Z.; Hu, M. Modeling and simulation of stranded passengers’ transferring decision-making on the basis of herd behaviors. Kybernetes 2012, 41, 963–976. [Google Scholar] [CrossRef]
- Wang, J.; Chen, M.; Yan, W.; Zhi, Y.; Wang, Z. A utility threshold model of herding–panic behavior in evacuation under emergencies based on complex network theory. Simulation 2017, 93, 123–133. [Google Scholar] [CrossRef] [Green Version]
- Muir, H.C. Research into the factors influencing survival in aircraft accidents. Aeronaut. J. 1996, 100, 177–182. [Google Scholar]
- Siebers, P.-O.; Aickelin, U. Introduction to Multi-Agent Simulation. In Encyclopedia of Decision Making and Decision Support Technologies; IGI Global: Hershey, PA, USA, 2008; Volume 2, pp. 554–564. [Google Scholar]
- Jérémy, P.; Mouaddib, A.I.; Gatepaille, S. Detection of Primitive Collective Behaviours in a Crowd Panic Simulation Based on Multi-Agent Approach. Int. J. Swarm Intell. Res. 2012, 3, 50–65. [Google Scholar]
- Minar, N.; Burkhart, R.; Langton, C.; Askenazi, M. The Swarm Simulation System: A Toolkit for Building Multi-Agent Simulations; Santa Fe Institute: Santa Fe, NM, USA, 1996. [Google Scholar]
- Tisue, S.; Wilensky, U. NetLogo: Design and implementation of a multi-agent modeling environment. In Proceedings of the Agent 2004 Conference on Social Dynamics: Interaction, Reflexivity and Emergence, Chicago, IL, USA, 7–9 October 2004; pp. 7–9. [Google Scholar]
- Collier, N.; Howe, T.R.; North, M.J. Onward and upward: The transition to Repast 2.0. In Proceedings of the First Annual North American Association for Computational Social and Organizational Science Conference, Pittsburgh, PA, USA, 1 January 2003; Volume 122, pp. 136–140. [Google Scholar]
- North, M.J.; Collier, N.T.; Vos, J.R. Experiences creating three implementations of the repast agent modeling toolkit. ACM Trans. Model. Comput. Simul. 2006, 16, 1–25. [Google Scholar] [CrossRef]
- Collier, N. RePast: An Extensible Framework for Agent Simulation. Univ. Chic. Soc. Sci. Res. 2003, 36, 371–375. [Google Scholar]
- North, M.J.; Howe, T.R.; Collier, N.T.; Vos, J.R. The Repast Simphony Runtime System. In Proceedings of the Agent 2005 Conference on Generative Social Processes, Models, and Mechanisms, Chicago, IL, USA, 13–15 October 2005; pp. 151–158. [Google Scholar]
- Malleson, N.; Heppenstall, A.; See, L. Crime reduction through simulation: An agent-based model of burglary. Comput. Environ. Urban Syst. 2010, 34, 236–250. [Google Scholar] [CrossRef]
- Wang, F.Y.; Carley, K.M.; Zeng, D.; Mao, W.J. Social computing: From social informatics to social intelligence. IEEE Intell. Syst. 2007, 22, 79–83. [Google Scholar] [CrossRef]
- Tong, W.; Cheng, L. Simulation of Pedestrian Flow based on Multi-agent. Procedia Soc. Behav. Sci. 2013, 96, 17–24. [Google Scholar] [CrossRef] [Green Version]
- Quarantelli, E. The behavior of panic participants. Sociol. Soc. Res. 1957, 41, 187–194. [Google Scholar]
- Keating, J.P. The myth of panic. Fire 1982, 147, 57–61. [Google Scholar]
- Wu, J.; Weng, W.; Ni, S. Urban emergency evacuation plans based on GIS and multi-agent systems. J. Tsing Huauni Univ. (Sci. Technol. ) 2010, 50, 1168–1172. (In Chinese) [Google Scholar]
- Dijkstra, E.W. A note on two problems in connexion with graphs. Numerischemathematik 1959, 1, 269–271. [Google Scholar] [CrossRef] [Green Version]
- Cuong, T.T. CrowdRoute: A crowd-sourced routing algorithm in public transit networks. GEOCROWD 2013. In Proceedings of the 2nd ACM SIGSPATIAL International Workshop on Crowdsourced and Volunteered Geographic Information, Orlando, FL, USA, 5 November 2013; pp. 9–14. [Google Scholar]
- Uno, K.; Kashiyama, K. Development of Simulation System for the Disaster Evacuation Based on Multi-Agent Model Using GIS. Tsinghua Sci. Technol. 2008, 13 (Suppl. 1), 348–353. [Google Scholar] [CrossRef]
- Fu, Y.; Liang, J.; Liu, Q.; Hu, X. Crowd Simulation for Evacuation Behaviors Based on Multi-agent System and Cellular Automaton. In Proceedings of the 2014 International Conference on Virtual Reality and Visualization (ICVRV), Shenyang, China, 30–31 August 2014. [Google Scholar]
- Helbing, D.; Farkas, I.; Vicsek, T. Simulating Dynamical Features of Escape Panic. Nature 2000, 407, 487–490. [Google Scholar] [CrossRef] [Green Version]
- Kasai, Y.; Sasabe, M.; Kasahara, S. Congestion-aware route selection in automatic evacuation guiding based on cooperation between evacuees and their mobile nodes. Eurasip J. Wirel. Commun. Netw. 2017, 2017, 164. [Google Scholar] [CrossRef] [Green Version]
- Iizuka, Y.; Iizuka, K. Disaster evacuation assistance system based on multi-agent cooperation. In Proceedings of the Annual Hawaii International Conference on System Sciences, Kauai, HI, USA, 5–8 January 2015; pp. 173–181. [Google Scholar]
- Chen, Y.; Liu, R.; Barrett, D.; Gao, L.; Zhou, M.; Renzullo, L.; Emelyanova, I. A spatial assessment framework for evaluating flood risk under extreme climates. Sci. Total Environ. 2015, 538, 512–523. [Google Scholar] [CrossRef]
- Liu, R.; Chen, Y.; Wu, J.; Gao, L.; Barrett, D.; Xu, T.; Li, X.; Li, L.; Huang, C.; Yu, J. Integrating Entropy-Based Naïve Bayes and GIS for Spatial Evaluation of Flood Hazard. Risk Anal. 2017, 37, 756–773. [Google Scholar] [CrossRef]
- Chang, M.; Tseng, Y.; Chen, J. A scenario planning approach for the floodemergency logistics preparation problem under uncertainty. Transp. Res. Part E Logist. Transp. Rev. 2007, 43, 737–754. [Google Scholar] [CrossRef]
- Wang, F.Y.; Wang, X.; Li, L.; Li, L. Steps toward Parallel Intelligence. IEEE/CAA J. Autom. Sin. 2016, 3, 345–348. [Google Scholar]
- Kongsomsaksakul, S.; Yang, C.; Chen, A. Shelter location-allocation model for flood evacuation planning. J. East. Asia Soc. Transp. Stud. 2005, 6, 4237–4252. [Google Scholar]
- Chu, J.Y.; Chen, L.L. The Research Progress on Site Selection of Disasters Mitigation Emergency Congregate Shelter. In Advanced Materials Research; Trans Tech Publication: Zurich, Switzerland, 2014. [Google Scholar]
- Chu, J.; Su, Y.; Ma, D. Study on design of emergency lodging plot in disasters mitigation congregate emergency shelter. World Inf. Earthq. Eng. 2014, 30, 80–85. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 1996, 96, 226–231. [Google Scholar]














| Variables | Symbols | Description |
|---|---|---|
| Probability | pij | probability of the agents start from i and the destination is shelter j |
| Replenishment capacity | replenishment capacity of the shelter j | |
| Distance | dij | distance between the nodes i and j |
| Number of pedestrians | M | co-occurrence amount of pedestrians in a route |
| Number of waterlogging points | r | number of waterlogging points in a route |
| Score of a route | S | the calculated score of a route by an agent crossing an intersection |
| speed | v0 | initial speed of an agent |
| v | current speed of an agent | |
| energy | E | current energy of an agent |
| E0 | initial energy of an agent | |
| Er | energy consumed by wading the waterlogging | |
| crowd density | crowd density around an agent | |
| information | I | information of an agent |
| Ratios | 1-1-1 | 1-1-2 | 1-2-3 | |||
|---|---|---|---|---|---|---|
| Rebellious | Following | Rebellious | Following | Rebellious | Following | |
| 6:4 | 18.89% | 21.74% | 14.01% | 18.13% | 22.44% | 43.15% |
| 5:5 | 14.10% | 13.91% | 14.69% | 20.39% | 21.32% | 36.36% |
| 4:6 | 19.80% | 23.15% | 11.28% | 10.82% | 19.38% | 35.74% |
| 3:7 | 14.04% | 10.64% | 23.08% | 20.06% | 17.04% | 40.82% |
| 2:8 | 13.59% | 14.86% | 14.44% | 16.34% | 13.86% | 31.83% |
| 1:9 | 6.25% | 20.18% | 14.29% | 24.61% | 20% | 50.43% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Sun, Y.; Liu, X.; Wang, J. MAS-Based Evacuation Simulation of an Urban Community during an Urban Rainstorm Disaster in China. Sustainability 2020, 12, 546. https://doi.org/10.3390/su12020546
Yang Q, Sun Y, Liu X, Wang J. MAS-Based Evacuation Simulation of an Urban Community during an Urban Rainstorm Disaster in China. Sustainability. 2020; 12(2):546. https://doi.org/10.3390/su12020546
Chicago/Turabian StyleYang, Qing, Ying Sun, Xingxing Liu, and Jinmei Wang. 2020. "MAS-Based Evacuation Simulation of an Urban Community during an Urban Rainstorm Disaster in China" Sustainability 12, no. 2: 546. https://doi.org/10.3390/su12020546
APA StyleYang, Q., Sun, Y., Liu, X., & Wang, J. (2020). MAS-Based Evacuation Simulation of an Urban Community during an Urban Rainstorm Disaster in China. Sustainability, 12(2), 546. https://doi.org/10.3390/su12020546




