Optimal Project Planning for Public Rental Housing in South Korea

Abstract

Although Korea has made notable progress in the availability of public rental housing, Korea’s public rental housing representing 6.3% of the country’s total housing is still below the 8% OECD average from 2016. The Seoul Metropolitan Area (composed of Seoul City, Incheon City, and Gyeonggi Province) has nearly 50% of the country’s population, but 11% of the nation’s territory, meaning the area suffers from an acute shortage of public rental housing. This is a serious problem which is hampering the sustainability of Korean society in general. We will examine the possibility of improving this public housing problem using certain algorithms to optimize decision making and resource allocation. This study reviews two pioneering studies on optimal investment portfolio for land development projects and optimal project combination for urban regeneration projects, and then optimizes a public housing investment combination to maximize the amount of public rental houses in Gyeonggi province using optimization techniques. Through the optimal investment combination, public rental houses were found to be more efficiently and sustainably planned for the community.

1. Introduction

Korea’s record for improving access to quality housing has been significant. This has been partially due to the introduction of minimum living standards (e.g., the number of rooms and floor space being differentiated by the size and composition of households) and by direct government support for housing construction. However, although the long-term public rental housing inventory has been steadily rising over the last decade, its share (6.3%) of total housing in 2016 is still below the OECD average (8%) according to the Korean Ministry of Land, Infrastructure, and Transport [1,2]. South Korea aims to increase the share of public rental housing to 9% by 2022 [1].

The scarcity of developable land for residential purposes in South Korea is more problematic in urban areas such as Seoul. The Seoul Metropolitan Area (SMA) —composed of Seoul city, Incheon city, and Gyeonggi province—represents 11% of Korea’s territory and accommodates almost 50% of the national population. As a result, housing demand in SMA is very high [2]. Strong demand, geographical constraint, and extensive land use regulation, such as greenbelt policy, may be leading to high house prices in SMA. Young, senior, and low-income households are particularly affected by soaring house prices in this region. The supply of public rental housing helps to solve this problem by expanding the stock of affordable housing, and it also indirectly contributes by keeping a lid on private rent prices.

According to Housing Welfare Road map [1], total housing stock increased by 3.58 million (22.0%) from 16.3 million in 2007 to 19.88 million in 2016 but housing prices increased by 24.9%, meaning it is not easy for ordinary people to buy houses. The Price to Income Ratio (PIR) is 5.6 and the PIR for the lowest-income group is 9.8 in South Korea.

So far, researchers have performed useful studies in the field of land-project optimization and public rental housing supply using optimization techniques such as the genetic algorithm (GA) and branch and bound method (B&B).

The genetic algorithm is useful tool which has been used to find the spatial optimization of multi-objective and multi-site land use allocation [3], to forecast the private housing demand in Hong Kong [4], to search for optimal solutions to a land use allocation problem with multiple objectives and constraints in case of Tongzhou Newtown in Beijing, China [5], to formulate and develop municipal land use plans in Galicia, Spain [6], and to undertake land-use spatial optimization in Gaoqiao Town, Zhejiang Province, China [7]. The genetic algorithm has also been used to maximize land prices and reduce incompatibility among land uses of an area for urban planners [8], enhance real estate appraisal forecasting with ridge regression [9], optimize transportation infrastructure planning in Provo, Utah, USA [10] or urban land-use allocation in the case study of Dhanmondi Residential Area, Dhaka, Bangladesh [11], search for a spatial multi-objective land use optimization model [12], solve multi-objective land use planning in the Netherlands [13], and support simulating multi-objective spatial optimization allocation of land in Changsha, Zhuzhou, Xiangttan city in China [14].

While the above studies used GA in real estate problems, other researchers have used other intelligent techniques. Jin and Yu [15] analyzed the risk of housing rearrangement projects using the technique of fuzzy theory [16], and Bae and Yu [17] predicted apartment housing prices using the technique of machine learning [18].

There are two pioneering studies in real estate optimization for South Korean projects. The first one considered the optimal investment portfolio for land development projects [19], and the second one considered the optimal project combination for urban regeneration projects [20]. Both studies used both the genetic algorithm and the branch and bound method to obtain combinatorial optimization solutions in real estate cases. Park et al. [21] also proposed an optimization model for another type of real estate problem involving investment scheduling for public rental housing projects. However, their initial study has the limitation of not considering real-world cases. Thus, this study aims to focus more on practical approach in investment optimization for public rental housing projects by considering real-world project data in South Korea.

2. Methodologies

The genetic algorithm is the optimal problem-solving method, and it involves using the natural selection phenomenon together with genetics-related operators such as crossover, mutation, and reproduction. The branch and bound method is a technique used for discrete and combinatorial optimization problems.

2.1. Genetic Algorithm

The Genetic algorithm was first introduced by John Holland in the 1960s [21]. GA is a technique for moving from one population of ‘chromosomes’ to a new population using selection operators such as crossover, mutation, and inversion. Each chromosome is composed of ‘genes (digital bits)’, and each gene is filled with a particular ‘allele (zero or one)’. In the selection operation, a group of chromosomes that are allowed to be reproduced is selected in the population, and the fitter chromosomes have a higher chance to produce offspring. Crossover exchanges subparts of two chromosomes, generally mimicking biological recombination between two chromosome organisms. Afterwards, mutation arbitrary changes the values of some places in the chromosomes and inversion reverses the order of an adjacent section of the chromosome, thus rearranging the order in which genes are spread.

2.2. Branch and Bound Method

The Branch and Bound method (B&B) was developed independently by Land and Doig in 1960 and by Murty, Karel, and Little in 1962 [19]. B&B is an analytical approach for discrete optimization problems. Unlike continuous optimization problems, discrete optimization problems are not smooth functions because integer restrictions are placed on (at least some of) the relevant variables. Discrete optimization problems are solved by enumerative methods that investigate the feasible solution set. B&B is an attractive partial enumeration strategy for optimization problems because it analyzes each subgroup with a lower bound or upper bound (branching and bounding) and deletes some groups with no feasibility (pruning), thus finding optimal combination in remaining groups (retracting). Therefore, B&B has four steps as follows: (1) branching, (2) bounding, (3) pruning, and (4) retracting.

3. Optimization for Land Development Projects

One of pioneering studies in public real estate optimization in South Korea focused on land development planning [19]. The summary of the study can be reviewed as follows.

Government-owned public companies often have a chance to decide the most reasonable investment portfolio from a number of new projects under a limited budget. Here, the limited budget can be a major constraint in this study. Another constraint in land development problems is the balance between profitability and public interest. If a public company chooses projects with a high profit margin but low public interest in order to maximize the total return on investment, its role for public good is likely to be reduced.

The third constraint in land optimization is the equitability in each region. If a project is concentrated on a specific region, it may be criticized for not focusing on regionally balanced development. The fourth constraint is the balance among land use purposes, such as new town, public rental housing, and industrial complexes. There is a minimally required amount constraint for each purpose.

The fifth constraint involves efficient allocation of human resources. Regarding human resources, it is necessary to minimize unassigned employees in order to maintain employment. The sixth constraint is the possibility of joint investment from cooperated companies. While there are some projects that can be jointly performed with a shared budget and risk, there are other projects that must be solely completed by a single company.

It is very important to find the best investment combination that will allow public companies to properly allocate financial resources and maximize return on investment among many new projects while meeting the constraints described above. It is not easy to rationally derive the optimal business combination that maximizes the return on investment among many new projects or maximizes the public interest while meeting the minimum profit goal because there is currently no customized methodology for achieving this in South Korea. As such, we must rely on the optimal business combination (combinatorial optimization) that maximizes the return on investment while meeting multiple constraints from a group of new project candidates that have different characteristics.

In line with the above-mentioned factors (return on investment maximization, budget limitation, public interest consideration, regional balance, land purpose balance, human resource management, joint investment possibility), an optimal land development model was proposed as follows:

- Objective function: $\mathrm{Max}{{\displaystyle \sum }}_i\left(R_i\cdot X_i\right)$: maximization of the return on investment ($R_i$ is the return on investment (%) for project i)

- Decision variable: $X_i$: the investment amount on project i (unit: 10¹⁰ KRW)

- Constraint 1. ${{\displaystyle \sum }}_i{X}_i\le 110$: the total investment amount is equal to or less than 110 × 10¹⁰ KRW

- Constraint 2. ${{\displaystyle \sum }}_k{X}_k\ge 0.3{{\displaystyle \sum }}_i{X}_i$, k ∊ Set of non-for-profit projects: the investment for non-for-profit projects is equal to or more than 30% of total investment

- Constraint 3. ${{\displaystyle \sum }}_k{X}_k\le 0.4{{\displaystyle \sum }}_i{X}_i$, k ∊ {East, West, North, South}: the investment in each area is equal to or less than 40% of total investment

- Constraint 4. ${{\displaystyle \sum }}_k{X}_k\ge 0.2{{\displaystyle \sum }}_i{X}_i$, k ∊ {New Town, Public Housing, Industrial Complex}: investment in each business division is equal to or more than 20% of total investment

- Constraint 5. ${{\displaystyle \sum }}_i{N}_i\cdot Sgn\left(X_i\right)\ge 250$: total employees in active projects are equal to or more than 250 ($N_i$ is the number of employees for performing project i; $Sgn()$ is a sign function representing the sign (0 or 1) of $X_i$)

- Constraint 6. $0\le X_i\le X_i^{Upper}$ and $X_i$ is an integer if i is a joint project. $X_i=0 or X_i=X_i^{Upper}$ if i is not a joint project. Projects that cannot be jointly invested such as E, F, G, H, M, N, O, P, S, and T have only two selections such as no investment or whole investment, while projects that can be jointly invested such as A, B, C, D, I, J, K, L, Q, and R have a partial investment option.

Park et al. [19] also provided a dataset of 20 new candidate projects in South Korea, as shown in Table 1. Each project has different characteristic in terms of investment amount, profit, public interest, investment area, business division, number of employees participated, and joint investment possibility.

Table 1. Candidate Land Development Projects.

Profit Type	Project	ROI *	Investment (108 KRW) **	Profit Type ***	Region	Biz Division	Partnership ****	Personnel
Low profit	A	−2%	1000	Non-for-profit	East	New town	Possible	30
	B	1%	800	Non-for-profit	West	New town	Possible	24
	C	−1%	600	Non-for-profit	South	New town	Possible	18
High profit	D	5%	400	For-profit	North	New town	Possible	12
	E	6%	200	For-profit	East	New town	Impossible	6
	F	5%	1000	For-profit	West	Industrial complex	Impossible	30
Low profit	G	2%	800	Non-for-profit	South	Industrial complex	Impossible	24
	H	1%	600	Non-for-profit	North	Industrial complex	Impossible	18
	I	−2%	400	Non-for-profit	East	Industrial complex	Possible	12
High profit	J	5%	200	For-profit	West	Industrial complex	Possible	6
	K	6%	1000	For-profit	South	Housing	Possible	30
	L	5%	800	For-profit	North	Housing	Possible	24
Low profit	M	−2%	600	Non-for-profit	East	Housing	Impossible	18
	N	1%	400	Non-for-profit	West	Housing	Impossible	12
	O	−2%	200	Non-for-profit	South	Housing	Impossible	6
High profit	P	5%	1000	For-profit	North	New town	Impossible	30
	Q	6%	800	For-profit	East	New town	Possible	24
	R	5%	600	For-profit	West	Industrial complex	Possible	18
Low profit	S	1%	400	Non-for-profit	South	Industrial complex	Impossible	12
	T	−2%	200	Non-for-profit	North	Housing	Impossible	6

* ROI was assumed based on real project performances. ** Total investment amount is 1.2 trillion KRW, which is over the total investment budget of 1.1 trillion Korean Won (KRW). *** Non-for-profit: New town projects that are not for profit but are for regional balance development; Public rental housing and Industrial complex projects that are not for profit but are for regional balance development. / For-profit: New town projects in attractive location; Public sale housing and Industrial complexes in attractive locations. **** Local government-owned company may invest with other public land development companies to reduce financial burden and business risk if partnerships are possible.

This optimization model has 20 decision variables, each of which has an integer or binary number, and the total number of possible candidate solutions is 3.3 × 10¹¹, which requires a considerable computation process.

After computation, this land development planning model found an optimal profit of 3.58 (10¹⁰ KRW), as shown in Table 2, which also satisfies the constraints as follows:

Table 2. Result of Land Development Optimization.

Project	Investment Amount	Non-for- Profit	Project Area				Business Division			Person	Profit (10 billion KRW)
			East	West	South	North	New Town	Industrial Complex	Housing
A	-	-	-	-	-	-	-	-	-	-	-
B	8	8	-	8	-	-	8	-	-	24	0.08
C	-	-	-	-	-	-	-	-	-	-	-
D	4	4	-	-	-	4	4	-	-	12	0.2
E	2	-	2	-	-	-	2	-	-	6	0.12
F	10	-	-	10	-	-	-	10	-	30	0.5
G	8	8	-	-	8	-	-	8	-	24	0.16
H	6	6	-	-	-	6	-	6	-	18	0.06
I	-	-	-	-	-	-	-	-	-	-	-
J	2	-	-	2	-	-	-	2	-	6	0.1
K	10	-	-	-	10	-	-	-	10	30	0.6
L	8	-	-	-	-	8	-	-	8	24	0.4
M	-	-	-	-	-	-	-	-	-	-	-
N	4	4	-	4	-	-	-	-	4	12	0.04
O	-	-	-	-	-	-	-	-	-	-	-
P	10	-	-	-	-	10	10	-	-	30	0.5
Q	8	-	8	-	-	-	8	-	-	24	0.48
R	6	-	-	6	-	-	-	6	-	18	0.3
S	4	4	-	-	4	-	-	4	-	12	0.04
T	-	-	-	-	-	-	-	-	-	-	-
Total	90	30	10	30	22	28	32	36	22	270	3.58

- Total investment amount: 90 (10¹⁰ KRW) which is less than 110 (10¹⁰ KRW).

- Non-for-profit ratio: 33% which is more than 30% of total investment.

- Investment area: East (10), West (30), South (22), North (28). Each area has less than 36 (10¹⁰ KRW) which is 40% of total investment.

- Investment division: new town (32), industrial complex (36), public housing (22). Each division is more than 18 (10¹⁰ KRW), which is 20% of total investment.

- Number of employees: 270 which is more than 250.

4. Optimization for Urban Regeneration Projects

Another pioneering study in public real estate optimization in South Korea is urban regeneration planning [20]. The summary of this study can be reviewed as follows.

According to Lee and Lim [22], urban growth in South Korea has reached its limit, and urban areas have started to decline. Urban decline has resulted in critical issues such as outflow of the population, ageing infrastructure, loss of economic capacity, etc. Thus, the ‘urban regeneration’ can be a new strategy in South Korea’s national urban policy for maintaining sustainable urban circumstances and revitalizing enervated communities. This concept of urban regeneration is not only for city planning-oriented approaches which can develop sustainable economic and physical city environments, but also for social and governance-oriented practices which can accumulate social capital. Thus, South Korea’s urban regeneration policy is highly related to the idea of urban sustainability.

There are various models such as the ‘Downtown model (DM)’, ‘Economic support model (ESM)’, and ‘Public company proposal model (PCPM)’ for urban regeneration projects. The DM is a project model used to support the recovery of public functions and the vitalization of commerce through cooperation with historical, cultural, and traveling resources in old downtown areas where the decline of public services and the decline of commerce are severe. The ESM is a project model that creates new industrial complexes to increase jobs in areas where urban decline is severe. The PCPM has been proposed by public companies as a plan for urban regeneration in certain cities, while other models were proposed by local governments.

Each project can be evaluated based on various criteria and correspondingly earned certain scores, as shown in Table 3.

Table 3. Evaluation Criteria and Score for Urban Regeneration Projects [23].

Evaluation Criteria	Score Points	Detail Evaluation Criteria	Score Points
Urgency and Necessity of project	30	Urgency of project (Region deterioration, Safety)	15
		Necessity of project (Community participation)	15
Feasibility of project plan	40	Local government’s organization for project	5
		Relevance of project plan	10
		Plan of land acquisition and finance for project	15
		Community participation and empowerment training	10
Effect of project	30	Housing welfare and improvement of quality of life	10
		Job creation effect	10
		Social integration and sustainability	5
		Countermeasure towards side-effects of the real estate market	5

The South Korean central government plans to choose 13 DM projects, 2 ESM projects, and 10 PCPM projects from a total of 66 projects developed by 16 local governments based on the evaluation of the Urban Regeneration Special Committee. Here, each local government can apply for a maximum of four projects. If the central government selects projects with respect to project effects themselves, there will be unselected regions, which will violate the principle of regionally balanced development. For this reason, a combinatorial optimization model was proposed and could provide optimal solutions while satisfying various constraints.

The model for optimally selecting urban regeneration projects can be formulated as follows:

- Objective function: $\mathrm{Max}{{\displaystyle \sum }}_i\left(S_i\cdot X_i\right)$: maximization of urban regeneration effect ($S_i$ is earned score for project i)

- Decision variable: $X_i\in \left\{0,1\right\}$: investment decision for project i (1 means investment; and 0 means no investment)

- Constraint 1.${{\displaystyle \sum }}_k{X}_k=13$, k ∊ Set of downtown-focused projects

- Constraint 2. ${{\displaystyle \sum }}_k{X}_k=2$, k ∊ Set of industry-oriented projects

- Constraint 3. ${{\displaystyle \sum }}_k{X}_k=10$, k ∊ Set of public-corporation-proposed projects

- Constraint 4. 1 $\le {{\displaystyle \sum }}_j{X}_j\le 3$, j ∊ Set of non-Gyeonggi province projects (Projects should be selected in each local government from a minimum of one project to a maximum of three for regionally balanced development)

- Constraint 5. 2 $\le {{\displaystyle \sum }}_j{X}_j\le 4$, j ∊ Set of Gyeonggi province projects (Because Gyeonggi province has lots of urban regeneration demand, projects should be selected from a minimum of two projects to a maximum of four)

Total number of candidate solutions for this combinatorial problem including constraint-violated ones is 2⁶⁶ (≈7.38 × 10¹⁹), which actually requires a major computation process.

The results of this optimal project combination problem using GA and B&B are shown in Table 4, Table 5 and Table 6. The total score (2198) from B&B as shown in Table 5 is slightly better than that (2173) of GA as shown in Table 4, and Table 6 shows the overall result from B&B. Here, Busan stands for Busan Metropolitan City, Daegu stands for Daegu Metropolitan City, Incheon stands for Incheon Metropolitan City, Gwangju stands for Gwangju Metropolitan City, Daejeon stands for Daejeon Metropolitan City, Ulsan stands for Ulsan Metropolitan City, Jeju stands for the Jeju Special Self-governing Province, and Sejong stands for the Sejong Special Self-governing City.

Table 4. Selected Projects of Urban Regeneration Planning using GA.

Project Model (Number)	Project Name
DM (13)	B1, C1, E1, F2, G3, H1, J2, K1, M1, M2, N1, O1, P1
ESM (2)	A4, B4
PCPM (10)	C3, D3, F3, G4, H2, I2, J3, K2, L3, M3

Table 5. Selected Projects of Urban Regeneration Planning using B&B.

Project Model (Number)	Project Name
DM (13)	B1, C1, E1, F2, G2, G3, H1, K1, L2, N1, O1, P1, P2
ESM (2)	D4, K4
PCPM (10)	A3, H2, I2, J3, K2, L3, M3, N2, O2, P3

Table 6. Overall Result of Urban Regeneration Planning using B&B.

Local Govt. (Number)	Project Name	Project Model	Score of Evaluation	Local Govt. (Number)	Project Name	Project Model	Score of Evaluation
Busan (1)	A1	DM	74	Chungcheong (North) (1)	I1	DM	73
	A2	DM	76		I2	PCPM	89
	A3	PCPM	86		I3	ESM	84
	A4	ESM	83		I4	ESM	76
Daegu (1)	B1	DM	83	Chungcheong (South) (1)	J1	DM	79
	B2	DM	83		J2	DM	82
	B3	PCPM	80		J3	PCPM	91
	B4	ESM	83		J4	ESM	79
Incheon (1)	C1	DM	88	Jeolla (North) (3)	K1	DM	88
	C2	DM	73		K2	PCPM	94
	C3	PCPM	86		K3	ESM	79
	C4	ESM	75		K4	ESM	86
Gwangju (1)	D1	DM	74	Jeolla (South) (2)	L1	DM	81
	D2	DM	73		L2	DM	85
	D3	PCPM	84		L3	PCPM	92
	D4	ESM	83		L4	ESM	79
Daejeon (1)	E1	DM	92	Gyeongsang (North) (1)	M1	DM	79
	E2	DM	84		M2	DM	82
	E3	PCPM	83		M3	PCPM	92
	E4	ESM	82		M4	ESM	78
Ulsan (1)	F1	DM	73	Gyeongsang (South) (2)	N1	DM	85
	F2	DM	86		N2	PCPM	89
	F3	PCPM	85		N3	ESM	84
	F4	ESM	77		N4	ESM	84
Gyeonggi (2)	G1	DM	80	Jeju (2)	O1	DM	87
	G2	DM	82		O2	PCPM	90
	G3	DM	86		O3	ESM	81
	G4	PCPM	85		O4	ESM	80
	G5	ESM	81	Sejong (3)	P1	DM	87
	G6	ESM	83		P2	DM	83
Gangwon (2)	H1	DM	95		P3	PCPM	90
	H2	PCPM	89		P4	ESM	77
	H3	ESM	81
	H4	ESM	83

5. Optimal Project Combination for Public Rental Housing

While previous real estate optimization studies [19,20] were based on artificial examples on investment amount, return on investment, the evaluation score for a urban regeneration project, etc., this study focused on a real-world case of a new town project in South Korea. We planned to find a optimal public housing investment combination to maximize the amount of public rental houses in Gwanggyo, which is one of the second-stage new towns. Gwanggyo new town is a planned city surrounding part of Suwon city and part of Yongin city. It is located 25 km south from Seoul, as shown with a red rectangle in Figure 1. In 2004, Gwanggyo new town was designated by Gyeonggi Province, Suwon city, Youngin city, and by a local-government-owned real-estate company named Gyeonggi Urban Innovation Corporation (GICO). Gwanggyo new town, which will accommodate more than 31,000 households, was not only intended for the purpose of providing increased housing supply but also for several regional purposes such as a local-government office, convention center, and commercial zone.

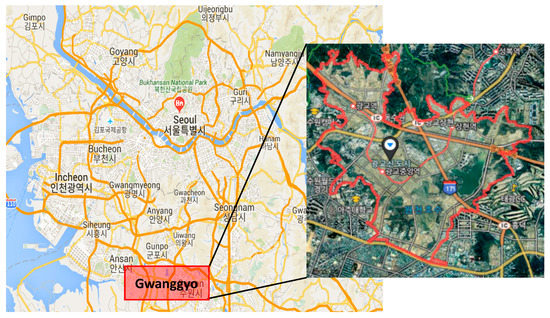
Figure 1. Map of Gwanggyo New Town (Google and Naver map).

The percentage of public rental housing investment from 2008 to 2018 by GICO was very low, and during this period the housing investment for public sale occupied most of relevant company activities, as seen in Table 7 (the data was extracted from an internal report).

Table 7. The Public Sale and Rental House Construction Record of GICO.

Type	Housing Project	Construction Period	Investment (108 KRW)	Detail of Investment
Sales Housing	Sub Total		30,345
	Gimpo-Yangchon	2008.4~2010.12	437	Land price +Construction cost
	Gwanggyo Edu-town 12	2009.11~2012.11	2613	Construction cost (GICO’s land)
	Gwanggyo Edu--town 13–15	2009.12~2012.12	2225	Construction cost (GICO’s land)
	Gimpo-Hangang Ab–1	2009.12~2013.2	2617	Land price +Construction cost
	Gimpo-Hangang Ab–7	2009.12~2013.2	3028	Land price +Construction cost
	Wirye A2–11	2014.4~2016.9	6758	Land price +Construction cost
	Wirye A2–2	2015.4~2017.9	4661	Land price +Construction cost
	Namyangju-Dasan B2	2015.4~2017.11	2166	Construction cost (GICO’s land)
	Namyangju-Dasan B4	2015.4~2017.11	2938	Construction cost (GICO’s land)
	Namyangju-Dasan S1	2015.12~2018.6	2902	Construction cost (GICO’s land)
Rental Housing	Gimpo-Hangang Ab-2	2012.1~2013.2	1091	Land price +Construction cost

On the other hand, all the public rental houses located in Gwanggyo New Town were supplied by the Korea Land Housing Corporation (KLHC), which is the central government-owned company with more than 32 trillion KRW of capital as of the first half of 2019 (www.lh.or.kr). GICO, who had about 1.6 trillion KRW of capital as of the first half of 2019 (www.gico.or.kr), did not build any public rental houses in Gwanggyo New Town. Because GICO had more than 4 trillion KRW of loans resulting from land acquisition and development expense with regard to Gwanggyo New Town from 2012 to 2014, it had to sell land for public rental housing to KLHC rather than construct and operate public rental houses. Table 8 shows the list of public rental house projects developed by KLHC and the corresponding construction costs. But it would be more desirable for GICO to supply some public rental houses to satisfy its mission statement. If the GICO had used 3034.5 billion won, which was originally invested for the 10 public sale house projects from 2008 to 2018, to construct rental houses and sales houses instead, it would have been a better decision that met the purpose of public interest.

Table 8. Estimated Cost of Public Rental House Projects.

Site Name	Number of Houses	ConstructionCompletion	Total Area (m2) (A)	Estimated Construction Cost (KRW) per m2 (B)	Total Construction Cost (108 KRW) of GICO
Total	6956		804,656		8673
A10	701	2013.11	111,002	1,077,893	1196
A11	637	2013.11	102,334		1103
A16	224	2014.7	34,680		374
A19	1373	2011.11	112,458		1212
A23	258	2014.2	39,979		431
A24	394	2014.2	54,883		592
A25	146	2011.10	13,091		141
A26	1132	2013.12	172,477		1859
A30	2091	2011.12	163,752		1765

According to a study on housing policy in South Korea [24], Korean housing authorities focused on the expansion of state-developed housing for sale rather than the provision of rental accommodation. In order to obtain adequate housing for poor and disadvantaged groups, adequate rental accommodation is needed to ensure legal security of tenure protection from discrimination and equal access to adequate housing for all persons and their families.

Here, the total number of combinations with 10 sales of housing sites and 10 rental housing sites (one rental housing project was developed by GICO as seen in Table 7 and nine projects were developed by KLHC as seen in Table 8) was 2²⁰ because we had to decide whether or not to select each of 20 housing projects. Thus, instead of total enumeration, we utilized optimization techniques such as GA and B&B to find an optimal solution.

The objective function and constraints for this housing combinatorial problem were as follows:

- Objective function: $\mathrm{Max}{{\displaystyle \sum }}_i\left(N_i\cdot X_i\right)$: Maximization of the number of supplied public rental houses ($N_i$ is the number of supplied houses from project i)

- Decision variable: $X_i\in \left\{0,1\right\}$: investment decision for project i (1 means investment; and 0 means no investment)

- Constraint 1$:{{\displaystyle \sum }}_i\left(B_i\cdot X_i\right)\le 3034.5$: Total investment amount should be less than 3034.5 billion KRW, which is the total investment amount for public sale house projects from 2008 to 2018 ($B_i$ is budget for project i)

- Constraint 2.${{\displaystyle \sum }}_k{X}_k=9$, k ∊ Set of public sale house projects: By slightly reducing the number of public sale house projects from 10 to 9, GICO can increase public rental houses more.

5.1. Public Rental Housing Planning by Arbitrary Selection #1

GICO usually invests two public sale house projects per one new town, for example Gimpo-Hangang Ab-1 and Ab-7 in Gimpo-Hangang new town, Wirye A2-2, and Wirye A2-11 in Wirye new town for their business portfolio. Gimpo-Yangchon (one project) and Namyangju-Dasan (three projects) are exceptional cases. Therefore, we excluded the biggest public sale house project, Namyangju-Dasan B4 among three Namyangju-Dasan projects. Then, we redistributed that investment amount of Namyangju-Dasan B4 (293,800 million KRW) to select public rental house projects. The result of arbitrary selection #1 is shown in Table 9.

Table 9. Result of Arbitrary Selection #1.

Name of Site		Number of Houses	Investment Amount (100m.)	Selection	Number of Selected Houses	Investment Amount (100m.)
Rental house (10)	Gwanggyo A10	701	1196	X	-	-
	Gwanggyo A11	637	1103	X	-	-
	Gwanggyo A16	224	374	X	-	-
	Gwanggyo A19	1373	1212	X	-	-
	Gwanggyo A23	258	431	X	-	-
	Gwanggyo A24	394	592	X	-	-
	Gwanggyo A25	146	141	X	-	-
	Gwanggyo A26	1132	1859	X	-	-
	Gwanggyo A30	2091	1765	O	2091	1765
	Gimpo Ab-2	559	1091	X	-	-
	Sub Total	7515	9764	1 site selected	2091	1765
Sales house (10)	Gimpo-Yangchon	743	437	O	743	437
	Gwanggyo-Edutown 12	1764	2613	O	1764	2613
	Gwanggyo-Edutown 13~15	1173	2225	O	1173	2225
	Gimpo-Hangang Ab-1	1167	2617	O	1167	2617
	Gimpo-Hangang Ab-7	1382	3028	O	1382	3028
	Wirye A2-11	1540	6758	O	1540	6758
	Wirye A2-2	1413	4661	O	1413	4661
	Namyangju-Dasan B2	1186	2166	O	1186	2166
	Namyangju-Dasan B4	1615	2938	X	-	-
	Namyangju-Dasan S1	1685	2902	O	1685	2902
	Sub Total	13,668	30,345	9 sites selected	12,053	27,407
Total		21,183	40,109	10 sites selected	14,144	29,172

As observed in Table 9, Constraint 1 is satisfied because total investment amount is 2,917,200 million KRW, which is less than 3,034,520 million KRW. Also, Constraint 2 is satisfied because only Namyangju-Dasan B4 was excluded.

The result of the objective function (maximization of the number of suppled public rental houses) is 2091. If GICO also includes Gwanggyo A19, the biggest remaining public rental house project, the total investment amount would be 3,384,000 million KRW which violates Constraint 1 (≤3,034,500 million KRW).

5.2. Public Rental Housing Planning by Arbitrary Selection #2

GICO excludes Wirye A2-11 (whose investment amount was the biggest) to supply more public rental houses. Then, GICO redistributes that investment amount of Wirye A2-11 (675,800 million KRW) in order to maximize the number of selected houses. The result of arbitrary selection #2 is as shown in Table 10.

Table 10. Result of Arbitrary Selection #2.

Name of Site		Number of Houses	Investment Amount (100m.)	Selection	Number of Selected Houses	Investment Amount (100m.)
Rental house (10)	Gwanggyo A10	701	1196	O	701	1196
	Gwanggyo A11	637	1103	X	-	-
	Gwanggyo A16	224	374	X	-	-
	Gwanggyo A19	1373	1212	O	1373	1212
	Gwanggyo A23	258	431	X	-	-
	Gwanggyo A24	394	592	X	-	-
	Gwanggyo A25	146	141	X	-	-
	Gwanggyo A26	1132	1859	O	1132	1859
	Gwanggyo A30	2091	1765	O	2091	1765
	Gimpo Ab-2	559	1091	X	-	-
	Sub Total	7515	9764	4 sites selected	5297	6032
Sales house (10)	Gimpo-Yangchon	743	437	O	743	437
	Gwanggyo-Edutown 12	1764	2613	O	1764	2613
	Gwanggyo-Edutown 13~15	1173	2225	O	1173	2225
	Gimpo-Hangang Ab-1	1167	2617	O	1167	2617
	Gimpo-Hangang Ab-7	1382	3028	O	1382	3028
	Wirye A2-11	1540	6758	X	-	-
	Wirye A2-2	1413	4661	O	1413	4661
	Namyangju-Dasan B2	1186	2166	O	1186	2166
	Namyangju-Dasan B4	1615	2938	O	1615	2938
	Namyangju-Dasan S1	1685	2902	O	1685	2902
	Sub Total	13,668	30,345	9 sites selected	12,128	23,587
Total		21,183	40,109	13 sites selected	17,425	29,619

As observed in Table 10, Constraint 1 is satisfied because total investment amount is 2,961,900 million KRW which is less than 3,034,520 million KRW. Also, Constraint 2 is satisfied because only Wirye A2-11 is excluded.

The result of objective function (maximization of the number of suppled public rental houses) is 5297. If GICO also includes Gwanggyo A11, the biggest remaining public rental house project, total investment amount would be 3,722,000 million KRW, which violates Constraint 1 (≤3,034,500 million KRW).

5.3. Public Rental Housing Planning Determined by the Branch and Bound Method

The result of the Branch and Bound Method is shown in Table 11. As observed in Table 11, Constraint 1 is satisfied because total investment amount is 2,929,800 million KRW, which is less than 3,034,520 million KRW. Also, Constraint 2 is satisfied because only Wirye A2-11 is excluded.

Table 11. Result of Branch & Bound Method.

Name of Site		Number of Houses	Investment Amount (100m.)	Selection	Number of Selected Houses	Investment Amount (100m.)
Rental house (10)	Gwanggyo A10	701	1196	O	701	1196
	Gwanggyo A11	637	1103	X	-	-
	Gwanggyo A16	224	374	O	224	374
	Gwanggyo A19	1373	1212	O	1373	1212
	Gwanggyo A23	258	431	O	258	431
	Gwanggyo A24	394	592	O	394	592
	Gwanggyo A25	146	141	O	146	141
	Gwanggyo A26	1132	1859	X	-	-
	Gwanggyo A30	2091	1765	O	2091	1765
	Gimpo Ab-2	559	1091	X	-	-
	Sub Total	7515	9764	7 sites selected	5187	5711
Sales house (10)	Gimpo-Yangchon	743	437	O	743	437
	Gwanggyo-Edutown 12	1764	2613	O	1764	2613
	Gwanggyo-Edutown 13~15	1173	2225	O	1173	2225
	Gimpo-Hangang Ab-1	1167	2617	O	1167	2617
	Gimpo-Hangang Ab-7	1382	3028	O	1382	3028
	Wirye A2-11	1540	6758	X	-	-
	Wirye A2-2	1413	4661	O	1413	4661
	Namyangju-Dasan B2	1186	2166	O	1186	2166
	Namyangju-Dasan B4	1615	2938	O	1615	2938
	Namyangju-Dasan S1	1685	2902	O	1685	2902
	Sub Total	13,668	30,345	9 sites selected	12,128	23,587
Total		21,183	40,109	16 sites selected	17,315	29,298

The result of objective function (maximization of the number of suppled public rental houses) is 5187.

5.4. Public Rental Housing Planning by Genetic Algorithm

The result of the Genetic Algorithm is shown in Table 12. As observed in Table 12, Constraint 1 is satisfied because total investment amount is 3,025,900 million KRW which is less than 3,034,520 million KRW. Also, Constraint 2 is satisfied because only Wirye A2-11 is excluded.

Table 12. Result of the Genetic Algorithm.

Name of Site		Number of Houses	Investment Amount (100m.)	Selection	Number of Selected Houses	Investment Amount (100m.)
Rental house (10)	Gwanggyo A10	701	1196	X	-	-
	Gwanggyo A11	637	1103	O	637	1103
	Gwanggyo A16	224	374	X	-	-
	Gwanggyo A19	1373	1212	O	1373	1212
	Gwanggyo A23	258	431	X	-	-
	Gwanggyo A24	394	592	O	394	592
	Gwanggyo A25	146	141	O	146	141
	Gwanggyo A26	1132	1859	O	1132	1859
	Gwanggyo A30	2091	1765	X	-	-
	Gimpo Ab-2	559	1091	X	-	-
	Sub Total	7515	9764	5 sites selected	5773	6672
Sales house (10)	Gimpo-Yangchon	743	437	O	743	437
	Gwanggyo-Edutown 12	1764	2613	O	1764	2613
	Gwanggyo-Edutown 13~15	1173	2225	O	1173	2225
	Gimpo-Hangang Ab-1	1167	2617	O	1167	2617
	Gimpo-Hangang Ab-7	1382	3028	O	1382	3028
	Wirye A2-11	1540	6758	X	-	-
	Wirye A2-2	1413	4661	O	1413	4661
	Namyangju-Dasan B2	1186	2166	O	1186	2166
	Namyangju-Dasan B4	1615	2938	O	1615	2938
	Namyangju-Dasan S1	1685	2902	O	1685	2902
	Sub Total	13,668	30,345	9 sites selected	12,128	23,587
Total		21,183	40,109	14 sites selected	17,901	30,259

The result of objective function (maximization of the number of suppled public rental houses) is 5773.

Table 13 is the comparison of each method. The result from the genetic algorithm is superior to those from arbitrary selection #1 and #2. Also, the result of the branch the bound method is not better than that of arbitrary selection #2.

Table 13. Comparison of the Supplied Number of Public Rental Houses.

Method	Arbitrary Selection #1	Arbitrary Selection #2	Branch & Bound Method	Genetic Algorithm
Number of Public Rental Houses	2091	5297	5187	5773

6. Conclusions

This study reviewed the optimal land development planning model and optimal urban regeneration planning model in South Korea. Then, it proposed an optimal project selection model to maximize the number of total supplied public rental houses with real-world project data.

There is a trade-off between the investment profit and investment amount needed to supply public rental houses. We applied a couple of optimization techniques such as the genetic algorithm and the branch and bound method to this combinatorial problem. The genetic algorithm obtained a superior result to those from arbitrary selections or the branch and bound method.

We think that this optimization model is a useful and practical planning tool for real estate investment projects while meeting various constraints including budget limitations, regional balance, and profit and welfare balance. Because real estate projects have no divisibility, we must decide whether or not to select any specific project. The genetic algorithm and branch and bound methods are useful tools for this kind of discrete optimization problems in real estate investment. Our optimization model may be applied to government-level infrastructure development plan in all over the country. With a limited budget, governments would select infrastructure (e.g., expressways, high-speed rail, facilities for disaster prevention, etc.) development projects which have different project effect, investment amount, and project location.

The model also can be applied to financial investment decisions with different returns of investment and risk among lots of bond, stock, commodities like gold or real estate. Investors would find an optimal investment portfolio obtaining objective profits under affordable risks with this model. The model saves considerable enumeration time with the trial and error method and proposes a reasonable basis for decisions.

Our research was limited by the amount of data available, thus we could not do a more detailed comparison between the various methods. If more data becomes available to us in the future, we can revisit this study and provide more precise comparisons between the different methods.