Optimal Operation of Integrated Electrical and Natural Gas Networks with a Focus on Distributed Energy Hub Systems

Abstract

Coordinated multi-carrier energy systems with natural gas and electricity energies provide specific opportunities to improve energy efficiency and flexibility of the energy supply. The interdependency of electricity and natural gas networks faces multiple challenges from power and gas flow in corresponding feeders and pipes and connection points between two infrastructures’ points of view. However, the energy hub concepts as the fundamental concept of multi-carrier energy systems with multiple conversion, storage, and generation facilities can be considered as a connection point between electricity and gas grids. Hence, this paper proposes an optimal operation of coordinated gas and electricity distribution networks by considering interconnected energy hubs. The proposed energy hub is equipped with combined heat and power units, a boiler, battery energy storage, a heat pump, and a gas-fired unit to meet the heating and electrical load demands. The proposed model is formulated as a two-stage scenario-based stochastic model aiming to minimize total operational cost considering wind energy, electrical load, and real-time power price uncertainties. The proposed integrated energy system can participate in real-time and day-ahead power markets, as well as the gas market, to purchase its required energy. The AC-power flow and Weymouth equation are extended to describe power and gas flow in feeders and gas pipelines, respectively. Therefore, a realistic model for the integrated electricity and gas grids considering coupling constraints is satisfied. The proposed model is tested on the integrated energy system and consists of a 33-bus electrical network and a 6-node gas grid with multiple interconnected energy hubs, where the numerical results reveal the effectiveness of the proposed model.

1. Introduction

The low cost and high energy efficiency of natural gas (NG) have concertedly promoted the fast growth of NG-fired units in the power system. For example, the total installed capacity of the NG-fired unit in the United States reached more than 42% of the total generation capacity by 2018 [1]. Multi-carrier energy systems (MCESs) are new frameworks to simultaneously supply heat and electricity to the end-user, and capture the interactions among multi-energy infrastructure, including electricity and NG. These coordinated energy systems provide high flexibility, which improves the performance and efficiency of the energy supply compared to conventional systems [2]. However, the optimal operation of the integrated energy system, such as coordinated electrical and gas grids, considering all interdependences of both networks, has been faced with multiple challenges from modeling and scheduling perspectives, which required more development.

Recently, the optimal operation of the multi-carrier energy system has received much attention from researchers. The optimal operation of the NG network was studied by [3] to solve the problem of NG transmission pipeline scheduling under a non-linear pressure-flow equation. For NG system fuel cost minimization, a dynamic programming based on the decomposition method was investigated in [4]. By considering NG price and pipeline congestion in [5], a two-stage optimization framework was developed to investigate the optimal operation of multi-energy resources. In [6], an optimal two-stage stochastic framework of a multi-carrier microgrid incorporated with an electrical and thermal demand response and a renewable energy source (RES) was extended. In [7], a geometric programming method was developed to optimize the NG network operation. The interaction between multiple energy carriers considering the impact of pipeline faults of the NG grid on the reliability and security of the power system was studied in [8,9]. In addition, the optimal hourly scheduling of coordinated NG and electrical systems in the presence of high penetration of wind energy [10] and demand response [11] were developed. The optimal operation of the integrated energy system of Great Britain, including NG and electrical grids considering wind power uncertainty with the aim of operation cost minimization, was developed by [12]. A novel optimization framework for the optimal operation of an integrated energy system was developed in [13]. The dynamic modeling of coordinated NG and electrical energy systems, in the form of microgrids, was investigated in [14]. In [15], the performance of the hybrid energy system with fuel-cell and hydrogen energy storage in buildings under a penetration of photovoltaic energy was developed.

The optimum energy flow in electrical and NG grids considering the security constraints of both systems was presented in [16] based on a mixed-integer linear programming (MILP) model. The stochastic security-constrained unit commitment problem, considering the interdependency between NG and power systems incorporated with wind and demand uncertainty, was studied in [17]. The effects of multi-carrier energy storage technologies incorporated with optimal scheduling of integrated energy systems, including heating, electrical, and NG networks, was studied by [18]. The co-optimization of the integrated NG and electrical networks, integrated with high penetration of wind energy, based on the hybrid stochastic/information gap decision theory (IGDT) framework, was evaluated in [19]. The effects of utilization of the power-to-gas facility, electrical storage, and NG-fired unit to handle the challenges in the integrated electrical and NG system were investigated by [20]. In [21], a bi-level optimization framework was investigated to determine the assailable equipment in the coordinated electricity and NG systems in the form of the microgrid. A large-scale non-linear programming approach for MCES power flow was developed by [22]. The multi-objective optimization framework for MCES, where the NG and electricity are considered as its inputs and heating and electricity as outputs with the aim of operation cost and reliability cost minimization, was developed by [23]. The effect of wind power penetration on MCES operation was presented by [24]. Therefore, the stochastic economic dispatch of MCES was investigated in this work. In [11], a probabilistic day-ahead operation of the integrated electrical and NG systems incorporated with demand response based on the linear approximation was developed. A two-stage robust strategy of the integrated electrical and NG grids considering the power and NG uncertainties was developed by [25], where the effects of the power-to-gas facility to facilitate the integration of wind energy were evaluated. In [26], a stochastic decentralized operation of the integrated electrical and NG grids to improve the operation economy of the whole system was proposed. The comprehensive study on the utilization of combined heat and power (CHP), gas boiler units, and NG-based units on the reduction in greenhouse gas emission was studied by [27].

Early investigations on the MCES are referred to as the energy hubs concept [28,29], which are introduced as an interface between the local demands and energy carriers through multiple energy storage and converter devices to serve the consumers. In [30], an optimization method was developed to model the MCES with energy hubs (EHs) to determine the optimal power flow in the integrated system, as well as economic dispatch between the energy converters. The optimal design of energy hubs considering the reliability constraints was addressed in [31]. In [32], a novel hybrid two-stage optimization approach for a multi-carrier microgrid based on electricity and hydrogen energies was developed. In [33], the operability and economic feasibility of power-to-gas facility are evaluated in the context of EHs. The fast developments in energy hub-based systems have revealed the need for extending efficient methods for optimal expansion planning, management, and scheduling of EHs. A model for optimal expansion planning of an EH in the MCES was studied in [34]. In this model, optimal investment solutions in the system, such as NG pipelines, transmission lines, and EH components, were determined. The optimal stochastic operation of EH integrated with renewable energy, CHP, power-to-gas (P2G) facility, and flexible demand response to meet gas, heating and electrical loads were developed by [35]. The effect of ice energy storage on the operation of EH incorporated with such renewable energies as solar and wind, as well as demand response based on a stochastic framework, was studied by [36]. In [37], the MCES-based EH equipped with energy storage, flexible loads, as well as an electric vehicle, was evaluated with the aim of emission cost and purchase cost minimization. The optimal scheduling of MCES incorporated with thermal infrastructure was developed by [38]. To handle the load demand uncertainty, the IGDT approach was extended.

The EH model of the residential integrated energy system was developed in [39] to optimize the operation of energy storage and responsible load with the aim of comfort level maximization. The optimal risk-based operation of EH system integrated demand response, and multiple energy storage as P2G and compressed air energy storage (CAES), was developed by [40]. The optimal short-term operation of a home-based EH system was studied in [41] to optimize the energy dispatch of multiple carriers to minimize the energy payments. The optimal short-term scheduling of EH integrated with wind energy was investigated by [42]. The bidding strategy of EHs in the competitive power market with the aim of operational cost minimization to supply both electricity and heat loads was presented in [43]. The real-time operation of EHs in a dynamic pricing energy market based on the decentralized energy management model was studied in [44]. The robust operation of MCES based on EH concepts integrated with electrical parking lots, as well as combined heat and power (CHP) units, was developed by [45]. The proposed model is subjected to high-level uncertainty caused by electrical, gas, and thermal loads, power prices, as well as electrical vehicle parameters. The multi-objective optimal scheduling of EH considering wind and load demand uncertainties was investigated by [46], where the operation cost, emission, and reliability cost are captured as objectives. The energy management model of an integrated microgrid or community system based on the EH model was investigated in [47].

The existing literature reviews show the significant growth of the utilization of NG-based generation units such as the NG-fired unit, CHP, boiler, etc., and the development of these resources in the form of multi-energy systems causes the interdependency of electricity and NG carriers. However, the optimal operation of the coordinated electricity and NG grid takes into account the security constraints of both networks incorporated with interconnected EHs (IEHs), and various uncertainties have rarely been examined. Hence, the paper proposes two-stage stochastic scheduling of the integrated electricity and NG systems, including distributed EHs to supply electrical and heating demands, with the aim of operational cost minimization. To model the realistic model of electricity and NG networks, the AC power flow and Weymouth equations are, respectively, applied to model energy dispatch in the transmission lines and gas pipelines. The proposed IEH in the coordinated electricity and gas systems, as connection points of NG and electricity carriers, are equipped with CHP, boiler, wind turbine, electrical and thermal storage, as well as a heat pump. The proposed integrated energy system can participate in both day-ahead and real-time power markets, as well as the gas market. The proposed scheduling of the integrated system is exposed to high-level uncertainty caused by real-time electricity prices, wind power, and electrical loads.

Table 1. Comparison of the key contributions of the proposed model with existing works.

Works	Integrated Gas-Electricity Scheduling	Network Constrained	Considering IEH	Participating in Markets		Existing Uncertainty			Uncertainty Modeling
				Day-Ahead	Real-Time	Wind	Load	Price
[11]	✓	✓	×	✓	×	✓	×	×	Robust
[17]	✓	✓	×	×	×	✓	✓	×	Stochastic
[19]	✓	✓	×	✓	×	✓		×	Stochastic
[44]	✓	×	×	×	✓		✓	✓	Stochastic
[45]	✓	×	✓	✓	×	✓	✓	×	Robust
Our work	✓	✓	✓	✓	✓	✓	✓	✓	Two-stage stochastic

compares the key components in this paper with existing works.

The main contributions of this work are outlined as follows:

• Proposing a novel optimal operation of integrated regional electrical and natural gas networks, considering security constraints pertaining to AC-power flow and gas flow in pipelines, to achieve a more realistic model.
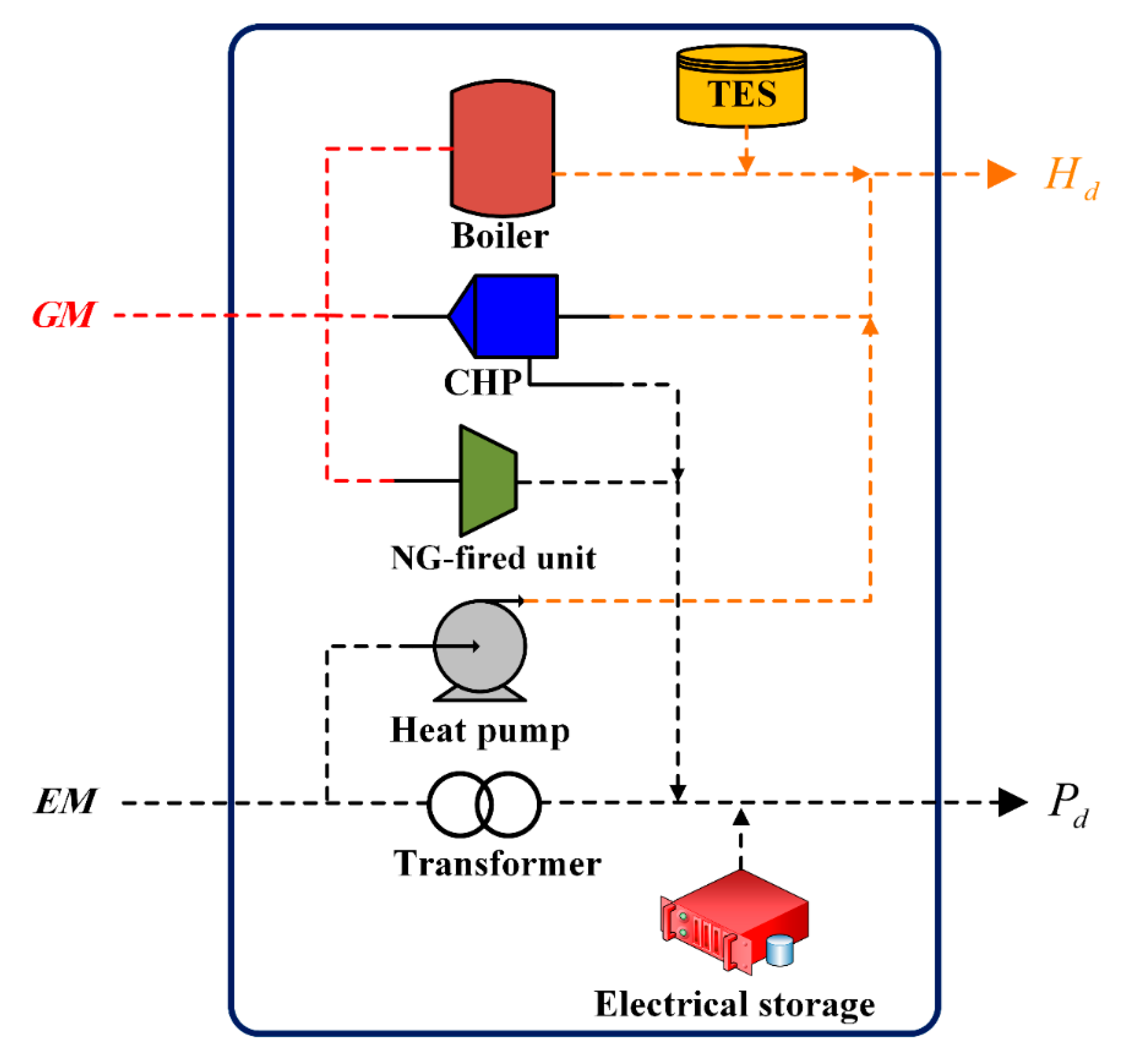
• Incorporating the interconnected energy hubs as connection points among multiple carriers to supply both electrical and thermal loads that are equipped with CHP, boiler, heat pump, and electrical and thermal storage systems. In this way, IEH systems can be considered a promising option to decentralize load management.
• Proposing a scenario-based stochastic approach to handle the uncertainty of real-time price, wind energy, as well as electrical loads in the integrated power and gas system’s operation.
• Analyzing the electricity and heating procurement of each IEH on the proposed scheduling to reveal their effects on the daily energy exchanged.

The rest of this paper is organized as follows: Section 2 provides the problem description and concepts of the interconnected energy system. The two-stage stochastic operation of MCES formulation, including objective function and corresponding constraints, is given in Section 3. Section 4 presents the numerical results and effectiveness of the proposed model for different cases. Finally, Section 5 concludes the paper.

2. Problem Description

The overall schematic of the proposed two-stage stochastic operation of the coordinated Ng and electrical networks are given in Figure 1. The system operator seeks to minimize the total operational cost of the whole system that is subjected to multiple constraints and uncertainties. At first, IEH’s component characteristics, load and wind data, as well as NG and electrical distribution network characteristics, are captured as input. The integrated energy system can participate in both the day-ahead market and real-time market, as well as the gas market, to supply the required energy. In the first stage, the operator makes a contract to purchase electricity from the day-ahead market for the next day. The day-ahead market and gas prices are not associated with uncertainty. In addition, the state operation (ON/OFF status) of dispatchable units (CHP, boiler, and NG-fired unit) is determined in the first stage. Based on historical data, a scenario generation procedure is applied to handle uncertainty associated with random variables (wind, real-time market price, and electrical load) in the second stage. After that, the AC power flow and Weymouth model run to find energy dispatch restricted to multiple operations and security constraints related to both networks. Real power dispatch, wind, electrical, and thermal load curtailment, as well as real power exchange with the real-time market and gas market, are determined in the second stage. The proposed model is formulated as a mixed-integer non-linear programming (MINLP) model. Using the appropriate solver (which will be described in a future section), the value of expected cost, real gas purchased, and power exchanged with three markets, gas and power in pipelines and feeders, real power dispatch, and energy procedure of each IEH are obtained. It should be noted, by determining the state operation and power procedure on NG-based generation units, the impact of NG congestion and gas flow in the pipeline on the security of the electrical grid will be analyzed.

Interconnected Energy Hub

The IEH systems model presents the conversion, generation, and storage devices that use multiple carriers such as electricity and NG to supply electrical and thermal loads as output [48]. Figure 2 shows the schematic of the proposed IEH, including electrical and thermal storage, the NG-fired unit, transformer, heat pump, CHP, and boiler units. The proposed IEH in Figure 2 receives electricity and NG as input from the corresponding electrical bus and gas node. Based on the energy efficiency, conversion, and generation characteristics of the embedded components, NG and electricity are delivered to electrical and thermal end-users.

The general matrix coupling for IEH, which makes the connection between input and output for IEH in Figure 2, can be presented as follows:

$$\left[\begin{array}{c}{P}_d\\ H_d\end{array}\right]=\left[\begin{array}{cccccc}1& 1& 0& 0& 1& 0\\ 0& 0& 1& {\eta }^{bo}& 0& {\alpha }^{hp}\end{array}\right]\left[\begin{array}{c}{P}_g\\ P_{chp}\\ H_{chp}\\ H^{bo}\\ P_{tr}\\ P^{hp}\end{array}\right]+\left[\begin{array}{c}{P}_b^{dis}\\ H_{}^{hs,dis}\end{array}\right]-\left[\begin{array}{c}{P}_b^{ch}\\ H_{}^{hs,ch}\end{array}\right]$$

(1)

The output matrix on the left side of Equation (1) represents the electrical and thermal loads. The matrix of efficiency for different components has multiplied the matrix of input, generation, and consumed power and gas. The two last matrices on the right side of Equation (1) represent stored and injected energy by the electrical and thermal storage systems.

3. Problem Formulation

In this section, the problem formulation and modeling of the integrated electrical and NG networks considering IEHs with multiple components are provided. The proposed model is formulated as a two-stage stochastic model where different terms will be solved in the first and second stages. In the following, the objective function of the proposed scheduling with the aim of total operational cost minimization is presented, then the related limitations of the operation and modeling of the two networks and multiple components are discussed.

3.1. Objective Function

The main objective of the proposed scheduling of the coordinated NG and electrical systems equipped with IEHs is to minimize operational costs, including different terms. The objective function Equation (2) represents the objective function, including 10 terms. The first term of Equation (2) expresses the power purchased cost from the day-ahead market. The start-up and shut-down cost of the NG-fired units, as well as CHP units in the first stage, are, respectively, represented by the second and third terms of the objective function (Equation (2)). The power purchased cost from the real-time market is represented by the fourth term of Equation (2). The generation cost function of the NG-fired unit is represented by the fifth term of the objective function( Equation (2)). In this paper, the quadratic cost function is considered for the NG-fired unit as [49]. The NG purchased cost from the gas market is expressed by the sixth term of Equation (2). Finally, the load demand curtailment cost for electrical and thermal loads are, respectively, established by the last two terms of the objective function (Equation (2)).

$$\begin{array}{l}Min\mathrm{OF}={\displaystyle \sum _{t=1}^T{\lambda }_t^D{E}_t^{day}+}{\displaystyle \sum _{t=1}^T\left[\left({\displaystyle \sum _{g=1}^{NU}S{U}_{g,t}+S{D}_{g,t}}\right)+\left({\displaystyle \sum _{n=1}^{NC}S{U}_{ch{p}_n,t}+S{D}_{ch{p}_n,t}}\right)\right]}\\ +{\displaystyle \sum _{s=1}^{NS}{\pi }_s[{\displaystyle \sum _{t=1}^T{\lambda }_{t,s}^R{E}_{t,s}^{real}}+{\displaystyle \sum _{t=1}^T{\displaystyle \sum _{g=1}^{NU}F\left(P_{g,t,s}\right)+}}}{\displaystyle \sum _{t=1}^T{\lambda }_t^{G}G{M}_{t,s}}+{\displaystyle \sum _{t=1}^{T}VOL{L}_e\times P_{d,t,s}^{curt}}+{\displaystyle \sum _{t=1}^{T}VOL{L}_h\times H_{d,t,s}^{curt}}]\end{array}$$

(2)

3.2. Problem Constraints

The proposed objective function of the assumed integrated electrical scheduling and NG systems, considering IEHs are restricted with multiple constraints, are represented as follows.

3.2.1. NG-Fired Unit Constraints

The NG-fired units have mainly attracted attention recently due to the appropriate features like high efficiency, low emission pollution, fast response, etc., which are the main generation units in EH. The set of constraints related to the NG-fired unit is represented by Equations (3)–(14). The active and reactive power limits for NG-fired units are, respectively, expressed by Equations (3) and (4). The ramp-up and ramp-down limitations are represented by Equations (5) and (6). The minimum up and downtime limits that restricted the NG-fired unit operation successive time are expressed by Equations (7)–(10) [49]. The start-up and shut-down limits for the NG-fired unit are represented by Equations (11)–(14).

$$P_g^{\min }{I}_{g,t}^{}\le P_{g,t,s}\le P_g^{\max }{I}_{g,t}^{}\hspace{0.17em}$$

(3)

$$Q_g^{\min }{I}_{g,t}^{}\le Q_{g,t,s}\le Q_g^{\max }{I}_{g,t}^{}\hspace{0.17em}$$

(4)

$$P_{g,t,s}-P_{g,t-1,s}\le R_g^{up}$$

(5)

$$P_{g,t-1,s}-P_{g,t,s}\le R_g^{dn}$$

(6)

$$I_{g,t}^{}-I_{g,t-1}^{}\le I_{g,t+U{T}_{g,u}}^{}$$

(7)

$$U{T}_{g,u}^{}=\{\begin{array}{l}u\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u\le MU{T}_g\\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u>MU{T}_g\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(8)

$$I_{g,t-1}^{}-I_{g,t}^{}\le 1-I_{g,t+D{T}_{g,u}}^{}$$

(9)

$$D{T}_{g,u}^{}=\{\begin{array}{l}u\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u\le MD{T}_g\\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u>MD{T}_g\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(10)

$$S{U}_{g,t}\ge SU{C}_g(I_{g,t}-I_{g,t-1})$$

(11)

$$S{U}_{g,t}\ge 0$$

(12)

$$S{D}_{g,t}\ge SD{C}_g(I_{g,t-1}-I_{g,t})$$

(13)

$$S{D}_{g,t}\ge 0$$

(14)

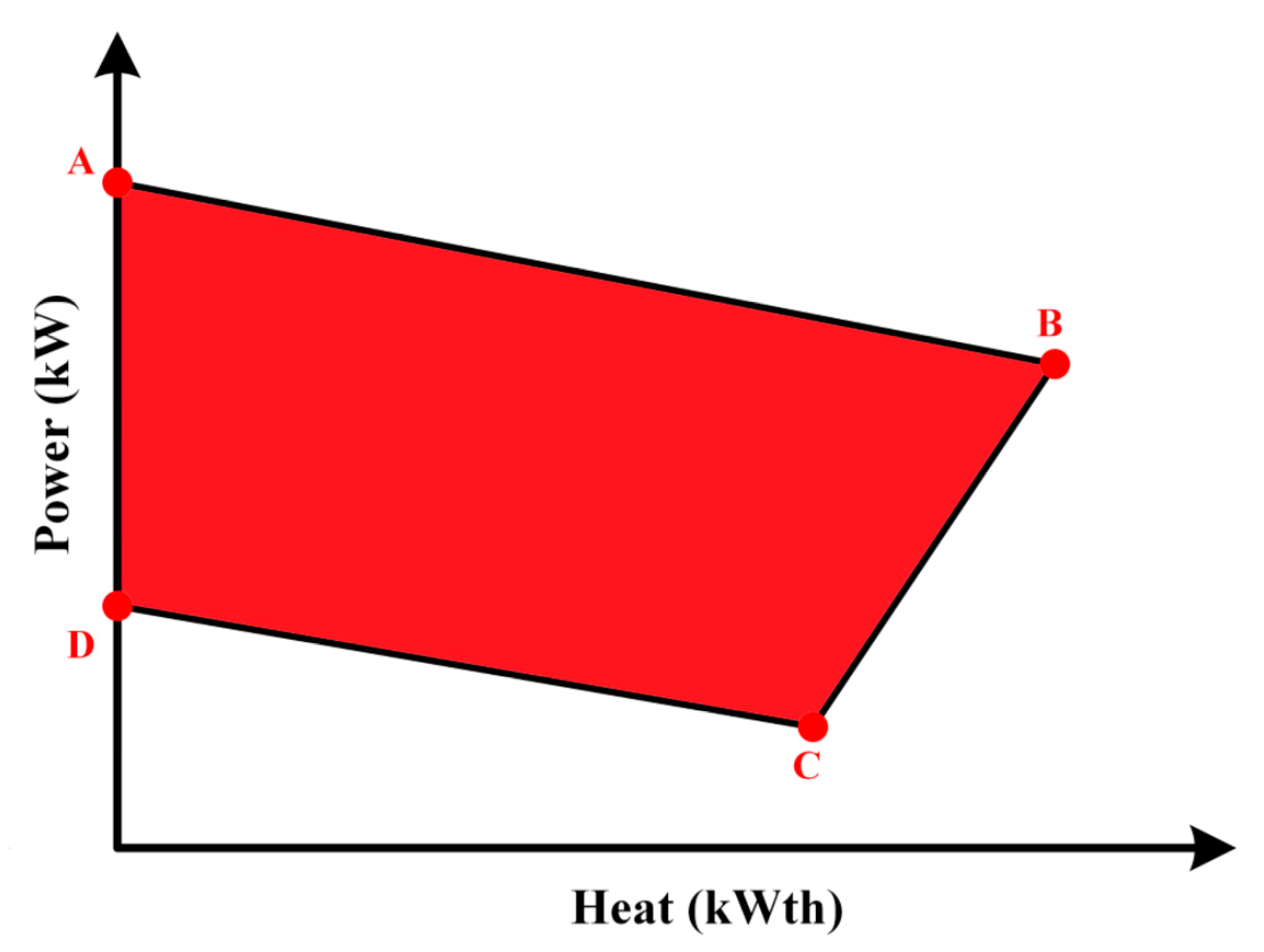
3.2.2. CHP Unit Constraints

The generated heat and power by the CHP unit depend on each other based on the feasible region operation, which is shown in Figure 3. The active power limit for the CHP unit is represented by Equation (15). The relationship between produced heat and power by CHP, based on the four operation points in Figure 3, is expressed by Equations (16)–(19). The ramp-up and ramp-down limits of the CHP unit are given by Equations (20) and (21). Minimum up and downtime limits of CHP are represented by Equations (22)–(25). The reactive power limit of the CHP unit is represented by Equation (26). The relationship between consumed NG and power produced by the CHP unit is calculated based on Equation (27).

$$P_{chp}^{min}{I}_{chp,t}\le P_{chp,t,s}\le P_{chp}^{max}{I}_{chp,t}$$

(15)

$$P_{chp,t,s}^{}-P_{chp}^A-\frac{P_{chp}^A-P_{chp}^B}{H_{chp}^A-H_{chp}^B}\times (H_{chp,t,s}^{}-H_{chp}^A)\le 0$$

(16)

$$P_{chp,t,s}^{}-P_{chp}^B-\frac{P_{chp}^B-P_{chp}^C}{H_{chp}^B-H_{chp}^C}\times H_{chp,t,s}^{}-H_{chp}^B)\ge -(1-I_{chp,t}^{})\times M$$

(17)

$$P_{chp,t,s}^{}-P_{chp}^C-\frac{P_{chp}^C-P_{chp}^D}{H_{chp}^C-H_{chp}^D}\times H_{chp,t,s}^{}-H_{chp}^C)\ge -(1-I_{chp,t}^{})\times M$$

(18)

$$0\le H_{chp,t,s}^{}\le H_{chp}^{\max }\times I_{chp,t}^{}$$

(19)

$$P_{chp,t,s}^{}-P_{chp,t-1,s}^{}\le R_{chp}^{UP}$$

(20)

$$P_{chp,t,s}^{}-P_{chp,t-1,s}^{}\le R_{chp}^{Dn}$$

(21)

$$I_{chp,t}^{}-I_{chp,t-1}^{}\le I_{chp,t+U{T}_{chp,u}}^{}$$

(22)

$$U{T}_{chp,u}^{}=\{\begin{array}{l}u\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u\le T_{chp}^{on}\\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u>T_{chp}^{con}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(23)

$$I_{chp,t-1}^{}-I_{chp,t}^{}\le 1-I_{chp,t+D{T}_{chp,u}}^{}$$

(24)

$$D{T}_{chp,u}^{}=\{\begin{array}{l}u\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u\le T_{chp}^{off}\\ 0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}u>T_{chp}^{off}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\end{array}$$

(25)

$$Q_{chp}^{\min }{I}_{n,t}^{}\le Q_{chp,t,s}\le Q_{chp}^{\max }{I}_{chp,t}^{}\hspace{0.17em}$$

(26)

$$G{C}_{t,s}=\frac{P_{chp,t,s}^{}}{{\eta }_{chp}}$$

(27)

3.2.3. Boiler Unit Constraints

The boiler unit consumed NG and generated heat to supply thermal load or save in the thermal energy storage (TES). The generated heat by the boiler unit is represented by Equation (28). The fuel function of the boiler unit is given in Equation (29).

$$H_{}^{bo,\min }\times I_{\hspace{0.17em}t}^{bo}\le H_{t,s}^{bo}\le H_{}^{bo,\max }\times I_t^{bo}$$

(28)

$$G{B}_{t,s}^{bo}={\eta }^{bo}{H}_{t,s}^{bo}$$

(29)

3.2.4. Thermal Energy Storage (TES) Constraints

TES is embedded in the IEH and is coupled with the boiler and CHP units to manage the heating load and thermal procedure in the integrated energy system. The set of limitations related to the TES is provided by Equations (30)–(35). The logical constraint that separates the charging and discharging modes of TES is represented by Equation (30). The heating charged and discharged values are bounded by minimum and maximum values, as expressed by Equations (31) and (32). The current energy capacity of TES is calculated based on Equation (33). The energy capacity of TES is bounded by minimum and maximum values as Equation (35). Finally, constraint (Equation (34)) expresses the equality condition for the initial and final energy capacity of TES.

$$I_{t,s}^{hs,dis}+I_{t,s}^{hs,ch}\le 1\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}$$

(30)

$$H_{}^{hs,dis,\min }\hspace{0.17em}{I}_{t,s}^{hs,dis}\le H_{t,s}^{hs,dis}\le H_{}^{hs,dis,\max }\hspace{0.17em}{I}_{t,s}^{hs,dis}$$

(31)

$$H_{}^{hs,ch,\min }\hspace{0.17em}{I}_{t,s}^{hs,ch}\le H_{t,s}^{hs,ch}\le H_{}^{hs,ch,\max }\hspace{0.17em}{I}_{t,s}^{hs,ch}$$

(32)

$$H{S}_{t,s}^{hs}=H{S}_{t-1,s}^{hs}+e{h}_{}^{ch}{H}_{t,s}^{hs,ch}-\frac{H_{t,s}^{hs,dis}}{e{h}_{}^{dis}}$$

(33)

$$H{S}_{}^{hs,\min }\le H{S}_{t,s}^{hs}\le H{S}_{}^{hs,\max }\hspace{0.17em}$$

(34)

$$H{S}_{t=0}=H{S}_{t=24}$$

(35)

3.2.5. Battery Constraints

The power charged and discharged limitations for battery energy storage are calculated by (36) and (37). The logical relationship between the charging and discharging modes of battery energy storage is given by (38). The state of charge limits for battery energy storage is given by Equations (39)–(41).

$$P_b^{dis,\min }{x}_{b,t,s}^{dis}\le P_{b,t,s}^{dis}\le P_b^{dis,\max }{x}_{b,t,s}^{dis}$$

(36)

$$P_b^{ch,\min }{x}_{b,t,s}^{ch}\le P_{b,t,s}^{ch}\le P_b^{ch,\max }{x}_{b,t,s}^{ch}$$

(37)

$$x_{b,t,s}^{ch}+x_{b,t,s}^{dis}\le 1$$

(38)

$$SO{C}_{b,t+1,s}^{}=SO{C}_{b,t,s}^{}+{\eta }_b^{ch}{P}_{b,t,s}^{ch}-\frac{P_{b,t,s}^{dis}}{{\eta }_b^{dis}}$$

(39)

$$SO{C}_{b,t=24,s}^{}=SO{C}_{b,\mathrm{int}}^{}$$

(40)

$$SO{C}_b^{\min }\le SO{C}_{b,t,s}^{}\le SO{C}_b^{\max }$$

(41)

3.2.6. Heat Pump Constraints

A heat pump consumed electricity to produce heating energy in the IEH. The consumed power by the heat pump is limited by upper and lower values as Equations (42) and (43). The generated heat by the heat pump is calculated based on the consumed maximum power and efficiency that is defined in the future.

$$0\le P_{t,s}^{hp}\le P_{}^{hp,\max }$$

(42)

$$0\le Q_{t,s}^{hp}\le Q_{}^{hp,\max }$$

(43)

3.2.7. Transformer Constraints

Transformer active and reactive power limits that are injected to the transformer are, respectively, established by Equations (44) and (45).

$$0\le P_{t,s}^{tr}\le P_{}^{tr,\max }$$

(44)

$$0\le Q_{t,s}^{tr}\le Q_{}^{tr,\max }$$

(45)

3.2.8. Power Flow and Distribution of Electrical Network Constraints

The set of the AC-power flow equations and electrical distribution limitations for the integrated energy system in the presence of IEH are presented by Equations (46)–(53). The active and reactive power balance limitations, including power exchanging with real-time and day-ahead markets, and the electrical procedure of multiple components, are represented by Equations (46) and (47), respectively. It should be noted that the first two terms in Equations (46) and (47) are established for nodes that are connected to the main grid. The heating energy balance for each IEH is examined by Equation (48), where the third term of Equation (48) is related to the heat pump thermal output based on its efficiency. Active and reactive power flow in electrical feeders is represented by Equations (49) and (50), respectively [6]. The exchanged power with markets is bounded by the maximum value as Equation (51). The value of power flows at the feeder is limited by the maximum rated value as Equation (52). Constraint (Equation (53)) represents the voltage magnitude limit for each electrical bus [50].

$$\begin{array}{l}\left(E_t^{day}+E_{t,s}^{real}\right)+{\displaystyle \sum _{g\in G_i}^{}{P}_{g,t,s}+P_{w_i,t,s}^{}+}{\displaystyle \sum _{b\in B_i}^{}\left(P_{b,t,s}^{dis}-P_{b,t,s}^{ch}\right)+{\displaystyle \sum _{n\in N_i}^{}{P}_{ch{p}_n,t,s}^{}}-{\displaystyle \sum _{tr\in T{R}_i}^{}{P}_{t,s}^{tr}}-{\displaystyle \sum _{hp\in H{p}_i}^{}{P}_{t,s}^{hp}}}\\ -{\displaystyle \sum _{d\in D_i}^{}{P}_{d,t,s}^{}-{\displaystyle \sum _{k\in i}^{}{P}_{d,t,s}^k}+{\displaystyle \sum _{d\in D_i}^{}{P}_{d,t,s}^{curt}}=}{\displaystyle \sum _{j\in J_i}^{}P{F}_{ij,t,s}}\end{array}$$

(46)

$$\begin{array}{l}\left(Q{E}_t^{day}+Q{E}_{t,s}^{real}\right)+{\displaystyle \sum _{g\in G_i}^{}{Q}_{g,t,s}+Q_{w_i,t,s}^{}+{\displaystyle \sum _{n\in N_i}^{}{Q}_{ch{p}_n,t,s}^{}}-{\displaystyle \sum _{tr\in T{R}_i}^{}{Q}_{t,s}^{tr}}-{\displaystyle \sum _{hp\in H{p}_i}^{}{Q}_{t,s}^{hp}}}\\ -{\displaystyle \sum _{d\in D_i}^{}{Q}_{d,t,s}^{}-{\displaystyle \sum _{k\in i}^{}{Q}_{d,t,s}^k}+{\displaystyle \sum _{d\in D_i}^{}{Q}_{d,t,s}^{curt}}=}{\displaystyle \sum _{j\in J_i}^{}Q{F}_{ij,t,s}}\end{array}$$

(47)

$${\displaystyle \sum _{n\in N_i}^{}{H}_{ch{p}_n,t,s}^{}}+{\displaystyle \sum _{bo\in B{o}_i}^{}{H}_{t,s}^{bo}}+{\displaystyle \sum _{hp\in H{p}_i}^{}{\alpha }^{hp}{P}_{t,s}^{hp}}+{\displaystyle \sum _{hs\in H{s}_i}^{}\left(H_{t,s}^{hs,dis}-H_{t,s}^{hs,ch}\right)}+{\displaystyle \sum _{d\in D_i}^{}{H}_{d,t,s}^{curt}}={\displaystyle \sum _{d\in D_i}^{}{H}_{d,t,s}^{}}$$

(48)

$$P{F}_{ij,t,s}=B_{ij}\left({\delta }_{i,t,s}-{\delta }_{j,t,s}\right)-G_{ij}\left(V_{i,t,s}-V_{j,t,s}\right)$$

(49)

$$Q{F}_{ij,t,s}=G_{ij}\left({\delta }_{i,t,s}-{\delta }_{j,t,s}\right)+B_{ij}\left(V_{i,t,s}-V_{j,t,s}\right)$$

(50)

$${\left(E_t^{day}+E_{t,s}^{real}\right)}^2+{\left(Q{E}_t^{day}+Q{E}_{t,s}^{real}\right)}^2\le {\left(S_{net}^{up}\right)}^2$$

(51)

$$P{F}_{ij,t,s}^2+Q{F}_{ij,t,s}^2\le {(S_{ij}^{\max })}^2$$

(52)

$$V_i^{\min }\le V_{i,t,s}\le V_i^{\max }$$

(53)

3.2.9. NG Network Constraints

The gas flow in gas pipelines is a complex phenomenon. In this paper, to model the NG network and gas flow in pipelines, the steady-state Weymouth gas flow equations are applied. The gas flow in the pipeline based on the pressure difference between two nodes as a non-linear function of pipeline characteristics is formulated as Equation (54). The NG balance at each node is examined by Equation (55). The maximum gas flow in the pipeline is restricted by the maximum value determined by Equation (56). The value of produced gas by the supplier is limited by the upper and lower values, as given in constraint (Equation (57)). The value of NG that should be purchased from the market is calculated based on Equation (58). In this constraint, to convert the volume of NG to the corresponding value of energy, the gross heating value (GHV) is applied [51]. The purchased NG from the gas market (calculated in Equation (58)), is limited by maximum value, as represented by Equation (59). Finally, the node pressure should not exceed the minimum and maximum pressure values, as given by constraint (Equation (60)).

$$G_{lm,t,s}^{line}=C_{lm}\sqrt{\left|\left({\rho }_{l,t,s}^2-{\rho }_{m,t,s}^2\right)\right|}$$

(54)

$${\displaystyle \sum _{d\in D_i}^{}{G}_{d,t,s}-{\displaystyle \sum _{m\in M_i}^{}{G}_{lm,t,s}^{line}}}=0$$

(55)

$$\left|G_{lm,t,s}^{line}\right|\le G_{lm}^{line,\max }$$

(56)

$$G_{sp}^{\min }\le G_{sp,t,s}^{}\le G_{sp}^{\max }$$

(57)

$$G{M}_{t,s}=GHV\times {\displaystyle \sum _{d\in D_i}^{}{G}_{d,t,s}}$$

(58)

$$0\le G{M}_{t,s}\le G{M}^{\max }$$

(59)

$${\rho }_l^{\min }\le {\rho }_{l,t,s}\le {\rho }_l^{\max }$$

(60)

3.2.10. Wind Power Modeling

The wind output is the main uncertain parameter effect on the system dynamic [52]. Wind power uncertainty is simulated by Monte-Carlo simulation (MCS). To this end, the 12-year wind speed data (2001 to 2012) is considered according to [53] as input data. In other words, 12 wind speeds are included for each hour of the day that belongs to a particular year [54]. After calculating the parameters of the Weibull distribution function (Equation (61)) based on the available data, its density function is obtained as follows:

$$r={\left(\frac{\sigma }{{\omega }_{mean}}\right)}^{-1.083}c=\frac{{\omega }_{mean}}{\mathrm{\Gamma }(1+\frac{1}{r})}$$

(61)

$$f(\omega )=\frac{r}{c}{\left(\frac{\omega }{c}\right)}^{r-1}\exp \left[-{\left(\frac{\omega }{c}\right)}^r\right]$$

(62)

By generating random numbers between [0, 1], and conforming them on the cumulative distribution function (CDF), the corresponding wind speed is obtained. This action is repeated 24 h a day. Then, according to Equation (63), wind power is calculated for each scenario.

$$P_{w,t,s}=\{\begin{array}{ll}0& 0\le {\omega }_{t,s}\le {\omega }_{cut-in}\\ (k_1+k_2{\omega }_{t,s}+k_3{\omega }_{t,s}{}^2)P_w^R& {\omega }_{cut-in}\le {\omega }_{t,s}\le {\omega }_{rated}\\ P_w^R& {\omega }_{rated}\le {\omega }_{t,s}\le {\omega }_{cut-out}\\ 0& {\omega }_{cut-out}\le {\omega }_{t,s}\end{array}$$

(63)

where $k_1$, $k_2$, and $k_3$ are the turbine coefficients, $P_w^R$ is rated power output of wind turbine, ${\omega }_{cut-in}$, ${\omega }_{cut-out}$, and ${\omega }_{rated}$ are cut-in, cut-out, and rated wind speed, respectively.

3.2.11. Load Curtailment Constraints

The total electrical and thermal load curtailment should be less than the rated value of load demand at time t. The load curtailment limits for electrical and thermal load are, respectively, represented by Equations (61) and (62).

$${\displaystyle \sum _{d\in D_i}^{}{P}_{d,t,s}^{curt}}\le {\displaystyle \sum _{d\in D_i}^{}{P}_{d,t,s}^{}}$$

(64)

$${\displaystyle \sum _{d\in D_i}^{}{H}_{d,t,s}^{curt}}\le {\displaystyle \sum _{d\in D_i}^{}{H}_{d,t,s}^{}}$$

(65)

4. Simulation and Numerical Results

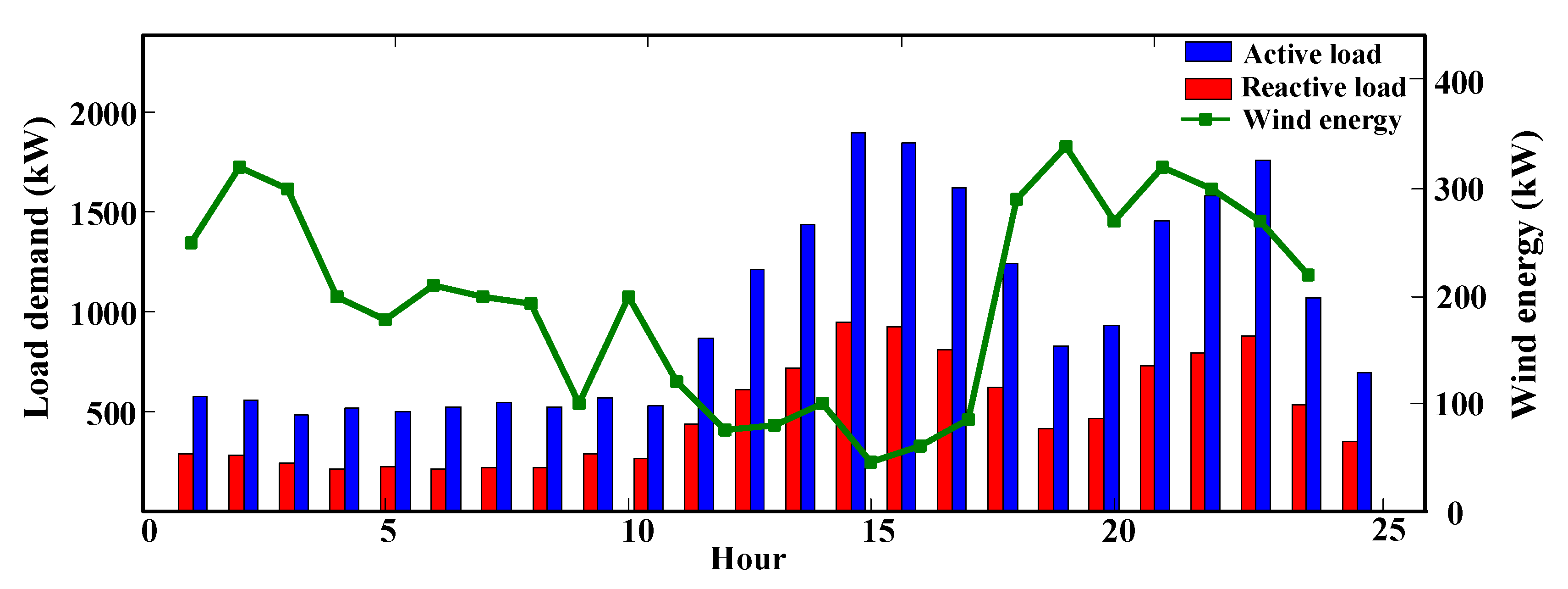
Case Study

The proposed two-stage stochastic scheduling of coordinated NG and electrical networks in the presence of IEH systems is examined on the integrated test system depicted in Figure 4. The proposed integrated system includes a 33-bus electrical grid and a 6-node NG system with four IEH systems. All the characteristics of the 33-bus test system can be found in [2]. In addition, the characteristics of the 6-node grid are given in [21]. Two 500-kW wind turbines are located on buses 14 and 16, with characteristics as in [55]. The components in each IEH are given in

Table 2. Component in each IEH.

Hub	Component
	CHP	Gas Boiler	NG-Fired Unit	Heat Pump	TES	Transformer	Battery
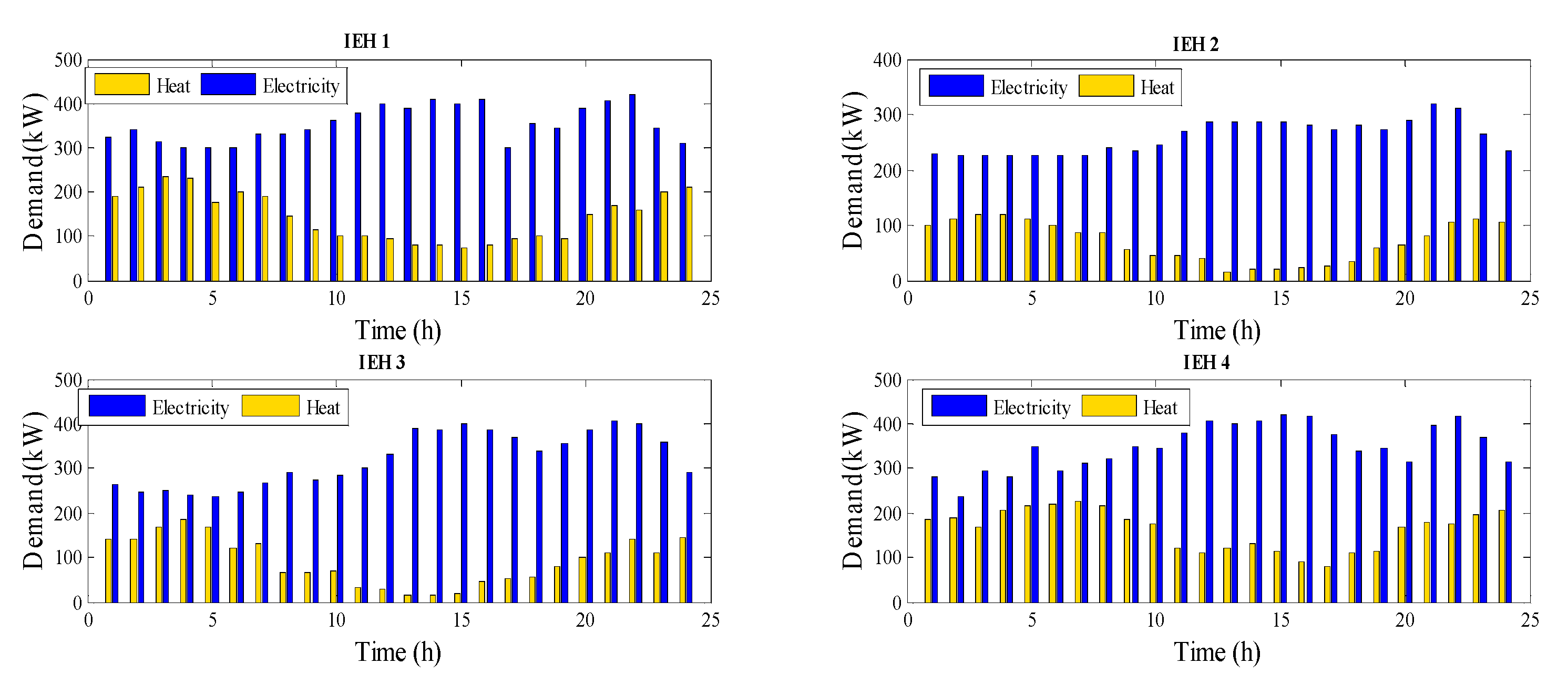
IEH 1	✓	✓	✓	✓	✓	✓	✓
IEH 2	×	✓	✓	✓	✓	✓	✓
IEH 3	✓	✓	✓	✓	✓	✓	×
IEH 4	✓	✓	✓	×	✓	✓	✓

. Furthermore, the characteristics of CHP, boiler, battery, NG-fired unit and TES are presented in

Table 3. Characteristics of the energy hub’s components.

CHP	$P_{chp}^{\min }/P_{chp}^{\max }$ 0/250	$T_{chp}^{on}/T_{chp}^{off}$ 1/1	$S{U}_{ch{p}_n}/S{D}_{ch{p}_n}$ 10
NG-fired unit	$P_g^{\min }/P_g^{\max }$ 0/200	$MU{T}_g/MD{T}_g$ 1/1	$S{U}_g/S{D}_g$ 10
Battery	$SO{C}_b^{\min }/SO{C}_b^{\max }$ 20/250	$P_b^{ch,\max }/P_b^{dis,\max }$ 50/50	${\eta }_b^{ch}/{\eta }_b^{dis}$ 0.8/0.9
TES	$H{S}_{}^{hs,\max }/H{S}_{}^{hs,\max }$ 50/500	$H_{}^{hs,ch,\max }/H_{}^{hs,dis,\max }$ 100/100	$e^{ch}/e^{dis}$ 0.8/0.9
Boiler	$H^{bo,\min }$ 0	$H^{bo,\max }$ 45	${\eta }^{bo}$ 0.8
Heat pump	$P_{}^{hp,\max }$ 135	${\alpha }^{hp}$ 2

.

To address the system uncertainties, including load demand, real-time power price, and wind power output, the scenario-based stochastic approach is applied. The load demand and real-time power price are subjected to the normal distribution with zero mean and 2% standard deviation. In addition, the wind power probability is subjected to the Weibull distribution function [56]. After the scenario generation via Monte-Carlo simulation, the SCENRED tool in GAMS software is used to reduce the generated scenarios to the 10 most probable scenarios. The scenario reduction procedure is a scenario-based approximation with a reduced number of scenarios, which provide a good approximation of the original system. The SCENRED tool, which is provided by General algebraic modeling system (GAMS) software, is a package that includes different scenario reduction techniques such as fast forward reduction and backward reduction. In this paper, the fast backward reduction technique is applied as the scenario reduction method. The reduced scenarios have to be defined before the equations of the scenario-based stochastic model are applied in a solve statement. The flowchart of the scenario generation and reduction procedure is shown in Figure 5. The reduced desired scenarios will be presented in the following. The proposed model and all the required coding were modeled in the GAMS software and solved with the DICOPT (GAMS Development Corporation, Washington D.C., USA) solver.

Figure 6 shows the load profile for four IEH systems. In addition, the load profile for other loads (loads not supplied by IEH) and wind power output is drawn in Figure 7. Day-ahead, real-time power price, and gas price curves are given in Figure 8. Furthermore, the value of loss of load for electrical and heating loads are, respectively, 1 $/kWh, 1 $/MBtu [21].

Table 4. The value of operation cost and the corresponding probability for each scenario

Scenario	Operation Cost ($)	Probability
1	5916.332	0.0321
2	5858.411	0.1376
3	5780.233	0.1991
4	5998.824	0.1076
5	6174.91	0.1402
6	6102.51	0.0352
7	6099.244	0.1322
8	6260.641	0.1333
9	6001.257	0.0225
10	5968.063	0.0602
Expected cost ($)	6016.0425

shows the operational cost for 10 reduced scenarios with corresponding probability. The scenario number eight is selected, as the worst scenario, to analyze the electricity and heating procedures.

The optimal hourly power exchanged with day-ahead and real-time markets is depicted in Figure 9. For the time periods 1–10, and 15–18, when the day-ahead market price is less than the real-time market, the operator purchases the required energy from the day-ahead market. When the real-time price reaches a lower value in comparison with the day-ahead market, the operator relies on the real-time market to supply the required energy. This action occurs at 12–14, and 19–22, and the main part of the power purchased of the integrated energy system is achieved from the real-time market.

The hourly gas purchased from the gas market is shown in Figure 10. According to this figure, for the time periods 1–10, the NG purchased is less than that of other periods. There are two main reasons for this phenomenon. First, for this time period, the operator tends to purchase more electricity and minimize the NG purchased to satisfy economic benefits and minimize total operation cost based on the energy price depicted in Figure 8. Second, the main part of the heating load is supplied by a heat pump, which consumes power to generate thermal energy. Therefore, injected NG is only burned by the NG-fired and gas boilers; consequently, the amount of NG purchased is reduced. The electricity and thermal scheduling of each IEH is presented in the following. For the time periods 12–24, the operator trends to purchase more NG to generate electricity instead of electricity purchased; consequently, the NG purchased is increased.

Table 5. The electricity and thermal energies scheduling for IEH 1.

	Electricity Energy Scheduling				Thermal Energy Scheduling
Hour	Power to Upstream Bus	Power by CHP	Power by NG-Fired	Battery Schedule	Heat by CHP	Heat by Boiler	Heat Pump	TES Schedule
1	0	0	200	−50	0	80	135	−25
2	0	0	200	−50	87.5	80	135	−90
3	0	0	200	−50	87.5	80	135	−67
4	0	0	200	0	87.5	80	135	−72
5	0	0	200	0	0	80	135	−40
6	0	0	200	0	0	80	135	−15
7	0	0	200	−50	0	80	45	65
8	0	83.5	200	−50	87.5	0	45	0
9	0	83.5	200	0	87.5	0	45	0
10	0	83.5	200	0	0	0	45	65
11	0	83.5	200	0	0	0	45	65
12	0	150	200	50	0	80	0	0
13	110	250	200	50	0	80	0	0
14	90	250	200	50	0	80	0	0
15	50	250	200	0	0	80	0	0
16	0	150	200	−25	0	80	0	0
17	0	83.5	200	−25	0	0	0	95
18	0	0	200	0	0	0	45	65
19	0	0	200	0	0	0	45	50
20	0	150	200	0	87.5	80	0	0
21	95	250	200	50	87.5	80	0	0
22	80	250	200	50	87.5	80	0	0
23	0	0	200	0	87.5	0	135	0
24	0	0	200	0	87.5	0	135	0

shows the electricity and thermal energy scheduling for IEH 1. Power and heating dispatch by multiple components can be seen in this table. For the time periods 1–6, when the heating load reaches maximum values, the heat pump operates with maximum capacity. Hence, the main part of the thermal energy is supplied by a heat pump. To this end, the embedded NG-fired unit in IEH 1 operates with maximum capacity to meet the local load and supply the heat pump for the first time of the day. The battery and TES follow the electrical and thermal load behavior. At the off-peak times, the electrical and heating storage are charged, then the stored energy is injected into the system at peak demand intervals. Based on the load condition for the IEH 1 depicted in Figure 5, the CHP unit is committed for the time periods 8–22. Because of the interdependency of power and heat produced by the CHP unit, when the CHP generated more power, the heat output is injected into the IEH and supply heating load or stored in the TES. For the time periods 13–15 and 21–22 (electrical demand peak hours), the CHP unit operates with maximum power capacity to meet the local load. At these periods, more NG is injected to the integrated energy system to produce more electricity and inject surplus power to the corresponding electrical bus that the IEH is connected to. The main reason for this phenomenon is higher electricity prices (day-ahead and real-time markets) for the time periods 13–15 and 21–22. Consequently, the operator tends to consume more NG to supply the required electricity without power being purchased, and reduces the total operation cost.

Table 6. The electricity and thermal energies scheduling for IEH 2.

	Electricity Energy Scheduling		Thermal Energy Scheduling
Hour	Power by NG-Fired	Battery Schedule	Heat by Boiler	Heat Pump	TES Schedule
1	150	−25	0	135	−35
2	150	−25	0	135	−25
3	150	−50	80	135	−95
4	150	0	80	135	−95
5	150	0	0	135	25
6	150	0	0	135	−35
7	150	−50	80	0	0
8	150	0	80	45	−40
9	150	0	40	0	15
10	150	0	0	0	45
11	150	0	0	0	45
12	150	0	0	0	40
13	150	50	0	0	15
14	150	50	0	0	20
15	150	50	0	0	20
16	150	50	0	0	22
17	150	0	0	0	25
18	150	0	0	0	35
19	150	0	60	0	0
20	150	0	65	0	0
21	150	50	80	0	0
22	150	0	65	0	40
23	150	−50	0	110	0
24	150	−50	0	110	0

shows the electricity and thermal energy scheduling for IEH 2. The IEH 2 does not contain the CHP unit. Therefore, the NG-fired unit operates with maximum capacity for the whole of the horizon scheduling. For the thermal load demand peak hours, the heat pump works with maximum capacity. TES and battery follow the electrical and heating load condition. At off-peak hours, TES and battery are charged, then at peak hours, they operate in discharging mode.

The electricity and thermal energy scheduling of IEH 3 are given in

Table 7. The electricity and thermal energies scheduling for IEH 3.

	Electricity Energy Scheduling			Thermal Energy Scheduling
Hour	Power to Upstream Bus	Power by CHP	Power by NG-Fired	Heat by CHP	Heat by Boiler	Heat Pump	TES Schedule
1	0	0	150	0	65	135	−60
2	0	0	150	0	65	135	−60
3	0	0	150	0	80	135	−45
4	0	0	150	0	80	135	−30
5	0	0	150	0	80	135	−45
6	0	0	150	0	0	135	0
7	0	0	150	0	0	135	0
8	0	0	150	0	0	0	67
9	0	0	150	0	0	0	67
10	0	0	150	0	0	0	70
11	0	83.5	150	87.5	0	0	32
12	0	180	150	112.5	0	0	0
13	60	250	200	0	0	0	15
14	65	250	200	0	0	0	15
15	50	250	200	0	0	0	20
16	64	250	200	0	0	45	0
17	0	83.5	200	87.5	0	45	0
18	0	0	200	0	0	55	0
19	0	83.5	200	87.5	80	0	0
20	−65	250	200	0	80	0	20
21	45	250	200	0	80	30	0
22	49	250	200	05	80	60	0
23	0	83.5	200	87.5	0	110	0
24	0	0	200	0	0	135	10

. For the time periods 1–7, the heat pump operates with the maximum capacity. At this time period, the injected NG and electricity to IEH 3 are high. As the electricity load reaches the higher value, the CHP unit and NG-fired unit are committed with the maximum capacity. For the time periods 13–16, and 21–22, the operator tends to inject more NG into the IEH 3 to generate electricity instead of power injection. In addition, in this period, the extra generated electricity goes back into the corresponding bus. This action results in the reduction in electricity purchased, and consequently, operation cost is reduced. TES is charged at the first hours of the day and discharged at the mid-day hours.

The electricity and thermal energy scheduling for IEH 4 are given in

Table 8. The electricity and thermal scheduling for IEH 4.

	Electricity Energy Scheduling				Thermal Energy Scheduling
Hour	Power to Upstream Bus	Power by CHP	Power by NG-Fired	Battery Schedule	Heat by CHP	Heat by Boiler	TES Schedule
1	0	0	200	−50	0	80	−10
2	0	0	200	−35	87.5	80	−15
3	0	0	200	−50	87.5	80	−15
4	0	0	200	0	87.5	80	0
5	0	0	200	0	0	80	39
6	0	0	200	0	0	80	42
7	0	0	200	0	0	80	45
8	0	0	200	0	87.5	80	43
9	0	0	200	0	87.5	80	0
10	0	0	200	0	0	80	0
11	0	0	200	50	0	80	−40
12	0	0	200	35	0	80	−70
13	0	0	200	0	0	80	−70
14	95	250	200	50	0	80	0
15	30	250	200	0	0	80	0
16	0	250	200	0	0	80	0
17	0	250	200	−50	0	80	0
18	0	0	200	−50	0	80	30
19	0	0	200	0	0	80	−53
20	0	0	200	0	87.5	80	0
21	105	250	200	50	87.5	80	70
22	85	250	200	50	87.5	80	70
23	0	0	200	0	87.5	80	−30
24	0	0	200	0	87.5	80	−30

. The NG-fired unit operates at the maximum capacity point for the whole of the horizon scheduling. Due to the absence of the heat pump, the CHP unit operates with maximum heating capacity for the first hours of the day. In addition, the gas boiler operates with the maximum capacity for the whole day. The battery is charged during off-peak hours, then is discharged at peak load demand hours. For the time periods 14–15 and 21–22, the extra power generated by the CHP unit back into the corresponding bus, and consequently, the power purchased from the electricity markets is reduced. In this way, the total operation cost decreases.

5. Conclusions

The need for sustainable energy supply has led to an increase in the trend towards an interconnected energy system based on the electricity and natural gas carriers. The energy hub system, as a fundamental concept of a multi-carrier energy system, plays a significant role in the flexible energy supply. Meanwhile, the interdependency of electricity and natural gas networks, due to multiple connection points, poses several challenges in terms of scheduling and modeling. Motivated by these challenges, this paper proposed a novel two-stage stochastic scheduling of coordinated electricity and natural gas systems in the presence of interconnected energy hubs under the probabilistic approach. The proposed model by applying AC-power flow and Weymouth equations for power and gas flow was formulated as an MINLP model with consideration of real-time power price, wind output, and load demand variability. The interconnected energy hub is equipped by combined heat and power units, a gas boiler, a gas-fired unit, multi-carrier energy storage systems, and a heat pump to supply local electrical and heating loads. The proposed scheduling was examined on the integrated energy system with a 33-bus distribution grid and a 6-node natural gas system with four interconnected energy hubs. The optimal electricity and thermal scheduling of each energy hub were presented individually and their effects on the daily power and gas purchased were analyzed. Numerical results reveal the effectiveness of the proposed model in terms of electrical and heating load supply, and consequently, economic benefits were satisfied.

In this paper, we proposed the two-stage scenario-based stochastic approach to handle the variation of the wind, load, and price. However, consideration of the other system dynamic techniques to better capture the existing uncertainties remains to be pursued in future works. In addition, the uncertainties of the decision (itself) are not modeled and can be considered using system dynamics-based or game theory-based methods in future works.