How Does Heterogeneity Affect Freeway Safety? A Simulation-Based Exploration Considering Sustainable Intelligent Connected Vehicles
Abstract
:1. Introduction
2. Methods
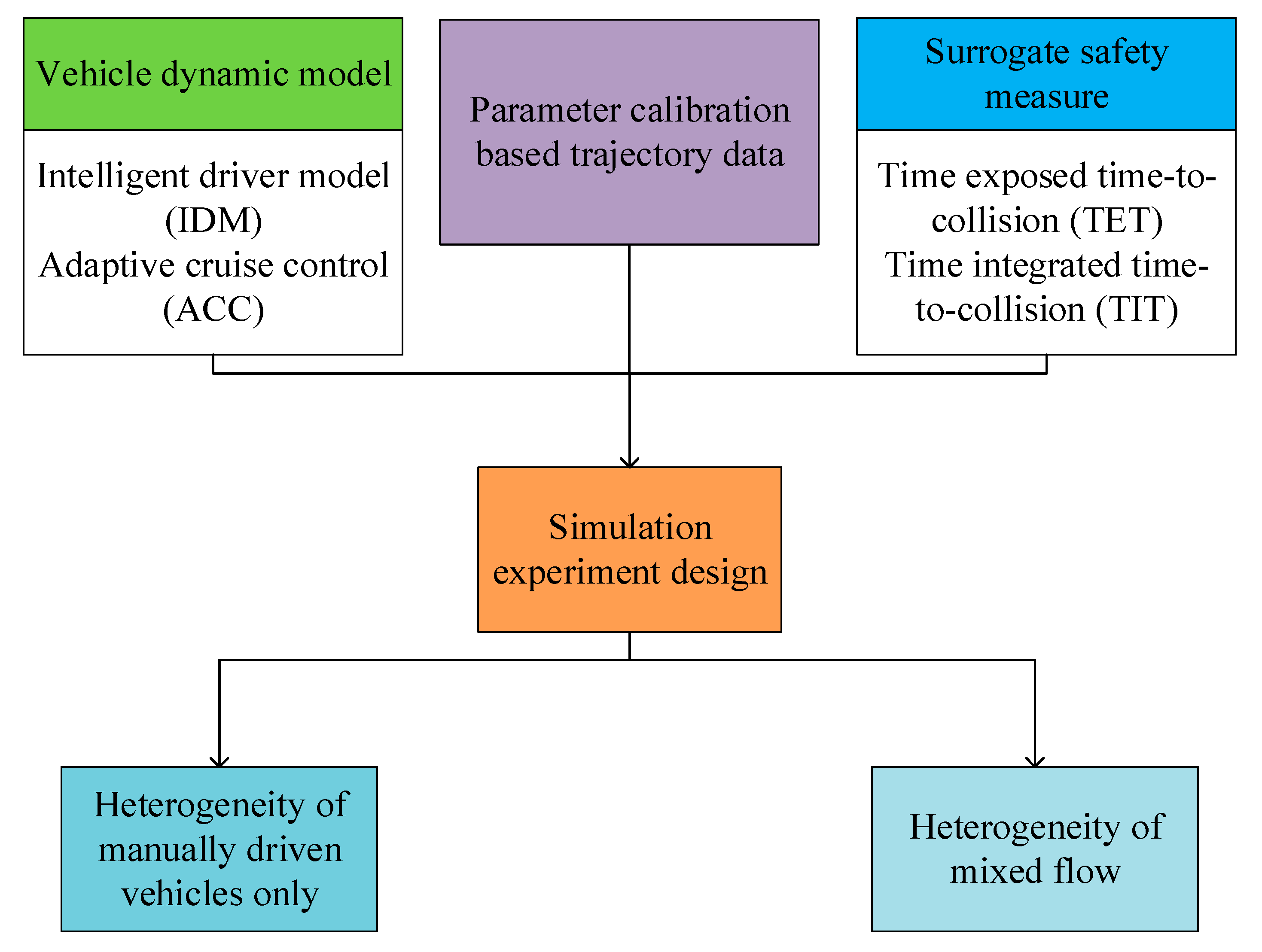
2.1. Research Framework
2.2. Vehicle Dynamic Models
2.2.1. Human Driver Model
2.2.2. ACC Models
2.3. Trajectory Data Collection and Parameter Calibration
2.3.1. Trajectory Data Collection
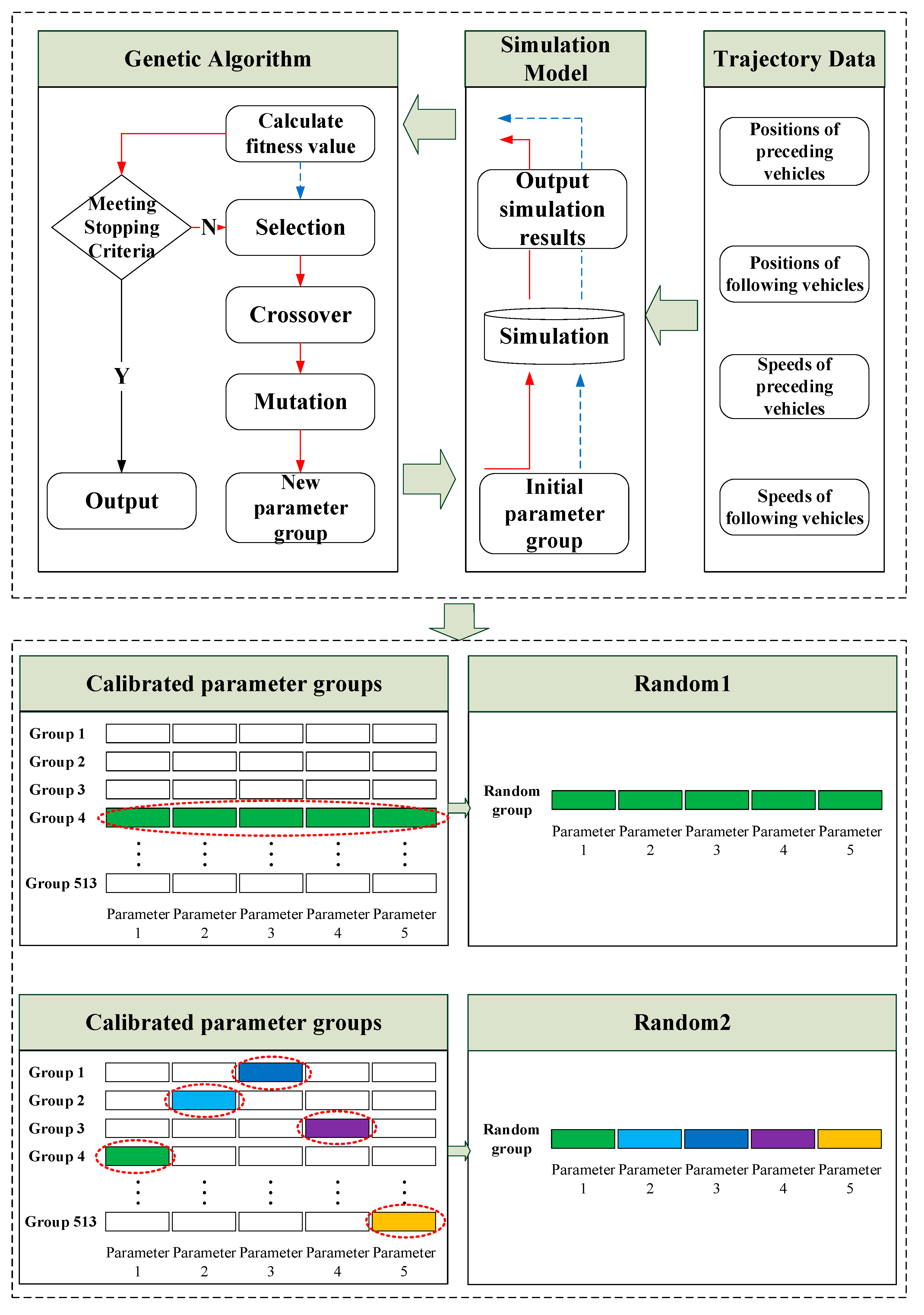
2.3.2. Parameter Calibration
- Step 1:
- Input the trajectory data of car-following vehicle pairs selected from the NGSIM dataset.
- Step 2:
- Generate initial parameter groups randomly by the genetic algorithm.
- Step 3:
- Obtain the real trajectory of front vehicle and the simulated trajectory of the following vehicle with current parameter groups.
- Step 4:
- Calculate the value of fitness function by Equation (6).
- Step 5:
- Determine whether the stopping criteria of genetic algorithm are met. If so, terminate and output the parameter group; otherwise, go to step 6.
- Step 6:
- Perform selection, crossover, and mutation operators to generate the new parameter groups and enter step 3.
- Step 7:
- Repeat the above steps until all the parameter groups are output.
2.4. Surrogate Safety Measures
2.5. Simulation Experiment Platform
3. Results and Discussion
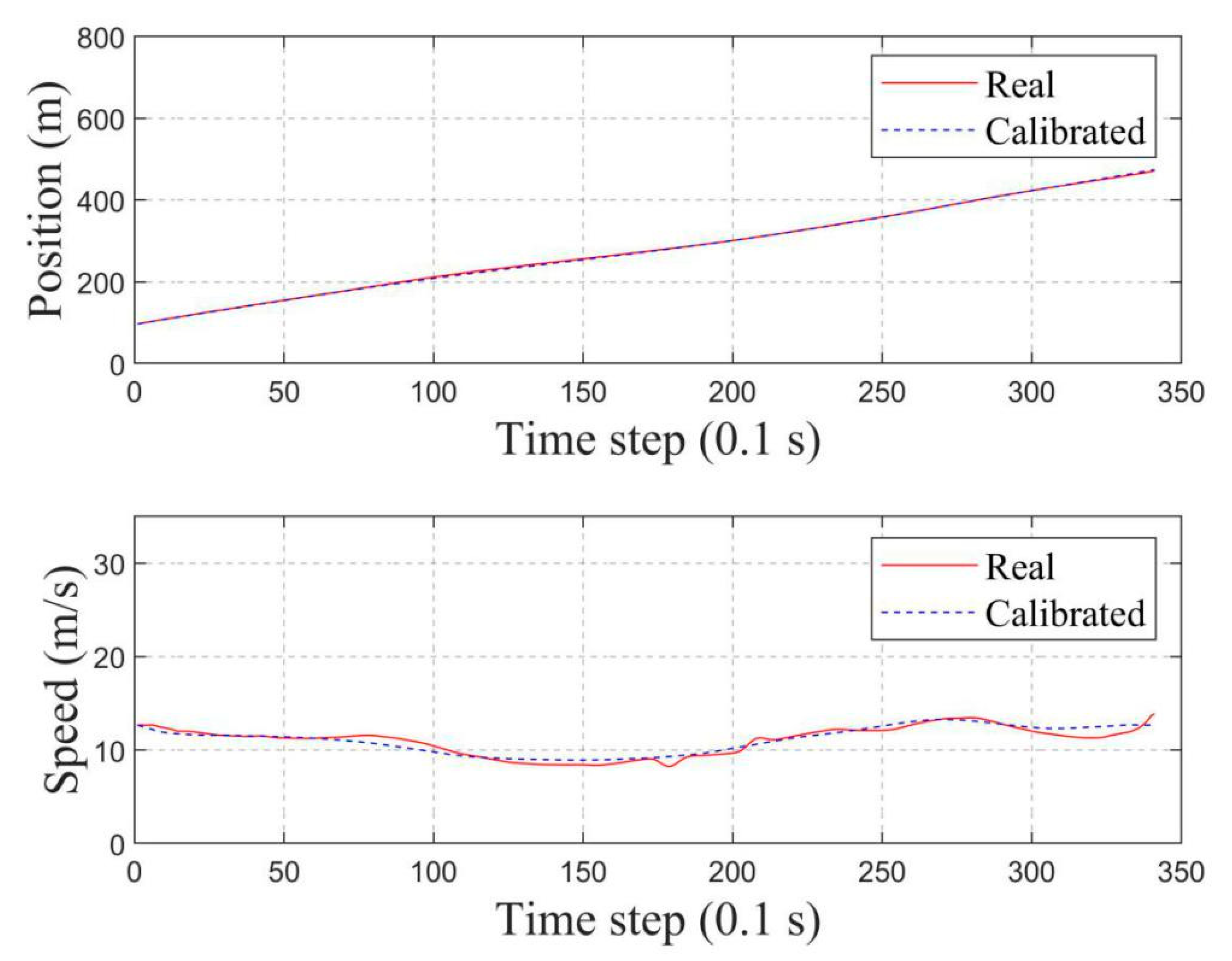
3.1. Results of Parameter Calibration
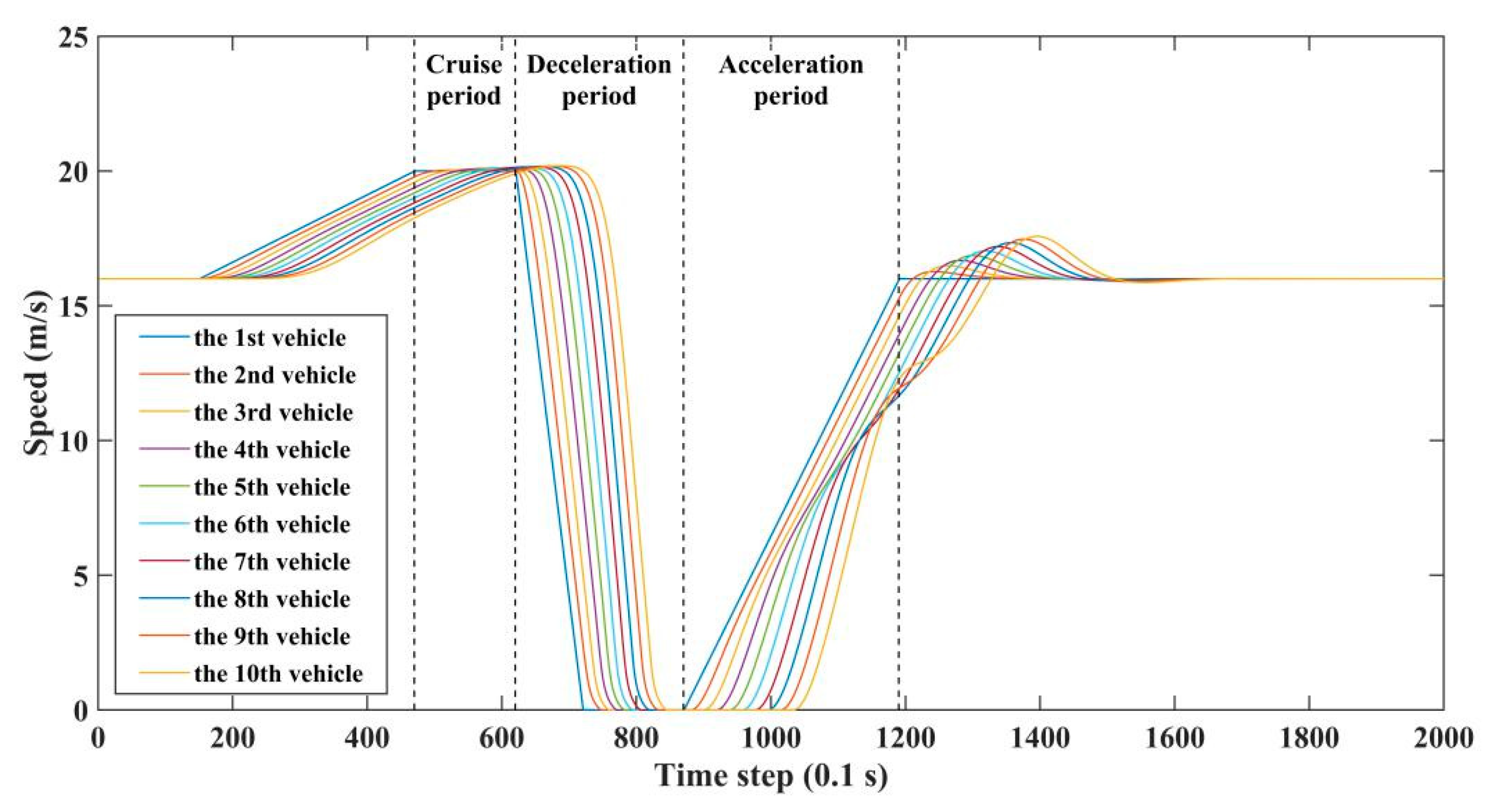
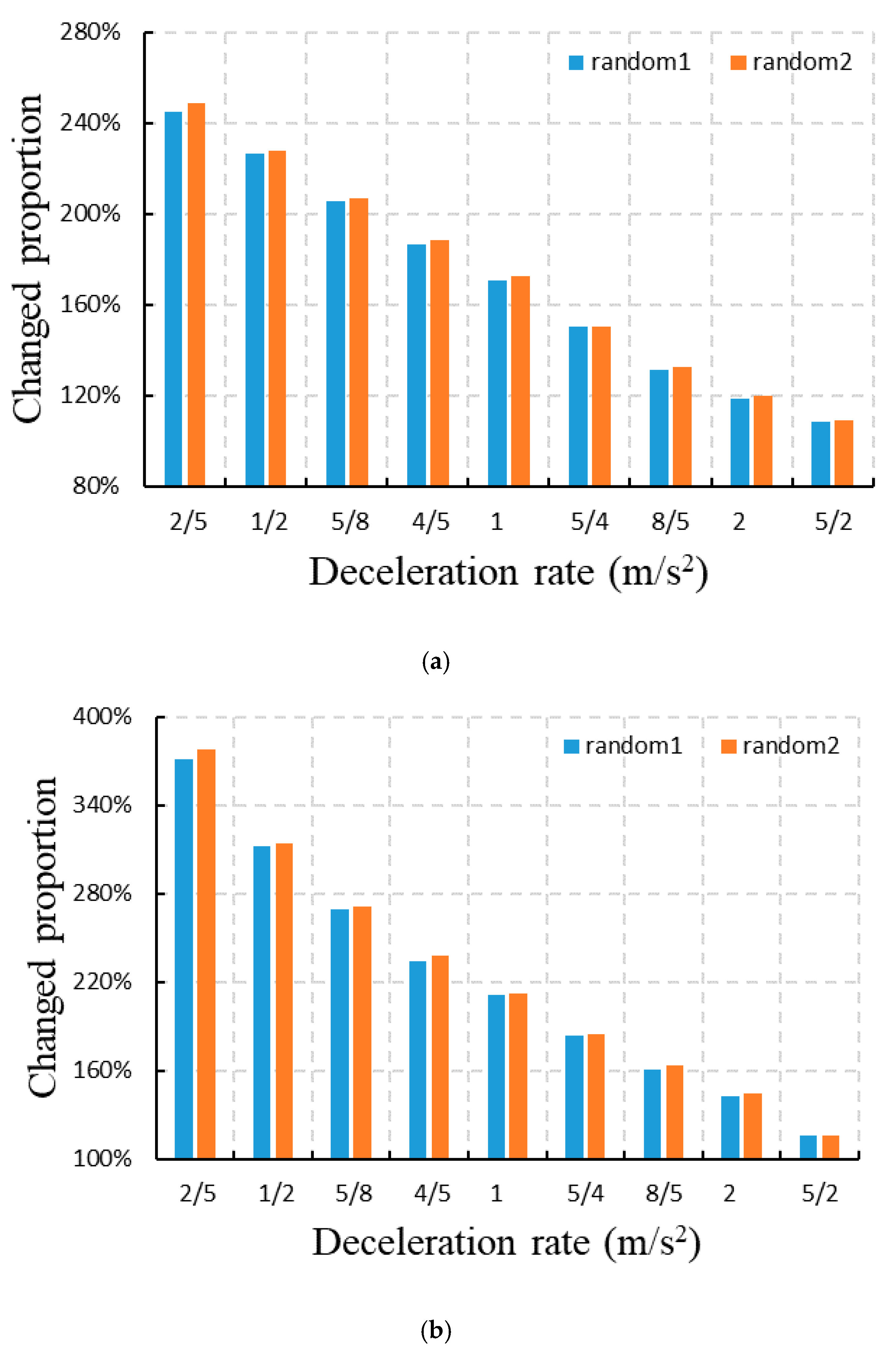
3.2. Traffic Flow of Only Manually Driven Vehicles
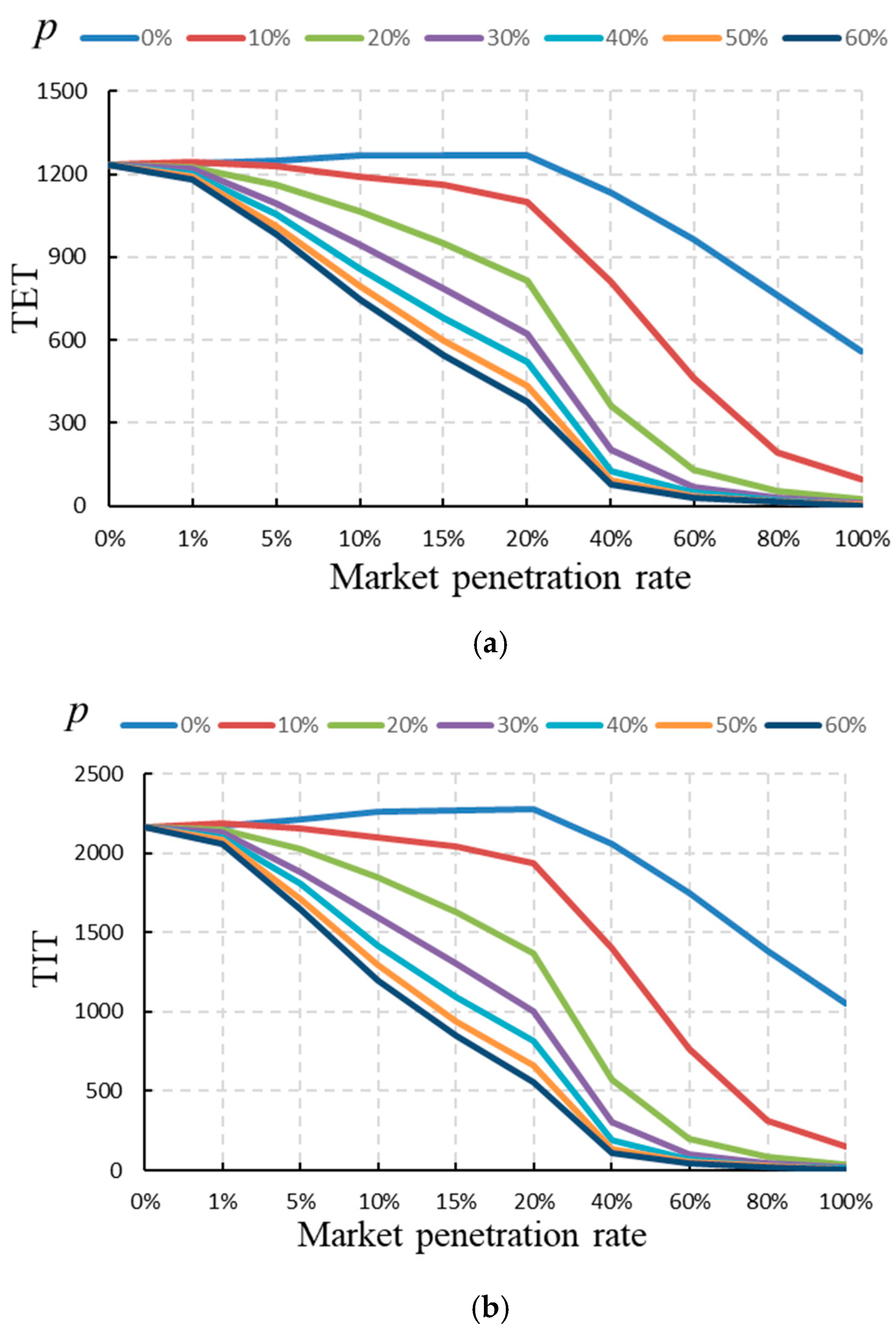
3.3. Impacts on Mixed Traffic Flow
4. Conclusions
- (1)
- Individual heterogeneity has negative effects on longitudinal safety—with the higher degree of heterogeneity, longitudinal collision risks are increased.
- (2)
- Compared to traffic flow consisting of manually driven vehicles only, mixed traffic flow with manually driven vehicles and ACC vehicles may be more dangerous when the market penetration rate of ACC is low, since the ACC system can be recognized as a new source of individual heterogeneity.
Author Contributions
Funding
Conflicts of Interest
References
- Itasca, I. National Safety Council—Injury Fact; National Safety Council: Itasca, IL, USA, 2015. [Google Scholar]
- Wu, K.F.; Thor, C.P. Method for the use of naturalistic driving study data to analyze rear-end crash sequences. Transp. Res. Record. 2015, 2518, 27–36. [Google Scholar] [CrossRef]
- Gao, J.; Davis, G.A. Using naturalistic driving study data to investigate the impact of driver distraction on driver’s brake reaction time in freeway rear-end events in car-following situation. J. Saf. Res. 2017, 63, 195–204. [Google Scholar] [CrossRef]
- Piccinini, G.B.; Engström, J.; Bärgman, J.; Wang, X. Factors contributing to commercial vehicle rear-end conflicts in China: A study using on-board event data recorders. J. Saf. Res. 2017, 62, 143–153. [Google Scholar] [CrossRef]
- Wu, Y.; Abdel-Aty, M.; Cai, Q.; Lee, J.; Park, J. Developing an algorithm to assess the rear-end collision risk under fog conditions using real-time data. Transp. Res. Part C-Emerg. Technol. 2018, 87, 11–25. [Google Scholar] [CrossRef]
- Wu, Y.; Abdel-Aty, M.; Wang, L.; Rahman, M.S. Combined connected vehicles and variable speed limit strategies to reduce rear-end crash risk under fog conditions. J. Intell. Transport. Syst. 2020, 24, 494–513. [Google Scholar] [CrossRef]
- Christoforou, Z.; Cohen, S.; Karlaftis, M.G. Identifying crash type propensity using real-time traffic data on freeways. J. Saf. Res. 2011, 42, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Wang, W.; Liu, P. Identifying crash-prone traffic conditions under different weather on freeways. J. Saf. Res. 2013, 46, 135–144. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Liu, P.; Wang, W.; Li, Z. Identification of freeway crash-prone traffic conditions for traffic flow at different levels of service. Transp. Res. Part A-Policy Pract. 2014, 69, 58–70. [Google Scholar] [CrossRef]
- Xu, C.; Liu, P.; Yang, B.; Wang, W. Real-time estimation of secondary crash likelihood on freeways using high-resolution loop detector data. Transp. Res. Part C-Emerg. Technol. 2016, 71, 406–418. [Google Scholar] [CrossRef]
- Pande, A.; Abdel-Aty, M.; Das, A. A classification tree based modeling approach for segment related crashes on multilane highways. J. Saf. Res. 2010, 41, 391–397. [Google Scholar] [CrossRef] [Green Version]
- Xing, L.; He, J.; Li, Y.; Wu, Y.; Yuan, J.; Gu, X. Comparison of different models for evaluating vehicle collision risks at upstream diverging area of toll plaza. Accid. Anal. Prev. 2020, 135, 105343. [Google Scholar] [CrossRef] [PubMed]
- Dinu, R.R.; Veeraragavan, A. Random parameter models for accident prediction on two-lane undivided highways in India. J. Saf. Res. 2011, 42, 39–42. [Google Scholar] [CrossRef] [PubMed]
- Yu, R.; Abdel-Aty, M. Investigating the different characteristics of weekday and weekend crashes. J. Saf. Res. 2013, 46, 91–97. [Google Scholar] [CrossRef] [PubMed]
- Xing, L.; He, J.; Abdel-Aty, M.; Cai, Q.; Li, Y.; Zheng, O. Examining traffic conflicts of up stream toll plaza area using vehicles’ trajectory data. Accid. Anal. Prev. 2019, 125, 174–187. [Google Scholar] [CrossRef]
- Xing, L.; He, J.; Abdel-Aty, M.; Wu, Y.; Yuan, J. Time-varying Analysis of Traffic Conflicts in Toll Plaza’s Upstream Diverging Area. Accid. Anal. Prev. 2020, 141, 105539. [Google Scholar] [CrossRef]
- Behnood, A.; Mannering, F. The effect of passengers on driver-injury severities in single-vehicle crashes: A random parameters heterogeneity-in-means approach. Anal. Methods Accid. Res. 2017, 14, 41–53. [Google Scholar] [CrossRef]
- Li, Y.; Xu, C.; Xing, L.; Wang, W. Integrated cooperative adaptive cruise and variable speed limit controls for reducing rear-end collision risks near freeway bottlenecks based on micro-simulations. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3157–3167. [Google Scholar] [CrossRef]
- Li, Y.; Wang, H.; Wang, W.; Xing, L.; Liu, S.; Wei, X. Evaluation of the impacts of cooperative adaptive cruise control on reducing rear-end collision risks on freeways. Accid. Anal. Prev. 2017, 98, 87–95. [Google Scholar] [CrossRef]
- Li, Y.; Xing, L.; Wang, W.; Wang, H.; Dong, C.; Liu, S. Evaluating impacts of different longitudinal driver assistance systems on reducing multi-vehicle rear-end crashes during small-scale inclement weather. Accid. Anal. Prev. 2017, 107, 63–76. [Google Scholar] [CrossRef]
- Li, Y.; Li, Z.; Wang, H.; Wang, W.; Xing, L. Evaluating the safety impact of adaptive cruise control in traffic oscillations on freeways. Accid. Anal. Prev. 2017, 104, 137–145. [Google Scholar] [CrossRef]
- Li, Y.; Tu, Y.; Fan, Q.; Dong, C.; Wang, W. Influence of cyber-attacks on longitudinal safety of connected and automated vehicles. Accid. Anal. Prev. 2018, 121, 148–156. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Ding, Z.; Wang, C.; Li, Z. Statistical analysis of the patterns and characteristics of connected and autonomous vehicle involved crashes. J. Saf. Res. 2019, 71, 41–47. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, Z.; Yin, Y.; Peeta, S. Deployment of roadside units to overcome connectivity gap in transportation networks with mixed traffic. Transp. Res. Part C-Emerg. Technol. 2020, 111, 496–512. [Google Scholar] [CrossRef]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested traffic states in empirical observations and microscopic simulations. Phys. Rev. E 2000, 62, 1805. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.S.; Abdel-Aty, M. Longitudinal safety evaluation of connected vehicles’ platooning on expressways. Accid. Anal. Prev. 2018, 117, 381–391. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, G.; Li, Y.; Li, Z. Optimal jam-absorption driving strategy for mitigating rear-end collision risks with oscillations on freeway straight segments. Accid. Anal. Prev. 2020, 135, 105367. [Google Scholar] [CrossRef]
- Milanés, V.; Shladover, S.E.; Spring, J.; Nowakowski, C.; Kawazoe, H.; Nakamura, M. Cooperative adaptive cruise control in real traffic situations. IEEE Trans. Intell. Transp. Syst. 2013, 15, 296–305. [Google Scholar] [CrossRef] [Green Version]
- Milanés, V.; Shladover, S.E. Modeling cooperative and autonomous adaptive cruise control dynamic responses using experimental data. Transp. Res. Part C-Emerg. Technol. 2014, 48, 285–300. [Google Scholar] [CrossRef] [Green Version]
- Xiao, L.; Wang, M.; Schakel, W.; Van Arem, B. Unravelling effects of cooperative adaptive cruise control deactivation on traffic flow characteristics at merging bottlenecks. Transp. Res. Part C-Emerg. Technol. 2018, 96, 380–397. [Google Scholar] [CrossRef]
- FHWA. Next Generation Simulation (NGSIM). 2006. Available online: https://ops.fhwa.dot.gov/trafficanalysistools/ngsim.htm (accessed on 1 December 2006).
- Kesting, A.; Treiber, M.; Schönhof, M.; Kranke, F.; Helbing, D. Jam-avoiding adaptive cruise control (ACC) and its impact on traffic dynamics. In Traffic and Granular Flow’05; Springer: Berlin/Heidelberg, Germany, 2007; pp. 633–643. [Google Scholar]
- Kesting, A.; Treiber, M.; Schönhof, M.; Helbing, D. Adaptive cruise control design for active congestion avoidance. Transp. Res. Part C-Emerg. Technol. 2008, 16, 668–683. [Google Scholar] [CrossRef]
- Kusano, K.D.; Chen, R.; Montgomery, J.; Gabler, H.C. Population distributions of time to collision at brake application during car following from naturalistic driving data. J. Saf. Res. 2015, 54, 95.e29–104. [Google Scholar]
- Lubbe, N. Brake reactions of distracted drivers to pedestrian Forward Collision Warning systems. J. Saf. Res. 2017, 61, 23–32. [Google Scholar]
- Tu, Y.; Wang, W.; Li, Y.; Xu, C.; Xu, T.; Li, X. Longitudinal safety impacts of cooperative adaptive cruise control vehicle’s degradation. J. Saf. Res. 2019, 69, 177–192. [Google Scholar]
- Li, Y.; Wu, D.; Lee, J.; Yang, M.; Shi, Y. Analysis of the transition condition of rear-end collisions using time-to-collision index and vehicle trajectory data. Accid. Anal. Prev. 2020, 144, 105676. [Google Scholar] [PubMed]
- Minderhoud, M.M.; Bovy, P.H. Extended time-to-collision measures for road traffic safety assessment. Accid. Anal. Prev. 2001, 33, 89–97. [Google Scholar]
- Meng, Q.; Qu, X. Estimation of rear-end vehicle crash frequencies in urban road tunnels. Accid. Anal. Prev. 2012, 48, 254–263. [Google Scholar]
- Chen, Z.; He, F.; Yin, Y.; Du, Y. Optimal design of autonomous vehicle zones in transportation networks. Transp. Res. Part B-Methodol. 2017, 99, 44–61. [Google Scholar]
- Calvert, S.C.; Schakel, W.J.; Van Lint, J.W.C. Will automated vehicles negatively impact traffic flow? J. Adv. Transp. 2017, 2017, 3082781. [Google Scholar]



| Statistics | (s) | Calibrated Objective Value | ||||
|---|---|---|---|---|---|---|
| Mean | 0.30 | 1.19 | 1.52 | 3.00 | 33.34 | 0.03 |
| Standard deviation | 0.92 | 0.39 | 0.81 | 1.95 | 3.94 | 0.01 |
| Maximum | 5.00 | 2.00 | 3.00 | 5.00 | 35.00 | 0.05 |
| Minimum | 0.00 | 0.10 | 0.50 | 0.00 | 20.01 | 0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Li, Y.; Cai, Q.; Zhang, H.; Wu, D. How Does Heterogeneity Affect Freeway Safety? A Simulation-Based Exploration Considering Sustainable Intelligent Connected Vehicles. Sustainability 2020, 12, 8941. https://doi.org/10.3390/su12218941
Shi Y, Li Y, Cai Q, Zhang H, Wu D. How Does Heterogeneity Affect Freeway Safety? A Simulation-Based Exploration Considering Sustainable Intelligent Connected Vehicles. Sustainability. 2020; 12(21):8941. https://doi.org/10.3390/su12218941
Chicago/Turabian StyleShi, Yuntao, Ye Li, Qing Cai, Hao Zhang, and Dan Wu. 2020. "How Does Heterogeneity Affect Freeway Safety? A Simulation-Based Exploration Considering Sustainable Intelligent Connected Vehicles" Sustainability 12, no. 21: 8941. https://doi.org/10.3390/su12218941




