A Framework for Identifying the Critical Region in Water Distribution Network for Reinforcement Strategy from Preparation Resilience
Abstract
:1. Introduction
2. Materials and Methods
2.1. System Resilience Definition and Hydraulic Calculation for WDN
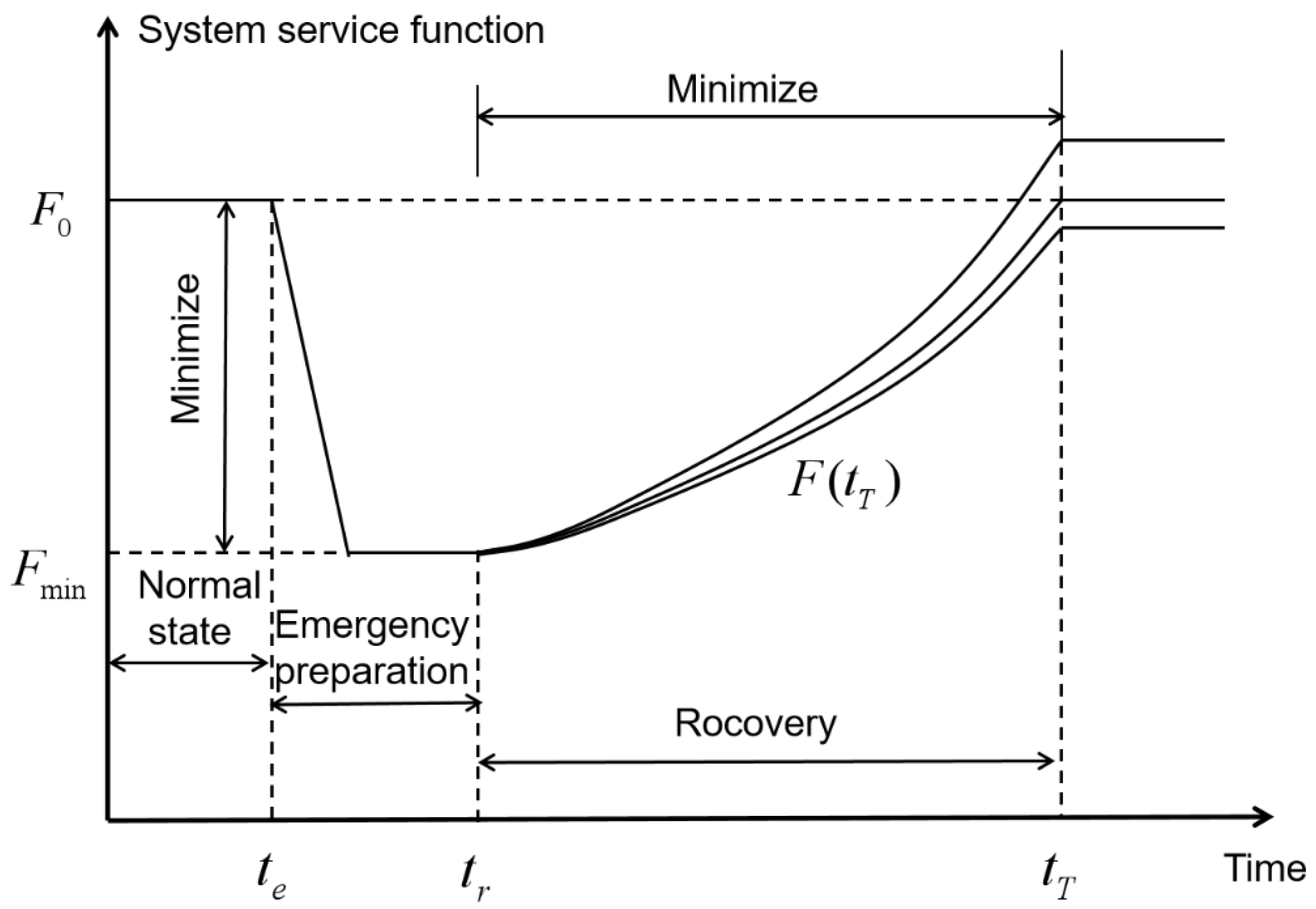
2.1.1. System Resilience
2.1.2. Representation and Hydraulic Calculation for WDNs
2.2. Failure Mode and Pressure-Driven Analysis
2.2.1. The Spatially Localized Attacks and Cascading Failures
2.2.2. Pressure-Driven Analysis
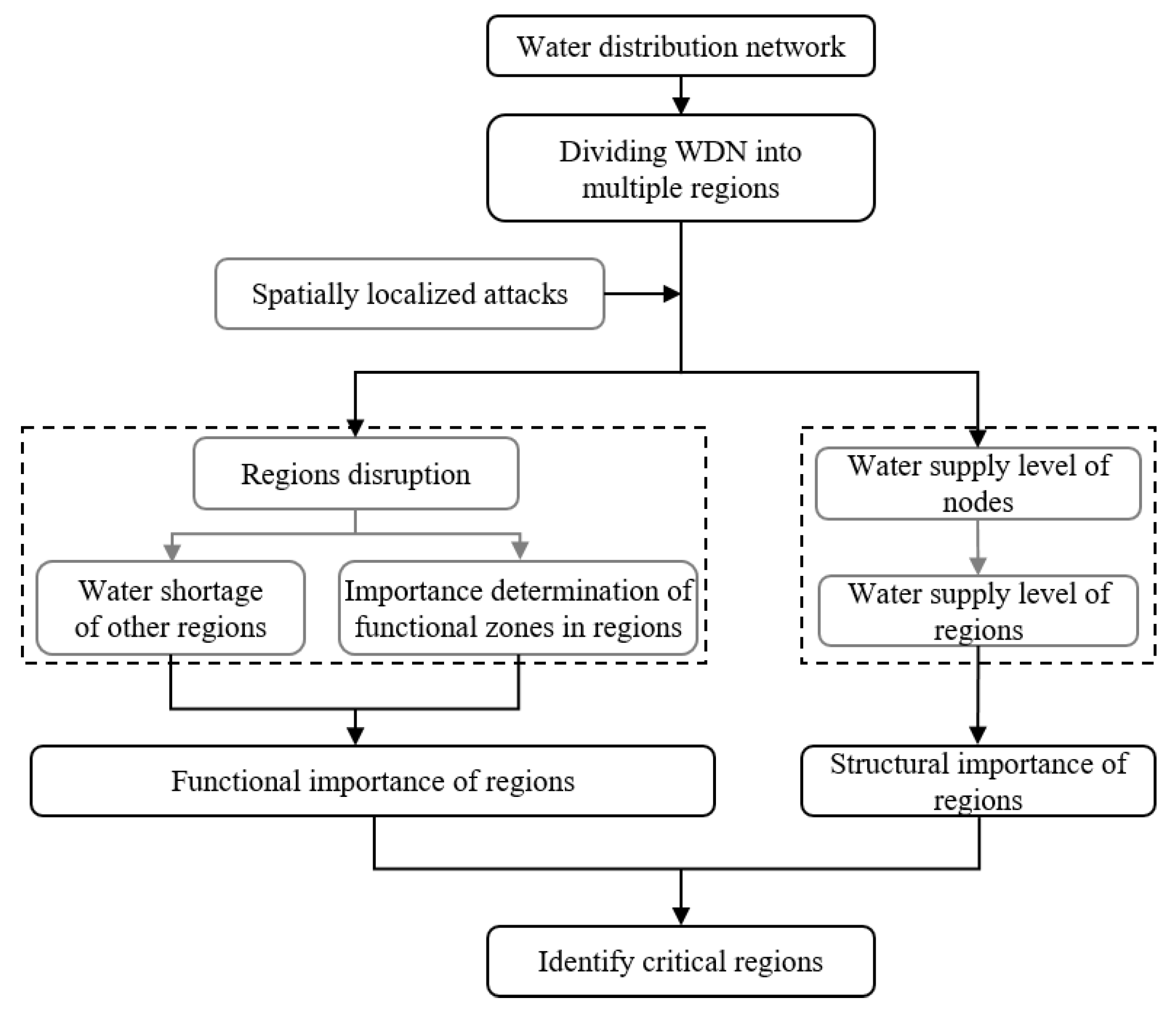
2.3. A Framework for Identifying the Critical Region in WDN
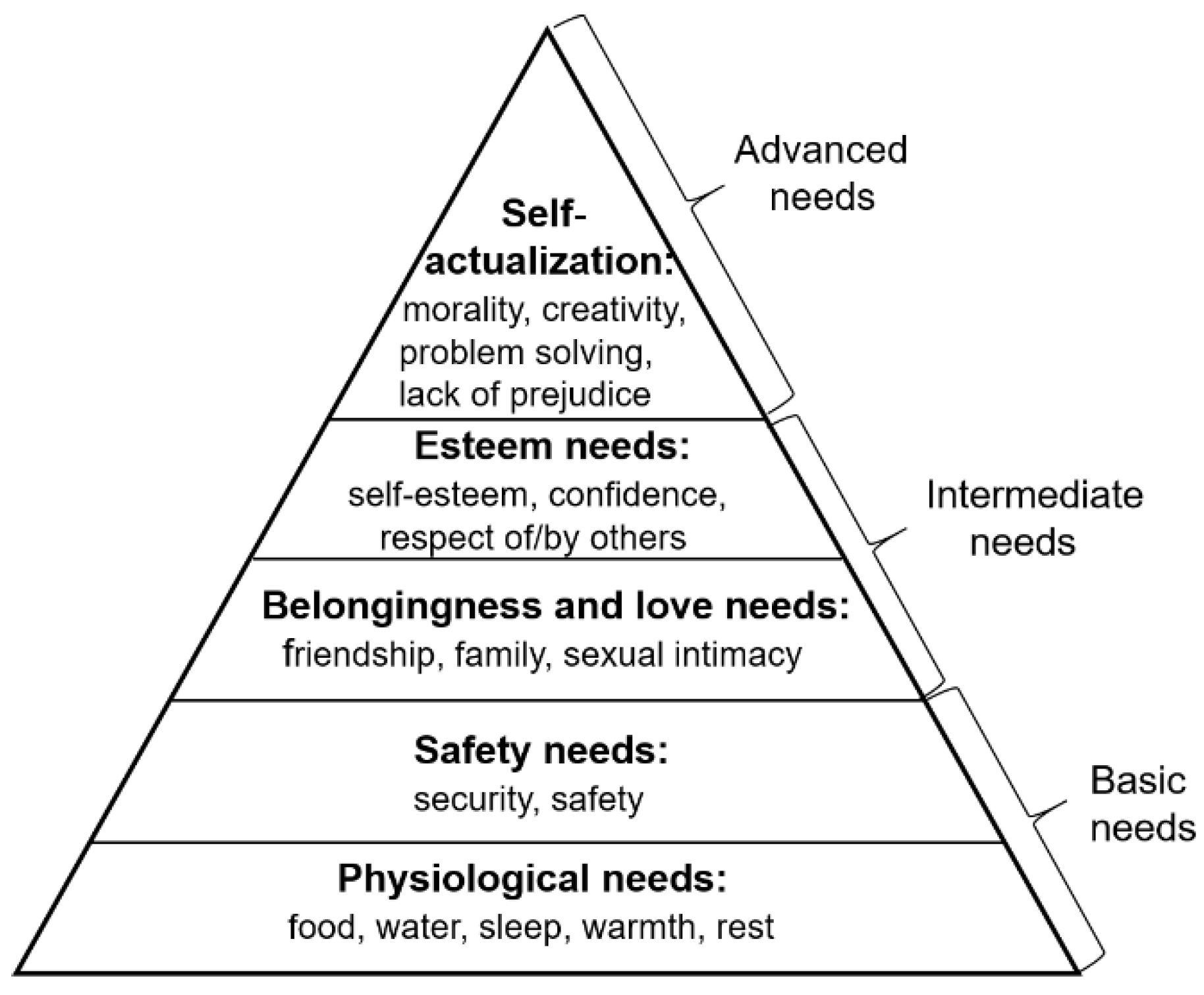
2.3.1. Evaluating the Weight of Urban Functional Zones
2.3.2. Evaluating the Structural and Functional Importance of Regions
2.3.3. Identifying the Critical Regions
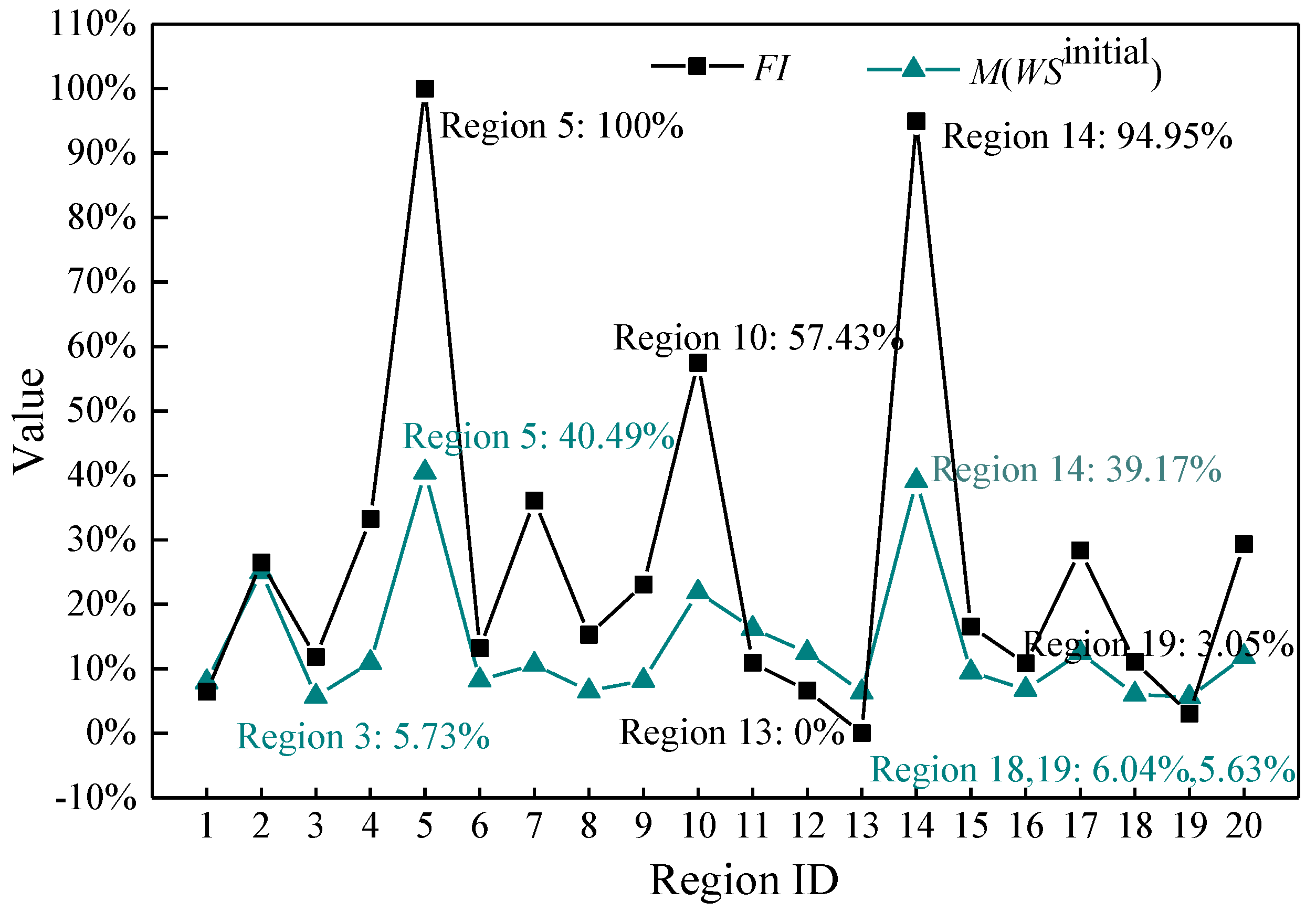
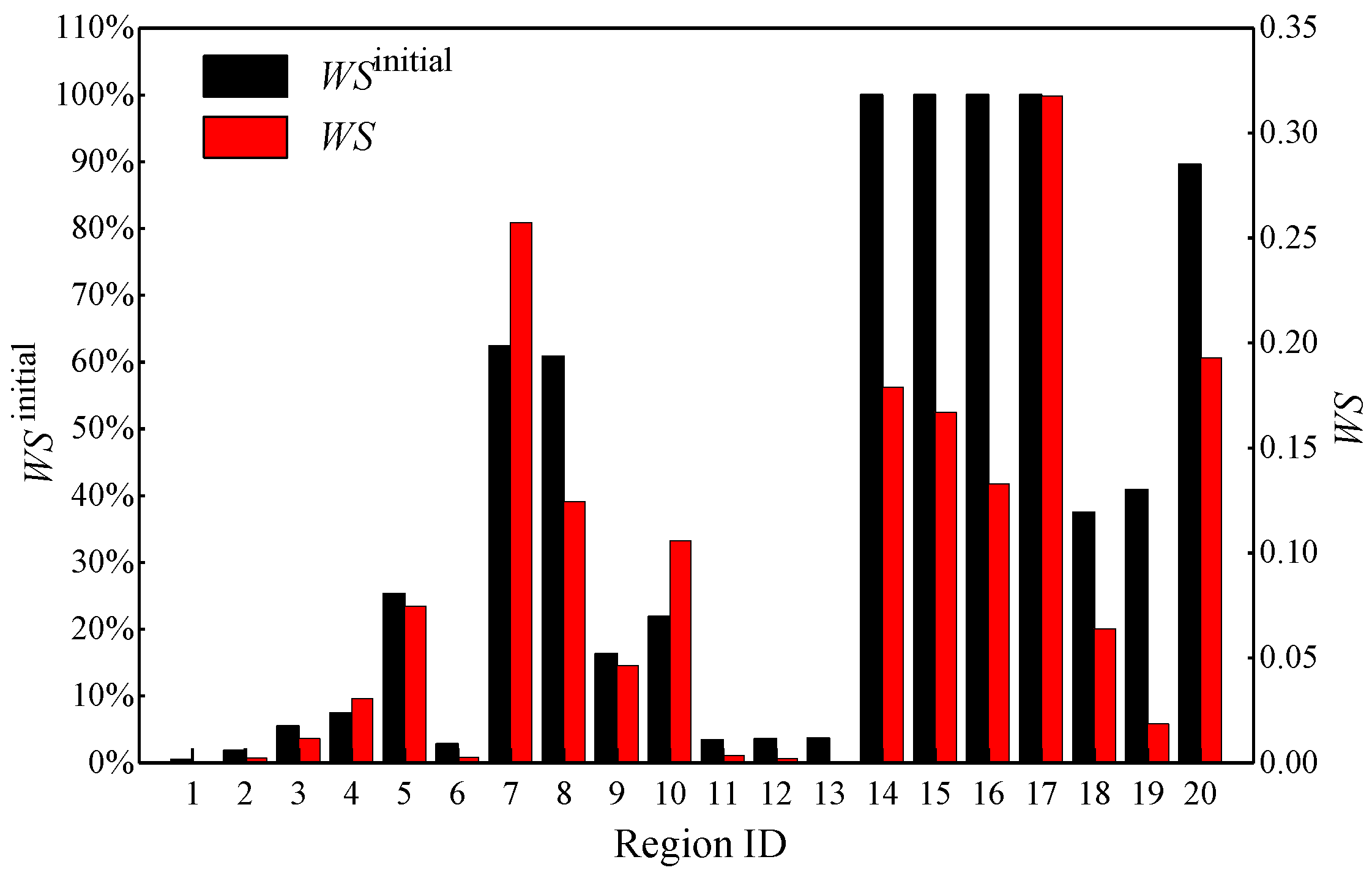
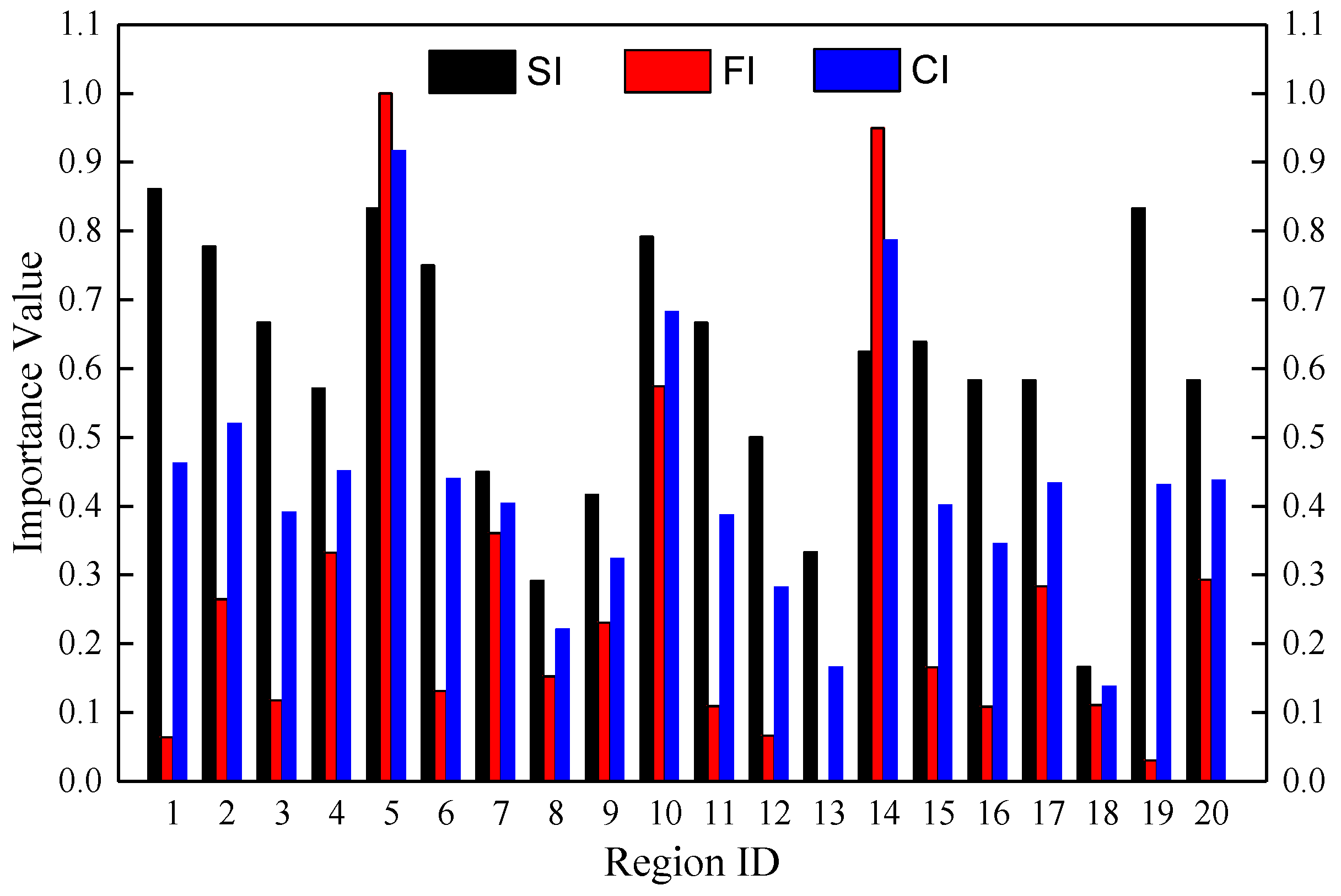
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, S.; Liu, X.; Zhuo, Y. Hybrid hidden markov models for resilience metrics in a dynamic infrastructure system. Reliab. Eng. Syst. Safety 2017, 164, 84–97. [Google Scholar] [CrossRef]
- Shuang, Q.; Zhang, M.Y.; Yuan, Y.B. Performance and Reliability Analysis of Water Distribution Systems under Cascading Failures and the Identification of Crucial Pipes. PLoS ONE 2014, 9, e88445. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, M. Critical location identification and vulnerability analysis of interdependent infrastructure systems under spatially localized attacks. Reliab. Eng. Syst. Safety 2016, 154, 106–116. [Google Scholar] [CrossRef]
- Shuang, Q.; Zhang, M.; Yuan, Y. Node vulnerability of water distribution networks under cascading failures. Reliab. Eng. Syst. Safety 2014, 124, 132–141. [Google Scholar] [CrossRef]
- Mazumder, R.K.; Salman, A.M.; Li, Y.; Yu, X. Seismic functionality and resilience analysis of water distribution systems. J. Pipel. Syst. Eng. Pract. 2019, 11, 04019045. [Google Scholar] [CrossRef]
- Zhang, Q.; Zheng, F.; Chen, Q.; Kapelan, Z.; Diao, K.; Zhang, K.; Huang, Y. Improving the resilience of postdisaster water distribution systems using dynamic optimization framework. J. Water Resour. Plan. Manag. 2020, 146, 04019075.1–04019075.12. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, M.; Wang, Z. Resilience assessment of interdependent infrastructure systems: With a focus on joint restoration modeling and analysis. Reliab. Eng. Syst. Safety 2015, 141, 74–82. [Google Scholar] [CrossRef]
- Francis, R.; Bekera, B.A. metric and frameworks for resilience analysis of engineered and infrastructure systems. Reliab. Eng. Syst. Safety 2014, 121, 90–103. [Google Scholar] [CrossRef]
- Khatavkar, P.; Mays, L.W. Resilience of water distribution systems during real-time operations under limited water and/or energy availability conditions. J. Water Resour. Plan. Manag. 2019, 145, 04019045.1–04019045.10. [Google Scholar] [CrossRef]
- Hosseini, S.; Barker, K.; Ramirez-Marquez, J.E. A review of definitions and measures of system resilience. Reliab. Eng. Syst. Safety 2016, 145, 47–61. [Google Scholar] [CrossRef]
- Jonas, J. Risk and Vulnerability Analysis of Interdependent Technical Infrastructures: Addressing Socio-Technical Systems. Risk Interdepend. Crit. Infrastruct. 2010. 978-91-88934-53-6. [Google Scholar]
- Ouyang, M.; DuenAs-Osorio, L.; Min, X. A three-stage resilience analysis framework for urban infrastructure systems. Struct. Safety 2012, 36–37, 23–31. [Google Scholar] [CrossRef]
- Meng, F.; Fu, G.; Farmani, R.; Sweetapple, C.; Butler, D. Topological attributes of network resilience: A study in water distribution systems. Water Res. 2018, 143, 376–386. [Google Scholar] [CrossRef] [PubMed]
- Pagano, A.; Sweetapple, C.; Farmani, R.; Giordano, R.; Butler, D. Water Distribution Networks Resilience Analysis: A Comparison between Graph Theory-Based Approaches and Global Resilience Analysis. Water Resour. Manag. 2019, 33, 2925–2940. [Google Scholar] [CrossRef]
- Porse, E.; Lund, J. Network analysis and visualizations of water resources infrastructure in california: Linking connectivity and resilience. J. Water Resour. Plan. Manag. 2016, 142, 04015041. [Google Scholar] [CrossRef]
- Butler, D.; Ward, S.; Sweetapple, C.; Astaraie-Imani, M.; Diao, K.; Farmani, R.; Fu, G. Reliable, resilient and sustainable water management: The Safe & SuRe approach. Glob. Chal. 2016, 1, 63–77. [Google Scholar] [CrossRef]
- Gheisi, A.; Naser, G. Water distribution system reliability under simultaneous multicomponent failure scenario. J. Am. Water Works Assoc. 2014, 106, E319–E327. [Google Scholar] [CrossRef]
- Berardi, L.; Ugarelli, R.; Røstum, J.; Giustolisi, O. Assessing mechanical vulnerability in water distribution networks under multiple failures. Water Resour. Res. 2014, 50, 2586–2599. [Google Scholar] [CrossRef]
- Nieminen, J. On the centrality in a graph. Scand. J. Psychol. 1974, 15, 332–336. [Google Scholar] [CrossRef]
- Knoke, D.; Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications. Contem. Sociol. 1996, 25, 275. [Google Scholar] [CrossRef]
- Freeman, L.C. Centrality in social networks: Conceptual clarification. Soc. Netw. 1979, 1, 215–239. [Google Scholar] [CrossRef] [Green Version]
- Zio, E.; Sansavini, G. Component Criticality in Failure Cascade Processes of Network Systems. Risk Anal. 2011, 31, 1196–1210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farahmandfar, Z.; Piratla, K.R. Comparative evaluation of topological and flow-based seismic resilience metrics for rehabilitation of water pipeline systems. J. Pipel. Syst. Eng. Pract. 2018, 9, 04017027. [Google Scholar] [CrossRef]
- He, X.; Yuan, Y. A framework of identifying critical water distribution pipelines from recovery resilience. Water Resour. Manag. 2019, 33, 3691–3706. [Google Scholar] [CrossRef]
- Giustolisi, O.; Savic, D. Identification of segments and optimal isolation valve system design in water distribution networks. Urban Water J. 2010, 7, 1–15. [Google Scholar] [CrossRef]
- Wang, S.; Hong, L.; Ouyang, M.; Zhang, J.; Chen, X. Vulnerability analysis of interdependent infrastructure systems under edge attack strategies. Safety Sci. 2013, 51, 328–337. [Google Scholar] [CrossRef]
- Zhou, F.; Yuan, Y.; Zhang, M. Robustness analysis of interdependent urban critical infrastructure networks against cascade failures. Arab. J. Ence Eng. 2019, 44, 2837–2851. [Google Scholar] [CrossRef]
- Ouyang, M. A mathematical framework to optimize resilience of interdependent critical infrastructure systems under spatially localized attacks. Eur. J. Oper. Res. 2017, 262, 1072–1084. [Google Scholar] [CrossRef]
- Wagner, J.M.; Shamir, U.; Marks, D.H. Water Distribution Reliability: Simulation Methods. J. Water Resour. Plan. Manag. 1988, 114, 276–294. [Google Scholar] [CrossRef] [Green Version]
- Walski, T.M.; Giustolisi, O. Demand components in water distribution network analysis. J. Water Resour. Plan. Manag. 2012, 138, 356–367. [Google Scholar]
- Zhuang, B.; Lansey, K.; Kang, D. Resilience/Availability Analysis of Municipal Water Distribution System Incorporating Adaptive Pump Operation. J. Hydr. Eng. 2013, 139, 527–537. [Google Scholar] [CrossRef]
- He, P.; Tao, T.; Xin, K.; Li, S.; Yan, H. Modelling water distribution systems with deficient pressure: An improved iterative methodology. Water Res. Manag. 2016, 30, 593–606. [Google Scholar] [CrossRef]
- Feng, K.; Wang, N.; Li, Q.; Lin, P. Measuring and enhancing resilience of building portfolios considering the functional interdependence among community sectors. Struct. Safety 2017, 66, 118–126. [Google Scholar] [CrossRef]
- Mieler, M.; Stojadinovic, B.; Budnitz, R.; Mahin, S. A framework for linking community resilience goals to specific performance targets for the built environment. Earthquake Spect. 2015, 31, 1267–1283. [Google Scholar] [CrossRef] [Green Version]
- Fang, D.P.; Li, Q.W.; Li, N. An evaluation system for community seismic resilience and its application in a typical community. Engin Mechan 2020. [Google Scholar] [CrossRef]
- Zhang, M.Y.; Gao, Y.; Yuan, Y.B. Nodal importance analysis of water supply system under cascade failure based on set pair potential. Nat. Disas. 2015, 24, 197–206. [Google Scholar]
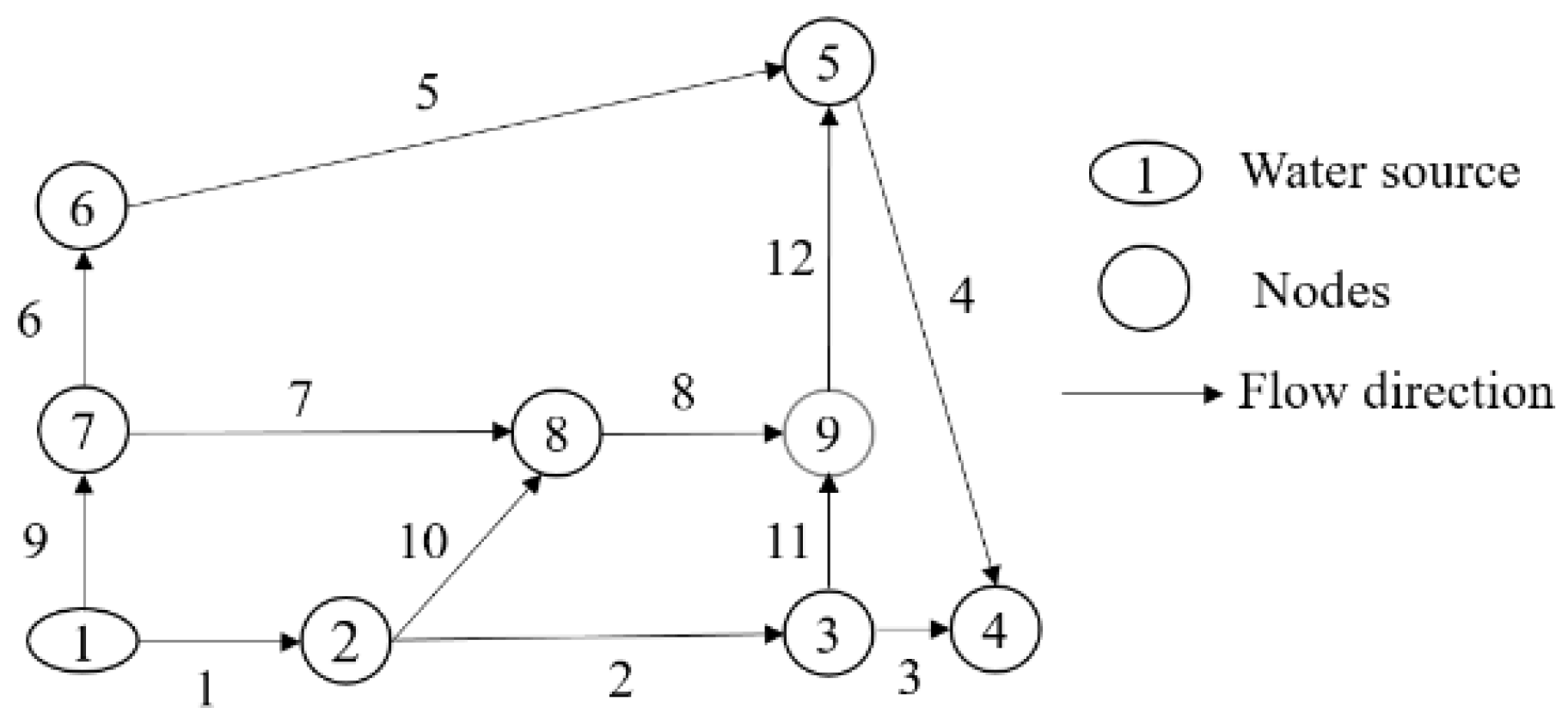
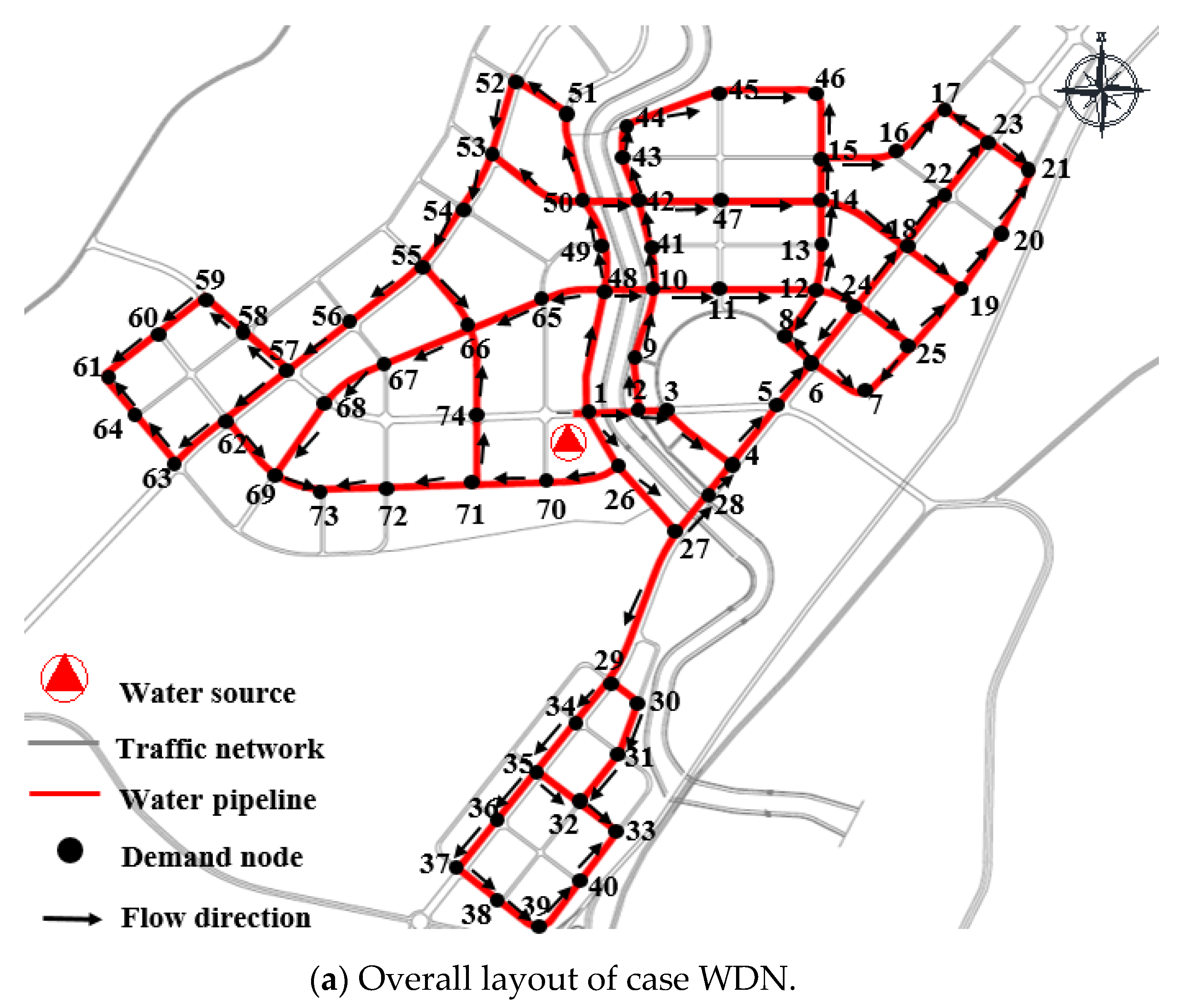
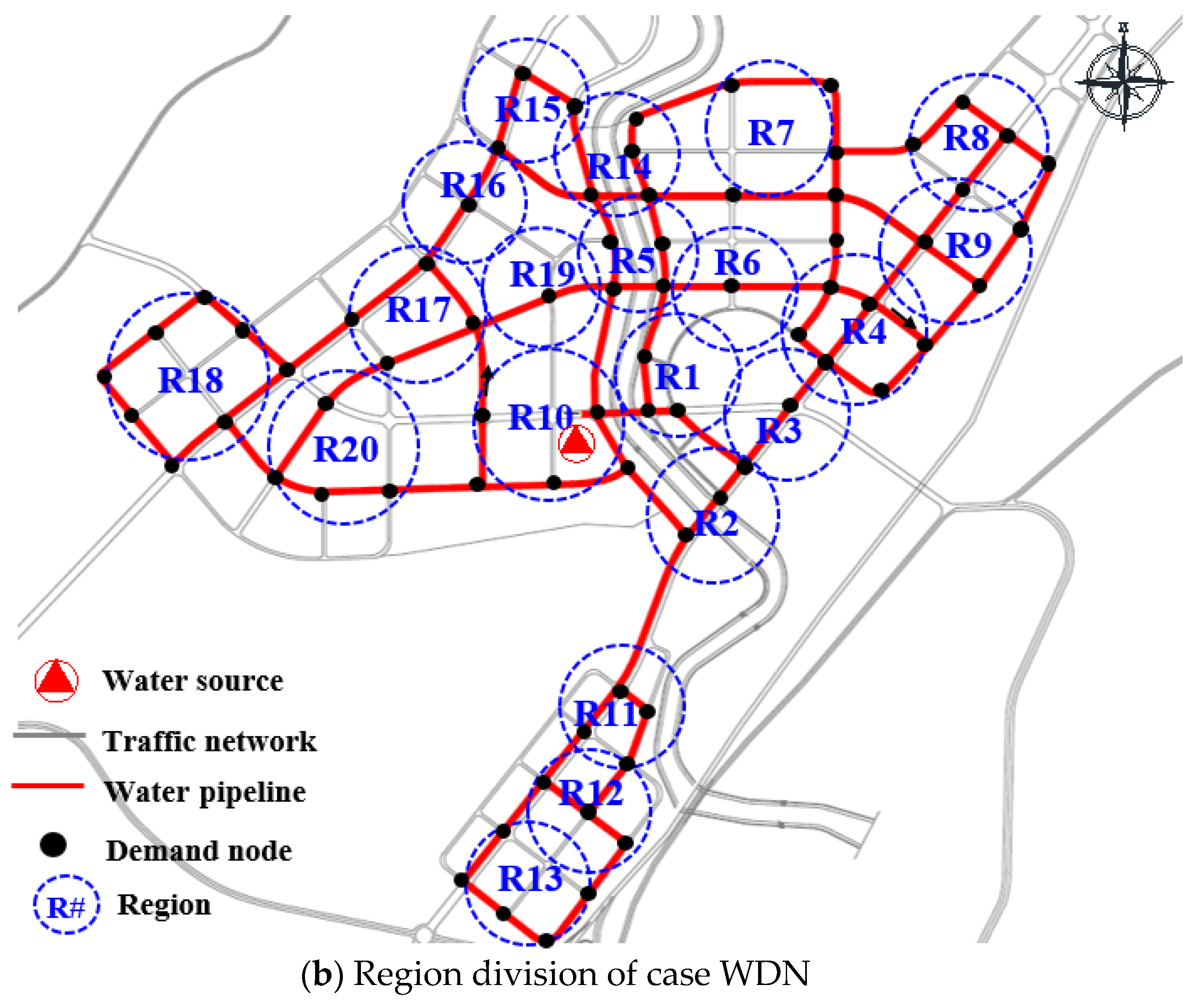

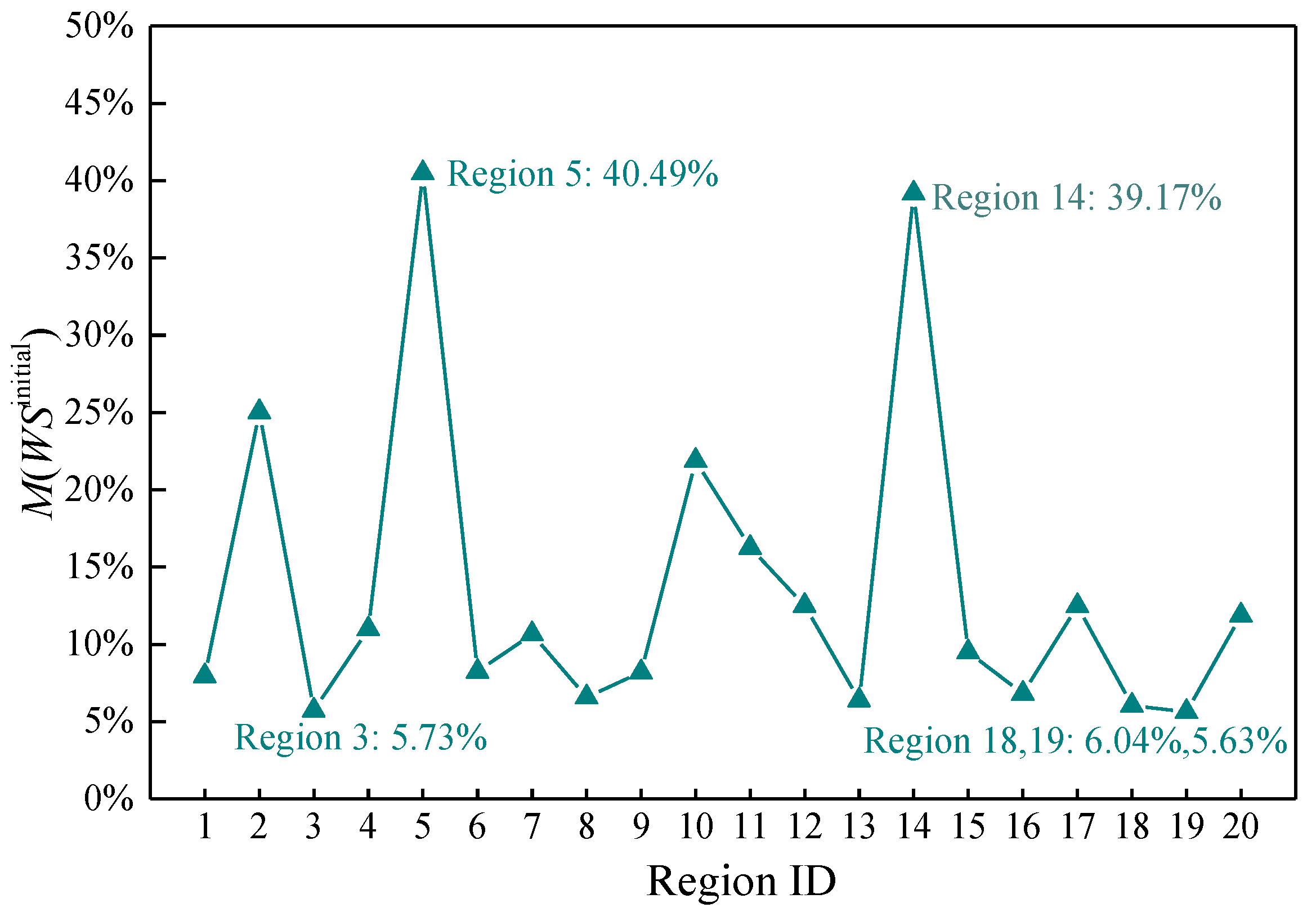
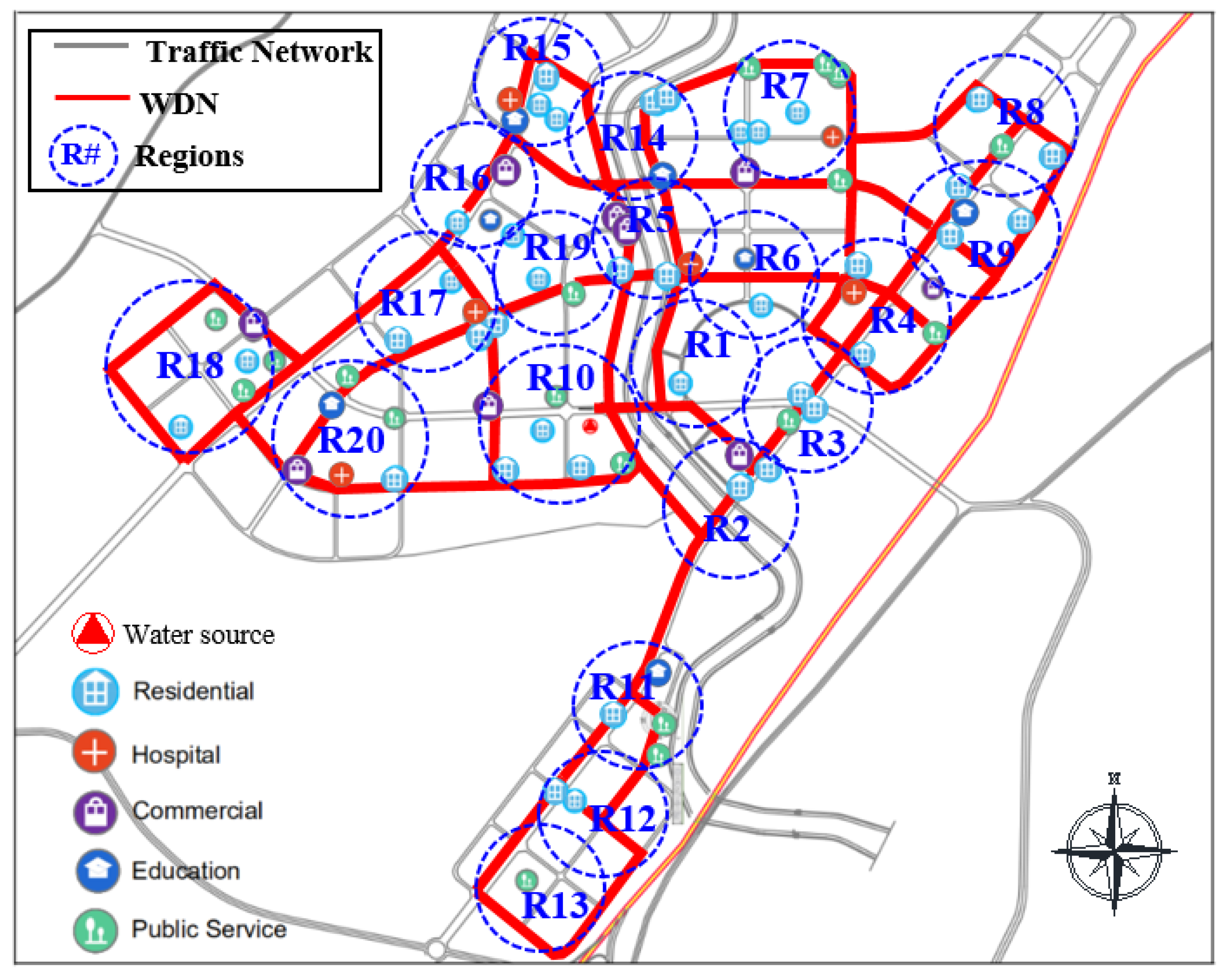

| Node # | WSL | Node # | WSL |
|---|---|---|---|
| 2 | 1 | 6 | 2 |
| 3 | 2 | 7 | 1 |
| 4 | 3 | 8 | 2 |
| 5 | 3 | 9 | 3 |
| Node# | Region# | Required Demand(L/s) | Elevation(m) | Pipe# | Region# | Diameter (mm) | Length (m) |
|---|---|---|---|---|---|---|---|
| 2 | 1 | 0.83 | 16.01 | 2–3 | 1 | 300 | 150.90 |
| 27 | 2 | 0 | 16.56 | 27–28 | 2 | 200 | 312.60 |
| 5 | 3 | 30.75 | 18.11 | 5–6 | 3 | 200 | 347.80 |
| 24 | 4 | 28.80 | 18.80 | 24–25 | 4 | 300 | 406.90 |
| 48 | 5 | 56.98 | 12.60 | 48–49 | 5 | 1000 | 265.10 |
| 11 | 6 | 19.04 | 20.64 | 11–12 | 6 | 500 | 556.70 |
| 45 | 7 | 20.53 | 24.60 | 45–46 | 7 | 200 | 584.40 |
| 23 | 8 | 23.70 | 32.33 | 23–17 | 8 | 200 | 329.20 |
| 18 | 9 | 42.05 | 24.60 | 18–19 | 9 | 300 | 424.20 |
| 1 | 10 | 21.44 | 16.14 | 1–26 | 10 | 700 | 367.20 |
| 29 | 11 | 16.27 | 21.35 | 29–30 | 11 | 200 | 217.30 |
| 32 | 12 | 11.94 | 19.42 | 32–33 | 12 | 200 | 279.80 |
| 38 | 13 | 1.13 | 21.30 | 38–39 | 13 | 200 | 277.80 |
| 43 | 14 | 20.53 | 11.00 | 43–44 | 14 | 300 | 194.60 |
| 52 | 15 | 28.84 | 27.72 | 52–53 | 15 | 1000 | 467.70 |
| 54 | 16 | 69.79 | 29.25 | 54–55 | 16 | 1000 | 410.10 |
| 55 | 17 | 59.10 | 32.04 | 55–66 | 17 | 700 | 488.10 |
| 60 | 18 | 12.65 | 66.40 | 60–61 | 18 | 200 | 409.60 |
| 65 | 19 | 56.98 | 25.00 | 65–66 | 19 | 500 | 457.20 |
| 68 | 20 | 33.60 | 38.25 | 68–69 | 20 | 300 | 532.10 |
| Region #. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Water supply level | 2.67 | 3.67 | 5.00 | 6.14 | 3.00 | 4.00 | 7.60 | 9.50 | 8.00 | 3.50 |
| Region #. | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Water supply level | 5.00 | 7.00 | 9.00 | 5.50 | 5.33 | 6.00 | 6.00 | 11.00 | 3.00 | 6.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Zhang, J.; Li, G.; Zhao, Y. A Framework for Identifying the Critical Region in Water Distribution Network for Reinforcement Strategy from Preparation Resilience. Sustainability 2020, 12, 9247. https://doi.org/10.3390/su12219247
Zhang M, Zhang J, Li G, Zhao Y. A Framework for Identifying the Critical Region in Water Distribution Network for Reinforcement Strategy from Preparation Resilience. Sustainability. 2020; 12(21):9247. https://doi.org/10.3390/su12219247
Chicago/Turabian StyleZhang, Mingyuan, Juan Zhang, Gang Li, and Yuan Zhao. 2020. "A Framework for Identifying the Critical Region in Water Distribution Network for Reinforcement Strategy from Preparation Resilience" Sustainability 12, no. 21: 9247. https://doi.org/10.3390/su12219247
APA StyleZhang, M., Zhang, J., Li, G., & Zhao, Y. (2020). A Framework for Identifying the Critical Region in Water Distribution Network for Reinforcement Strategy from Preparation Resilience. Sustainability, 12(21), 9247. https://doi.org/10.3390/su12219247





