Optimum Design and Control of Heat Pumps for Integration into Thermohydraulic Networks
Abstract
:1. Introduction
1.1. Industrial Heating and Cooling Networks
1.2. Heat Pumps in Industrial Sites
1.3. Methods for Optimal Integration of Heat Pumps
2. Materials and Methods
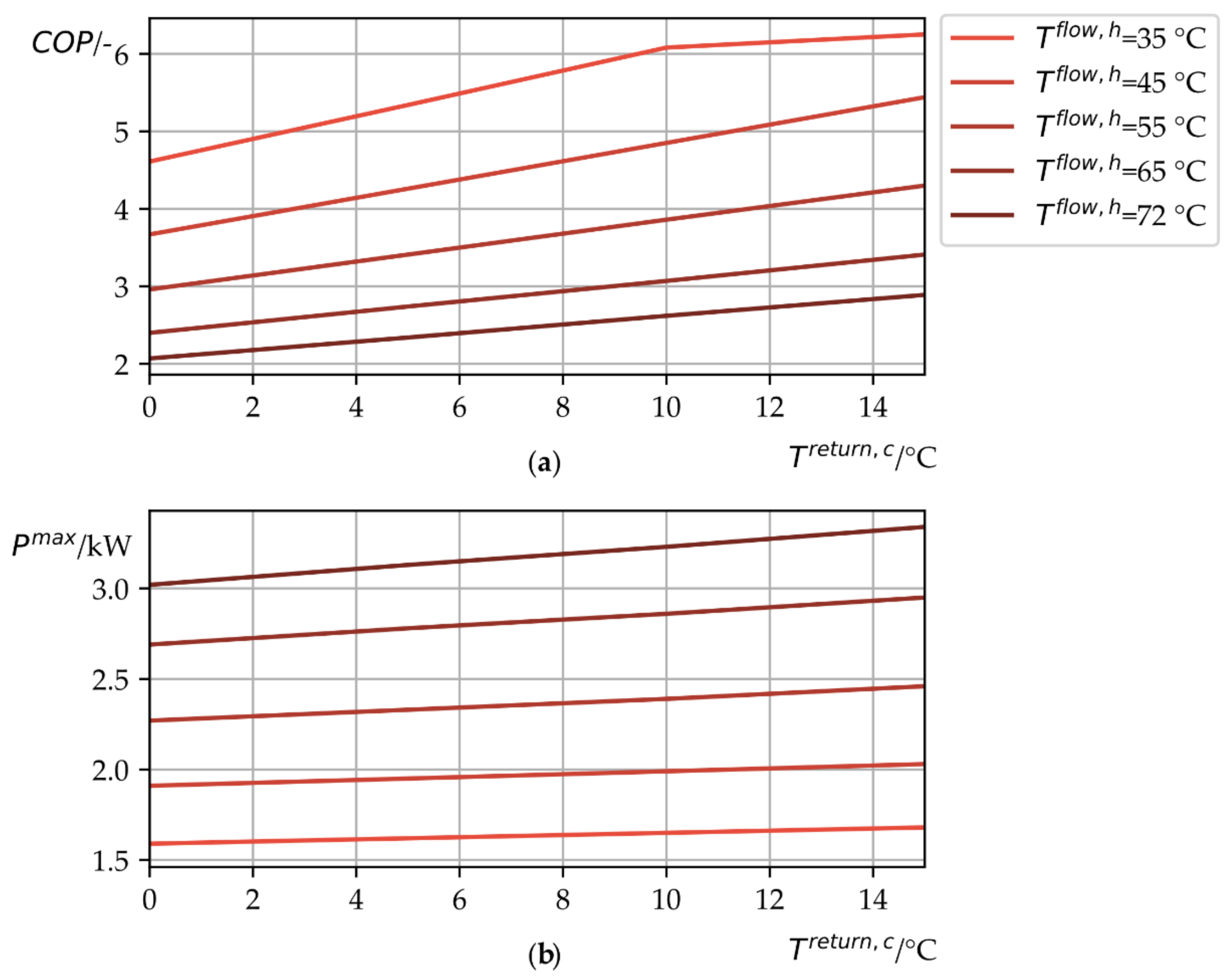
2.1. Mathematical Model
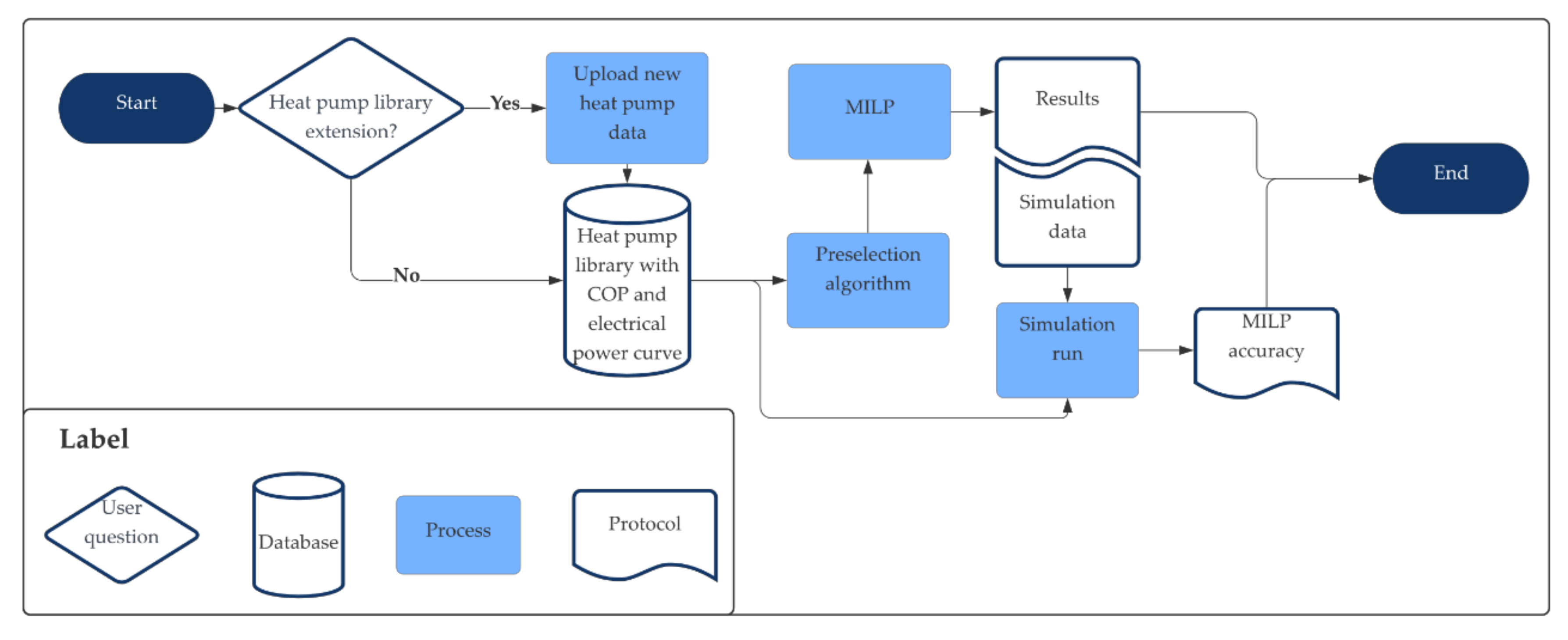
2.2. Preselection Algorithm
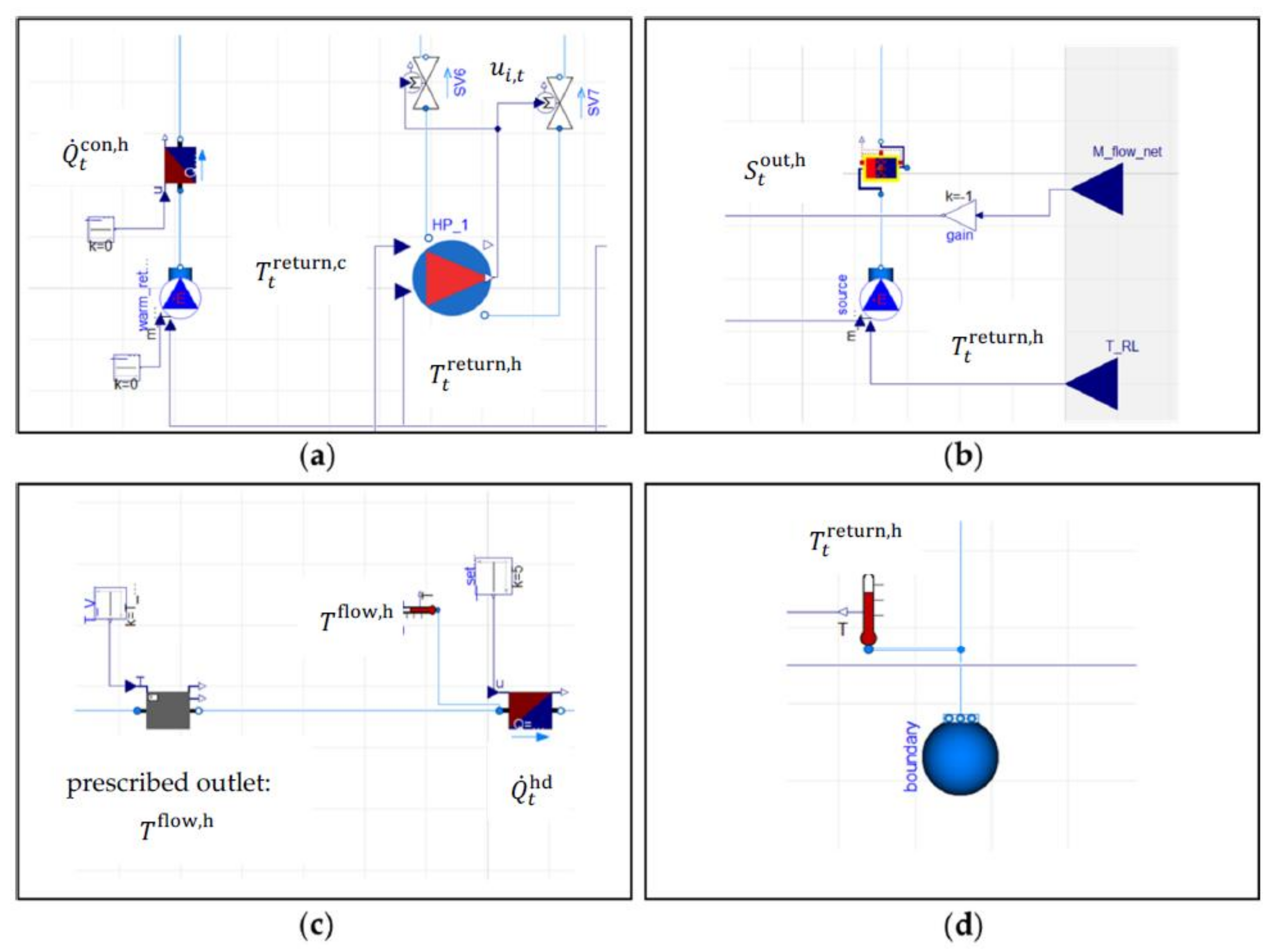
2.3. Simulation Model
- flow temperatures to adjust the heat pump operation,
- regression function to calculate the and the maximum electrical power for the heat pump operation in the simulation with the simulation’s return temperature and the passed flow temperature ,
- minimum electrical power to limit the heat pumps’ operation in the simulation,
- time step to adjust the time series in the simulation,
- buying decision to implement the heat pump constellation into the simulation,
- storage volumes and to pass the dimension into the simulation,
- heating and cooling demand at each time step to model the consumer in the simulation,
- conventional heating and cooling at each time step to model a conventional energy converter in the simulation,
- value of the objective function to insert it into Equation (17),
- heat and cold flow rate of every heat pump at each time step to calculate the mass flow rates in the simulation,
- loading and unloading heat flow rate for the storage to set it in the simulation.
3. Results
3.1. Industrial Use Case
3.2. Sensitivity Analysis
3.2.1. Standard Case
3.2.2. Demand
- The tool will always try to completely cover the lower demand with heat pumps (in this example, this refers to the cooling demand).
- The chosen volume of storage might not make sense despite the tool’s selection, as it may be primarily loaded.
- The size of cold water storage depends on both the heating and cooling demand.
- The NPV is primarily dependent on the lower demand curve (in this example, this refers to the cooling demand).
3.2.3. Temperature
- A rising temperature spread between the heat source and the heat sink leads to lower efficiency.
- As long as the purchase of a heat pump is economical, the cooling demand will be covered fully by heat pumps.
- With a flow temperature of the cooling circuit of 5 °C and a flow temperature of the heating circuit of 90 °C, the purchase of a heat pump is no longer economical.
3.2.4. Costs
3.2.5. Storage
3.2.6. Preselection Algorithm
3.3. Analysis with the Simulation Model
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Heat Pump | ||
|---|---|---|
| BWC 351 A07 | 3.44 | 6 |
| BW 351 A07 | 3.38 | 0 |
| BW 351 A18 | 3.44 | 8 |
| BW 301 A10 | 2.89 | 0 |
| BWC 201 A17 | 2.83 | 0 |
| Heat Pump | ||
|---|---|---|
| BW 351 A18 | 3.02 | 8 |
| BWC 351 A07 | 2.97 | 8 |
| BW 351 A07 | 2.93 | 1 |
| BWC 201 A17 | 2.19 | 0 |
| BW 301 A10 | 2.18 | 0 |
| Heat Pump | ||
|---|---|---|
| BW 351 A18 | 2.39 | 8 |
| BWC 351 A07 | 2.26 | 8 |
| BW 351 A07 | 2.25 | 8 |
| BWC 201 A17 | 1.23 | 0 |
| BWC 201 A10 | 1.13 | 0 |
| Passed Object | Type of Parameter | Information |
|---|---|---|
| regressor function for and | equation | calculates the and depending on the temperatures in the simulation |
| initial parameter | limits the electrical power of every heat pump | |
| parameter for equation | time information (time step length) | |
| initial parameter | purchased heat pumps to be installed in the simulation | |
| initial parameter | dimension of the storages in the simulation | |
| time-dependent parameter | heating and cooling demand for the simulation | |
| time-dependent parameter | conventional heating and cooling at each time step for the simulation | |
| initial parameter | flow temperatures are set before the simulation start | |
| initial parameter | value of the objective function for comparison | |
| time-dependent parameter | storage loading and unloading at each time step for the simulation | |
| time-dependent parameter | heat/cold flow rate to calculate mass flow rates for every heat pump at each time step |
| Symbol | Unit | Description |
|---|---|---|
| - | amount of purchases of the same heat pump model | |
| a | payback period | |
| - | binary buying option of heat pump i chosen by optimizer | |
| J·(kgK)−1 | specific heat capacity of water | |
| €·kWh−1 | specific costs for cooling energy | |
| €·kWh−1 | specific costs for electricity | |
| €·kWh−1 | specific costs for heating energy | |
| €·m−3 | specific volume price for stratified thermal storage tank | |
| € | price for heat pump i | |
| € | NPV of optimization (objective function value) chosen by optimizer | |
| € | NPV of simulation (objective function value) | |
| - | COP of heat pump i at time step t | |
| - | averaged COP of heat pump i | |
| - | constant COP for preselection algorithm | |
| kJ | SOC of the storage (hot/cold) at time step t chosen by optimizer | |
| - | error between simulation () and optimization () | |
| - | heat pump | |
| kg·s−1 | mass flow rate for loading and unloading the storage | |
| - | heat pump models | |
| - | Big-M-Coefficient | |
| - | number of heat pumps | |
| kW | electrical power of heat pump i at time step t chosen by optimizer | |
| kW | max. electrical power of heat pump i at time step t | |
| kW | min. electrical power of heat pump i | |
| kW | electrical power of heat pump i at time step t in the simulation | |
| kW | heat/cold flow rate | |
| kW | heating/cooling demand at time step t | |
| kW | conv. heat/cold flow rate at time step t chosen by optimizer | |
| kW | conv. heat/cold flow rate at each time step t in the simulation | |
| kW | heat/cold flow rate of heat pump i at time step t chosen by optimizer | |
| kW | nominal heat flow rate of heat pump | |
| kW | heat/cold flow rate for storage loading/unloading at time step t chosen by optimizer | |
| - | time step of optimization | |
| - | time step length | |
| K | cold/hot flow temperature | |
| min | minimum runtime of heat pump | |
| K | cold/hot return temperature at time step t | |
| - | binary variable for on-/off-switch of heat pump i at time step t chosen by optimizer | |
| m3 | cold/hot water storage volume chosen by optimizer | |
| - | binary variable to forbid bidirectional flow chosen by optimizer | |
| - | loading/unloading efficiency | |
| kg·m−3 | density of the fluid (water) | |
| - | number of time steps | |
| h | operating hours | |
| - | energy efficiency of the storage from time step to |
References
- Ittershagen, M. Erneuerbare Energien in Zahlen. Available online: https://www.umweltbundesamt.de/themen/klima-energie/erneuerbare-energien/erneuerbare-energien-in-zahlen#uberblick (accessed on 1 July 2020).
- Hüttmann, M. CO2-Freie Wärme für Industrie und Gewerbe mit Solarthermie. Available online: https://www.dgs.de/news/en-detail/211218-co2-freie-waerme-fuer-industrie-und-gewerbe-mit-solarthermie/ (accessed on 7 September 2020).
- Deutscher Bundestag. Klimaschutzprogramm 2030 der Bundesregierung zur Umsetzung des Klimaschutzplans 2050. Available online: https://www.bundesregierung.de/resource/blob/975226/1679914/e01d6bd855f09bf05cf7498e06d0a3ff/2019-10-09-klima-massnahmen-data.pdf?download=1 (accessed on 1 July 2020).
- Wolf, S.; Fahl, U.; Blesl, M.; Voß, A.; Jakobs, R. Analyse des Potenzials von Industriewärmepumpen in Deutschland; Final Report to Federal Ministry for Economic Affairs and Energy (BMWi) and Energy Baden-Wuerttemberg AG (EnBW); Institute for Energy Economics and Rational Energy Use (IER) and Information Center for Heat Pumps and Refrigeration Technology (IZW): Stuttgart, Germany, 2014. [Google Scholar]
- Nowak, T. Heat Pumps. In Integrating Technologies to Decarbonise Heating and Cooling; Technical Report of European Copper Institute: Brussels, Belgium, 2018. [Google Scholar]
- Verein Deutscher Ingenieure. Hydraulik in Anlagen der Technischen Gebäudeausrüstung Hydraulische Schaltungen, 23.100.01, 91.140.10 (VDI 2073). Available online: https://www.vdi.de/richtlinien/details/vdi-2073-blatt-2-hydraulik-in-anlagen-der-technischen-gebaeudeausruestung-hydraulischer-abgleich-1 (accessed on 8 October 2019).
- Viessmann. Planungsanleitung. Sole/Wasser- und Wasser/Wasser-Wärmepumpenein- und Zweistufig, 5,8 bis 117,8 kW. Available online: https://www.manualslib.de/manual/441762/Viessmann-Vitocal-300-G-Typ-Bw-301-A.html#manual (accessed on 11 August 2020).
- Heinrich, C.; Wittig, S.; Albring, P.; Richter, L.; Safarik, M.; Böhm, U.; Hantsch, A. Nachhaltige Kälteversorgung in Deutschland an den Beispielen Gebäudeklimatisierung und Industrie. Clim. Chang. 2014, 25, 82–83. [Google Scholar]
- Frisch, S.; Pehnt, M.; Otter, P.; Nast, M. Prozesswärme im Marktanreizprogramm. In Zwischenbericht zu Perspektivische Weiterentwicklung des Marktanreizprogramms FKZ 03MAP123; Interim Report to Federal Ministry for Economic Affairs and Energy (BMWi); Institute for Energy and Environmental Research (ifeu): Heidelberg, Germany; German Aerospace Center (DLR): Stuttgart, Germany, 2010. [Google Scholar]
- Vardakas, J.S.; Zorba, N.; Verikoukis, C.V. A Survey on Demand Response Programs in Smart Grids: Pricing Methods and Optimization Algorithms. IEEE Commun. Surv. Tutor. 2014, 17, 152–178. [Google Scholar] [CrossRef]
- Hart, W.E. Pyomo-Optimization Modeling in Python, 2nd ed.; Springer: Cham, Switzerland, 2017; ISBN 978-3-319-58819-3. [Google Scholar]
- Schütz, T.; Harb, H.; Streblow, R.; Mueller, D. Comparison of models for thermal energy storage units and heat pumps in mixed integer linear programming. In Proceedings of the 28th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems (ECOS), Pau, France, 29 June 2015. [Google Scholar]
- Fang, C.; Xu, Q.; Wang, S.; Ruan, Y. Operation optimization of heat pump in compound heating system. Energy Procedia 2018, 152, 45–50. [Google Scholar] [CrossRef]
- Schlosser, F.; Seevers, J.-P.; Peesel, R.-H. System efficient integration of standby control and heat pump storage systems in manufacturing processes. Energy 2019, 181, 395–406. [Google Scholar] [CrossRef]
- Kanga, Z.; Zhoua, X.; Zhaoa, Y.; Wanga, R.; Wang, X. Study on Optimization of Underground Water Source Heat Pump. Procedia Eng. 2017, 205, 1691–1697. [Google Scholar] [CrossRef]
- Held, E. Wie funktioniert eigentlich eine Wärmepumpe? Gezügelte Leistung. SBZ Monteur 2017, 21, 10–15. [Google Scholar]
- Oppelt, T. Modell zur Auslegung und Betriebsoptimierung von Nah- und Fernkältenetzen. Ph.D. Thesis, Technical University of Chemnitz, Chemnitz, Germany, 2015. Available online: https://monarch.qucosa.de/api/qucosa%3A20314/attachment/ATT-0/ (accessed on 30 October 2020).
- Malherbe, A. DYMOLA Systems Engineering. Available online: https://www.3ds.com/de/produkte-und-services/catia/produkte/dymola/ (accessed on 15 July 2020).
- Functional Mock-Up Interface. Available online: https://fmi-standard.org/ (accessed on 15 July 2020).
- Konstantin, P. Praxisbuch Energiewirtschaft: Energieumwandlung, Transport und Beschaffung, Übertragungsnetzausbau und Kernenergieausstieg, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2017; p. 14. ISBN 978-3-662-49822-4. [Google Scholar]
- Chiasson, A. Geothermal heat pump and heat engine systems. In Theory and Practice; Wiley: Hoboken, NJ, USA, 2016; pp. 312–314, 327–328. ISBN 9781118961971. [Google Scholar]
- Weisberg, S. Applied Linear Regression, 4th ed.; Wiley: Hoboken, NJ, USA, 2014; pp. 51–53. ISBN 9781118386088. [Google Scholar]
- Müller, C. Leistungszahlen für Kälte-, Klima- und Wärmepumpensysteme. Friscaldo 2008, 1, 31–33. [Google Scholar]
- Hülsken, C. Erneuerbare energie für die industrie: Prozesswärme aus bioenergie sorgt für unabhängigkeit und klimaschutz. Renews Kompakt 2017, 38, 1–5. [Google Scholar]
- Modelica Association. Modelica Libraries. Available online: https://www.modelica.org/libraries (accessed on 8 October 2020).
- Grave, K.; Hazrat, M.; Boeve, S.; Blücher, F.V.; Bourgault, C.; Bader, N.; Breitschopf, B.; Friedrichsen, N.; Arens, M.; Aydemir, A.; et al. Stromkosten der energieintensiven Industrie. In Ein Internationaler Vergleich; Technical Report to Federal Ministry for Economic Affairs and Energy (BMWi); Fraunhofer ISI and ECOFYS Germany GmbH: Berlin, Germany, 2015. [Google Scholar]
- Illner, B.; Bünting, F. Industrie 4.0: Finanzierung von Investitionen. Available online: https://www.vdma.org/documents/105628/878344/Investitionen+in+Industrie+40.pdf/abafbde7-51d8-4281-af3e-f567361ef979 (accessed on 9 October 2019).
- Stiebel Eltron. OPERATION AND INSTALLATION: DHW Heat Pump. Available online: https://www.stiebel-eltron.com.au/download/1540529916_STIEBEL_ELTRON_Operation_and_Installation_WWK.pdf (accessed on 16 September 2020).
- Viessmann. Preisliste 2018 DE Heizsysteme. Available online: https://www.meinhausshop.de/media/pdf/meinhausshop-Viessmann-Hetzsysteme-Teil%201.PDF (accessed on 17 October 2019).
- Pang, X.-F. Water. In Molecular Structure and Properties; World Scientific Publishing Company: Singapore, 2014; pp. 92, 97. ISBN 9789814440431. [Google Scholar]








| Heat Pump | Heat Pump | ||||
|---|---|---|---|---|---|
| BWC 201 A06 | 57.6 | 18,642.24 | BW 301 A08 | 103.6 | 24,166.07 |
| BWC 201 A08 | 76.3 | 21,109.58 | BW 301 A10 | 134 | 27,077.49 |
| BWC 201 A10 | 97.4 | 23,515.66 | BW 301 A13 | 171.3 | 30,182.80 |
| BWC 201 A13 | 130 | 26,717.13 | BW 351 A07 | 73.5 | 20,763.52 |
| BWC 201 A17 | 172 | 30,237.27 | BW 351 A18 | 186.5 | 31,338.81 |
| BWT 221 A06 | 59 | 18,841.22 | BWC 351 A07 | 73.3 | 20,738.53 |
| BWT 221 A08 | 77 | 21,194.98 | BW 301 A06 | 78.6 | 21,388.57 |
| BWT 221 A10 | 100 | 23,791.15 |
| Symbol | Value | Symbol | Value |
|---|---|---|---|
| 6000 h [4] (p. 54) | 6 K | ||
| 6 [4] (p. 66) | 0.04 €·kWh−1 | ||
| 85 kg·s−1 | 0.06 €·kWh−1 | ||
| 1000 kg·s−1 | 0.12 €·kWh−1 [26] (p. 2) | ||
| 0.06 [20] (p. 14) | 60 min | ||
| 5 a [27] (p. 5) | 60 min [28] (p. 7) | ||
| 3186.36 €·m−3 [29] (pp. 288–290) | 1 | ||
| 10 kg·s−1 | 0.98 | ||
| 4.182 kJ·kg−1·K−1 [30] (p. 97) | 5 | ||
| 997 kg·m−3 [30] (p. 92) | 8 | ||
| 60 °C | 108 | ||
| 16 °C |
| Name | Parameter | Variation |
|---|---|---|
| 1. Standard case | none | none |
| 2. Demand | 80% , 60% 40% | |
| 80% 60% 40% | ||
| 80% 60% 40% | ||
| 3. Temperature | , | = 5 °C and = 60 °C = 5 °C and = 66 °C = 5 °C and = 75 °C |
| 4. Costs | , , | = 0.04 €·kWh−1 = 0.02 €·kWh−1 = 0.14 €·kWh−1 |
| 5. Storage | = 0 | |
| 6. Preselection algorithm | , | = 15 and = 3 |
| Heat Pump | ||
|---|---|---|
| BWC 351 A07 | 4.39 | 0 |
| BW 351 A07 | 4.29 | 0 |
| BW 351 A18 | 4.27 | 8 |
| BW 301 A10 | 4.25 | 0 |
| BW 301 A08 | 4.08 | 0 |
| Heat Pump | ||
|---|---|---|
| BWC 351 A07 | 4.39 | 2 |
| BW 351 A07 | 4.29 | 0 |
| BW 351 A18 | 4.27 | 6 |
| BW 301 A10 | 4.25 | 0 |
| BW 301 A08 | 4.08 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sporleder, M.; Burkhardt, M.; Kohne, T.; Moog, D.; Weigold, M. Optimum Design and Control of Heat Pumps for Integration into Thermohydraulic Networks. Sustainability 2020, 12, 9421. https://doi.org/10.3390/su12229421
Sporleder M, Burkhardt M, Kohne T, Moog D, Weigold M. Optimum Design and Control of Heat Pumps for Integration into Thermohydraulic Networks. Sustainability. 2020; 12(22):9421. https://doi.org/10.3390/su12229421
Chicago/Turabian StyleSporleder, Maximilian, Max Burkhardt, Thomas Kohne, Daniel Moog, and Matthias Weigold. 2020. "Optimum Design and Control of Heat Pumps for Integration into Thermohydraulic Networks" Sustainability 12, no. 22: 9421. https://doi.org/10.3390/su12229421
APA StyleSporleder, M., Burkhardt, M., Kohne, T., Moog, D., & Weigold, M. (2020). Optimum Design and Control of Heat Pumps for Integration into Thermohydraulic Networks. Sustainability, 12(22), 9421. https://doi.org/10.3390/su12229421





