A Model for Managing Packaging in the Product Life Cycle in the Automotive Industry

Abstract

Due to its many benefits, the automotive industry is increasingly focused on the use of returnable packaging, but the benefits of using it can only be fully realized if the system is properly managed. This study therefore aims to build a model that enables a comparison between different sustainable packaging systems: non-returnable packaging, returnable packaging, and returnable foldable packaging. The applicability of the model was verified in a multinational manufacturing company that is a development supplier in the international automotive industry. The results highlight the main advantages of the model: enabling the comparison between the use of different sustainable packaging systems; when simulating different scenarios, it takes into account several different cost components and ensures a systematic selection of the packaging system in the early phase of product development. The high degree of practicality and usability of the model was also validated by the sensitivity analysis, as the longer the transport distance, the more acceptable the use of non-returnable packaging. In addition, higher demand for the product was correlated with a reduction in the total cost of all three aspects of packaging choice. The model upgrades existing studies and represents a practical decision-making tool for manufacturing companies and the logistics industry. It will contribute to the systematic construction of a packaging management system at an early stage of product development, which will reduce costs in the long run, improve the quality of logistics processes, and ensure an effective sustainable packaging management system.

1. Introduction

Returnable transport items (RTI), such as pallets, trays, crates, or refillable liquid or gas containers/bottles, play an important role in modern logistics. The use of RTIs to transport products down the supply chain can bring a number of benefits, including reduced packaging and waste, better product protection and safety, more efficient handling, better opportunities for outsourcing, combining, and standardization, and lower CO₂ emissions throughout the life of the packaging material [1,2,3]. These are also the reasons why returnable packaging has been widely accepted in the automotive industry’s supply chains, as packaging management is an important issue in automotive parts logistics, especially for an industry facing cost-cutting pressures due to high competition and lower profit margins [4].

Although the automotive industry has been increasingly adopting returnable packaging due to its many benefits, it is clear that the benefits of using RTIs can only be fully realized if the system is properly managed. Mason et al. [5] highlighted the potential problems that may arise in the management of a returnable packaging system, which are related to flow management, higher transport costs, shipment collection, repair, cleaning, storage, and additional investments. Therefore, various mathematical models have been developed in recent years to support the cost optimization of the use of different sustainable packaging systems, which represent the basic direction of research and a key practical tool for logistics management. These models became the basis for optimization programs that were later developed in companies, however, Rybakov [6] points out that attempts to execute optimization models in practice in companies’ logistics systems do not always result in the achievement of certain goals. The discrepancy between the actual results and the specific objectives of optimization programs based on mathematical models is emphasized.

Opportunities for cost model improvements can also be identified based on an analysis of the scientific literature. Most model simulations take into account mainly transport costs, labour costs, maintenance costs (packaging washing, repairing, and cleaning), administration costs, purchase costs, and material-handling costs. However, no model has been found which would account for all these costs at the same time in a simulation. To upgrade the existing research, a model has therefore been developed that addresses several different cost components. This is especially important in the automotive industry, which focuses on cost optimization and the need to estimate all costs in a company’s logistics process [7]. For this reason, several different cost components are examined through the model, with their amounts depending on the choice of each individual packaging system. The choice of a packaging management system is a complex process that requires detailed modelling of various costs. The proposed model addresses them at an early stage of product development, where we must define the method of distribution, the quantity of stocks, the type of packaging, the purchasing of goods, and the internal business processes that support the development and production of the product. Since packaging management is part of this process, the systematic use of the model at an early stage of product development reduces any potential errors that might occur later in the company’s logistics system. The advantage of the model is that by simulating the choice of packaging at the product development stage, all future logistics processes in product distribution (transport method, warehousing method, and other supporting processes) can be defined, which also contributes to a better overview of the company’s logistics. Unlike other models, which only compare non-returnable and returnable packaging systems, the developed model adds returnable foldable packaging to the comparison.

The goal of the study is therefore to upgrade existing studies by developing a model for an optimal choice of packaging throughout the product life cycle, which can be an important decision-making tool at an early stage of logistics management. Improving the quality of information regarding the choice of an appropriate packaging system in the automotive industry will help ensure sustainable environmental and economic development. The applicability of the proposed model was verified in a multinational manufacturing company that is a development supplier in the international automotive industry. Testing was performed on a product selected at random and encompassed its entire life cycle. A comparison between the current situation and the model testing results obtained identifies suggestions for improvements to how packaging choice is optimised in the analysed company. The proposed model complements existing knowledge in the field of packaging management and is characterised by a high degree of practicality and usability. It will contribute to designing a more efficient packaging management system at an early stage of product development, which will reduce overall logistics costs in the long run, improve the quality of business processes, and ensure an effective sustainable packaging management system.

2. Literature Review

Efficient use of returnable packaging contributes to reducing waste, costs, and potential damage during transport, while the use of reusable packaging can help companies achieve economic and environmental benefits [4,8]. These are the reasons that led to returnable packaging gaining wide acceptance in supply chains in the automotive industry as early as thirty years ago. This is followed by various studies addressing the optimization of returnable packaging management in the automotive industry [4,9,10,11,12]. The number of studies on the subject has increased, as Glock [3] writes that research on the RTI supply chain (Returnable Transport Items) is becoming increasingly popular, as the number of publications has grown from an average of 0.56 contributions per year between 1986 and 2010 to an average of 3.16 contributions/year since 2011.

The field split into the following three directions of research: comparing different packaging systems, forecasting RTI returns, and managing container systems. The development of models for comparing different sustainable packaging systems is the most prevalent, as it is aimed at providing the environmental and economic perspectives that companies need most in practice. Mollenkopf et al. [13] developed a simulation model for comparing the performance of two different container systems, namely a single-use system (with recycling) and a reusable container system. The authors modelled the total costs for each system, taking into account aspects such as delivery distance, level of demand, and quantity of goods per container. With the use of regression analysis, they determined that the container cost ratio, the average daily volume of products to be transported, and the delivery distance are the three parameters that influence the relative advantage of an individual packaging management system the most. Cheng and Yang [14] went in a similar direction with their research, developing a model to compare three different container systems, namely disposable containers, recyclable containers, and reusable containers (RTI). Using the method they developed, the authors calculated both optimal container quantities for each system and the minimal costs for operating the systems. Empirical findings suggest that the operational cost benefits of using reusable containers are greater than those of disposable containers.

Duhaime et al. [15] examined the use of reusable containers between Canada Post and its large mailing customers. The authors developed a minimum-cost-flow model and confirmed that Canada Post has enough containers to satisfy demand, and that their regular shortage of containers is due to an inventory imbalance between supply locations and demand locations. Grimes-Casey et al. [16] developed a game-theoretic model designed to help companies in analysing and developing an optimal strategy of choice between disposable bottles and returnable bottles (RTIs). The study highlighted that companies are only motivated to use reusable bottles if customer return rates are high enough, as otherwise the operating costs of the RTI system increase. This, in turn, encourages companies to rely on disposable containers. Levi et al. [17] developed a model that enables a comparison between a one-way paper packaging system and a returnable plastic packaging system, with special emphasis on fruits and vegetables distribution. The results of the study show that both packaging use systems can be acceptable and depend on the simulated scenario (type of product being transported, number of RTI reuses, and transport distances). Menesatti et al. [18] conducted a simulation study on a practical example, where they compared the use of non-returnable and returnable packaging in the transport of flowers. Using the developed model, they found that the use of a reusable packaging system that ensures production with less waste and less environmental pressures is also more economically advantageous. The use of returnable packaging required a larger initial investment, but became less expensive from the second year of the investment and maintained a reasonable cost level, even taking into account all the costs associated with returning the items. Silva et al. [19] developed and tested a returnable packaging model using the example of a Brazilian manufacturer of cylinder heads. During the case study, a returnable packaging system was replaced by a disposable packaging system, resulting in an 18% reduction in material costs, greater protection of exported products, and reduced waste generation with the end customer. In terms of environmental performance, the returnable packaging model has proven to be the best alternative, as it has a lower environmental impact compared to the disposable packaging model. The practice of reverse logistics has shown benefits that contribute to the sustainability of operations from a technical, economic and environmental point of view.

Palsson et al. [9] developed a model that was tested with the Volvo Car Corporation and the Volvo Logistics Corporation. They compared the use of newly developed, one-way packaging with the sustainability of returnable packaging. The model compares the environmental and economic impacts of the two packaging systems in a specific supply chain. In the case study, one-way (non-returnable) packaging caused fewer economic and environmental impacts, thereby indicating the importance for companies to question their packaging systems. Accorsi et al. [20] compared a multi-use system to traditional single-use packaging (e.g., wooden boxes, disposable plastic crates, and cardboard boxes) to quantify the economic returns and environmental impacts of the reusable plastic container (RPC). The authors showed that a number of factors, such as the lifetime of the containers, washing speed, waste treatment, and network geography, can affect the environmental and economic costs of reuse. The paper proposed an original conceptual framework for the integrated design of a food packaging and distribution network. Zhang et al. [4] conducted a study comparing two different modes, i.e., dedicated mode and shared mode, used in packaging management in automotive parts logistics. The authors estimated the costs of transport and the cost of reusable container inventories under different management strategies. The study showed that in shared mode, cost savings have a negative correlation with the number of package categories.

Carrano et al. [21] developed a model for evaluating the impact of three different pallet management strategies, namely single-use expandable pallets, reusable (purchased) pallets, and reusable (leased/pooled) pallets. The environmental impact for each pallet system was measured by calculating the CO₂ footprint, taking into account the entire life cycle of the pallet. The life cycle of the pallet was divided into five phases—extraction of raw materials, production, transport and use, recovery, and disposal at the end of its life cycle. In this case, too, the results of the paper show that none of the pallet management strategies prevails over the others, and that a suitable pallet management strategy should be chosen instead according to the specific requirements of the application. Katephap and Limnararat [22] developed a mathematical model to calculate the total effective cost of packaging for a Thai automotive parts manufacturer. In the study, a switch was made from the currently disposable packaging to the standardized returnable packaging under three reverse logistics arrangements: single-, round-, and multi-trip arrangements. The authors found that the multi-trip reverse logistics arrangement was most operationally and environmentally viable, with the largest total packaging cost reduction and packaging waste reduction of 61% and 68%, relative to the disposable packaging. Meanwhile, the single-trip reverse logistics arrangement was most favourable economically due to its shortest payback period of 0.33 year. Na et al. [8] performed a cost simulation of the use of expendable containers and returnable containers in the automotive industry. The results of the study indicate that a greater initial purchase of returnable packages is desirable for longer operation duration, higher demand variability, and higher lead time variability. However, if operation duration is short and the uncertainty is high, then there may be little benefit in using reusable packages.

Table 1. Review of the literature in the field of models for the comparison of different packaging systems.

Authors	Costs Taken into Account	Num. of Packaging Systems Analysed	Orientation of Research
			Product Logistics Costs	Product Life Cycle
Our proposed model	Transport, warehousing, external warehousing, warehousing equipment, administration, labour, material-handling, packaging, maintenance, purchasing.	3	x	x
Duhaime et al. (2001)	Transport, packaging, material-handling, labour.	1
Mollenkopf et al. (2005)	Transport, packaging, material-handling, labour, purchasing.	2
Cheng & Yang (2005)	Transport, packaging, labour, purchasing, damage costs.	3
Grimes-Casey et al. (2007)	Packaging, purchasing, maintenance.	2
Levi et al. (2011)	Transport (Evaluates environmental issues throughout the life cycle of containers).	2
Menesatti et al. (2012)	Transport, packaging, purchasing, administration, labour, material-handling.	2
Silva et al., (2013)	Transport, packaging, material-handling, purchasing, maintenance.	2
Palsson et al. (2013)	Transport, packaging, material-handling, maintenance, administration.	2
Accorsi et al. (2014)	Transport, warehousing, packaging, labour, material-handling, other costs.	2
Carrano et al. (2015)	Calculating the CO2 footprint of the respective system.	3
Zhang et al. (2015)	Transport, inventory, holding, packaging.	2
Katephap & Limnararat (2017)	Transport, packaging, labour, maintenance.	3
Na et al. (2019)	Transport, material-handling, holding, packaging.	2

summarizes the scientific literature in the field of development of models for the comparison of different sustainable packaging systems. Based on a detailed analysis, it can be concluded that most models take into account several different cost components. Most simulations take into account mainly transport costs, labour costs, maintenance costs (packaging washing, repairing, and cleaning), administration costs, purchase costs, and material-handling costs. However, none of the models can simulate all these costs at the same time when comparing the use of different packaging systems. The proposed model therefore upgrades the existing optimization models, as it takes into account several different cost components. In addition to the above, there are only four models that analyse the use of three different packaging systems, including the proposed model. What represents a significant upgrade of existing research is the fact that the developed model is designed to calculate all logistics costs at an early stage of product development and takes into account the costs throughout the product’s life cycle. This systematic approach highlights the importance of defining packaging management as early as at the product development stage, enabling companies to avoid potential costs that may arise later as a result of the wrong choice of packaging system.

Based on the analysis of the scientific literature, where current research has been verified with the developed model, the following research questions are presented, which will be the subject of verification in the experimental part:

• Does the developed model enable the simultaneous analysis of different packaging systems for the entire life cycle of an individual product?
• Which type of packaging system use results in the lowest costs and which one in the highest?
• Is the model able to simultaneously analyse different cost components and which cost components have the greatest impact on the costs of the packaging system?
• How does changing the input data affect the behaviour of the model in selecting the most cost-optimal packaging system?

3. Model Formulation

The applicability of the model was verified in a multinational manufacturing company that is a development supplier in the international automotive industry. Testing of the optimal packaging cost choice model was performed on a randomly selected product for its entire life cycle. The data for model verification were obtained from the controlling department, which provided information on the value of individual cost items, and from the logistics department, which provided data on individual logistics activities and on the value of logistics items. To facilitate the review of the data, the model was structured and developed in Excel, where data entry was enabled. Upon entering the data, the user of the model is given an overview of the most optimal choice of packaging system for a product’s life cycle, as all the variables are interconnected. Figure 1 illustrates the process of data entry into the model. Data entry begins with data for the product for which the optimal cost choice of packaging will be defined. It continues with entering data on various types of packaging (non-returnable, returnable, and returnable foldable) and data on other logistics processes that are part of the proposed model.

The authors define a disposable packaging system as packaging that is not returned to the sender, such as single-use expandable pallets [21], expendable container [8], disposable bottles [16]. RTI is defined as a special type of reusable packaging materials such as pallets, trays, boxes, or crates [3]. The same definition of reusable packaging is also used by The Reusable Packaging Association [23]. The terms ‘reusable packaging’ and ‘returnable packaging’ are used both in theory and in practice [8,23]. In the developed model, we used the term non-returnable packaging for the disposable packaging system. The first simulation was conducted with the use of the EPAL (European Pallet Association) wooden pallet currently used in the tested company. The terms ‘returnable packaging’ and ‘returnable foldable packaging’ were used in the model under the packaging system with reusable containers. The second simulation was made for the use of Gitterbox returnable wire mesh containers, which is the most commonly used packaging in the automotive industry as well as the most suitable. A third simulation was performed using foldable wire mesh containers.

A general Total Choice of Packaging (TCP) model is composed as follows:

$$\mathrm{TCP}={{\displaystyle \sum }}_{i=1}^{n}Ci,$$

(1)

where i is the cost component; n is the number of individual logistics costs components; and Ci is the cost per the selected individual logistics cost component. The model consists of three main logistics cost components, where:

• $C_1$—packaging cost
• $C_2$—warehousing costs
• $C_3$—transport costs

4. Model Formulation

Based on the data given in Figure 1, testing was performed next. To make it easier to understand the model, abbreviations are used for each variable. The basic formula of the model consists of calculations of total packaging costs, warehousing costs, and transport costs, where:

TCP = PC(R,F) + WC(R,F) + TC(R,F).

(2)

4.1. Packaging Costs

Three cost aspects of packaging use are calculated. If returnable packaging (R) is marked with NO and foldable (F) with NO, the cost of non-returnable packaging per piece (NRPC) is calculated. If returnable packaging (R) is marked with YES and foldable (F) with NO, the cost of returnable packaging per piece (RPC) is calculated. If returnable packaging (R) is marked with YES and foldable (F) with YES, the cost of returnable foldable packaging per piece (RFPC) is calculated.

$$\mathrm{PC}\left(\mathrm{R},\mathrm{F}\right)\left\{\begin{array}{c}NRPC;R=NO;F=NO\\ \\ RPC;R=YES;F=NO\\ \\ RFPC;R=YES;F=YES\end{array}\right.$$

(3)

The calculation of the NRPC starts with the definition of the average quantity required for the order (AQO), where the average annual need of products (ANP) is divided by the number of shipments per year (NSY).

$$\mathrm{AQO}=\frac{\mathrm{ANP}}{\mathrm{NSY}}$$

(4)

The calculation continues with the definition of the number of packaging units required for the execution of the order (PU), where the average quantity required for the order (AQO) is divided by the number of products in the packaging unit. Where ceil(x) is a function that rounds to the smallest integer not less than x.

$$\mathrm{PU}=\mathrm{ceil}(\frac{\mathrm{AQO}}{\mathrm{NP}})$$

(5)

To determine the cost of using non-returnable packaging (NRPC), the resulting number is multiplied by the packaging cost per pallet (PCP) and then divided by the average quantity required for the order (AQO). The packaging cost per pallet (PCP) is the sum of all the material required to assemble one non-returnable packaging unit. The following material was used: metal staples, packaging tape, cardboard divider, wooden pallet, label, and other material.

$$\mathrm{PCP}={\mathrm{PM}}^1(\mathrm{num}.\mathrm{pcs}\times \mathsf{€}/\mathrm{pcs})+\dots {\mathrm{PM}}^{\mathrm{n}}(\mathrm{num}.\mathrm{pcs}.\times \mathsf{€}/\mathrm{pcs})$$

(6)

$$\mathrm{NRPC}=\frac{\mathrm{PCP}\times \mathrm{PU}}{\mathrm{AQO}}$$

(7)

The calculation is as follows:

$$\mathrm{AQO}=\frac{151,200\mathrm{pcs}}{250}=604.8\mathrm{pcs},$$

(8)

$$\mathrm{PU}=\frac{604.8\mathrm{pcs}}{196\mathrm{pcs}}=4\mathrm{units}\mathrm{for}\mathrm{order},$$

(9)

$$\mathrm{PCP}={\mathrm{PM}}^1(\mathrm{num}.\mathrm{pcs}\times \mathsf{€}/\mathrm{pcs})+\dots {\mathrm{PM}}^{\mathrm{n}}(\mathrm{num}.\mathrm{pcs}.\times \mathsf{€}/\mathrm{pcs}),$$

(10)

$$\mathrm{NRPC}=\frac{\mathrm{€}15.328\times 4}{604.8\mathrm{pcs}}=\mathrm{€}0.1013\mathrm{pcs}.$$

(11)

The cost of non-returnable packaging is €0.1013/pcs. The cost of returnable packaging is calculated in the next step. The amount of packaging required in circulation (PRC), which is the sum of the anticipated days of product stock, must be determined first: in the company (PS—packaging stock), in transport (PT), and in manufacturing (PM). The sum of the days is multiplied by the average quantity of products needed to execute the order (AQO) and then divided by the number of pieces in the packaging unit (NP). The number of empty packaging at the customer (EPC) is then added to the result. Where ceil(x) is a function that rounds to the smallest integer not less than x.

$$\mathrm{PRC}=\mathrm{ceil}(\frac{\mathrm{PS}\times \mathrm{AQO}+\mathrm{PT}\times \mathrm{AQO}+\mathrm{PM}\times \mathrm{AQO}}{\mathrm{NP}}+\mathrm{EPC})$$

(12)

Once the number of returnable packaging in circulation (PRC) has been determined, the total value of returnable packaging (VRP) is calculated, therefore the value of a single returnable packaging unit or packaging unit purchase value (PUPV) must be taken into account.

VRP = PUPV ∗ PRC

(13)

Since the DIN (Deutsches Institut für Normung) standard [24] requires that returnable packaging be changed every six years, the following formula is used to calculate the cost of using returnable packaging for the product life cycle—VRPL. The total value of the total returnable packaging (VRP) is divided by the number of years when returnable packaging is replaced (replacement of packaging—RP). The value obtained is multiplied by the number of years of the product life cycle (PLC).

$$\mathrm{VRPL}=\frac{\mathrm{VRP}}{\mathrm{RP}}\times \mathrm{PLC}$$

(14)

In the final calculation of the cost of returnable packaging per piece (RPC), the value of the total quantity of returnable packaging for the product life cycle (VRPL) is divided by the number of all the pieces in the product life cycle (PPLC).

$$\mathrm{RPC}=\frac{\mathrm{VRPL}}{\mathrm{PPLC}}$$

(15)

The calculation is as follows:

$$\mathrm{PRC}=\mathrm{ceil}(\frac{5\times 604.8+1\times 604.8+2\times 604.8}{196}+5)=30\mathrm{units},$$

(16)

VRP = 100.00 €/unit ∗ 30 units = €3000.00,

(17)

$$\mathrm{VRPL}=\frac{3000.00}{6}\times 6=\mathrm{€}3000.00,$$

(18)

$$\mathrm{RPC}=\frac{3000.00\mathrm{€}}{907,200}=\mathrm{€}0.0033\mathrm{pcs}.$$

(19)

The cost of using returnable packaging (RPC) is €0.0033 pcs. When calculating the cost of returnable foldable packaging (RFPC), the PRC (Formula (12)) is also calculated first. The VRP for foldable packaging is calculated next (Formula (13)). According to the DIN standard [24], returnable foldable packaging must be changed every three years, which is taken into account when calculating the VRPL (Formula (14)). This result is then multiplied by the index of loading (IL), which is calculated by dividing the number of packaging required to complete the order (PU) by the number of packaging on vehicle (PV).

$$\mathrm{IL}=\frac{\mathrm{PU}}{\mathrm{PV}}$$

(20)

In the final calculation of the cost of returnable foldable packaging per piece (RPCC), the value of the total quantity of returnable foldable packaging for the product life cycle (VRPL) is divided by the number of all the pieces in the product life cycle (PPLC) and multiplied by the index of loading (IL).

$$\mathrm{RFPC}=\frac{\mathrm{VRPL}}{\mathrm{PPLC}}\times \mathrm{IL}$$

(21)

The calculation is as follows:

$$\mathrm{PRC}=\mathrm{ceil}(\frac{5\times 604.8+1\times 604.8+2\times 604.8}{196}+195)=220\mathrm{units},$$

(22)

VRP = 250.00 €/unit ∗ 220 units = €55,000.00,

(23)

$$\mathrm{VRPL}=\frac{55,000.00}{3}\times 6=\mathrm{€}110,000.00,$$

(24)

$$\mathrm{IL}=\frac{4}{66}=0.06,$$

(25)

$$\mathrm{RFPC}=\frac{110,000.00}{907,200}\times 0.06=\mathrm{€}0.0072\mathrm{pcs}.$$

(26)

The cost of using returnable foldable packaging (RFPC) is €0.0072 pcs.

4.2. Warehousing Costs

The use of three types of packaging affects the calculation of the three different procedures for calculating warehousing costs. If returnable packaging (R) is marked with NO and foldable (F) with NO, the warehousing costs of non-returnable packaging (WCNR) are calculated. If returnable packaging (R) is marked with YES, and foldable (F) with NO, the warehousing costs of returnable packaging (WCR) are calculated. If returnable packaging (R) is marked with YES and foldable (F) with YES, the warehousing costs of foldable returnable packaging (WCFR) are calculated.

$$\mathrm{WC}\left(\mathrm{R},\mathrm{F}\right)\left\{\begin{array}{c}WCNR;R=NO;F=NO\\ \\ WCR;R=YES;F=NO\\ \\ WCFR;R=YES;F=YES\end{array}\right.$$

(27)

Warehousing costs for all three types of packaging use are calculated using the same procedure. Warehousing costs per piece (WC) consist of warehouse equipment costs per piece (WECP), warehouse staff costs per piece (WSCP), and external warehousing costs per piece (EWC). The calculation begins by defining the average value of the equipment owned by the company (AEV) and the average value of rented equipment (AER).

$$\mathrm{AEV}=\frac{\mathrm{TWEV}}{\mathrm{TWE}}$$

(28)

$$\mathrm{AER}=\frac{\mathrm{TWERV}}{\mathrm{TWER}}$$

(29)

The average value of the equipment (AEV) is divided by the amortization period (AP) and the number of monthly working hours (MWH). The average value of rented equipment (AER) is divided by the number of monthly working hours (MWH). With the sum of both results, the value of the warehouse equipment costs per hour (WEC) is obtained.

$$\mathrm{WEC}=\frac{\mathrm{AEV}}{\mathrm{AP}\times \mathrm{MWH}}+\frac{\mathrm{AER}}{\mathrm{MWH}}$$

(30)

Prior to calculating the cost of warehouse equipment per piece (WECP), the processed packaging units per hour (PPH) is calculated, where the number of minutes in one hour is divided by the sum of the preparation and packing (PP), the cleaning time per packaging unit (cleaning—packaging—CP) and the stacking on return of packaging time (S), where ceil(x) is a function that rounds to the smallest integer not less than x.

$$\mathrm{PPH}=\mathrm{ceil}(\frac{60}{\mathrm{PP}+\mathrm{CP}+\mathrm{S}})$$

(31)

The number of packaging units required for the order (PU), which is calculated using formula (5), is divided by the average processed packaging per hour (PPH). The warehouse equipment costs per hour (WEC) are divided by the average quantity of products required for the order (AQO). The two results obtained are multiplied by each other.

$$\mathrm{WECP}=\frac{\mathrm{PU}}{\mathrm{PPH}}\times \frac{\mathrm{WEC}}{\mathrm{AQO}}$$

(32)

When calculating the warehouse staff costs per hour (WSCH), the total personal incomes per month (TPIM) and the number of monthly working hours (MWH) are taken into account.

$$\mathrm{WSCH}=\frac{\mathrm{TPIM}}{\mathrm{MWH}}$$

(33)

When calculating the warehouse staff costs per piece (WSCP), the following is taken into account: the number of packaging units required for the order (PU), which is calculated using formula (5), is divided by the average processed packaging per hour (PPH). The warehouse staff costs per hour (WSCH) value is divided by the average quantity of products required for the order (AQO), after which both results are multiplied.

$$\mathrm{WSCP}=\frac{\mathrm{PU}}{\mathrm{PPH}}\times \frac{\mathrm{WSCH}}{\mathrm{AQO}}$$

(34)

When using external warehousing, the cost of external warehousing per pallet (EWP) is multiplied by the number of packaging units required for the order (PU), which is calculated using formula (5) and divided by the average quantity of products required for the order (AQO).

$$\mathrm{EWC}=\frac{\mathrm{EWP}\times \mathrm{PU}}{\mathrm{AQO}}$$

(35)

Warehousing costs per piece (WC) for the use of each type of packaging (WCNR, WCR, and WCFR) are the sum of the results of the warehouse equipment costs per piece (WECP), the warehouse staff costs per piece (WSCP), and the external warehousing costs per piece (EWC).

WC (WCNR, WCR, WCFR) = WECP + WSCP + EWC

(36)

Warehousing costs of non-returnable packaging (WCNR) are calculated using the following formula.

$$\mathrm{AEV}=\frac{\mathrm{€}60,000.00}{4}=\mathrm{€}\mathrm{15,000.00}$$

(37)

$$\mathrm{AER}=\frac{\mathrm{€}1500.00}{2}=\mathrm{€}750.00$$

(38)

$$\mathrm{WEC}=\frac{\mathrm{€}15,000.00}{5\times 160}+\frac{\mathrm{€}750.00}{160}=\mathrm{€}23.44$$

(39)

$$\mathrm{PPH}=\mathrm{ceil}(\frac{60}{7})=9\mathrm{units}$$

(40)

$$\mathrm{WECP}=\frac{4}{9}\times \frac{\mathrm{€}23.44}{604.8}=\mathrm{€}0.017\mathrm{pcs}$$

(41)

$$\mathrm{WSCH}=\frac{\mathrm{€}\mathrm{19,085.00}}{160}=\mathrm{€}119.28\mathrm{h}$$

(42)

$$\mathrm{WSCP}=\frac{4}{9}\times \frac{\mathrm{€}119.28\mathrm{h}}{604.8}=\mathrm{€}0.0867\mathrm{pcs}$$

(43)

WCNR = €0.017 pcs + €0.0867 pcs = €0.1037 pcs

(44)

Warehousing costs of non-returnable packaging (WCNR) amount to €0.1037 pcs. In the calculation of warehousing costs of returnable packaging (WCR), the value of WEC is the same as in the calculation of WCNR (the result of formula (39)), which is €23.44. However, PPH and WECP must be calculated:

$$\mathrm{PPH}=\mathrm{ceil}(\frac{60}{3+0.5+0.5})=15\mathrm{units},$$

(45)

$$\mathrm{WECP}=\frac{4}{15}\times \frac{\mathrm{€}23.44}{604.8}=\mathrm{€}0.0103\mathrm{pcs}.$$

(46)

The WSCH value is the same as in the calculation of WCNR (result of formula (42)), which is €119.28h. The PPH for the calculation of warehousing costs of returnable packaging (WCR) is 15 units (formula (45)), which requires the calculation of WSCP:

$$\mathrm{WSCP}=\frac{4}{15}\times \frac{\mathrm{€}119.28\mathrm{h}}{604.8}=\mathrm{€}0.0525\mathrm{pcs},$$

(47)

WCR = €0.0103 pcs + €0.0525 pcs = €0.0628 pcs

(48)

Warehousing costs of returnable packaging (WCR) amount to €0.0628 pcs. In the calculation of warehousing costs of returnable foldable packaging (WCRF), the value of WEC is the same as in the calculation of WCNR (the result of formula (39)), which is €23.44. However, PPH and WECP must be calculated:

$$\mathrm{PPH}=\mathrm{ceil}(\frac{60}{3+0.5+3})=10\mathrm{units},$$

(49)

$$\mathrm{WECP}=\frac{4}{10}\times \frac{\mathrm{€}23.44}{604.8}=\mathrm{€}0.0155\mathrm{pcs}.$$

(50)

The WSCH value is the same as in the calculation of WCNR (result of formula (42)), which is €119.28h. The PPH for the calculation of warehousing costs of returnable foldable packaging (WCRF) is 10 units (formula (49)), which requires the calculation of WSCP:

$$\mathrm{WSCP}=\frac{4}{10}\times \frac{\mathrm{€}119.28\mathrm{h}}{604.8}=\mathrm{€}0.0788\mathrm{pcs},$$

(51)

WCRF = €0.0155 pcs + €0.0788 pcs = €0.0943 pcs.

(52)

Warehousing costs of returnable foldable packaging (WCRF) are €0.0943 pcs.

4.3. Transport Costs

The use of three types of packaging affects the calculation of the three procedures for defining transport costs. If returnable packaging (R) is marked with NO and foldable (F) with NO in the model, transport costs of non-returnable packaging (TCNR) are calculated. If returnable packaging (R) is marked with YES, and foldable (F) with NO, the transport costs of returnable packaging (TCR) are calculated. If returnable packaging (R) is marked with YES and foldable (F) with YES, the transport costs of foldable returnable packaging (TCRF) are calculated.

$$\mathrm{TC}\left(\mathrm{R},\mathrm{F}\right)\left\{\begin{array}{c}TCNR;R=NO;F=NO\\ \\ TCR;R=YES;F=NO\\ \\ TCRF;R=YES;F=YES\end{array}\right.$$

(53)

The same procedure is used to calculate transport costs for the three types of packaging use. First, the value of transport for the product life cycle (TV) is calculated. The monthly frequency of one-way journeys (MFO) is multiplied by the price of one-way journeys (OP). The monthly return trip frequency (MFR) is multiplied by the return trip price (PR). The value obtained is multiplied by twelve months and by the number of years of the product life cycle (PLC).

$$\mathrm{TV}=\left(\mathrm{MFO}\times \mathrm{OP}+\mathrm{MFR}\times \mathrm{PR}\right)\times 12 \mathrm{months}\times \mathrm{PLC}$$

(54)

This result is then multiplied by the index of loading (IL), which is calculated by dividing the number of packaging required to complete the order (PU) by the number of packaging on vehicle (PV).

$$\mathrm{IL}=\frac{\mathrm{PU}}{\mathrm{PV}}$$

(55)

In the calculation of the final transport cost (TCNR), the transport value for the product life cycle (TV) is multiplied by the index of loading (IL) and then divided by the number of all the pieces in the product life cycle (PPLC).

$$\mathrm{TCNR}=\frac{\mathrm{TV}\times \mathrm{IL}}{\mathrm{PPLC}}$$

(56)

The calculation of transport costs for non-returnable packaging (TCNR) is as follows:

$$\mathrm{TV}=\left(20\times \mathrm{€}1100.00+0\times \mathrm{€}1100.00\right)\times 12\times 6=\mathrm{€}1,584,000.00,$$

(57)

$$\mathrm{IL}=\frac{4}{52}=0.0769,$$

(58)

$$\mathrm{TCNR}=\frac{\mathrm{€}1,584,000.00\times 0.0769}{907,200}=\mathrm{€}0.1342\mathrm{pcs}.$$

(59)

The transport cost of non-returnable packaging (TCNR) is €0.1342 pcs. The transport cost of returnable packaging (TCR) is calculated in the next step:

$$\mathrm{TV}=\left(20\times \mathrm{€}1100.00+20\times \mathrm{€}1100.00\right)\times 12\times 6=\mathrm{€}3,168,000.00,$$

(60)

$$\mathrm{IL}=\frac{4}{66}=0.0606,$$

(61)

$$\mathrm{TCR}=\frac{\mathrm{€}3,168,000.00\times 0.0606}{907,200}=\mathrm{€}0.2116\mathrm{pcs}.$$

(62)

The transport cost of returnable packaging (TCR) is €0.2116 pcs. The transport cost of returnable foldable packaging (TCRF) is then calculated as follows:

$$\mathrm{TV}=\left(20\times \mathrm{€}1100.00+6\times \mathrm{€}1100.00\right)\times 12\times 6=\mathrm{€}2,059,200.00,$$

(63)

$$\mathrm{IL}=\frac{4}{66}=0.0606,$$

(64)

$$\mathrm{TCRF}=\frac{\mathrm{€}2,059,200.00\times 0.0606}{907,200}=\mathrm{€}0.1375\mathrm{pcs}.$$

(65)

The transport cost of returnable foldable packaging (TCRF) is €0.1375 pcs.

4.4. Comparison of the Results of Model Testing and Sensitivity Analysis

A comparison of the results of model testing shows that returnable foldable packaging is the most cost-optimal, as the total cost in the product life cycle is €0.2390 pcs (

Table 2. Comparison of the Results of Model Testing.

	Packaging Costs	Warehousing Costs	Transport Costs	Total
Nonreturnable packaging	€0.1013	€0.1037	€0.1342	€0.3392
Returnable packaging	€0.0033	€0.0628	€0.2116	€0.2777
Returnable foldable packaging	€0.0072	€0.0943	€0.1375	€0.2390

). The use of returnable packaging (€0.2777 pcs) is closely behind, while the least cost-effective is the use of non-returnable packaging (€0.3392 pcs), which is the type of packaging currently used in the tested company.

Figure 2 shows the changes in individual cost items according to the choice of packaging. Packaging costs are highest for non-returnable packaging and lowest for returnable packaging. The same applies to the impact of the choice of use of each type of packaging on the cost of warehousing, which is the lowest when returnable packaging is used. The cost picture changes significantly in transport costs, as these are highest when using returnable packaging. Transport costs are lowest when non-returnable packaging is used.

Sensitivity analysis was performed to examine the parameters that may affect the management of the proposed model. Our intention was to gain certain knowledge about the behaviour of the model, which will help decision-makers in the concrete application of the model in practice. The company where the proposed model was tested uses non-returnable packaging. The results showed that this is the least cost-effective solution. Based on the observation of Na et al. [8], who pointed out that there are trade-offs between returnable packaging and non-returnable packaging, the impact of the change in the transport price on the final cost of choosing a particular type of packaging was tested. The reason behind this, as highlighted by Na et al. [8], is that when the delivery distance is longer and therefore the transport price is higher, the use of non-returnable packaging generally represents an advantage over the use of returnable packaging. This is due to the high transport costs of return transport of empty containers. The results of the sensitivity analysis in Figure 3 show that the longer the transport distance and thus the price, the more acceptable the use of non-returnable packaging. In this case, the use of returnable packaging would be the least rational solution. However, the fact remains that the use of returnable foldable packaging is still the most cost-optimal aspect of packaging management.

Sensitivity analysis continued with the analysis of the behaviour of the model as the demand for the product increases. Figure 4 shows that if the demand for a product increases by 30%, the total costs of all three aspects of packaging choice are reduced. Returnable foldable packaging costs decrease by 3.86%, returnable packaging costs decrease by 4.28%, and non-returnable packaging costs decrease by 3.98%.

5. Discussion

Testing of the model was performed on a randomly selected product for its entire life cycle and confirmed that the model allows simultaneous calculation of the use of the non-returnable packaging system, the returnable packaging system, and the returnable foldable packaging system. This answered the first research question and confirmed the results of the literature analysis, as there are only four models that analyse the use of three different packaging systems, besides the developed model. The second research question aimed to determine which type of packaging system results in the lowest costs and which one in the highest. The results showed that the use of returnable foldable packaging is the most optimal choice for the company. The company currently uses a non-returnable packaging system for the randomly selected product, which is 22.14% more expensive than a returnable packaging system and as much as 42% more expensive than a returnable foldable packaging system. This answered the second research question. The results of the answer to this question are consistent with the global trend of replacing disposable packaging with returnable packaging, where, as highlighted by Zhang [4], the advantages generally exceed the drawbacks. It is emphasized that the use of returnable packaging, in addition to reducing logistics costs, reduces transport damage, improves productivity, and enhances the cleanliness of the assembly line [10]. The results are consistent with studies conducted for the automotive industry, where Cheng and Yang [14] found that using reusable containers has greater operational cost benefits than using disposable containers by testing a model at Toyota. Silva et al. [19] also replaced a disposable packaging system with a returnable packaging system, thereby achieving an 18% reduction in material costs, greater protection of exported products, and reduced waste generation with the end customer.

The third research question focused on determining whether the model allows the simultaneous analysis of different cost components and which of the components has the greatest impact on the costs of the packaging system. It was determined that the model addresses several different cost components. It takes into account the costs of packaging, within which the costs of materials and packaging for non-returnable packaging, the costs of purchasing returnable packaging, and the costs of purchasing returnable foldable packaging are calculated. Warehousing costs include warehouse equipment costs, warehouse staff costs, external warehousing costs, preparation and packaging costs, packaging cleaning costs, and stacking costs. Transport costs include the price of one-way journeys and the return trip price. The analysis revealed that transport costs represent the cost component with the strongest impact on the selection of an individual packaging system, as their share when non-returnable packaging is used is 39.6% (packaging costs 29.8%; warehousing costs 30.5%); when returnable packaging is used, their share is 76.2% (packaging costs 1.2%; warehousing costs 22.6%); and when returnable foldable packaging is used, their share is 57.6% (packaging costs 3.0%; warehousing costs 39.4%). This provided a clear answer to the third research question.

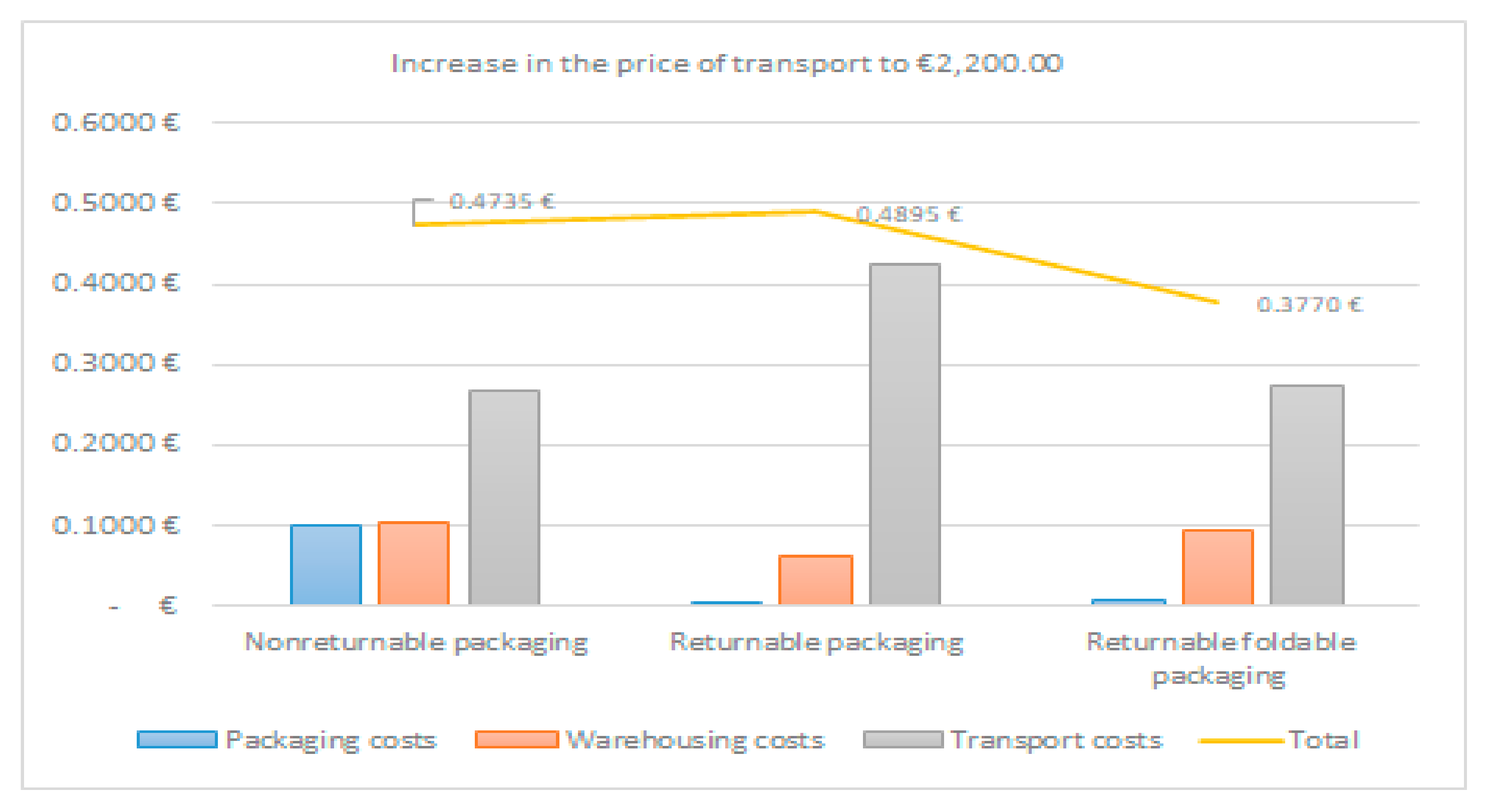
The fourth research question was a continuation of the third, as it aimed to determine how changing the input data affects the behaviour of the model in selecting the most cost-optimal packaging system. For this purpose, a sensitivity analysis was performed, as the results of the third research question confirmed that transport costs have the strongest impact on the selection of an individual packaging system. The results of the sensitivity analysis show that the longer the transport distance and thus the price, the more acceptable the use of non-returnable packaging. In this case, the use of returnable packaging would be the least rational solution. This answered the fourth research question and confirmed the claims of previous studies [4,8,25], which came to the same conclusions. Despite the fact that the use of returnable foldable packaging is still the most cost-optimal aspect of packaging management, the cost ratio between non-returnable and returnable foldable packaging drastically decreased from 42% to 25.36% in favour of non-returnable packaging in this simulation.

5.1. Contribution to Theory and Practice

The innovativeness of the results of the study concerns the following theoretical and practical areas of packaging management.

Analysis of different sustainable packaging systems: Glock [3] points out that the benefits of using RTIs can only be fully realized if the system is properly managed. This was also the basic purpose behind building the model, as it enables a comparison between the use of different sustainable packaging systems. Unlike other studies conducted in the automotive industry [9,14,19], the results of the model do not exclusively favour one type of packaging over another. As reported by Mollenkopf et al. [13], Grimes-Casey et al. [16], Levi et al. [17], and Carrano et al. [21], both packaging systems can be acceptable, depending on the simulated scenario. This was confirmed by a sensitivity analysis, which indicated that the choice of packaging system depends on the specific circumstances from practice and the specific requirements of the business process. The model therefore represents an important tool for decision-makers in the concrete application of the model in practice and the selection of the most optimal packaging system.

Cost model optimization: Most model simulations take into account mainly transport costs, labour costs, maintenance costs (packaging washing, repairing, and cleaning), administration costs, purchase costs, and material-handling costs. Literature analysis showed that none of the existing models can simulate all these costs at the same time when comparing the use of different packaging systems. The model therefore upgrades existing studies by providing wider coverage of individual logistics processes, as it takes into account several different cost components when simulating different scenarios. This also improves the quality of information on the selection of a suitable packaging system.

Improving the management of sustainable packaging systems: To ensure better packaging system management, planning has to start as early as at the product development stage, as this is also when future logistics processes and costs related to the product (mode of transport, warehousing method, and other support processes) are defined. Several authors [7,26] point out that such a systematic approach is especially important in the automotive industry, which focuses on cost optimization and the need to estimate all costs in a company’s logistics process. The proposed model addresses these costs at an early stage of product development since packaging management is also part of this process. The model therefore improves the management of packaging in practice, as the systematic use of the model in the initial stage of product development can reduce any errors and costs that could later occur in the company’s logistics system as a result of the wrong choice of packaging. The results of testing the proposed model provide theoretical grounds for the need for a systematisation of the choice of packaging in the initial phase of logistics management, as opposed to when the system is already operational. This is also the first study to use an optimisation model to illustrate the impact of choosing a particular packaging system on the cost of an individual product. The presented approach to packaging management therefore represents a novelty in the field that is the focus of this study. It will contribute to designing a more efficient packaging management system at an early stage of product development, which will reduce overall logistics costs in the long run, improve the quality of business processes and ensure an effective sustainable packaging management system.

The research synthesizes and analyses the existing literature in the field of developing models for choosing the optimal packaging management system, which represents an important framework for future empirical studies in the logistics industry and in the field of ensuring sustainable development in supply chains.

5.2. Limitations and Recommendations for Future Studies

The developed model, like most models, is focused on the cost comparison of the use of different packaging systems. Although it does introduce innovative solutions for packaging management both in theory and in practice, it has certain limitations, as it does not compare all the environmental impacts of the choice of individual packaging systems. Glock [27] specifically points out that, from an environmental point of view, the fact that RTIs need to be returned, possibly over long distances, and the specific characteristics of the materials needed to manufacture them may lead to situations where one-way packaging materials could have an advantage over RTIs, especially from the point of view of reducing the impact of the supply chain on the environment. However, as the RTI system is widely accepted globally and its use provides many benefits (also in terms of environmental perspectives), future efforts should definitely focus on the development of a model that would evaluate an individual packaging system from both an economic and environmental point of view. There is only one study [9] that has attempted to compare the environmental and economic impacts of two packaging systems in a specific supply chain but it failed to focus extensively on the cost aspects of the choice.

The second limitation stems from the fact that testing was performed for a randomly selected product only. It is therefore necessary to examine the possibilities of integrating the model into larger IT software solutions within the company, for companies that produce several different products.

The third limitation stems from the fact that the proposed model does not take into account all aspects of the end-of-life phase of the analysed packaging scenarios and uncertainties regarding the durability of packaging.

6. Conclusions

The study represents one of the first contributions that examine the field of packaging systems management for the product life cycle, during its development phase. Testing the applicability of the proposed model in a multinational manufacturing company that is a development supplier in the international automotive industry enabled a comparison between different sustainable packaging systems, in order to select the most optimal one. The answers to the research questions have confirmed the results of the analysis of the scientific literature, highlighting the differences between current research and the developed model. The model therefore upgrades existing studies by providing a wider coverage of individual logistics processes, as it takes into account several different cost components when simulating different scenarios. Unlike other studies, it provides a systematic choice of packaging system in the initial phase of product development. This also improves the quality of information on the selection of a suitable packaging system. The high level of practicality and usability of the model was also validated by the sensitivity analysis, as the longer the transport distance, and thus the price, the more acceptable the use of non-returnable packaging. In addition, higher demand for the product was correlated with a reduction in the total cost of all three aspects of packaging choice.

The model upgrades existing studies and represents a practical decision-making tool for the logistics industry. It will contribute a more efficient design of the packaging management system at an early stage of product development, which will reduce costs in the long run, improve the quality of logistics processes, and ensure an effective sustainable packaging management system.

However, the model does not compare all the environmental impacts of the choice of individual packaging systems, which is why it is important for future efforts to focus on the development of a model that would evaluate an individual packaging system from both an economic and environmental point of view. A new methodology was presented on a randomly selected product in an international company operating in the automotive industry. Therefore, there is a need for additional empirical verification in various other organisations and sectors.