Coordinated Voltage Regulation Methods in Active Distribution Networks with Soft Open Points
Abstract
1. Introduction
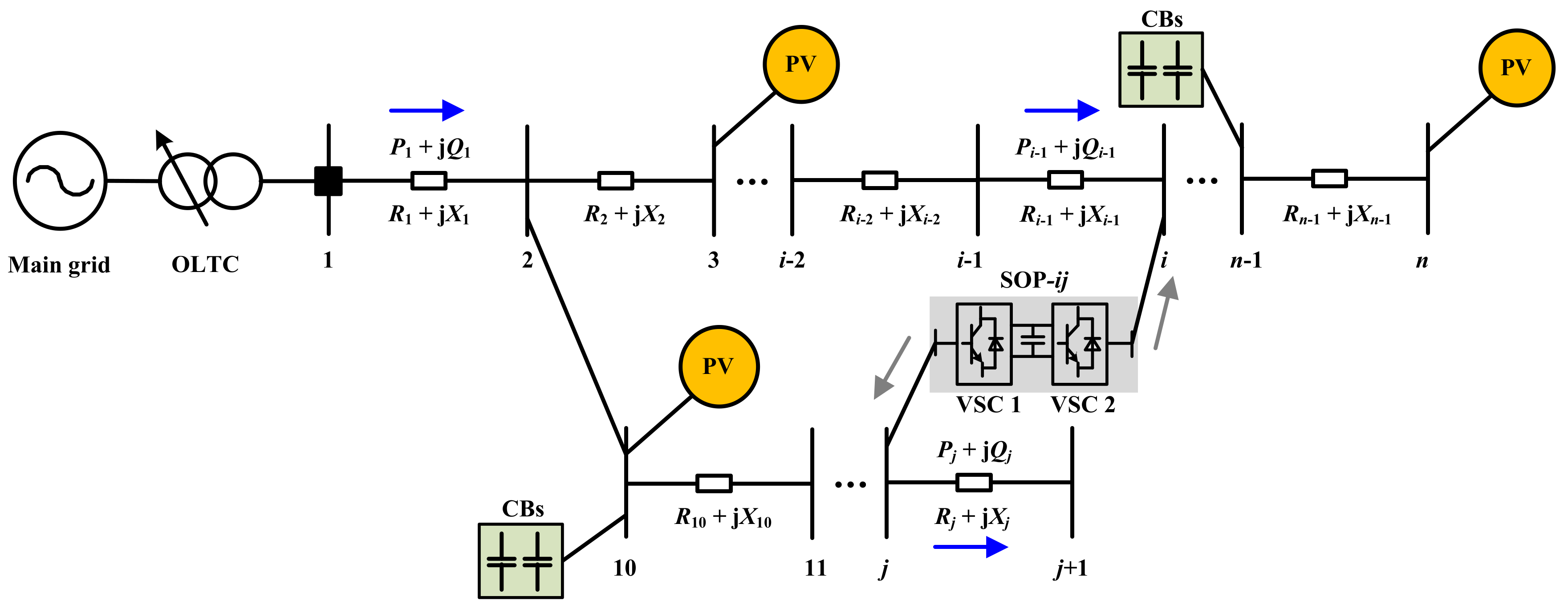
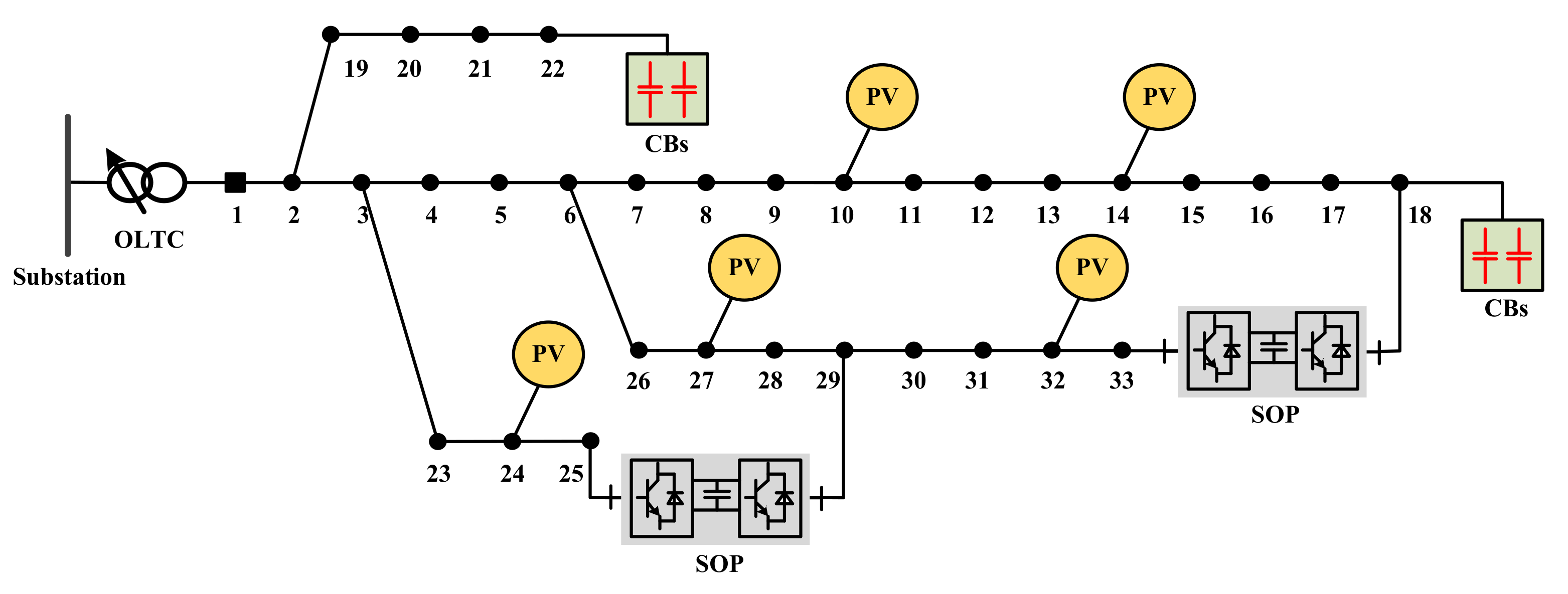
2. System Description
3. Coordinated Voltage Regulation Methods
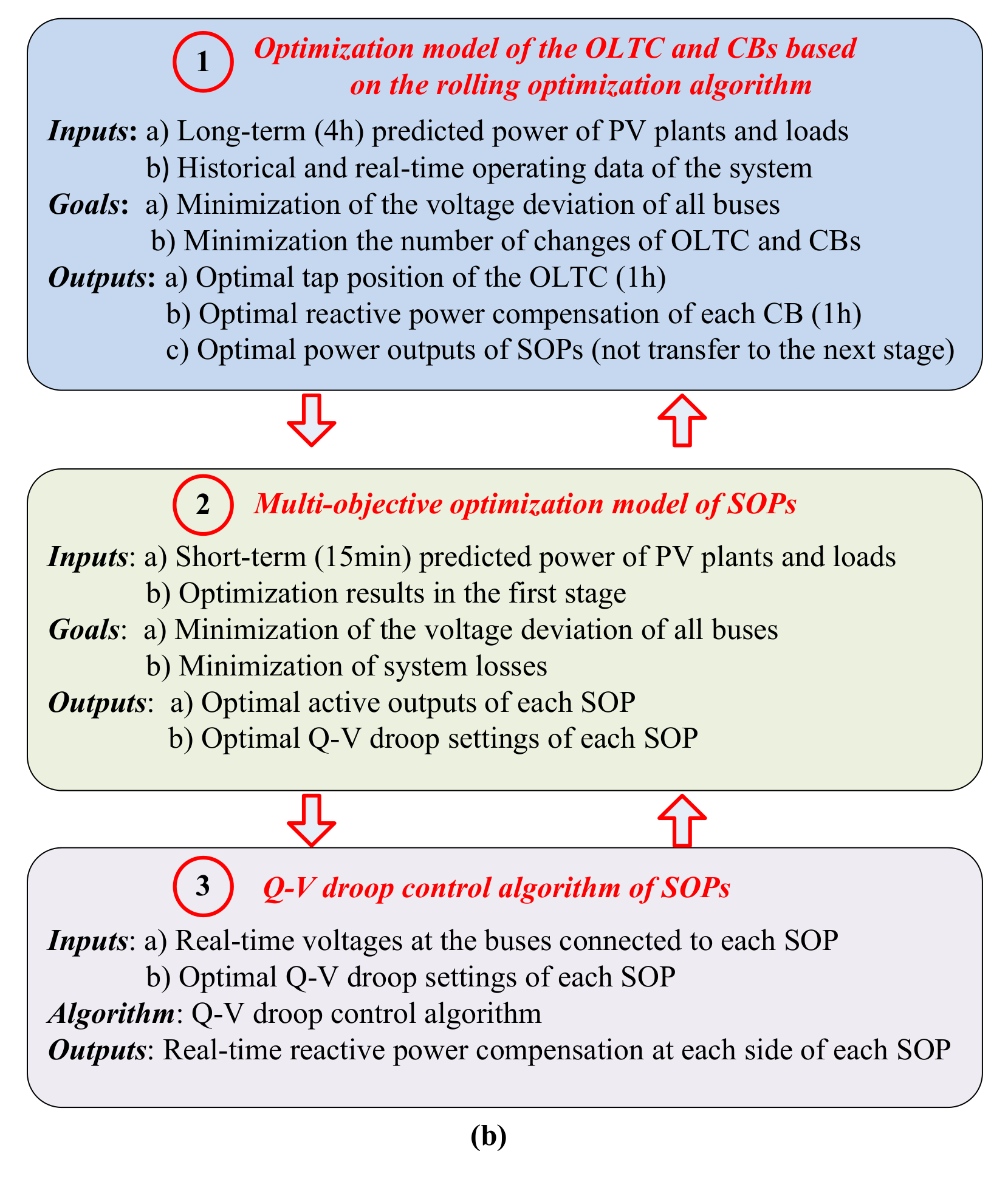
3.1. Overall Idea of the Proposed Voltage Regulation Methods
3.1.1. First Stage (Long-Term Optimization)
3.1.2. Second Stage (Short-Term Optimization)
3.1.3. Third Stage (Real-Time Control)
3.2. Optimization Models of the OLTC and CBs
3.2.1. Rolling Optimization Framework
3.2.2. Mathematical Models
3.3. Optimization Models of SOPs
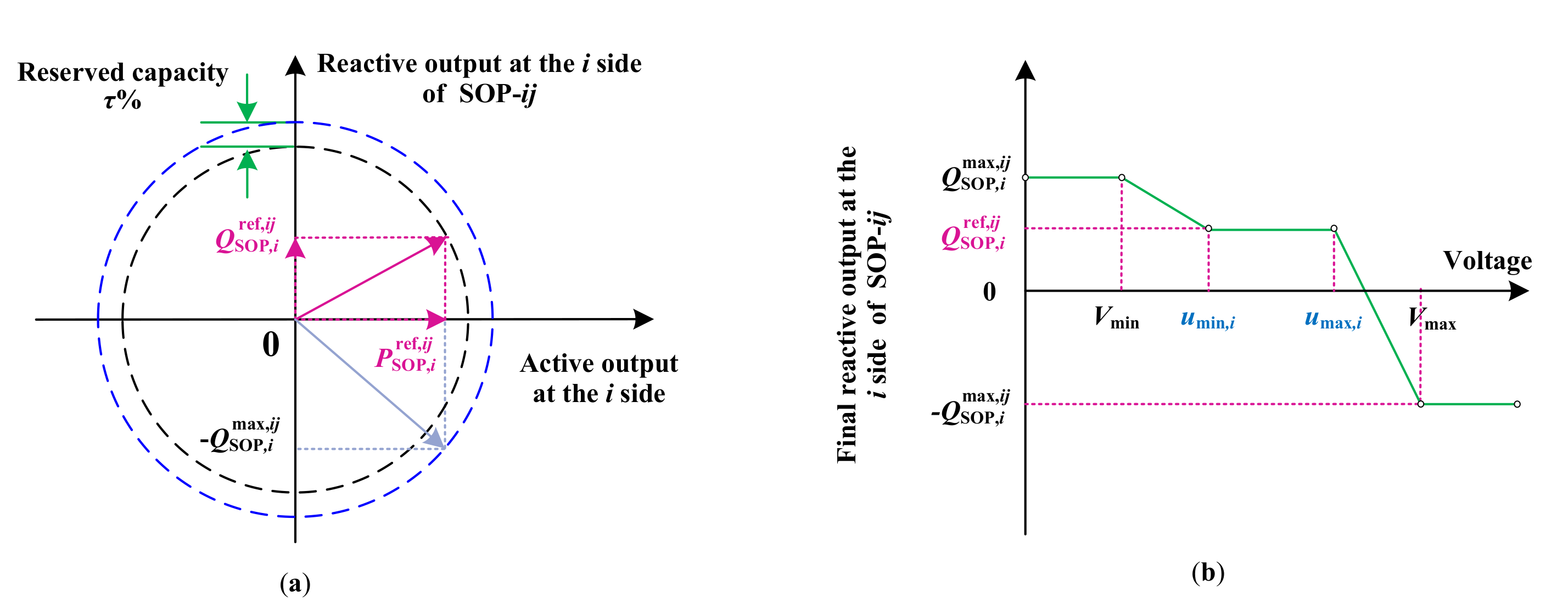
3.3.1. Optimization of Active and Reactive Power of SOPs
3.3.2. Optimization of Q-V Droop Coefficients of SOPs
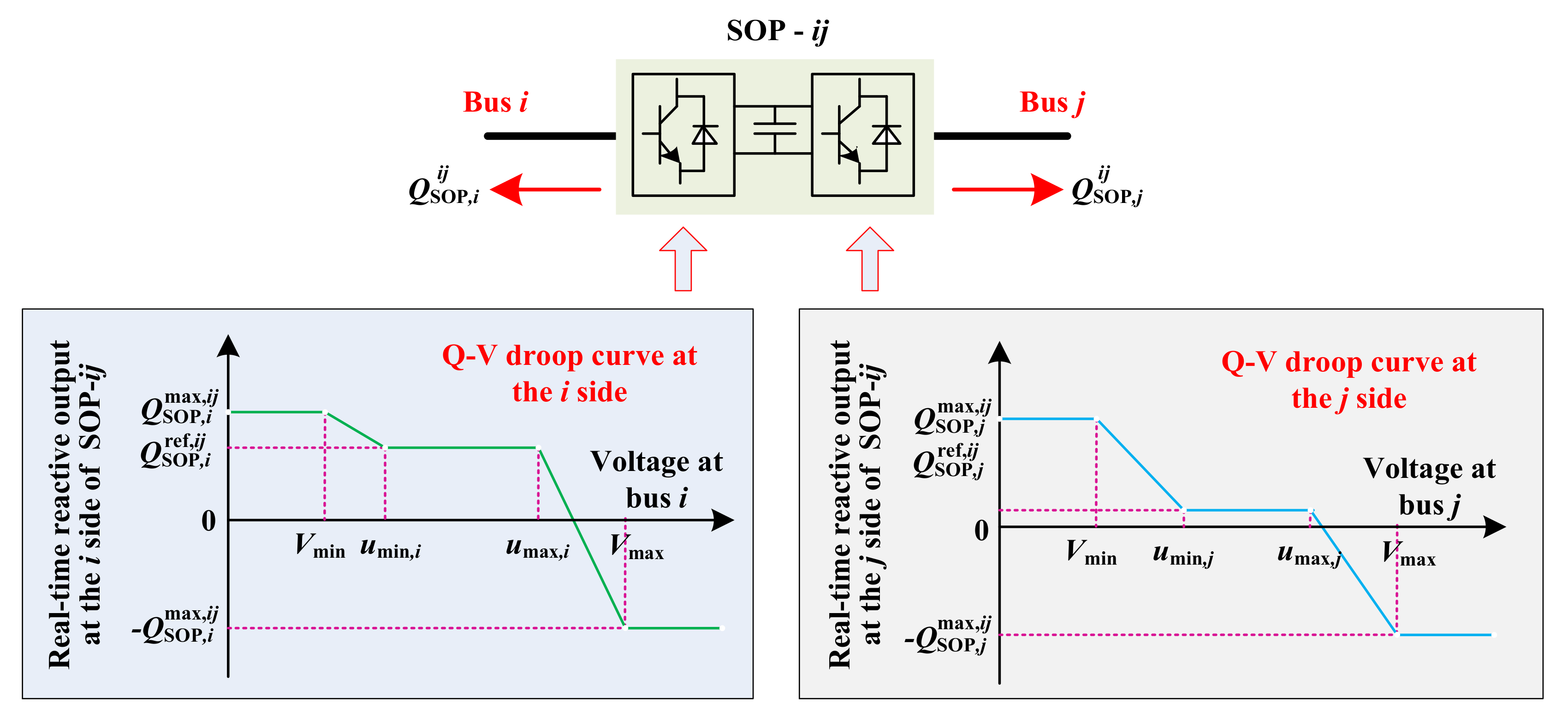
3.4. Q-V Droop Control of SOPs
3.5. Solution Algorithms of All Established Models
3.5.1. Conversion to an MISOCP Model
- (1)
- Power flow constraints: (5)–(12).
- (2)
- Operation constraints of OLTCs and CBs: (13)–(18).
- (3)
- SOP constraints: (19)–(23) and (26)–(27).
- (4)
- Constraints related to droop control of SOPs: (28)–(30).
3.5.2. Calculation
4. Case Study
4.1. Simulation Parameters
4.2. Simulation Results
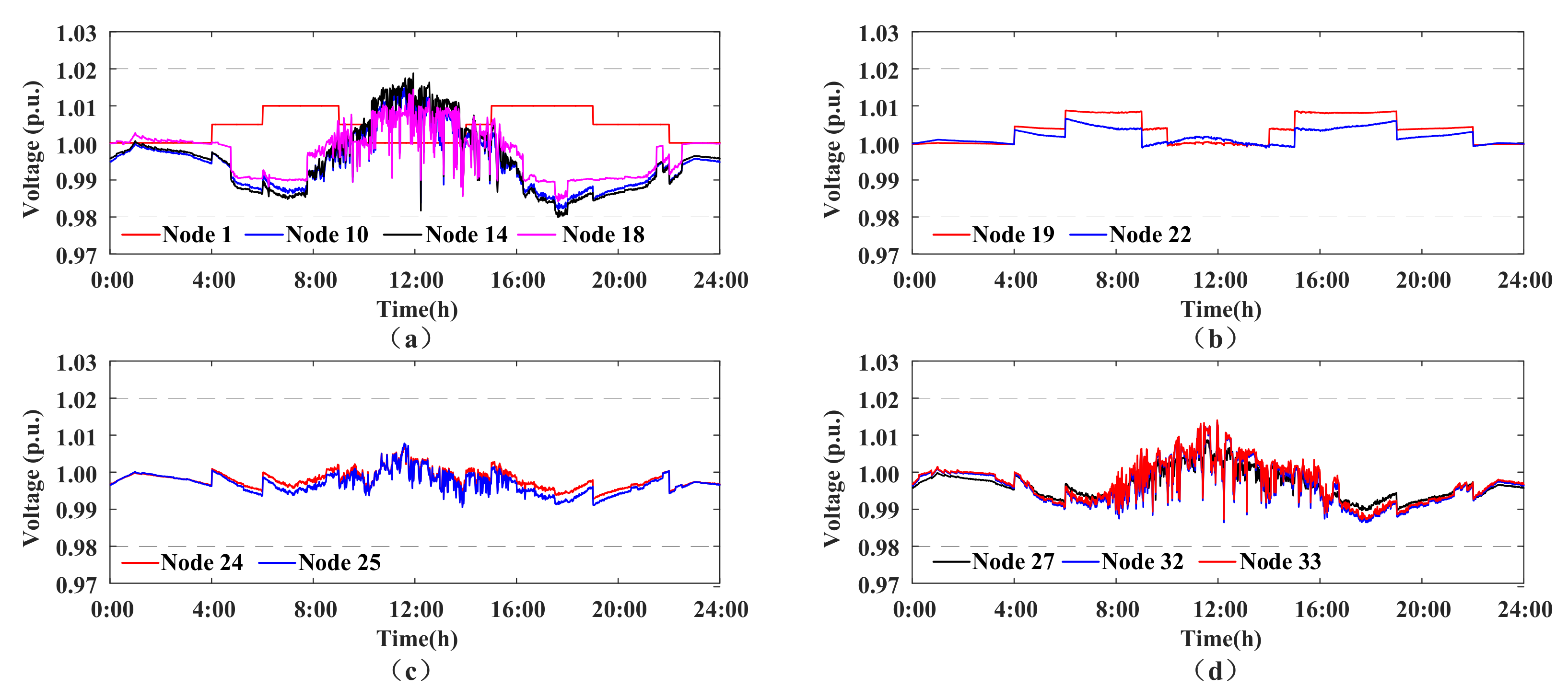
4.2.1. Voltage Regulation Results
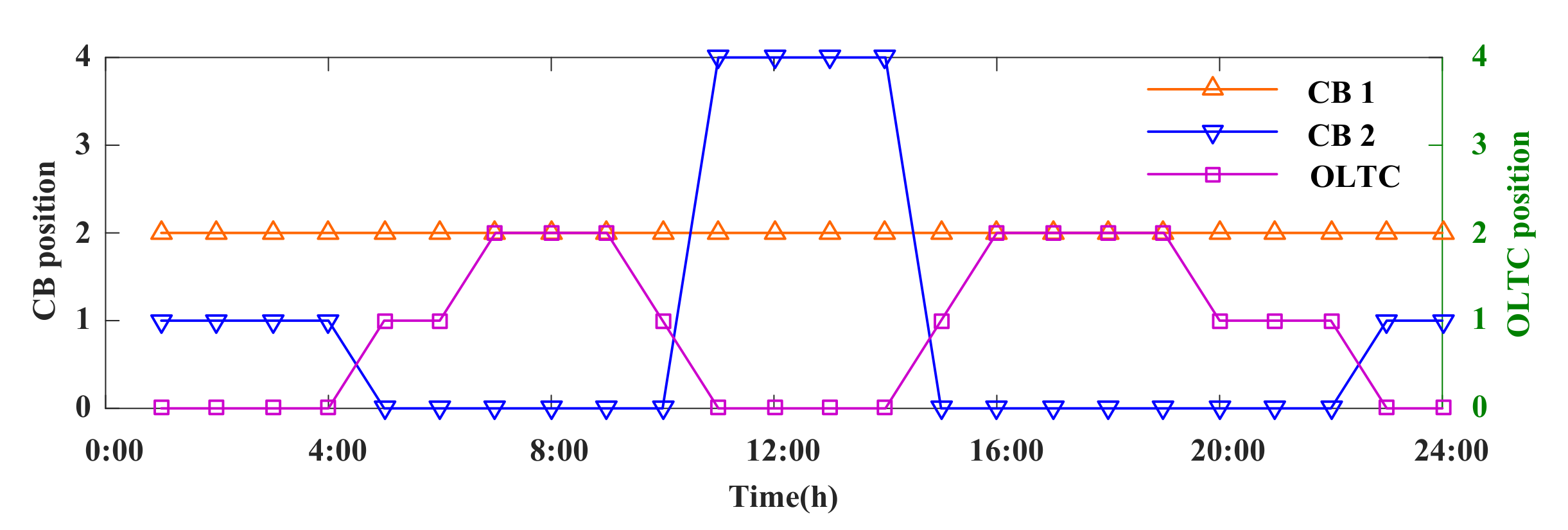
4.2.2. Optimization Results of the OLTC and CBs
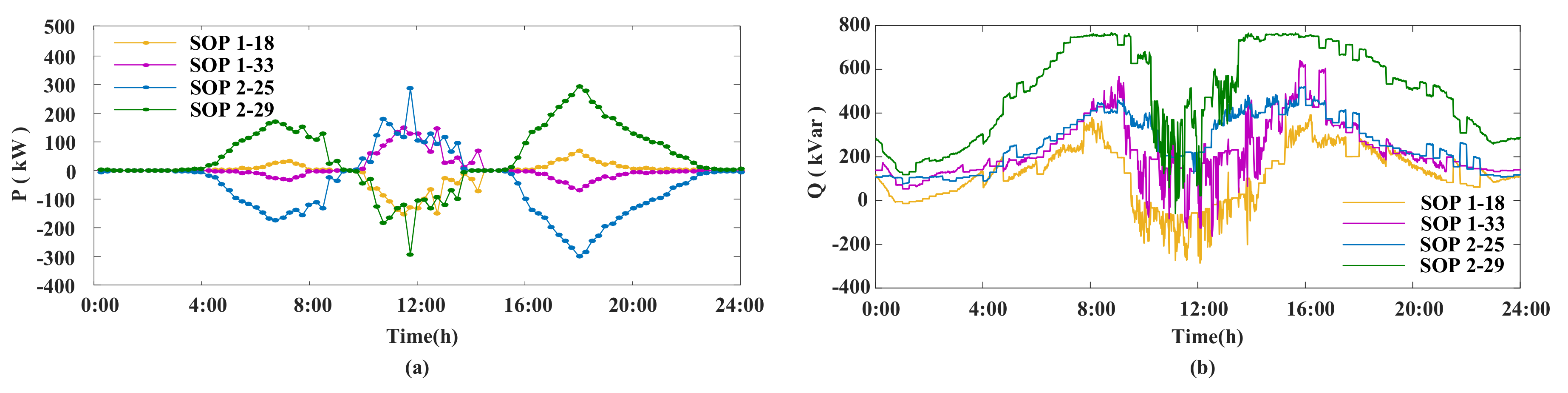
4.2.3. Optimal Active and Reactive Power Profiles of SOPs
4.3. Comparisons of Different Voltage Regulation Methods
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sarkar, M.N.I.; Meegahapola, L.G.; Datta, M. Reactive power management in renewable rich power grids: A review of grid-codes, renewable generators, support devices, control strategies and optimization algorithms. IEEE Access 2018, 6, 41458–41489. [Google Scholar] [CrossRef]
- Ma, C.; Dong, S.; Lian, J.; Pang, X. Multi-objective sizing of hybrid energy storage system for large-scale photovoltaic power generation system. Sustainability 2019, 11, 5441. [Google Scholar] [CrossRef]
- Wang, H.; Wang, J.; Piao, Z.; Meng, X.; Sun, C.; Yuan, G.; Zhu, S. The optimal allocation and operation of an energy storage system with high penetration grid-connected photovoltaic systems. Sustainability 2020, 12, 6154. [Google Scholar] [CrossRef]
- Aziz, T.; Ketjoy, N. Enhancing PV penetration in LV networks using reactive power control and on load tap changer with existing transformers. IEEE Access 2018, 6, 2683–2691. [Google Scholar] [CrossRef]
- Kacejko, P.; Adamek, S.; Wydra, M. Optimal voltage control in distribution networks with dispersed generation. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenberg, Sweden, 11–13 October 2010; pp. 1–4. [Google Scholar]
- Krata, J.; Saha, T.K.; Yan, R. Model-driven real-time control coordination for distribution grids with medium-scale photovoltaic generation. IET Renew. Power Gener. 2017, 11, 1603–1612. [Google Scholar] [CrossRef]
- Wang, L.; Yan, R.; Saha, T.K. Voltage management for large scale PV integration into weak distribution systems. IEEE Trans. Smart Grid 2018, 9, 4128–4139. [Google Scholar] [CrossRef]
- Zhang, C.; Xu, Y.; Dong, Z.; Ravishankar, J. Three-stage robust inverter-based voltage/var control for distribution networks with high-level PV. IEEE Trans. Smart Grid 2019, 10, 782–793. [Google Scholar] [CrossRef]
- Xu, Y.; Dong, Z.Y.; Zhang, R.; Hill, D.J. Multi-timescale coordinated voltage/var control of high renewable-penetrated distribution systems. IEEE Trans. Power Syst. 2017, 32, 4398–4408. [Google Scholar] [CrossRef]
- Ma, W.; Wang, W.; Wu, X.; Hu, R.; Tang, F.; Zhang, W.; Han, X.; Ding, L. Optimal allocation of hybrid energy storage systems for smoothing photovoltaic power fluctuations considering the active power curtailment of photovoltaic. IEEE Access 2019, 7, 74787–74799. [Google Scholar] [CrossRef]
- Aziz, T.; Ketjoy, N. PV penetration limits in low voltage networks and voltage variations. IEEE Access 2017, 5, 16784–16792. [Google Scholar] [CrossRef]
- Liu, X.; Cramer, A.M.; Liao, Y. Reactive power control methods for photovoltaic inverters to mitigate short-term voltage magnitude fluctuations. Electr. Power Syst. Res. 2015, 127, 213–220. [Google Scholar] [CrossRef]
- Turitsyn, K.; Sulc, P.; Backhaus, S.; Chertkov, M. Options for control of reactive power by distributed photovoltaic generators. Proc. IEEE 2011, 99, 1063–1073. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Homaee, O.; Jadid, S.; Siano, P. A new approach for real time voltage control using demand response in an automated distribution system. Appl. Energy 2014, 117, 157–166. [Google Scholar] [CrossRef]
- Ma, W.; Wang, W.; Wu, X.; Hu, R.; Tang, F.; Zhang, W. Control strategy of a hybrid energy storage system to smooth photovoltaic power fluctuations considering photovoltaic output power curtailment. Sustainability 2019, 11, 1324. [Google Scholar] [CrossRef]
- Fang, L.; Luo, A.; Xu, X.; Fang, H.; Ma, F.; Wang, W. Voltage control for static var compensator using novel optimal nonlinear PI. J. Control Theory Appl. 2012, 10, 35–43. [Google Scholar] [CrossRef]
- Collins, L.; Ward, J.K. Real and reactive power control of distributed PV inverters for overvoltage prevention and increased renewable generation hosting capacity. Renew. Energy 2015, 81, 464–471. [Google Scholar] [CrossRef]
- Ghasemi, M.A.; Parniani, M. Prevention of distribution network overvoltage by adaptive droop-based active and reactive power control of PV systems. Electr. Power Syst. Res. 2016, 133, 313–327. [Google Scholar] [CrossRef]
- Wang, J.; Bharati, G.R.; Paudyal, S.; Ceylan, O.; Bhattarai, B.P.; Myers, K.S. Coordinated electric vehicle charging with reactive power support to distribution grids. IEEE Trans. Ind. Inform. 2019, 15, 54–63. [Google Scholar] [CrossRef]
- Shafik, M.B.; Chen, H.; Rashed, G.I.; El-Sehiemy, R.A.; Elkadeem, M.R.; Wang, S. Adequate topology for efficient energy resources utilization of active distribution networks equipped with soft open points. IEEE Access 2019, 7, 99003–99016. [Google Scholar] [CrossRef]
- Long, C.; Wu, J.; Thomas, L.; Jenkins, N. Optimal operation of soft open points in medium voltage electrical distribution networks with distributed generation. Appl. Energy 2016, 184, 427–437. [Google Scholar] [CrossRef]
- Cao, W.; Wu, J.; Jenkins, N.; Wang, C.; Green, T. Benefits analysis of soft open points for electrical distribution network operation. Appl. Energy 2016, 165, 36–47. [Google Scholar] [CrossRef]
- Bloemink, J.M.; Green, T.C. Benefits of Distribution-Level Power Electronics for Supporting Distributed Generation Growth. IEEE Trans. Power Deliv. 2013, 28, 911–919. [Google Scholar] [CrossRef]
- Gu, H.; Chu, X.; Tang, M. Coordinated control of tie switch and soft normally open point for harnessing flexibility in active distribution systems. J. Phys. Conf. Ser. 2019, 1176, 62052. [Google Scholar] [CrossRef]
- Aithal, A.; Li, G.; Wu, J.; Yu, J. Performance of an electrical distribution network with soft open point during a grid side AC fault. Appl. Energy 2018, 227, 262–272. [Google Scholar] [CrossRef]
- Diaaeldin, I.; Abdel Aleem, S.; El-Rafei, A.; Abdelaziz, A.; Zobaa, A.F. Optimal network reconfiguration in active distribution networks with soft open points and distributed generation. Energies 2019, 12, 4172. [Google Scholar] [CrossRef]
- Zheng, Y.; Song, Y.; Hill, D.J. A general coordinated voltage regulation method in distribution networks with soft open points. Int J. Electr. Power 2020, 116, 105571. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Wang, C.; Zhao, J.; Song, G.; Ding, F.; Wu, J. Coordinated control method of voltage and reactive power for active distribution networks based on soft open point. IEEE Trans. Sustain. Energy 2017, 8, 1430–1442. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.; Yu, H.; Zhao, J.; Wang, C.; Song, G.; Wu, J. Combined decentralized and local voltage control strategy of soft open points in active distribution networks. Appl. Energy 2019, 241, 613–624. [Google Scholar] [CrossRef]
- Zhao, J.; Yao, M.; Yu, H.; Song, G.; Ji, H.; Li, P. Decentralized voltage control strategy of soft open points in active distribution networks based on sensitivity analysis. Electronics 2020, 9, 295. [Google Scholar] [CrossRef]
- Ji, H.; Wang, C.; Li, P.; Ding, F.; Wu, J. Robust operation of soft open points in active distribution networks with high penetration of photovoltaic integration. IEEE Trans. Sustain. Energy 2019, 10, 280–289. [Google Scholar] [CrossRef]
- O’Connell, A.; Flynn, D.; Keane, A. Rolling multi-period optimization to control electric vehicle charging in distribution networks. IEEE Trans. Power Syst. 2014, 29, 340–348. [Google Scholar] [CrossRef]
- Dhulipala, S.C.; Monteiro, R.V.A.; Silva Teixeira, R.F.D.; Ruben, C.; Bretas, A.S.; Guimaraes, G.C. Distributed model-predictive control strategy for distribution network volt/var control: A smart-building-based approach. IEEE Trans. Ind. Appl. 2019, 55, 7041–7051. [Google Scholar] [CrossRef]






| PV Plants | Location | Rated Capacity (kVA) |
|---|---|---|
| PV 1 | Bus 10 | 600 |
| PV 2 | Bus 14 | 800 |
| PV 3 | Bus 24 | 800 |
| PV 4 | Bus 27 | 600 |
| PV 5 | Bus 32 | 800 |
| Methods | Overall Operating Losses (kWh) | Minimum Voltage (p.u.) | Maximum Voltage (p.u.) | Average Voltage Deviation (p.u.) |
|---|---|---|---|---|
| Method I | 1113.65 | 0.9352 | 1.0260 | 1.7854 |
| Method II | 799.94 | 0.9567 | 1.0240 | 1.3219 |
| Method III | 791.46 | 0.9816 | 1.0200 | 1.1485 |
| Method IV | 913.06 | 0.9800 | 1.0120 | 1.1088 |
| Method V | 594.81 | 0.9770 | 1.0260 | 1.2176 |
| Proposed method | 594.98 | 0.9800 | 1.0195 | 1.1588 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, R.; Wang, W.; Chen, Z.; Wu, X.; Jing, L.; Ma, W.; Zeng, G. Coordinated Voltage Regulation Methods in Active Distribution Networks with Soft Open Points. Sustainability 2020, 12, 9453. https://doi.org/10.3390/su12229453
Hu R, Wang W, Chen Z, Wu X, Jing L, Ma W, Zeng G. Coordinated Voltage Regulation Methods in Active Distribution Networks with Soft Open Points. Sustainability. 2020; 12(22):9453. https://doi.org/10.3390/su12229453
Chicago/Turabian StyleHu, Ruonan, Wei Wang, Zhe Chen, Xuezhi Wu, Long Jing, Wei Ma, and Guohong Zeng. 2020. "Coordinated Voltage Regulation Methods in Active Distribution Networks with Soft Open Points" Sustainability 12, no. 22: 9453. https://doi.org/10.3390/su12229453
APA StyleHu, R., Wang, W., Chen, Z., Wu, X., Jing, L., Ma, W., & Zeng, G. (2020). Coordinated Voltage Regulation Methods in Active Distribution Networks with Soft Open Points. Sustainability, 12(22), 9453. https://doi.org/10.3390/su12229453









