Assessing Landscape Fragmentation: A Composite Indicator
Abstract
:1. Introduction
2. A State-of-the-Art Summary on Composite Indicators Design: General Perspective and Focus on Landscape Fragmentation Assessment
3. Methodology
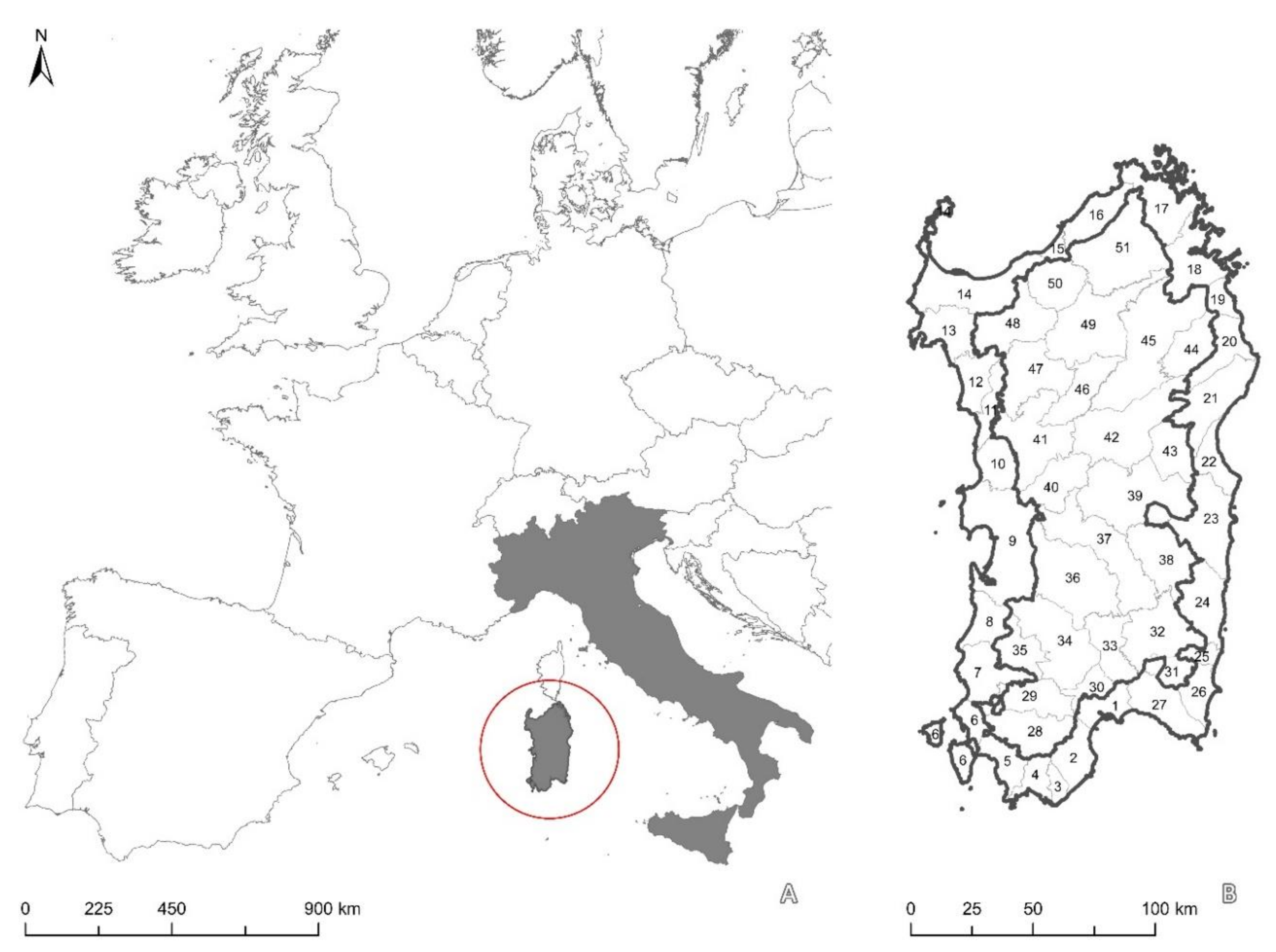
4. Applying the CI Design Method to the Context of Sardinia: The Composite Indicator of Landscape Fragmentation
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| LU | 2003 | 2008 | ||||||
|---|---|---|---|---|---|---|---|---|
| CILFBAM Rank | CILFMMAM Rank | CILFMAM Rank | CILFBGM Rank | CILFBAM Rank | CILFMMAM Rank | CILFMAM Rank | CILFBGM Rank | |
| N | vs. CILFMMGGM rank | vs. CILFMMGGM rank | ||||||
| 1 | −4 | 0 | 0 | −2 | 2 | 0 | 0 | 0 |
| 2 | 2 | 0 | 0 | 1 | 1 | 1 | 1 | 2 |
| 3 | 13 | −11 | −10 | −4 | 12 | −11 | −11 | 1 |
| 4 | 1 | −3 | −3 | −4 | 0 | −9 | −8 | −7 |
| 5 | −5 | 4 | 4 | 0 | −4 | −1 | −1 | −3 |
| 6 | −3 | 0 | 0 | −2 | −3 | 0 | 0 | −1 |
| 7 | 3 | 2 | 2 | 7 | 1 | −1 | −1 | 5 |
| 8 | −3 | 0 | 0 | −1 | −1 | 3 | 3 | 2 |
| 9 | 3 | 1 | 1 | 2 | 2 | 1 | 1 | 3 |
| 10 | −3 | 0 | 0 | −2 | −4 | −1 | −1 | −2 |
| 11 | −5 | 2 | 3 | −5 | 0 | 1 | 1 | −1 |
| 12 | −12 | −1 | −1 | −14 | −7 | 1 | 1 | −7 |
| 13 | −3 | 2 | 1 | −1 | −3 | 3 | 2 | −1 |
| 14 | 1 | 0 | 0 | 0 | 2 | 0 | 0 | 0 |
| 15 | 3 | 0 | 0 | 0 | 3 | 0 | 0 | 0 |
| 16 | 1 | 2 | 1 | 4 | 3 | 3 | 3 | 7 |
| 17 | −1 | 0 | 0 | 1 | 1 | 0 | 0 | 2 |
| 18 | 0 | 0 | 0 | 1 | −4 | 0 | 0 | −3 |
| 19 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 20 | −5 | 2 | 2 | 6 | −6 | 3 | 3 | −2 |
| 21 | 1 | 4 | 4 | 4 | 0 | 4 | 4 | 1 |
| 22 | −3 | 0 | 0 | −4 | −5 | −2 | −2 | −6 |
| 23 | −2 | −5 | −5 | 1 | 0 | 2 | 1 | 2 |
| 24 | 7 | 2 | 2 | 8 | 3 | 1 | 1 | 3 |
| 25 | 8 | −3 | −3 | 1 | 11 | −3 | −2 | 5 |
| 26 | −1 | −5 | −5 | −1 | −1 | −4 | −3 | −2 |
| 27 | 2 | −1 | −1 | 0 | 2 | −1 | −1 | 3 |
| 28 | 7 | 1 | 1 | 8 | 6 | 2 | 2 | 6 |
| 29 | 2 | 0 | 0 | 5 | 3 | −3 | −3 | 6 |
| 30 | 4 | −1 | −1 | 0 | 3 | −1 | −1 | −1 |
| 31 | −3 | −9 | −8 | −14 | −2 | −12 | −12 | −12 |
| 32 | −3 | 0 | 0 | −3 | −1 | 3 | 3 | −1 |
| 33 | −4 | 2 | 2 | 0 | −4 | 4 | 4 | −1 |
| 34 | 0 | 2 | 2 | 0 | −1 | 1 | 1 | −1 |
| 35 | −7 | −1 | −1 | −3 | −5 | 0 | 1 | 1 |
| 36 | 6 | 0 | 0 | 1 | 7 | 0 | 0 | 1 |
| 37 | 3 | 4 | 4 | −4 | 4 | 0 | −1 | −3 |
| 38 | −1 | 4 | 4 | 0 | −2 | 1 | 1 | −1 |
| 39 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 40 | −5 | 6 | 6 | 1 | −4 | 3 | 3 | 1 |
| 41 | 9 | 2 | 1 | 0 | 5 | 0 | 0 | −1 |
| 42 | 4 | 0 | 0 | −2 | −3 | −2 | −2 | −7 |
| 43 | 1 | 0 | 0 | 0 | 0 | −2 | −2 | 0 |
| 44 | −3 | 1 | 1 | −2 | −6 | 2 | 2 | −4 |
| 45 | −1 | 0 | 0 | −2 | −1 | −1 | −1 | −1 |
| 46 | 5 | 3 | 3 | 6 | 4 | 5 | 5 | 5 |
| 47 | 1 | 5 | 5 | 4 | −2 | 3 | 3 | 3 |
| 48 | −2 | 3 | 3 | 1 | 1 | 5 | 5 | 3 |
| 49 | 2 | −3 | −3 | 1 | −5 | −1 | −2 | −2 |
| 50 | −1 | −5 | −5 | 3 | 5 | 0 | 0 | 5 |
| 51 | 0 | −7 | −7 | 3 | 2 | 2 | 2 | 3 |
References
- Blancas, F.J.; Lozano-Oyola, M.; González, M. A european sustainable tourism labels proposal using a composite indicator. Environ. Impact Assess. Rev. 2015, 54, 39–54. [Google Scholar] [CrossRef]
- Nardo, M.; Saisana, M. OECD/JRC Handbook on Constructing Composite Indicators. Putting Theory into Practice 2009. Available online: https://ec.europa.eu/eurostat/documents/1001617/4398416/S11P3-OECD-EC-HANDBOOK-NARDO-SAISANA.pdf (accessed on 17 November 2020).
- Karagiannis, R.; Karagiannis, G. Constructing composite indicators with Shannon entropy: The case of Human Development Index. Socio Econ. Plan. Sci. 2020, 70. [Google Scholar] [CrossRef]
- Attardi, R.; Cerreta, M.; Sannicandro, V.; Torre, C.M. Non-compensatory composite indicators for the evaluation of urban planning policy: The Land-Use Policy Efficiency Index (LUPEI). Eur. J. Oper. Res. 2018, 264, 491–507. [Google Scholar] [CrossRef]
- Zhang, L.P.; Zhou, P.; Qiu, Y.Q.; Su, Q.; Tang, Y.L. Reassessing the climate change cooperation performance via a non-compensatory composite indicator approach. J. Clean. Prod. 2020, 252, 119387. [Google Scholar] [CrossRef]
- European Environment Agency. Landscape Fragmentation in Europe, Joint EEA-FOEN Report; European Environment Agency: Copenhagen, Denmark, 2011; ISBN 978-92-9213-215-6. [Google Scholar]
- Jaeger, J.A.G. Landscape division, splitting index, and effective mesh size: New measures of landscape fragmentation. Landsc. Ecol. 2000, 15, 115–130. [Google Scholar] [CrossRef]
- Harris, L.D. The Fragmented Forest: Island Biogeography Theory and the Preservation of Biotic Diversity; University of Chicago Press: Chicago, IL, USA, 1984; ISBN 978-0-226-31764-9. [Google Scholar]
- Saunders, D.A.; Hobbs, R.J.; Margules, C.R. Biological consequences of ecosystem fragmentation: A review. Conserv. Biol. 1991, 5, 18–32. [Google Scholar] [CrossRef]
- Forman, R.T.T. Land Mosaics: The Ecology of Landscapes and Regions; Cambridge University Press: Cambridge, UK, 1995; ISBN 978-0-521-47462-7. [Google Scholar]
- United Nations. World Urbanization Prospects: The 2014 Revision, Highlights (ST/ESA/SER.A/352); Department of Economic and Social Affairs, Population Division: New York, NY, USA, 2014. [Google Scholar]
- Jaeger, J.A.G.; Bertiller, R.; Schwick, C.; Kienast, F. Suitability criteria for measures of urban sprawl. Ecol. Indic. 2010, 10, 397–406. [Google Scholar] [CrossRef]
- Romano, B. Evaluation of urban fragmentation in the ecosystems. In Proceedings of the International Conference on Mountain Environment and Development (ICMED), Chengdu, China, 20–26 May 2002. [Google Scholar]
- Floridi, M.; Pagni, S.; Falorni, S.; Luzzati, T. An exercise in composite indicators construction: Assessing the sustainability of Italian regions. Ecol. Econ. 2011, 70, 1440–1447. [Google Scholar] [CrossRef]
- OECD. Handbook on Constructing Composite Indicators: Methodology and User Guide; Organisation for Economic Co-operation and Development: Paris, France, 2008; ISBN 978-92-64-04345-9. [Google Scholar]
- Autonomous Region of Sardinia. Decree of the President of the Region n. 82, 7 September 2006, Approval of the Regional Landscape Plan-First Homogeneous Part-Decision of the Regional Government n. 36/7, 5 September 2006, Official Bulletin of the Autonomous Region of Sardinia, 58(30), 8 September 2006; Autonomous Region of Sardinia: Sardinia, Italy, 2006. [Google Scholar]
- Bunge, M. What is a quality of life indicator? Soc. Indic. Res. 1975, 2, 65–79. [Google Scholar] [CrossRef]
- Abberger, K.; Graff, M.; Siliverstovs, B.; Sturm, J.-E. Using rule-based updating procedures to improve the performance of composite indicators. Econ. Model. 2018, 68, 127–144. [Google Scholar] [CrossRef]
- Ciommi, M.; Gigliarano, C.; Emili, A.; Taralli, S.; Chelli, F.M. A new class of composite indicators for measuring well-being at the local level: An application to the Equitable and Sustainable Well-being (BES) of the Italian Provinces. Ecol. Indic. 2017, 76, 281–296. [Google Scholar] [CrossRef]
- Gómez-Vega, M.; Picazo-Tadeo, A.J. Ranking world tourist destinations with a composite indicator of competitiveness: To weigh or not to weigh? Tour. Manag. 2019, 72, 281–291. [Google Scholar] [CrossRef]
- Rogge, N. On aggregating Benefit of the Doubt composite indicators. Eur. J. Oper. Res. 2018, 264, 364–369. [Google Scholar] [CrossRef]
- Mendola, D.; Volo, S. Building composite indicators in tourism studies: Measurements and applications in tourism destination competitiveness. Tour. Manag. 2017, 59, 541–553. [Google Scholar] [CrossRef]
- Omrani, H.; Valipour, M.; Jafari Mamakani, S. Construct a composite indicator based on integrating Common Weight Data Envelopment Analysis and principal component analysis models: An application for finding development degree of provinces in Iran. Socio-Econ. Plan. Sci. 2019, 68, 100618. [Google Scholar] [CrossRef]
- Badea, A.C.; Rocco, S.C.M.; Tarantola, S.; Bolado, R. Composite indicators for security of energy supply using ordered weighted averaging. Reliab. Eng. Syst. Saf. 2011, 96, 651–662. [Google Scholar] [CrossRef]
- Miller, P.; De Barros, A.G.; Kattan, L.; Wirasinghe, S.C. Managing uncertainty in the application of composite sustainability indicators to transit analysis. Transp. Res. Procedia 2017, 25, 4003–4018. [Google Scholar] [CrossRef]
- Requejo-Castro, D.; Giné-Garriga, R.; Pérez-Foguet, A. Bayesian network modelling of hierarchical composite indicators. Sci. Total Environ. 2019, 668, 936–946. [Google Scholar] [CrossRef]
- Zanella, A.; Camanho, A.S.; Dias, T.G. Undesirable outputs and weighting schemes in composite indicators based on data envelopment analysis. Eur. J. Oper. Res. 2015, 245, 517–530. [Google Scholar] [CrossRef]
- Caschili, S.; De Montis, A.; Trogu, D. Accessibility and rurality indicators for regional development. Comput. Environ. Urban Syst. 2015, 49, 98–114. [Google Scholar] [CrossRef]
- Ghosh, B.; Chakma, N. Composite indicator of land, water and energy for measuring agricultural sustainability at micro level, Barddhaman District, West Bengal, India. Ecol. Indic. 2019, 102, 21–32. [Google Scholar] [CrossRef]
- Xavier, A.; Costa Freitas, M.D.B.; Fragoso, R.; Rosário, M.D.S. A regional composite indicator for analysing agricultural sustainability in Portugal: A goal programming approach. Ecol. Indic. 2018, 89, 84–100. [Google Scholar] [CrossRef]
- Wang, H. A generalized MCDA-DEA (multi-criterion decision analysis-data envelopment analysis) approach to construct slacks-based composite indicator. Energy 2015, 80, 114–122. [Google Scholar] [CrossRef]
- Singh, R.K.; Murty, H.R.; Gupta, S.K.; Dikshit, A.K. An overview of sustainability assessment methodologies. Ecol. Indic. 2012, 15, 281–299. [Google Scholar] [CrossRef]
- Abenayake, C.C.; Mikami, Y.; Matsuda, Y.; Jayasinghe, A. Ecosystem services-based composite indicator for assessing community resilience to floods. Environ. Dev. 2018, 27, 34–46. [Google Scholar] [CrossRef]
- Alam, M.; Dupras, J.; Messier, C. A framework towards a composite indicator for urban ecosystem services. Ecol. Indic. 2016, 60, 38–44. [Google Scholar] [CrossRef]
- Mao, F.; Zhao, X.; Ma, P.; Chi, S.; Richards, K.; Clark, J.; Hannah, D.M.; Krause, S. Developing composite indicators for ecological water quality assessment based on network interactions and expert judgment. Environ. Model. Softw. 2019, 115, 51–62. [Google Scholar] [CrossRef]
- Speak, A.; Escobedo, F.J.; Russo, A.; Zerbe, S. An ecosystem service-disservice ratio: Using composite indicators to assess the net benefits of urban trees. Ecol. Indic. 2018, 95, 544–553. [Google Scholar] [CrossRef]
- Llauss, A.; Nogué, J. Indicators of landscape fragmentation: The case for combining ecological indices and the perceptive approach. Ecol. Indic. 2012, 15, 85–91. [Google Scholar] [CrossRef]
- Opdam, P.; Verboom, J.; Pouwels, R. Landscape cohesion: An index for the conservation potential of landscapes for biodiversity. Landsc. Ecol. 2003, 18, 113–126. [Google Scholar] [CrossRef]
- Becker, W.; Saisana, M.; Paruolo, P.; Vandecasteele, I. Weights and importance in composite indicators: Closing the gap. Ecol. Indic. 2017, 80, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, F.; El Gibari, S.; Cabello, J.M.; Gómez, T. MRP-WSCI: Multiple reference point based weak and strong composite indicators. Omega 2020, 95. [Google Scholar] [CrossRef]
- Luzzati, T.; Gucciardi, G. A non-simplistic approach to composite indicators and rankings: An illustration by comparing the sustainability of the EU Countries. Ecol. Econ. 2015, 113, 25–38. [Google Scholar] [CrossRef]
- Bruschi, D.; Astiaso Garcia, D.; Gugliermetti, F.; Cumo, F. Characterizing the fragmentation level of Italian’s National Parks due to transportation infrastructures. Transp. Res. Part D Transp. Environ. 2015, 36, 18–28. [Google Scholar] [CrossRef]
- Astiaso Garcia, D.; Bruschi, D.; Cinquepalmi, F.; Cumo, F. An estimation of urban fragmentation of natural habitats: Case studies of the 24 italian national parks. Chem. Eng. Trans. 2013, 32, 49–54. [Google Scholar] [CrossRef]
- Battisti, C.; Romano, B. Frammentazione e Connettività. Dall’analisi Ecologica alla Pianificazione Ambientale; Città Studi: Torino, Italy, 2007; ISBN 978-88-251-7314-7. [Google Scholar]
- Biondi, M.; Corridore, G.; Romano, B.; Tamburini, G.; Tetè, P. Evaluation and planning control of the ecosystem fragmentation due to urban development. In Proceedings of the 50th Conference of the European Regional Science Association (ERSA), Jyväskylä, Finland, 27–30 August 2003. [Google Scholar]
- Romano, B.; Zullo, F. Valutazione della pressione insediativa: Indicatori e sperimentazione di soglie. In Biodiversità, Disturbi, Minacce; Battisti, C., Conigliaro, M., Poeta, G., Teofili, C., Eds.; Editrice Universitaria Udinese: Udine, Italy, 2013; pp. 170–177. ISBN 978-88-8420-803-3. [Google Scholar]
- Battisti, C.; Conigliaro, M.; Poeta, G.; Teofili, C. Biodiversità, Disturbi, Minacce. Dall’ecologia di Base alla Gestione e Conservazione Degli Ecosistemi; Forum Edizioni: Udine, Italy, 2013; ISBN 978-88-8420-803-3. [Google Scholar]
- De Montis, A. Impacts of the European Landscape Convention on national planning systems: A comparative investigation of six case studies. Landsc. Urban Plan. 2014, 124, 53–65. [Google Scholar] [CrossRef]
- De Montis, A. Measuring the performance of planning: The conformance of Italian landscape planning practices with the European Landscape Convention. Eur. Plan. Stud. 2016, 24, 1727–1745. [Google Scholar] [CrossRef]
| N | Description | Rationale |
|---|---|---|
| 1 | Theoretical framework | Simplification of decisional processes through the construction of a unique CILF for LF and considering three relevant aspects. The context is strategic landscape analysis and planning in a Mediterranean region: the DMUs correspond to the 51 landscape units designed by the Regional Landscape Plan of Sardinia [16]. |
| 2 | Variables | CILF derives from a combination of three indicators, IFI, UFI, and Seff, measuring LF due to transport and mobility infrastructure, urban settlements, and landscape subdivision per se in several patches. |
| 3 | Normalization | The indicators are normalized according to three transformations: distance of Borda, distance from minimum normalized by the range (min-max transformation), rescaling with respect to the maximum value. |
| 4 | Aggregation | Normalized indicators are aggregated by means of three rules: arithmetic, geometric, and generalized geometric mean. |
| 5 | Robustness and sensitivity | Sensitivity analysis is performed to ascertain the robustness of CILF expressions obtained according to the various normalization and aggregation patterns. Various metrics characterize the variation of the shift in ranking of the DMUs. |
| Key Elements | Data | Year | Scale | Source | Website |
|---|---|---|---|---|---|
| Patches, human settlements | Land Use map of Sardinia, areas | 2003, 2008 | 1:25,000 | Sardinia Geoportal, Autonomous Region of Sardinia | http://www.sardegnageoportale.it/ |
| Linear infrastructures | Land Use map of Sardinia, linear elements |
| RLP Landscape Units | Indicators (2003) | Indicators (2008) | ||||||
|---|---|---|---|---|---|---|---|---|
| Homogeneous Part | N | Denomination | IFI | UFI | Seff | IFI | UFI | Seff |
| Coastal | 1 | Golfo di Cagliari | 928.41 | 0.73 | 17.75 | 1265.16 | 3.62 | 18.49 |
| 2 | Nora | 135.19 | 0.57 | 3.54 | 134.35 | 0.89 | 3.68 | |
| 3 | Chia | 16.17 | 0.07 | 11.56 | 15.87 | 0.13 | 11.68 | |
| 4 | Golfo di Teulada | 91.88 | 0.02 | 5.19 | 92.06 | 0.04 | 5.20 | |
| 5 | Anfiteatro del Sulcis | 274.32 | 0.26 | 4.15 | 274.47 | 0.56 | 4.25 | |
| 6 | Carbonia e Isole sulcitane | 1855.18 | 1.59 | 11.46 | 1900.10 | 1.86 | 11.91 | |
| 7 | Bacino metallifero | 460.89 | 0.60 | 2.46 | 476.51 | 0.77 | 2.47 | |
| 8 | Arburese | 230.97 | 0.15 | 3.65 | 251.15 | 0.17 | 3.65 | |
| 9 | Golfo di Oristano | 13,959.40 | 1.35 | 2.57 | 14,267.11 | 1.71 | 3.17 | |
| 10 | Montiferru | 337.44 | 0.12 | 4.03 | 340.94 | 0.17 | 4.05 | |
| 11 | Planargia | 1122.35 | 0.13 | 5.22 | 1209.16 | 0.22 | 7.94 | |
| 12 | Monteleone | 747.12 | 0.01 | 3.41 | 780.40 | 0.04 | 3.42 | |
| 13 | Alghero | 2243.81 | 0.48 | 3.04 | 2225.22 | 0.96 | 3.13 | |
| 14 | Golfo dell’Asinara | 19,156.42 | 1.60 | 3.28 | 20,719.70 | 2.23 | 3.37 | |
| 15 | Bassa valle del Coghinas | 147.00 | 0.62 | 15.51 | 163.33 | 0.80 | 15.91 | |
| 16 | Gallura costiera nord-occidentale | 196.40 | 0.19 | 2.52 | 196.40 | 0.30 | 2.62 | |
| 17 | Gallura costiera nord-orientale | 13,290.97 | 0.99 | 3.05 | 13,797.54 | 1.65 | 3.07 | |
| 18 | Golfo di Olbia | 6028.91 | 1.44 | 2.42 | 6225.49 | 1.95 | 4.13 | |
| 19 | Budoni - S.Teodoro | 229.60 | 0.92 | 8.56 | 263.07 | 1.14 | 9.81 | |
| 20 | Monte Albo | 638.49 | 0.39 | 3.21 | 841.50 | 0.58 | 3.25 | |
| 21 | Baronia | 1297.30 | 0.19 | 1.76 | 1298.95 | 0.32 | 1.85 | |
| 22 | Supramonte di Baunei e Dorgali | 164.90 | 0.02 | 4.00 | 281.12 | 0.03 | 4.00 | |
| 23 | Ogliastra | 638.60 | 0.43 | 1.51 | 656.63 | 0.49 | 1.52 | |
| 24 | Salto di Quirra | 56.64 | 0.15 | 2.19 | 117.31 | 0.19 | 2.20 | |
| 25 | Bassa valle del Flumendosa | 107.67 | 0.23 | 10.07 | 117.49 | 0.27 | 10.15 | |
| 26 | Castiadas | 84.09 | 0.29 | 4.39 | 91.37 | 0.35 | 4.41 | |
| 27 | Golfo orientale di Cagliari | 755.98 | 1.41 | 2.52 | 783.48 | 1.57 | 2.52 | |
| Internal | 28 | Sulcis | 54.08 | 0.19 | 2.14 | 84.59 | 0.32 | 2.17 |
| 29 | Valle del Cixerri | 114.07 | 0.23 | 2.54 | 120.35 | 0.46 | 2.57 | |
| 30 | Basso Campidano | 218.89 | 1.33 | 23.19 | 396.05 | 1.66 | 24.60 | |
| 31 | Serpeddì-Monte Genis | 23.32 | 0.01 | 5.25 | 23.32 | 0.02 | 5.26 | |
| 32 | Gerrei | 453.67 | 0.05 | 1.68 | 568.60 | 0.07 | 1.68 | |
| 33 | Parteolla Trexenta | 2162.33 | 0.47 | 3.06 | 2352.74 | 0.71 | 3.13 | |
| 34 | Campidano | 2386.31 | 0.54 | 1.59 | 2423.93 | 1.02 | 1.64 | |
| 35 | Monte Linas | 427.44 | 0.18 | 4.00 | 433.93 | 0.27 | 4.01 | |
| 36 | Regione delle giare basaltiche | 9260.50 | 0.39 | 1.46 | 9522.59 | 0.49 | 1.47 | |
| 37 | Flumendosa-Sarcidano-Araxisi | 2844.21 | 0.23 | 1.31 | 3048.57 | 0.29 | 1.31 | |
| 38 | Regione dei tacchi calcarei | 507.99 | 0.06 | 1.87 | 508.89 | 0.06 | 1.86 | |
| 39 | Gennargentu e Mandrolisai | 250.39 | 0.10 | 1.02 | 251.51 | 0.11 | 1.02 | |
| 40 | Media valle del Tirso | 1406.12 | 0.18 | 2.66 | 1517.20 | 0.33 | 2.70 | |
| 41 | Altopiani di Macomer | 3770.56 | 0.17 | 1.55 | 3808.67 | 0.27 | 1.55 | |
| 42 | Valli del Rio Isalle e Liscoi | 2721.64 | 0.39 | 1.21 | 2677.18 | 0.49 | 1.21 | |
| 43 | Supramonti interni | 57.76 | 0.05 | 2.94 | 76.31 | 0.05 | 2.94 | |
| 44 | La valle del Rio Mannu | 332.31 | 0.03 | 2.90 | 567.71 | 0.05 | 2.91 | |
| 45 | Altopiani e Alta Valle del Tirso | 380.55 | 0.06 | 0.90 | 447.21 | 0.10 | 0.90 | |
| 46 | Marghine - Goceano | 115.84 | 0.15 | 2.61 | 303.31 | 0.16 | 2.62 | |
| 47 | Meilogu | 1347.16 | 0.17 | 1.80 | 1622.18 | 0.35 | 1.82 | |
| 48 | Logudoro | 1662.05 | 0.22 | 1.91 | 2049.52 | 0.47 | 1.95 | |
| 49 | Piana del Rio Mannu di Ozieri | 1393.85 | 0.38 | 1.21 | 1424.82 | 0.51 | 1.22 | |
| 50 | Anglona | 66.68 | 0.24 | 2.68 | 73.19 | 0.36 | 2.70 | |
| 51 | Massiccio del Limbara | 364.86 | 0.42 | 1.14 | 366.39 | 0.47 | 1.14 | |
| Mean values | All LUs | 1912.13 | 0.42 | 4.23 | 2028.52 | 0.63 | 4.44 | |
| Coastal LUs | 2414.67 | 0.55 | 5.30 | 2547.62 | 0.85 | 5.62 | ||
| Internal LUs | 1346.77 | 0.26 | 3.02 | 1444.53 | 0.38 | 3.10 | ||
| LU | MM-Normalized Indicators (2003) | MM-Normalized Indicators (2008) | GGM Aggregated CI | ||||||
|---|---|---|---|---|---|---|---|---|---|
| N | IFI | UFI | Seff | IFI | UFI | Seff | CILF (2003) | CILF (2008) | CILF (AAV) |
| 1 | 0.05 | 0.46 | 0.77 | 0.06 | 1.00 | 0.75 | 0.35 | 0.50 | 8.42% |
| 2 | 0.01 | 0.35 | 0.15 | 0.01 | 0.25 | 0.15 | 0.13 | 0.10 | −3.75% |
| 3 | 0.00 | 0.05 | 0.50 | 0.00 | 0.04 | 0.48 | 0.10 | 0.09 | −1.70% |
| 4 | 0.00 | 0.01 | 0.22 | 0.00 | 0.01 | 0.21 | 0.05 | 0.04 | −1.51% |
| 5 | 0.01 | 0.16 | 0.18 | 0.01 | 0.16 | 0.17 | 0.10 | 0.10 | −0.88% |
| 6 | 0.10 | 1.00 | 0.49 | 0.09 | 0.51 | 0.48 | 0.45 | 0.33 | −5.49% |
| 7 | 0.02 | 0.37 | 0.11 | 0.02 | 0.21 | 0.10 | 0.13 | 0.10 | −5.54% |
| 8 | 0.01 | 0.10 | 0.16 | 0.01 | 0.05 | 0.15 | 0.07 | 0.06 | −4.91% |
| 9 | 0.73 | 0.85 | 0.11 | 0.69 | 0.47 | 0.13 | 0.49 | 0.39 | −4.18% |
| 10 | 0.02 | 0.08 | 0.17 | 0.02 | 0.05 | 0.16 | 0.08 | 0.06 | −3.28% |
| 11 | 0.06 | 0.08 | 0.23 | 0.06 | 0.06 | 0.32 | 0.11 | 0.12 | 1.99% |
| 12 | 0.04 | 0.00 | 0.15 | 0.04 | 0.01 | 0.14 | 0.05 | 0.05 | 1.39% |
| 13 | 0.12 | 0.30 | 0.13 | 0.11 | 0.27 | 0.13 | 0.17 | 0.16 | −1.70% |
| 14 | 1.00 | 1.00 | 0.14 | 1.00 | 0.62 | 0.14 | 0.63 | 0.52 | −3.55% |
| 15 | 0.01 | 0.39 | 0.67 | 0.01 | 0.22 | 0.65 | 0.26 | 0.21 | −4.08% |
| 16 | 0.01 | 0.12 | 0.11 | 0.01 | 0.08 | 0.11 | 0.07 | 0.06 | −3.00% |
| 17 | 0.69 | 0.62 | 0.13 | 0.67 | 0.45 | 0.12 | 0.44 | 0.38 | −2.73% |
| 18 | 0.31 | 0.90 | 0.10 | 0.30 | 0.54 | 0.17 | 0.37 | 0.32 | −2.99% |
| 19 | 0.01 | 0.58 | 0.37 | 0.01 | 0.32 | 0.40 | 0.24 | 0.19 | −4.34% |
| 20 | 0.03 | 0.24 | 0.14 | 0.04 | 0.16 | 0.13 | 0.12 | 0.10 | −3.07% |
| 21 | 0.07 | 0.12 | 0.08 | 0.06 | 0.09 | 0.08 | 0.09 | 0.07 | −2.61% |
| 22 | 0.01 | 0.02 | 0.17 | 0.01 | 0.01 | 0.16 | 0.04 | 0.04 | −1.48% |
| 23 | 0.03 | 0.27 | 0.07 | 0.03 | 0.13 | 0.06 | 0.10 | 0.07 | −6.21% |
| 24 | 0.00 | 0.10 | 0.09 | 0.01 | 0.05 | 0.09 | 0.05 | 0.04 | −3.90% |
| 25 | 0.01 | 0.15 | 0.43 | 0.01 | 0.07 | 0.41 | 0.14 | 0.11 | −4.20% |
| 26 | 0.00 | 0.18 | 0.19 | 0.00 | 0.10 | 0.18 | 0.10 | 0.07 | −5.02% |
| 27 | 0.04 | 0.88 | 0.11 | 0.04 | 0.43 | 0.10 | 0.24 | 0.15 | −7.24% |
| 28 | 0.00 | 0.12 | 0.09 | 0.00 | 0.09 | 0.09 | 0.05 | 0.05 | −2.40% |
| 29 | 0.01 | 0.14 | 0.11 | 0.01 | 0.13 | 0.10 | 0.07 | 0.06 | −1.58% |
| 30 | 0.01 | 0.83 | 1.00 | 0.02 | 0.46 | 1.00 | 0.45 | 0.37 | −3.85% |
| 31 | 0.00 | 0.01 | 0.23 | 0.00 | 0.01 | 0.21 | 0.04 | 0.04 | −1.32% |
| 32 | 0.02 | 0.03 | 0.07 | 0.03 | 0.02 | 0.07 | 0.04 | 0.04 | −2.19% |
| 33 | 0.11 | 0.29 | 0.13 | 0.11 | 0.20 | 0.13 | 0.17 | 0.14 | −3.26% |
| 34 | 0.12 | 0.34 | 0.07 | 0.12 | 0.28 | 0.07 | 0.16 | 0.14 | −2.12% |
| 35 | 0.02 | 0.11 | 0.17 | 0.02 | 0.07 | 0.16 | 0.09 | 0.07 | −3.35% |
| 36 | 0.48 | 0.24 | 0.06 | 0.46 | 0.14 | 0.06 | 0.23 | 0.18 | −3.97% |
| 37 | 0.15 | 0.14 | 0.06 | 0.15 | 0.08 | 0.05 | 0.11 | 0.09 | −3.98% |
| 38 | 0.03 | 0.04 | 0.08 | 0.02 | 0.02 | 0.08 | 0.05 | 0.03 | −4.67% |
| 39 | 0.01 | 0.06 | 0.04 | 0.01 | 0.03 | 0.04 | 0.04 | 0.03 | −5.56% |
| 40 | 0.07 | 0.11 | 0.11 | 0.07 | 0.09 | 0.11 | 0.10 | 0.09 | −1.73% |
| 41 | 0.20 | 0.11 | 0.07 | 0.18 | 0.07 | 0.06 | 0.12 | 0.10 | −2.82% |
| 42 | 0.14 | 0.24 | 0.05 | 0.13 | 0.14 | 0.05 | 0.13 | 0.10 | −5.09% |
| 43 | 0.00 | 0.03 | 0.13 | 0.00 | 0.01 | 0.12 | 0.04 | 0.03 | −4.12% |
| 44 | 0.02 | 0.02 | 0.13 | 0.03 | 0.01 | 0.12 | 0.04 | 0.04 | 0.27% |
| 45 | 0.02 | 0.04 | 0.04 | 0.02 | 0.03 | 0.04 | 0.03 | 0.03 | −1.99% |
| 46 | 0.01 | 0.09 | 0.11 | 0.01 | 0.04 | 0.11 | 0.06 | 0.05 | −3.32% |
| 47 | 0.07 | 0.11 | 0.08 | 0.08 | 0.10 | 0.07 | 0.08 | 0.08 | −0.34% |
| 48 | 0.09 | 0.14 | 0.08 | 0.10 | 0.13 | 0.08 | 0.10 | 0.10 | 0.13% |
| 49 | 0.07 | 0.24 | 0.05 | 0.07 | 0.14 | 0.05 | 0.11 | 0.08 | −4.79% |
| 50 | 0.00 | 0.15 | 0.12 | 0.00 | 0.10 | 0.11 | 0.07 | 0.06 | −3.90% |
| 51 | 0.02 | 0.26 | 0.05 | 0.02 | 0.13 | 0.05 | 0.08 | 0.06 | −6.81% |
| CILFBAM | CILFMMAM | CILFMAM | CILFBGM | CILFMMGM | CILFMGM | CILFBGGM | CILFMMGGM | CILFMGGM | |
|---|---|---|---|---|---|---|---|---|---|
| CILFBAM | 0.22 | 0.22 | 0.22 | 0.27 | 0.22 | 0.22 | 0.22 | 0.22 | |
| CILFMMAM | 0.00 | 0.00 | 0.06 | 0.00 | 0.00 | 0.00 | 0.00 | ||
| CILFMAM | 0.00 | 0.06 | 0.00 | 0.00 | 0.00 | 0.00 | |||
| CILFBGM | 0.06 | 0.00 | 0.00 | 0.00 | 0.00 | ||||
| CILFMMGM | −0.06 | −0.06 | −0.06 | −0.06 | |||||
| CILFMGM | 0.00 | 0.00 | 0.00 | ||||||
| CILFBGGM | 0.00 | 0.00 | |||||||
| CILFMMGGM | 0.00 | ||||||||
| CILFMGGM |
| CILFBAM | CILFMMAM | CILFMAM | CILFBGM | CILFMMGM | CILFMGM | CILFBGGM | CILFMMGGM | CILFMGGM | |
|---|---|---|---|---|---|---|---|---|---|
| CILFBAM | 0.22 | 0.22 | 0.20 | 0.27 | 0.22 | 0.20 | 0.22 | 0.22 | |
| CILFMMAM | 0.00 | −0.02 | 0.06 | 0.00 | −0.02 | 0.00 | 0.00 | ||
| CILFMAM | −0.02 | 0.06 | 0.00 | −0.02 | 0.00 | 0.00 | |||
| CILFBGM | 0.08 | 0.02 | 0.00 | 0.02 | 0.02 | ||||
| CILFMMGM | −0.06 | −0.08 | −0.06 | −0.06 | |||||
| CILFMGM | −0.02 | 0.00 | 0.00 | ||||||
| CILFBGGM | 0.02 | 0.02 | |||||||
| CILFMMGGM | 0.00 | ||||||||
| CILFMGGM |
| 2003 | 2008 | |||||
|---|---|---|---|---|---|---|
| Mean | Max | Min | Mean | Max | Min | |
| ASR | 0.05 | 0.27 | 0.00 | 0.05 | 0.27 | 0.00 |
| SRmax | 12 | 25 | 1 | 11 | 26 | 1 |
| SRMin | −14 | −1 | −36 | −13 | −1 | −37 |
| SSRunder5 | 49.35% | 94.12% | 25.49% | 50.54% | 92.16% | 23.53% |
| SSRunder10 | 57.46% | 94.12% | 35.29% | 58.33% | 92.16% | 33.33% |
| 2003 | 2008 | |||||
|---|---|---|---|---|---|---|
| Mean | Max | Min | Mean | Max | Min | |
| ASR | 0.02 | 0.22 | 0.00 | 0.03 | 0.22 | 0.00 |
| SRmax | 12 | 25 | 5 | 12 | 26 | 4 |
| SRMin | −10 | −5 | −14 | −9 | −3 | −12 |
| SSRunder5 | 54.90% | 72.55% | 31.37% | 51.82% | 68.63% | 29.41% |
| SSRunder10 | 59.66% | 74.51% | 39.22% | 54.90% | 68.63% | 37.25% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Montis, A.; Serra, V.; Ganciu, A.; Ledda, A. Assessing Landscape Fragmentation: A Composite Indicator. Sustainability 2020, 12, 9632. https://doi.org/10.3390/su12229632
De Montis A, Serra V, Ganciu A, Ledda A. Assessing Landscape Fragmentation: A Composite Indicator. Sustainability. 2020; 12(22):9632. https://doi.org/10.3390/su12229632
Chicago/Turabian StyleDe Montis, Andrea, Vittorio Serra, Amedeo Ganciu, and Antonio Ledda. 2020. "Assessing Landscape Fragmentation: A Composite Indicator" Sustainability 12, no. 22: 9632. https://doi.org/10.3390/su12229632
APA StyleDe Montis, A., Serra, V., Ganciu, A., & Ledda, A. (2020). Assessing Landscape Fragmentation: A Composite Indicator. Sustainability, 12(22), 9632. https://doi.org/10.3390/su12229632








