Analysis of Contact Stresses and Rolling Resistance of Truck-Bus Tyres under Different Working Conditions
Abstract
1. Introduction
2. Establishment and Verification of Tyre–Pavement Finite Element Model
2.1. The Constitutive Model of Rubber Material
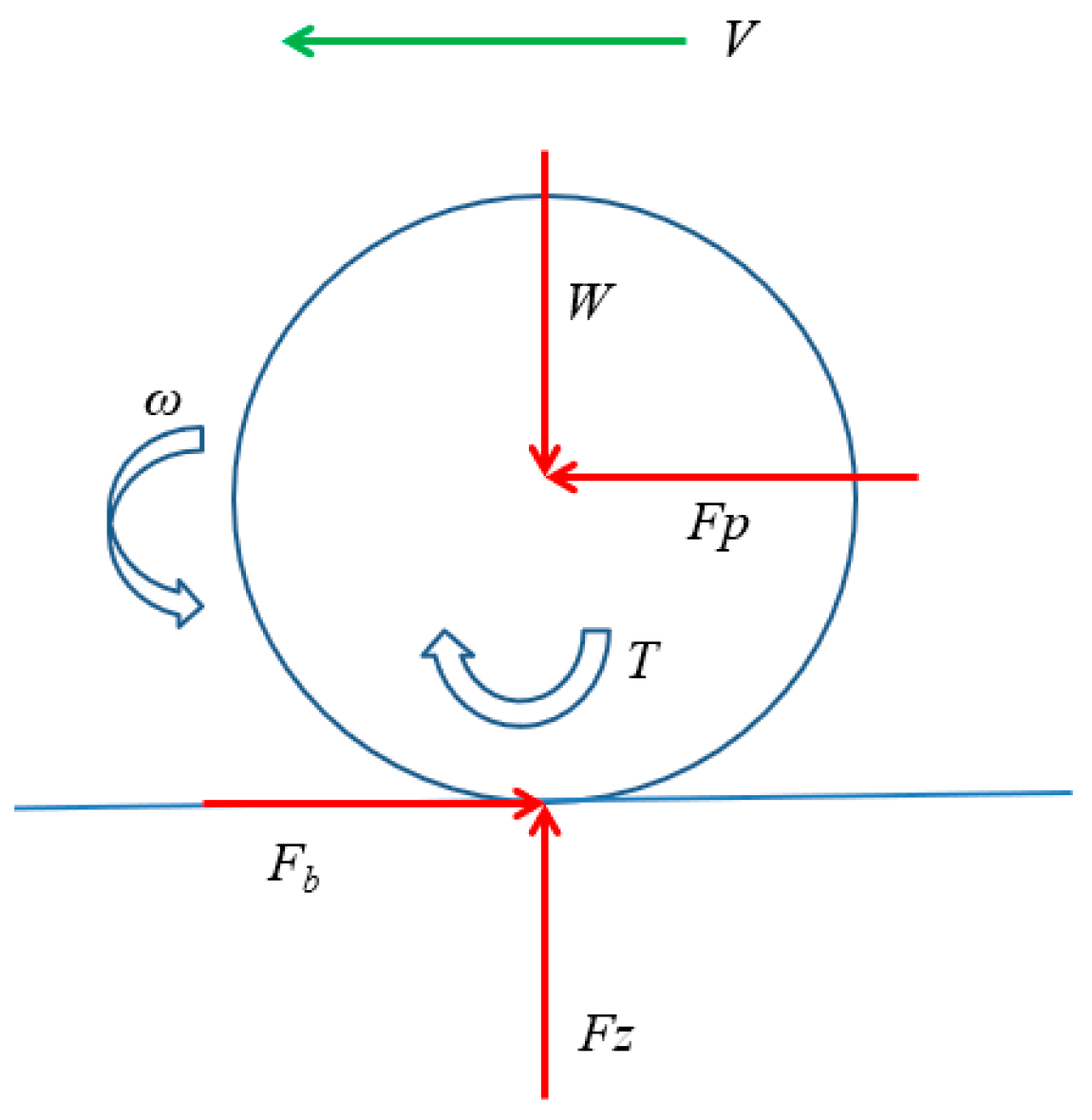
2.2. Rolling Resistance of the Tyre
2.3. Development of a Complete 3D Tyre Model
2.4. Modelling Tyre-Pavement Contact
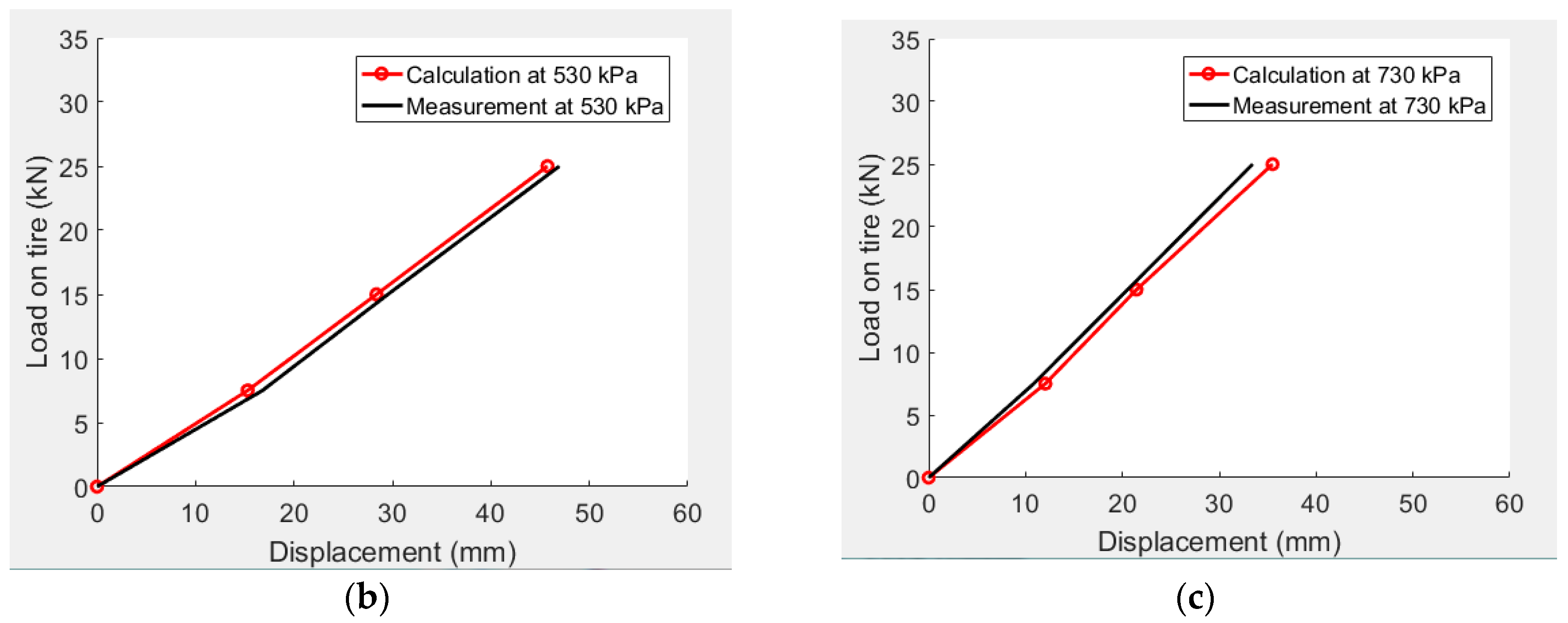
2.5. Validation of the 3D Contact Model
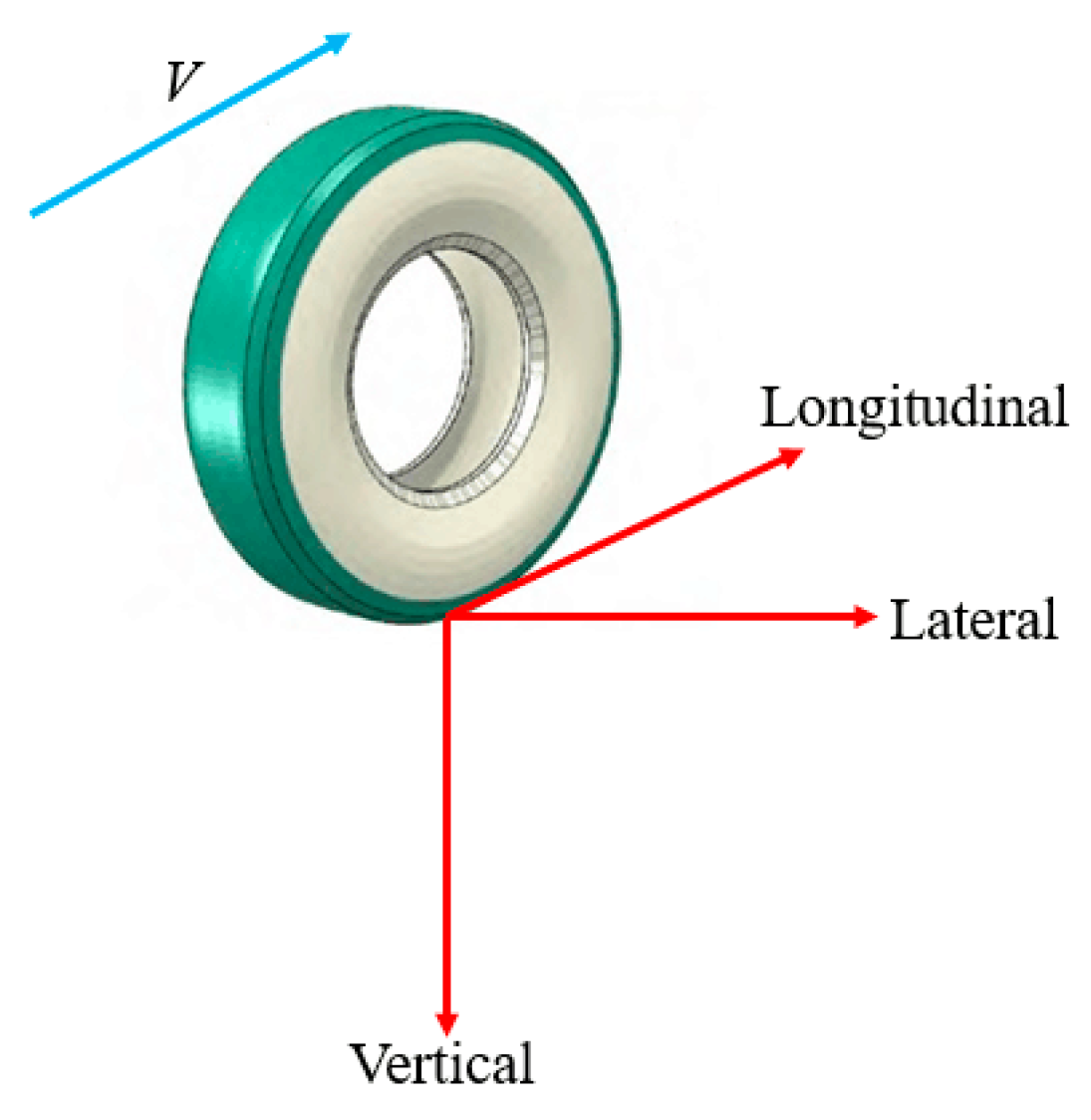
3. Effects of Tyre Working Conditions on Contact Stresses
3.1. Simulation Condition Design of Tyre–Pavement Contact
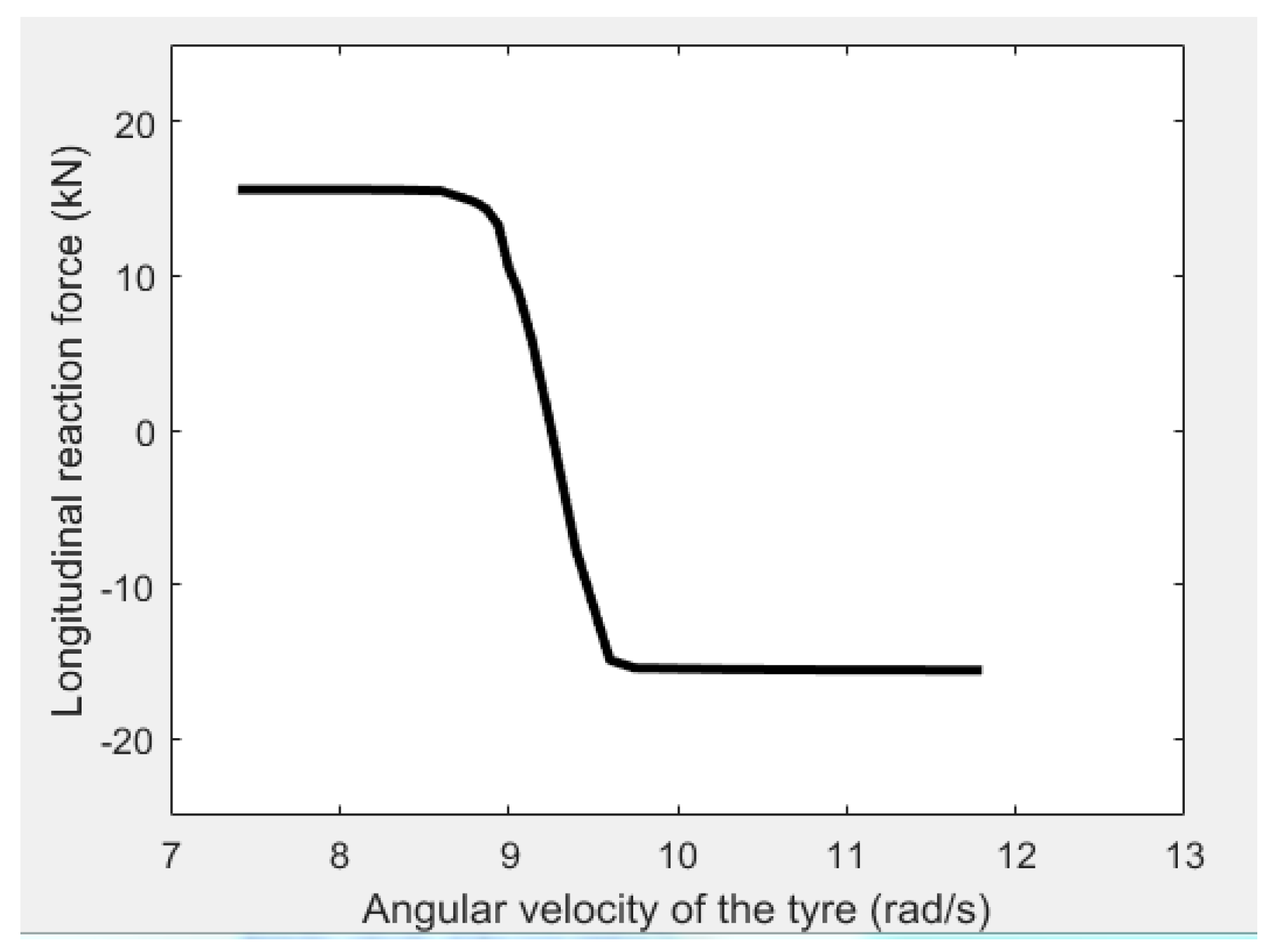
3.2. Realisation of the Steady Rolling State
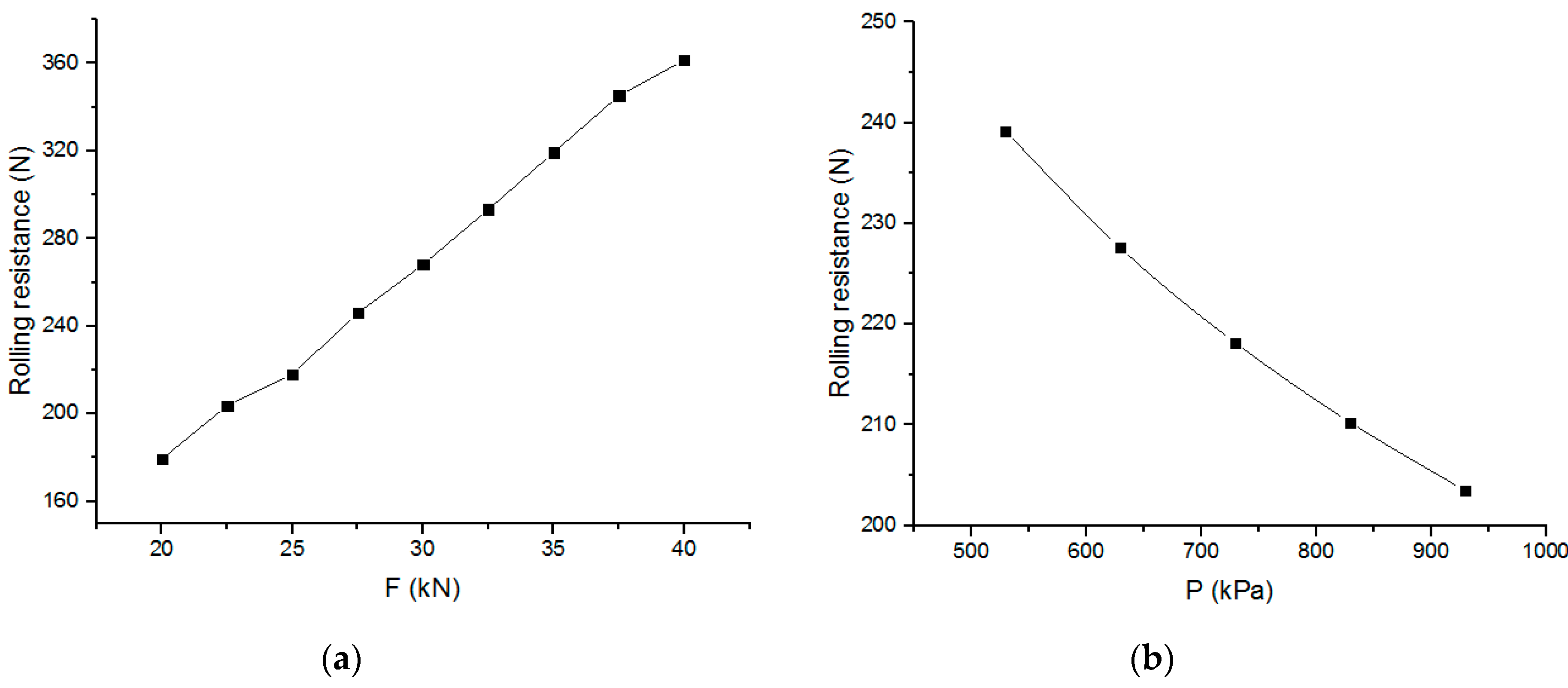
3.3. Effect of Tyre Load on the Change Characteristics of Contact Stresses
3.4. Effect of Inflation Pressure on the Change Characteristics of Contact Stresses
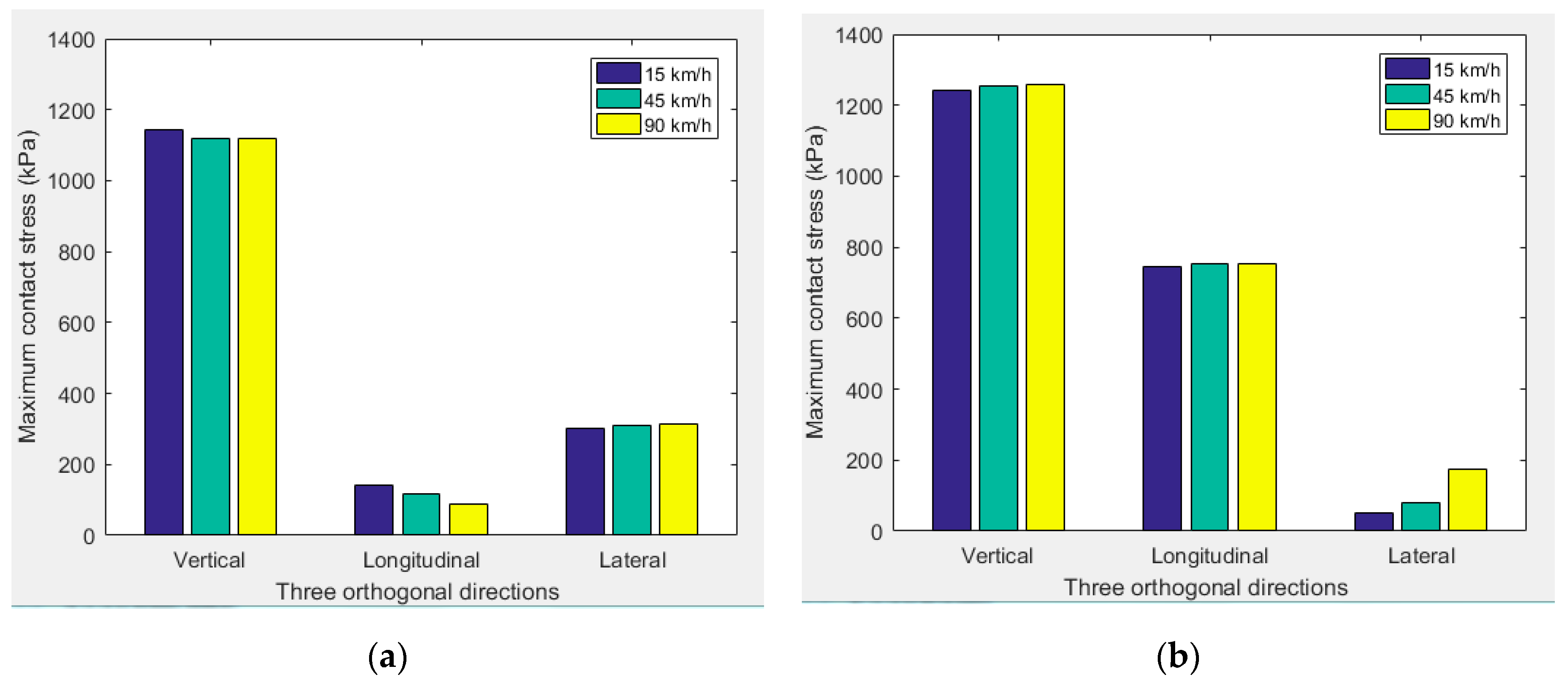
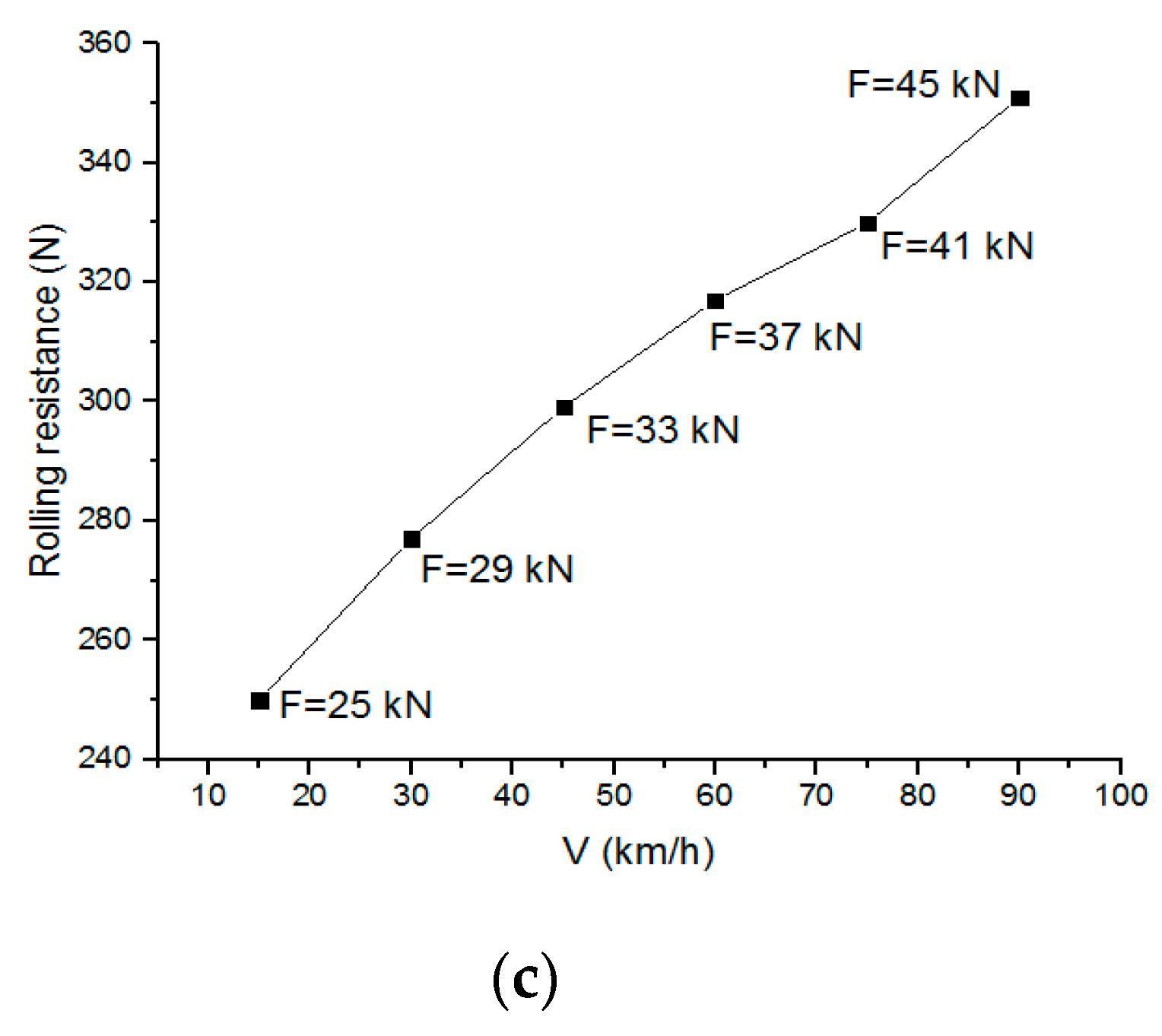
3.5. Effect of the Tyre Speed on the Change Characteristics of Contact Stresses
4. Effects of Tyre Working Conditions on Rolling Resistance
5. Conclusions
- (1)
- The maximum value of the transverse contact stress is greater than the longitudinal contact stress under the free-rolling condition. However, the situation under the full-braking condition is the opposite.
- (2)
- Longitudinal contact stresses under the free-rolling and full-braking conditions were symmetrically distributed in a longitudinal direction, while the lateral contact stress presented an almost antisymmetric distribution in a longitudinal direction. Under the full-braking condition, longitudinal stress is the main component of the horizontal contact stresses.
- (3)
- The tyre load and inflation pressure have significant impacts on contact stresses. Overload and low tyre pressure are important contributors to the wear of the tyre shoulder. Properly increasing the inflation pressure can effectively relieve damage to the tyre shoulder caused by overloading. Additionally, compared with the tyre load and inflation pressure, the impact of tyre speed on contact stress is relatively weak.
- (4)
- The proposed exponential equation describes a method that can forecast the RR related to the working conditions of truck-bus tyres, and a similar method can be used to predict the RRs of other types of tyres.
Author Contributions
Funding
Conflicts of Interest
References
- Guan, Y.J.; Zhao, G.C.; Cheng, G. FEA and testing studies on static camber performance of the radial tire. J. Reinf. Plast. Comp. 2007, 26, 1921–1936. [Google Scholar]
- Guan, Y.J.; Zhao, G.C.; Cheng, G. 3-Dimensional non-linear FEM modeling and analysis of steady-rolling of radial tires. J. Reinf. Plast. Comp. 2011, 30, 229–240. [Google Scholar] [CrossRef]
- Park, S.; Yoo, W.; Cho, J.; Kang, B. Pressure-sensing pad test and computer simulation for the pressure distribution on the contact patch of a tyre. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2007, 221, 25–31. [Google Scholar] [CrossRef]
- Wang, W.; Yan, S.; Zhao, S. Experimental verification and finite element modeling of radial truck tire under static loading. J. Reinf. Plast. Comp. 2013, 32, 490–498. [Google Scholar] [CrossRef]
- De Beer, M.; Fisher, C. Evaluation of non-uniform tire contact stresses on thin asphalt pavements. In Proceedings of the 9th International Conference on Asphalt Pavements, Copenhagen, Denmark, 17–22 August 2002. [Google Scholar]
- Elseifi, M.A.; Al-Qadi, I.L.; Yoo, P.J.; Janajreh, I. Quantification of pavement damage caused by dual and wide-base tires. Transp. Res. Rec. 2005, 1940, 125–135. [Google Scholar] [CrossRef]
- Al-Qadi, I.L.; Yoo, P.J. Effect of surface tangential contact stress on flexible pavement response. In Proceedings of the Journal of Association of Asphalt Paving Technologists: From the Proceedings of the Technical Sessions, San Antonio, TX, USA, 11–14 March 2007. [Google Scholar]
- Al-Qadi, I.L.; Wang, H.; Yoo, P.J.; Dessouky, S.H. Dynamic analysis and in-situvalidation of perpetual pavement response to vehicular loading. Transp. Res. Rec. 2008, 2087, 29–39. [Google Scholar] [CrossRef]
- Wang, H.; Al-Qadi, I.L. Evaluation of surface-related pavement damage due to tire braking. Road. Mater. Pavement. 2010, 11, 101–122. [Google Scholar] [CrossRef]
- Wang, G.; Roque, R. Three-dimensional finite element modeling of static tire–pavement interaction. Transp. Res. Rec. 2010, 2155, 158–169. [Google Scholar] [CrossRef]
- Wang, G.; Roque, R. Impact of wide-based tires on the near-surface pavement stress states based on three-dimensional tire-pavement interaction model. Road. Mater. Pavement. 2011, 12, 639–662. [Google Scholar] [CrossRef]
- Ghosh, S.; Sengupta, R.A.; Kaliske, M. Prediction of rolling resistance for truck bus radial tires with nanocomposite based tread compounds using finite element simulation. Rubber. Chem. Technol. 2014, 87, 276–290. [Google Scholar] [CrossRef]
- Hernandez, J.A.; Al-Qadi, I.L. Semicoupled Modeling of Interaction between Deformable Tires and Pavements. J. Transp. Eng. A Syst. 2017, 143, 1–9. [Google Scholar] [CrossRef]
- De Beer, M.; Fisher, C.; Jooste, F.J. Determination of pneumatic tire pavement interface contact stresses under moving loads and some effects on pavements with thin asphalt surfacing layers. In Proceedings of the 8th International Conference on Asphalt Pavements, Seattle, WA, USA, 10–14 August 1997; pp. 179–227. [Google Scholar]
- Assogba, O.C.; Tan, Y.; Sun, Z.; Lushinga, N.; Zheng, B. Effect of vehicle speed and overload on dynamic response of semi-rigid base asphalt pavement. Road. Mater. Pavement. 2019, 1–31. [Google Scholar] [CrossRef]
- Si, C.; Chen, E.; You, Z.; Zhang, R.; Qiao, P.; Feng, Y. Dynamic response of temperature-seepage-stress coupling in asphalt pavement. Constr. Build. Mater. 2019, 211, 824–836. [Google Scholar] [CrossRef]
- Alireza, S. Numerical comparison of flexible pavement dynamic response under different axles. Int. J. Pavement. Eng. 2016, 17, 377–387. [Google Scholar]
- Tarefder, R.A.; Ahmed, M.U.; Islam, M.R. Impact of cross-anisotropy on embedded sensor stress–strain and pavement damage. Eur. J. Environ. Civ. Eng. 2014, 18, 845–861. [Google Scholar] [CrossRef]
- Ahmed, M.U.; Rahman, A.; Islam, M.R.; Tarefder, R.A. Combined effect of asphalt concrete cross-anisotropy and temperature variation on pavement stress–strain under dynamic loading. Constr. Build. Mater. 2015, 93, 685–694. [Google Scholar] [CrossRef]
- Tarefder, R.A.; Ahmed, M.U.; Rahman, A. Effects of cross-anisotropy and stress-dependency of pavement layers on pavement responses under dynamic truck loading. J. Rock. Mech. Geotech. Eng. 2016, 8, 366–377. [Google Scholar] [CrossRef]
- Wang, H.; Al-Qadi, I.L.; Stanciulescu, I. Simulation of tyre–pavement interaction for predicting contact stresses at static and various rolling conditions. Int. J. Pavement Eng. 2012, 13, 310–321. [Google Scholar] [CrossRef]
- Wang, H.; Al-Qadi, I.L.; Stanciulescu, I. Effect of surface friction on tire-pavement contact stress during vehicle maneuvering. J. Eng. Mech. 2014, 140, 1–8. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, G.; Ding, Y. Effect of Friction Model and Tire Maneuvering on Tire-Pavement Contact Stress. Adv. Mater. Sci. Eng. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Cho, J.R.; Lee, H.W.; Jeong, W.B.; Jeong, K.M.; Kim, K.W. Finite element estimation of hysteretic loss and rolling resistance of 3-D patterned tire. Int. J. Mech. Mater. Des. 2013, 9, 355–366. [Google Scholar] [CrossRef]
- Aldhufairi, H.S.; Essa, K. Tire rolling-resistance computation based on material viscoelasticity representation. Adv. Automot. Eng. 2019, 2, 167–183. [Google Scholar]
- Rafei, M.; Ghoreishy, M.H.R.; Naderi, G. Computer simulation of tire rolling resistance using finite element method: Effect of linear and nonlinear viscoelastic models. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 233, 2746–2760. [Google Scholar] [CrossRef]
- Anghelache, G.; Moisescu, R.; Sorohan, S.; Buretea, D. Measuring system for investigation of tri-axial stress distribution across the tyre–road contact patch. Measurement 2011, 44, 559–568. [Google Scholar] [CrossRef]
- Anghelache, G.; Moisescu, R. Measurement of stress distributions in truck tyre contact patch in real rolling conditions. Vehicle. Syst. Dyn. 2012, 50, 1747–1760. [Google Scholar] [CrossRef]
- De Beer, M.; Fisher, C. Stress-In-Motion (SIM) system for capturing tri-axial tyre–road interaction in the contact patch. Measurement 2013, 46, 2155–2173. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, X.; Yu, J. Impact of contact stress distribution on skid resistance of asphalt pavements. Constr. Build. Mater. 2017, 133, 330–339. [Google Scholar] [CrossRef]
- Knothe, K.; Wille, R.; Zastrau, B.W. Advanced contact mechanics-Road and rail. Veh. Syst. Dyn. 2001, 35, 361–407. [Google Scholar]
- Hurtford, S. Improving the Quality of Terrain Measurement. Master’s Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2009. [Google Scholar]
- Cho, J.R.; Lee, H.W.; Jeong, W.B.; Jeong, K.M.; Kim, K.W. Numerical estimation of rolling resistance and temperature distribution of 3-D periodic patterned tire. Int. J. Solids. Struct. 2013, 50, 86–96. [Google Scholar]
- Guo, M.; Zhou, X. Tire-Pavement Contact Stress Characteristics and Critical Slip Ratio at Multiple Working Conditions. Adv. Mater. Sci. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Laursen, A.; Stanciulescu, I. An algorithm for incorporation of frictional sliding conditions within a steady state rolling framework. Commun. Numer. Methods Eng. 2006, 22, 301–318. [Google Scholar] [CrossRef]
- Zhang, X. Nonlinear Finite Element Modeling and Incremental Analysis of a Composite Truck Tire Structure. Ph.D. Dissertation, Concordia University, Montreal, QC, Canada, 2001. [Google Scholar]
- Meng, L. Truck Tire/Pavement Interaction Analysis by the Finite Element Method. Ph.D. Dissertation, Michigan State University, East Lansing, MI, USA, 2002. [Google Scholar]
- Ghoreishy, M.H.R.; Malekzadeh, M.; Rahimi, H. A parametric study on the steady state rolling behaviour of a steel-belted radial tyre. Iran. Polym. J. 2007, 16, 539–548. [Google Scholar]
- China Communications Construction Group Road and Bridge Technology Co., Ltd. Specifications for Design of Highway Asphalt Pavement: JTG D50—2017[S]; People’s Transportation Press: Beijing, China, 2017. [Google Scholar]
- Lv, J.; Mao, J.; Feng, Y.; Xiang, Z. Size Designation, Dimensions, Inflation Pressure and Load Capacity for Truck Tyres: GB/T 2977—2016 [S]; China National Standardization Administration: Beijing, China, 2016. [Google Scholar]
- Ye, J. Finite Element Simulation and Validation of All-Steel Radial Truck Tire Rolling Resistance; Tsinghua University: Beijing, China, 2007. [Google Scholar]
- Schuring, D.J. The Rolling Loss of Pneumatic Tires; The Firestone Tire and Rubber Company, Central Research Laboratories: Akron, OH, USA, 1980. [Google Scholar]



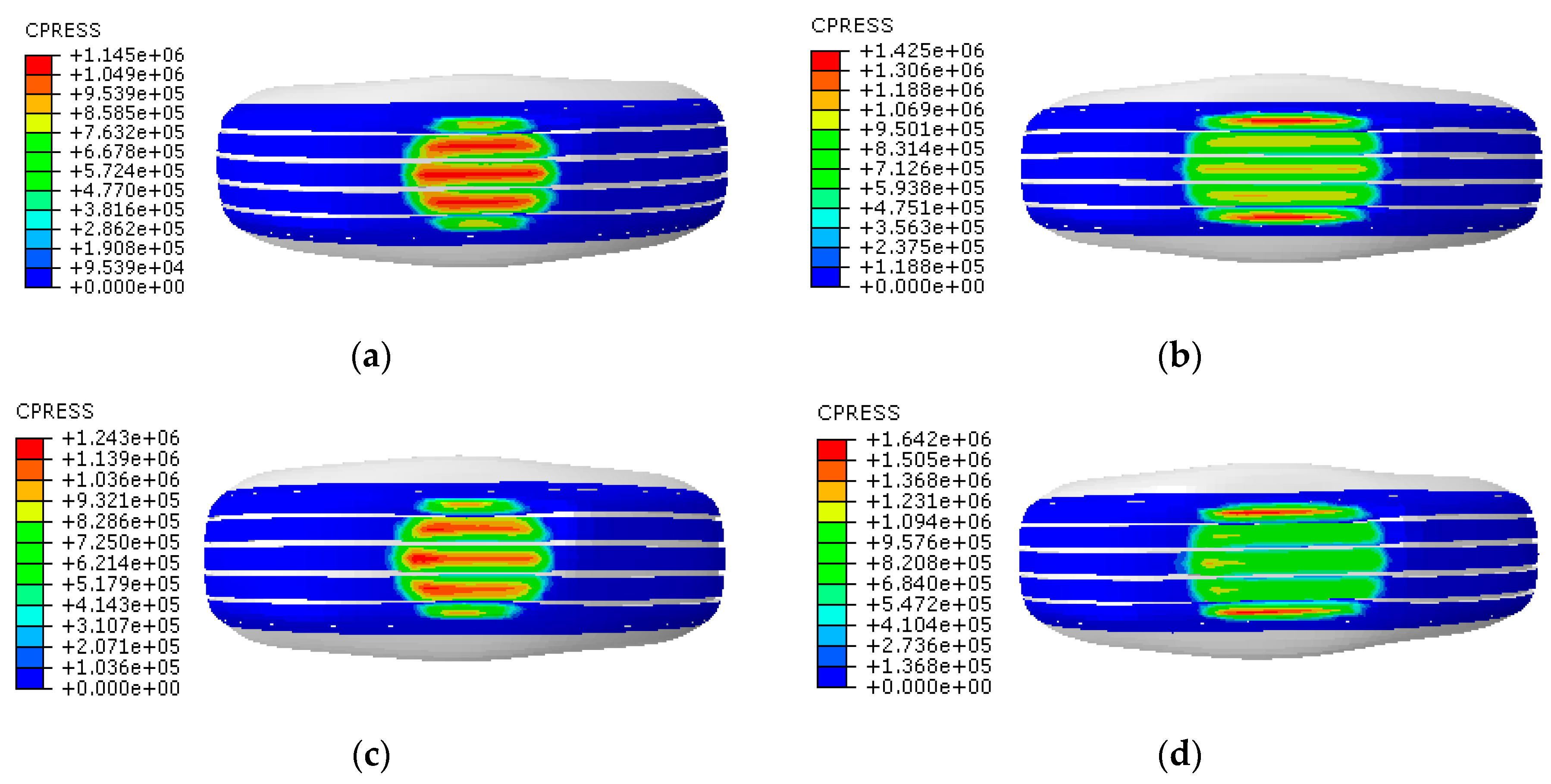

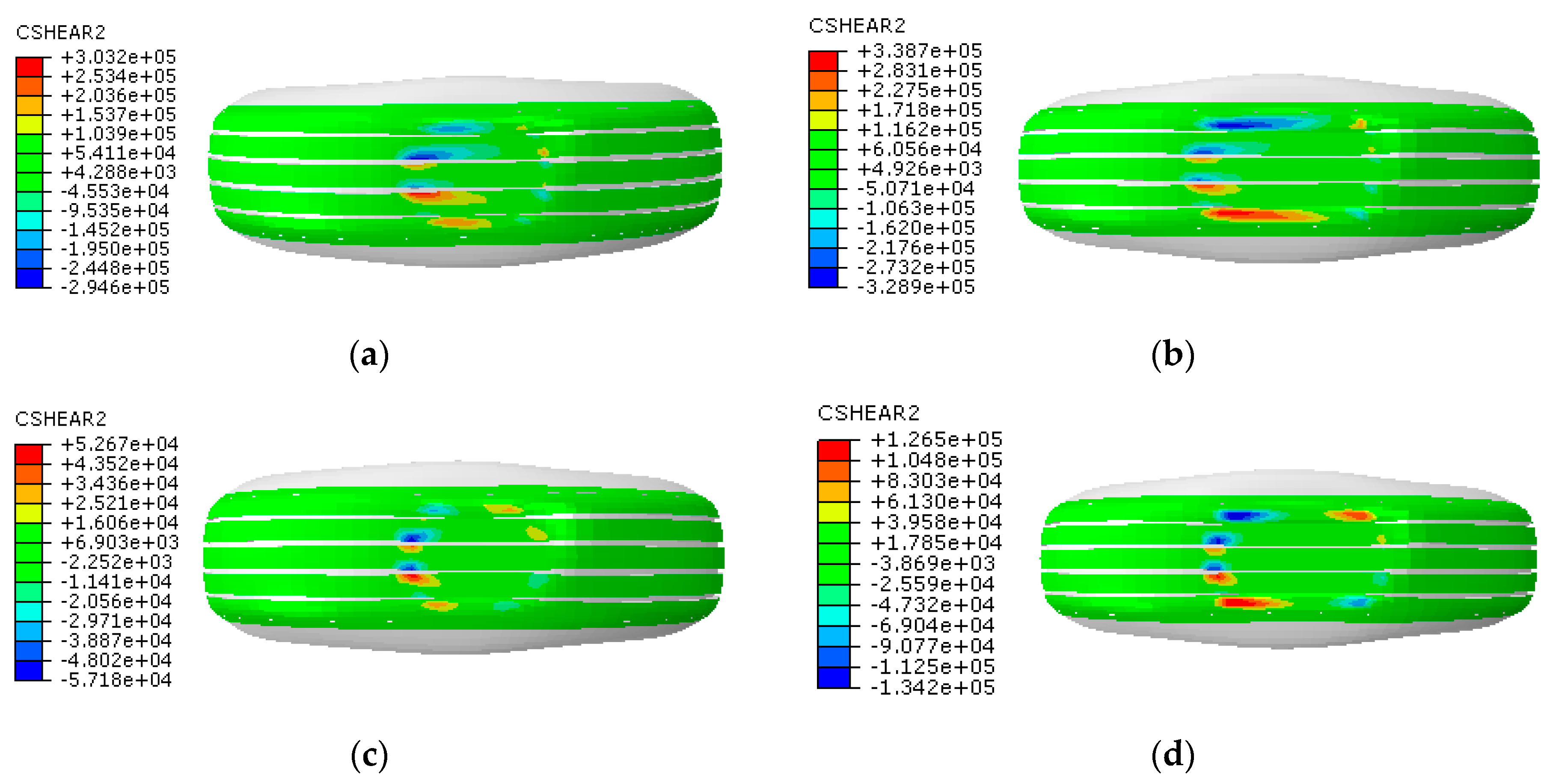
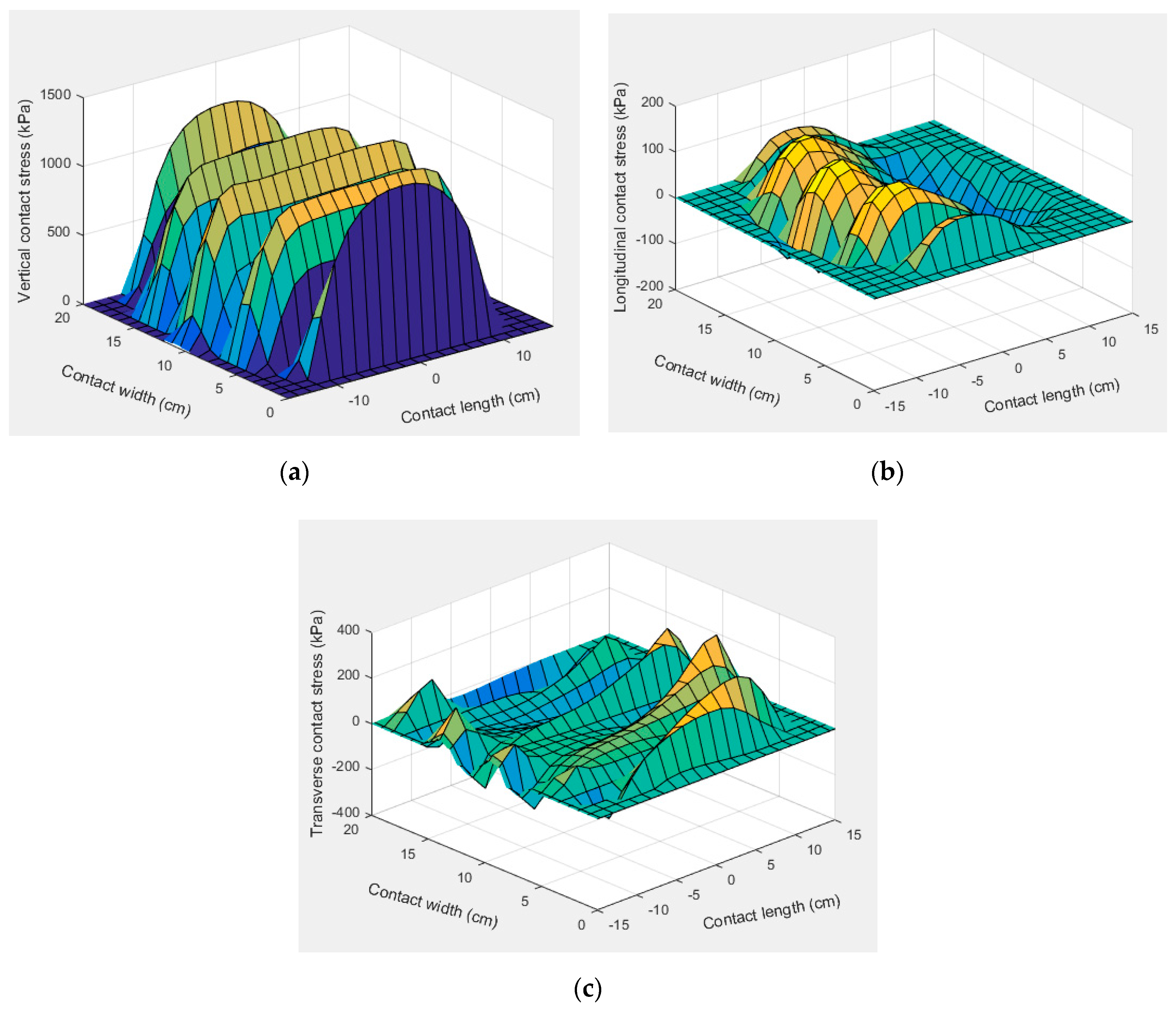
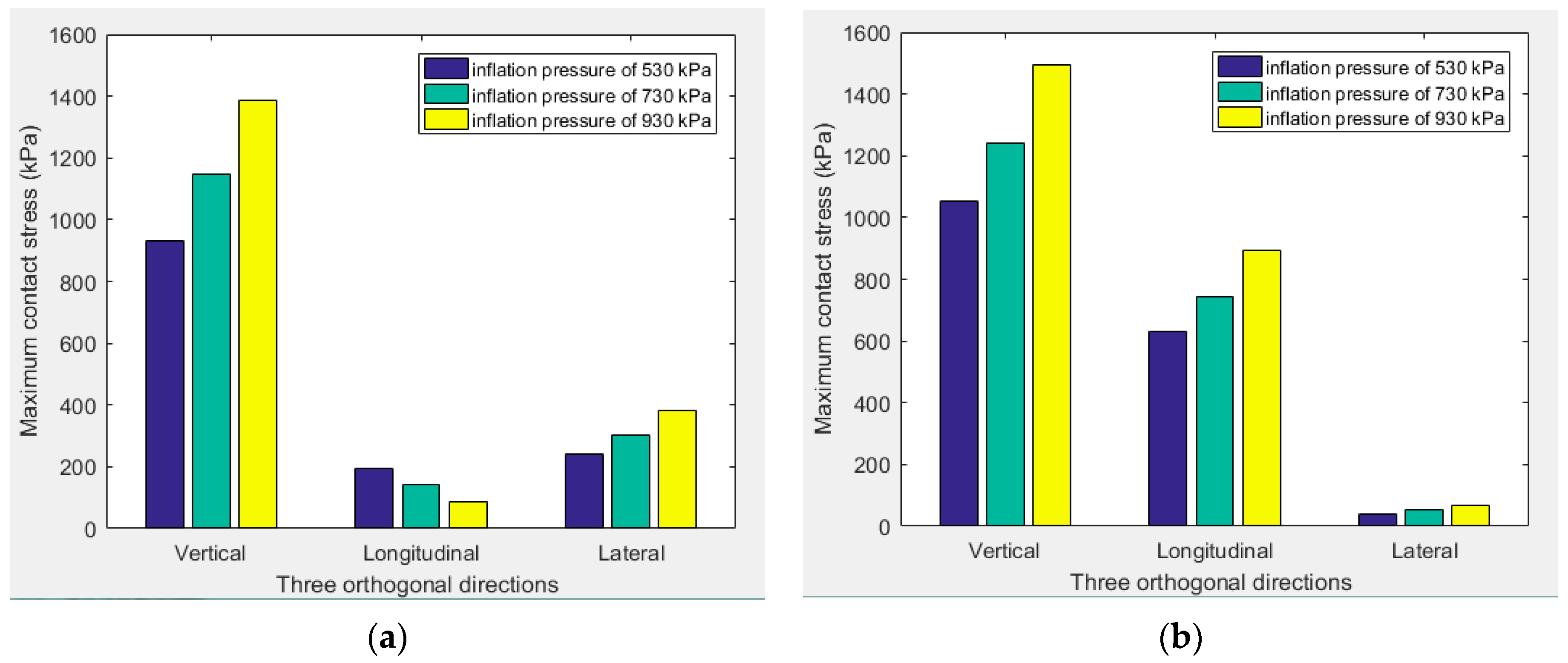

| Inflation Pressure (kPa) | Maximum Contact Stress during Free Rolling (kPa) | Maximum Contact Stress during Full Braking (kPa) | ||||
|---|---|---|---|---|---|---|
| Vertical | Longitudinal | Lateral | Vertical | Longitudinal | Lateral | |
| 530 | 931 | 194 | 240 | 1052 | 631 | 40 |
| 730 | 1145 | 142 | 303 | 1243 | 745 | 52 |
| 930 | 1386 | 86 | 381 | 1495 | 896 | 66 |
| Speed (km/h) | Maximum Contact Stress During Free Rolling (kPa) | Maximum Contact Stress During Full Braking (kPa) | ||||
|---|---|---|---|---|---|---|
| Vertical | Longitudinal | Lateral | Vertical | Longitudinal | Lateral | |
| 15 | 1145 | 142 | 303 | 1243 | 745 | 52 |
| 45 | 1120 | 116 | 308 | 1254 | 752 | 82 |
| 90 | 1117 | 87 | 315 | 1256 | 753 | 175 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, M.; Li, X.; Ran, M.; Zhou, X.; Yan, Y. Analysis of Contact Stresses and Rolling Resistance of Truck-Bus Tyres under Different Working Conditions. Sustainability 2020, 12, 10603. https://doi.org/10.3390/su122410603
Guo M, Li X, Ran M, Zhou X, Yan Y. Analysis of Contact Stresses and Rolling Resistance of Truck-Bus Tyres under Different Working Conditions. Sustainability. 2020; 12(24):10603. https://doi.org/10.3390/su122410603
Chicago/Turabian StyleGuo, Minrui, Xiangwen Li, Maoping Ran, Xinglin Zhou, and Yuan Yan. 2020. "Analysis of Contact Stresses and Rolling Resistance of Truck-Bus Tyres under Different Working Conditions" Sustainability 12, no. 24: 10603. https://doi.org/10.3390/su122410603
APA StyleGuo, M., Li, X., Ran, M., Zhou, X., & Yan, Y. (2020). Analysis of Contact Stresses and Rolling Resistance of Truck-Bus Tyres under Different Working Conditions. Sustainability, 12(24), 10603. https://doi.org/10.3390/su122410603




