Sustainability of Reinforced Concrete Beams with/without BF Influenced by Cracking Capacity and Chloride Diffusion
Abstract
:1. Introduction
2. Experiment Method
2.1. Raw Materials and Mix Proportion of Tested Concrete
2.2. Test Methods and Exposure Environment
2.3. Chloride Concentrations Measure Method
2.4. Calculation Model for Chloride Diffusion Coefficients in Concrete under Flexural Loads
3. Theoretic Analytical Methods
3.1. Life Cycle Assessment (LCA)
Goal and Scope Definition
3.2. Life Cycle Inventory and Impact Assessment
4. Results and Discussion
4.1. Related Parameters Profile of Chloride Diffusion
4.1.1. Free Chloride Ion Concentration in Concrete
4.1.2. Chloride Diffusion Coefficients in Concrete
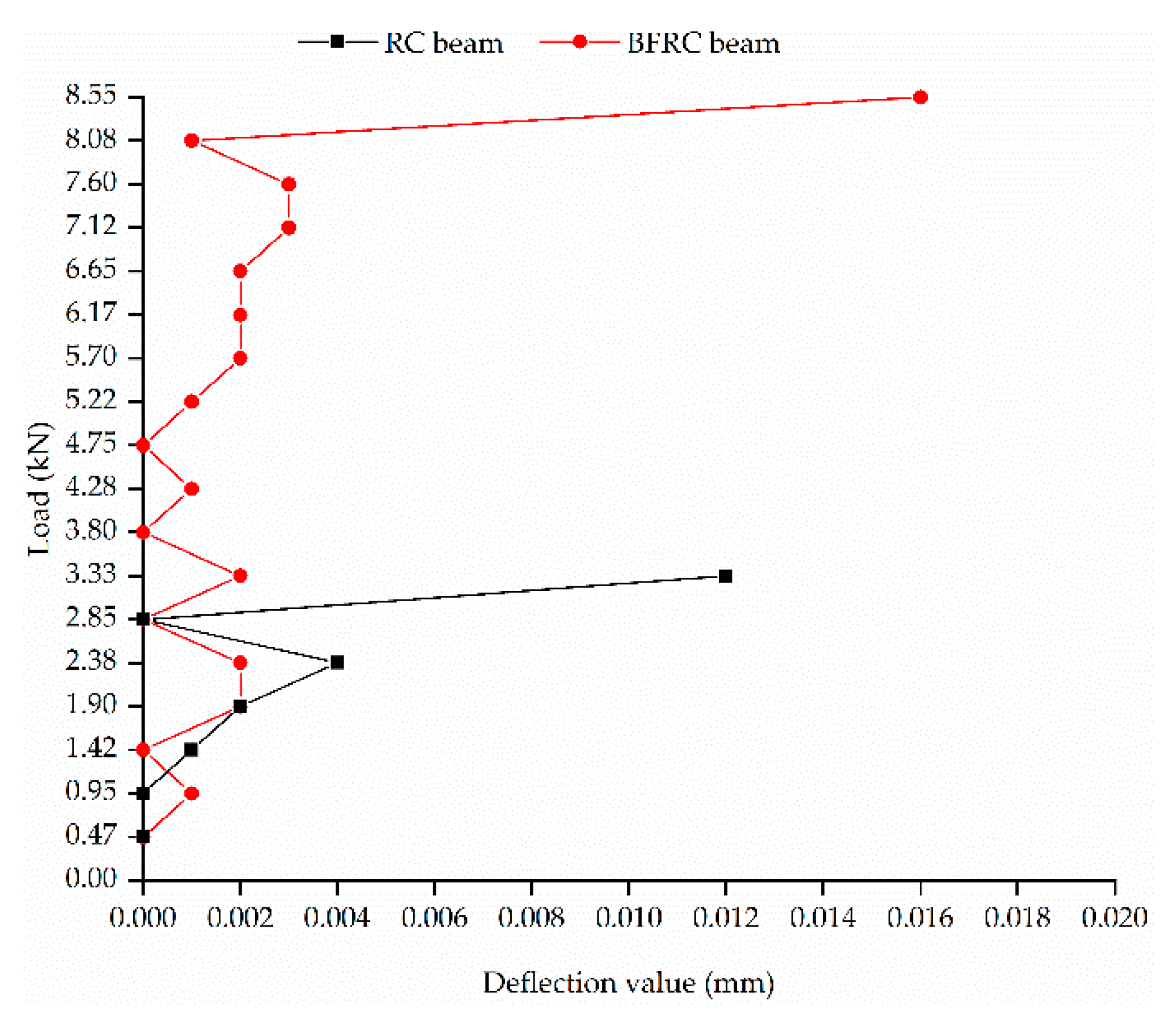
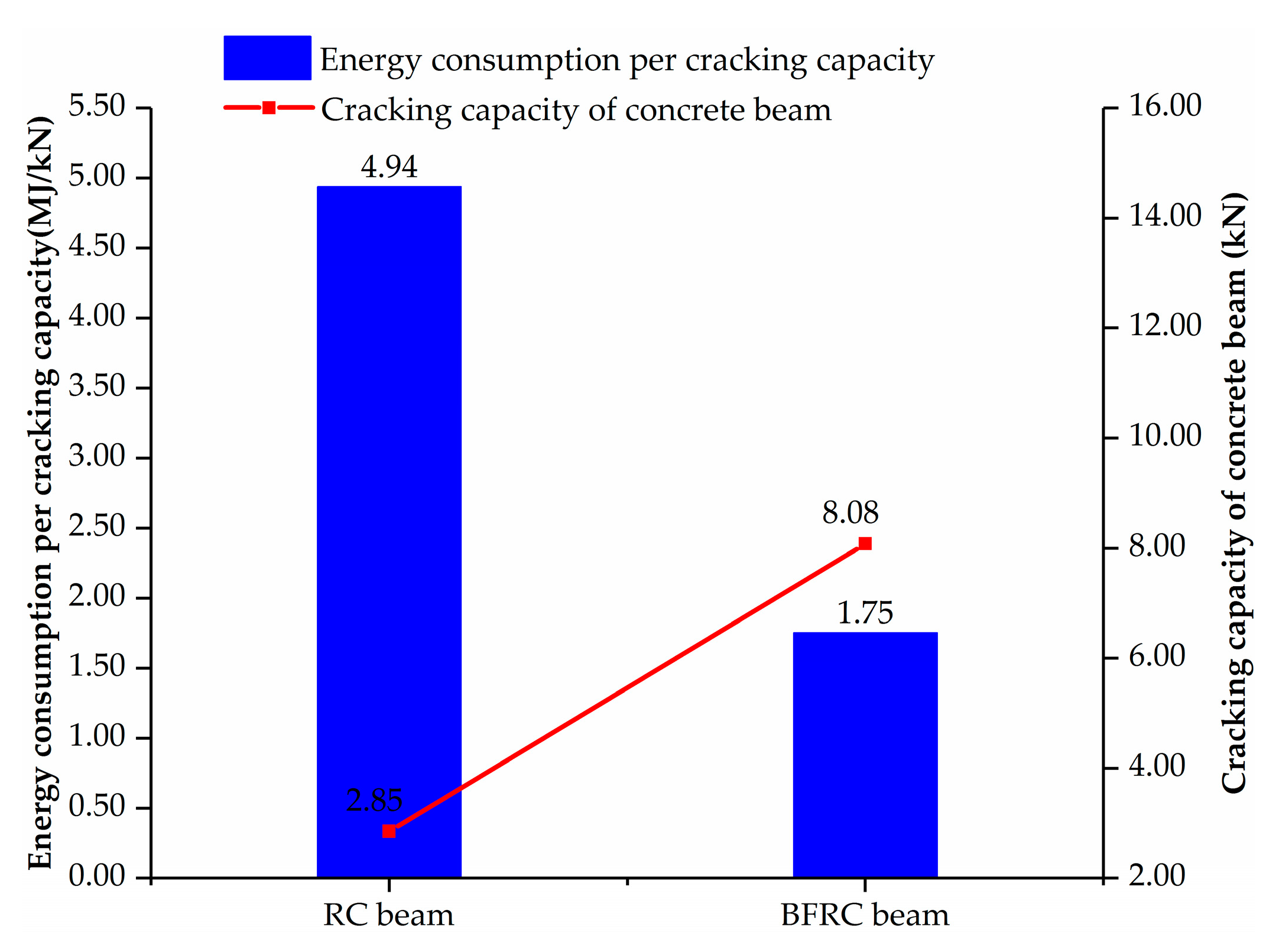
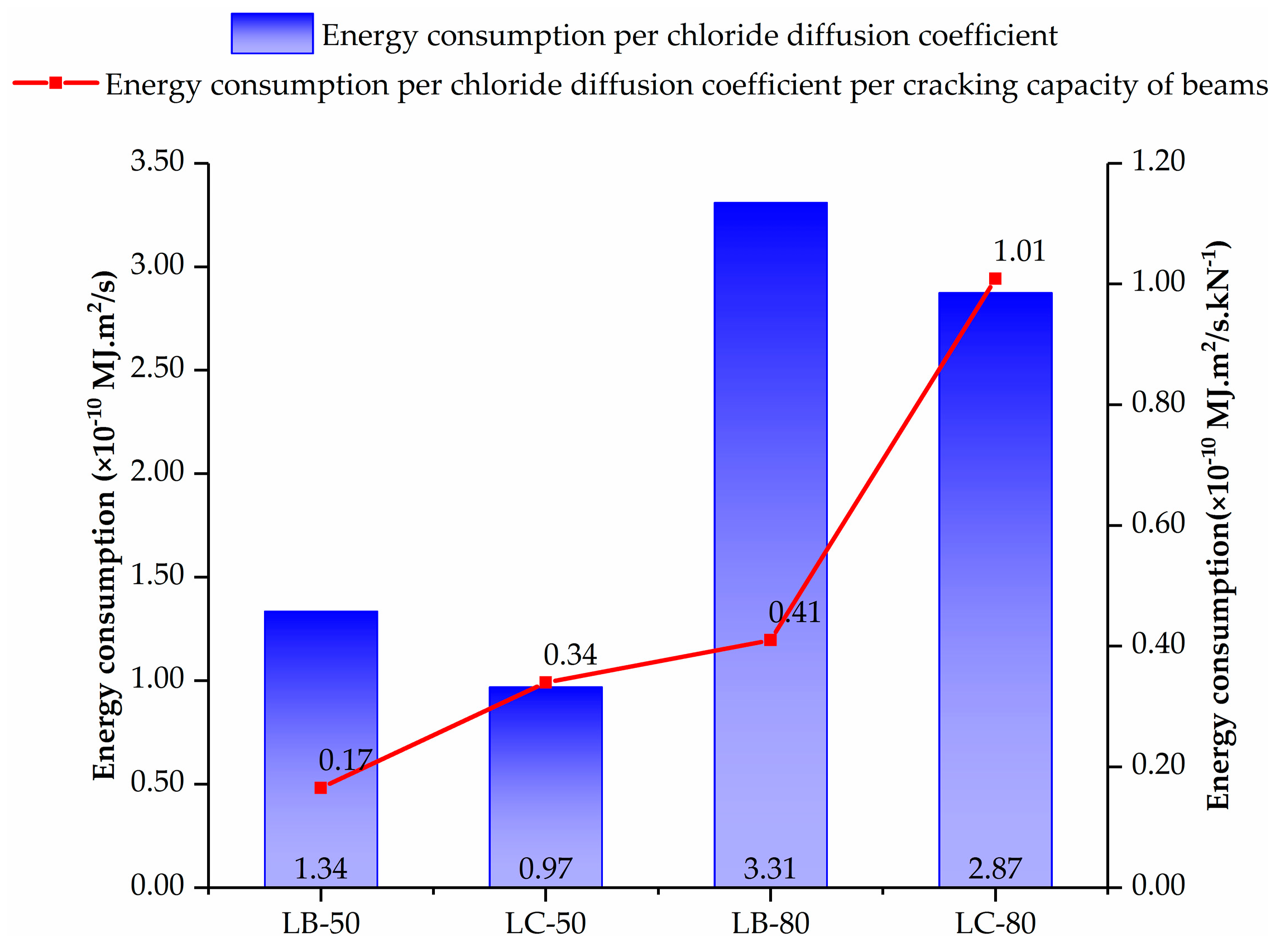
4.2. Energy Consumption of Concrete Member with/without BF under Different Stress Levels
5. Conclusions and Limitations
5.1. Conclusions
5.2. Limitations
Author Contributions
Funding
Conflicts of Interest
References
- Fiore, V.; Scalici, T.; Di Bella, G.; Valenza, A. A review on basalt fibre and its composites. Compos. Part B Eng. 2015, 74, 74–94. [Google Scholar] [CrossRef]
- Ramakrishnan, V.; Panchalan, R.K. A new construction Material-Non-corrosive basalt bar reinforced concrete. Spec. Publ. 2005, 229, 253–270. Available online: https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/14741 (accessed on 1 October 2019).
- Elshafie, S.; Whittleston, G. A Review of the Effect of Basalt Fibre Lengths and Proportions on the Mechanical Properties of Concrete. Int. J. Res. Eng. Technol. 2015, 4, 458–465. [Google Scholar]
- Katkhuda, H.; Shatarat, N. Improving the mechanical properties of recycled concrete aggregate using chopped basalt fibers and acid treatment. Constr. Build. Mater. 2017, 140, 328–335. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, B.; Xie, A.; Qi, Y. Experimental study on dynamic mechanical properties and constitutive model of basalt fiber reinforced concrete. Constr. Build. Mater. 2017, 152, 154–167. [Google Scholar] [CrossRef]
- Mehta, P.K. Durability of concrete-fifty years of progress. ACI Spec. Publ. 1991, 126, 1–32. Available online: https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/1998 (accessed on 1 October 2019).
- Suryavanshi, A.K.; Swamy, R.N.; Cardew, G.E. Estimation of diffusion coefficients for chloride ion penetration into structural concrete. Mater. J. 2002, 99, 441–449. [Google Scholar]
- Zhu, H. Experimental Study on Durability of Basalt Fiber Concrete. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2009. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10497-2009102680.htm (accessed on 1 October 2019). (In Chinese).
- Ghahari, S.A.; Ramezanianpour, A.M.; Esmaeili, M. An Accelerated Test Method of Simultaneous Carbonation and Chloride Ion Ingress: Durability of Silica Fume Concrete in Severe Environments. Adv. Mater. Sci. Eng. 2016, 2016, 1–12. Available online: https://www.hindawi.com/journals/amse/2016/1650979/ (accessed on 1 October 2019). [CrossRef] [Green Version]
- Al-Kutti, W.A.; Rahman, M.K.; Shazali, M.A.; Baluch, M.H. Enhancement in Chloride Diffusivity due to Flexural Damage in Reinforced Concrete Beams. J. Mater. Civ. Eng. 2014, 26, 658–667. [Google Scholar] [CrossRef]
- Wu, J.; Li, H.; Wang, Z.; Liu, J. Transport model of chloride ions in concrete under loads and drying-wetting cycles. Constr. Build. Mater. 2016, 112, 733–738. [Google Scholar] [CrossRef]
- Wang, H.; Lu, C.; Jin, W.; Bai, Y. Effect of External Loads on Chloride Transport in Concrete. J. Mater. Civ. Eng. 2011, 23, 1043–1049. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, C.; Cui, Y. Experiments of Chloride Ingression in Loaded Concrete Members under the Marine Environment. J. Mater. Civ. Eng. 2014, 26, 04014012. [Google Scholar] [CrossRef]
- International Standard Organization (ISO). ISO 14040-Environmental Management-Life Cycle Assessment-Principles and Framework; International Organization for Standardization: Geneva, Switzerland, 2006; Available online: https://www.iso.org/standard/37456.html (accessed on 1 October 2019).
- Jamshaid, H.; Mishra, R. A green material from rock: basalt fiber—A review. J. Text. Inst. Proc. Abstracts 2016, 107, 923–937. [Google Scholar] [CrossRef]
- De Fazio, P. Basalt fibra: from earth an ancient material for innovative and modern application. Energia, Ambiente Innovazione 2011, 3, 89–96. Available online: https://www.researchgate.net/publication/298105370_Basalt_fiber_From_earth_an_ancient_material_for_innovative_and_modern_application (accessed on 1 October 2019).
- Zhang, J.; Zheng, Y.; Wang, J.; Zhang, Y.; Gao, Y. Chloride Transport in Concrete under Flexural Loads in a Tidal Environment. J. Mater. Civ. Eng. 2018, 30, 04018285. [Google Scholar] [CrossRef]
- GB/T 50152–2012. Standard for Test Method of Concrete Structures. 2012. Available online: http://www.mohurd.gov.cn/wjfb/201203/t20120326_209263.html (accessed on 1 October 2019).
- China Meteorological Data, Qiantang River Weather. Available online: http://www.weatherr40d/101210305.shtml (accessed on 1 March 2019).
- Gao, Y.-H.; Zhang, J.-Z.; Zhang, S.; Zhang, Y.-R. Probability distribution of convection zone depth of chloride in concrete in a marine tidal environment. Constr. Build. Mater. 2017, 140, 485–495. [Google Scholar] [CrossRef]
- China Association for Engineering Construction Standardization (CECS). Standard for Durability Assessment of Concrete Structures; CECS: Beijing, China, 2007; Available online: http://www.cecs.org.cn/a/infos/xiehuibiaozhun/2013/0921/619.html (accessed on 1 October 2019). (In Chinese)
- International Standard Organization (ISO). ISO 14044: Environmental Management-Life Cycle Assessment-Requirements and Guidelines; International Organization for Standardization: Geneva, Switzerland, 2006; Available online: https://www.iso.org/standard/38498.html (accessed on 1 October 2019).
- Hischier, R.; Reichart, I. Multifunctional electronic media-traditional media: The problem of an adequate functional unit. Int. J. Life Cycle Assess. 2003, 8, 201–208. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Dale, B. Ethanol Fuels: E10 or E85—Life Cycle Perspectives. Int. J. Life Cycle Assess. 2006, 11, 117–121. [Google Scholar] [CrossRef]
- Damineli, B.L.; Kemeid, F.M.; Aguiar, P.S.; John, V.M. Measuring the eco-efficiency of cement use. Cem. Concr. Compos. 2010, 32, 555–562. [Google Scholar] [CrossRef]
- Picandet, V.; Khelidj, A.; Bellegou, H. Crack effects on gas and water permeability of concretes. Cem. Concr. Res. 2009, 39, 537–547. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Hu, S.; Zhang, J.; Cai, C.; Li, L.-Y. Influence of cracks on chloride diffusivity in concrete: A five-phase mesoscale model approach. Constr. Build. Mater. 2019, 197, 587–596. [Google Scholar] [CrossRef]
- Chen, L. The Study on Chloride Corrosion and Bending Cracking Performance of CRC Reinforced Concrete Beams. Master’s Thesis, Tianjin University, Tianjin, China, 2009. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10056-2010090595.htm (accessed on 1 October 2019). (In Chinese).
- Müller, H.S.; Haist, M.; Vogel, M. Assessment of the sustainability potential of concrete and concrete structures considering their environmental impact, performance and lifetime. Constr. Build. Mater. 2014, 67, 321–337. [Google Scholar] [CrossRef]
- Gu, L. Research on Environmental Impact of China Construction Industry Based on Life Cycle Assessment. Doctoral Dissertation, Tsinghua University, Beijing, China, 2009. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10003-2010214944.htm (accessed on 1 October 2019). (In Chinese).
- Oss, H.G.; Padovani, A.C. Cement Manufacture and the Environment Part II: Environmental Challenges and Opportunities. J. Ind. Ecol. 2003, 7, 93–126. [Google Scholar] [CrossRef] [Green Version]
- Wang, S. Study on life Cycle Environmental Impact Assessment of Commercial Concrete. Master’s Thesis, Tsinghua University, Beijing, China, 2009. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10003-2010215358.htm (accessed on 1 October 2019). (In Chinese).
- Huijbregts, M. Uncertainty and variability in environmental life-cycle assessment. Int. J. Life Cycle Assess. 2001, 7, 173. [Google Scholar] [CrossRef] [Green Version]
- Weidema, B.P.; Wesnæs, M.S. Data quality management for life cycle inventories—An example of using data quality indicators. J. Clean. Prod. 1996, 4, 167–174. [Google Scholar] [CrossRef]



| No. | Cement | Sand | Gravel | Water | BF | 28 d Compressive Strength (MPa) | |
|---|---|---|---|---|---|---|---|
| Proportion | Mass | ||||||
| C | 316.70 | 596.50 | 1269.10 | 190.00 | / | / | 18.80 |
| B | 316.70 | 596.50 | 1269.10 | 190.00 | 0.10% | 0.29 | 20.10 |
| No. | Load Level/% | Load F/kN | No. | Load Level/% | Load F/kN |
|---|---|---|---|---|---|
| LC-80 | 80 | 2.28 | LB-80 | 80 | 6.46 |
| LC-50 | 50 | 1.43 | LB-50 | 50 | 4.04 |
| Simulation Environment | Spring | Summer | Autumn | Winter |
|---|---|---|---|---|
| Temperature (°C) | 34 | 53 | 34 | 12 |
| Relative humidity (%) | 78 | 80 | 80 | 75 |
| No. | (MJ) | (MJ/kN) | (×10−10 MJ·m2/s) | (×10−10 MJ·m2/s·kN−1) |
|---|---|---|---|---|
| Detailed description |
| Raw Material | Cement [30] | BF [16] | Coarse Aggregate Fine Aggregate [31] | Water [32] | |
|---|---|---|---|---|---|
| 2358.02 | 18,000.00 | 50.00 | 70.00 | 2.40 | |
| Distance from the Surface of the Tensile Zone of Test Beam (mm) | ||||||
|---|---|---|---|---|---|---|
| No. | 0 | 2 | 4 | 6 | 8 | 10 |
| LC-50 | / | / | / | / | 5.67 | 3.85 |
| LB-50 | / | / | 14.66 | 7.25 | 8.86 | 7.38 |
| LC-80 | / | / | / | / | 17.24 | 14.09 |
| LB-80 | / | / | / | / | / | 14.27 |
| No. | 12 | 14 | 16 | 18 | 20 | Average |
| LC-50 | 4.85 | 5.63 | 8.19 | 8.87 | 11.12 | 6.88 |
| LB-50 | 7.92 | 8.71 | 9.14 | 10.69 | 10.35 | 9.44 |
| LC-80 | 18.41 | 23.80 | 21.54 | 22.66 | 25.27 | 20.43 |
| LB-80 | 20.49 | 25.08 | 28.35 | 24.62 | 27.56 | 23.39 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Mao, C.; Wang, J.; Gao, Y.; Zhang, J. Sustainability of Reinforced Concrete Beams with/without BF Influenced by Cracking Capacity and Chloride Diffusion. Sustainability 2020, 12, 1054. https://doi.org/10.3390/su12031054
Zhang Y, Mao C, Wang J, Gao Y, Zhang J. Sustainability of Reinforced Concrete Beams with/without BF Influenced by Cracking Capacity and Chloride Diffusion. Sustainability. 2020; 12(3):1054. https://doi.org/10.3390/su12031054
Chicago/Turabian StyleZhang, Yurong, Chaojun Mao, Jiandong Wang, Yanhong Gao, and Junzhi Zhang. 2020. "Sustainability of Reinforced Concrete Beams with/without BF Influenced by Cracking Capacity and Chloride Diffusion" Sustainability 12, no. 3: 1054. https://doi.org/10.3390/su12031054




