Analysis of the Indoor Thermal Environment and Passive Energy-Saving Optimization Design of Rural Dwellings in Zhalantun, Inner Mongolia, China
Abstract
:1. Introduction
2. Methodology
2.1. Description of Zhalantun Climate and Local Rural Dwellings
2.2. Measurement of Indoor Thermal Environment
2.3. Investigation of Indoor Thermal Comfort
2.4. Simulation of Energy Consumption
2.5. Orthogonal Experimental Design
2.5.1. Basic Principle
2.5.2. Schematic Design
2.5.3. Data Analysis
3. Results and Discussion
3.1. Analysis of Testing Results
3.2. Threshold Value of Thermal Comfort Temperature
3.2.1. Characteristics of Respondents and Indoor Environment
3.2.2. Thermal Environment Evaluation
3.2.3. Neutral Temperature and Acceptable Temperature Range
3.3. Analysis of Simulation Results
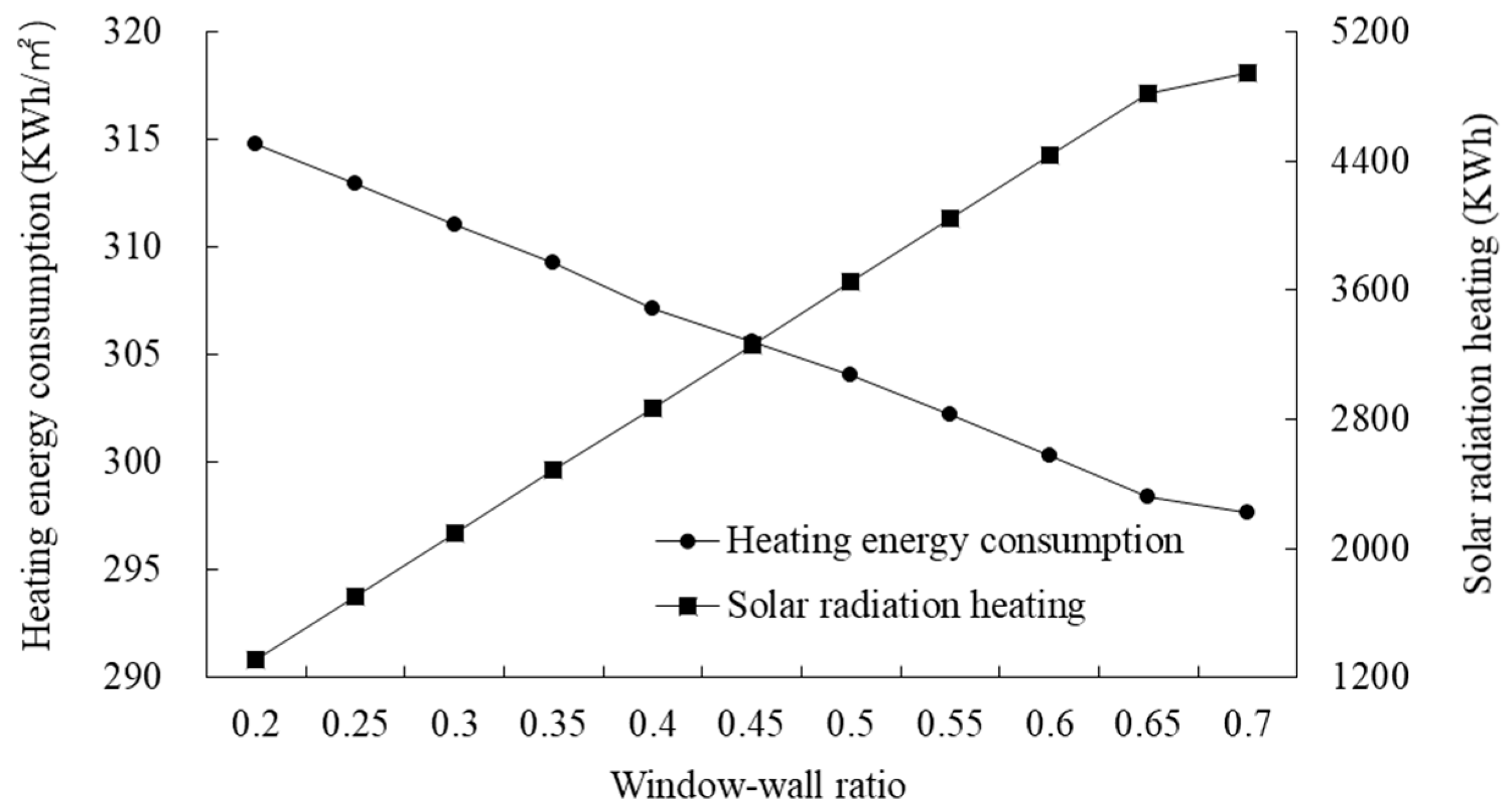
3.3.1. Effect of a Single Factor on Energy Consumption
3.3.2. Comprehensive Optimization for Energy Saving
3.4. Economic Evaluation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| No. | A | B | C | D | E | F | G | H | I | J | Blank Column | Energy Consumption |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | South by east 10° | 1.2 | 2.6 | 70 | 70 | 70 | 2.4 | 0.4 | 0.4 | 1.8 | 4 | 155.98 |
| 2 | South by west 10° | 1.0 | 2.9 | 70 | 130 | 30 | 1.5 | 0.4 | 0.3 | 1.5 | 3 | 145.20 |
| 3 | South by west 10° | 1.2 | 2.6 | 70 | 130 | 30 | 2.7 | 0.3 | 0.4 | 1.5 | 1 | 146.47 |
| 4 | South by west 20° | 1.3 | 2.8 | 70 | 90 | 50 | 2.4 | 0.3 | 0.1 | 1.2 | 4 | 144.45 |
| 5 | South by east 10° | 1.0 | 2.8 | 110 | 110 | 30 | 1.5 | 0.6 | 0.2 | 1.2 | 2 | 131.28 |
| 6 | South by west 20° | 1.0 | 2.9 | 70 | 90 | 50 | 2.7 | 0.5 | 0.3 | 1.2 | 1 | 157.91 |
| 7 | South by west 20° | 1.1 | 2.9 | 90 | 110 | 70 | 2.7 | 0.3 | 0.1 | 1.5 | 2 | 133.38 |
| 8 | South (0°) | 1.2 | 2.6 | 70 | 110 | 90 | 2.1 | 0.5 | 0.4 | 0.9 | 2 | 135.82 |
| 9 | South by west 10° | 1.3 | 2.9 | 110 | 90 | 70 | 1.5 | 0.3 | 0.4 | 0.9 | 2 | 135.67 |
| 10 | South by east 10° | 1.3 | 2.7 | 50 | 90 | 90 | 2.7 | 0.3 | 0.3 | 1.5 | 3 | 155.17 |
| 11 | South by east 10° | 1.3 | 2.8 | 70 | 70 | 70 | 1.5 | 0.5 | 0.1 | 1.8 | 3 | 146.06 |
| 12 | South (0°) | 1.2 | 2.9 | 50 | 130 | 70 | 2.4 | 0.3 | 0.2 | 1.2 | 2 | 155.02 |
| 13 | South by west 10° | 1.1 | 2.7 | 70 | 130 | 30 | 2.4 | 0.5 | 0.2 | 1.5 | 4 | 143.28 |
| 14 | South by west 10° | 1.3 | 2.6 | 90 | 70 | 90 | 2.7 | 0.5 | 0.2 | 1.2 | 2 | 139.40 |
| 15 | South by west 10° | 1.1 | 2.9 | 90 | 70 | 90 | 1.5 | 0.6 | 0.1 | 1.2 | 4 | 139.62 |
| 16 | South (0°) | 1.0 | 2.9 | 70 | 110 | 90 | 2.4 | 0.6 | 0.3 | 0.9 | 4 | 147.16 |
| 17 | South by east 10° | 1.0 | 2.7 | 90 | 130 | 50 | 2.7 | 0.4 | 0.4 | 0.9 | 2 | 137.91 |
| 18 | South by west 20° | 1.2 | 2.9 | 50 | 70 | 30 | 2.7 | 0.4 | 0.2 | 0.9 | 3 | 174.73 |
| 19 | South by east 10° | 1.3 | 2.6 | 90 | 130 | 50 | 2.4 | 0.6 | 0.2 | 0.9 | 3 | 127.30 |
| 20 | South (0°) | 1.3 | 2.6 | 90 | 90 | 30 | 2.1 | 0.3 | 0.2 | 1.8 | 1 | 138.72 |
| 21 | South by west 10° | 1.1 | 2.6 | 110 | 90 | 70 | 2.7 | 0.4 | 0.3 | 0.9 | 4 | 131.43 |
| 22 | South by west 20° | 1.1 | 2.6 | 110 | 130 | 90 | 1.5 | 0.5 | 0.3 | 1.8 | 2 | 113.87 |
| 23 | South by west 10° | 1.3 | 2.8 | 70 | 130 | 30 | 2.1 | 0.6 | 0.1 | 1.5 | 2 | 140.78 |
| 24 | South by east 10° | 1.0 | 2.9 | 70 | 70 | 70 | 2.1 | 0.3 | 0.3 | 1.8 | 2 | 159.35 |
| 25 | South (0°) | 1.3 | 2.7 | 50 | 130 | 70 | 1.5 | 0.6 | 0.3 | 1.2 | 1 | 137.96 |
| 26 | South by west 10° | 1.0 | 2.6 | 50 | 110 | 50 | 2.7 | 0.6 | 0.1 | 1.8 | 3 | 143.93 |
| 27 | South by west 20° | 1.2 | 2.6 | 70 | 90 | 50 | 1.5 | 0.6 | 0.4 | 1.2 | 3 | 138.79 |
| 28 | South by west 10° | 1.2 | 2.9 | 50 | 110 | 50 | 1.5 | 0.5 | 0.2 | 1.8 | 1 | 152.02 |
| 29 | South by west 20° | 1.1 | 2.7 | 70 | 90 | 50 | 2.1 | 0.4 | 0.2 | 1.2 | 2 | 142.79 |
| 30 | South by west 10° | 1.2 | 2.8 | 90 | 70 | 90 | 2.1 | 0.4 | 0.3 | 1.2 | 1 | 146.85 |
| 31 | South by west 20° | 1.0 | 2.7 | 90 | 110 | 70 | 2.1 | 0.6 | 0.4 | 1.5 | 1 | 136.23 |
| 32 | South (0°) | 1.1 | 2.9 | 90 | 90 | 30 | 2.4 | 0.4 | 0.1 | 1.8 | 3 | 148.36 |
| 33 | South (0°) | 1.1 | 2.8 | 50 | 130 | 70 | 2.7 | 0.5 | 0.4 | 1.2 | 3 | 156.61 |
| 34 | South by west 20° | 1.3 | 2.7 | 50 | 70 | 30 | 2.1 | 0.5 | 0.3 | 0.9 | 4 | 167.77 |
| 35 | South by east 10° | 1.0 | 2.6 | 50 | 90 | 90 | 2.4 | 0.5 | 0.1 | 1.5 | 2 | 144.67 |
| 36 | South (0°) | 1.3 | 2.9 | 110 | 70 | 50 | 2.4 | 0.5 | 0.4 | 1.5 | 1 | 161.84 |
| 37 | South (0°) | 1.0 | 2.8 | 110 | 70 | 50 | 2.7 | 0.3 | 0.2 | 1.5 | 4 | 144.51 |
| 38 | South by west 20° | 1.2 | 2.7 | 110 | 130 | 90 | 2.1 | 0.3 | 0.1 | 1.8 | 3 | 114.79 |
| 39 | South by east 10° | 1.2 | 2.8 | 90 | 130 | 50 | 1.5 | 0.3 | 0.3 | 0.9 | 4 | 128.09 |
| 40 | South by east 10° | 1.1 | 2.7 | 70 | 70 | 70 | 2.7 | 0.6 | 0.2 | 1.8 | 1 | 152.08 |
| 41 | South (0°) | 1.1 | 2.7 | 70 | 110 | 90 | 1.5 | 0.3 | 0.2 | 0.9 | 3 | 127.86 |
| 42 | South (0°) | 1.0 | 2.6 | 50 | 130 | 70 | 2.1 | 0.4 | 0.1 | 1.2 | 4 | 134.08 |
| 43 | South (0°) | 1.2 | 2.8 | 90 | 90 | 30 | 2.7 | 0.6 | 0.3 | 1.8 | 2 | 154.77 |
| 44 | South by west 20° | 1.0 | 2.6 | 50 | 70 | 30 | 1.5 | 0.3 | 0.1 | 0.9 | 1 | 154.77 |
| 45 | South by west 20° | 1.0 | 2.8 | 110 | 130 | 90 | 2.4 | 0.4 | 0.2 | 1.8 | 1 | 125.22 |
| 46 | South (0°) | 1.3 | 2.8 | 70 | 110 | 90 | 2.7 | 0.4 | 0.1 | 0.9 | 1 | 133.68 |
| 47 | South by east 10° | 1.3 | 2.9 | 110 | 110 | 30 | 2.1 | 0.4 | 0.4 | 1.2 | 3 | 148.65 |
| 48 | South by east 10° | 1.1 | 2.6 | 110 | 110 | 30 | 2.4 | 0.3 | 0.3 | 1.2 | 1 | 134.54 |
| 49 | South (0°) | 1.1 | 2.6 | 110 | 70 | 50 | 2.1 | 0.6 | 0.3 | 1.5 | 3 | 140.70 |
| 50 | South by west 10° | 1.2 | 2.7 | 110 | 90 | 70 | 2.4 | 0.6 | 0.1 | 0.9 | 1 | 126.70 |
| 51 | South by west 10° | 1.0 | 2.7 | 90 | 70 | 90 | 2.4 | 0.3 | 0.4 | 1.2 | 3 | 148.95 |
| 52 | South by east 10° | 1.1 | 2.9 | 90 | 130 | 50 | 2.1 | 0.5 | 0.1 | 0.9 | 1 | 130.35 |
| 53 | South (0°) | 1.0 | 2.7 | 90 | 90 | 30 | 1.5 | 0.5 | 0.4 | 1.8 | 4 | 142.29 |
| 54 | South (0°) | 1.2 | 2.7 | 110 | 70 | 50 | 1.5 | 0.4 | 0.1 | 1.5 | 2 | 133.12 |
| 55 | South by west 20° | 1.2 | 2.8 | 90 | 110 | 70 | 2.4 | 0.5 | 0.3 | 1.5 | 3 | 141.19 |
| 56 | South by west 20° | 1.1 | 2.8 | 50 | 70 | 30 | 2.4 | 0.6 | 0.4 | 0.9 | 2 | 179.23 |
| 57 | South by west 10° | 1.3 | 2.7 | 50 | 110 | 50 | 2.4 | 0.4 | 0.3 | 1.8 | 2 | 155.47 |
| 58 | South by east 10° | 1.1 | 2.8 | 50 | 90 | 90 | 1.5 | 0.4 | 0.4 | 1.5 | 1 | 151.70 |
| 59 | South by east 10° | 1.2 | 2.9 | 50 | 90 | 90 | 2.1 | 0.6 | 0.2 | 1.5 | 4 | 157.62 |
| 60 | South by east 10° | 1.2 | 2.7 | 110 | 110 | 30 | 2.7 | 0.5 | 0.1 | 1.2 | 4 | 130.63 |
| 61 | South by west 10° | 1.1 | 2.8 | 50 | 110 | 50 | 2.1 | 0.3 | 0.4 | 1.8 | 4 | 158.21 |
| 62 | South by west 20° | 1.3 | 2.6 | 90 | 110 | 70 | 1.5 | 0.4 | 0.2 | 1.5 | 4 | 121.26 |
| 63 | South by west 20° | 1.3 | 2.9 | 110 | 130 | 90 | 2.7 | 0.6 | 0.4 | 1.8 | 4 | 150.39 |
| 64 | South by west 10° | 1.0 | 2.8 | 110 | 90 | 70 | 2.1 | 0.5 | 0.2 | 0.9 | 3 | 131.28 |
References
- Pachauri, R.K.; Reisinger, A. Climate Change 2007. Synthesis Report. Contribution of Working Groups I, II and III to The Fourth Assessment Report. Speculum 2007, 77, 586–588. [Google Scholar]
- Liu, G.; Peng, S.; Liu, J. Research on the development history and trend of abroad building energy saving standards. Constr. Sci. Tech. 2015, 14, 18–23. [Google Scholar]
- Feldmann, C. French building regulation sets 50 kWh/(m2·a) a limit for primary energy use. REHVA J. 2013, 10, 29–32. [Google Scholar]
- Pan, W.; Garmston, H. Building regulations in energy efficiency: Compliance in England and Wales. Energy Policy 2012, 45, 594–605. [Google Scholar] [CrossRef]
- Hou, S.; Thomas, A.; Jones, P.J. A detailed review of the development of building regulations in relation to energy efficiency and carbon reduction in the UK. Synchrotron Radiat. News 2015, 8, 19–21. [Google Scholar]
- Melo, A.P.; Sorgato, M.J. Lamberts R. Building energy performance assessment: Comparison between ASHRAE standard 90.1 and Brazilian regulation. Energy Build. 2014, 70, 372–383. [Google Scholar] [CrossRef]
- Lau, L.C.; Tan, K.T.; Lee, K.T.; Mohamed, A.R. A comparative study on the energy policies in Japan and Malaysia in fulfilling their nations’ obligations towards the Kyoto Protocol. Energy Policy 2009, 37, 4771–4778. [Google Scholar] [CrossRef]
- Evans, M.; Shui, B.; Takagi, T. Country Report on Building Energy Codes in Japan; Pacific Northwest National Laboratory: Richland, WA, USA, 2009; pp. 100–103.
- Building Energy Conservation Research Center, Tsinghua University. Annual Development Research Report of China Building Energy Conservation; China Architecture & Building Press: Beijing, China, 2012. [Google Scholar]
- Building Energy Statistics Committee, China Association of Building Energy Efficiency. Research Report of China Building Energy Consumption (2016); China Association of Building Energy Efficiency: Shanghai, China, 2017. [Google Scholar]
- Building Energy Statistics Committee, China Association of Building Energy Efficiency. Research Report of China Building Energy Consumption (2017); China Association of Building Energy Efficiency: Shanghai, China, 2018. [Google Scholar]
- Ministry of Housing and Urban–Rural Development of PRC. The 13th Five-Year Plan of Building Energy Conservation and Green Building Development; Ministry of Housing and Urban–Rural Development of PRC: Beijing, China, 2017.
- Hamdy, M.; Hasan, A.; Kai, S. Applying a multi-objective optimization approach for Design of low-emission cost-effective dwellings. Build. Environ. 2011, 46, 109–123. [Google Scholar] [CrossRef]
- Wang, L.; Gwilliam, J.; Jones, P. Case study of zero energy house design in UK. Energy Build. 2009, 41, 1215–1222. [Google Scholar] [CrossRef]
- Lai, C.M.; Wang, Y.H. Energy-Saving Potential of Building Envelope Designs in Residential Houses in Taiwan. Energies 2011, 4, 2061–2076. [Google Scholar] [CrossRef]
- Setiawan, A.F.; Huang, T.-L.; Tzeng, C.-T.; Lai, C.-m. The Effects of Envelope Design Alternatives on the Energy Consumption of Residential Houses in Indonesia. Energies 2015, 8, 2788–2802. [Google Scholar] [CrossRef]
- Çay, Y.; Gürel, A.E. Determination of optimum insulation thickness, energy savings, and environmental impact for different climatic regions of Turkey. Curr. Eye Res. 2013, 38, 729–735. [Google Scholar] [CrossRef]
- Skarning, G.C.J.; Hviid, C.A.; Svendsen, S. Roadmap for Improving Roof and Façade Windows in Nearly Zero-Energy Houses in Europe. Energy Build. 2016, 116, 602–613. [Google Scholar] [CrossRef] [Green Version]
- Monge Barrio, A.; Sánchez Ostiz, A. Energy efficiency and thermal behaviour of attached sunspaces, in the residential architecture in Spain, Summer Conditions. Energy Build. 2015, 108, 244–256. [Google Scholar] [CrossRef]
- Jermyn, D.; Richman, R. A Process for Developing Deep Energy Retrofit Strategies for Single-Family Housing Typologies: Three Toronto Case Studies. Energy Build. 2016, 116, 522–534. [Google Scholar] [CrossRef]
- ECGB Editorial Department. Regional Green Building in the Background of Urban-Rural Integration: Interview with Academician Liu Jiaping, Professor of College of Architecture, Xi’an University of Architecture & Technology. Eco-city Green Build. 2014, 1, 16–17. [Google Scholar]
- Zhu, X.; Liu, J.; Yang, L.; Hu, R. Energy performance of a new Yaodong dwelling, in the Loess Plateau of China. Energy Build. 2014, 70, 159–166. [Google Scholar] [CrossRef]
- Yang, W.; Gao, Q.; Xu, B.; Yin, S.S. Inheriting and Updating the Technology of Low Energy Consumption Used in Waterside Vernacular Dwellings in the Lower Yangtze Basin. Archit. J. 2015, 1, 66–69. [Google Scholar]
- Yang, W.; Xu, B.; Chang, L. Research on the Ecological Design Strategy of Rural Housing in Qinghai. Eco-city Green Build. 2015, 1, 112–119. [Google Scholar]
- Zhou, T.; Liu, H. A Study on the Application of Low-tech Energy-saving Strategies in the New Rural Residence in Sichuan Province-Exampled by the Residential Design of the No.2 Settlements in Nanlin Village, Xiwai Township, Guanghan City. Hum. Settl. Forum West China 2014, 3, 32–37. [Google Scholar]
- He, Q.; Gao, H.Q.; Liu, D.L.; Zhu, X.R. Study on Energy Saving Optimization of Traditional Houses in Lhasa. Archit. Cult. 2019, 180, 243–245. [Google Scholar]
- Hao, S.M.; Song, Y.H.; Li, J.J.; Zhu, N. Field Study on Indoor Thermal and Luminous Environment in Winter of Vernacular Houses in Northern Hebei Province of China. J. Harbin Inst. Tech. 2014, 21, 77–83. [Google Scholar]
- Sun, H.; Leng, M. Analysis on building energy performance of Tibetan traditional dwelling in cold rural area of Gannan. Energy Build. 2015, 96, 251–260. [Google Scholar] [CrossRef]
- Liu, S.; Huang, C. Analysis of the Thermal Environment and Energy-Saving Retrofitting of a Traditional Dwelling in Western Hunan. Build. Sci. 2016, 6, 27–32, 38. [Google Scholar]
- Xu, G.; Jin, H.; Kang, J. Experimental Study on the Indoor Thermo-Hygrometric Conditions of the Mongolian Yurt. Sustainability 2019, 11, 687. [Google Scholar] [CrossRef] [Green Version]
- Li, G.; Feng, G.; Wang, L.; Wang, Q. Energy consumption simulation and analysis on energy saving reconstruction of rural house in China extreme cold areas. J. Shenyang Jianzhu Univ. 2012, 28, 884–890. [Google Scholar]
- Zhang, X.Y.; Jin, H. Strategies of function improvement on existing rural housing in severe cold and cold regions. J. Harbin Inst. Tech. 2011, 18, 117–121. [Google Scholar]
- Jin, H.; Ling, W. Low Energy Consumption, Low-tech and Low Cost: Study on the Design for Rural Energy-saving Housing in Cold Region. Archit. J. 2010, 8, 14–16. [Google Scholar]
- Cao, B.; Zhu, Y.; Ouyang, Q.; Zhou, X.; Huang, L. Field study of human thermal comfort and thermal adaptability during winter in Beijing. Heat. Vent. Air Cond. 2010, 40, 98–101. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, J. Research on the Indoor Thermal Environment of Rural Architecture in Winter in Northwestern Areas. China Civ. Eng. J. 2010, 43, 400–403. [Google Scholar]
- Yang, L.; Yang, Q.; Yan, H.-Y.; Liu, J.-P. Field study on thermal comfort of rural houses in winter in a the Guanzhong region, Shaanxi Province. J. Xi’an Univ. Archit. Tech. 2011, 43, 551–556. [Google Scholar]
- Wang, Z.; Sheng, X.; Ren, J.; Ji, Y. Field survey on indoor thermal comfort in rural houses around Harbin in winter. Heat. Vent. Air Cond. 2014, 12, 71–75. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of China. Code for Thermal Design of Civil Building (GB 50176-2016); China Building Industry Press: Beijing, China, 2016.
- China Meteorological Information Center, Building Science and Technology Department of Tsinghua University. Chinese Building Thermal Environment Analysis of Specialized Meteorological Data Collection; Chinese Architecture Industry Press: Beijing, China, 2005. [Google Scholar]
- ISO 7726. Ergonomics of the Thermal Environment—Instruments for Measuring Physical Quantities; International Standard: Geneva, Switzerland, 1998. [Google Scholar]
- Liu, Z.M.; Jin, Y.M.; Jin, H. The Effects of Different Space Forms in Residential Areas on Outdoor Thermal Comfort in Severe Cold Regions of China. Int. J. Environ. Res. Public Health 2019, 16, 3960. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- ASHRAE 55. Thermal Environmental Condition for Human Occupancy; American Society of Heating, Refrigerating and Air-Conditioning Engineers, Inc.: Atlanta, GA, USA, 2013. [Google Scholar]
- Gagge, A.P. An Effective Temperature Scale Based on a Simple Model of Human Physiological Regulatory Response. ASHRAE Trans. 1972, 77, 21–36. [Google Scholar]
- Gagge, A.P.; Fobelets, A.P.; Berglund, L.G. A standard predictive index of human response to the thermal environment. ASHRAE Trans. 1986, 92, 709–731. [Google Scholar]
- De Dear, R.; Brager, G.S. Thermal comfort in naturally ventilated buildings: Revisions to ASHRAE Standard 55. Energy Build. 2002, 34, 549–561. [Google Scholar] [CrossRef] [Green Version]
- Fanger, P.O. Thermal Comfort; Robert E krieger Publish Company: New York, NY, USA, 1982. [Google Scholar]
- De Dear, R. Thermal comfort in practice. Indoor Air 2004, 14, 32–39. [Google Scholar] [CrossRef]
- ANSI/ASHRAE Standard 140-2004 Building Thermal Envelope and Fabric Load Tests—DesignBuilder Version 1.2.0. Available online: https://www.batisim.net/images/stories/cetteg/ansi_ashrae.pdf (accessed on 28 January 2020).
- Rahman, M.M.; Rasul, M.G.; Khan, M.M.K. Energy conservation measures in an institutional building in sub-tropical climate in Australia. Appl. Energy 2010, 87, 2994–3004. [Google Scholar] [CrossRef]
- Liang, X.; Wang, Y.; Zhang, Y.; Jiang, J.; Chen, H.; Zhang, X.; Guo, H.; Roskilly, T. Analysis and Optimization on Energy Performance of a Rural House in Northern China Using Passive Retrofitting. Energy Procedia 2017, 105, 3023–3030. [Google Scholar] [CrossRef]
- Cho, H.M.; Park, J.H.; Wi, S.; Chang, S.J.; Yun, G.Y.; Kim, S. Energy retrofit analysis of cross-laminated timber residential buildings in Seoul, Korea: Insights from a case study of packages. Energy Build. 2019, 202. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Q.; Wang, F.; Wang, Q.; Liang, R. Study on Influencing Factors of Energy Consumption in Traditional Rural Dwellings of Kangding Prefecture Based on DesignBuilder. Build. Sci. 2019, 35, 108–115. [Google Scholar]
- Jin, H.; Shao, T. Optimal Design of Energy Saving for Rural Housing of Severe Cold Regions. Archit. J. 2015, S1, 218–220. [Google Scholar]
- Nguyen, A.T.; Reiter, S. Passive designs and strategies for low-cost housing using simulation-based optimization and different thermal comfort criteria. J. Build. Perform. Simul. 2014, 7, 68–81. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, A.T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Bre, F.; Roman, N.; Fachinotti, V.D. An efficient metamodel-based method to carry out multi-objective building performance optimizations. Energy Build. 2020, 206. [Google Scholar] [CrossRef]
- Zhao, X. Experimental Design Methods; China Science Press: Beijing, China, 2010. [Google Scholar]
- Zhang, W.; Wu, J.; Wei, Y.; Wei, Y. Analysis on affecting factors of building cooling load by orthogonal experiment method. Heat. Vent. Air Cond. 2006, 36, 77–80. [Google Scholar]
- Wang, S.; Li, Y.; Zhang, Y. Comparison of the concrete orthogonal experimental results in method of range analysis and variance analysis. Dev. Guide Build. Mater. 2016, 14, 44–48. [Google Scholar] [CrossRef]
- China Academy of Building Research. Design Standard for Energy Efficiency of Rural Residential Buildings (GB/T50824-2013); Chinese Architecture Industry Press: Beijing, China, 2012. [Google Scholar]
- Chongqing University. Evaluation Standard for Indoor Thermal Environment in Civil Buildings (GB/T 50785-2012); Chinese Architecture Industry Press: Beijing, China, 2012. [Google Scholar]
- Wang, Z.; Fang, X.; Lian, L. Field experiments on occupant thermal comfort in Harbin. J. Harbin Inst. Tech. 2002, 34, 500–504. [Google Scholar]
- Lan, B.; Huang, L. Query on Relationship Between Shape Coefficient of Building and Energy Efficiency. Constr. Conserves Energy 2013, 5, 65–70. [Google Scholar]
- Zhao, H.; Jin, H. Research on the local optimum eco-technologies of rural housing in the chill region of China. J. Harbin Inst. Tech. 2007, 39, 235–237, 291. [Google Scholar]
- Sun, S.; Yu, Y.; Chen, Q. Energy saving on ground floor of building. J. Harbin Inst. Tech. 2003, 35, 573–575, 580. [Google Scholar]
- Harbin Institute of Technology. Design Standard for Energy Efficiency of Rural Residential Buildings in Heilongjiang Province (DB 23/T 1537–2013); Department of Housing and Urban-Rural Development of Heilongjiang: Harbin, China, 2013.
- Hasan, A.; Mika Vuolle, M.; Kai, S. Minimization of life cycle cost of detached house using combined simulation and optimization. Build. Environ. 2008, 43, 2022–2034. [Google Scholar] [CrossRef]


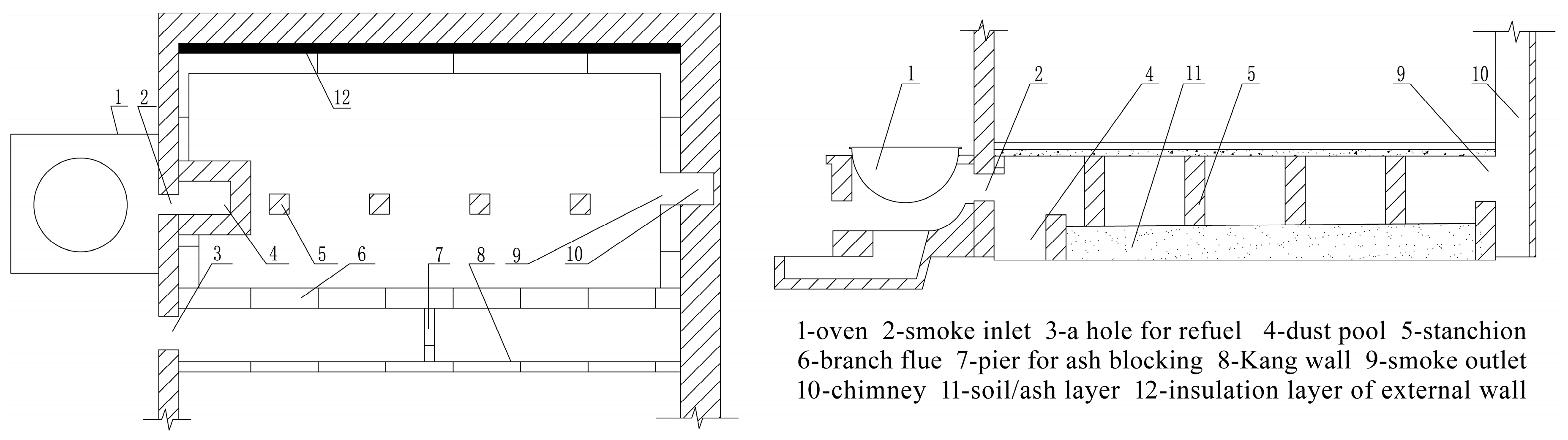



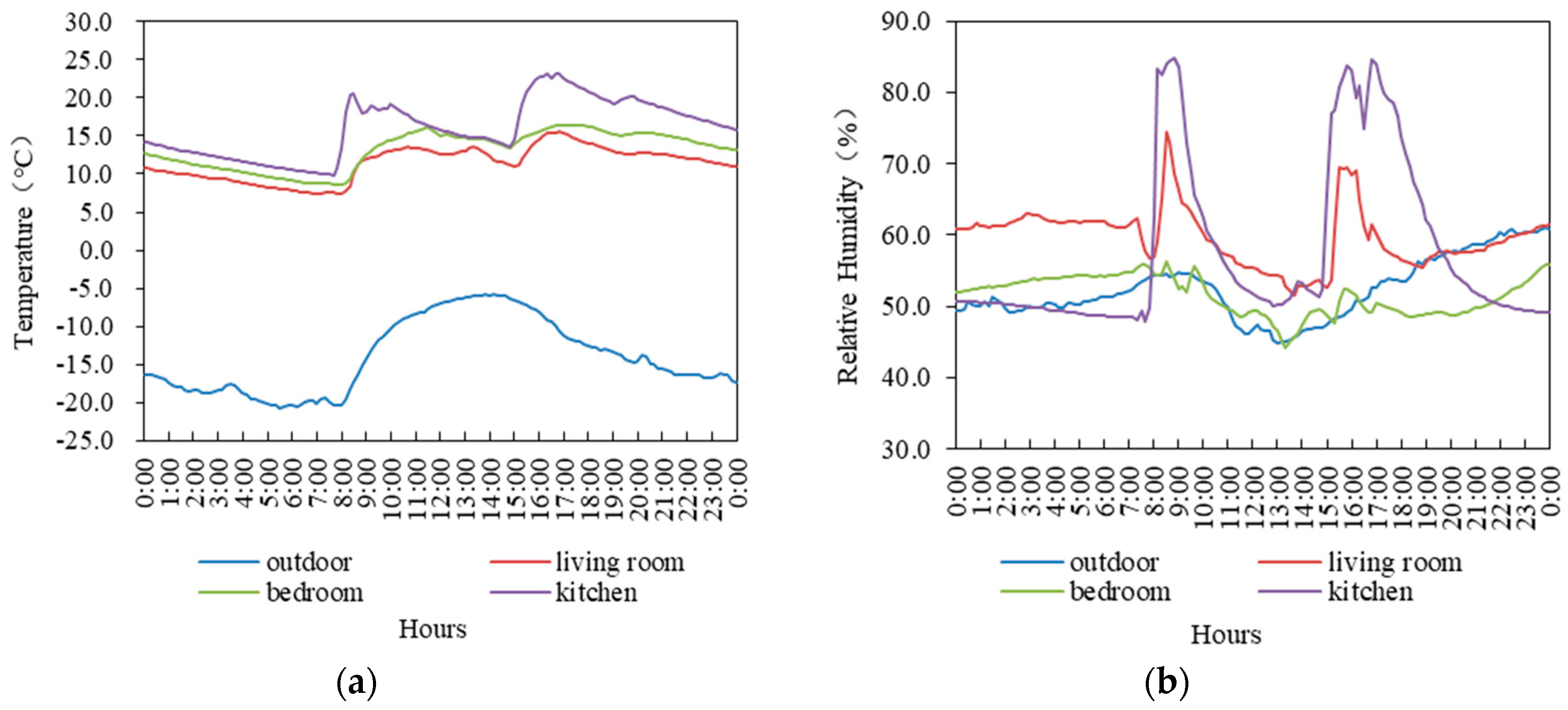
























| Parameter | Model | Range | Accuracy |
|---|---|---|---|
| Air temperature (Ta) and relative humidity (RH) | BES-02 | −30 to 50 °C, 0–99% | ±0.5 °C, ±3% |
| Surface temperature (Ts) | BES-01 (external sensor) | −30 to 50 °C | ±0.5 °C |
| Globe temperature (Tg) | BES-01 (external black globe, diameter 0.15 m) | −30 to 50 °C | ±0.5°C |
| Wind speed (V) | KANOMAX | 0.01–20 m/s | ±0.01 m/s |
| Heat transfer coefficient (K) | BES-Aa | −40 to 100 °C, 0–±20 mV | ±0.2 °C, ±0.01 mV |
| Infrared thermal imaging | Fluke | −20 to 550 °C | ±2°C |
| Parameter | Mean Value | Standard Deviation | Max Value | Min Value |
|---|---|---|---|---|
| Air temperature (°C) | 15.0 | 3.39 | 22.0 | 7.0 |
| Mean radiant temperature (°C) | 11.0 | 3.47 | 19.0 | 3.0 |
| Relative humidity (%) | 51.0 | 11.04 | 75.0 | 22.0 |
| Air velocity (m/s) | 0.02 | 0.01 | 0.06 | 0.01 |
| Operating Temperature | MTS | Operating Temperature | MTS | Operating Temperature | MTS | Operating Temperature | MTS |
|---|---|---|---|---|---|---|---|
| 4.75 | −2 | 8.75 | −1 | 12.75 | −0.45 | 16.75 | 0 |
| 5.25 | −2 | 9.25 | −1.25 | 13.25 | −0.44 | 17.25 | 0 |
| 5.75 | −2 | 9.75 | −1.25 | 13.75 | −0.63 | 17.75 | 0 |
| 6.25 | −2 | 10.25 | −1 | 14.25 | −0.44 | 18.25 | 0 |
| 6.75 | −2 | 10.75 | −1 | 14.75 | −0.33 | 18.75 | 0.4 |
| 7.25 | −2 | 11.25 | −0.9 | 15.25 | −0.38 | 19.25 | 1 |
| 7.75 | −2 | 11.75 | −1.2 | 15.75 | −0.1 | 19.75 | 1 |
| 8.25 | −2 | 12.25 | −0.7 | 16.25 | 0 | 20.25 | 1 |
| Name | Diagram | Structures |
|---|---|---|
 |  | 1. Interior surface 2. 370 mm solid brick 3. Cement mortar 4. Cementing compound 5. EPS board 6. Alkali resistant glass fiber mesh cloth (8 mm, double layer) 7. Exterior surface |
 |  | 1. Tile 2 Waterproof layer 3. Plank 4. Wood (or steel) roof truss 5. EPS board 6. Vapor barrier (plastic film) 7. Wood joist 8. Suspended ceiling |
 |  | 1. Surface course 2. Protective layer 3. EPS board 4. Damp roof course 5. 20 mm cement mortar 6. 100 mm concrete cushion 7. Rammed earth |
| Number | Window Type | K | SHGC |
|---|---|---|---|
| 1 | 6 mm clear + 6A + 6 mm clear | 3.1 | 0.700 |
| 2 | 6 mm clear + 6A + 6 mm bronze | 3.1 | 0.504 |
| 3 | 6 mm clear + 6A + 6 mm gray | 3.1 | 0.485 |
| 4 | 6 mm clear + 12A + 6 mm clear | 2.7 | 0.715 |
| 5 | 6 mm clear + 6A + 6 mm low-e | 2.4 | 0.569 |
| 6 | 6 mm clear + 6A + 6 mm clear + 6A + 6 mm clear | 2.1 | 0.624 |
| 7 | 6 mm g clear + 6A + 6 mm clear + 100A + 6 mm clear + 6A + 6 mm clear | 1.5 | 0.554 |
| K (W/m2·K) | SHGC | |
|---|---|---|
| Pearson correlation | 0.949 ** | −0.296 |
| Significance (bilateral) | 0.001 | 0.520 |
| Regression Equation | Regression Coefficient (R2) | Significance Test (Sig.) | |
|---|---|---|---|
| South window–wall ratio | Y = −35.164X + 321.594 | 0.998 | 0.000 |
| North window–wall ratio | Y = 17.876X + 321.286 | 0.980 | 0.000 |
| Level | Factor | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | |
| 1 | South by west 20° | 1.0 | 2.6 | 50 | 70 | 30 | 1.5 | 0.3 | 0.1 | 0.9 |
| 2 | South by west 10° | 1.1 | 2.7 | 70 | 90 | 50 | 2.1 | 0.4 | 0.2 | 1.2 |
| 3 | South (0°) | 1.2 | 2.8 | 90 | 110 | 70 | 2.4 | 0.5 | 0.3 | 1.5 |
| 4 | South by east 10° | 1.3 | 2.9 | 110 | 130 | 90 | 2.7 | 0.6 | 0.4 | 1.8 |
| Mean Value (KWh/m²) | Factors | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | G | H | I | J | Blank Column | |
| 143.55 | 142.79 | 137.61 | 154.93 | 152.81 | 148.84 | 137.47 | 142.50 | 137.46 | 141.86 | 142.94 | |
| 142.83 | 142.75 | 140.81 | 144.85 | 143.90 | 143.59 | 142.75 | 142.90 | 141.52 | 142.97 | 143.28 | |
| 143.28 | 143.29 | 144.62 | 138.42 | 139.46 | 140.89 | 146.21 | 143.44 | 144.84 | 143.57 | 143.10 | |
| 143.21 | 144.04 | 149.83 | 134.66 | 136.71 | 139.55 | 146.44 | 144.03 | 149.04 | 144.47 | 143.55 | |
| Ri | 0.72 | 1.29 | 12.22 | 20.27 | 16.10 | 9.29 | 8.97 | 1.53 | 11.58 | 2.61 | 0.61 |
| ≤17 °C | 17–21 °C | 21–26 °C | <26 °C | |
|---|---|---|---|---|
| Ambient temperature (h) | 6295 | 974 | 1059 | 432 |
| Indoor temperature (h) | 6198 | 2106 | 456 | 0 |
| After energy-saving design (h) | 5125 | 1152 | 2121 | 362 |
| III Type Quadratic Sum | df | MS | F | Sig. | |
|---|---|---|---|---|---|
| A: Building orientation | 4.233 | 3 | 1.411 | 0.246 | 0.864 |
| B: Length–width ratio | 17.113 | 3 | 5.704 | 0.993 | 0.409 |
| C: Indoor height | 1326.900 | 3 | 442.300 | 76.995 | 0.000 |
| D: External wall insulation thickness | 3779.036 | 3 | 1259.679 | 219.282 | 0.000 |
| E: Roof insulation thickness | 2383.959 | 3 | 794.653 | 138.331 | 0.000 |
| F: Ground insulation thickness | 810.240 | 3 | 270.080 | 47.015 | 0.000 |
| G: Window heat transfer coefficient | 840.762 | 3 | 280.254 | 48.786 | 0.000 |
| H: South window–wall ratio | 21.333 | 3 | 7.111 | 1.238 | 0.313 |
| I: North window–wall ratio | 1161.877 | 3 | 387.292 | 67.419 | 0.000 |
| J: Sunspace depth | 57.550 | 3 | 19.183 | 3.339 | 0.032 |
| K: Blank column | 3.278 | 3 | 1.093 | 0.190 | 0.902 |
| Deviation | 172.337 | 30 | 5.745 |
| Parts | Additional or Replacement Material | Price | Area (m2) | Difference in Investment Cost (CNY) | ||
|---|---|---|---|---|---|---|
| Wall | EPS | 360 CNY/m3 | 67.20 | 2661.1 | ||
| Roof | EPS | 360 CNY/m3 | 54.12 | 2532.8 | ||
| Ground | EPS | 360 CNY/m3 | 54.12 | 1753.5 | ||
| Sunspace | Single-glass with aluminum alloy frame | 120 CNY/m2 | 31.63 | 3795.6 | ||
| Window replacement | Reference building | Single-frame double-glass window | 270 CNY/m2 | 14.04 | 3790.8 | 118.8 |
| Energy-saving house | Two single-frame double-glass window | 540 CNY/m2 | 7.24 | 3909.6 | ||
| Total | 10,861.8 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shao, T.; Zheng, W.; Jin, H. Analysis of the Indoor Thermal Environment and Passive Energy-Saving Optimization Design of Rural Dwellings in Zhalantun, Inner Mongolia, China. Sustainability 2020, 12, 1103. https://doi.org/10.3390/su12031103
Shao T, Zheng W, Jin H. Analysis of the Indoor Thermal Environment and Passive Energy-Saving Optimization Design of Rural Dwellings in Zhalantun, Inner Mongolia, China. Sustainability. 2020; 12(3):1103. https://doi.org/10.3390/su12031103
Chicago/Turabian StyleShao, Teng, Wuxing Zheng, and Hong Jin. 2020. "Analysis of the Indoor Thermal Environment and Passive Energy-Saving Optimization Design of Rural Dwellings in Zhalantun, Inner Mongolia, China" Sustainability 12, no. 3: 1103. https://doi.org/10.3390/su12031103
APA StyleShao, T., Zheng, W., & Jin, H. (2020). Analysis of the Indoor Thermal Environment and Passive Energy-Saving Optimization Design of Rural Dwellings in Zhalantun, Inner Mongolia, China. Sustainability, 12(3), 1103. https://doi.org/10.3390/su12031103







