Asset Allocation Model for a Robo-Advisor Using the Financial Market Instability Index and Genetic Algorithms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Literature Review
2.1.1. p-Value Derived from the iFMII
2.1.2. Risk Parity Model
2.1.3. Genetic Algorithms
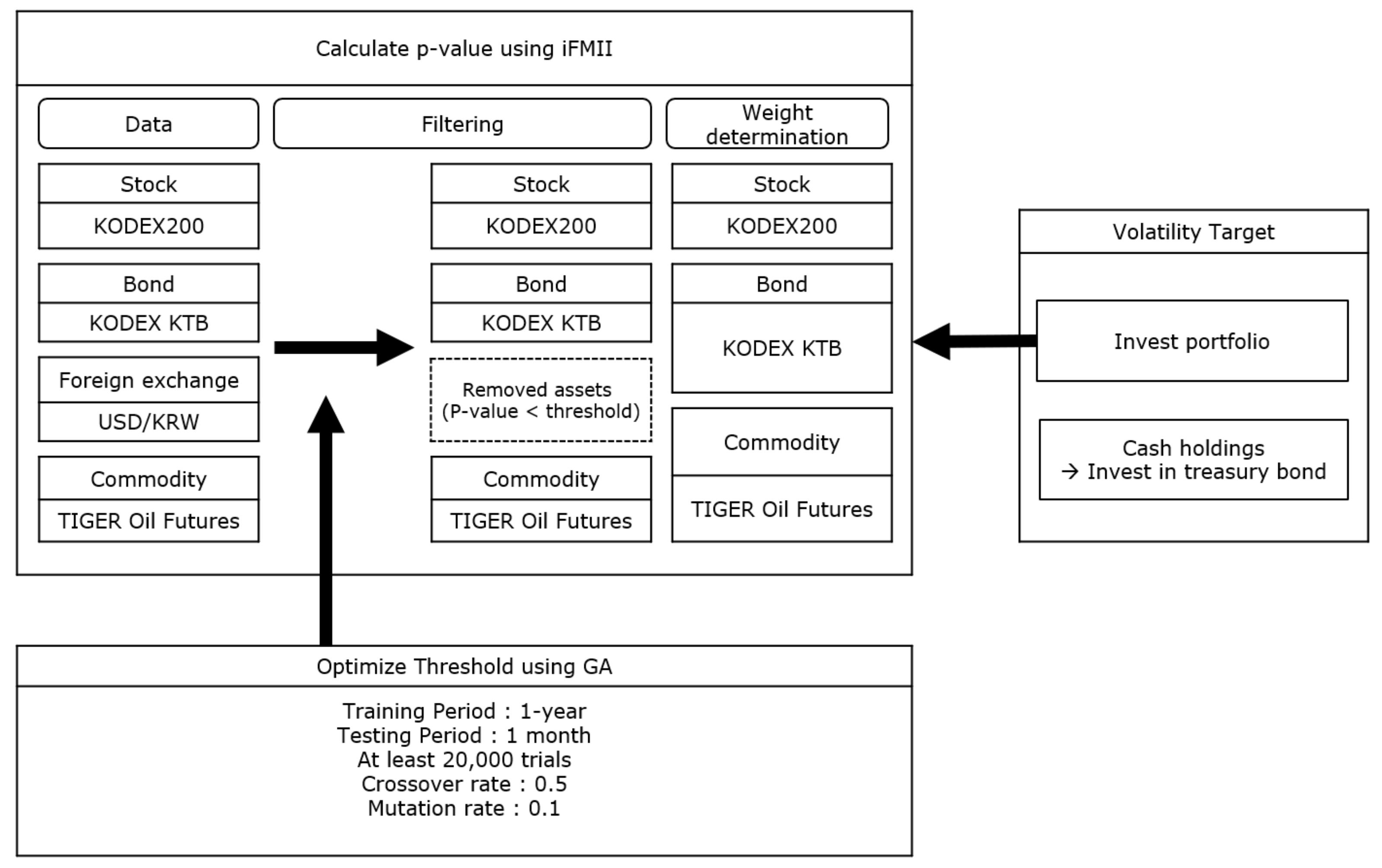
2.2. Proposed Model
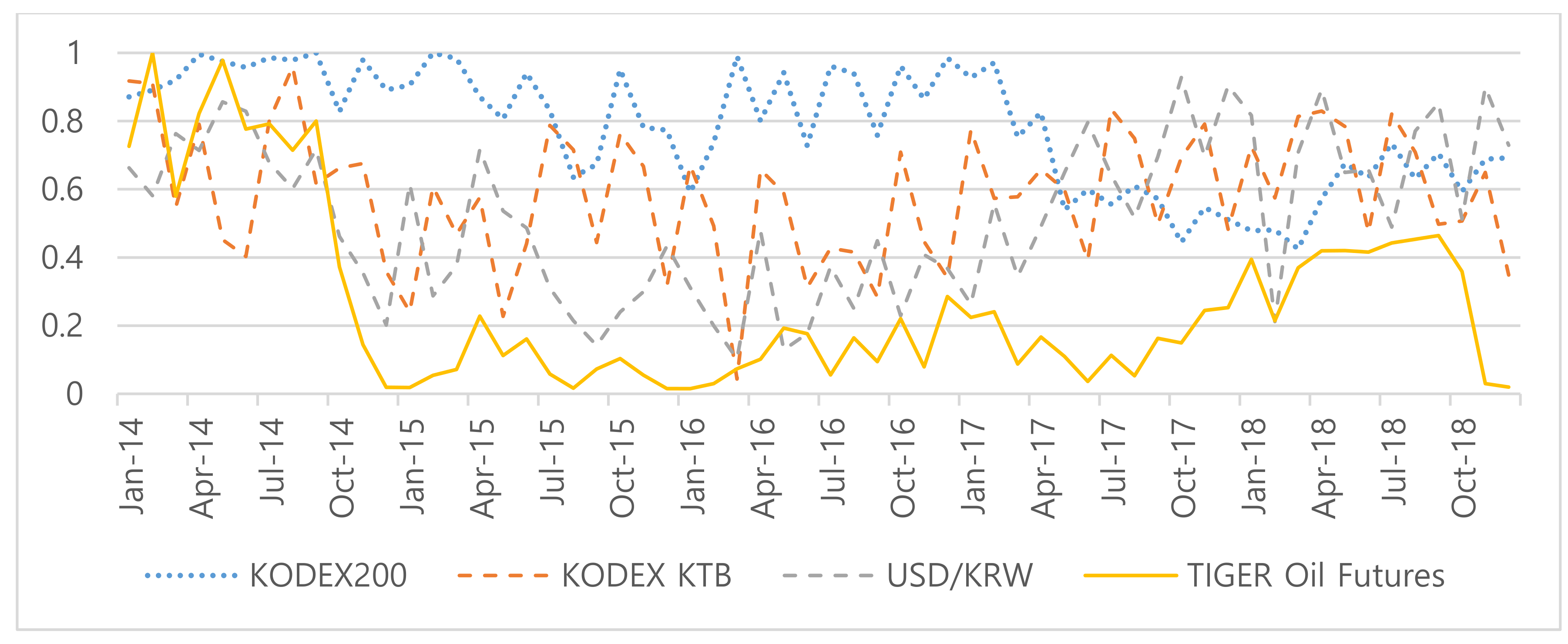
2.2.1. Phase 1: Calculate the ip-Value from the IFMII
2.2.2. Phase 2: Determine the Allocation of Assets
2.2.3. Phase 3: Volatility Target
2.3. Application of the Proposed Model to Build a Robo-Advisor
3. Results
3.1. Experimental Environments
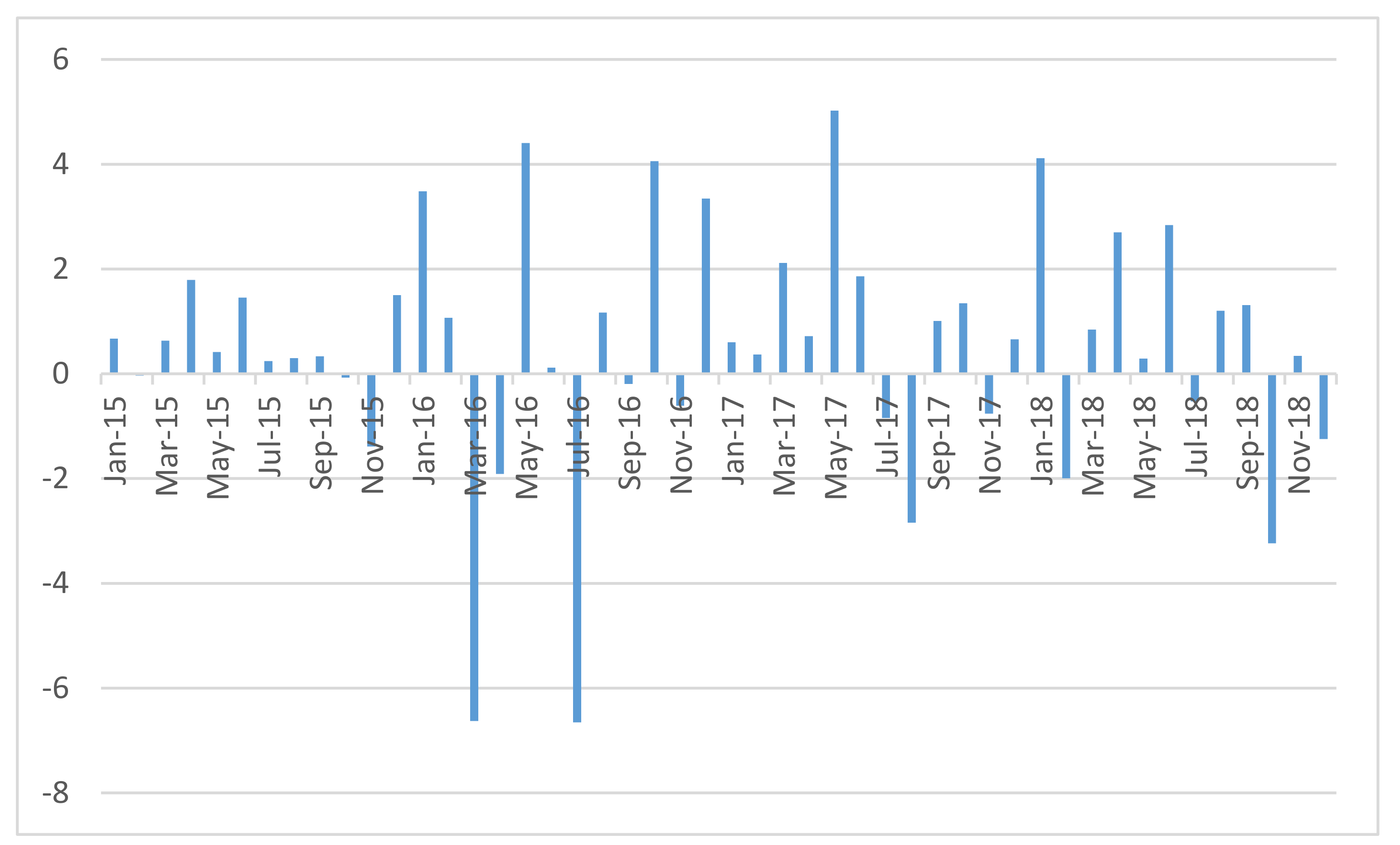
3.2. Experimental Results
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Faloon, M.; Scherer, B. Individualization of Robo-Advice. J. Wealth Manag. 2017, 20, 30–36. [Google Scholar] [CrossRef] [Green Version]
- Yanagawa, E. Trends and initiatives about robo-advisers: Pioneering unexplored areas in Japan. J. Digit. Bank. 2017, 2, 58–73. [Google Scholar]
- Poterba, J.M.; Shoven, J.B. Exchange-Traded Funds: A New Investment Option for Taxable Investors. Am. Econ. Rev. 2002, 92, 422–427. [Google Scholar] [CrossRef] [Green Version]
- Musto, C.; Semeraro, G.; Lops, P.; De Gemmis, M.; Lekkas, G. Personalized finance advisory through case-based recommender systems and diversification strategies. Decis. Support Syst. 2015, 77, 100–111. [Google Scholar] [CrossRef]
- Lopez, J.C.; Babcic, S.; De La Ossa, A. Advice goes virtual: How new digital investment services are changing the wealth management landscape. J. Financ. Perspect. 2015, 3, 1–18. [Google Scholar]
- Gomes, C.P.; Selman, B. Algorithm portfolios. Artif. Intell. 2001, 126, 43–62. [Google Scholar] [CrossRef] [Green Version]
- Trippi, R.R.; Turban, E. Neural Networks in Finance and Investing: Using Artificial Intelligence to Improve Real World Performance; McGraw-Hill, Inc.: New York, NY, USA, 1992. [Google Scholar]
- Bahrammirzaee, A. A comparative survey of artificial intelligence applications in finance: Artificial neural networks, expert system and hybrid intelligent systems. Neural Comput. Appl. 2010, 19, 1165–1195. [Google Scholar] [CrossRef]
- Markowitz, H. Portfolio selection. J. Financ. 1952, 7, 77–91. [Google Scholar]
- Rubinstein, M.E. A mean-variance synthesis of corporate financial theory. J. Financ. 1973, 28, 167–181. [Google Scholar] [CrossRef]
- Li, D.; Ng, W.-L. Optimal Dynamic Portfolio Selection: Multiperiod Mean-Variance Formulation. Math. Financ. 2000, 10, 387–406. [Google Scholar] [CrossRef]
- Gruber, M.J.; Ross, S.A. The current status of the capital asset pricing model (CAPM). J. Financ. 1978, 33, 885–901. [Google Scholar] [CrossRef]
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar]
- Lintner, J. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. In Stochastic Optimization Models in Finance; Academic Press: Cambridge, MA, USA, 1975; pp. 131–155. [Google Scholar]
- Fama, E.F.; French, K.R. The Value Premium and the CAPM. J. Financ. 2006, 61, 2163–2185. [Google Scholar] [CrossRef]
- Black, F.; Litterman, R. Global Portfolio Optimization. Financ. Anal. J. 1992, 48, 28–43. [Google Scholar] [CrossRef]
- Drobetz, W. How to avoid the pitfalls in portfolio optimization? Putting the Black-Litterman approach at work. Financ. Mark. Portf. Manag. 2001, 15, 59–75. [Google Scholar] [CrossRef]
- Chaves, D.; Hsu, J.; Li, F.; Shakernia, O. Risk Parity Portfolio vs. Other Asset Allocation Heuristic Portfolios. J. Invest. 2011, 20, 108–118. [Google Scholar] [CrossRef] [Green Version]
- Anderson, R.M.; Bianchi, S.W.; Goldberg, L.R. Will my risk parity strategy outperform? Financ. Anal. J. 2012, 68, 75–93. [Google Scholar] [CrossRef] [Green Version]
- Clarke, R.; De Silva, H.; Thorley, S. Risk parity, maximum diversification, and minimum variance: An analytic perspective. J. Portf. Manag. 2013, 39, 39–53. [Google Scholar] [CrossRef]
- Roncalli, T.; Weisang, G. Risk parity portfolios with risk factors. Quant. Financ. 2016, 16, 377–388. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.H.; Lee, S.J.; Oh, K.J.; Kim, T.Y. An early warning system for financial crisis using a stock market instability index. Expert Syst. 2009, 26, 260–273. [Google Scholar] [CrossRef]
- Oh, K.J.; Kim, T.Y.; Kim, C. An early warning system for detection of financial crisis using financial market volatility. Expert Syst. 2006, 23, 83–98. [Google Scholar] [CrossRef]
- Kim, Y.M.; Han, S.K.; Kim, T.Y.; Oh, K.J.; Luo, Z.; Kim, C. Intelligent stock market instability index: Application to the Korean stock market. Intell. Data Anal. 2015, 19, 879–895. [Google Scholar] [CrossRef]
- Qian, E. Risk parity and diversification. J. Invest. 2011, 20, 119. [Google Scholar] [CrossRef]
- Lohre, H.; Opfer, H.; Ország, G. Diversifying risk parity. J. Risk 2014, 16, 53–79. [Google Scholar] [CrossRef]
- Benson, R.; Furbush, T.; Goolgasian, C. Targeting Volatility: A Tail Risk Solution When Investors Behave Badly. J. Index Invest. 2014, 4, 88–101. [Google Scholar] [CrossRef]
- Hocquard, A.; Ng, S.; Papageorgiou, N. A constant-volatility framework for managing tail risk. J. Portf. Manag. 2013, 39, 28–40. [Google Scholar] [CrossRef] [Green Version]
- Perchet, R.; De Carvalho, R.L.; Moulin, P. Intertemporal risk parity: A constant volatility framework for factor investing. J. Invest. Strateg. 2014, 4, 19–41. [Google Scholar] [CrossRef]
- Bai, X.; Scheinberg, K.; Tutuncu, R. Least-squares approach to risk parity in portfolio selection. Quant. Financ. 2016, 16, 357–376. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Goldberg, D.E.; Holland, J.H. Genetic algorithms and machine learning. Mach. Learn. 1988, 3, 95–99. [Google Scholar] [CrossRef]
- Cheong, D.; Kim, Y.M.; Byun, H.W.; Oh, K.J.; Kim, T.Y. Using genetic algorithm to support clustering-based portfolio optimization by investor information. Appl. Soft Comput. 2017, 61, 593–602. [Google Scholar] [CrossRef]
- Kim, Y.; Ahn, W.; Oh, K.J.; Enke, D. An intelligent hybrid trading system for discovering trading rules for the futures market using rough sets and genetic algorithms. Appl. Soft Comput. 2017, 55, 127–140. [Google Scholar] [CrossRef]
- Chang, T.-J.; Yang, S.-C.; Chang, K.-J. Portfolio optimization problems in different risk measures using genetic algorithm. Expert Syst. Appl. 2009, 36, 10529–10537. [Google Scholar] [CrossRef]
- Jiao, J.; Zhang, Y.; Wang, Y. A heuristic genetic algorithm for product portfolio planning. Comput. Oper. Res. 2007, 34, 1777–1799. [Google Scholar] [CrossRef]
- Butler, A.; Philbrick, M.; Gordillo, R.; Faber, M.T. Global Cape Model Optimization. 2012. Available online: https://ssrn.com/abstract=2163486 (accessed on 18 October 2012).


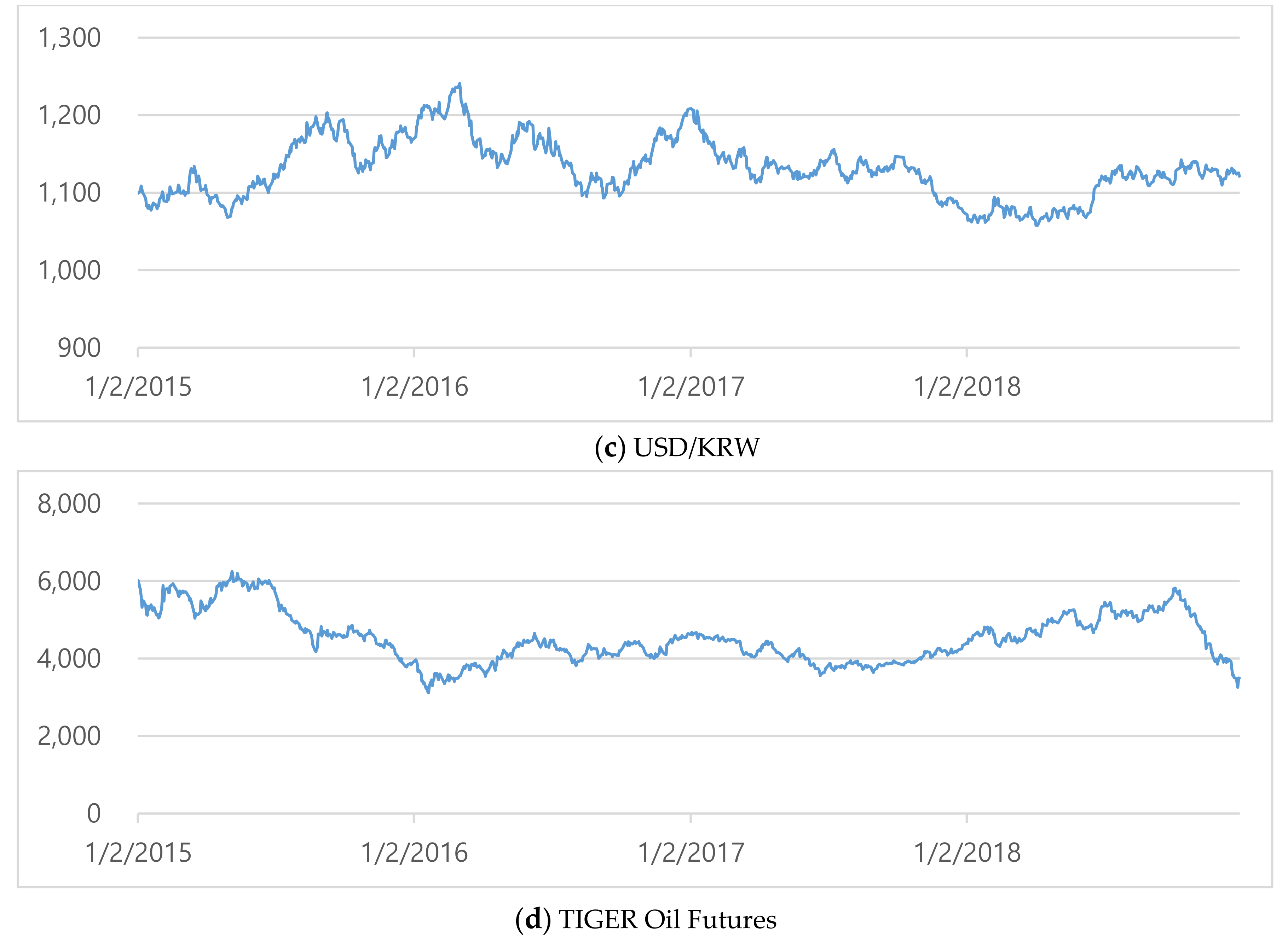




| Sector | Korean ETF Market | U.S. ETF Market |
|---|---|---|
| Stock | KODEX200 | iShares MSCI Emerging Markets |
| Bond | KODEX KTB | iShares 20+ Year Treasury Bond |
| Currency | Won/Dollar exchange rate | iShares Currency Hedged MSCI Canada |
| Commodity | TIGER crude oil futures | iShares Silver Trust |
| Window Number | Training Period | Testing Period |
|---|---|---|
| 1 | January 2014~December 2014 | January 2015 |
| 2 | February 2014~January 2015 | February 2015 |
| 3 | March 2014~February 2015 | March 2015 |
| 4 | April 2014~March 2015 | April 2015 |
| 5 | May 2014~April 2015 | May 2015 |
| … | … | … |
| 43 | July 2017~June 2018 | July 2018 |
| 44 | August 2017~July 2018 | August 2018 |
| 45 | September 2017~August 2018 | September 2018 |
| 46 | October 2017~September 2018 | October 2018 |
| 47 | November 2017~October 2018 | November 2018 |
| 48 | December 2017~November 2018 | December 2018 |
| Experiment * | Mean Monthly Return | Cumulative Return | Standard Deviation | Downside Risk | Skewness | Kurtosis | Sharpe Ratio | Sortino Ratio |
|---|---|---|---|---|---|---|---|---|
| Experiment 1 | 0.04% | 2.08% | 0.45% | 0.34% | 0.81 | 1.38 | −0.199 | −0.260 |
| Experiment 2 | 0.18% | 8.69% | 2.75% | 2.16% | −1.05 | 2.39 | 0.017 | 0.022 |
| Experiment 3 | 0.31% | 14.64% | 1.81% | 1.23% | −0.36 | 1.96 | 0.095 | 0.140 |
| Experiment 4.1 | 0.49% | 23.39% | 2.32% | 1.63% | −0.94 | 2.47 | 0.153 | 0.217 |
| Experiment 4.2 | 0.35% | 16.89% | 2.30% | 1.59% | −0.49 | 0.90 | 0.095 | 0.138 |
| Experiment 5 | 0.42% | 20.54% | 3.60% | 2.18% | 0.52 | 0.14 | 0.081 | 0.135 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, W.; Lee, H.S.; Ryou, H.; Oh, K.J. Asset Allocation Model for a Robo-Advisor Using the Financial Market Instability Index and Genetic Algorithms. Sustainability 2020, 12, 849. https://doi.org/10.3390/su12030849
Ahn W, Lee HS, Ryou H, Oh KJ. Asset Allocation Model for a Robo-Advisor Using the Financial Market Instability Index and Genetic Algorithms. Sustainability. 2020; 12(3):849. https://doi.org/10.3390/su12030849
Chicago/Turabian StyleAhn, Wonbin, Hee Soo Lee, Hosun Ryou, and Kyong Joo Oh. 2020. "Asset Allocation Model for a Robo-Advisor Using the Financial Market Instability Index and Genetic Algorithms" Sustainability 12, no. 3: 849. https://doi.org/10.3390/su12030849
APA StyleAhn, W., Lee, H. S., Ryou, H., & Oh, K. J. (2020). Asset Allocation Model for a Robo-Advisor Using the Financial Market Instability Index and Genetic Algorithms. Sustainability, 12(3), 849. https://doi.org/10.3390/su12030849






