Seismic Fragility Analysis of Tunnels with Different Buried Depths in a Soft Soil
Abstract
1. Introduction
2. Seismic Fragility Analysis Methodology of Tunnels
2.1. Procedure of Seismic Fragility Analysis
- The suite of applicable ground motion is chosen for analysis according to the site information.
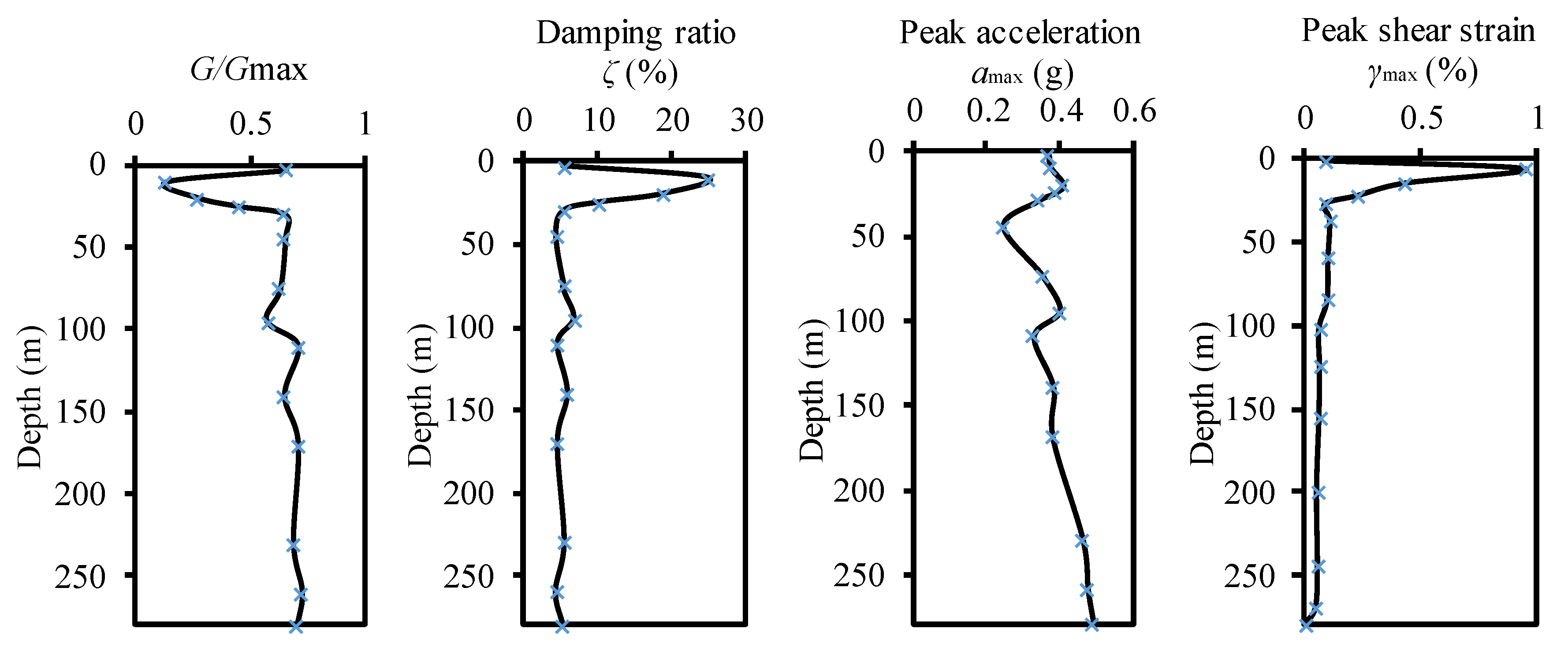
- Free site response analysis is conducted through a 1D equivalent linear analysis on the soil profiles, paired with input motions at different seismic intensity levels, to acquire the dynamic characteristics of soil layers. The nonlinear soil behavior is considered through equivalent shear modulus G and damping ratio ζ compatible with shear strain.
- Establish the finite element soil-tunnel model and evaluate seismic response by dynamic time history analysis in a finite element software such as ABAQUS.
- Selection of the intensity measure (IM) parameter of input ground motions for developing the fragility curves.
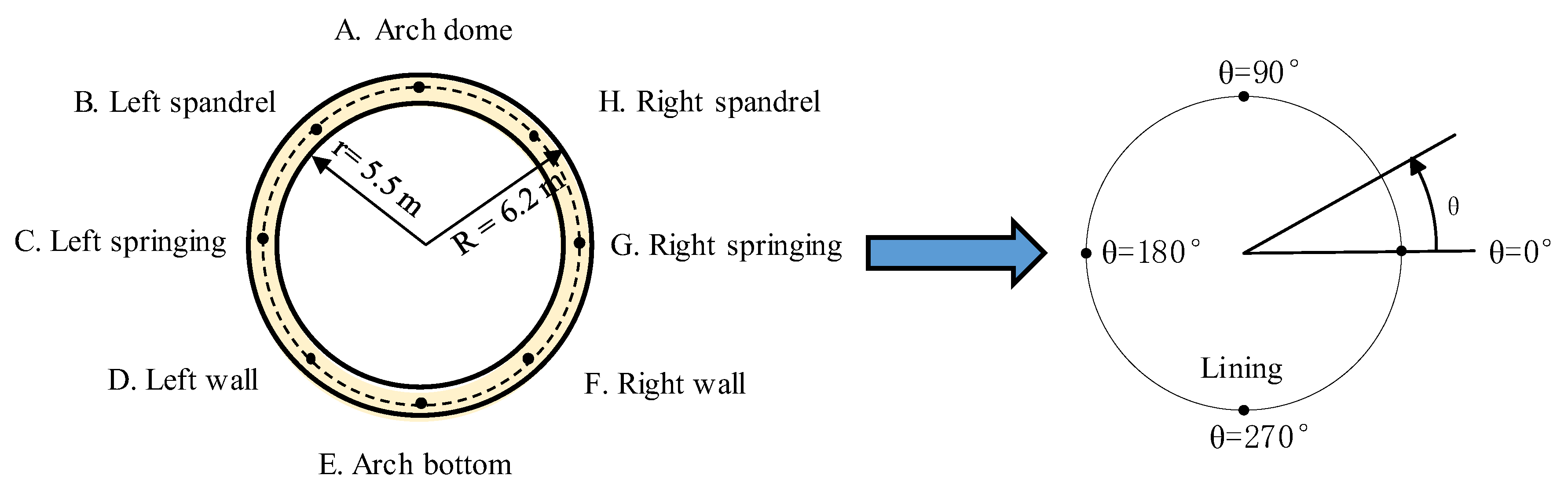
- Definition of damage states (DS) corresponding to the damage index (DI) for determining the damage of tunnel lining.
- The damage assessment can be performed based on lognormal approach with linear regression to determine the relationship of DI and IM.
- A lognormal standard deviation (βtot) that describes the total variability associated with each fragility curve must be estimated.
- These outputs are obtained and used for developing the fragility curves of tunnels.
2.2. Intensity Measure (IM) Selection
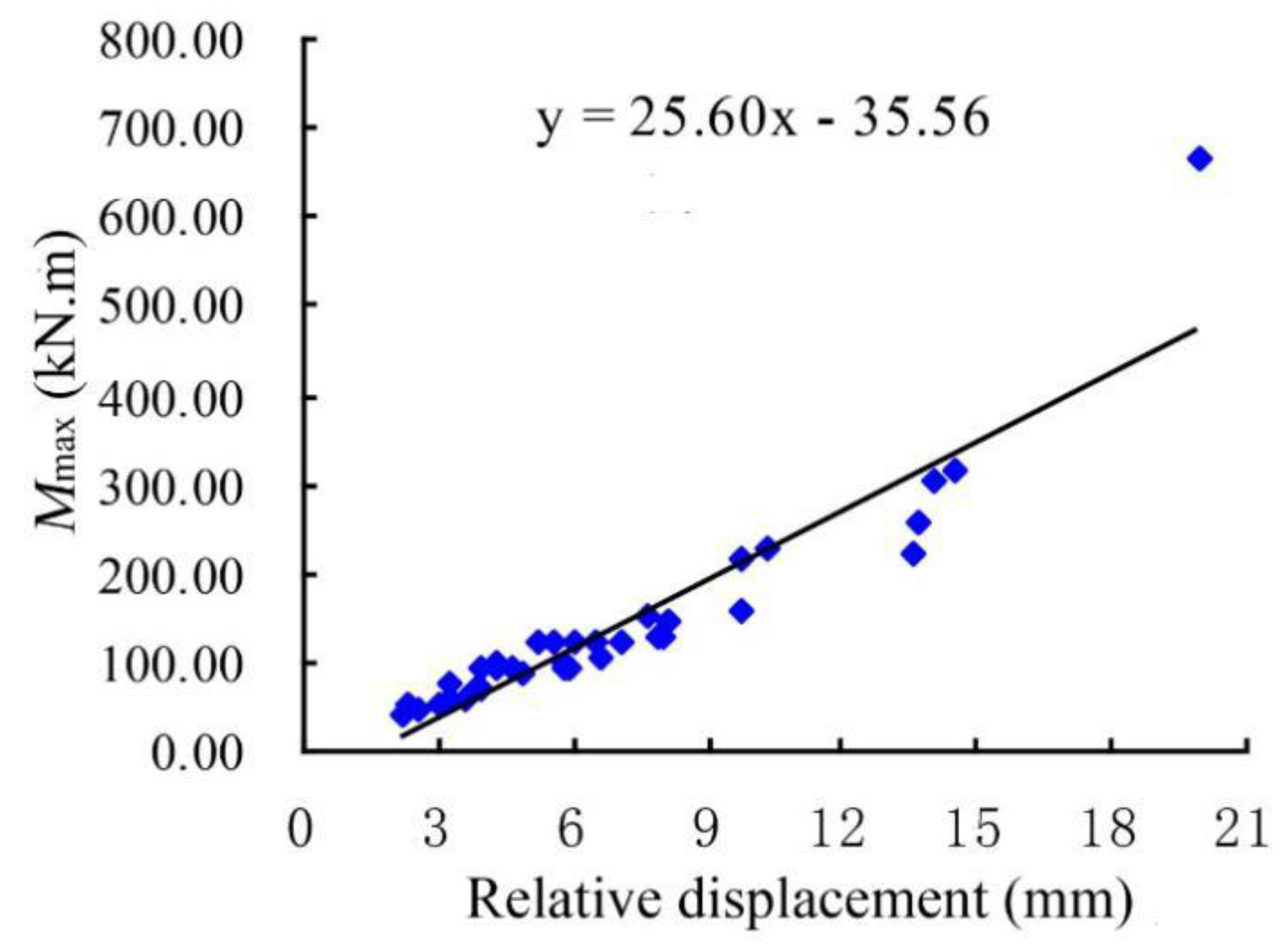
2.3. Definition of Damage States (DS)
2.4. Derivation of Fragility Function
3. Numerical Model of Soil-Tunnel System
3.1. Specification of Tunnel Lining
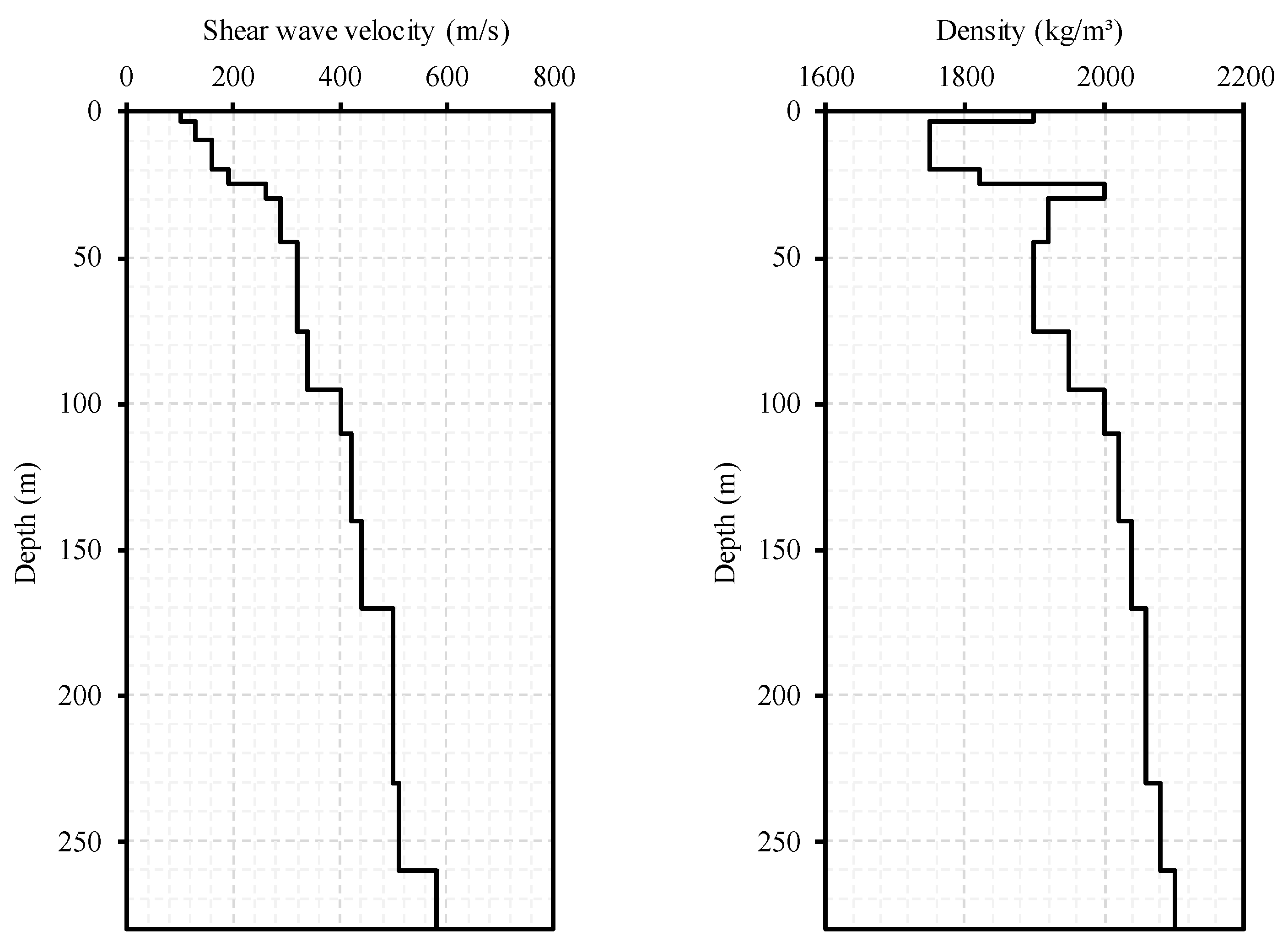
3.2. Soil Profile
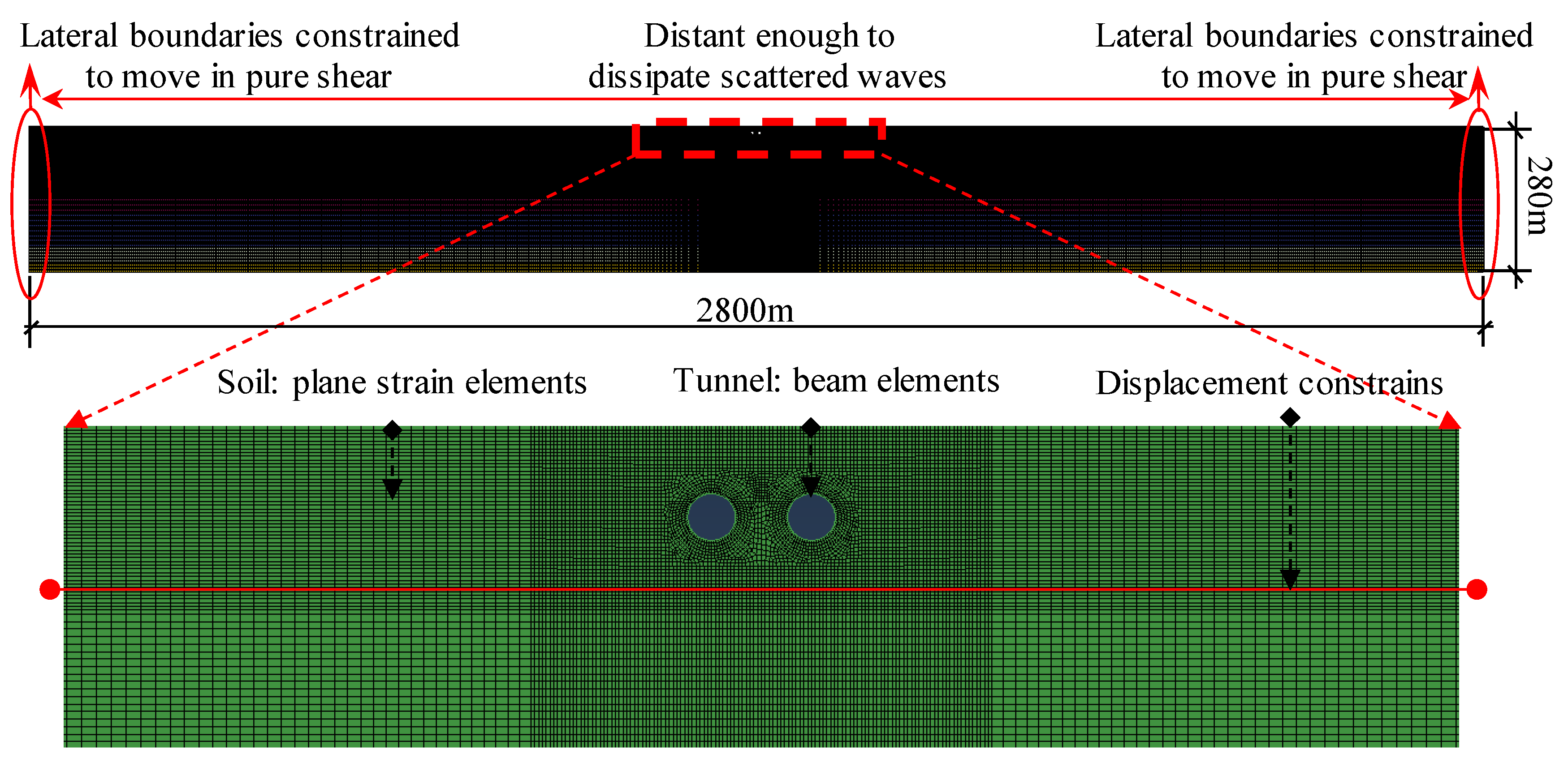
3.3. Establishment of Soil-Tunnel Model and Boundary Condition
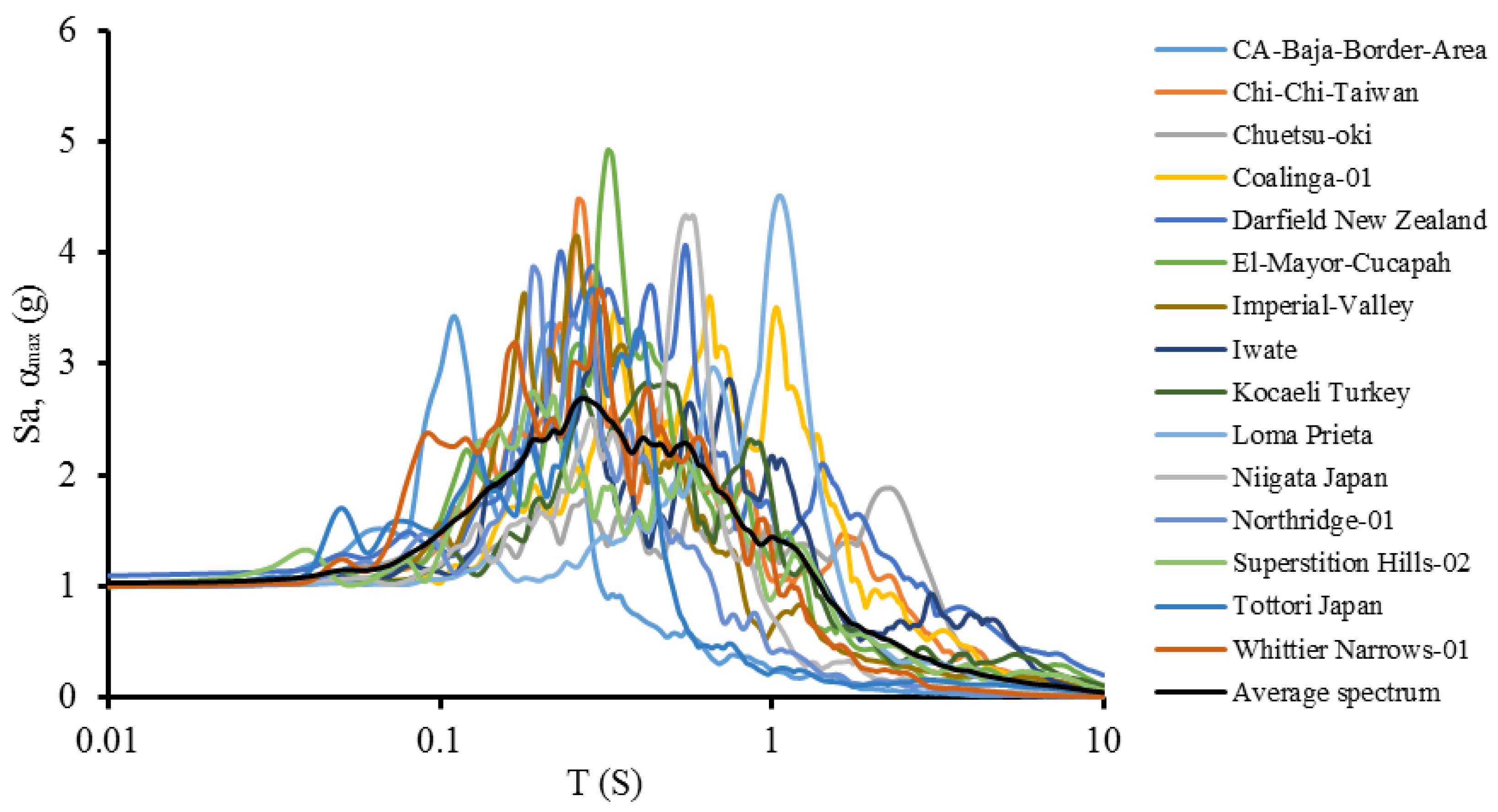
3.4. Selection of Input Ground Motions
- In reference to Chinese codes for seismic design of buildings, the seismic wave whose shear wave velocity Vs_30 m is less than 200 m/s is selected firstly.
- To reduce the effect of near-field effects, the epicentral distance of the selected seismic waves must be more than 10 km.
- To avoid the influence of the same focal mechanism, only one horizontal seismic wave is selected for each station and each seismic event.
- To avoid the dependence of the selected seismic waves on the recording direction, only one of the larger PGA is selected for the two horizontal time history recording curves of the same seismic event.
- Fifteen different seismic waves are selected, and the seismic waves with larger magnitudes are prioritized in the wave selection process to eliminate the earthquake that is unlikely to affect structural safety.
4. Fragility Analysis with Different Buried Depths
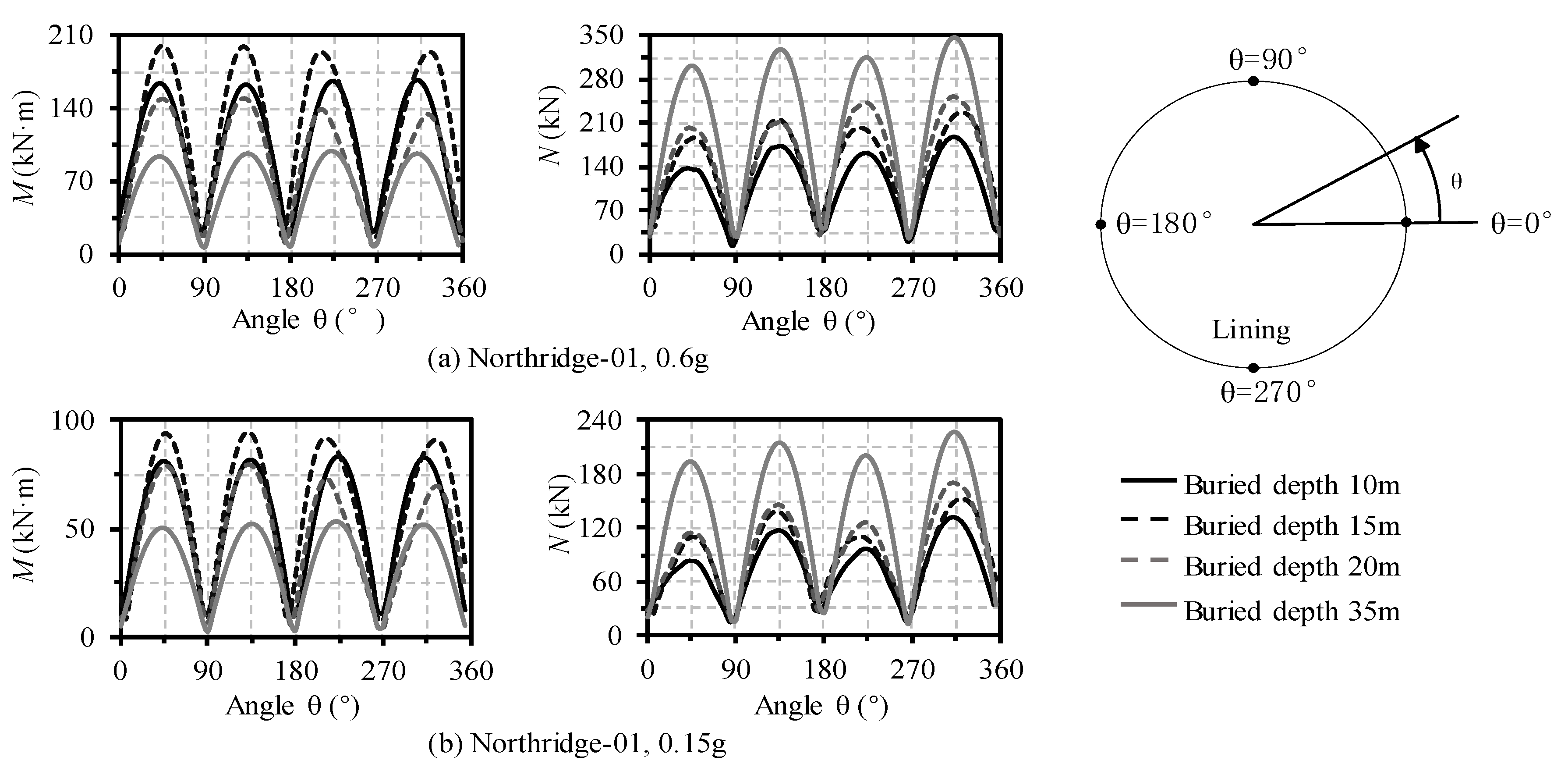
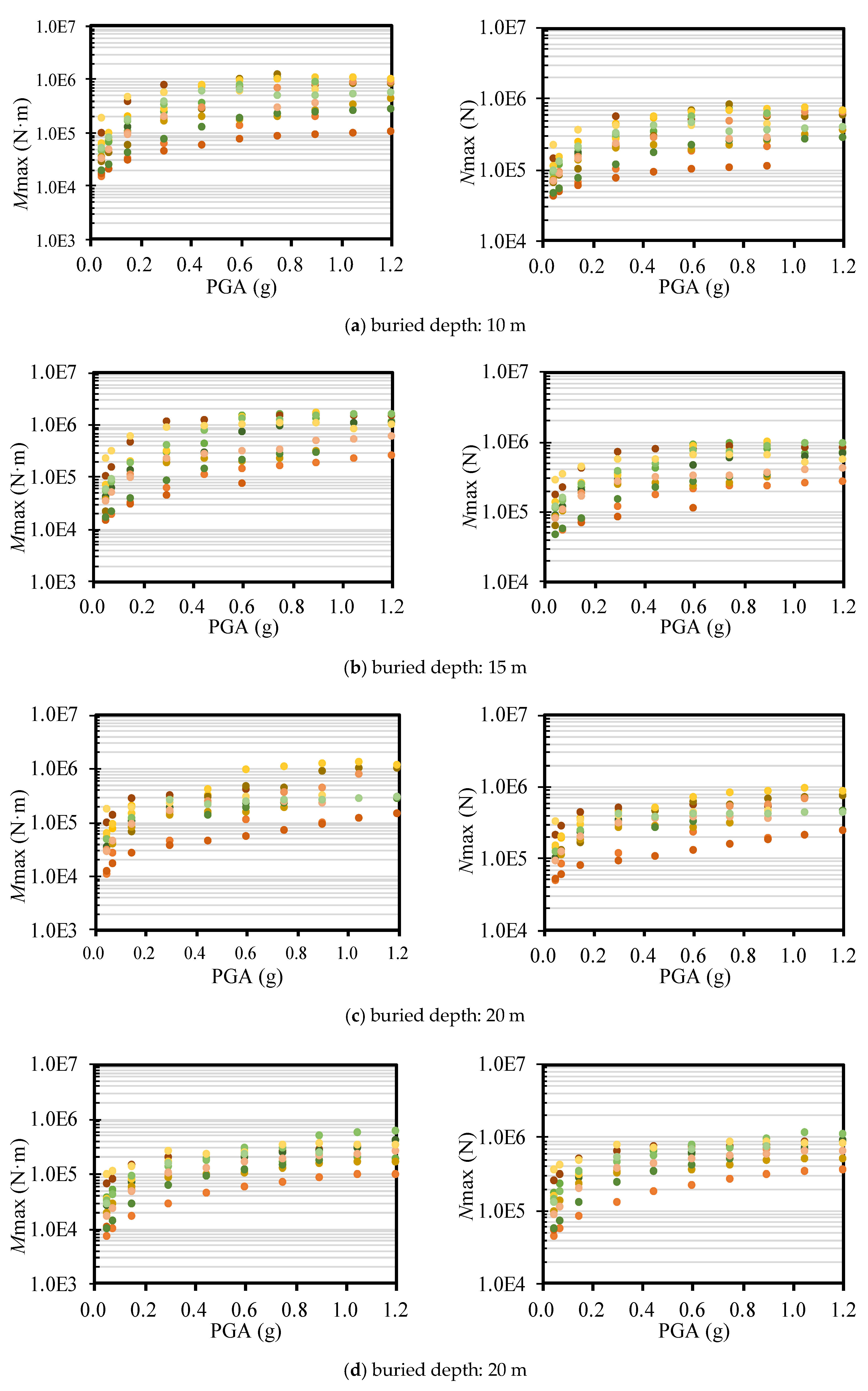
4.1. Internal Forces and Deformation of the Lining
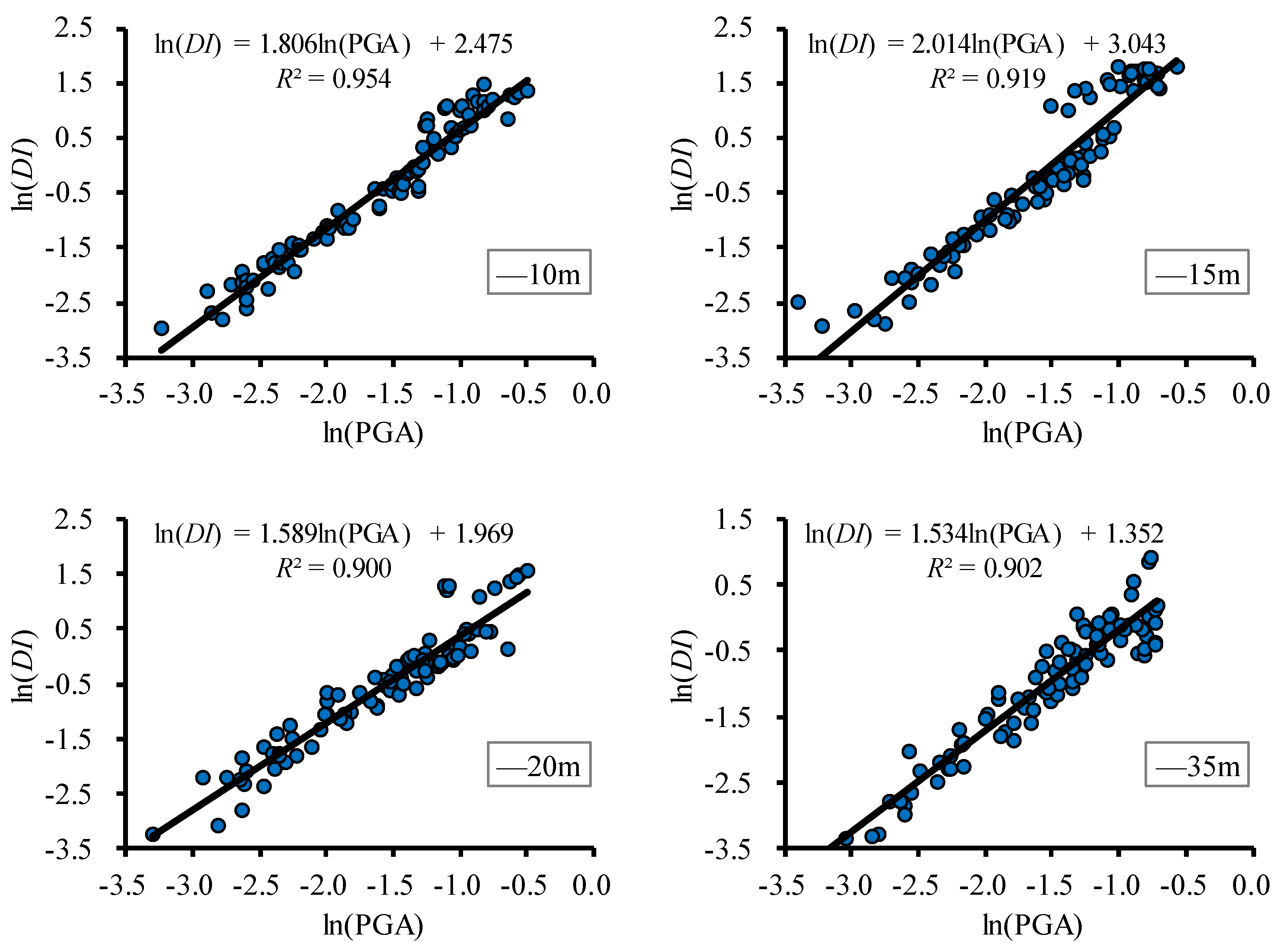
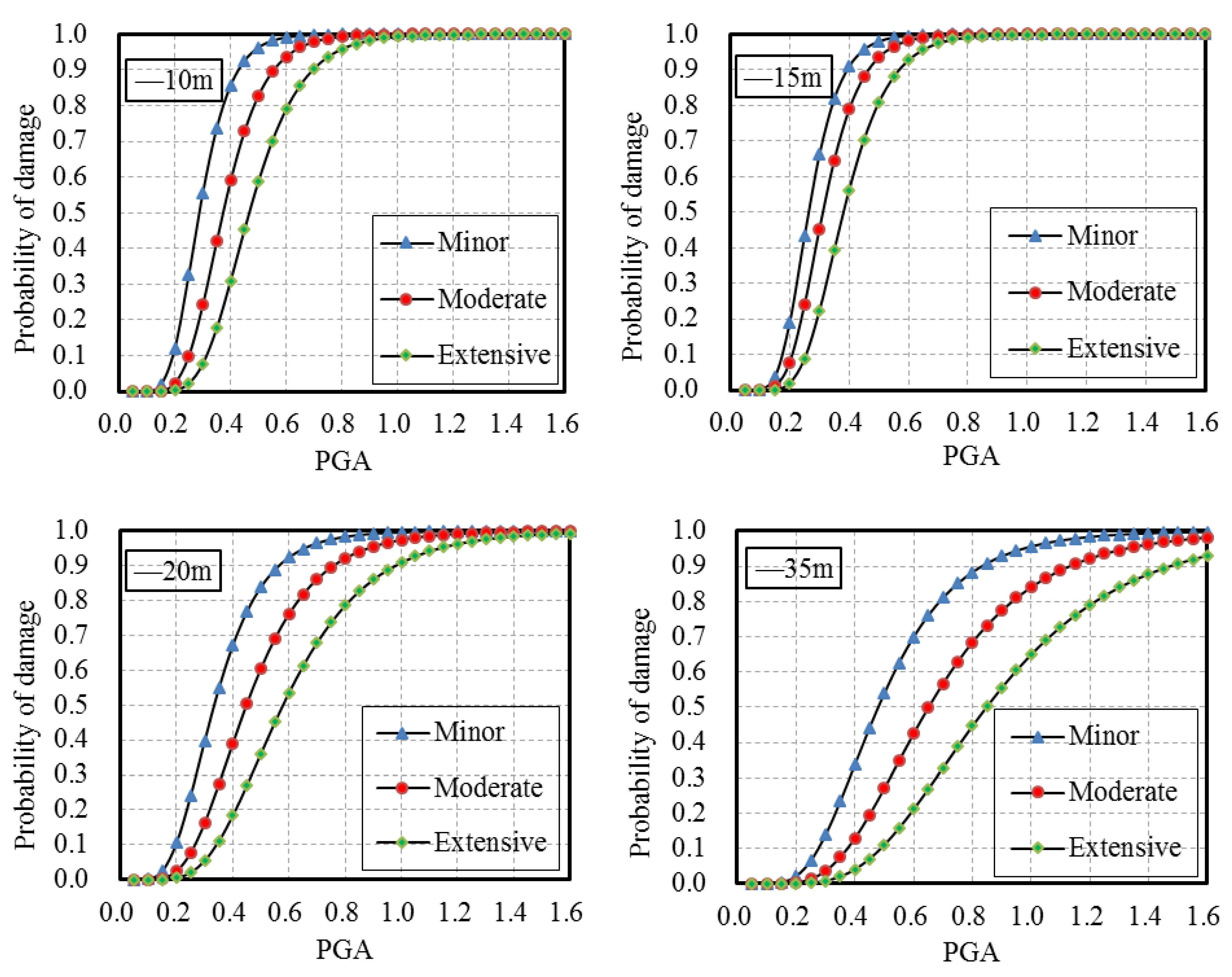
4.2. Seismic Fragility Curves with Different Buried Depths
4.3. Comparison Between Numerical and Empirical Fragility Curves
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zheng, Y.L.; Yang, L.D. Earthquake damages and countermeasures of underground structures. Earthq. Resist. Eng. 1999, 4, 23–28. (In Chinese) [Google Scholar]
- American Lifelines Alliance (ALA). Seismic Fragility Formulations for Water Systems, part 1—Guideline; ASCE-FEMA: Reston, VA, USA, 2001. [Google Scholar]
- Applied Technology Council-ATC-13. Earthquake Damage Evaluation Data for California; Applied Technology Council: Redwood City, CA, USA, 1985. [Google Scholar]
- National Institute of Building Sciences (NIBS). HAZUS-MH: Technical Manuals; Federal Emergency Management Agency and National Institute of Building Science: Washington, DC, USA, 2004. [Google Scholar]
- Kappos, A.; Panagopoulos, G.; Panagiotopoulos, C.; Penelis, G. A hybrid method for the vulnerability assessment of R/C and URM buildings. Bull. Earthq. Eng. 2006, 4, 391–413. [Google Scholar] [CrossRef]
- Lu, X.Z.; Shi, W.; Zhang, W.K.; Ye, L.P.; Ma, Y.H. Influence of Three-dimensional Ground Motion Input on IDA-based Collapse Fragility Analysis. Earthq. Resist. Eng. Retrofit. 2011, 33, 1–7. (In Chinese) [Google Scholar]
- Yu, X.H.; Lu, D.G. Seismic collapse fragility analysis considering structural uncertainties. J. Build. Struct. 2012, 33, 8–14. (In Chinese) [Google Scholar]
- Karim, K.R.; Yamazaki, F. Effect of earthquake ground motions on fragility curves of highway bridge piers based on numerical simulation. Earthq. Eng. Struct. Dyn. 2001, 30, 1839–1856. [Google Scholar] [CrossRef]
- Hwang, H.; Liu, J.B. Seismic Fragility Analysis of Reinforced Concrete Bridges. China Civ. Eng. J. 2004, 37, 47–51. (In Chinese) [Google Scholar]
- Miano, A.; Sezen, H.; Jalayer, F.; Prota, A. Performance-Based Assessment Methodology for Retrofit of Buildings. J. Struct. Eng. 2019, 145, 04019144. [Google Scholar] [CrossRef]
- Jalayer, F.; Ebrahimian, H.; Miano, A.; Manfredi, G.; Sezen, H. Analytical fragility assessment using un-scaled ground motion records. Earthq. Eng. Struct. Dyn. 2017, 46, 2639–2663. [Google Scholar] [CrossRef]
- Cornell, C.A.; Krawinkler, H. Progress and challenges in seismic performance assessment. PEER Cent. News 2000, 3, 1–3. [Google Scholar]
- Villaverde, R. Methods to assess the seismic collapse capacity of building structures: State of the art. J. Struct. Eng. ASCE 2007, 133, 57–66. [Google Scholar] [CrossRef]
- Baker, J.W. Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Argyroudis, S.; Pitilakis, K. Seismic fragility curves of shallow tunnels in alluvial deposits. Soil Dyn. and Earthq. Eng. 2012, 35, 1–12. [Google Scholar] [CrossRef]
- Le, T.S.; Huh, J.; Park, J.H. Earthquake Fragility Assessment of the Underground Tunnel Using an Efficient SSI Analysis Approach. J. Appl. Math. Phys. 2014, 2, 1073–1078. [Google Scholar] [CrossRef][Green Version]
- Osmi, C.; Khadijah, S.; Ahmad, S.M. Seismic Fragility Curves for Shallow Circular Tunnels under Different Soil Conditions. Int. J. Civ. Environ. Eng. 2016, 10, 1351–1357. [Google Scholar]
- Sharma, S.; Judd, W.R. Underground opening damage from earthquakes. Eng. Geol. 1991, 30, 263–276. [Google Scholar] [CrossRef]
- Gao, F.; Tan, X.K.; Sun, C.X.; Zhu, Y.; Li, H. Shaking table tests for seismic response of tunnels with different depths. Rock Soil Mech. 2015, 36, 2517–2522. (In Chinese) [Google Scholar]
- Idriss, I.M.; Seen, H.B. Seismic response of horizontal soil layers. J. Soil Mech. Found. Div. Am. Soc. Civ. Eng. 1968, 95, 693–698. [Google Scholar]
- Liu, D.D.; Qi, W.H.; Zhang, Y.D.; Lan, J.Y. Problem existing in current seismic response analysis for soil layers. J. Inst. Disaster Prev. Sci. Technol. 2009, 11, 34–37. (In Chinese) [Google Scholar]
- ABAQUS, version 6.14; Dassault Systemes Simulia Corp.: Providence, RI, USA, 2014.
- Bardet, J.P.; Ichii, K.; Lin, C. EERA-A Computer Program for Equivalent-linear Earthquake site Response Analysis of Layered Soil Deposits, User’s Manual; University of Southern California: Los Angeles, CA, USA, 2000; pp. 1–38. [Google Scholar]
- Osmi, S.C.; Ahmad, S.M.; Adnan, A. Seismic fragility analysis of underground tunnel buried in rock. In Proceedings of the International Conference on Earthquake Engineering and Seismology, MSC ORCHESTRA, Germany, 12–16 May 2015. [Google Scholar]
- Alam, J.; Kim, D.; Choi, B. Uncertainty reduction of seismic fragility of intake tower using Bayesian Inference and Markov Chain Monte Carlo simulation. Struct. Eng. Mech. 2017, 63, 47–53. [Google Scholar]
- Serdar Kirçil, M.; Polat, Z. Fragility analysis of mid-rise R/C frame buildings. Eng. Struct. 2006, 28, 1335–1345. [Google Scholar] [CrossRef]
- Hashash, Y.A.; Hook, J.; Schmidt, B.; Chiangyao, J. Seismic design and analysis of underground structures. Tunn. Undergr. Sp. Technol. 2001, 16, 247–293. [Google Scholar] [CrossRef]
- Shinozuka, M.; Feng, M.Q.; Lee, J.; Naganuma, T. Statistical analysis of fragility curves. J. Eng. Mech. 2000, 126, 1224–1231. [Google Scholar] [CrossRef]
- Salmon, M.; Wang, J.; Jones, D.; Wu, C. Fragility formulations for the BART system. In Proceedings of the 6th U.S. Conference on Lifeline Earthquake Engineering, TCLEE, Long Beach, CA, USA, 10–13 August 2003. [Google Scholar]
- Zheng, Y.L.; Liu, S.G.; Yang, L.D.; Tong, F. A Study on Seismic Design of Subway Tunnel in Soft Clay. Undergr. Sp. 2003, 23, 113–118. (In Chinese) [Google Scholar]
- Huang, Y.; Ye, W.M.; Tang, Y.Q.; Chen, Z.C. Coupled seismic response analysis of deep saturated soil covering layers in Shanghai. Rock Soil Mech. 2002, 23, 411–416. (In Chinese) [Google Scholar]
- Zhang, Y.J.; Lan, H.L.; Cui, Y.G. Statistical studies on shear modulus ratios and damping ratios of soil in Shanghai area. World Earthq. Eng. 2010, 26, 171–175. (In Chinese) [Google Scholar]
- Gutierrez, J.A.; Chopra, A.K. A substructure method for earthquake analysis of structures including structure-soil interaction. Earthq. Eng. Struct. Dyn. 1978, 6, 51–69. [Google Scholar] [CrossRef]
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div. ASCE 1973, 99, 421–427. [Google Scholar]
- Pitilakis, K.; Tsinidis, G. Earthquake Geotechnical Engineering Design, Chapter11: Performance and Seismic Design of Underground Structures; Springer International Publishing: Cham, Switzerland, 2014; pp. 279–335. [Google Scholar]
- Coleman, J.L.; Bolisetti, C.; Whittaker, A.S. Time-domain soil-structure interaction analysis of nuclear facilities. Nucl. Eng. Design 2016, 298, 264–270. [Google Scholar] [CrossRef]
- Qu, Z.; Ye, L.P.; Pan, P. Comparative study on methods of selecting earthquake ground motions for nonlinear time history analyses of building structures. China Civ. Eng. J. 2011, 44, 10–21. (In Chinese) [Google Scholar]
- Applied Technology Council-ATC-63. Quantification of Building Seismic Performance Factors; Applied Technology Council: Redwood City, CA, USA, 2008. [Google Scholar]


| . none | - | |
| . minor | 1.25 | |
| . moderate | 2.00 | |
| . extensive | 3.00 | |
| . collapse | - |
| Shear Strain γ (%) | Clay | Mucky Clay | Silty Clay | Fine Sand | Clayey Sand | Medium Sand | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| G/Gmax | ζ (%) | G/Gmax | ζ (%) | G/Gmax | ζ (%) | G/Gmax | ζ (%) | G/Gmax | ζ (%) | G/Gmax | ζ (%) | |
| 0.0005 | 0.992 | 0.9 | 0.00 | 1.1 | 0.989 | 1.1 | 0.994 | 0.5 | 0.993 | 0.7 | 0.995 | 0.66 |
| 0.001 | 0.986 | 0.9 | 0.982 | 1.2 | 0.981 | 1.2 | 0.989 | 0.6 | 0.987 | 0.8 | 0.990 | 1.0 |
| 0.005 | 0.936 | 1.5 | 0.923 | 1.8 | 0.924 | 1.9 | 0.945 | 1.2 | 0.936 | 1.4 | 0.953 | 2.5 |
| 0.01 | 0.882 | 2.0 | 0.86 | 2.6 | 0.865 | 2.6 | 0.896 | 1.7 | 0.881 | 2.0 | 0.991 | 3.6 |
| 0.05 | 0.605 | 6.1 | 0.549 | 7.4 | 0.564 | 7.8 | 0.64 | 4.5 | 0.606 | 5.8 | 0.682 | 7.2 |
| 0.1 | 0.433 | 10.5 | 0.366 | 12.5 | 0.378 | 13.3 | 0.476 | 7.1 | 0.442 | 9.7 | 0.522 | 8.6 |
| 0.5 | 0.128 | 24.7 | 0.086 | 27.3 | 0.085 | 28.7 | 0.164 | 15.8 | 0.147 | 22.3 | 0.182 | 10.6 |
| 1 | 0.067 | 26.2 | 0.041 | 28.8 | 0.039 | 30.5 | 0.093 | 16.8 | 0.082 | 23.7 | 0.103 | 11.0 |
| No. | Year | Earthquake | Magnitude | VS_30 (m/s) | Epicentral Distance (km) | PGA (g) |
|---|---|---|---|---|---|---|
| 1 | 1979 | Imperial Valley-06 | 6.53 | 196.25 | 12.56 | 0.38 |
| 2 | 1983 | Coalinga-01 | 6.36 | 178.27 | 41.99 | 0.14 |
| 3 | 1987 | Whittier Narrows-01 | 5.99 | 160.58 | 20.03 | 0.11 |
| 4 | 1987 | Superstition Hills-02 | 6.54 | 192.05 | 18.20 | 0.36 |
| 5 | 1989 | Loma Prieta | 6.93 | 133.11 | 43.23 | 0.27 |
| 6 | 1994 | Northridge-01 | 6.69 | 191.06 | 24.08 | 0.46 |
| 7 | 1999 | Kocaeli Turkey | 7.51 | 175.00 | 69.62 | 0.25 |
| 8 | 1999 | Chi-Chi Taiwan | 7.62 | 169.52 | 24.13 | 0.18 |
| 9 | 2000 | Tottori Japan | 6.61 | 169.16 | 45.98 | 0.19 |
| 10 | 2002 | CA/Baja Border Area | 5.31 | 196.25 | 52.30 | 0.13 |
| 11 | 2004 | Niigata Japan | 6.63 | 134.50 | 48.79 | 0.20 |
| 12 | 2007 | Chuetsu Oki, Japan | 6.80 | 198.26 | 10.78 | 0.68 |
| 13 | 2008 | Iwate, Japan | 6.90 | 146.72 | 10.39 | 0.24 |
| 14 | 2010 | Darfield, New Zealand | 7.00 | 141.00 | 19.48 | 0.26 |
| 15 | 2010 | El Mayor Cucapah | 7.20 | 196.25 | 16.21 | 0.59 |
| Buried Depth (m) | ||||
|---|---|---|---|---|
| 10 | 0.4 | 0.3 | 0.26 | 0.56 |
| 15 | 0.39 | 0.63 | ||
| 20 | 0.42 | 0.65 | ||
| 35 | 0.43 | 0.66 |
| D-10 m | D-15 m | D-20 m | D-35 m | HAZUS | ALA | |
|---|---|---|---|---|---|---|
| . minor | 0.29 | 0.26 | 0.33 | 0.48 | 0.51 | 0.59 |
| . moderate | 0.38 | 0.31 | 0.45 | 0.65 | 0.69 | 0.80 |
| . extensive | 0.47 | 0.37 | 0.58 | 0.84 | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Zhou, Z.; Chen, H.; Ren, Y. Seismic Fragility Analysis of Tunnels with Different Buried Depths in a Soft Soil. Sustainability 2020, 12, 892. https://doi.org/10.3390/su12030892
Hu X, Zhou Z, Chen H, Ren Y. Seismic Fragility Analysis of Tunnels with Different Buried Depths in a Soft Soil. Sustainability. 2020; 12(3):892. https://doi.org/10.3390/su12030892
Chicago/Turabian StyleHu, Xiaorong, Zhiguang Zhou, Hao Chen, and Yongqiang Ren. 2020. "Seismic Fragility Analysis of Tunnels with Different Buried Depths in a Soft Soil" Sustainability 12, no. 3: 892. https://doi.org/10.3390/su12030892
APA StyleHu, X., Zhou, Z., Chen, H., & Ren, Y. (2020). Seismic Fragility Analysis of Tunnels with Different Buried Depths in a Soft Soil. Sustainability, 12(3), 892. https://doi.org/10.3390/su12030892




