A Dynamic Model for the Financial Sustainability of the Restoration Sponsorship

Abstract

The paper addresses the theme of sponsorship as the main form of public–private partnership through which to finance restoration/recovery interventions for the historical–architectural heritage. The goal is the maximization of sponsorship profitability for companies. Specifically, an existing dynamic model through which it was possible to estimate the optimal annual amount to be invested in sponsorship to maximize the current value of expected profits has been analyzed, reworked and for the first time applied to an Italian company. It was therefore assumed that the company is intent on supporting a multi-year program of sponsorship investment. It is also assumed that the corporation is a single-product company, operating in monopolistic competition and characterized by a Cobb–Douglas production function with decreasing returns to scale. The work is in continuity with a previous publication focused on the application and validation of a static model. The final goal is to provide tools for applied analysis of the financial sustainability of the sponsorship that forms incentive for companies to implement its use, facilitating the recovery of the historical–architectural heritage. Public bodies can thus benefit from the greater contribution of resources from private financiers for a zero-cost and sustainable valorization of cultural heritage.

1. Introduction

Italy is among the countries with the largest cultural heritage. The country has more than 3400 museums, around 2100 archaeological parks and 54 of the 1092 sites included in the World Heritage List of the UNESCO (United Nations Educational, Scientific and Cultural Organization).

Given the premises, one would expect substantial revenues in the coffers of the Italian state from the management of the cultural heritage. However, these expectations are denied. Reading the RAC, the index analyzing the Economic Return on Cultural Assets of UNESCO sites, shows that the USA, despite owning less than half of Italy’s cultural sites, manages to achieve a higher economic return of about 16 times compared to the Italian one [1]. Furthermore, concerning the other European States there are some noticeable differences: in Spain the economic activities related to the cultural and tourism supply chain account about 21% of Gross Domestic Product (for around 225 billion euros) while in Italy they represent only 13% (about 203 billion euros).

It is clear, therefore, that the Italian cultural heritage is not properly capitalized, i.e., these resources are not used efficiently. Paradoxically, one of the major causes is to be attributed to many sites owned: in fact, the maintenance and management of such a vast heritage have proved to be difficult tasks in the absence of a valid management strategy.

Nevertheless, in recent years, thanks to more careful planning, important steps forward have been recorded in Italy [2]. In fact, between 2013 and 2016 there is a 38.4% increase in revenues linked to cultural activities (i.e., around 50 million euros) and the trend is still growing in 2017 (+13.5%).

Moreover, together with the revenues generated by the management of cultural heritage, public spending on culture and investments in the protection and enhancement of cultural heritage has also increased. This data is comforting as it is an indicator of a growing sensitivity to the issues of protection and conservation of this heritage, which has recently been made particularly fragile due to the constraints imposed by the economic crisis [3].

In fact, in 2017 there was a strong increase in Public Administration expenditure for the mission Protection and enhancement of cultural and landscape assets and activities. Not only were current expenses up (+27.6%) but also investments in protection and enhancement (+23.7%) [4].

The progressive increase in cultural investment and economic revenue are undoubtedly positive factors for Italy and its historical–artistic heritage. However, these factors are not the only variables to be considered. Recent administrative actions aimed at profit maximization place emphasis on achieving financial results, leaving aside other equally relevant aspects such as the greater value that historical–artistic assets derive from their relationship with the surrounding environment.

As well, momentum for sustainable growth of the values of the country’s cultural heritage and landscape derives from an increase in human capital: in fact, this productive factor can increase the value of cultural resources [5]. But, as mentioned, the enhancement and protection activities to be implemented are so expensive for the State [6] that collaboration with the private entrepreneur is necessary. In fact, the scarcity of resources for the preservation of the historical–architectural heritage generates the search for alternative sources to public funding. Thus, in recent years, rights, incentives and tax breaks have been made available to private entrepreneurs who are committed to ensuring an efficient valorization of cultural heritage [7]. Various instruments have therefore been used with the aim of creating partnership models between businesses and public administrations [8]. The public–private partnership (P.P.P.) is defined by the World Bank Institute [9] as a long-term contract between a government agency and a private entity. The latter not only provides a public good or service but also assumes considerable responsibility in terms of management and risk. According to Roehrich et al. [10] through public–private partnerships, it is possible to obtain multiple benefits through the combination of characteristics typical of private actors (such as innovation, technical knowledge and management efficiency) with those of public actors (such as social justice, local knowledge and public responsibility). There are many partnership instruments in support of cultural heritage. On the Italian scene, the Decree of the Ministry of Cultural Heritage and Activities and Tourism of 19th of December 2012 [11] identifies the following forms of private funding in support of culture: patronage, the adoption of a monument, cultural enhancement agreements, project financing, the granting of advertising space and sponsorship.

Sponsorship of cultural heritage is the most widespread legal instrument in Italy for the application of the constitutional principle of horizontal subsidiarity [12], by which individuals can intervene in favor of the enhancement and conservation of the historical–architectural heritage [13].

Sponsorship involves the establishment of a synergistic relationship between two parties: the sponsor who financially or in-kind supports a specific activity or project and the sponsee which, in exchange for such support, undertakes to promote the name and/or brand of the lender, allowing it to achieve commercial objectives. Sponsorship, therefore, is an innovative promotion strategy that uses the initiative supported as a communication channel, thus guaranteeing the sponsor high visibility. This characteristic makes it the form of partnership in support of the culture most used by companies. Moreover, due to its advertising nature, it also provides benefits in terms of tax breaks. The objectives of companies that use sponsorship are mainly the following: the growth of their reputation in the markets and with resource holders, the improvement of the company’s image and reputation and the increase in sales of the goods or services they offer [14,15,16]. For this reason, sponsorship can be used by companies both as a corporate communication (or institutional) tool and as a real marketing (or product) strategy. In the first case, the goal of the sponsor will be to increase the image and reputation of its brand in public opinion. In the case of marketing communication, instead, the message will be focused more on the final consumer in both directly (first-person involvement) and indirectly (media influence). In this latter case, sponsorship is closer to traditional advertising, since its main objective is the increase in turnover by the company.

But, regardless of the goal to be pursued, the most delicate phase for the sponsor is the evaluation of its work. The results obtained from a sponsorship campaign are often not easily measurable. This feature is valid both for measuring intangible effects (related to brand value and retention) and for tangible ones (such as business volume growth) [17]. As a direct consequence, it is just as complicated for the sponsor to establish the budget to be allocated to sponsorships to pursue the two previously mentioned goals. The international literature has produced numerous studies aimed at evaluating the effects of sponsorship [18,19,20,21], systematizing and analyzing validly and accurately the various techniques used to measure its effectiveness [22]. In these studies, sponsorship is considered above all as an important marketing strategy and means of corporate communication, leaving aside in many cases those aspects that lead back to the world of public–private partnerships. However, the evaluation of the effects generated by sponsorship is only the last step in the management process that a company’s management is called upon to follow to best promote an initiative. In fact, it is first necessary to verify that certain basic prerequisites are met, without which sponsorship could lose its effectiveness. Sponsorship must be functional to the objectives, both financial and image, established during the design and planning phase. In fact, if the objectives in question have been defined in detail, the subsequent phase of effectiveness assessment will be more precise [23,24]. Moreover, the business objectives are often not aligned with those of the public body. It is therefore only after public and private stakeholders have a perfect understanding and sharing of the objectives that a partnership instrument can be considered truly effective [25]. This presupposes a more accurate definition of them at the planning stage. Consequently, an ex-post measurement of the effectiveness of a sponsorship that has returned positive results for the company does not necessarily imply that the objectives set out in the partnership agreement have been fully achieved. Moreover, most of the models in the literature focus only on the concept of sponsorship effectiveness, not considering the economic efficiency of the investment. In this sense, the ROI (Return on investment) of sponsorship investment should also be assessed, expressed in terms of results obtained (monetary and image returns) compared to the total capital invested in this form of communication [23]. The index should then be compared with the budget (expressed as a percentage of turnover) that has been allocated to the sponsorship investment in the planning phase. There is, therefore, a gap in the literature regarding the purely financial aspects of sponsorship.

About this last point, in the 2017 work, a methodology was identified and analyzed for determining the optimal percentage of turnover to be allocated to sponsorships in order to guarantee the maximization of business profit [26]. Specifically, an existing model [27] was tested for the first time on a real company involved in cultural sponsorship. The main hypotheses underlying the model are the independence from the time of the investment in sponsorship (static model hypothesis) and the assumption of a Cobb–Douglas production function with constant returns to scale.

The purpose of this paper is instead to test, again through an application on a real case, a second theoretical model; the latter too was proposed by the authors of the static model [27]. The objective of the study remains to evaluate the optimal level of sponsorship (intended both as the number of events to be sponsored and as financial capital to be invested in sponsorship) that allows the company to maximize profits. This time, however, the model under study envisages that the analyses should be conducted in dynamic conditions.

It will then be possible to determine the optimal amount to invest annually in sponsorship that will maximize the NPV generated by the investment program. Specifically, the question to be answered will be: how many interventions in support of cultural heritage will the company have to sponsor over time (what is the amount that the company will have to invest each year in sponsorship) to maximize the present value of expected profits?

The model in question will be applied to a company (Caffè Moreno) operating in the coffee roasting and distribution sector which has already gained over time some experience in the field of sponsorship aimed at redeveloping the historical–architectural heritage.

The objectives of the model are the following: to implement the use of sponsorship to facilitate the sustainable recovery of the historical and architectural heritage, both public and private; to clarify to the companies the limits and convenience of the investment in cultural sponsorship; to provide a tool to assess the financial sustainability (private operator’s point of view) of the investment in sponsorship. Specifically, sponsorship is financially sustainable when it aims to create value for the company through a medium–long term-oriented investment strategy and when, through it, it is possible to obtain profits capable of self-financing further investments in the sector.

The model can also be useful to the sponsee, the organizer of the cultural initiative, which is often represented by a public administration. Knowing the optimal budget that the company should invest in sponsorship, the public body may, in turn, request a higher amount during the negotiation phase than is necessary for the realization of the initiative, given the greater attractiveness of the investment for the sponsor. The surcharge thus created can be used by sponsee both to enhance the initiative promoted, for example by improving its social or cultural impact, and to fund other sectors. The model can, therefore, represent a useful tool through which to guarantee economic sustainability (from the public operator’s point of view) of the investment in sponsorship. Sponsorship is economically sustainable for the public body if it can attract the financial resources needed to carry out an initiative in respect of cultural, social and environmental issues.

Another important goal of this paper is to evaluate the actual level of complexity of the model in its application to the operational reality to try to translate it into little complex software that is useful for companies.

The final aim is to fill at least part of the gaps in the literature, by proposing a model for estimating the optimal budget for sponsorship that allows the financial aspect of this form of partnership to be explored in greater depth.

That said, it should be noted that the dynamic model is also applicable to enterprises in other countries provided that the necessary data and information are available. In the present work, the model is applied to the Italian context because of the central role that the themes of cultural sponsorship and enhancement of the historical–architectural heritage assume in the country. Also, the application lends itself to further modifications and can be used in optimization problems both in areas like the one under analysis (such as advertising) and in different areas.

Nonetheless, further aspects of the issue that will eventually be addressed in the future remain to be defined. First, the sponsoring companies are not only interested in maximizing profit, but also in quantifying the return on image and reputation. In this sense, one could think of a synthesis model (partly applicable a priori and partly a posteriori) through which it would be possible to estimate all the information requested by the company regarding sponsorship activities. At this stage, it will be essential to estimate the media coverage of the sponsored event [18,19,20,21].

Moreover, the effects generated by traditional advertising on profits and the results obtained from the interactions between advertising and sponsorship have not been considered.

Finally, it should be stressed that, unlike the original model, the proposed revision did not take into account the learning capacity of the company through which, due to the experience gained from the initiatives sponsored in the past, it can reduce the organizational efforts for future initiatives and thus to contain the costs of sponsorship. In other words, from past sponsorships, you could learn to be more efficient in investing in future ones [27]. However, the estimation of a possible parameter representative of the learning level of the enterprise remains difficult to assess.

2. Conceptual Background and Theoretical Development

The classic approach to sponsorship by marketing and corporate communication scholars has produced many studies whose aim is to understand the following: the reasons why companies sponsor an event [15,22,28,29,30,31], the psychological processes triggered by sponsorship in the individual’s mind [32,33,34,35], the image transfer mechanism that allows the association between the initiative promoted and the company’s image [21,29,36,37], and the value creation process for the sponsor [38]. Of great importance are the studies on the evaluation of the effects of sponsorship, based mainly on the estimation of direct and indirect audience [19,39,40,41,42], on consumer surveys [20,43,44] or social experiments [21]. Despite the enormous importance of the topics covered, there are some gaps. First, few studies address the issue of sponsorship from the broader perspective of public–private partnerships. For example, as highlighted by Caldwell [25], the existing literature offers a limited understanding of social value creation mechanisms. This is especially true for cultural sponsorships, where the relationship between sponsors and sponsee is often built only on a contractual basis, not considering the benefits of mutual knowledge and alignment of objectives [45,46]. According to Kivleniece and Quelin [47], the opportunism of public partners and external stakeholders can undermine the success of the partnership and penalize the private funder. In such a highly competitive environment, measures are therefore needed to quantify the amount of funding to be provided by the sponsor to enable it to pursue its objectives in terms of both monetary return and image.

Secondly, most studies on the effects of sponsorship give little relevance to the financial value of the investment. The proposed models are very effective in determining how companies should operate in sponsorships to achieve their awareness and image promotion objectives. They also offer valuable results in quantifying changes in consumer preferences and tastes induced by sponsorship. However, these results are hardly ever translated into monetary terms. According to Pham [21], cost–benefit analysis is not the most effective tool to measure the impact of sponsorship. This is because, due to the complexity of establishing a direct relationship between sponsorship revenues and costs, the measure of effectiveness based on cost–benefit analysis is rarely appropriate. Although this statement is true, it is undeniable that companies show a strong interest in financial aspects. The same applies to public bodies, often eager to understand which potential sponsor is willing to provide the most funding. It is, therefore, necessary to propose further models to estimate the financial impact of sponsorship. However, these models should consider the theoretical and empirical aspects on sponsorship developed by the most authoritative scholars, both in the application phase and in the verification of results, integrating marketing and corporate communication models with the tools of the economic-financial evaluation of investment projects (as done, for example, in the recent work of Nickell et al. [48]).

Having defined the gaps in the literature, it is necessary to highlight the problems that businesses and public administrations encounter in practice.

As previously anticipated, it is quite complicated for the sponsors to be able to measure the actual increase in sales and the higher level of loyalty that may be found following the conclusion and execution of a sponsorship contract. Public administrations and private companies measuring the impact of sponsorships generally rely on a series of questionnaires, which usually provide results whose validity is acceptable almost exclusively in the short term [49]. Moreover, sponsors, since their work is constantly influenced by various external factors, generally prefer to evaluate the monetary and image return only after sponsorship is complete. For this reason, several a posteriori survey models have been proposed over the years, the aim of which is to measure the level of effectiveness of sponsorship activity. These models often make use of questionnaires, focus groups, direct and telephone interviews, surveys and social experiments through which it is possible to identify and analyze the responses to the stimuli that sponsorship transmits to the target audience [20,21,43,44,45].

There is also a further family of models, most of which, depending on the needs, is applicable both prior and posterior. They use economic applications of mathematical analysis to assess the effects (actual or potential) generated by sponsorship or other forms of advertising that a company could use [50,51,52,53,54,55,56,57,58,59].

These models should lead to more reliable results than those mentioned above, as they use the mathematical tool. However, they can be subject to considerable errors depending on the type and number of simplifying assumptions adopted. Moreover, in most cases, they are poorly applied by enterprises due to the high level of complexity of their functional relationships, so that they are almost entirely replaced by the more intuitive survey models.

In the latter family of models, those proposed by Bucci A., Castellani M. and Figini P. in the paper L’investimento in sponsorizzazione delle imprese: un’analisi economica in termini statici e dinamici assume certain importance [27]. The objective of the study is to estimate, using mathematical models applied to the microeconomics in both static and dynamic conditions, the optimal level of sponsorship that maximizes business profit.

The present work analyses the dynamic model of investment in sponsorship, with the intention of explaining those logical-mathematical passages summarized by the authors in the original text and of reducing, where possible, their original level of complexity by introducing some simplifying hypotheses. However, the main objective is to test the model, currently formalized only on a theoretical level, adapting and applying it through a case study to a company active in the field of cultural sponsorship. This not only provides a further useful tool for business practice but also partially closes gaps in the literature on the issues of public–private partnerships and sponsorship.

Following the model is illustrated and analyzed in detail in its individual parts. In particular, the basic hypotheses adopted in its original formalization are recalled, specifying which of these are confirmed and which are instead simplified in the application phase.

2.1. The Basic Hypotheses of the Model

The basic hypotheses adopted by the authors in the formalization of the original model refer to the following three characteristics of the company that invests in sponsorship: the type of company, the form of market in which it operates and the production function that best approximates its real behavior.

2.1.1. Type of Company

In the original model, the hypothesis of a single-product company was assumed. In contrast, it is easy to see that in a not ideal economic system most corporations are considered multi-products companies.

However, it is useful to remember that a single-product company is defined as a company which simply offers a single good or service to its customers and a company which, although it maintains several goods or services on the market, obtains a considerable percentage of its turnover from the sale of only one of them.

By contrast, multi-product companies are defined as companies offering a high range of goods or services or companies whose total turnover does not derive mainly from the sale of a given good or service [60].

As mentioned above, the company to which the model has been applied operates mainly in the sector of coffee roasting and distribution and offers its customers different types of products (coffee beans, powder, pods and capsules). Also, the company sells machines for pods and/or capsules as well as equipment, kits and various gadgets. It would appear, therefore, that the corporation is a multi-product company. However, from the notes to the ordinary financial statements (closing date 31 of December 2017) filed with the Register of Companies of the Chamber of Commerce, Industry, Crafts and Agriculture of Naples [61], the sale of coffee goods has an incidence of 98.93% on total revenues and is much higher than the incidence relating to the sale of machinery (0.69%) and that relating to the sale of various equipment and kits (0.38%). In the notes to the financial statements it is also stated that the company’s main activity is the production and sale of coffee intended for bars and that the company obtains a substantial proportion of its turnover (around 80%) from the sale of coffee beans. Therefore, it falls fully within the definition of a single-product company and, as a result, it was not considered necessary to modify the first basic hypothesis of the dynamic model.

Consequently, in the application phase it was possible to introduce a further simplification: in the equations characterizing the model only the price p of the asset which has the greatest impact on the company’s overall turnover was considered.

Finally, it can be observed that the single-product company hypothesis does not affect the sponsorship results in any way. Sponsorship promotes the overall image of the company, i.e., it acts at the brand level, unlike traditional advertising, which refers to individual products [27]. It follows that sponsorship contributes to an overall increase in sales of all products offered so that its effects remain the same for both single-product and multi-product companies.

2.1.2. Market Form

The original model assumes that the company operates in perfect competition. Under this assumption, the unit price of the goods offered by the single-product company is independent of the quantity of product required by the market (and vice versa). This choice allows to keep the price constant and not to consider the inverse demand curve, which complicates the equations of the dynamic model.

However, the hypothesis of perfect competition does not fit in with the theme of sponsorship, leading to a conceptual error. In perfect competition, there is an infinite number of companies producing homogeneous goods, that is, perfectly identical to each other. Therefore, according to this hypothesis, it makes no sense to implement marketing policies, since companies being price takers cannot influence the market. In perfect competition, any advertising and promotional strategy would be useless, since the products of the individual companies, being homogeneous, do not differ from each other. Under these circumstances, all efforts by an undertaking to differentiate itself from its competitors would be in vain.

On the contrary, in so-called markets of imperfect competition there are many (but not infinite) companies that produce non-homogeneous goods. In this case, marketing techniques and communication strategies such as sponsorship can influence consumers’ choices since product differentiation leads to a change in their preferences as each good is distinct from the others by differences both tangible (technical characteristics, objective quality, etc.) and intangible (brand reputation, perceived quality, etc.) [62].

It is therefore considered necessary to modify the second basic hypothesis of the dynamic model assuming that the studied company operates in a monopolistic competition market.

In the application phase, the dynamic model of the reverse demand function for the monopoly was therefore considered in the equations. This function expresses the law of variation of the price that the good undergoes to vary of the demanded quantity. Moreover, in the present case, it has been assumed that the price also depends on the number of events sponsored by the company until that moment. Although this hypothesis could be a problematic aspect of modelling and requires an analysis of the price trend as the sponsorship stock changes, it is essential if the company’s behavior is to be analyzed as realistically as possible. In fact, the hypothesis is supported by the real observation of the price of the main good offered by the company as the number of sponsorships varies. It should be noted, however, that this observation did not prove to be overly complex, as the overall stock of sponsorships accumulated over time by the company was limited. Specifically, the price trend was analyzed only in the last four years, during which the number of sponsorships increased from 1 to 3. Also, the good offered by the company is of prime necessity so that its price does not change significantly with the amount requested and the number of sponsored restorations, thus remaining almost constant. The representative equation of the reverse market demand function is shown below:

p_t = b − c · Q_(t−1) + d · S_(t−1),

(1)

which, in this simplified form, identifies a plan along which the price of the good of the single-product company changes with the variation of the requested quantity of the same (Q_t) and with the number of events sponsored in the past by the company (S_t). It has been assumed that the price increases in proportion to the number of sponsorships because a socially and culturally committed company is generally perceived as more reliable by consumers and its products are usually of better quality than those of its competitors. For this reason, they will be willing to buy them at a slightly higher price.

2.1.3. Production Function

According to the original model, a Cobb–Douglas production function is assumed with decreasing returns to scale [63]. Generally, there are decreasing returns to scale when the increase in the quantity of production factors used corresponds to an increase in the quantity of finished product that is less than proportional [64]. The less than proportional growth of the level of total productivity is mainly due to the hypothesis of limited organizational capacity of the company: as the size of the production increases, the waste of resources linked to problems of management and organization increases. This assumption is consistent with the company under analysis. Decreasing returns to scale usually characterize those companies that, like the one under examination, do not have a very high technological component, while generally increasing returns to scale are associated with those companies with a high innovative component (IT or industrial sector). Specifically, the company under study is active in the production and distribution of coffee, for which it does not require a very high level of technological specialization [65,66]. Moreover, as will be illustrated in the following paragraphs, the assumption of a technology with decreasing returns to scale has also been demonstrated empirically through the application of multiple linear regression analysis to the historical series of input and output data of the company under examination.

The authors of the dynamic model have reworked the Cobb–Douglas function (which in the original version considers only the factors of production, labor and capital) introducing as the third factor of production the stock of intangible capital invested in sponsorships. Considering a generic instant of time t, the characteristic equation of the Cobb–Douglas, therefore, assumes the following form:

Q_t = K_t^αL_t^βS_t^γ,

(2)

where Q_t is the output of the single-product company, K_t is capital, L_t is labour, and S_t represents the stock of sponsorship intangible capital (i.e., the number of events sponsored in the past by the company). The constants 0 < α < 1, 0 < β < 1 and 0 < γ < 1 constitute instead a measure of the elasticity of the production and of the marginal return (decreasing because all three less than 1) respectively of K_t, L_t and S_t. The sum of the three constants determines the type of returns to scale. In the proposed model the authors have assumed that it is α + β + γ < 1; this means that the production technology of the company has decreasing returns to scale [67,68,69].

In the specific case of the application covered by this publication, the output Q_t was obtained by dividing the production value, which we indicate with R_t, by the unit price p_t of the good that has the greatest impact on total turnover. The production value has been extrapolated from the Income Statement of the company’s Financial Statements for the year 2017. About capital K_t, it was associated with the value of the assets taken from the Balance Sheet (i.e., the value of the investments to which the company has allocated the means found in the conduct of its business). It was also decided to represent labor L_t through the number of workers, which was extrapolated from the Notes to the Financial Statements. Finally, the number of sponsorships (S_t) supported by the company over the years and aimed at recovering the historical and architectural heritage was easy to identify, given the media coverage of the initiatives in question.

Compared to the model proposed by Bucci et al. the multiplicative constant T > 0, which is instead present in the original formalization of the Cobb–Douglas function, was also introduced. This constant, whose rate of change indicates the technical progress of the company, represents the efficiency of the simultaneous use of all factors and therefore indicates the technology productivity degree used by the organizational apparatus [67,70,71].

The production function adopted ultimately takes the following form:

Q_t = T · K_t^αL_t^βS_t^γ.

(3)

For the estimation of the parameters T, α, β and γ see the following paragraphs.

In the following section we will analyze the mathematical principle through which it is possible to solve the fundamental question of the model.

2.2. Pontryagin’s Maximum Principle and Dynamic Model

The objective of the dynamic model is not only to identify the conditions of equilibrium of a company that invests in sponsorships, but also to establish the dynamic process that leads to the optimal path of growth. The aim is therefore to determine the amount of long-term investment in sponsorship that will maximize the present value of the company’s expected profits [27].

In the case of the dynamic model, the function of profit to be maximized depends, therefore, also on the time t. This makes the resolution of the problem rather complex. Variables will not only change over time but will also be subject to the laws of financial mathematics. We will therefore have that the annual profits to be maximized can only be added together if they are transformed into their present value through a constant assumed financial discount rate ρ.

The technique used to solve the endogenous growth model is that of the Maximum Principle elaborated by the Russian mathematician Pontryagin [72]. The basic elements of this principle and how it was contextualized within the dynamic model of investment in sponsorship are presented below. Given a dynamic system, it is possible to divide its variables into two categories:

• state variables: these are those variables which are associated with a law of movement whose value cannot be chosen or controlled by the agent, since it is historically predetermined. These are usually quantities without a time dimension, i.e., stock variables (such as the amount of wealth).
• control variables: these are those variables that can be controlled by the decision-maker, such as, for example, investment in capital goods (both tangible and intangible). In this case, the agent can “choose” the value of the variable in each time interval that has not yet occurred, that is, to control it according to his needs. They therefore generally represent flow variables, i.e., those quantities measured in units of time (such as, for example, investments).

Once the value of the control variable has been fixed by the decision-maker, the change in the state variable in each period is determined accordingly. For example, by choosing the optimal investment flow (control) a company determines the dynamics of the capital stock given the initial endowment and the programming interval. It is, therefore, possible to describe the growth rate of state variables in the form of differential equations. The fundamental problem is to choose a sequence of controls that ensures the maximization or minimization of some objective function (in the present case we are interested in the maximization of the profit function).

The Pontryagin’s Maximum Principle was therefore adopted by Bucci, Castellani and Figini [27] to identify the optimal level of investment in sponsorship that maximizes at all times the function of the discounted profits of a representative company. The variables and starting conditions considered by the model are as follows:

• S_t: stock of sponsorship (number of events sponsored in the past by the enterprise up to time t). It is the state variable of the problem;
  I_St: investment in sponsorships (number of new events to be sponsored in time unit t). Represents the control variable;
  L_t: non-specialized labor employed at time t. It is supposed to be constant in the planning horizon as the purpose of the work is to determine, under the same conditions, only the amount of optimal investment in sponsorship (for this reason, the subscript t will be omitted below);
  K_t: stock of capital (cash and cash equivalents and fixed assets, tangible and intangible, held at time t). For similar reasons to those mentioned for unskilled work, it was assumed that it remains constant in the programming horizon (even in this case the subscript t will be omitted in the following);
• δS_t/δt = I_St is the law of motion of the state variable (i.e., of the stock of sponsorships). Conceptually, it coincides with the number of new events to be sponsored in the time unit. It represents a constraint of the problem;
  π_t [S_t; I_St]: is the objective function that is intended to be maximized, i.e., the profit function of the company. Its arguments are the status variable S_t and the control variable I_St.
  [0; ∞]: is the programming horizon, where 0 is the starting instant and the ending instant is at infinity;
• t: is the generic instant time in the range [0; ∞];
• S₀: is the initial value of the stock of sponsorship, i.e., of the state variable (known data, and therefore another constraint of the problem);
• ρ: is the discount rate;
• e^−ρt: is the discount factor.

In its simplest form an optimal control problem consists in finding, for each t, the value of I_St that maximizes the following function:

$${V=MAX}_{\{S_t,I_{S_t}\}}{{\displaystyle \int }}_0^{\infty }{e}^{-\rho t}{\pi }_{t}dt,$$

(4)

where S_t is the state variable while I_st is the control variable of the dynamic optimization problem. Maximizing the objective function is subject to the following constraints:

$$\begin{array}{c}{\stackrel{.}{S}}_t=\frac{\partial S_t}{\partial t}=I_{S_t},\\ {S(0)=S}_0.\end{array}$$

(5)

The first equation of (5) expresses the motion law of the state variable: it tells us that the variation of the state of the system in an infinitesimal time depends on the value possessed by the state variable at time t and by the one chosen for the control variable at the same time.

The corporate profit at the generic time t is equal to:

$${\pi }_t{=R}_t({K,L,S}_t){-C}_{S_t}(I_{S_t})-wL-rK,$$

(6)

where R(K, L, S_t) is the production value, CS_t(I_St) is the total cost of sponsorship, wL is labor cost (calculated as the product of the number of workers L for the average cost of a single worker w) and rK is capital cost (calculated as the product of K expressed in terms of value for a return rate r which represents the cost that at time t must possibly be incurred to increase the capital stock and, consequently, the value of K).

The necessary conditions that constitute the Maximum Principle require the introduction of a variable of convenience called costate variable and denoted with μ_t. In the present case, this variable coincides with the shadow price of sponsorship, since it expresses the usefulness that the current choice of investment in sponsorship has for the company net of the distortions found on the market (such as taxes, VAT, taxation, etc.). It is the opportunity cost of resources and it is a useful quantity to express the value of the resources themselves about the conditions of their specific use [73]. Shadow prices, in problems of constrained optimization, are related to the change in the level of the target function, resulting from a relaxation of the constraint. In problems of production maximization, the shadow price corresponds to the marginal utility at the optimum point of the resource (input) binding. It is in the specific case the highest price the company is willing to pay for an additional investment in sponsorship [74,75]. Introduced such variable, it is possible to define in every instant a new function called Hamiltonian, defined by the sum of the objective function v[s(t), c(t)] evaluated in an instant of time and of a function that identifies the intertemporal constraints, that is the law of motion multiplied by the costate variable, which measures how tight the constraint is.

The Hamiltonian function associated with the problem of dynamic optimization will be equal to:

$$H_t=e^{-\rho t}{\pi }_t+\mu (t)\stackrel{.}{S}=e^{-\rho t}\{R_t(K,L,S_t)-C_{S_t}(I_{S_t})-wL-rK\}+{\mu }_t\stackrel{.}{S}.$$

(7)

According to the principle of the maximum, the control variable in every instant of time t must be chosen in order to maximize the Hamiltonian, known the values of the state and the costate variables.

It is also possible to calculate the costate variable in current value by multiplying the costate variable by the capitalization factor:

$${\lambda }_t=e^{\rho t}{\mu }_t.$$

(8)

Considering the costate variable in current value and remembering that, from the first equation of (5), the variation of the sponsorship stock in the unit of time coincides with I_St, the Hamiltonian can therefore also take the following form:

$$H_t=e^{-\rho t}{\pi }_t+\mu (t)\stackrel{.}{S}=e^{-\rho t}\{R_t(K,L,S_t)-C_{S_t}(I_{S_t})-wL-rK+{\lambda }_t{I}_{S_t}\}.$$

(9)

With the introduction of the Hamiltonian, the function to be maximized through the action of the variable of cost has been corrected; the objective function can be rewritten as follows:

$$V={MAX}_{\left\{S_t,I_{S_t}\right\}}{{\displaystyle \int }}_0^{\infty }{H}_{t}dt.$$

(10)

It is shown that an excellent solution to the problem is a triplet I_St, S_t, µ_t that meets an algebraic condition and two differential equations.

In particular, the algebraic condition is that the control variable I_St maximizes the function H_t [I_St; S_t; µ_t]. This consists in imposing that the partial derivative of the Hamiltonian concerning the control variable is equal to zero (first order condition):

$$\frac{\partial H_t}{\partial I_{S_t}}=0.$$

(11)

The pair of differential equations that the µ_t costate variable and the S_t state variable must satisfy is the following:

$$\stackrel{.}{\mu }(t)=-\frac{\partial H_t}{\partial S_t};{\stackrel{.}{S}}_t=\frac{\partial H_t}{\partial {\mu }_t}.$$

(12)

Therefore, the optimal triplet consists of two differential equations that describe the dynamics of the state variable S_t and that of the costate variable µ_t plus an algebraic equation obtained from the first-order condition that allows choosing optimally the control I_St [58,76,77,78].

3. The Case Study and the Revision of the Model

In this paragraph the model is contextualized concerning the case study. First, basic information on the analysis is introduced (Caffè Moreno S.r.l.). Then, we proceed to the phase of partial revision of the dynamic model considering the real behavior of the company and introducing further simplifying hypotheses.

3.1. The Company Chosen for the Case Study

A valid example of ongoing sponsorship is the Monumentando initiative, proposed by the City of Naples. The project started on September 16, 2013, when a public call for proposals was launched for the selection of a single sponsor to be entrusted with the design and execution of the restoration of 27 city monuments. The official sponsor could resell the advertising space intended to be installed on the scaffolding of the yards to other companies that are the real financiers of the works. The winner of the public tender was Uno Outdoor a large integrated communication agency that has been chosen as an intermediary between the City of Naples and the financing companies. The latter, therefore, are the real sponsors, as all the activities planned are at their expense.

Among the various sponsors recruited by Uno Outdoor stands out Caffè Moreno a company active in the roasting and distribution of wholesale coffee. Between 2014 and 2016 the company has financed the restoration of the following three monuments [79]:

• Artichoke Fountain (location: Piazza Trieste and Trento; advertising exposure time: about 6 months; monthly exposure cost: €80,000; total sponsorship cost: €480,000);
• Obelisk of Portosalvo (location: Via De Gasperi–Via Cristoforo Colombo; advertising exposure time: about 2 months; monthly exposure cost: €80,000; total sponsorship cost: €160,000);
• Armando Diaz Monument (location: Rotonda Diaz; advertising exposure time: approximately 2 months; monthly exposure cost: €100,000; total sponsorship cost: €200,000).

It is easy to see how Caffè Moreno has invested a total of €840,000 in sponsorships in three years, and that therefore the average cost for sponsoring a restoration project was €280,000 [80].

The dynamic model of investment in sponsorship has been applied to the company in question. In the following, we will highlight the fundamental steps taken during the phases of characterization and partial revision of the model.

3.2. Characterization and Revision of the Model

Let us start with the characterization phase of the model introducing the profit function at time t, expressed in generic form:

$${\pi }_t=R_t-C_t\to {\pi }_t=p_t{Q}_t-C_t,$$

(13)

where R_t and C_t indicate respectively the production value and the production cost at time t. In turn, the value of production can be expressed as the product between the unit price of the offered good (p_t) and the output (Q_t) obtained at time t. Assuming, moreover, a non-linear Cobb–Douglas production function with decreasing returns to scale, for the (1) and the (3), the (13) becomes:

$${\pi }_t=(b-c T{K}^{\alpha }{L}^{\beta }{S_{t-1}}^{\gamma }+d{S}_{t-1})T{K}^{\alpha }{L}^{\beta }{S_t}^{\gamma }-C_t.$$

(14)

In parentheses, the function of unit price expressed in terms of reverse market demand is indicated. For the estimation of the coefficients b, c and d, the demand for coffee beans, that is the product from which the company obtains about 80% of its turnover, was analyzed. Following research carried out at various points of sale and on the web, the variation in the unit price of coffee beans (for each of the product lines in which it differs in quality and aroma) was recorded when the requested tons varied. This operation was carried out over three different periods, during which the number of events sponsored by the company increased from 1 to 3.

It was, therefore, possible to apply multiple linear regression analysis for each price i recorded (varying by S and Q) and for each product line j of coffee beans offered by the company. Different values of the regression coefficients b_ij, c_ij and d_ij were thus obtained. Their average was then calculated, thus obtaining the following values: b = 20; c = 0.0000057; d = 0.0005. The quantity Q₀ of goods virtually produced by the company at time 0 was determined by dividing the value of production R₀ taken from the financial statements by the unit price p₀ of the goods offered at time 0. For the latter, an average value of around €15 per kilogram has been estimated.

About the production costs C_t, we can explain to them as follows:

$$C_t=C_{S_t}+wL+rK,$$

(15)

where, as seen above, C_St represents the function of the total cost of sponsorship, wL is labor cost and rK is capital cost.

Specifically, agreeing with the original dynamic model, we express the C_St function through a standard investment model [81,82,83]. In particular, the total cost of sponsorship is represented by the following function:

$$C_{S_t}=A{I_{S_t}}^2+B{I}_{S_t},$$

(16)

where AI_St² represents the sponsorship adjustment cost, increasing and convex in I_St > 0, while BI_St represents the sponsorship direct cost. Parameters A > 0 and B > 0 are constant.

The direct cost represents the set of items of expenditure directly and objectively attributable to the individual sponsorships. These are costs which have a specific relationship with the investments concerned and which relate to a specific moment t [84,85]. B is the unit sponsorship direct cost (i.e., when I_St = 1). In the present discussion it has therefore been made to coincide with the cost that on average the company has incurred to sponsor a restoration (B = €280,000). With this term we refer, therefore, both to the financial expenditure necessary for the design and execution of restoration work on a monument and to all the costs of advertising and propaganda, the costs of design and installation of the exhibition panels and the costs for the acquisition of additional specific rights provided for in the individual contract.

The adjustment cost, on the other hand, represents the additional cost that the company must bear in order to make a further investment in sponsorship. That is, when at time t you decide to increase the stock of sponsorships accumulated over the years through an additional investment I_St, you must bear a series of costs that are increasing more than proportionally to the increase in the size of the investment. The company that therefore decides to intensify its investment policy in sponsorships will have to provide additional expenses: for the organization of conferences and press reviews, for the communication plan, for the recruitment of consultants experts in marketing and communication, for the ongoing training of that part of the management that deals with public relations, for investigations aimed at assessing the effectiveness of sponsorship [86,87,88]. Adjustment costs are usually assumed to grow more than proportionally to the increase in the number of sponsorship investments made by the company. This behavior is justified by the following reason: each event to be sponsored generally requires a very specific organization (from a legal, administrative and financial point of view) and therefore difficult to share among several initiatives sponsored at the same time. In the presence of numerous sponsorships, congestion effects are created that lead to a more than proportional increase in adjustment costs [27]. In addition, we can note that parameter A represents the unit sponsorship adjustment cost (i.e., the adjustment cost that the company incurs when I_St = 1). In this application, parameter A has been set equal to the share of the marketing budget that a company uses on average in activities complementary to the sponsorship of a single event. In order to be able to define this quota, the overall budget that ideally should be invested in marketing and communication has been estimated in advance. The latter, for a small to medium sized company such as the one under review (so classifiable according to Commission Directive 96/280/EC in terms of volume of turnover and number of employees recruited), according to the most accredited estimation models should be about 15% of annual turnover [89,90,91]. Since the turnover of the company at the time t is €13,875,998, the optimal amount to be allocated to marketing and communication activities during the year is approximately €2,000,000. This amount includes the direct unit cost of sponsorship, for which €280,000 must be deducted. Of the remaining €1,720,000, it is assumed that 90%, i.e., the most significant part is allocated to other marketing and communication strategies (advertising, direct marketing, sales promotions, public relations, company website, etc.) and that the remaining 10% is used in complementary activities and support to sponsorship, constituting the cost of adjusting the investment. Therefore, the unit adjustment cost A was assumed to be €172,000. The total cost of sponsorship (C_St) to be incurred when I_St = 1 is obtained as the sum of A and B and is €452,000. It is assumed that approximately 23% of the marketing mix is used to finance the investment in sponsorship and other related activities.

Once the production costs have been fully defined, the total profit function expressed by (14) becomes the following:

$${\pi }_t=(b-cT{K}^{\alpha }{L}^{\beta }{S_{t-1}}^{\gamma }+d{S}_{t-1})T{K}^{\alpha }{L}^{\beta }{S_t}^{\gamma }-A{I_{S_t}}^2-B{I}_{S_t}-wL-rK.$$

(17)

The Hamiltonian function associated with the dynamic optimization problem will therefore be equal to:

$$H_t=e^{-\rho t}\{(b-cT{K}^{\alpha }{L}^{\beta }{S_{t-1}}^{\gamma }+d{S}_{t-1})T{K}^{\alpha }{L}^{\beta }{S_t}^{\gamma }-A{I_{S_t}}^2-B{I}_{S_t}-wL-rK+{\lambda }_t{I}_{S_t}\}.$$

(18)

We now move on to the partial revision of the model. At this stage, two of the basic hypotheses have been modified in order to make the choices regarding the investment program more realistic:

• Finite-time horizon within which to evaluate the financial convenience of the investment program and set the problem of dynamic optimization: we have chosen a time horizon of twenty years (0 ˂ t ˂ T = 20), taking into account both the effects of medium–long duration of sponsorship and the fact that discounting the profits generated after a large number of years usually obtains a present value almost negligible.
• Discrete-time variable instead of continuous: the objective becomes to maximize the profits discounted year by year, and no longer instant by instant. The transition from the continuous to the discrete field is necessary because the data extrapolated from the official financial statements are generally representative of the company’s performance during each financial year. Furthermore, from an operational point of view, investment plans are drawn up considering the total amount that will be invested during each year.

In the transition from the continuous to the discrete the structure of the constraint, expressed through the law of motion, changes in the following way:

$${\stackrel{.}{S}}_t=I_{S_t}\to \frac{\partial S_t}{\partial t}=I_{S_t}\to \frac{\Delta S_t}{\Delta t}=I_{S_t}\to \frac{S_t-S_{(t-1)}}{t-(t-1)}=I_{S_t}\to I_{S_t}-S_t+S_{(t-1)}=0.$$

(19)

When the constraint is expressed in finite form, the auxiliary function given by the sum of the objective function and the constraint function is no longer called Hamiltonian but Lagrangian. In this last function is introduced, as in the infinitesimal case, the variable of convenience λ_t that represents once again the shadow price of sponsorship [92]. However, in the discrete case λ_t is called Lagrange multiplier and expresses the marginal variation in the optimized value of the target function to a unitary variation of the constraint [93]. The Lagrangian function $ℒ$_t associated with the problem of dynamic optimization can be written as follows:

$${ℒ}_t=e^{-\rho t}\{p_{t}T{K}^{\alpha }{L}^{\beta }{S_t}^{\gamma }-A{I_{S_t}}^2-B{I}_{S_t}-wL-rK+{\lambda }_t(I_{S_t}-S_t+S_{(t-1)})\}.$$

(20)

The price of the good produced by the company at time t can be written in equation (20) in compact form p_t because, although it varies over time, it is a function of the quantity and stock of sponsorships referred to the previous instant t-1. This means that, not being dependent on Q_t and S_t at time t, it is possible to consider p_t constant concerning these two variables.

The Lagrangian function can be expressed as follows:

$${ℒ}_t=e^{-\rho t}\{p_{t}T{K}^{\alpha }{L}^{\beta }{S_t}^{\gamma }-A{I_{S_t}}^2-B{I}_{S_t}-wL-rK+{\lambda }_t{I}_{S_t}-{\lambda }_t{S}_t+{\lambda }_t{S}_{(t-1)}\}.$$

(21)

Equations (11) and (12) in the case of a constraint defined in a discrete time assume the following form (the two differential equations of (12) become ordinary equations):

$$\{\begin{array}{c}\frac{\partial {ℒ}_t}{\partial S_t}=0\\ \frac{\partial {ℒ}_t}{\partial I_{S_t}}=0\\ \frac{\partial {ℒ}_t}{\partial {\lambda }_t}=0.\end{array}$$

(22)

In the discrete case the problem of dynamic optimization consists therefore in solving the system of three equations in three unknowns (22) obtained by placing equal to zero the derivatives of the Lagrangian function concerning S_t, I_st and λ_t. Deriving the Lagrangian compared to the three variables we get:

$$\{\begin{array}{c}\gamma p_{t}T{K}^{\alpha }{L}^{\beta }{S_t}^{\gamma -1}={\lambda }_t\\ I_{S_t}=\frac{{\lambda }_t-B}{2A}\\ I_{S_t}=S_t-S_{(t-1)}.\end{array}$$

(23)

We notice how the third equation of the system coincides with the law of the expressed motion of the equation (19). We solve the system by first equating the second equation with the third and isolating the unknown λ_t:

$$\frac{{\lambda }_t-B}{2A}=S_t-S_{(t-1)}\to {\lambda }_t=2A{S}_t-2A{S}_{(t-1)}+B.$$

(24)

Substituting the expression of λ_t in the first equation of the system we obtain the following equation in the only unknown S_t:

$$\gamma p_{t}T{K}^{\alpha }{L}^{\beta }{S_t}^{\gamma -1}-2A{S}_t+2A{S}_{(t-1)}-B=0.$$

(25)

Equation (25) cannot be solved in a closed form, as it is of grade γ − 1. For the purpose of its resolution, it was necessary to use, for each t, the solver function of Excel, which allows estimating the value of S_t that cancel the objective function f(S_t). Once solved the (25) and known S_t it is enough to replace the value of this variable in the (24) and in the third equation of the (23) to obtain respectively λ_t and I_St. The resolution of the system of equations must be repeated for every 0 ˂ t ˂ 20. After this it is possible to verify how the value of the control variable I_St maximizes in every instant the discounted sum of the expected profits, that in the discreet case is expressed in the following way:

$$V={MAX}_{\{S_t,I_{S_t}\}}{{\displaystyle \sum }}_0^{20}{ℒ}_t={{\displaystyle \sum }}_0^{20}({\pi }_t·e^{-\rho t}),$$

(26)

being ${\mathrm{I}}_{{\mathrm{S}}_{\mathrm{t}}}{-\mathrm{S}}_{\mathrm{t}}{+\mathrm{S}}_{(\mathrm{t}-1)}=0$. Maximized then the sum of the Lagrangian over time, the problem of dynamic optimization can be considered solved.

At this point all that remains is to describe the procedures applied to estimate the constants of the Cobb–Douglas function and the financial discount rate used.

3.2.1. Estimation of the constants T, α, β and γ of the Cobb–Douglas function

The value of the three constants T, α, β and γ was determined by exploiting the log-linearity property of the Cobb–Douglas production function. Being such a linear function in the logarithms, it is possible to write the (3) in the following form:

$$ln{Q}_t=lnT+\alpha ln{K}_t+\beta ln{L}_t+\gamma ln{S}_t.$$

(27)

At this point it has been possible to apply the multiple linear regression analysis considering the historical series of Q, K, L and S. The following values of the Cobb–Douglas function constants were then estimated: T = 19,188.09, α = 0.11, β = 0.53 and γ = 0.12. These parameters may be applied to estimate the production value of the company for each moment t. It should be noted that the hypothesis of decreasing return to scale is confirmed, as it is α + β + γ = 0.75 ˂ 1.

3.2.2. Estimation of the Financial Discount Rate

The financial discount rate ρ at which the expected future profits are to be discounted at the present has been estimated using the Weighted Average Cost of Capital (WACC) method. It has been assumed that the company has recourse to debt for current investments and that the debt to equity ratio remains constant over the planning horizon. In estimating the average market risk β market for investment in sponsorship, was considered both advertising nature of the investment in question and the ordinary characteristics of the companies which, like the one being analyzed, are active in the production and distribution of food products. Specifically, it has been assumed that the market risk of the investment is equal to the average market risk of the advertising sector, the market risk of the food production sector and the market risk of its distribution, weighted with respect to the average market yields of the three sectors considered [94,95].

The rate estimated with the WACC method, equal to 4.27%, is consistent with the financial discount rate suggested in the Guidelines for the Cost–Benefit Analysis of Investment Projects (2014) of the European Commission [96], Directorate-General for Regional and Urban Policy (the indicative reference value of the financial discount rate for the European Union Member States is 4%).

4. Results and Discussion

Once the revision phase of the model has been completed, the only thing left to do is to apply it, considering the changes introduced in the previous paragraph. For each time 0 ˂ t ˂ 20 equations (23), (24) and (25) shall be applied and resolved to calculate the variables I_St, S_t and λ_t. It should be noted that the values of I_St, S_t and λ_t are known a priori only at the instant t = 0, for which you have: I_S0 = 0, S₀ = 3 and λ₀ = B = €280,000. It is easy to see how, in the initial moment, the company is not making any investment, even though in the past it has already sponsored three restoration projects. At the same time, moreover, we have that the shadow price of a sponsorship is equal to the direct unit cost of the same.

Once the three unknowns of the problem have been determined, by applying the (16), it is possible to determine the total cost of sponsorship C_St(I_St) for each year of the programming horizon. Also known as S_t for each t, from (1), (3) and (17) it is possible to estimate the values of p_t, Q_t, R_t and π_t. Finally, equation (21) gives $ℒ$_t = e^-ρtπ_t, which is the objective function to be maximized for each year.

Table 1. Starting data of the problem of dynamic optimization.

K0	L0	S0 = S−1	R0	p0 (S−1;Q−1)	b	C	d	Q0 = R0/p0
18,337,735.00	38.00	3.00	13,875,998.00	15.00	20.00	0.0000057	0.0005	13,875,998.00
rK0	wL0	r	w	α	β	γ	T	K0αL0βS0γ
10,643,139.00	1501,221.00	0.58	39,505.82	0.11	0.53	0.12	19,188.09	48.21
A	B	ρ	CSt (ISt = 1)	λ0 = B	IS0	CS0	R−1	Q−1 = R−1/p−1
172,000.00	280,000.00	0.0417	452,000.00	280,000.00	0.00	0.00	13,059,321.00	870,621.40

shows the starting points of the problem, most of which are extrapolated from the ordinary balance sheet (year-end date 31/12/2017).

In

Table 2. Estimated values of p_t, S_t, Q_t, R_t, π_t, $ℒ$_t, λ_t, I_St e C_St through the dynamic model.

t	pt	St	Qt	Rt	πt	$ℒ$t = e−ρt πt	λt	ISt	CSt
1	14.69	3.51	941,801.18	13,832,447.23	1502,662.05	1441,235.40	453,841.96	0.51	185,425.19
2	14.59	3.89	953,074.04	13,906,630.00	1630,182.83	1499,627.93	411,431.61	0.38	132,087.17
3	14.53	4.19	961,278.05	13,964,269.12	1720,131.24	1517,687.63	383,467.31	0.30	99,777.88
4	14.48	4.43	967,535.20	14,009,710.91	1787,132.30	1512,345.85	363,612.99	0.24	78,218.62
5	14.44	4.63	972,460.95	14,046,197.16	1838,943.41	1492,575.76	348,813.56	0.20	62,893.75
6	14.42	4.80	976,427.52	14,075,957.63	1880,090.57	1463,593.24	337,397.17	0.17	51,507.05
7	14.39	4.94	979,676.22	14,100,548.10	1913,421.42	1428,650.04	328,364.85	0.14	42,766.68
8	14.37	5.06	982,371.90	14,121,082.26	1940,832.69	1389,878.80	321,079.46	0.12	35,889.57
9	14.36	5.16	984,631.81	14,138,378.12	1963,645.11	1348,731.30	315,113.68	0.10	30,373.01
10	14.35	5.25	986,542.12	14,153,050.76	1982,811.49	1306,223.42	310,169.20	0.09	25,879.26
11	14.34	5.32	988,167.82	14,165,572.17	1999,039.34	1263,080.37	306,030.89	0.08	22,172.83
12	14.33	5.39	989,559.02	14,176,311.08	2012,866.70	1219,827.06	302,539.33	0.07	19,084.37
13	14.32	5.45	990,755.09	14,185,559.99	2024,711.02	1176,846.71	299,573.71	0.06	16,488.97
14	14.31	5.50	991,787.40	14,193,554.09	2034,901.71	1134,420.04	297,040.67	0.05	14,292.38
15	14.31	5.54	992,681.32	14,200,484.65	2043,702.47	1092,752.30	294,866.85	0.04	12,422.18
16	14.30	5.58	993,457.57	14,206,508.84	2051,327.07	1051,992.33	292,993.82	0.04	10,821.77
17	14.30	5.61	994,133.27	14,211,756.96	2057,950.67	1012,246.37	291,374.41	0.03	9446.29
18	14.29	5.64	994,722.66	14,216,337.82	2063,718.10	973,588.07	289,970.15	0.03	8259.72
19	14.29	5.66	995,237.68	14,220,342.97	2068,750.12	936,066.09	288,749.38	0.03	7232.85
20	14.29	5.69	995,688.40	14,223,849.87	2073,148.14	899,709.73	287,685.78	0.02	6341.73
TOTAL			19,631,989.22	282,348,549.72	38,589,968.45	25,161,078.45		2.69	1993,455.39

the values of the fundamental variables that have been possible to estimate by applying the equations of the dynamic model are reported.

It is easy to see that as t increases, the shadow price of sponsorship λ_t again tends to equal the direct unit cost of investment B.

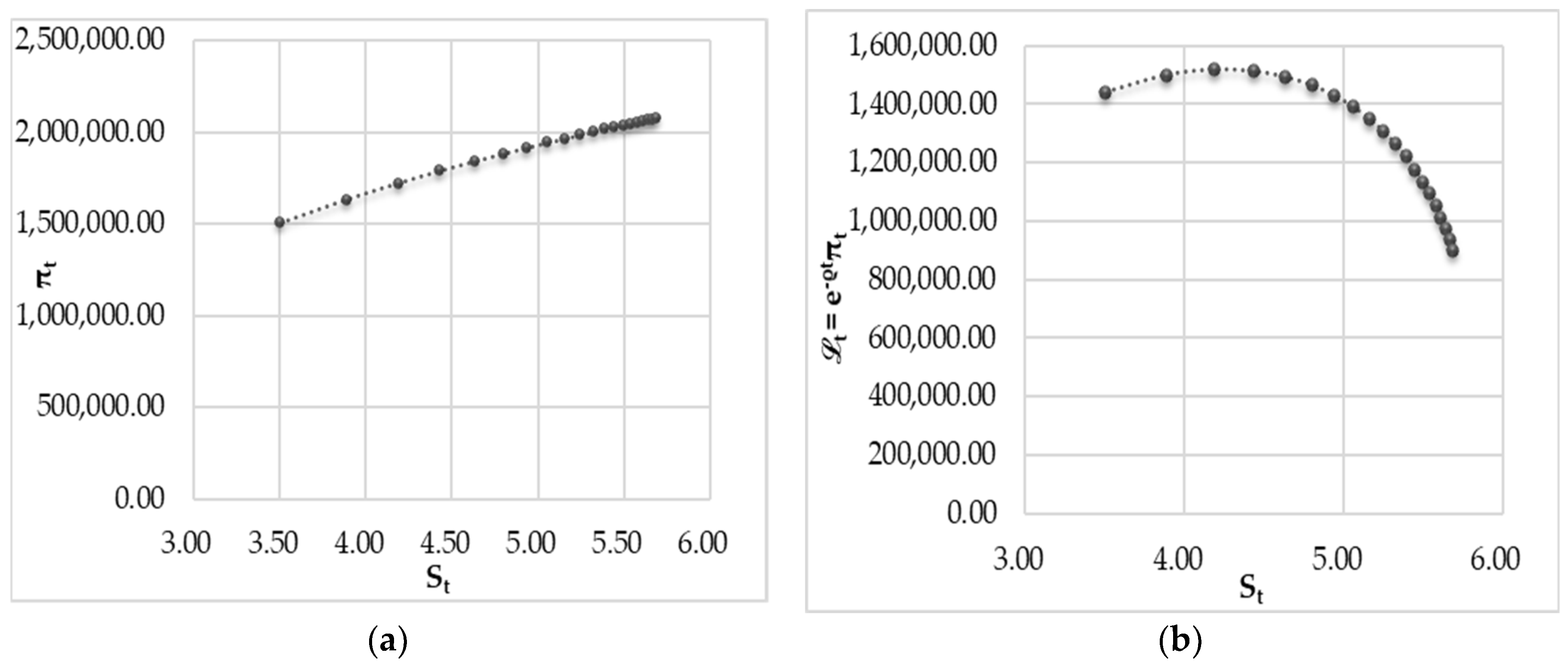
From the interpretation of the results, several points for reflection emerge. The target function e^-ρtπ_t represents the discounted profits for each year of the time horizon and coincides with the Lagrangian auxiliary function of the optimization problem. Figure 1 shows the trend of profits and discounted profits to the growth of the stock of sponsorship.

It is possible to notice how, as the number of sponsorships increases up to a certain instant t, the current profit is also growing and increases in a little less than proportional way. But a very interesting aspect is the reading of the evolution of profits in terms of present value (discounted profits). With the growth of the stock S_t over time as a result of the investment I_St, there are discounted profits initially increasing and then becoming gradually decreasing. Specifically, once the threshold of 4.20 total sponsored events has been exceeded (and this occurs between the third and fourth years), current profit becomes decreasing. This means that, after the third year of the investment program, the effects of the laws of financial mathematics on profits are beginning to be felt, even if current profit is always increasing in the planning horizon (which is why, assuming that K and L remain constant over time, it is always convenient to sponsor, provided that the right amount to invest is identified).

Furthermore, we can see that, as the investment in sponsorship increases, the stock of sponsorship never reaches 6 events (in fact, for a planning horizon of twenty years, in the last year we have S₂₀ = 5.69).

In Figure 2 it is possible to observe the evolution of current profits and discounted profits over time.

We can see once again that the current profit is always increasing over time and that, instead, discounted profit become decreasing after the third year.

From Figure 3, in which the evolution over time of I_St and S_t is represented, it is evident that I_St represents the marginal level of sponsorship, i.e., the increase in the stock of sponsorship that occurred each year of the period of analysis considered.

The number of new restoration/recovery interventions to be sponsored over the years to maximize the present value of future profits is decreasing over time. This means that marginal sponsorship is becoming smaller and smaller from time to time. In other words, if in the first year it is enough to maximize profits to sponsor an intervention of approximately 51% of the average of the interventions carried out in the past by the company, for the second year this percentage drops to 38%.

The stock of events sponsored by the company from year to year, understood as the number of sponsorships carried out up to a certain moment t, is on the other hand growing over time. We are witnessing less than proportional growth precisely because there is a decrease over time in the level of marginal sponsorship I_St. The trend of the total cost of sponsorship (C_St) is shown in Figure 4:

We note that as the number of investments in sponsorships made per unit of time increases, the total cost of the investment increases more than proportionally (Figure 4 (a)). The more than proportional growth can be attributed to the adjustment costs (AI_St²). These costs, as we have seen, are difficult to share between several initiatives sponsored at the same time. Nevertheless, the total cost of the investment is decreasing over time (Figure 4 (b)), from the moment when the flow of new sponsored events capable of maximizing the present value of the business profit is decreasing over time.

In summary, the application has led to the following results: the optimal annual investment in I_St sponsorship capable of maximizing the function of discounted profits is decreasing over time. In particular, in the first year it is sufficient to maximize the profit to sponsor an intervention of approximately 51% of the average of the interventions carried out in the past by the company, while in the twentieth year this percentage drops to 2%. Nevertheless, the current profits π_t are growing less than proportionally over time, while the discounted profits e − ^ρtπ_t are first increasing after which, reached in the third year their maximum (with I_St equal to 0.30), then become decreasing. The total cost CS_t of the marginal investment, being function of I_St, is also decreasing over time. During the first year the company should invest about €185,000 in sponsorships, while in the last year the ideal investment falls to about €6300. Overall, over twenty years, the company should invest almost €2,000,000 in sponsorship. This investment corresponds, over the entire programming period, to approximately 2.69 recovery/restoration interventions structurally comparable to the average type of intervention sponsored in the past by the company. Therefore, to maximize the NPV generated by the investment program, the company will have to sponsor a lower number of recovery/restoration operations in twenty years than those financed in the last four years (which is equal to 3). This result can be interpreted as follows: for a company that has already been active for some time in the field of cultural sponsorship, it is sufficient to sponsor a few other restorations works in the following years. This is because, given the long-term effects that this marketing and communication strategy can generate, the influence on the growth in turnover of sponsorships supported in the past is still strong. The result obtained is in line with the study conducted by Edeling et al. [97], which shows that the sponsor can exploit the positive effects of a previous sponsorship by promoting a new, lower level sponsorship in the same area. A similar position is that of McAlister et al. [98], according to which a new sponsor should not support an event promoted in the past by another company. This is because, according to the processes of cognitive psychology, the memory of the previous sponsor negatively influences the association of the current sponsor to the event. Therefore, a company should enter into several consequential sponsorship agreements with the same sponsee in the same or related areas, with a view to a medium to a long-term partnership. From this point of view, the sponsor can align its objectives, monetary, image and communication, with those of the sponsee, whose aim is, in this case, to find the financial resources necessary for the enhancement and conservation of the historical–architectural heritage.

However, a second point must be made. The development of the discounted profit function suggests that the third is a year of sensitivity, from which the investment program starts to be less effective. From t = 3 onwards, the maximum achievable discounted profit becomes decreasing. Therefore, in year 3 it would be better to reset the dynamic analysis by using the updated production and cost data and elaborating a new forecast. The analyst could also propose to the company a reshaping of the company’s policies to make the discounted profits grow again. In this regard, the company could make changes to its sponsorship strategy, for example by sponsoring the restoration of monumental assets of greater (historical, cultural, social and mediatic) importance than those promoted so far. Also, after the critical year, the discount rate should be monitored. If there were to be a substantial change in the discount rate in that year, it would be necessary to remodel the communication strategy making it more impactful.

Furthermore, it is necessary to compare the results of the dynamic model with those obtained by applying the static model to the same company in 2014. In that year the company sponsored a single restoration project. The application of the static model showed that to maximize profits, the company should have sponsored at least two other restorations similar (in terms of financial weight and characteristics) to the one promoted, reaching a total of 3 sponsorships. The cost of three interventions amounted to €1,440,000 (about 12% of turnover), so the differential expense required was €960,000. This investment was expected to generate an increase in profits of about €192,797 (see

Table 3. Static and dynamic models in comparison.

Models	t	S0	St*	ISt = St* − S0	C0(ISt)	Δπ
Static	year 2014	1.00	3.00	2.00	960,000	192,798
	year 2018	3.00	3.61	0.61	274,072	23,175
Dynamic	years 2018–2028	3.00	5.69	2.69	1,993,455	25,161,079

).

However, the actual behavior of the company was quite different. The company sponsored two other interventions but distributed them for over three years (between 2014 and 2017). This did not allow it to maximize profit for each of the years considered. Moreover, its structure in the initial year of the dynamic analysis (2018) has inevitably changed. By reapplying the static model to 2018, it appears that the company would have had to sponsor an additional 0.61 interventions, i.e., invest in that year about €274,072. This would have guaranteed a profit increase of about €23,175. This result does not differ much from that obtained by applying the dynamic analysis at the end of the first year (2019), being I_St = 0.51 and C_St = €185,425 (first line from Table 2). The slight difference found is justifiable. The static model allows to maximize the profit at the moment of analysis, i.e., it is assumed that the optimal investment is made immediately by the company. The dynamic model, on the other hand, returns the first profit after one year. This is to allow the company to adjust the sponsorships stock to changes in the consumer demand and the sponsorship value (shadow price).

Comparing the dynamic model implemented at the end of the 20 years with the static model applied in 2014, it is clear that in the former case, by investing just over twice as much as the static situation, a profit increase of about 131 times higher is achieved at the end of the planning period. That is, in average terms, a discounted profit of about €1,250,000 per year is obtained (about 6.5 times higher than €192,798 of the static model). This not only shows that a long-term partnership relationship can bring greater benefits to potential sponsors, but also that, if perfectly quantified, frequent and small sponsorship investments are preferable to sporadic but larger ones. The mathematical functions of the dynamic model would, therefore, seem to describe quite plausibly the recall effect on consumers resulting from previous sponsorships [97,98].

Finally, the comparison shows that both models, static and dynamic, are useful tools for practice and company policy. In particular, the static model applies to those companies that, through a short-term communication policy, want to obtain rapid results from sponsorship and an immediate impact on the market (as in the case of a company that decides to launch a new product or promotional offer). Differently, the dynamic model, being part of long-term communication policy, can be used to estimate the optimal sponsorship budget for those companies whose main objectives are to assign new values to the corporation or change the brand perception for the target audience. In this case, it takes several years for the positive values of the sponsored cultural activities to be automatically associated with the brand. Sponsoring initiatives in the same sector over the years, even if at a decreasing relevance, can, therefore, contribute to the perfect sedimentation of these values. Once the objectives of sponsorship have been defined (in terms of intensity, audience and time), it is possible, through the above-mentioned models, to quantify the optimal budget to be used for investment, bearing in mind that it must include not only the amount for the sponsorship itself (direct cost) but also the amount for all the expenses related to the collateral and support initiatives necessary to fully exploit the company’s intervention (adjustment cost). This study shows that, although the use of statistical-mathematical methods for the ex-ante evaluation of the effects of the sponsorship investment is not widespread among company operators, however, it is advisable if you want to limit the risk of possible failure. Moreover, as mentioned above, these models may also prove useful for public bodies. This is because when sponsee asks for a cash contribution it should consider not only the amount needed to carry out the recovery/restoration work but also the value of the economic counterpart it is able to offer the sponsor. Moreover, when defining this contribution, administrations should, in turn, consider the optimal budget for businesses. In this way, public authorities can avoid asking potential sponsors for amounts that do not allow them to maximize profit. Only then can alignment and sharing of objectives between public and private actors be ensured.

The proposed models also make it possible to partially fill some gaps in the reference literature on two aspects of cultural sponsorship that are often overlooked: the framing of the instrument in the public–private partnership perspective and the estimation of the financial results of the sponsorship investment.

5. Conclusions

The theme of the valorization of the historical–architectural patrimony has taken on certain importance in Italy for several years now, becoming the object of investigation by numerous scholars [99,100].

Recently, both because of the large number of cultural assets spread throughout Italy, and because of the multiplicity of subjects and organizations, public or private, involved in the process of increasing their value, some difficulties have emerged about the definition of strategies aimed at enhancing and managing the collective heritage [101,102,103]. This is because historical and architectural heritage not only has a cultural, but also social, environmental and monetary value [104,105].

Let us remember that, in the economic language, to valorize means to increase the value of a resource or to make it manifest if it is not explicitly known, as often happens in the case of buildings with historical–architectural value that are in conditions of degradation [106,107]. About this last aspect, it is necessary to carry out recovery or restoration work to better conserve, and therefore enhance, the monumental goods. Unfortunately, in recent years, due to cuts in public investment, there has been a shortage of financial resources for various sectors (such as, for example, the residential construction, industrial and water services sectors [108,109,110]), including that of cultural heritage. Private support for the historical and architectural heritage has therefore become of fundamental importance. This made forms of collaboration between public and private necessary to assist the institutions in the protection of the monumental heritage.

Sponsorship contracts are the form of public–private partnerships most commonly used by companies. However, the objective difficulties encountered in measuring the effectiveness of the investment in sponsorship could lead to a tendency for companies to make little use of the instrument.

The new Public Contracts Code [111] has repealed the previous regulations regarding sponsorships and, to encourage private intervention in the cultural sector, has sought to simplify and facilitate the selection procedure for sponsors. Nonetheless, many of the concerns of companies about the convenience of sponsorships investment remain unresolved. This work is part of the theme of cultural sponsorship and its primary objective, in continuity with a previous publication, is to resolve at least in part some doubts about the profitability of sponsorship for businesses. This is to facilitate and implement the use of the cultural heritage tool.

This paper aims to revise, apply and finally validate an existing dynamic model whose purpose is to assess the optimal level of investment in sponsorship able to maximize over time the present value of the expected profits by the company. The intention is to be able to define a possible application through which to assess the financial sustainability of the investment in sponsorship. In the first phase of the study, the original model, proposed by Bucci A., Castellani M. and Figini P. in their paper entitled L’investimento in sponsorizzazione delle imprese: un’analisi economica in termini statici e dinamici [27], was first analyzed and explained in detail. In the second phase of the study, however, part of the original model was revised and modified to make it more responsive to the real characteristics of the sponsorship market.

In the last phase of the work, the revised version of the model was applied, to verify its validity, for the first time to a company active in the field of cultural sponsorship (Caffè Moreno). The application has made it possible to partially fill some gaps in the literature on the themes of public–private partnerships and cultural sponsorship. Specifically, sponsorship is considered not only as a marketing strategy and means of corporate communication but also as a partnership tool through which the company can pursue its financial objectives (profit maximization) and the public body can benefit from more resources to enhance the cultural heritage. Estimating the optimal budget to invest in sponsorship, therefore, allows for more effective alignment of the sponsor’s objectives with those of sponsee. The precise knowledge on the part of the companies of the right amount to allocate to sponsorships may encourage them to support a greater number of recovery/restoration interventions for the benefit of the historical–architectural heritage. Therefore, the model represents a tool for evaluating not only the financial sustainability (private entrepreneur’s point of view) but also the economic sustainability (public administration’s point of view) of sponsorship.

Although the results obtained are in line with expectations, the dynamic model analyzed, both in its original version and in the revised version, has several limitations related to the hypotheses adopted simplifying. In particular, the corporation under analysis was considered as a single-product company. It is clear, therefore, that in the case of multi-product companies some purely mathematical simplifications are no longer possible, and therefore more data and accounting details (unit prices, quantities produced for each product line, etc.) are needed.

Another limit is represented by the function of price adopted: in the model it is of linear type and identifies a plan of the prices function of Q_t and S_t; however, it could be better represented by a more complex functional relation that represents, for example, a curved surface in the space.

The assumption of a non-linear production function of the Cobb–Douglas type with decreasing returns to scale is quite acceptable, especially for the companies in the sector in question, which have a low technological component. However, depending on the type of company to which the model is to be applied, other production functions more representative of the economic reality under investigation could be adopted.

Finally, there is a further limitation. A large part of the model is based on the observation of historical company data. For this reason, the application provides more reliable results for companies that have sponsored more events in the past. On the other hand, due to the lack of data, the model is difficult to apply to companies that have recently started to invest in sponsorship. In this case, the estimation of the γ parameter representative of the rate of variation of the marginal productivity of sponsorship becomes problematic. For these companies, a possible solution could consist in estimating an average γ of the sector, obtained taking into consideration those companies active in the same market segment and that present a dimension like the one under study. The same applies to the coefficients b, c and d of the reverse demand curve.

The goal of future research is to overcome these limits, proposing a summary model that reconciles the needs of both the sponsor and the sponsee in an integrated perspective of sharing sponsorship results.