The Spatial Optimization and Evaluation of the Economic, Ecological, and Social Value of Urban Green Space in Shenzhen
Abstract
1. Introduction
2. Study Area and Data Sources
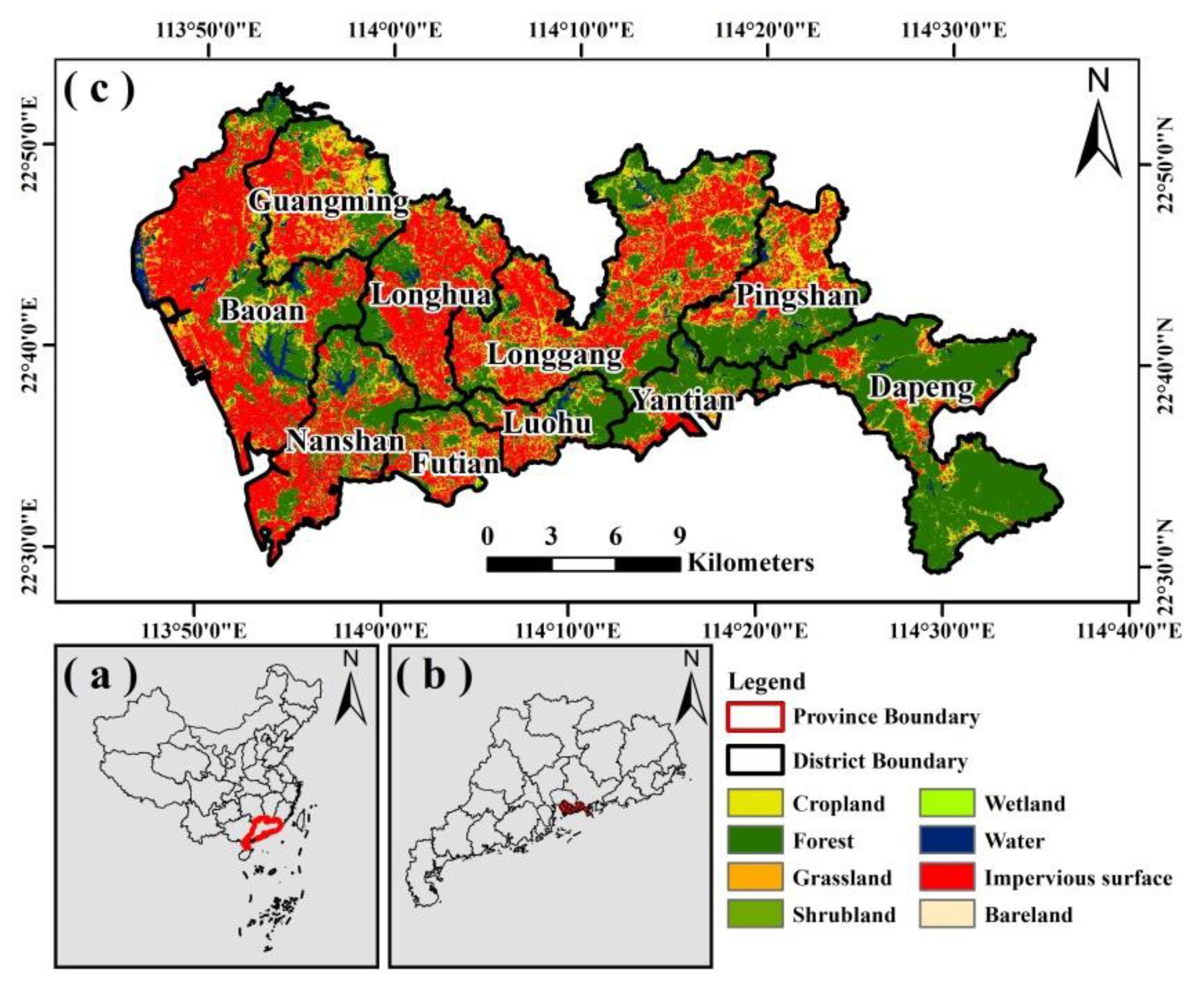
2.1. Study Area
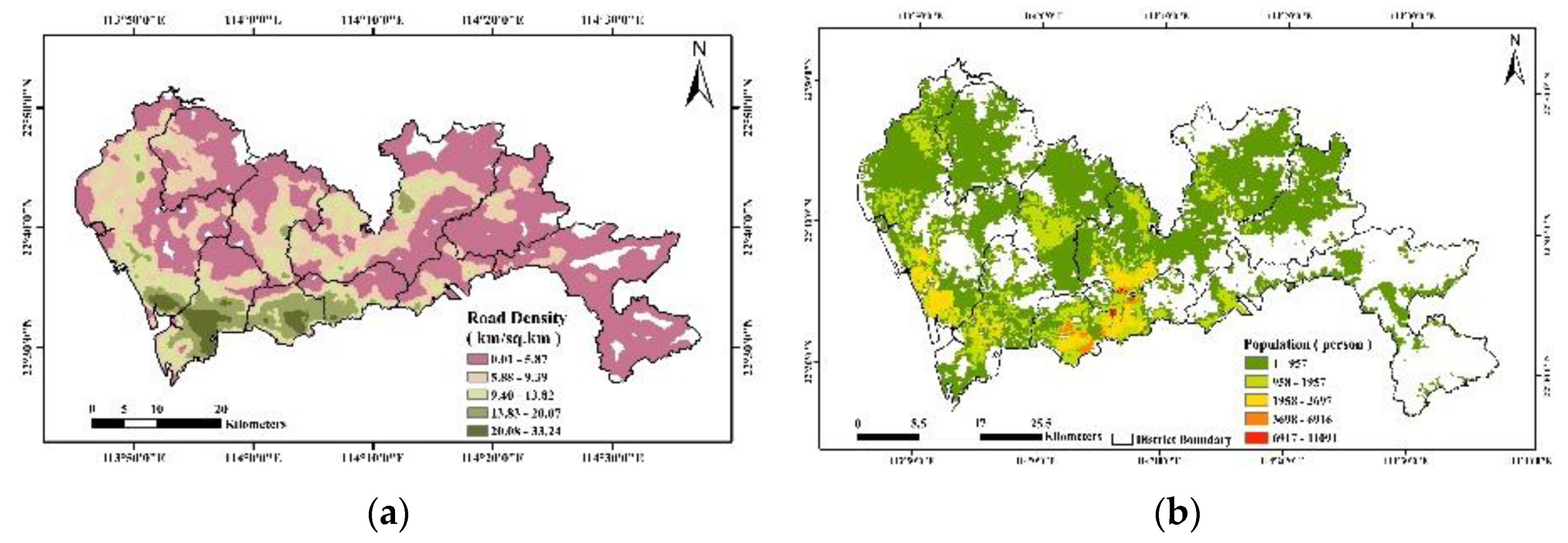
2.2. Data Sources and Processing
2.2.1. Land-use Datasets and UGS in China
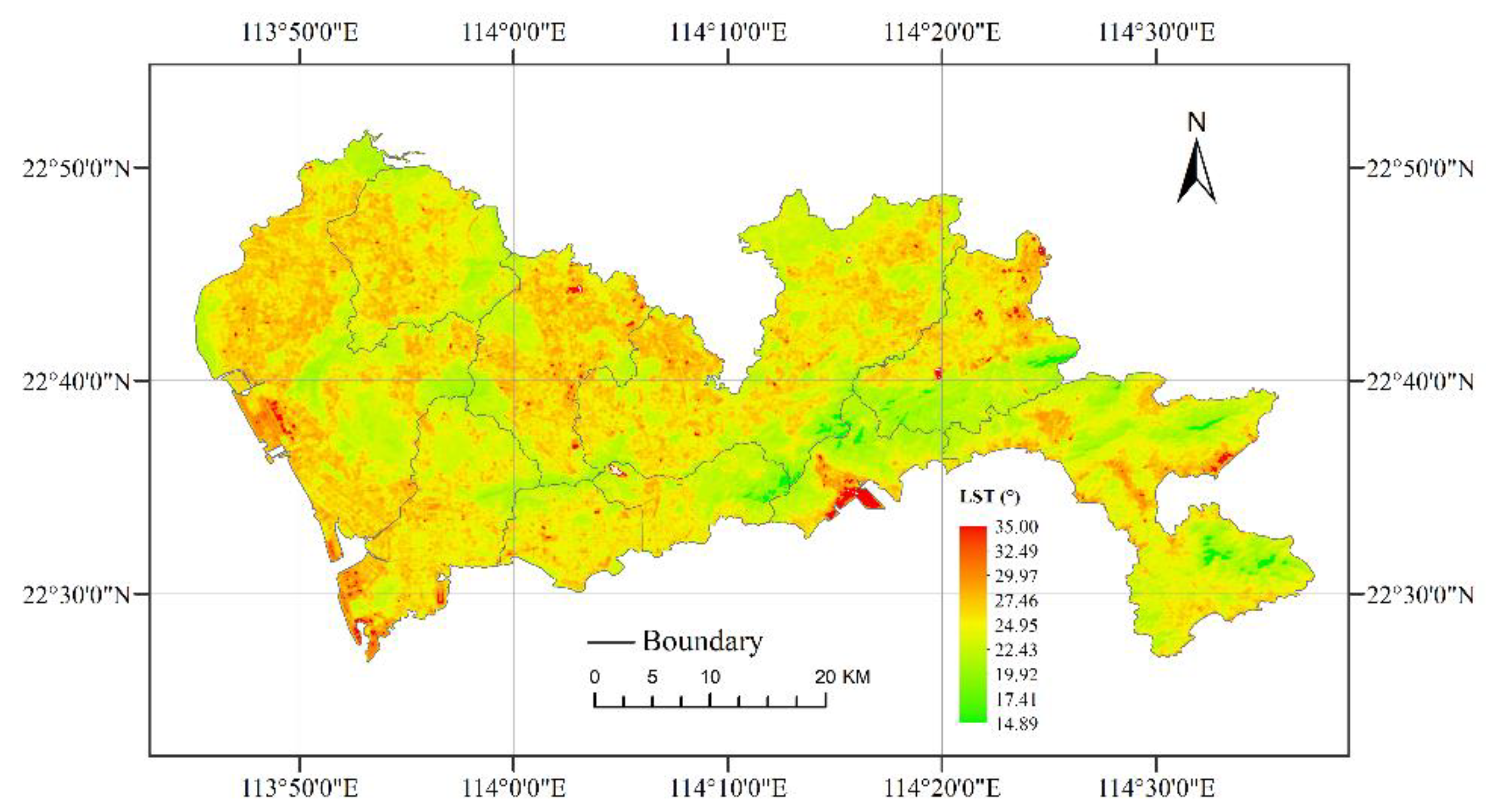
2.2.2. Land Surface Temperature (LST) Retrieval
2.2.3. Point of Interest Retrieval
2.2.4. Housing Rental Price Retrieval
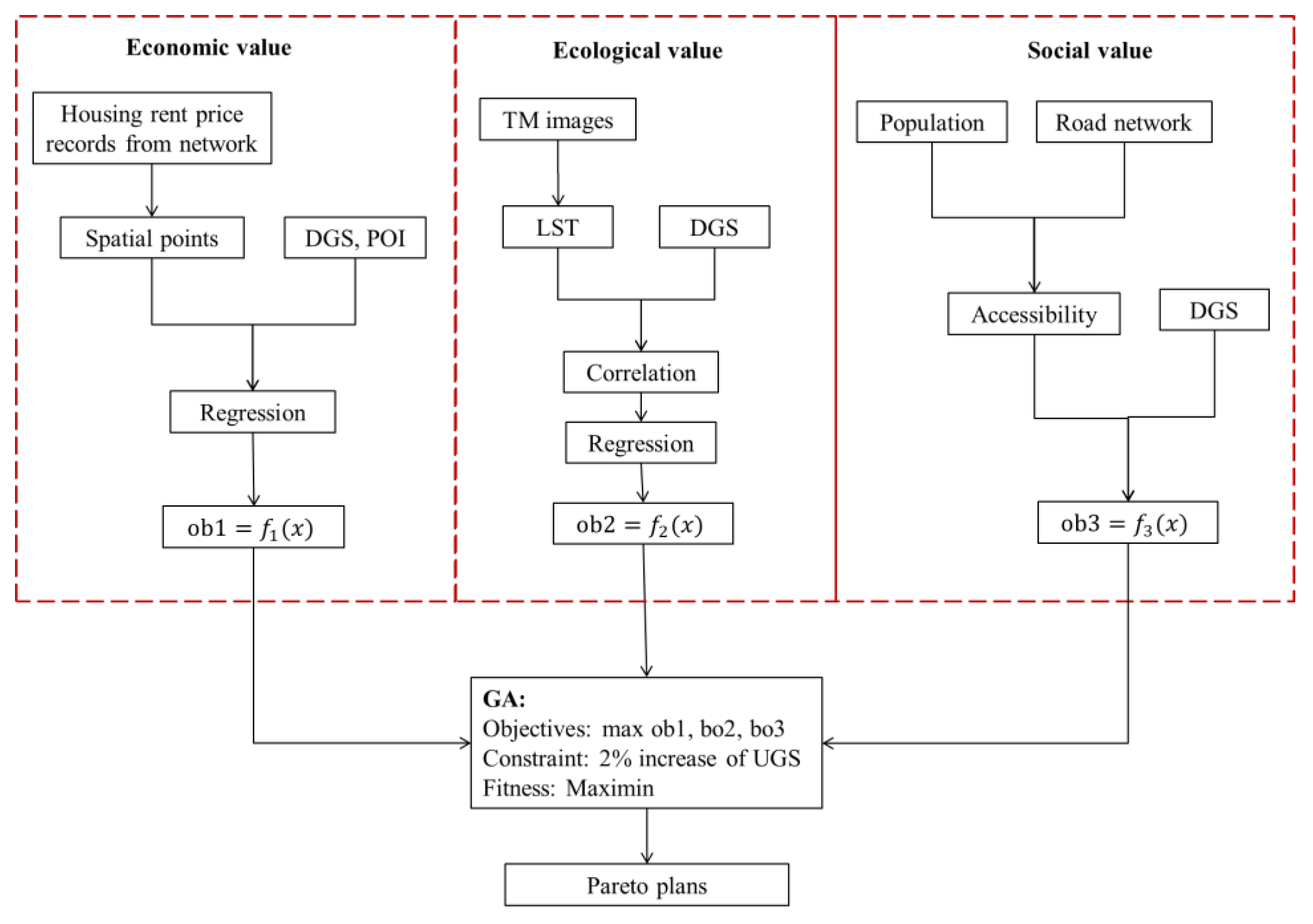
3. Methods
3.1. Economic Value Evaluation
3.1.1. Evaluating Model
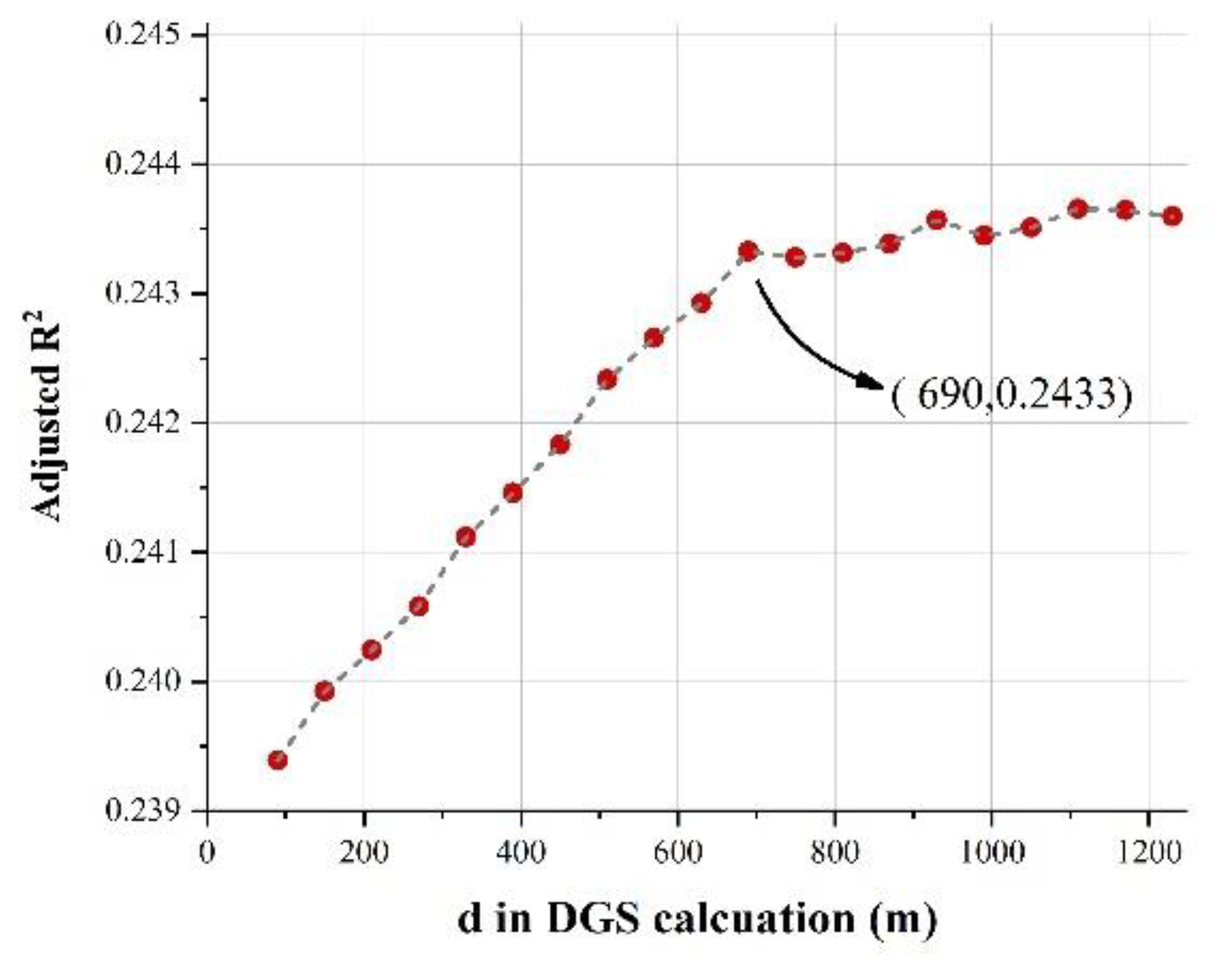
3.1.2. Dependent and Independent Variables
3.2. Ecological Value Evaluation
3.2.1. Correlation Analysis
3.2.2. Evaluating Model
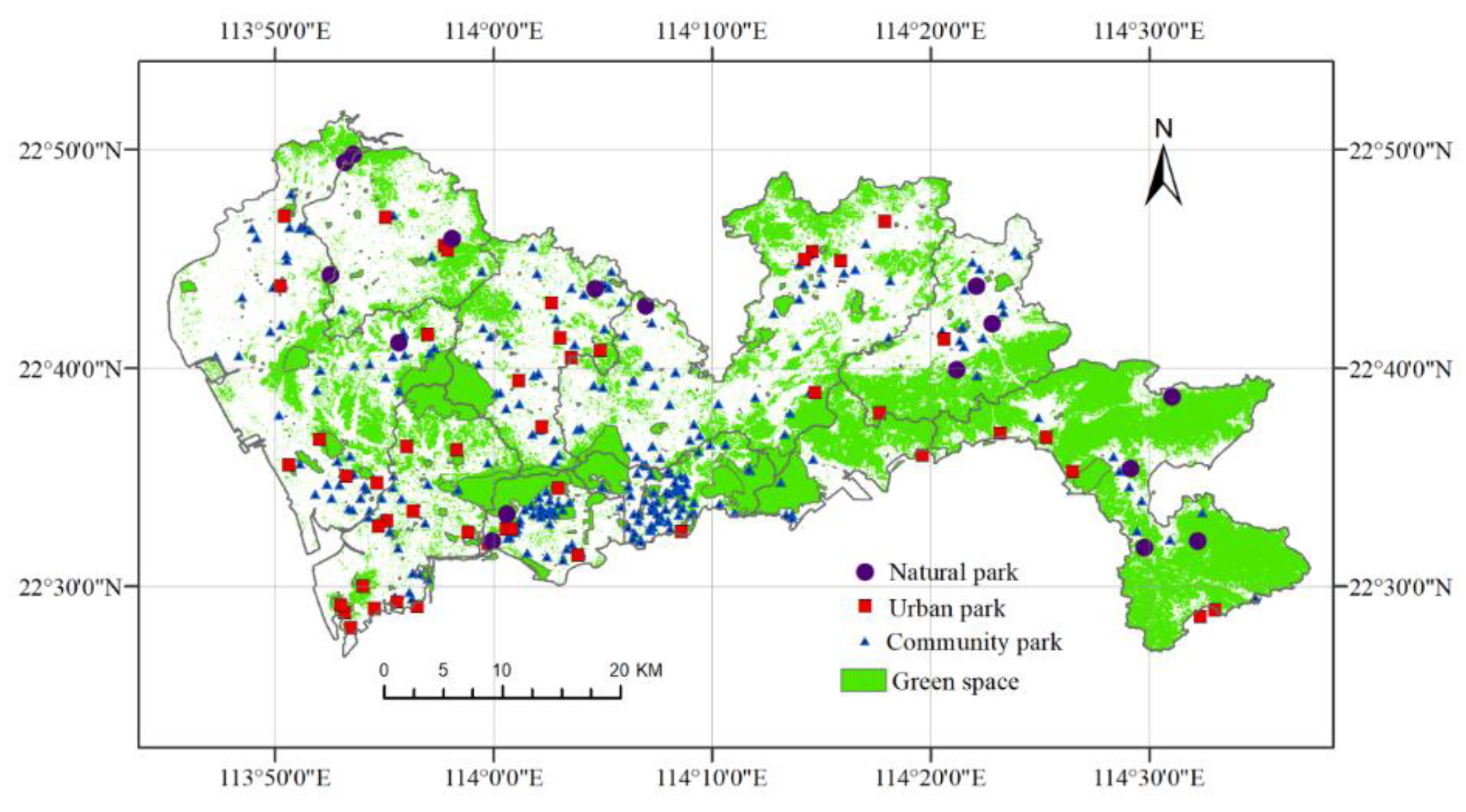
3.3. Social Value Evaluation
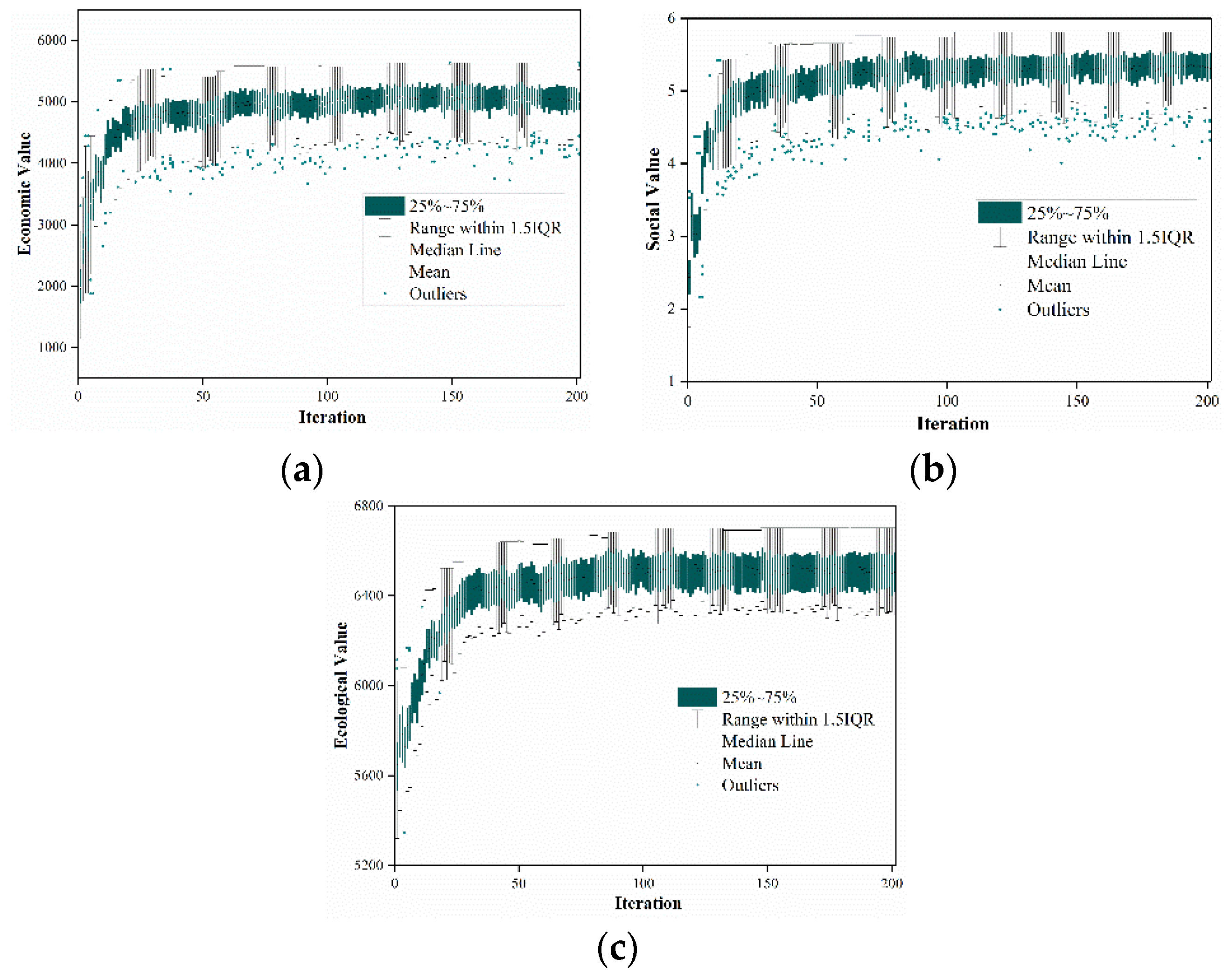
Multi-Objective Optimization
4. Results
4.1. The Economic Value of Green Space
4.2. The Ecological Value of Green Space
4.3. The Social Value of Green Space
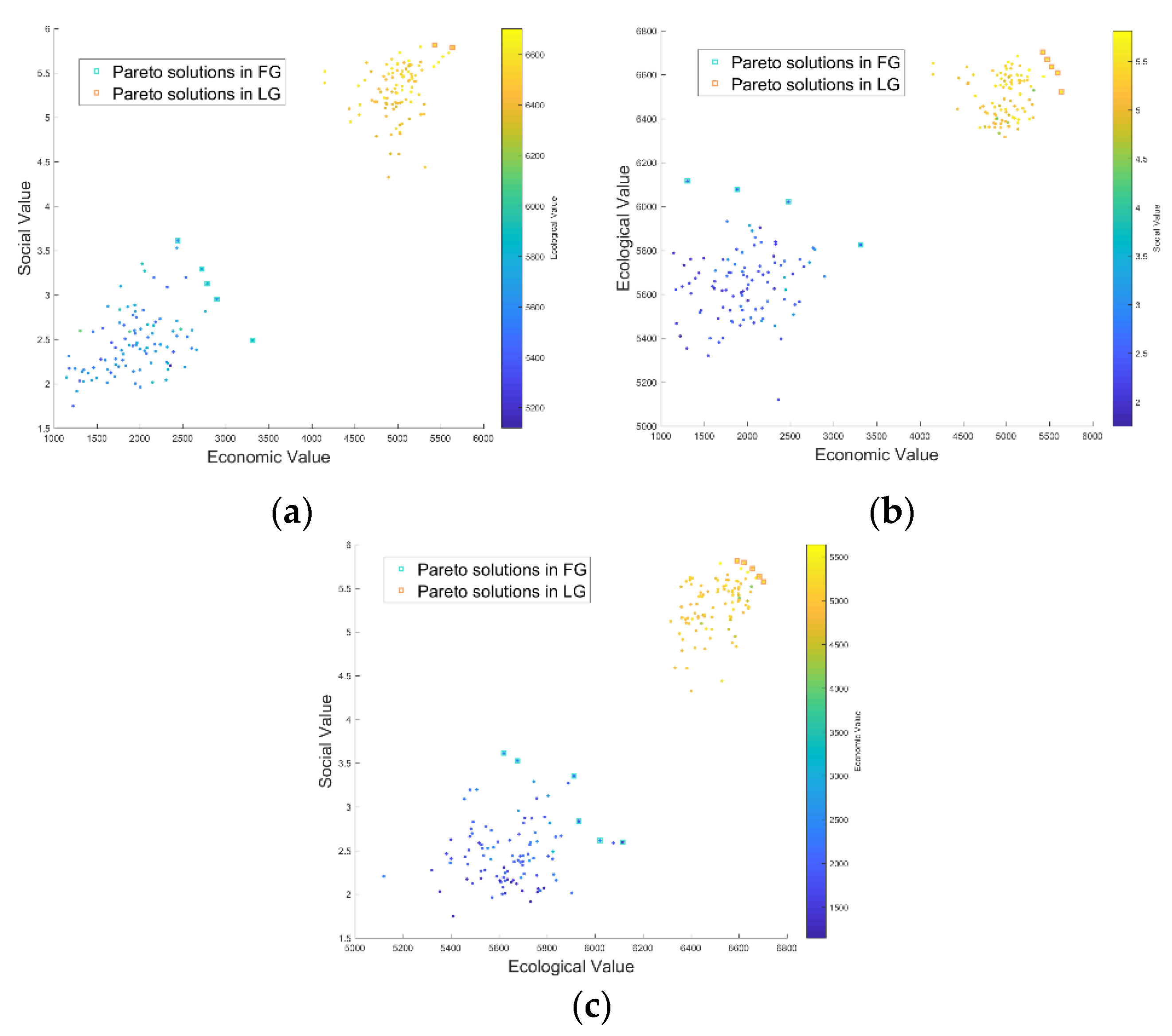
4.4. Green Space Optimization for Shenzhen
5. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, L.; Lee, X.; Smith, R.B.; Oleson, K. Strong contributions of local background climate to urban heat islands. Nature 2014, 511, 216–219. [Google Scholar] [CrossRef]
- Bao, T.; Li, X.; Zhang, J.; Zhang, Y.; Tian, S. Assessing the distribution of urban green spaces and its anisotropic cooling distance on urban heat island pattern in Baotou, China. ISPRS Int. J. Geo inf. 2016, 5, 12. [Google Scholar] [CrossRef]
- van den Berg, A.E.; Maas, J.; Verheij, R.A.; Groenewegen, P.P. Green space as a buffer between stressful life events and health. Soc. Sci. Med. 2010, 70, 1203–1210. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.Y.; Liu, X.P.; Gao, W.X.; Wang, R.Y.; Li, Y.; Tu, W. Emerging social media data on measuring urban park use. Urban. For. Urban. Green. 2018, 31, 130–141. [Google Scholar] [CrossRef]
- Xu, M.; Xin, J.; Su, S.; Weng, M.; Cai, Z. Social inequalities of park accessibility in Shenzhen, China: The role of park quality, transport modes, and hierarchical socioeconomic characteristics. J. Transp. Geogr. 2017, 62, 38–50. [Google Scholar] [CrossRef]
- Pearce, D. Nature’s services. Societal dependence on natural ecosystems—Daily, GC. Science 1997, 277, 1783. [Google Scholar] [CrossRef]
- Hong, W.; Guo, R. Indicators for quantitative evaluation of the social services function of urban greenbelt systems: A case study of Shenzhen, China. Ecol. Indic. 2017, 75, 259–267. [Google Scholar] [CrossRef]
- Maas, J.; Verheij, R.A.; de Vries, S.; Spreeuwenberg, P.; Schellevis, F.G.; Groenewegen, P.P. Morbidity is related to a green living environment. J. Epidemiol. Commun. H 2009, 63, 967–973. [Google Scholar] [CrossRef]
- Villeneuve, P.J.; Jerrett, M.; Su, J.G.; Burnett, R.T.; Chen, H.; Wheeler, A.J.; Goldberg, M.S. A cohort study relating urban green space with mortality in Ontario, Canada. Environ. Res. 2010, 115, 51–58. [Google Scholar] [CrossRef]
- Alexander, D.S.; Huber, R.L.; Piper, C.R.; Tanner, A.E. The association between recreational parks, facilities, and childhood obesity: A cross-sectional study of the 2007 National Survey of Children’s Health. J. Epidemiol. Community Health 2013, 67, 427–431. [Google Scholar] [CrossRef]
- Troy, A.R.; Grove, J.M.; O’Neill-Dunne, J.P.M.; Pickett, S.T.A.; Cadenasso, M.L. Predicting opportunities for greening and patterns of vegetation on private urban lands. J. Environ. Manag. 2007, 40, 394–412. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zhang, Z. Examining social inequalities in urban public leisure spaces provision using principal component analysis. Qual. Quant. 2017, 51, 2409–2420. [Google Scholar] [CrossRef]
- Song, Y.; Huang, B.; Cai, J.; Chen, B. Dynamic assessments of population exposure to urban greenspace using multi-source big data. Sci. Total Environ. 2018, 634, 1315–1325. [Google Scholar] [CrossRef] [PubMed]
- Nesbitt, L.; Meitner, M.J.; Girling, C.; Sheppard, S.R.J.; Lu, Y. Who has access to urban vegetation? A spatial analysis of distributional green equity in 10 US cities. Landsc. Urban. Plan. 2019, 181, 51–79. [Google Scholar] [CrossRef]
- Li, W.; Saphores, J.M.; Gillespie, T.W. A comparison of the economic benefits of urban green spaces estimated with NDVI and with high-resolution land cover data. Landsc. Urban. Plan. 2015, 133, 105–117. [Google Scholar] [CrossRef]
- Qiu, G.Y.; Zou, Z.; Li, X.; Li, H.; Guo, Q.; Yan, C.; Tan, S. Experimental studies on the effects of green space and evapotranspiration on urban heat island in a subtropical megacity in China. Habitat Int. 2017, 68, 30–42. [Google Scholar] [CrossRef]
- Xiao, X.D.; Dong, L.; Yan, H.; Yang, N.; Xiong, Y. The influence of the spatial characteristics of urban green space on the urban heat island effect in Suzhou Industrial Park. Sustain. Cities. Soc. 2018, 40, 428–439. [Google Scholar] [CrossRef]
- Nowak, D.J.; Civerolo, K.L.; Rao, S.T.; Sistla, G.; Luly, C.J.; Crane, D.E. A modeling study of the impact of urban trees on ozone. Atmos. Environ. 2000, 34, 1601–1613. [Google Scholar] [CrossRef]
- Nowak, D.J.; Crane, D.E.; Stevens, J.C. Air pollution removal by urban trees and shrubs in the United States. Urban. For. Urban. Green. 2006, 4, 115–123. [Google Scholar] [CrossRef]
- Escobedo, F.J.; Nowak, D.J. Spatial heterogeneity and air pollution removal by an urban forest. Landsc. Urban. Plan. 2009, 90, 102–110. [Google Scholar] [CrossRef]
- Nowak, D.J.; Crane, D.E. Carbon storage and sequestration by urban trees in the USA. Environ. Pollut. 2002, 116, 381–389. [Google Scholar] [CrossRef]
- Morancho, A.B. A hedonic valuation of urban green areas. Landsc. Urban. Plan. 2003, 66, 35–41. [Google Scholar] [CrossRef]
- Luttik, J. The value of trees, water, and open space as reflected by house prices in the Netherlands. Landsc Urban. Plan. 2000, 48, 161–167. [Google Scholar] [CrossRef]
- Jim, C.Y.; Chen, W.Y. External effects of neighborhood parks and landscape elements on high-rise residential value. Land Use Policy 2010, 27, 662–670. [Google Scholar] [CrossRef]
- Bolitzer, B.; Netusil, N.R. The impact of open spaces on property values in Portland, Oregon. J. Environ. Manag. 2000, 59, 185–193. [Google Scholar] [CrossRef]
- Poudyal, N.C.; Hodges, D.G.; Merrett, C.D. A hedonic analysis of the demand for and benefits of urban recreation parks. Land Use Policy 2009, 26, 975–983. [Google Scholar] [CrossRef]
- Huang, C.; Huang, P.; Wang, X.; Zhou, Z. Assessment and optimization of green space for urban transformation in resources-based city—A case study of Lengshuijiang city, China. Urban. For. Urban. Green. 2018, 30, 295–306. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Murray, A.T.; Murray, B.L. Optimizing green space locations to reduce daytime and nighttime urban heat island effects in Phoenix, Arizona. Landsc. Urban. Plan. 2017, 165, 162–171. [Google Scholar] [CrossRef]
- Unal, M.; Uslu, C. Evaluating and optimizing urban green spaces for compact urban areas: Cukurova District in Adana, Turkey. ISPRS Int. J. Geoinf. 2018, 7, 70. [Google Scholar] [CrossRef]
- Yoon, E.J.; Kim, B.; Lee, D.K. Multi-objective planning model for urban greening based on optimization algorithms. Urban. For. Urban. Green. 2019, 40, 183–194. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, B. Soil erosion evaluation in a rapidly urbanizing city (Shenzhen, China) and implementation of spatial land-use optimization. Environ. Sci. Pollut. Res. 2014, 22, 4475–4490. [Google Scholar] [CrossRef] [PubMed]
- Cao, K.; Huang, B.; Wang, S.; Lin, H. Sustainable Land Use Optimization Using Boundary-based Fast Genetic Algorithm. Comput. Environ. Urban Syst. 2012, 36, 257–269. [Google Scholar] [CrossRef]
- Cao, K.; Batty, M.; Huang, B.; Liu, Y.; Yu, L.; Chen, J. Spatial Multi-objective Land Use Optimization: Extensions to the Non-dominated Sorting Genetic Algorithm-II. Inter. J. Geogr. Inf. Sci. 2011, 25, 1949–1969. [Google Scholar] [CrossRef]
- Steuer, R.E. Multiple Criteria Optimization: Theory, Computation, and Application; Wiley: Hoboken, NJ, USA, 1989. [Google Scholar]
- Miettinen, K. Nonlinear Multiobjective Optimization; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Cao, K.; Zhang, W.; Liu, S.; Huang, B.; Huang, W. Pareto law-based regional inequality analysis of PM2.5 air pollution and economic development in China. J. Environ. Manag. 2019, 252, 109635. [Google Scholar] [CrossRef]
- Kong, F.; Yin, H.; Nakagoshi, N. Using GIS and landscape metrics in the hedonic price modeling of the amenity value of urban green space: A case study in Jinan City, China. Landsc. Urban. Plan. 2007, 79, 240–252. [Google Scholar] [CrossRef]
- You, H. Characterizing the inequalities in urban public green space provision in Shenzhen, China. Habitat Int. 2016, 56, 176–180. [Google Scholar] [CrossRef]
- Li, Q.; Yu, Y.; Jiang, X.; Guan, Y. Multifactor-based environmental risk assessment for sustainable use planning in Shenzhen, China. Sci. Total Environ. 2019, 657, 1051–1063. [Google Scholar] [CrossRef] [PubMed]
- Gong, C.; Yu, S.; Chen, J. Spatiotemporal dynamics of urban forest conversion through model urbanization in Shenzhen, China. Int. J. Remote Sens. 2011, 32, 9071–9092. [Google Scholar] [CrossRef]
- Gong, C.; Chen, J.; Yu, S. Biotic homogenization and differentiation of the flora in artificial and near-natural habitats across urban green spaces. Landsc. Urban. Plan. 2013, 120, 158–169. [Google Scholar] [CrossRef]
- Zheng, C.; Cao, C.; Cheng, J.; Wu, Y.; Xie, X.; Xu, M. A study on land use and land cover change during urbanization in Shenzhen using data from Chinese satellites. Sci. Sin. 2011, 41, 140–152. [Google Scholar] [CrossRef]
- Chen, Z.; Gong, C.; Wu, J.; Yu, S. The influence of socioeconomic and topographic factors on nocturnal urban heat islands: A case study in Shenzhen, China. Int. J. Remote Sens. 2012, 33, 3834–3849. [Google Scholar] [CrossRef]
- Burak, G.; Seto, K.C. Environmental impacts of urban growth from an integrated dynamic perspective: A case study of Shenzhen, South China. Glob. Environ. Chang. 2008, 18, 0–735. [Google Scholar]
- Li, L.; Du, Q.; Ren, F.; Ma, X. Assessing spatial accessibility to hierarchical urban parks by multi-types of travel distance in Shenzhen, China. Int. J. Environ. Res. Public Health 2019, 16, 1038. [Google Scholar] [CrossRef] [PubMed]
- The Global Ecosystems and Environment Observation Analysis Research Cooperation. Available online: http://data.ess.tsinghua.edu.cn/ISLandCoverAfrica.html (accessed on 12 December 2018).
- Wolch, J.R.; Byrne, J.; Newell, J.P. Urban green space, public health, and environmental justice: The challenge of making cities “just green enough”. Landsc. Urban. Plan. 2014, 125, 234–244. [Google Scholar] [CrossRef]
- Urban Management and Comprehensive Law Enforcement Bureau of Shenzhen. Statistic Book for Green Parks in Shenzhen. 2018. Available online: http://cgj.sz.gov.cn/zwgk/tjsj/zxtjxx/201805/t20180525_11941634.htm (accessed on 25 December 2018).
- Naeem, S.; Cao, C.; Qazi, W.A.; Zamani, M.; Wei, C.; Acharya, B.K.; Rehman, A.U. Studying the association between green space characteristics and land surface temperature for sustainable urban environments: An analysis of Beijing and Islamabad. ISPRS Int. J. Geo Inf. 2018, 7, 38. [Google Scholar] [CrossRef]
- Garcia-Santos, V.; Cuxart, J.; Martinez-Villagrasa, D.; Jimenez, M.A.; Simo, G. Comparison of three methods for estimating land surface temperature from Landsat 8-TIRS sensor data. Remote Sens. 2018, 10, 1450. [Google Scholar] [CrossRef]
- Witte, A.D.; Sumka, H.J.; Erekson, H. An estimate of a structural hedonic price model of the housing market: An application of Rosen’s theory of implicit markets. Econometrica 1979, 47, 1151–1173. [Google Scholar] [CrossRef]
- Saphores, J.D.; Li, W. Estimating the value of urban green areas: A hedonic pricing analysis of the single-family housing market in Los Angeles, CA. Landsc. Urban. Plan. 2012, 104, 373–387. [Google Scholar] [CrossRef]
- Panduro, T.E.; Veie, K.L. Classification and valuation of urban green spaces: A hedonic house price valuation. Landsc. Urban. Plan. 2013, 120, 119–128. [Google Scholar] [CrossRef]
- Chen, W.Y. Environmental externalities of urban river pollution and restoration: A hedonic analysis in Guangzhou (China). Landsc. Urban. Plan. 2017, 157, 170–179. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, Y. Spatial variation of urban thermal environment and its relation to green space patterns: Implication to sustainable landscape planning. Sustainability 2018, 10, 2249. [Google Scholar] [CrossRef]
- Balling, R. The Maximin Fitness Function; Multi-objective City and Regional Planning. International conference on Evolutionary Multi-Criterion Optimization; Springer: Berlin, Germany, 2003; pp. 1–15. [Google Scholar]







| Category | Number | Retrieval Date |
|---|---|---|
| Train station | 13 | 23 December 2018 |
| Subway station | 327 | |
| Bus station | 5049 | |
| Scenery | 2081 | |
| School | 1240 | |
| Hospital | 380 | |
| Swimming pool | 400 | |
| Sum | 9490 |
| Type | Value |
|---|---|
| 1 bedroom | 1 |
| 1 bedroom with 1 hall | 2 |
| 2 bedrooms with 1 hall | 3 |
| 2 bedrooms with 2 halls | 4 |
| 3 bedrooms with 1 hall | 5 |
| 3 bedrooms with 2 halls | 6 |
| 4 bedrooms with 2 halls | 7 |
| 5 bedrooms with 2 halls | 8 |
| Name | Variables | Description |
|---|---|---|
| Area | Area (sq. m) of room or house for samples. | |
| Type | The number of bedrooms and halls of samples. | |
| Distance from train station | Euclidean distance from the sample point to the closest train station. | |
| Distance from subway station | Euclidean distance from the sample point to the closest subway station. | |
| Density of schools | Density of schools at the location of the sample. | |
| Distance from hospital | Euclidean distance from the sample point to the closest hospital. | |
| Density of swimming pools | Density of swimming pools at the location of the sample. | |
| Distance from scenery | Euclidean distance from the sample point to the closest scenery. | |
| Distance from river | Euclidean distance from the sample point to the closest river. | |
| Distance from urban park | Euclidean distance from the sample point to the closest urban park. | |
| Density of green space | Density of green space at the location of the sample. | |
| Distance from bus station | Euclidean distance from the sample point to the closest bus station. |
| Length (meter) | Model1 | Model2 | Model3 | Model4 | Model5 | Model6 | Model7 | Model8 | Model9 | Model10 | Model11 | Model12 | Model13 | Model14 | Model15 | Model16 | Model17 | Model18 | Model19 | Model20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 90 | - | |||||||||||||||||||
| 150 | 0.0227 * | |||||||||||||||||||
| 210 | 0.0299 * | |||||||||||||||||||
| 270 | 0.0372 * | |||||||||||||||||||
| 330 | 0.0532 * | |||||||||||||||||||
| 390 | 0.0597 * | |||||||||||||||||||
| 450 | 0.0656 * | |||||||||||||||||||
| 510 | 0.0726 * | |||||||||||||||||||
| 570 | 0.0777 * | |||||||||||||||||||
| 630 | 0.0822 * | |||||||||||||||||||
| 690 | 0.0879 * | |||||||||||||||||||
| 750 | 0.0883 * | |||||||||||||||||||
| 810 | 0.0891 * | |||||||||||||||||||
| 870 | 0.0902 * | |||||||||||||||||||
| 930 | 0.0926 * | |||||||||||||||||||
| 990 | 0.0923 * | |||||||||||||||||||
| 1050 | 0.0936 * | |||||||||||||||||||
| 1110 | 0.0956 * | |||||||||||||||||||
| 1170 | 0.0963 * | |||||||||||||||||||
| 1230 | 0.0970 * | |||||||||||||||||||
| 0.2469 * | 0.2463 * | 0.2459 * | 0.2454 * | 0.2462 * | 0.2458 * | 0.2453 * | 0.2449 * | 0.2448 * | 0.2442 * | 0.2436 * | 0.2437 * | 0.2435 * | 0.2434 * | 0.2434 * | 0.2437 * | 0.2439 * | 0.2439 * | 0.2438 * | 0.2440 * | |
| −0.0650 * | −0.0654 * | −0.0655 * | −0.0656 * | −0.0668 * | −0.0667 * | −0.0667 * | −0.0666 * | −0.0667 * | −0.0667 * | −0.0666 * | −0.0666 * | −0.0662 * | −0.0660 * | −0.0658 * | −0.0655 * | −0.0653 * | −0.0651 * | −0.0647 * | −0.0650 * | |
| −0.2449 * | −0.2428 * | −0.2421 * | −0.2413 * | −0.2387 * | −0.2380 * | −0.2372 * | −0.2361 * | −0.2353 * | −0.2345 * | −0.2337 * | −0.2334 * | −0.2331 * | −0.2328 * | −0.2322 * | −0.2321 * | −0.2318 * | −0.2314 * | −0.2312 * | −0.2310 * | |
| −0.2207 * | −0.2228 * | −0.2236 * | −0.2250 * | −0.2276 * | −0.2285 * | −0.2287 * | −0.2292 * | −0.2295 * | −0.2293 * | −0.2296 * | −0.2292 * | −0.2293 * | −0.2294 * | −0.2296 * | −0.2294 * | −0.2294 * | −0.2298 * | −0.2301 * | −0.2301 * | |
| −0.1207 * | −0.1191 * | −0.1183 * | −0.1174 * | −0.1162 * | −0.1154 * | −0.1146 * | −0.1137 * | −0.1129 * | −0.1122 * | −0.1115 * | −0.1113 * | −0.1110 * | −0.1107 * | −0.1103 * | −0.1103 * | −0.1101 * | −0.1098 * | −0.1097 * | −0.1096 * | |
| −0.0376 | −0.0404 * | −0.0414 * | −0.0418 * | −0.0412 * | −0.0423 * | −0.0432 * | −0.0440 * | −0.0444 * | −0.0449 * | −0.0458 * | −0.0462 * | −0.0466 * | −0.0468 * | −0.0471 * | −0.0471 * | −0.0472 * | −0.0474 * | −0.0475 * | −0.0477 * | |
| 0.1561 * | 0.1565 * | 0.1567 * | 0.1568 * | 0.1552 * | 0.1558 * | 0.1566 * | 0.1576 * | 0.1583 * | 0.1590 * | 0.1598 * | 0.1601 * | 0.1603 * | 0.1608 * | 0.1613 * | 0.1616 * | 0.1621 * | 0.1626 * | 0.1630 * | 0.1633 * | |
| −0.0854 * | −0.0829 * | −0.0822 * | −0.0815 * | −0.0795 * | −0.0791 * | −0.0785 * | −0.0778 * | −0.0774 * | −0.0772 * | −0.0769 * | −0.0769 * | −0.0766 * | −0.0764 * | −0.0760 * | −0.0759 * | −0.0756 * | −0.0753 * | −0.0751 * | −0.0748 * | |
| −0.1391 * | −0.1413 * | −0.1418 * | −0.1423 * | −0.1436 * | −0.1441 * | −0.1448 * | −0.1455 * | −0.1461 * | −0.1465 * | −0.1470 * | −0.1472 * | −0.1475 * | −0.1478 * | −0.1482 * | −0.1484 * | −0.1488 * | −0.1493 * | −0.1497 * | −0.1500 * | |
| −0.1129 * | −0.1066 * | −0.1045 * | −0.1024 * | −0.0996 * | −0.0979 * | −0.0962 * | −0.0942 * | −0.0931 * | −0.0920 * | −0.0906 * | −0.0903 * | −0.0898 * | −0.0891 * | −0.0883 * | −0.0883 * | −0.0880 * | −0.0873 * | −0.0870 * | −0.0868 * | |
| 0.0363 * | 0.0304 * | 0.0284 | 0.0267 | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | - | |
| Constant | 0.4811 | 0.4773 | 0.4761 | 0.4747 | 0.4776 | 0.4761 | 0.4744 | 0.4721 | 0.4705 | 0.4693 | 0.4676 | 0.4671 | 0.4664 | 0.4655 | 0.4642 | 0.4637 | 0.4628 | 0.4616 | 0.4609 | 0.4606 |
| 0.2394 | 0.2399 | 0.2402 | 0.2406 | 0.2411 | 0.2415 | 0.2418 | 0.2423 | 0.2427 | 0.2429 | 0.2433 | 0.2433 | 0.2433 | 0.2434 | 0.2436 | 0.2434 | 0.2435 | 0.2437 | 0.2436 | 0.2436 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Zhang, W.; Fu, P.; Huang, W.; Li, K.; Cao, K. The Spatial Optimization and Evaluation of the Economic, Ecological, and Social Value of Urban Green Space in Shenzhen. Sustainability 2020, 12, 1844. https://doi.org/10.3390/su12051844
Yu Y, Zhang W, Fu P, Huang W, Li K, Cao K. The Spatial Optimization and Evaluation of the Economic, Ecological, and Social Value of Urban Green Space in Shenzhen. Sustainability. 2020; 12(5):1844. https://doi.org/10.3390/su12051844
Chicago/Turabian StyleYu, Yuhan, Wenting Zhang, Peihong Fu, Wei Huang, Keke Li, and Kai Cao. 2020. "The Spatial Optimization and Evaluation of the Economic, Ecological, and Social Value of Urban Green Space in Shenzhen" Sustainability 12, no. 5: 1844. https://doi.org/10.3390/su12051844
APA StyleYu, Y., Zhang, W., Fu, P., Huang, W., Li, K., & Cao, K. (2020). The Spatial Optimization and Evaluation of the Economic, Ecological, and Social Value of Urban Green Space in Shenzhen. Sustainability, 12(5), 1844. https://doi.org/10.3390/su12051844




