Abstract
Enteromorpha is a species of algae biomass that is spread widely and has resulted in green tides in China in recent years. It was urgent to explore an appropriate method for taking advantage of the ocean waste as an energy supply in the current sustainable development. Pyrolysis, as the first step of thermochemical conversion in energy utilization, was given attention in order to study its behavior based on thermogravimetric experiments over a wide heating-rate range from 5 to 60 K/min. The whole pyrolysis process was divided into three stages: water evaporation, the main components decomposition, and carbonate decomposition. To estimate the detailed kinetic parameters (activation energy, the pre-exponential factor, and reaction order etc.), the Kissinger method was used to establish the original kinetic parameters at different stages and provide the parameter search range for the next heuristic algorithm, and then the Shuffled Complex Evolution optimization algorithm was coupled and first applied to the algae biomass pyrolysis. Eventually, the predicted results of mass loss rate based on the optimized kinetic parameters agreed well with the thermogravimetric experimental data, with the R2 value being up to 0.92 for all the heating rates.
1. Introduction
Many countries are surrounded by wide coastal areas and territorial seas. There are a lot of algae biomass species living along 32 thousand kilometers of coastline in China. With a short life cycle and fast breeding, they are easy to breed [1,2]. However, due to global climate change and water body eutrophication, the accumulating of massive amounts of Enteromorpha occurs, named “green tide”, which has become one of the major marine environmental problems all over the world, resulting in the damage of marine ecosystems, waterways, biodiversity, and even the coastal aquaculture, fishery, and tourism industry [3]. For example, green tide broke out in Qingdao (China’s yellow sea) in the summer of the 2008 Beijing Olympics, and more than 60 million tons of two green algae species (Enteromorpha clathrata and Enteromorpha compressa) grew very rapidly [4]. Thirty percent of the sailing competition area was covered by Enteromorpha with a direct economic loss of 1.322 billion RMB [3]. Such green tide is not accidental and it continues to thrive today. Green tide appears frequently along coastlines and has caused extensive ocean pollution and big economic losses over the years [3]. Therefore, it is very urgent to explore how to solve this problem.
Energy supply is one of the greatest challenges for the sustainable development of the current society [5]. The exploration and development of safe and sustainable alternatives to fossil fuels are given important global priorities [6]. Accordingly, renewable energy has gained more attention to address this problem. Algae biomass which lives in the largest aquatic environment area of the earth, as an important kind of renewable energy, shows several main advantages compared with terrestrial biomass, including no competition for arable land, cultivation in fresh or saltwater, no need for fertilizer or pesticide application, year-round production capability, high photosynthetic capacity, and high CO2 capture efficiency. Moreover, it also reveals other benefits, such as sequestering environmental contaminants [7,8]. Therefore, algae biomass, categorized as a third-generation biofuel resource, is not only ocean waste but also one of renewable energy [3,9]. Furthermore, it has become the biomass resource with most potential and is currently cultivated on an industrial scale for energy utilization [10]. Namely, a practical and feasible technology to solve the problem of green tide is to take advantage of these algae wastes for energy supply. At present, thermal-chemical conversion processes are regarded as an important energy utilization approach to algal biomass, especially pyrolysis [11,12,13,14]. Pyrolysis is not only a direct pathway for biomass thermal conversion, but also the first step in combustion and gasification reactions [7,15,16,17,18]. Thus, an improved understanding of this process would be helpful for thermochemical system design. Following this, an evaluation of the pyrolysis behaviors and kinetic characteristics of algae biomasses is needed.
Thermogravimetric analysis (TGA) is a technology widely used to explore the thermal conversion of biomass pyrolysis as a function of temperature and/or time in a controlled atmosphere [7,12], which will be applied here. Moreover, various reactions might be involved in the pyrolysis process with lots of kinetic parameters (activation energy, pre-exponential factor, reaction order etc.) need to be calculated. It is difficult for traditional kinetic methods to estimate so many parameters, therefore heuristic algorithms have to be considered to solve this problem. The Shuffled Complex Evolution (SCE) optimization algorithm, as a classic heuristic algorithm, is proposed by Duan et al. [19,20]. Its applicability and effectiveness to terrestrial lignocellulosic biomass pyrolysis have been verified in our previous study [21,22]. However, the optimization algorithm has not been applied to algae biomass pyrolysis. In order to fill the gaps in knowledge, Enteromorpha clathrate, as a typical algae biomass in green tide, is used in our current study. Thermogravimetric analysis is conducted at various heating rates to explore its pyrolysis behaviors, and its kinetic parameters are estimated by coupling the Kissinger method and the SCE optimization algorithm.
2. Materials and Methods
2.1. Thermogravimetric Measurements
Enteromorpha clathrate was collected from the Qingdao coast and sun dried for 10 days. The detailed properties of this sample, including ultimate analysis and biochemical composition are listed in Table 1. To conduct thermogravimetric experiments, all the samples were milled to powder with a size of less than 0.01 mm. A SDT Q600 thermal analyzer (TA Instruments, New Castle, DE, USA) was applied in the pyrolysis process with five heating rates (5–60 K/min) from 300 to 1200 K. All the samples were evenly placed in an Alumina cup without a lid, and a high purity nitrogen flow (100 mL/min) was used for all the experimental runs.

Table 1.
Properties of Enteromorpha clathrate 1 (% mass, dry basis).
2.2. Pyrolysis Kinetics
A pyrolysis kinetic equation can be expressed based on conversion rate α as follows:
where k(T) and f(α) are the reaction rate constant and reaction mechanism function, respectively. Whereby, α and k(T) can be further calculated via the following equations:
where m0, mt, and m∞ represent the sample mass at the initial time, time t, and the end, respectively. A and E are the pre-exponential factor and activation energy of the reaction, respectively.
Then Equation (1) can be written as
where the linear heating rate β = dT/dt.
Based on the basic pyrolysis kinetic equation, the Kissinger method was applied to calculate the activation energy and pre-exponential factor at the peak locations, as a reference of the parameter search range of the SCE algorithm.
2.2.1. Kissinger Method
Assuming that the reaction-order model should be responsible for our current reaction, the reaction mechanism function was defined as f(α) = (1 − α)n, and then the time derivative of Equation (4) at peak locations could be expressed as
Kissinger regarded that n(1 − ap)n − 1 was independent of the heating rate β, with the value being approximately equal to 1. Then the Kissinger kinetic equation was obtained by taking the logarithm of the following equation:
The plot of ln(β/T2p) versus 1/T gave a straight line, whose slope and intercept could be used to determine the activation energy E and pre-exponential factor A.
2.2.2. SCE Optimization Algorithm
The SCE global optimization algorithm is an effective method for optimizing the pyrolysis kinetic parameters of biomass pyrolysis. This has been proved in our previous study [21,22,23]. There are four concepts for this algorithm: the combination of probabilistic and deterministic approaches, clustering, the systematic evolution of a complex of points spanning the space in the direction of global improvement, and competitive evolution [19]. In the optimization process, an initial population composed of parameters that need to be optimized is generated. Next, these parameters (called individuals) are ranked and partitioned into multiple complexes. Then each complex is evolved independently according to the Competitive Complex Evolution algorithm and the second generation is produced by combining all the individuals in each complex. For each generation, the fittest individuals can be survived based on the objective function until convergence is achieved. The more detailed optimization process can be referred to Duan and Chaos et al. [19,20,24]. For the current thermogravimetric experiment, the objective function φmlr was the least error of mass loss rate (MLR) between the predicted results and experimental data:
where N and λ are the number of experiments and experimental data points for each experiment, respectively.
3. Results and Discussion
3.1. Thermogravimetric Analysis
The thermogravimetric experimental data, including the conversion rate and mass loss rate of Enteromorpha clathrate pyrolysis at various heating rates, are shown in Figure 1. Ross et al. [25] found that there were significant differences in the pyrolysis properties between algae biomass and terrestrial lignocellulosic biomass. Different from lignocellulosic biomass, whose main components are hemicellulose, cellulose, and lignin [26,27], the main components of algal biomass are protein, carbohydrate, and lipid.
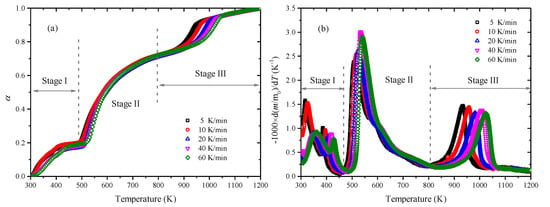
Figure 1.
Pyrolysis behaviors at different heating rates: (a) conversion rate and (b) mass loss rate.
Figure 1 shows that the main pyrolysis process was divided into three parts: Stage I in the temperature range of 300–460 K, Stage II in the temperature range of 460–800 K, and Stage III in the temperature range of 800–1100 K, which is marked in the figure. In Stage I, a dehydration process—namely, the evaporation of water happens—which was also observed by Wang, Kim and Zhao et al. [4,28,29] in a similar temperature range. The total conversion rate in this stage was about 20%. In Stage II, the main components of Enteromorpha clathrate started to decompose. Namely, protein, carbohydrate, and lipid should have been responsible for the pyrolysis in this stage with about a 50% total conversion rate. The obvious peaks were observed within the temperature range of 520–570 K. The higher the heating rate was, the greater the mass loss rate of peak was. In Stage III, the reaction occurred at a high temperature, which might be attributed to the carbonate decomposition or volatile metal loss [4]. The total conversion rate in this stage was about 30% and the peak location was between 930 and 1030 K. Differently from the change trend of the peak in Stage II, the higher the heating rate was, the smaller the mass lose rate of peak was in Stage III.
In the whole pyrolysis process, the main decomposition reactions of Enteromorpha clathrate happened in Stage II and III, which can be expressed as
where v is the residue yield, ComponentA and ComponentB are the hypothetical reactants that should have been responsible for Stages II and III, respectively.
3.2. Kinetic Analysis Based on the Kissinger Method
To calculate the activation energy and pre-exponent factor, the peak location should first be established, then the second derivative of m/m0 (DTG) is used here [23,30,31]:
Li et al. [30] stressed that if a major component was near the maximum decomposition rate, then the value of |DDTG| would be likely to drop rapidly to a local minimum (LM). The curve of |DDTG| in Stages II and III at 40 and 60 K/min is shown in Figure 2 and the local minimum locations (LM) are still marked. By coupling the DTG and |DDTG| curves, it was convenient to establish the peak temperature, namely 533.97 and 1006.57 K at 40 K/min, and 540.79 and 1023.11 K at 60 K/min. The detailed peak temperature for all the heating rates is listed in Table 2.
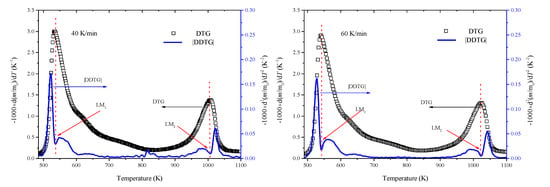
Figure 2.
Estimation of peak locations based on second derivative of m/m0 (|DDTG|).

Table 2.
Peak temperatures at different heating rate.
Based on the established peak locations and Equation (6), the slope and intercept were obtained in Figure 3, and the activation energy and pre-exponent factor were calculated by the Kissinger method: Ep1 = 166.45 kJ/mol, Ep2 = 209.34 kJ/mol, Ap1 = 8.50 × 1011 s−1, and Ap2 = 1.21 × 106 s−1, respectively.
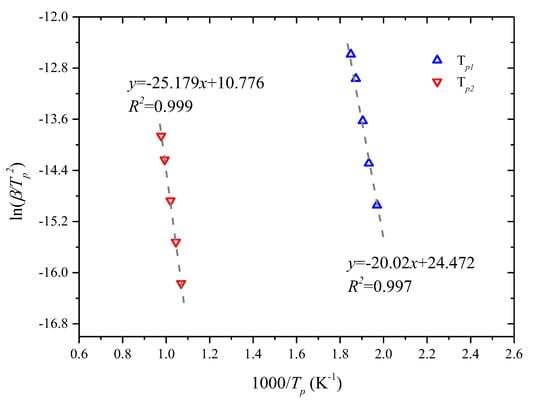
Figure 3.
Kissinger plots for peak locations.
3.3. Estimation of Kinetic Parameters by SCE
The obtained activation energy and pre-factor were defined as the original value V0, and the parameter search range of the SCE was set to 0.5–1.5V0, as listed in Table 3.

Table 3.
Optimized parameters by Shuffled Complex Evolution at multiple heating rates.
For Equation (8), the reaction rates of the hypothetical reactants and produced residue could be represented by the nth order reaction-order model
Then the predicted value of total mass loss rate was expressed as
The above predicted results were compared with thermogravimetric experimental data by the object function of Equation (7). There were 9 kinetic parameters that needed to be optimized at the same time. Eventually, the optimized results were obtained by SCE based on all five heating rates, as shown in Figure 4, taking the results of 5–40 K/min, for example. The mass loss rates of separate component are further displayed in Figure 5, taking the results of 5 and 10 K/min, for example. Moreover, the optimized parameters are listed in Table 3.
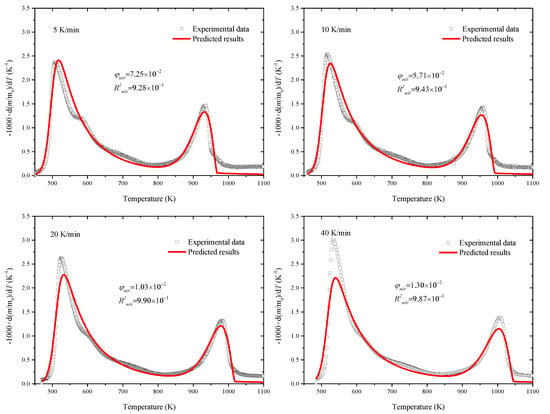
Figure 4.
Predicted mass loss rates based on the optimized parameters (lines) compared with experimental data (symbols).
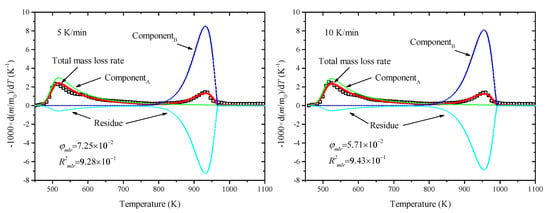
Figure 5.
Predicted mass loss rates of separated components.
This shows that the predicted results agreed well with the experiment data with R2 being up to 0.92, especially the peak locations, which were captured exactly in both Stages II and III. The activation energy and pre-exponent factor in Stages II and III were Ep1 = 199.85 kJ/mol, Ap1 = 7.75 × 1017 s−1, Ep2 = 208.91 kJ/mol, and Ap2 = 1.25 × 109 s−1, respectively. The optimized parameters could be used in the pyrolysis reactor design and numerical simulation. Our previous study proved the applicability of optimized parameters in the pyrolysis model coupled with mass and heat transfer [32] and even the complicated direct combustion process in the field of numerical simulation [33].
4. Conclusions
A series of thermogravimetric experiments from 5 to 60 K/min was conducted to explore the pyrolysis behaviors of the typical algae biomass Enteromorpha clathrate, which results in green tide in China. The whole pyrolysis behavior was composed of three stages, including water evaporation, main-component (protein, carbohydrate, and lipid) decomposition and carbonate decomposition. To explore the kinetic parameters (such as the activation energy, pre-exponential factor, and reaction order etc.) in the main reaction stages, the second derivative of mass loss rate was used to establish the peak locations. Then a traditional kinetic method called Kissinger was used to calculate the original kinetic parameters according to the above peak locations. Furthermore, the Shuffled Complex Evolution algorithm was coupled and first applied to the algae biomass pyrolysis. Eventually, the optimized kinetic parameters were obtained based on all the heating rates. The predicted mass loss rates agreed well with the thermogravimetric experimental data, with R2 being up to 0.92.
Author Contributions
Conceptualization, L.Z. and Y.D.; methodology, L.Z. and Y.D.; validation, L.Z., J.Z., and Y.D.; investigation, L.Z.; data curation, J.Z.; writing—original draft preparation, L.Z.; writing—review and editing, J.Z. and Y.D.; supervision, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant numbers 51806202 and 51806106, the Natural Science Foundation of Hubei Province of China, grant number 2018CFB352 and the Research Fund of The State Key Laboratory of Coal Resources and Safe Mining, CUMT, grand number SKLCRSM19KF021.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, S.; Jiang, X.; Wang, N.; Yu, L.; Li, Z.; He, P. Research on pyrolysis characteristics of seaweed. Energy Fuels 2007, 21, 3723–3729. [Google Scholar] [CrossRef]
- Zhao, B.; Fang, Y.; Wu, K.; Zhang, F.; Wang, J. A Method of Large-Scale Resource Utilization of Algae—Eutrophic Waste from Lake Chao, China: Preparation and Performance Optimization of Composite Packaging Materials. Sustainability 2019, 11, 6462. [Google Scholar] [CrossRef]
- Gao, X.; Xing, W.; Zhou, J.; Wang, G.; Zhuo, S.; Liu, Z.; Xue, Q.; Yan, Z. Superior capacitive performance of active carbons derived from Enteromorpha prolifera. Electrochim. Acta 2014, 133, 459–466. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, X.; Han, X.; Liu, J. Combustion characteristics of seaweed biomass. 1. Combustion characteristics of Enteromorpha clathrata and Sargassum natans. Energy Fuels 2009, 23, 5173–5178. [Google Scholar] [CrossRef]
- Li, D.; Chen, L.; Zhao, J.; Zhang, X.; Wang, Q.; Wang, H.; Ye, N. Evaluation of the pyrolytic and kinetic characteristics of Enteromorpha prolifera as a source of renewable bio-fuel from the Yellow Sea of China. Chem. Eng. Res. Des. 2010, 88, 647–652. [Google Scholar] [CrossRef]
- Hua, M.-Y.; Li, B.-X. Co-pyrolysis characteristics of the sugarcane bagasse and Enteromorpha prolifera. Energy Convers. Manag. 2016, 120, 238–246. [Google Scholar] [CrossRef]
- Ceylan, S.; Goldfarb, J.L. Green tide to green fuels: TG–FTIR analysis and kinetic study of Ulva prolifera pyrolysis. Energy Convers. Manag. 2015, 101, 263–270. [Google Scholar] [CrossRef]
- Guo, Y.; Tan, C.; Wang, P.; Sun, J.; Li, W.; Zhao, C.; Lu, P. Structure-performance relationships of magnesium-based CO2 adsorbents prepared with different methods. Chem. Eng. J. 2020, 379, 122277. [Google Scholar] [CrossRef]
- Pal, P.; Chew, K.W.; Yen, H.-W.; Lim, J.W.; Lam, M.K.; Show, P.L. Cultivation of Oily Microalgae for the Production of Third-Generation Biofuels. Sustainability 2019, 11, 5424. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, D.; Cao, B.; Qian, L.; Hu, Y.; Liu, L.; Yuan, C.; Abomohra, A.E.-F.; He, Z.; Wang, Q. Bio-char and bio-oil characteristics produced from the interaction of Enteromorpha clathrate volatiles and rice husk bio-char during co-pyrolysis in a sectional pyrolysis furnace: A complementary study. J. Anal. Appl. Pyrolysis 2018, 135, 219–230. [Google Scholar] [CrossRef]
- Wang, S.; Cao, B.; Liu, X.; Xu, L.; Hu, Y.; Afonaa-Mensah, S.; Abomohra, A.E.-F.; He, Z.; Wang, Q.; Xu, S. A comparative study on the quality of bio-oil derived from green macroalga Enteromorpha clathrata over metal modified ZSM-5 catalysts. Bioresour. Technol. 2018, 256, 446–455. [Google Scholar] [CrossRef] [PubMed]
- Perrot, J.-F.; Subiantoro, A. Municipal waste management strategy review and waste-to-energy potentials in New Zealand. Sustainability 2018, 10, 3114. [Google Scholar] [CrossRef]
- Xu, Z.; Xiao, X.; Fang, P.; Ye, L.; Huang, J.; Wu, H.; Tang, Z.; Chen, D. Comparison of Combustion and Pyrolysis Behavior of the Peanut Shells in Air and N2: Kinetics, Thermodynamics and Gas Emissions. Sustainability 2020, 12, 464. [Google Scholar] [CrossRef]
- Chen, R.; Li, Q.; Zhang, Y.; Xu, X.; Zhang, D. Pyrolysis kinetics and mechanism of typical industrial non-tyre rubber wastes by peak-differentiating analysis and multi kinetics methods. Fuel 2019, 235, 1224–1237. [Google Scholar] [CrossRef]
- Kong, D.; Peng, R.; Sun, X.; Zhang, J.; Ping, P.; Du, J. Study of the influence of crude oil on the spontaneous combustion risk of sulfurized rust in crude oil tanks. Fuel 2019, 255, 115816. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, D.; Li, M.; He, J.-J.; Gao, Z.-H.; Zhou, Y.; Sun, J.-H. Pyrolytic behavior of waste extruded polystyrene and rigid polyurethane by multi kinetics methods and Py-GC/MS. Fuel 2018, 222, 11–20. [Google Scholar] [CrossRef]
- Zhou, Y.; Bu, R.; Gong, J.; Yan, W.; Fan, C. Experimental investigation on downward flame spread over rigid polyurethane and extruded polystyrene foams. Exp. Therm. Fluid Sci. 2018, 92, 346–352. [Google Scholar] [CrossRef]
- Kong, B.; Wang, E.; Lu, W.; Li, Z. Application of electromagnetic radiation detection in high-temperature anomalous areas experiencing coalfield fires. Energy 2019, 189, 116144. [Google Scholar] [CrossRef]
- Duan, Q.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Ding, Y.; Wang, C.; Chaos, M.; Chen, R.; Lu, S. Estimation of beech pyrolysis kinetic parameters by shuffled complex evolution. Bioresour. Technol. 2016, 200, 658–665. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Zhang, J.; He, Q.; Huang, B.; Mao, S. The application and validity of various reaction kinetic models on woody biomass pyrolysis. Energy 2019, 179, 784–791. [Google Scholar] [CrossRef]
- Ding, Y.; Huang, B.; Li, K.; Du, W.; Lu, K.; Zhang, Y. Thermal interaction analysis of isolated hemicellulose and cellulose by kinetic parameters during biomass pyrolysis. Energy 2020, 195, 117010. [Google Scholar] [CrossRef]
- Chaos, M. Spectral aspects of bench-scale flammability testing: Application to hardwood pyrolysis. Fire Saf. Sci. 2014, 11, 165–178. [Google Scholar] [CrossRef]
- Ross, A.; Jones, J.; Kubacki, M.; Bridgeman, T. Classification of macroalgae as fuel and its thermochemical behaviour. Bioresour. Technol. 2008, 99, 6494–6504. [Google Scholar] [CrossRef]
- Ding, Y.; Ezekoye, O.A.; Lu, S.; Wang, C.; Zhou, R. Comparative pyrolysis behaviors and reaction mechanisms of hardwood and softwood. Energy Convers. Manag. 2017, 132, 102–109. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, W.; Yu, L.; Lu, K. The accuracy and efficiency of GA and PSO optimization schemes on estimating reaction kinetic parameters of biomass pyrolysis. Energy 2019, 176, 582–588. [Google Scholar] [CrossRef]
- Kim, S.-S.; Ly, H.V.; Kim, J.; Choi, J.H.; Woo, H.C. Thermogravimetric characteristics and pyrolysis kinetics of Alga Sagarssum sp. biomass. Bioresour. Technol. 2013, 139, 242–248. [Google Scholar] [CrossRef]
- Zhao, H.; Yan, H.; Dong, S.; Zhang, Y.; Sun, B.; Zhang, C.; Ai, Y.; Chen, B.; Liu, Q.; Sui, T. Thermogravimetry study of the pyrolytic characteristics and kinetics of macro-algae Macrocystis pyrifera residue. J. Therm. Anal. Calorim. 2013, 111, 1685–1690. [Google Scholar] [CrossRef]
- Li, K.-Y.; Huang, X.; Fleischmann, C.; Rein, G.; Ji, J. Pyrolysis of medium-density fiberboard: Optimized search for kinetics scheme and parameters via a genetic algorithm driven by Kissinger’s method. Energy Fuels 2014, 28, 6130–6139. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Y.; Zhang, J.; Zhou, R.; Ren, Z.; Guo, H. Kinetic parameters estimation of pinus sylvestris pyrolysis by Kissinger-Kai method coupled with Particle Swarm Optimization and global sensitivity analysis. Bioresour. Technol. 2019, 293, 122079. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Ezekoye, O.A.; Zhang, J.; Wang, C.; Lu, S. The effect of chemical reaction kinetic parameters on the bench-scale pyrolysis of lignocellulosic biomass. Fuel 2018, 232, 147–153. [Google Scholar] [CrossRef]
- Ding, Y.; Fukumoto, K.; Ezekoye, O.A.; Lu, S.; Wang, C.; Li, C. Experimental and numerical simulation of multi-component combustion of typical charring material. Combust. Flame 2020, 211, 417–429. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).