Next Article in Journal
Uncertainty in Flood Mitigation Practices: Assessing the Economic Benefits of Property Acquisition and Elevation in Flood-Prone Communities
Previous Article in Journal
Opening up the Black Box of Group Decision-Making on Solar Energy: The Case of Strata Buildings in Amsterdam, the Netherlands
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 12
Issue 5
10.3390/su12052099
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimating Ecosystem Respiration in the Grasslands of Northern China Using Machine Learning: Model Evaluation and Comparison

by
Xiaobo Zhu
1,2,3,4,
Honglin He
3,4,5,*,
Mingguo Ma
1,2,*,
Xiaoli Ren
3,4,
Li Zhang
3,4,5,
Fawei Zhang
6,
Yingnian Li
6,
Peili Shi
3,5,
Shiping Chen
7,
Yanfen Wang
8,
Xiaoping Xin
9,
Yaoming Ma
8,10,11,
Yu Zhang
12,
Mingyuan Du
13,
Rong Ge
3,4,8,
Na Zeng
3,4,8,
Pan Li
14,
Zhongen Niu
3,4,8,
Liyun Zhang
3,4,8,
Yan Lv
3,4,8,
Zengjing Song
1,2 and
Qing Gu
1,2add Show full author list remove Hide full author list
1
Southwest University, School of Geographical Sciences, Chongqing Jinfo Mountain Field Scientific Observation and Research Station for Karst Ecosystem, Ministry of Education, Chongqing 400715, China
2
Chongqing Engineering Research Center for Remote Sensing Big Data Application, School of Geographical Sciences, Southwest University, Chongqing 400715, China
3
Key Laboratory of Ecosystem Network Observation and Modeling, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
4
National Ecosystem Science Data Center, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
5
College of Resources and Environment, University of Chinese Academy of Sciences, Beijing 100049, China
6
Northwest Institute of Plateau Biology, Chinese Academy of Sciences, Xining 810001, China
7
State Key Laboratory of Vegetation and Environmental Change, Institute of Botany, Chinese Academy of Sciences, Beijing 100093, China
8
University of Chinese Academy of Sciences, Beijing 100049, China
9
Institute of Agricultural Resources and Regional Planning, Chinese Academy of Agricultural Sciences, Beijing 100081, China
10
Key Laboratory of Tibetan Environment Changes and Land Surface Processes, Institute of Tibetan Plateau Research, Chinese Academy of Sciences, Beijing 100101, China
11
CAS Center for Excellence in Tibetan Plateau Earth Science, Chinese Academy of Sciences, Beijing 100101, China
12
Northwest Institute of Eco-Environment and Resources, Chinese Academy of Sciences, Lanzhou 730000, China
13
Institute for Agro-Environmental Sciences, National Agriculture and Food Research Organization, Tsukuba, Ibaraki 3058604, Japan
14
Institute of Surface-Earth System Science, Tianjin University, Tianjin 300072, China
 
add Show full affiliation list
 
remove Hide full affiliation list
*
Authors to whom correspondence should be addressed.
Sustainability 2020, 12(5), 2099; https://doi.org/10.3390/su12052099
Submission received: 15 January 2020 / Revised: 2 March 2020 / Accepted: 4 March 2020 / Published: 9 March 2020
(This article belongs to the Section Environmental Sustainability and Applications)
Browse Figures
Versions Notes

Abstract

:
While a number of machine learning (ML) models have been used to estimate RE, systematic evaluation and comparison of these models are still limited. In this study, we developed three traditional ML models and a deep learning (DL) model, stacked autoencoders (SAE), to estimate RE in northern China’s grasslands. The four models were trained with two strategies: training for all of northern China’s grasslands and separate training for the alpine and temperate grasslands. Our results showed that all four ML models estimated RE in northern China’s grasslands fairly well, while the SAE model performed best (R2 = 0.858, RMSE = 0.472 gC m−2 d−1, MAE = 0.304 gC m−2 d−1). Models trained with the two strategies had almost identical performances. The enhanced vegetation index and soil organic carbon density (SOCD) were the two most important environmental variables for estimating RE in the grasslands of northern China. Air temperature (Ta) was more important than the growing season land surface water index (LSWI) in the alpine grasslands, while the LSWI was more important than Ta in the temperate grasslands. These findings may promote the application of DL models and the inclusion of SOCD for RE estimates with increased accuracy.

1. Introduction

Ecosystem respiration (RE) is a major flux in the global carbon cycle. Small changes in RE can have a significant impact on the atmospheric CO2 concentration and thus be a potentially positive feedback mechanism to the warming climate [1,2]. However, RE varies greatly at temporal and spatial scales due to the complex interactions among chemical, physical, and biological processes [3]. Numerous studies at regional and global scales indicate that RE estimates remain rather uncertain [4,5]. Therefore, it is necessary but challenging to accurately estimate RE at regional and global scales to quantitatively assess the terrestrial carbon budget and its response to global changes.
RE is often quantified using process-based models (e.g., the Lund–Potsdam–Jena model [6]), semi-empirical models (e.g., RECO model [5]), and empirical models (e.g., Arrhenius model [7]). In recent years, empirical models based on machine learning (ML) algorithms have become widely used because they are driven by observational data without complex assumptions and a large number of parameters [8,9]. In general, there are three well-known and commonly applied ML models for RE estimation: the back propagation artificial neural network (BP–ANN) model, the support vector regression (SVR) model, and the random forests (RF) model. For example, Zhao et al. [10] developed a BP–ANN model to predict global soil respiration (Rs, which is a major component of RE) from 1960 to 2012 using field records reported in the scientific literature. Ueyama et al. [9] estimated RE in Alaska by using flux observations and remote sensing data with the SVR model. Jian et al. [11] obtained global Rs using different timescales of Rs and climate data with the RF model. Although these ML models have been successful in estimating RE at different temporal and spatial scales, some uncertainties still exist. For instance, these ML models are usually constructed based on different learning principles; however, few attempts have been made to compare the predictive performance of these models in estimating RE [12]. Some advanced ML models, such as deep learning (DL) models, have not yet been tested for estimating RE. Moreover, RE under different environmental conditions may have different responses to climate change [13,14], and whether separately training ML models for each ecosystem type can improve performance is unclear. In addition, few studies have adequately explored the effects of different environmental variables on the performance of ML models in estimating RE. Thus, systematic evaluation and comparison of the performance of these ML models in estimating RE are essential.
In this study, with the integration of flux, meteorological, remote sensing, and soil map data, we developed four ML models for estimating RE in northern China’s grasslands. The four models include the three commonly used traditional ML models (BP–ANN, SVR, and RF) and a DL model named the stacked autoencoders (SAE) model. The main objectives of this study are (1) to compare the performance of the four ML models in estimating RE in the grasslands of northern China; (2) to compare the performance of the ML models trained for all of northern China’s grasslands and separately trained for each ecosystem type; and (3) to analyze the effects of different environmental variables on the performance of the ML models in estimating RE.

2. Materials and Methods

2.1. Study Area

Northern China’s grasslands are mainly composed of alpine and temperate grasslands, which are widely distributed in the Tibetan Plateau (TP) and Inner Mongolian Plateau (IM), respectively (Figure 1). The TP and IM have distinct environmental features [13]. The TP is in the alpine climate zone, and the average elevation of TP is over 4000 m. The range of mean annual precipitation is from 200 to 600 mm, and the range of mean annual temperature is from −5.75 to 2.57 °C. The alpine grasslands represent a typical ecosystem in the central Asia alpine environment and cover more than 60% of the plateau [15]. The IM is under arid and semi-arid conditions, with an average elevation of approximately 1000 m. The range of mean annual precipitation is from 200 to 350 mm, and the range of mean annual temperature is from 3 to 6 °C. The temperate grasslands growing on the IM are an important component of the Eurasian grasslands, and represent a typical vegetation type under the temperate continental climate [16].
Fully considering the spatial representativeness of the flux sites in this study, we focused on three grassland types: (a) alpine meadow, (b) alpine meadow steppe, and (c) temperate steppe. According to the Atlas of Grasslands Resources of China (1:1,000,000) [17], the alpine meadow was further reclassified into three types: alpine swamp meadow, alpine shrub meadow, and alpine Kobresia meadow. The temperate steppe was also reclassified into three types: desert steppe, typical steppe, and meadow steppe. The distribution of these grassland types, as well as the typical grassland flux sites, is exhibited in Figure 1.

2.2. Data

2.2.1. Flux and Meteorological Observations

In this study, we used 52 site-year eddy covariance (EC) flux and meteorological observations from 18 grassland sites over 2003 to 2014 in northern China’s grasslands, including 34 site-years from 9 sites on the TP and 18 site-years from 9 sites on the IM (Figure 1 and Table 1). These data were collected from the ChinaFLUX [18], the Coordinated Observations and Integrated Research over Arid and Semi-arid China (COIRAS) [19], and the Heihe Watershed Allied Telemetry Experimental Research (HiWATER) [20]. The flux and meteorological data were processed by the ChinaFLUX CO2 data processing system [21], including triple coordinate rotation, the Webb–Pearman–Leuning (WPL) correction [22], abnormal data rejection [23], and nighttime data filtering with the friction velocity (μ*) threshold obtained from the algorithm provided by Reichstein et al. [24]. The missing nighttime RE and daytime RE data were calculated with the Lloyed–Taylor equation based on nighttime net ecosystem exchange observations [24]. The air temperature (Ta) and photosynthetically active radiation (PAR) data were gap-filled following the methods provided by Schwalm et al. [25]. The half-hourly RE, Ta, and PAR data were integrated into daily values, and the site-years with more than 30% of the daily RE missing were eliminated. To match the 8-day compositing intervals of the moderate resolution imaging spectroradiometer (MODIS) data, the processed daily RE, Ta, and PAR data were averaged within the same periods.

2.2.2. Remote Sensing Data

The following MODIS products (Collection 6) during 2003 to 2014 were used in this study: normalized difference vegetation index (NDVI), enhanced vegetation index (EVI) (MOD13A2) [26], and surface reflectance (MOD09A1) [27]. These data were obtained from the Land Processes Distributed Active Archive Center. NDVI and EVI are at 16-day temporal resolution and 1000 m spatial resolution, while surface reflectance is at 8-day temporal resolution and 500 m spatial resolution. The obtained data were further processed for quality control and gap-filling [28,29]. Each 16-day NDVI/EVI composite was used for two 8-day intervals corresponding to the composting interval of other MODIS products [30]. The surface reflectance data were further processed to generate the land surface water index (LSWI) data [31]. We used MODIS subsets of 3 × 3 km pixels centered on each flux tower to better represent the EC footprint area and to reduce the effect of geolocation errors [30].

2.2.3. SOCD Data

The Harmonized World Soil Database (HWSD) data were used to derive soil organic carbon density (SOCD) data of the surface (0–30 cm) soil layer [32]. SOCD (kgC m−2) was estimated from the organic carbon content (wt %), gravel content (vol %), layer thickness (m), and bulk density (kg m−3). Further details about the estimation are provided by Carvalhais et al. [33]. Then, we extracted the SOCD of each site from the HWSD-derived SOCD data [34].

2.3. Model Development

2.3.1. Environmental Variables

A variety of environmental factors influencing RE, including temperature [35,36], moisture [37,38], plant productivity [3,39] and substrate availability [1,40]. Grassland type represents the spatial distribution of different grassland community types, which have different physiological characteristics and responses to climate change [41,42]. The TP and IM have distinct elevational gradients, which influence the vertical zonality of grasslands [13,43]. Variations in Ta have significant effects on the intensity of vegetation and microbial activities, and many studies have indicated that Ta strongly regulates RE [1,3,13]. The growing season LSWI is strongly correlated with leaf water content and soil moisture in grasslands [37,44,45]. PAR is crucial for photosynthesis [46], thus influencing the photosynthetic supply of RE. The NDVI is closely correlated to fractional vegetation cover and vegetation biomass [45,47]. We also incorporated the EVI because, in comparison to the NDVI, it is more responsive to canopy structural variations, such as plant physiognomy, canopy type, and canopy architecture [48]. SOCD represents the quantity of carbon input of Rs [40]. Taken together, we selected grassland type, elevation, Ta, LSWI, PAR, NDVI, EVI, and SOCD as the environmental variables to account for the variation in RE in northern China’s grasslands.

2.3.2. Machine Learning Algorithms

ML algorithms focus on how to automatically improve their performance through experience [49]. In regression problems, ML algorithms try to automatically learn the dependencies between input and target variables from historical observations and make predictions. These algorithms mainly differ in structure and learning principle [8,50]. In this study, we developed models to estimate RE using four ML algorithms. The four algorithms include three traditional ML algorithms and a DL algorithm, which represented four broad families in ML [8]. The four traditional algorithms are the back propagation artificial neural network (BP-ANN), the support vector regression (SVR), and the random forests (RF), respectively. The DL algorithm is the stacked autoencoders (SAE). The four algorithms were implemented using the “scikit-learn” and “keras” packages in Python [51]. A brief description of the characteristics of each algorithm follows.
BP-ANN is one of the most widely used artificial neural networks and simulates the behavior of biological nervous networks. BP-ANN is composed of input, hidden, and output layers. Each layer contains many artificial neurons. An artificial neuron can be seen as a linear function with a non-linear function connected with its output. The input layer contains the input variables to perform the prediction, and the output layer contains the target variable. The input and output layers are connected by a hidden layer. Weights in the three layers represent the linkages between the input and target variables. In the training of BP-ANN, the weights are automatically adjusted along a negative gradient to minimize the error between the predicted and observed target variables using the back propagation algorithm [10]. BP-ANN has self-organizing, self-adaptive, and self-learning abilities, which can represent the complex relationship between the input and target variables [50].
SVR is an algorithm based on the kernel method [8]. Generally, the original regression problem is represented in a low dimensional space that is nonlinear [50]. SVR can transform the nonlinear regression into linear regression by projecting the input data of the original low-dimensional space into a higher-dimensional space with a kernel function. Thus, a global optimal solution is obtained by solving the convex quadratic programming problem [52]. The radial basis kernel function is usually used as the kernel function [53]. The training of SVR can always converge to the global optimal solution [9].
RF is a tree-based algorithm that combines decision tree and ensemble methods [54]. For regression problems, the basic unit in the RF is the regression tree, which is the decision tree with a continuous target variable. Each independent regression tree is developed using input samples selected by the bootstrap sampling method, and at each node, a random subset of input variables is selected [55]. The prediction results of all trees are averaged to make final predictions. RF is able to handle high-dimensional data and avoid overfitting in practice [54].
SAE has been one of the most typical and widely used DL algorithms over the past few years [56,57]. A single autoencoder (AE) is a neural network that attempts to reconstruct its inputs [58]. A basic AE has three neural layers, the first layer and the third layer are the input layer and the output layer, respectively, and the second layer is the hidden layer. The number of artificial neurons in the hidden layer is smaller than the input layer and the output layer; thus the AE can learn the main features that form a good representation of its input. An SAE is a deep neural network consisting of multiple layers of AEs in which the outputs of each layer are wired to the inputs of the successive layer [59,60]. For the purpose of prediction, a regressor is often added on the top layer. The AEs are pre-trained one by one in an unsupervised layer-wise manner, and the trained weights are used to initialize the SAE. Then, the SAE is fine-tuned to achieve a better convergence using the back propagation algorithm [61]. SAE can capture high-level features from input data for robust prediction [57].

2.3.3. Model Training and Evaluation

The performances of the four ML models (BP-ANN, SVR, RF, and SAE) in estimating RE were evaluated using a sample-based 10-fold cross-validation strategy [62], in which all of the RE observations were averagely split into 10 folds randomly. In each training, one fold was used as the validation data, and the remaining nine folds were used as training data. This process was repeated 10 times. Parameters in the four models were optimized and determined using the grid-search method [63]. The predicted RE from all 10 folds were compared with the observed RE. In addition, we trained the ML models with two strategies: training for all of northern China’s grasslands and separate training for the alpine and temperate grasslands.
The coefficient of determination (R2), root mean squared error (RMSE), and mean absolute error (MAE) were selected as evaluation metrics. These metrics were calculated as follows:
R 2 = ( ∑ i = 1 n ( O i − O ¯ ) ( P i − P ¯ ) ∑ i = 1 n ( O i − O ¯ ) 2 ∑ i = 1 n ( P i − P ¯ ) 2 ) 2
RMSE = 1 n ∑ i = 1 n ( O i − P i ) 2
MAE = 1 n ∑ i = 1 n | O i − P i |
where Oi is the ith observed value of RE, Pi is the ith predicted value of RE, O ¯ and P ¯ are the means of the observed RE and predicted RE, respectively; and n is the number of RE observation samples.

2.4. Variable Relative Importance Evaluation

To analyze the effects of different environmental variables on the performance of the ML models in estimating RE, we evaluated the relative importance of each variable by sequentially removing one of the environmental variables and repeating the cross-validation process [53,64]. The relative importance of each variable was quantified by the variation in the RMSE in percentage form. Since NDVI and EVI are highly consistent in representing vegetation cover and growth [26], we first compared the predictive performance of NDVI and EVI and then selected one of them for subsequent analysis. Moreover, we also tested the predictive performance of combining the NDVI and EVI. As the alpine grasslands and the temperate grasslands exist under different environmental conditions [13,37], we evaluated the relative importance of the environmental variables in the alpine grasslands and in the temperate grasslands.

3. Results

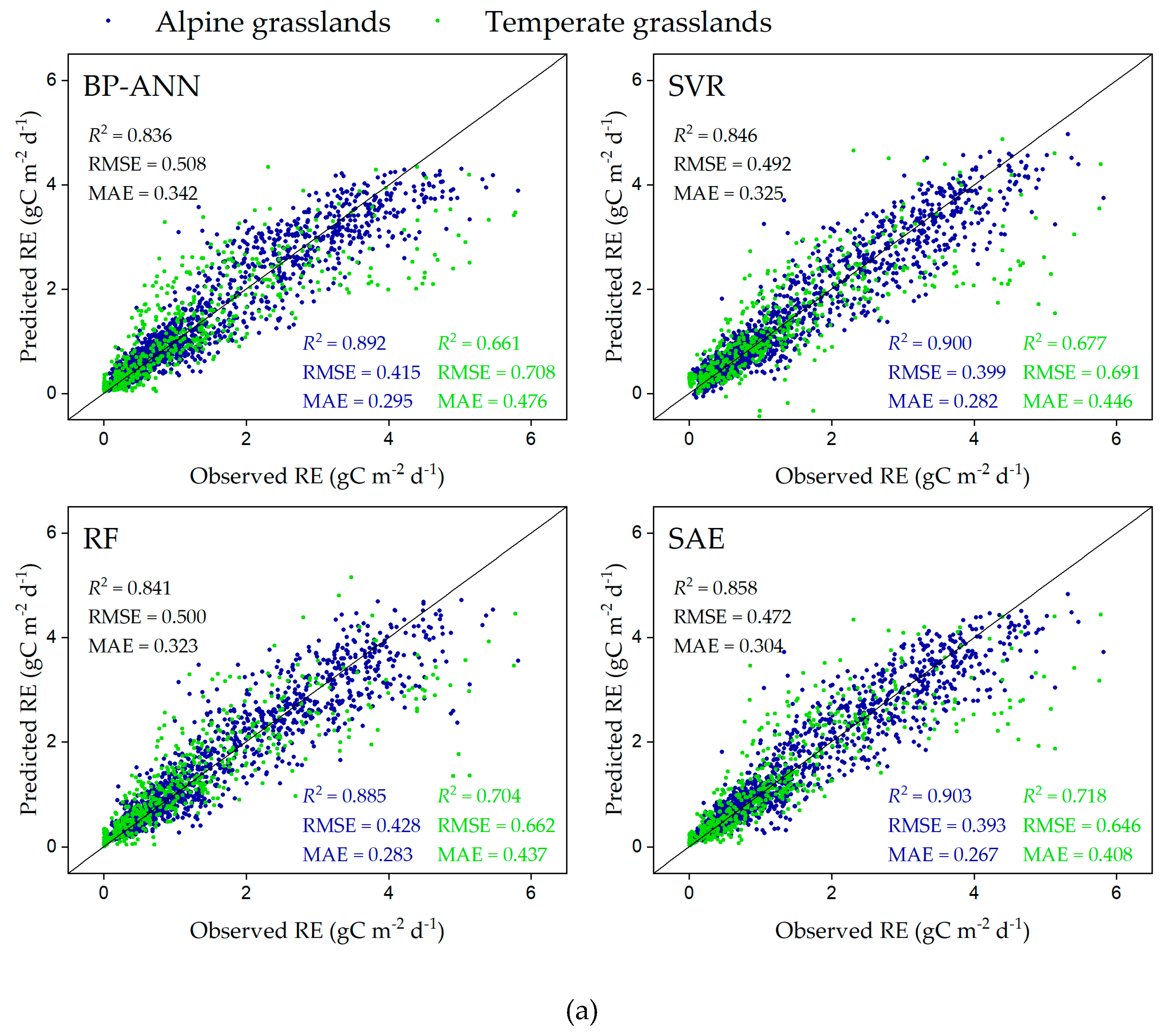
3.1. Model Performance

We first trained the BP–ANN, SVR, RF, and SAE models for all of northern China’s grasslands. The predicted RE from the four models agreed well with the observed RE and occurred at approximately the 1:1 line, indicating that all four ML models estimated RE in the grasslands of northern China fairly well (Figure 2a). However, there were still appreciable differences in the performances among the four models. The SAE model produced the lowest RMSE (0.472 gC m−2 d−1) and MAE (0.304 gC m−2 d−1) and the highest R2 (0.858), demonstrating that of the four models, SAE performed best in estimating RE. The SVR prediction performed the second-best with higher RMSE (0.492 gC m−2 d−1) and MAE (0.325 gC m−2 d−1) and lower R2 (0.846) than those of SAE. RF had slightly higher RMSE (0.500 gC m−2 d−1) and lower R2 (0.841) than those of SVR, but had slightly lower MAE (0.323 gC m−2 d−1) than that of SVR. BP-ANN produced the highest RMSE (0.508 gC m−2 d−1) and MAE (0.342 gC m−2 d−1) and the lowest R2 (0.836).
We then separately trained the ML models for the alpine and temperate grasslands. The two strategies had similar R2, RMSE, and MAE values in estimating RE for the alpine grasslands, temperate grasslands, and all of northern China’s grasslands (Figure 2). This result indicated that the difference between the performance of the two strategies was minimal. For example, in the alpine grasslands, the overall R2 of the two strategies ranged from 0.885 to 0.903. In the temperate grasslands, the overall R2 of the two strategies ranged from 0.656 to 0.718. In all of northern China’s grasslands, the overall R2 of the two strategies ranged from 0.836 to 0.858.
The results also showed that the performance of the four ML models varied with ecosystem type. More specifically, the four models performed better in estimating RE in the alpine grasslands than in the temperate grasslands in general (Figure 2). For the alpine grasslands, the four models with the two strategies produced RMSEs lower than 0.430 gC m−2 d−1, MAEs lower than 0.300 gC m−2 d−1, and R2 values higher than 0.880. In contrast, for the temperate grasslands, the four models produced RMSEs higher than 0.640 gC m−2 d−1, MAEs higher than 0.400 gC m−2 d−1, and R2 values lower than 0.720.

3.2. Relative Importance of Environmental Variables

All four ML models produced higher R2 and lower RMSE while using the EVI as the input vegetation index than while using the NDVI as the input vegetation index (Table 2), indicating that in comparison to the NDVI, the EVI better reflected the RE variations in the grasslands of northern China. By using both the EVI and NDVI as input vegetation indices, however, the BP–ANN, SVR, RF, and SAE models performed best in estimating RE.
Considering that the four models performed better while using EVI than using NDVI, we evaluated the relative importance of the environmental variables while using the EVI as the input vegetation index. The removal of each environmental variable caused an increase in the RMSE (Figure 3), illustrating that the four models performed best in estimating RE in northern China’s grasslands when all the environmental variables were used as input variables. However, the relative importance of the environmental variables varied with the model, indicating that environmental variables had different effects on different ML models in estimating RE.
The relative importance of the environmental variables also varied with the ecosystem type (Figure 3), indicating that the environmental variables had different effects on the RE estimation in different ecosystem types. For the Tibetan alpine grasslands (Figure 3a), the removal of the EVI caused the largest mean increase in RMSE (14.02%) of the four models, indicating that the EVI was the most important environmental variable for estimating RE in the alpine grasslands. The next most important environmental variables were SOCD, Ta, LSWI, grassland type, and elevation, with comparatively minor mean increases in the RMSE (10.64%, 5.53%, 4.70%, 3.50%, and 2.78%, respectively). The removal of PAR caused the smallest mean increase in the RMSE (1.50%). For the Inner Mongolian temperate grasslands (Figure 3b), the rank of the relative importance of the environmental variables was EVI, SOCD, LSWI, grassland type, Ta, elevation, and PAR. The removal of the EVI, SOCD, LSWI, grassland type, Ta, elevation, and PAR caused 8.44%, 6.57%, 5.07%, 4.09%, 3.44%, 2.55%, and 1.23% mean increases in the RMSE, respectively.

4. Discussion

In recent years, several ML models have been widely used to estimate RE at regional and global scales [8,9,30,62]. However, few studies have systematically evaluated and compared the performance of different ML models in estimating RE. In this study, we evaluated and compared the performance of three traditional ML models (BP–ANN, SVR, and RF) and a DL model (SAE) for estimating RE in the grasslands of northern China. We found that all four models could estimate RE fairly well in the study area (Figure 2). This can be explained by the fact that RE has strong dependencies on the selected environmental variables in the grasslands of northern China, and all four ML models have sufficient capabilities to learn these underlying dependencies to estimate RE, although they have different learning principles (introduced in Section 2.2.2). However, REs predicted from ML models were underestimated while the RE was getting larger (Figure 2). This may be caused by two reasons. First, we estimated RE for each 8-day interval. The 8-day Ta, LSWI, PAR, NDVI and EVI values may not represent some weather events influencing RE during that period [45,65], such as extreme heat and precipitation in summer. Second, some large RE values may be caused by certain atmospheric turbulent events rather than real ecological processes [66]. ML models are well known for having the ability to automatically learn complex nonlinear relationships from input data [49,67]. Given that RE is difficult to constrain due to our limited understanding of the complex interactions among physical, chemical, and biological processes [5,14], ML models can help us accurately quantify the spatiotemporal variation in RE at regional or global scales.
In addition, our results show that the SAE model performed best in estimating RE in the grasslands of northern China (Figure 2). As a DL model, SAE is able to automatically extract higher-level features in the environmental variables with unsupervised pre-training than traditional ML models. These higher-level features are more robust to outliers in input data and can better reflect the inherent nature of environmental variables [68,69]. Then, these higher-level features can be utilized to predict RE more effectively and accurately in the fine-tuning process [56]. Previous studies have shown that SAE or other DL models can perform better than traditional ML models in air quality prediction [59,70], digital soil mapping [71], and soil moisture prediction [72]. However, few studies have applied SAE or other DL models to estimate RE or other carbon fluxes. Our results suggest that the SAE model can be successfully applied to RE estimation and may perform better than traditional ML models, although with relatively small datasets. Moreover, with the rapid increase in EC flux observations and the development of DL approaches, we expect that DL models will be more widely used in quantifying RE or other carbon fluxes at different scales.
We developed ML models to estimate RE in northern China’s grasslands using two different strategies: training for all of northern China’s grasslands and separate training for each ecosystem type. Both strategies have been used to estimate RE or other carbon fluxes in previous studies. For example, Xiao et al. [30] developed a regression tree model to estimate RE for all ecosystem types over North America. In contrast, Liu et al. [73] separately trained general regression neural networks to estimate gross primary productivity and net ecosystem exchanges for each ecosystem type in the conterminous United States. Our results show that the two strategies differed little in estimating RE in northern China’s grasslands (Figure 2). This can be explained by two aspects. First, by training with samples from all the ecosystem types together, the four ML models may have been able to learn the underlying dependencies between RE and environmental variables both in the alpine and temperate grasslands, although the RE may have different responses to environmental change in the two ecosystem types [13,37]. Then, the four models had the generalization capacity to accurately estimate RE in the entire study area. Second, this similar performance may be due to the high variability among sites within the same ecosystem type, which is comparable to the variability among different ecosystem types [74]. We suggest training ML models for all ecosystem types together, which is more expedient in practice and can be more independent of the land cover and vegetation maps and related uncertainty [74,75]. In addition, we found that the four models generally performed better in the alpine grasslands than in the temperate grasslands (Figure 2). This may be due to the higher spatial and temporal variability in RE in the temperate grasslands (CV = 91.64%) than in the alpine grasslands (CV = 84.86%) [74].
All four ML models performed better in estimating RE while using the EVI as the input vegetation index than using the NDVI as the input vegetation index (Table 2). The NDVI uses red and infrared reflectance, which are sensitive to the soil background [26]. Studies have also shown that the NDVI could be saturated in grasslands with highly fractional vegetation cover [76]. As an improved vegetation index, EVI overcomes these shortcomings [26]. Moreover, in comparison to the NDVI, the EVI is more responsive to canopy structural variations, such as canopy architecture, plant physiognomy, and canopy type [48]. Therefore, in comparison to the NDVI, the EVI can better reflect the variation in RE in the grasslands of northern China. Furthermore, we found that the four models performed best in estimating RE while using both the EVI and NDVI as input vegetation indices, which may be due to the synergy of the two vegetation indices.
By using all the environmental variables as input variables, the four models performed best (Figure 3), implying that all the selected environmental variables account for the variation in RE in northern China’s grasslands. However, the results showed that environmental variables have different effects on different ML models in estimating RE (Figure 3). As the same training data were used for the four models, this may be caused by their different sampling strategies or learning methods [50]. The environmental variables also had different effects on the RE estimation in different ecosystem types (Figure 3). In general, the EVI and SOCD were the two most important environmental variables for estimating RE in both the alpine and temperate grasslands. This is not surprising, given that the EVI and SOCD can represent the variability of plant productivity and soil organic carbon pool, respectively [44,77], which are two main sources of carbon substrate supply for RE [1,40,78]. The important role of plant productivity and the soil carbon pool in regulating RE variations is also consistent with the results of many previous studies [3,5,42,79]. The most obvious differences in the effects of environmental variables on estimating RE in the two ecosystem types are Ta and LSWI (Figure 3). For the Tibetan alpine grasslands, Ta was more important than LSWI in estimating RE (Figure 3a). This result indicates that RE is more responsive to temperature variations than moisture variations in the alpine grasslands, which is consistent with the results of previous studies [13,36,80,81]. Alpine grasslands on the TP are generally thermal limited [13]; thus, temperature strongly controls the RE process by affecting enzyme activity [1,82]. Geng et al. [38] indicated that the spatial variation in Rs in Tibetan alpine grasslands can be better explained by soil moisture than by soil temperature. The different conclusions may be due to the differential responses of RE components to temperature variations [83]. In contrast, RE is more responsive to moisture variations than temperature variations in temperate grasslands (Figure 3b). Being mainly distributed in arid and semi-arid environments, vegetation and microbial activities in the Inner Mongolian temperate grasslands are strongly limited by moisture, thus leading to the strong control of moisture on RE variations [13,42]. Although ML models are usually called “black box” models, our results suggest that they still have some level of interpretability to improve our understanding of RE dynamics [84].
We evaluated and compared the performance of four ML models in estimating RE in the grasslands of northern China in our study; however, some limitations still exist. On the one hand, some other ML models have been used to estimate RE, such as the model tree ensembles [62] and Cubist [30], which are not included in our study. However, they are similar to the RF model that we have already evaluated. On the other hand, although we found that the soil carbon pool is important for RE estimation, the application of ML models that consider the effects of the soil carbon pool on regional RE estimation is still limited since spatially explicit information on the soil carbon pool is not readily available or contains considerable uncertainty [30,33,85]. With the development of ML, especially DL, the increase in soil carbon inventory data, and the development of digital soil mapping, we may be able to quantify the dynamics of RE more accurately and reasonably at regional and global scales.

5. Conclusions

In this study, we systematically evaluated and compared three traditional machine learning (ML) models (back propagation artificial neural network, support vector regression, and random forests models) and a deep learning (DL) model (stacked autoencoders model) in terms of estimating ecosystem respiration (RE) in northern China’s grasslands. Our results show that all four ML models estimated RE in the grasslands of northern China fairly well, while the stacked autoencoders model performed best (R2 = 0.858, RMSE = 0.472 gC m−2 d−1, MAE = 0.304 gC m−2 d−1). The ML models that were trained for all of northern China’s grasslands and separately trained for the alpine and temperate grasslands had almost identical performances, indicating that ML models for RE estimations can be developed for all ecosystem types together. Moreover, by evaluating the relative importance of environmental variables, we found that the enhanced vegetation index (EVI) and soil organic carbon density (SOCD) were the two most important variables in estimating RE in the grasslands of northern China. Air temperature (Ta) was more important than the growing season land surface water index (LSWI) in the Tibetan alpine grasslands, while LSWI was more important than Ta in the Inner Mongolian temperate grasslands. We suggest that RE estimation will benefit from the advanced algorithms in ML models, and some important environmental variables, such as SOCD, should be incorporated into RE estimations at regional and global scales.

Author Contributions

Conceptualization, H.H., M.M. and X.Z.; methodology, X.Z., X.R. and L.Z. (Li Zhang); validation, X.Z. and R.G.; formal analysis, X.Z. and H.H.; resources, M.M., F.Z., Y.L. (Yingnian Li), P.S., S.C., Y.W., X.X., Y.M., Y.Z. and M.D.; data curation, X.Z., R.G., N.Z., P.L., Z.N., L.Z. (Liyun Zhang), Y.L. (Yan Lv), Z.S., and Q.G.; writing—original draft preparation, X.Z.; writing—review and editing, H.H., M.M., and X.Z.; funding acquisition, H.H. and M.M.; All of the authors contributed to the result discussion and paper writing. All authors have read and agreed to the published version of the manuscript.

Funding

This work was jointly supported by the National Natural Science Foundation of China (grant number: 41571424, 41830648, 41771453) and the Strategic Priority Research Program of the Chinese Academy of Sciences (grant number: XDA19020301).

Acknowledgments

We thank the staff of ChinaFLUX, COIRAS and HiWATER for their dedication in observation to data processing. We also thank the principle contributors of the MODIS products, the Distributed Active Archive Center of the Oak Ridge National Laboratory and the Earth Observing System Data.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Davidson, E.A.; Janssens, I.A.; Luo, Y. On the variability of respiration in terrestrial ecosystems: Moving beyond Q10. Glob. Chang. Biol. 2006, 12, 154–164. [Google Scholar] [CrossRef]
  2. Heimann, M.; Reichstein, M. Terrestrial ecosystem carbon dynamics and climate feedbacks. Nature 2008, 451, 289–292. [Google Scholar] [CrossRef] [PubMed]
  3. Migliavacca, M.; Reichstein, M.; Richardson, A.D.; Colombo, R.; Sutton, M.A.; Lasslop, G.; Tomelleri, E.; Wohlfahrt, G.; Carvalhais, N.; Cescatti, A.; et al. Semiempirical modeling of abiotic and biotic factors controlling ecosystem respiration across eddy covariance sites. Glob. Chang. Biol. 2011, 17, 390–409. [Google Scholar] [CrossRef]
  4. Byrne, B.; Wunch, D.; Jones, D.B.A.; Strong, K.; Deng, F.; Baker, I.; Kohler, P.; Frankenberg, C.; Joiner, J.; Arora, V.K.; et al. Evaluating GPP and respiration estimates over northern midlatitude ecosystems using solar-induced fluorescence and atmospheric CO2 measurements. J. Geophys. Res. Biogeosci. 2018, 123, 2976–2997. [Google Scholar] [CrossRef]
  5. Jagermeyr, J.; Gerten, D.; Lucht, W.; Hostert, P.; Migliavacca, M.; Nemani, R. A high-resolution approach to estimating ecosystem respiration at continental scales using operational satellite data. Glob. Chang. Biol. 2014, 20, 1191–1210. [Google Scholar] [CrossRef]
  6. Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.O.; Levis, S.; Lucht, W.; Sykes, M.T.; et al. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Chang. Biol. 2003, 9, 161–185. [Google Scholar] [CrossRef]
  7. Kätterer, T.; Reichstein, M.; Andrén, O.; Lomander, A. Temperature dependence of organic matter decomposition: A critical review using literature data analyzed with different models. Biol. Fertil. Soils 1998, 27, 258–262. [Google Scholar] [CrossRef]
  8. Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Raduly, B.; Reichstein, M.; Arain, M.A.; Cescatti, A.; Kiely, G.; et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef] [Green Version]
  9. Ueyama, M.; Ichii, K.; Iwata, H.; Euskirchen, E.S.; Zona, D.; Rocha, A.V.; Harazono, Y.; Iwama, C.; Nakai, T.; Oechel, W.C. Upscaling terrestrial carbon dioxide fluxes in Alaska with satellite remote sensing and support vector regression. J. Geophys. Res. Biogeosci. 2013, 118, 1266–1281. [Google Scholar] [CrossRef]
  10. Zhao, Z.Y.; Peng, C.H.; Yang, Q.; Meng, F.R.; Song, X.Z.; Chen, S.T.; Epule, T.E.; Li, P.; Zhu, Q. Model prediction of biome-specific global soil respiration from 1960 to 2012. Earths Future 2017, 5, 715–729. [Google Scholar] [CrossRef]
  11. Jian, J.S.; Steele, M.K.; Thomas, R.Q.; Day, S.D.; Hodges, S.C. Constraining estimates of global soil respiration by quantifying sources of variability. Glob. Chang. Biol. 2018, 24, 4143–4159. [Google Scholar] [CrossRef] [PubMed]
  12. Dou, X.; Yang, Y. Estimating forest carbon fluxes using four different data-driven techniques based on long-term eddy covariance measurements: Model comparison and evaluation. Sci. Total Environ. 2018, 627, 78–94. [Google Scholar] [CrossRef] [PubMed]
  13. Liu, D.; Li, Y.; Wang, T.; Peylin, P.; MacBean, N.; Ciais, P.; Jia, G.S.; Ma, M.G.; Ma, Y.M.; Shen, M.G.; et al. Contrasting responses of grassland water and carbon exchanges to climate change between Tibetan Plateau and Inner Mongolia. Agric. For. Meteorol. 2018, 249, 163–175. [Google Scholar] [CrossRef]
  14. Yuan, W.P.; Luo, Y.Q.; Li, X.L.; Liu, S.G.; Yu, G.R.; Zhou, T.; Bahn, M.; Black, A.; Desai, A.R.; Cescatti, A.; et al. Redefinition and global estimation of basal ecosystem respiration rate. Glob. Biogeochem. Cycles 2011, 25. [Google Scholar] [CrossRef]
  15. Zhang, J.-W. Vegetation of Xizang (Tibet); Science Press: Beijing, China, 1988. [Google Scholar]
  16. Bai, Y.F.; Wu, J.G.; Xing, Q.; Pan, Q.M.; Huang, J.H.; Yang, D.L.; Han, X.G. Primary production and rain use efficiency across a precipitation gradient on the Mongolia plateau. Ecology 2008, 89, 2140–2153. [Google Scholar] [CrossRef] [PubMed]
  17. Su, D. The Atlas of Grassland Resources of China (1:1000000); Press of Map: Beijing, China, 1993. (In Chinese) [Google Scholar]
  18. Yu, G.R.; Wen, X.F.; Sun, X.M.; Tanner, B.D.; Lee, X.H.; Chen, J.Y. Overview of ChinaFLUX and evaluation of its eddy covariance measurement. Agric. For. Meteorol. 2006, 137, 125–137. [Google Scholar] [CrossRef]
  19. Wang, H.S.; Jia, G.S.; Fu, C.B.; Feng, J.M.; Zhao, T.B.; Ma, Z.G. Deriving maximal light use efficiency from coordinated flux measurements and satellite data for regional gross primary production modeling. Remote Sens. Environ. 2010, 114, 2248–2258. [Google Scholar] [CrossRef]
  20. Li, X.; Cheng, G.D.; Liu, S.M.; Xiao, Q.; Ma, M.G.; Jin, R.; Che, T.; Liu, Q.H.; Wang, W.Z.; Qi, Y.; et al. Heihe Watershed Allied Telemetry Experimental Research (HiWATER): Scientific Objectives and Experimental Design. B Am. Meteorol. Soc. 2013, 94, 1145–1160. [Google Scholar] [CrossRef]
  21. Li, C.; He, H.; Liu, M.; Su, W.; Fu, Y.; Zhang, L.; Wen, X.; Yu, G. The design and application of CO2 flux data processing system at ChinaFLUX. Geo Inf. Sci. 2008, 10, 557–565. [Google Scholar]
  22. Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water-vapor transfer. Q. J. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
  23. Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of net ecosystem exchange measured with eddy covariance technique: Algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef] [Green Version]
  24. Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
  25. Schwalm, C.R.; Williams, C.A.; Schaefer, K.; Anderson, R.; Arain, M.A.; Baker, I.; Barr, A.; Black, T.A.; Chen, G.S.; Chen, J.M.; et al. A model-data intercomparison of CO2 exchange across North America: Results from the North American Carbon Program site synthesis. J. Geophys. Res. Biogeosci. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
  26. Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
  27. Vermote, E.; Vermeulen, A. MODIS Algorithm Technical Background Document, Atmospheric Correction Algorithm: Spectral Reflectances (MOD09); NASA Contract NAS5-96062; University of Maryland: College Park, MD, USA, 1999. [Google Scholar]
  28. Ma, M.G.; Veroustraete, F. Reconstructing pathfinder AVHRR land NDVI time-series data for the Northwest of China. Adv. Space Res. Ser. 2006, 37, 835–840. [Google Scholar] [CrossRef]
  29. Xiao, J.F.; Zhuang, Q.L.; Baldocchi, D.D.; Law, B.E.; Richardson, A.D.; Chen, J.Q.; Oren, R.; Starr, G.; Noormets, A.; Ma, S.Y.; et al. Estimation of net ecosystem carbon exchange for the conterminous United States by combining MODIS and AmeriFlux data. Agric. For. Meteorol. 2008, 148, 1827–1847. [Google Scholar] [CrossRef] [Green Version]
  30. Xiao, J.F.; Ollinger, S.V.; Frolking, S.; Hurtt, G.C.; Hollinger, D.Y.; Davis, K.J.; Pan, Y.D.; Zhang, X.Y.; Deng, F.; Chen, J.Q.; et al. Data-driven diagnostics of terrestrial carbon dynamics over North America. Agric. For. Meteorol. 2014, 197, 142–157. [Google Scholar] [CrossRef] [Green Version]
  31. Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
  32. FAO; IIASA/ISRIC/ISSCAS/JRC. Harmonized World Soil Database (Version 1.2); FAO: Rome, Italy; IIASA: Laxenburg, Austria, 2012. [Google Scholar]
  33. Carvalhais, N.; Forkel, M.; Khomik, M.; Bellarby, J.; Jung, M.; Migliavacca, M.; Mu, M.; Saatchi, S.; Santoro, M.; Thurner, M.; et al. Global covariation of carbon turnover times with climate in terrestrial ecosystems. Nature 2014, 514, 213–217. [Google Scholar] [CrossRef] [Green Version]
  34. Smallman, T.L.; Exbrayat, J.F.; Mencuccini, M.; Bloom, A.A.; Williams, M. Assimilation of repeated woody biomass observations constrains decadal ecosystem carbon cycle uncertainty in aggrading forests. J. Geophys. Res. Biogeosci. 2017, 122, 528–545. [Google Scholar] [CrossRef]
  35. Lloyd, J.; Taylor, J.A. On the temperature-dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
  36. Hu, Y.; Jiang, L.; Wang, S.; Zhang, Z.; Luo, C.; Bao, X.; Niu, H.; Xu, G.; Duan, J.; Zhu, X.; et al. The temperature sensitivity of ecosystem respiration to climate change in an alpine meadow on the Tibet plateau: A reciprocal translocation experiment. Agric. For. Meteorol. 2016, 216, 93–104. [Google Scholar] [CrossRef]
  37. Ge, R.; He, H.L.; Ren, X.L.; Zhang, L.; Li, P.; Zeng, N.; Yu, G.R.; Zhang, L.Y.; Yu, S.Y.; Zhang, F.W.; et al. A satellite-based model for simulating ecosystem respiration in the Tibetan and Inner Mongolian grasslands. Remote Sens. 2018, 10, 149. [Google Scholar] [CrossRef] [Green Version]
  38. Geng, Y.; Wang, Y.; Yang, K.; Wang, S.; Zeng, H.; Baumann, F.; Kuehn, P.; Scholten, T.; He, J.S. Soil respiration in Tibetan alpine grasslands: Belowground biomass and soil moisture, but not soil temperature, best explain the large-scale patterns. PLoS ONE 2012, 7, e34968. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  39. Janssens, I.A.; Lankreijer, H.; Matteucci, G.; Kowalski, A.S.; Buchmann, N.; Epron, D.; Pilegaard, K.; Kutsch, W.; Longdoz, B.; Grünwald, T.; et al. Productivity overshadows temperature in determining soil and ecosystem respiration across European forests. Glob. Chang. Biol. 2001, 7, 269–278. [Google Scholar] [CrossRef]
  40. Chen, S.T.; Huang, Y.; Zou, J.W.; Shen, Q.R.; Hu, Z.H.; Qin, Y.M.; Chen, H.S.; Pan, G.X. Modeling interannual variability of global soil respiration from climate and soil properties. Agric. For. Meteorol. 2010, 150, 590–605. [Google Scholar] [CrossRef]
  41. Kang, L.; Han, X.; Zhang, Z.; Sun, O.J. Grassland ecosystems in China: Review of current knowledge and research advancement. Philos. Trans. R. Soc. B 2007, 362, 997–1008. [Google Scholar] [CrossRef]
  42. Chen, Q.S.; Wang, Q.B.; Han, X.G.; Wan, S.Q.; Li, L.H. Temporal and spatial variability and controls of soil respiration in a temperate steppe in northern China. Glob. Biogeochem. Cycles 2010, 24. [Google Scholar] [CrossRef]
  43. Gao, M.; Piao, S.; Chen, A.; Yang, H.; Liu, Q.; Fu, Y.H.; Janssens, I.A. Divergent changes in the elevational gradient of vegetation activities over the last 30 years. Nat. Commun. 2019, 10, 2970. [Google Scholar] [CrossRef]
  44. Xiao, X.M.; Zhang, Q.Y.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Berrien, M.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sens. Environ. 2004, 91, 256–270. [Google Scholar] [CrossRef]
  45. Xiao, J.F.; Zhuang, Q.L.; Law, B.E.; Chen, J.Q.; Baldocchi, D.D.; Cook, D.R.; Oren, R.; Richardson, A.D.; Wharton, S.; Ma, S.Y.; et al. A continuous measure of gross primary production for the conterminous United States derived from MODIS and AmeriFlux data. Remote Sens. Environ. 2010, 114, 576–591. [Google Scholar] [CrossRef] [Green Version]
  46. Ren, X.L.; He, H.L.; Zhang, L.; Yu, G.R. Global radiation, photosynthetically active radiation, and the diffuse component dataset of China, 1981-2010. Earth Syst. Sci. Data 2018, 10, 1217–1226. [Google Scholar] [CrossRef] [Green Version]
  47. Myneni, R.B.; Dong, J.; Tucker, C.J.; Kaufmann, R.K.; Kauppi, P.E.; Liski, J.; Zhou, L.; Alexeyev, V.; Hughes, M.K. A large carbon sink in the woody biomass of Northern forests. Proc. Natl. Acad. Sci. USA 2001, 98, 14784–14789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  48. Gao, X.; Huete, A.R.; Ni, W.G.; Miura, T. Optical-biophysical relationships of vegetation spectra without background contamination. Remote Sens. Environ. 2000, 74, 609–620. [Google Scholar] [CrossRef]
  49. Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
  50. Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating different machine learning methods for upscaling evapotranspiration from flux towers to the gegional scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
  51. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
  52. Yang, F.H.; White, M.A.; Michaelis, A.R.; Ichii, K.; Hashimoto, H.; Votava, P.; Zhu, A.X.; Nemani, R.R. Prediction of continental-scale evapotranspiration by combining MODIS and AmeriFlux data through support vector machine. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3452–3461. [Google Scholar] [CrossRef]
  53. Yang, F.H.; Ichii, K.; White, M.A.; Hashimoto, H.; Michaelis, A.R.; Votava, P.; Zhu, A.X.; Huete, A.; Running, S.W.; Nemani, R.R. Developing a continental-scale measure of gross primary production by combining MODIS and AmeriFlux data through Support Vector Machine approach. Remote Sens. Environ. 2007, 110, 109–122. [Google Scholar] [CrossRef]
  54. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  55. Siewert, M.B. High-resolution digital mapping of soil organic carbon in permafrost terrain using machine learning: A case study in a sub-Arctic peatland environment. Biogeosciences 2018, 15, 1663–1682. [Google Scholar] [CrossRef] [Green Version]
  56. Zhang, Q.C.; Yang, L.T.; Chen, Z.K.; Li, P. A survey on deep learning for big data. Inf. Fusion 2018, 42, 146–157. [Google Scholar] [CrossRef]
  57. Ma, L.; Liu, Y.; Zhang, X.L.; Ye, Y.X.; Yin, G.F.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogram. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
  58. Lv, Y.S.; Duan, Y.J.; Kang, W.W.; Li, Z.X.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Trans. Syst. 2015, 16, 865–873. [Google Scholar] [CrossRef]
  59. Li, X.; Peng, L.; Hu, Y.; Shao, J.; Chi, T. Deep learning architecture for air quality predictions. Environ. Sci. Pollut. Res. Int. 2016, 23, 22408–22417. [Google Scholar] [CrossRef]
  60. Gehring, J.; Miao, Y.; Metze, F.; Waibel, A. Extracting deep bottleneck features using stacked auto-encoders. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 3377–3381. [Google Scholar]
  61. Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [Green Version]
  62. Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.Q.; et al. Global patterns of land-atmosphere fluxes of carbon dioxide, latent heat, and sensible heat derived from eddy covariance, satellite, and meteorological observations. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
  63. Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
  64. Were, K.; Bui, D.T.; Dick, O.B.; Singh, B.R. A comparative assessment of support vector regression, artificial neural networks, and random forests for predicting and mapping soil organic carbon stocks across an Afromontane landscape. Ecol. Indic. 2015, 52, 394–403. [Google Scholar] [CrossRef]
  65. von Buttlar, J.; Zscheischler, J.; Rammig, A.; Sippel, S.; Reichstein, M.; Knohl, A.; Jung, M.; Menzer, O.; Arain, M.A.; Buchmann, N.; et al. Impacts of droughts and extreme-temperature events on gross primary production and ecosystem respiration: A systematic assessment across ecosystems and climate zones. Biogeosciences 2018, 15, 1293–1318. [Google Scholar] [CrossRef] [Green Version]
  66. Gu, L.; Baldocchi, D.; Verma, S.B.; Black, T.A.; Vesala, T.; Falge, E.M.; Dowty, P.R. Advantages of diffuse radiation for terrestrial ecosystem productivity. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef] [Green Version]
  67. Liu, Z.L.; Peng, C.H.; Work, T.; Candau, J.N.; DesRochers, A.; Kneeshaw, D. Application of machine-learning methods in forest ecology: Recent progress and future challenges. Environ. Rev. 2018, 26, 339–350. [Google Scholar] [CrossRef] [Green Version]
  68. Sun, A.Y.; Scanlon, B.R. How can Big Data and machine learning benefit environment and water management: A survey of methods, applications, and future directions. Environ. Res. Lett. 2019, 14, 073001. [Google Scholar] [CrossRef]
  69. Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
  70. Li, T.W.; Shen, H.F.; Yuan, Q.Q.; Zhang, X.C.; Zhang, L.P. Estimating Ground-Level PM2.5 by Fusing Satellite and Station Observations: A Geo-Intelligent Deep Learning Approach. Geophys. Res. Lett. 2017, 44, 11985–11993. [Google Scholar] [CrossRef] [Green Version]
  71. Padarian, J.; Minasny, B.; McBratney, A.B. Using deep learning for digital soil mapping. Soil 2019, 5, 79–89. [Google Scholar] [CrossRef] [Green Version]
  72. Song, X.D.; Zhang, G.L.; Liu, F.; Li, D.C.; Zhao, Y.G.; Yang, J.L. Modeling spatio-temporal distribution of soil moisture by deep learning-based cellular automata model. J. Arid Land 2016, 8, 734–748. [Google Scholar] [CrossRef] [Green Version]
  73. Liu, S.Q.; Zhuang, Q.L.; He, Y.J.; Noormets, A.; Chen, J.Q.; Gu, L.H. Evaluating atmospheric CO2 effects on gross primary productivity and net ecosystem exchanges of terrestrial ecosystems in the conterminous United States using the AmeriFlux data and an artificial neural network approach. Agric. For. Meteorol. 2016, 220, 38–49. [Google Scholar] [CrossRef] [Green Version]
  74. Papale, D.; Black, T.A.; Carvalhais, N.; Cescatti, A.; Chen, J.Q.; Jung, M.; Kiely, G.; Lasslop, G.; Mahecha, M.D.; Margolis, H.; et al. Effect of spatial sampling from European flux towers for estimating carbon and water fluxes with artificial neural networks. J. Geophys. Res. Biogeosci. 2015, 120, 1941–1957. [Google Scholar] [CrossRef] [Green Version]
  75. Giri, C.; Zhu, Z.L.; Reed, B. A comparative analysis of the Global Land Cover 2000 and MODIS land cover data sets. Remote Sens. Environ. 2005, 94, 123–132. [Google Scholar] [CrossRef]
  76. Meng, B.P.; Gao, J.L.; Liang, T.G.; Cui, X.; Ge, J.; Yin, J.P.; Feng, Q.S.; Xie, H.J. Modeling of alpine grassland cover based on unmanned aerial vehicle technology and multi-factor methods: A case study in the east of Tibetan Plateau, China. Remote Sens. 2018, 10, 320. [Google Scholar] [CrossRef] [Green Version]
  77. Yang, Y.; Li, P.; Ding, J.; Zhao, X.; Ma, W.; Ji, C.; Fang, J. Increased topsoil carbon stock across China’s forests. Glob. Chang. Biol. 2014, 20, 2687–2696. [Google Scholar] [CrossRef] [PubMed]
  78. Gao, Y.N.; Yu, G.R.; Li, S.G.; Yan, H.M.; Zhu, X.J.; Wang, Q.F.; Shi, P.L.; Zhao, L.; Li, Y.N.; Zhang, F.W.; et al. A remote sensing model to estimate ecosystem respiration in Northern China and the Tibetan Plateau. Ecol. Model. 2015, 304, 34–43. [Google Scholar] [CrossRef]
  79. Valentini, R.; Matteucci, G.; Dolman, A.J.; Schulze, E.D.; Rebmann, C.; Moors, E.J.; Granier, A.; Gross, P.; Jensen, N.O.; Pilegaard, K.; et al. Respiration as the main determinant of carbon balance in European forests. Nature 2000, 404, 861–865. [Google Scholar] [CrossRef] [PubMed]
  80. Lin, X.W.; Zhang, Z.H.; Wang, S.P.; Hu, Y.G.; Xu, G.P.; Luo, C.Y.; Chang, X.F.; Duan, J.C.; Lin, Q.Y.; Xu, B.R.B.Y.; et al. Response of ecosystem respiration to warming and grazing during the growing seasons in the alpine meadow on the Tibetan plateau. Agric. For. Meteorol. 2011, 151, 792–802. [Google Scholar] [CrossRef]
  81. Kato, T.; Tang, Y.H.; Gu, S.; Cui, X.Y.; Hirota, M.; Du, M.Y.; Li, Y.N.; Zhao, Z.Q.; Oikawa, T. Carbon dioxide exchange between the atmosphere and an alpine meadow ecosystem on the Qinghai-Tibetan Plateau, China. Agric. For. Meteorol. 2004, 124, 121–134. [Google Scholar] [CrossRef]
  82. Davidson, E.A.; Belk, E.; Boone, R.D. Soil water content and temperature as independent or confounded factors controlling soil respiration in a temperate mixed hardwood forest. Glob. Chang. Biol. 1998, 4, 217–227. [Google Scholar] [CrossRef] [Green Version]
  83. Chen, J.; Luo, Y.Q.; Xia, J.Y.; Shi, Z.; Jiang, L.F.; Niu, S.L.; Zhou, X.H.; Cao, J.J. Differential responses of ecosystem respiration components to experimental warming in a meadow grassland on the Tibetan Plateau. Agric. For. Meteorol. 2016, 220, 21–29. [Google Scholar] [CrossRef] [Green Version]
  84. He, H.; Yu, G.; Zhang, L.; Sun, X.; Su, W. Simulating CO2 flux of three different ecosystems in ChinaFLUX based on artificial neural networks. Sci. China Ser. D Earth Sci. 2006, 36, 234–243. [Google Scholar] [CrossRef]
  85. Luo, Y.Q.; Ahlstrom, A.; Allison, S.D.; Batjes, N.H.; Brovkin, V.; Carvalhais, N.; Chappell, A.; Ciais, P.; Davidson, E.A.; Finzi, A.C.; et al. Toward more realistic projections of soil carbon dynamics by Earth system models. Glob. Biogeochem. Cycles 2016, 30, 40–56. [Google Scholar] [CrossRef]
Sustainability 12 02099 g001 550
Figure 1. Spatial distribution of the alpine and temperate grasslands in northern China. Triangles denote the 18 flux sites.
Figure 1. Spatial distribution of the alpine and temperate grasslands in northern China. Triangles denote the 18 flux sites.
Sustainability 12 02099 g001
Sustainability 12 02099 g002a 550Sustainability 12 02099 g002b 550
Figure 2. Performance of the back propagation artificial neural network (BP–ANN), support vector regression (SVR), random forests (RF), and stacked autoencoders (SAE) models (a) trained for all of northern China’s grasslands and (b) separately trained for the alpine and temperate grasslands. The black text in the figures represent the coefficient of determination (R2), root mean squared error (RMSE), and mean absolute error (MAE) of the whole northern China’s grasslands. The blue and green points and text in the figures represent the alpine and temperate grassland samples, respectively.
Figure 2. Performance of the back propagation artificial neural network (BP–ANN), support vector regression (SVR), random forests (RF), and stacked autoencoders (SAE) models (a) trained for all of northern China’s grasslands and (b) separately trained for the alpine and temperate grasslands. The black text in the figures represent the coefficient of determination (R2), root mean squared error (RMSE), and mean absolute error (MAE) of the whole northern China’s grasslands. The blue and green points and text in the figures represent the alpine and temperate grassland samples, respectively.
Sustainability 12 02099 g002aSustainability 12 02099 g002b
Sustainability 12 02099 g003 550
Figure 3. Relative importance of the environmental variables in predicting RE (a) in the alpine grasslands and (b) in the temperate grasslands. List of acronyms: back propagation artificial neural network (BP–ANN), support vector regression (SVR), random forests (RF), stacked autoencoders (SAE), enhanced vegetation index (EVI), soil organic carbon density (SOCD), land surface water index (LSWI), air temperature (Ta), photosynthetically active radiation (PAR), root mean squared error (RMSE).
Figure 3. Relative importance of the environmental variables in predicting RE (a) in the alpine grasslands and (b) in the temperate grasslands. List of acronyms: back propagation artificial neural network (BP–ANN), support vector regression (SVR), random forests (RF), stacked autoencoders (SAE), enhanced vegetation index (EVI), soil organic carbon density (SOCD), land surface water index (LSWI), air temperature (Ta), photosynthetically active radiation (PAR), root mean squared error (RMSE).
Sustainability 12 02099 g003
Table
Table 1. Main characteristics of the 18 flux sites in northern China’s grasslands.
Table 1. Main characteristics of the 18 flux sites in northern China’s grasslands.
SiteLatitude (°N)Longitude (°E)Elevation (m)YearGrassland Type
AR38.04100.4630332014Alpine Kobresia meadow
GL34.35100.5639802007, 2010–2011, 2013
HBKO37.61101.3131482003–2004
HBSH37.67101.3332932003–2012Alpine shrub meadow
DXSW30.4791.0642862009–2010Alpine swamp meadow
HBSW37.61101.3331602004–2008, 2010–2012
DXST30.5091.0643332004–2005, 2007, 2009–2010Alpine meadow steppe
NMC30.7790.9647302009
ZF28.3686.9542932009
HLBE49.06119.406282012Meadow steppe
TY44.57122.921512008–2009
DL42.05116.2813242010–2011Typical steppe
NMG43.53116.2812002004, 2007–2008, 2010–2011
XLHT44.13116.3211872010–2011
YZ35.95104.1319682008–2009
DS44.09113.579902008–2009Desert steppe
SZWQ41.80111.9014382012
XLS35.77104.0524812008
Table
Table 2. Comparison of the predictive performance of the different vegetation index combinations as input.
Table 2. Comparison of the predictive performance of the different vegetation index combinations as input.
R2RMSE (gC m−2 d−1)
BP–ANNSVRRFSAEBP–ANNSVRRFSAE
NDVI0.8310.8410.8370.8460.5150.5000.5060.493
EVI0.8350.8440.8380.8540.5090.4950.5050.479
EVI and NDVI0.8360.8460.8410.8580.5080.4920.5000.472
List of abbreviations and acronyms: coefficient of determination (R2), root mean squared error (RMSE), back propagation artificial neural network (BP–ANN), support vector regression (SVR), random forests (RF), stacked autoencoders (SAE), normalized difference vegetation index (NDVI), enhanced vegetation index (EVI).

Share and Cite

MDPI and ACS Style

Zhu, X.; He, H.; Ma, M.; Ren, X.; Zhang, L.; Zhang, F.; Li, Y.; Shi, P.; Chen, S.; Wang, Y.; et al. Estimating Ecosystem Respiration in the Grasslands of Northern China Using Machine Learning: Model Evaluation and Comparison. Sustainability 2020, 12, 2099. https://doi.org/10.3390/su12052099

AMA Style

Zhu X, He H, Ma M, Ren X, Zhang L, Zhang F, Li Y, Shi P, Chen S, Wang Y, et al. Estimating Ecosystem Respiration in the Grasslands of Northern China Using Machine Learning: Model Evaluation and Comparison. Sustainability. 2020; 12(5):2099. https://doi.org/10.3390/su12052099

Chicago/Turabian Style

Zhu, Xiaobo, Honglin He, Mingguo Ma, Xiaoli Ren, Li Zhang, Fawei Zhang, Yingnian Li, Peili Shi, Shiping Chen, Yanfen Wang, and et al. 2020. "Estimating Ecosystem Respiration in the Grasslands of Northern China Using Machine Learning: Model Evaluation and Comparison" Sustainability 12, no. 5: 2099. https://doi.org/10.3390/su12052099

APA Style

Zhu, X., He, H., Ma, M., Ren, X., Zhang, L., Zhang, F., Li, Y., Shi, P., Chen, S., Wang, Y., Xin, X., Ma, Y., Zhang, Y., Du, M., Ge, R., Zeng, N., Li, P., Niu, Z., Zhang, L., ... Gu, Q. (2020). Estimating Ecosystem Respiration in the Grasslands of Northern China Using Machine Learning: Model Evaluation and Comparison. Sustainability, 12(5), 2099. https://doi.org/10.3390/su12052099

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop