Daily Photovoltaic Power Generation Forecasting Model Based on Random Forest Algorithm for North China in Winter
Abstract
1. Introduction
- Topic: In this paper, a daily PV power generation forecasting model for North China in winter is proposed. The proposed forecasting model is based on the random forest algorithm and can obtain satisfactory forecasting results using small samples. The results of this study provide a reference to the sustainable development of PV generation in this area.
- Influence factor selection: The unique winter climatic characteristics of North China were considered. In consideration of the serious air pollution in winter, “PM2.5” is especially selected as one of the influence factors.
- Weather classification: To ensure the operation of the model, the weather classification analysis is used to fix the varied weather. By combining weather types with similar characteristics, the problem of balance between category and sample number was solved.
- Methodology: The application of RF for solar PV systems, as most of the previous researches are focused on trend extrapolation methods, artificial intelligence methods or support vector machines.
2. Influence Factors and Weather Classification
2.1. Influence Factor Selection
2.2. Weather Classification
3. RF Forecasting Model
3.1. RF Algorithm
- Select samples by Bootstrap method [35] and regard them as a training set.
- Grow an initial tree in the set.
- Calculate the best node split of the initial tree according to its features.
- Split the nodes until the samples belong to the same class.
- Aggregate all trees into a forest, and then consider the mean value of the results given by each tree as the final prediction of the forest.
- Number of estimators or the number of trees in the forest.
- Criterion index measures the quality of the split. Alternatives include the mean absolute error (MAE) or mean square error (MSE) criteria.
- Max features. A function is chosen to select the best number of features when searching for the best node. Three options are available: (1) original value, corresponding to the function auto, (2) square root of original value, corresponding to sqrt, and (3) the logarithm of original value, corresponding to log2.
3.2. Forecasting Process
3.3. Performance Evaluation Indicators
4. Model Application and Evaluation
4.1. Model Application
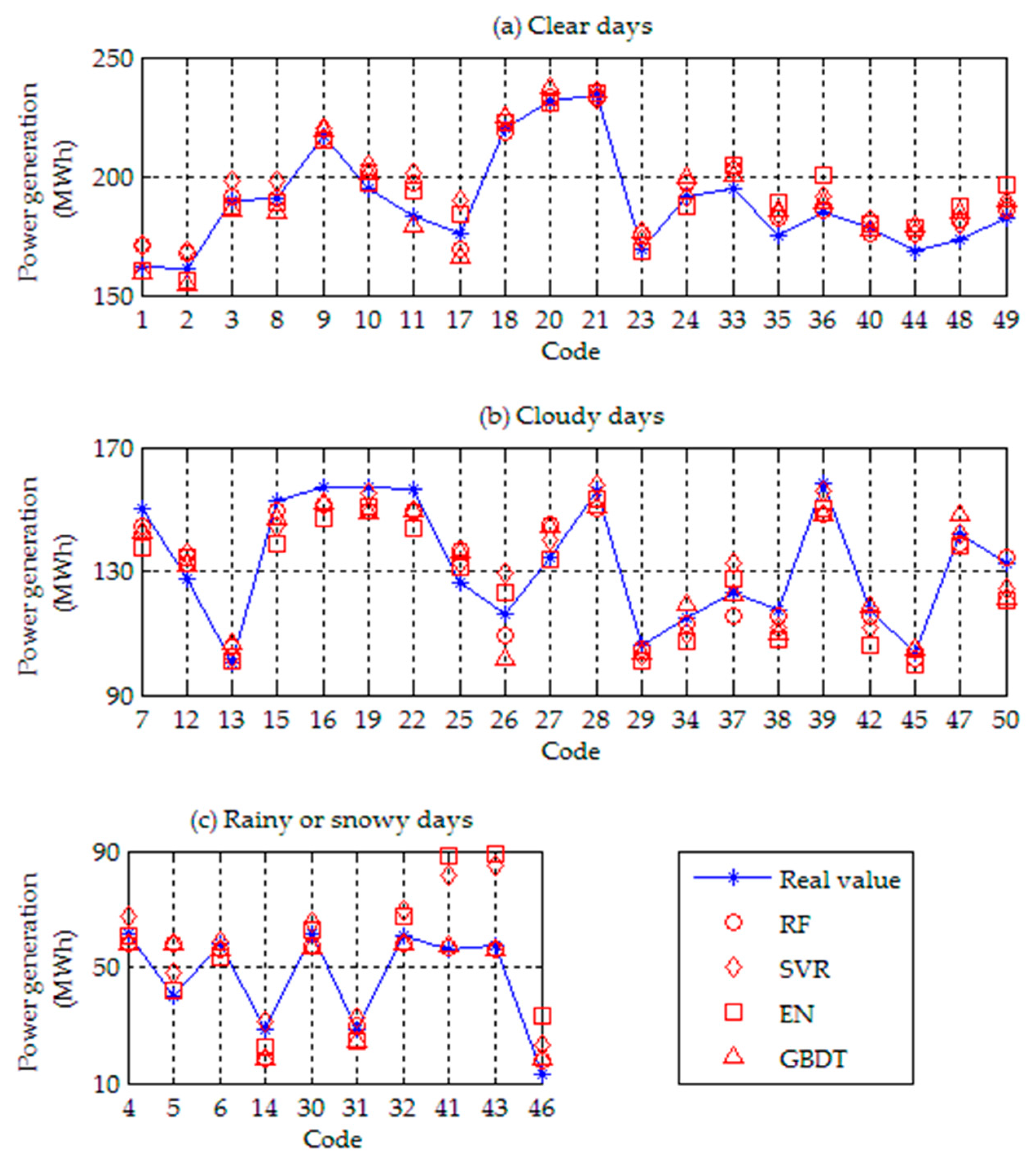
4.2. Forecasting Results Analysis
4.3. Performance Evaluation
5. Conclusion
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Date | Classification 1 | Temperature (°C) | Atmospheric Pressure (kPa) | Relative Humidity (%) | Wind Speed (m/s) | PM2.5 (μg/m3) | Radiant Exposure (0.01 MJ/m2) | Daily Power Generation (MWh) |
|---|---|---|---|---|---|---|---|---|
| Nov.2.2016 | Clear | 6.1 | 101.34 | 85 | 1.2 | 110 | 1251 | 233.72 |
| Nov.3.2016 | Clear | 7.4 | 100.53 | 90 | 1.8 | 129 | 1120 | 197.05 |
| Nov.5.2016 | Clear | 10.2 | 99.92 | 90 | 2.4 | 127 | 1164 | 208.24 |
| Nov.7.2016 | Cloudy | 7.3 | 101.56 | 91 | 1.3 | 109 | 424 | 76.66 |
| Nov.8.2016 | Clear | 6.1 | 102.11 | 77 | 1.4 | 81 | 1376 | 260.91 |
| Nov.9.2016 | Cloudy | 6.1 | 101.52 | 81 | 3 | 138 | 577 | 108.90 |
| Nov.10.2016 | Clear | 8.1 | 100.25 | 62 | 2.1 | 51 | 1185 | 231.03 |
| Nov.11.2016 | Clear | 8.2 | 99.91 | 65 | 1.4 | 112 | 1118 | 210.87 |
| Nov.12.2016 | Clear | 8 | 100.6 | 77 | 2 | 115 | 934 | 154.30 |
| Nov.14.2016 | Cloudy | 7 | 100.75 | 85 | 1.3 | 67 | 583 | 108.29 |
| Nov.15.2016 | Cloudy | 6 | 101.15 | 73 | 1.5 | 161 | 993 | 151.00 |
| Nov.16.2016 | Cloudy | 7 | 100.66 | 69 | 1.3 | 141 | 861 | 148.59 |
| Nov.17.2016 | Cloudy | 6.7 | 100.93 | 79 | 1.4 | 132 | 526 | 90.14 |
| Nov.19.2016 | Cloudy | 9 | 100.44 | 84 | 1.1 | 157 | 429 | 83.41 |
| Nov.20.2016 | R or S | 6.5 | 100.89 | 90 | 2 | 74 | 230 | 18.55 |
| Nov.21.2016 | R or S | 0.9 | 101.47 | 95 | 4.6 | 43 | 54 | 5.98 |
| Nov.23.2016 | Clear | −1.7 | 102.22 | 71 | 1.3 | 112 | 910 | 191.26 |
| Nov.24.2016 | Clear | −0.7 | 101.58 | 76 | 2 | 166 | 974 | 201.23 |
| Nov.25.2016 | Clear | 1.1 | 101.14 | 81 | 1.8 | 242 | 848 | 161.25 |
| Nov.26.2016 | Clear | 6.6 | 100.78 | 48 | 2.2 | 160 | 1048 | 210.21 |
| Nov.27.2016 | Clear | 4.6 | 101.28 | 58 | 2.2 | 108 | 998 | 199.54 |
| Nov.28.2016 | Cloudy | 2.7 | 101.85 | 62 | 1.4 | 143 | 796 | 147.18 |
| Nov.29.2016 | Cloudy | 3.5 | 101.9 | 70 | 1.4 | 220 | 313 | 50.09 |
| Nov.30.2016 | Clear | 4.8 | 101.18 | 72 | 1.4 | 222 | 1026 | 196.39 |
| Dec.1.2016 | Clear | 4.3 | 101.83 | 59 | 1.8 | 162 | 906 | 185.11 |
| Dec.2.2016 | Clear | 3.3 | 101.58 | 70 | 1.1 | 194 | 885 | 180.53 |
| Dec.3.2016 | Cloudy | 4.4 | 100.71 | 81 | 1.4 | 276 | 621 | 116.64 |
| Dec.4.2016 | Cloudy | 3.5 | 100.29 | 80 | 1.4 | 260 | 712 | 122.56 |
| Dec.5.2016 | Cloudy | 4.4 | 101.31 | 72 | 2.9 | 99 | 563 | 89.90 |
| Dec.6.2016 | Clear | 2.6 | 100.95 | 75 | 1.5 | 133 | 947 | 199.79 |
| Dec.7.2016 | Clear | 5.7 | 100.97 | 57 | 2 | 74 | 894 | 183.91 |
| Dec.8.2016 | Cloudy | 5.2 | 100.35 | 53 | 2.3 | 52 | 791 | 146.21 |
| Dec.10.2016 | Cloudy | −0.5 | 101.53 | 72 | 1.1 | 79 | 666 | 112.29 |
| Dec.12.2016 | R or S | 3.8 | 100.96 | 86 | 1.9 | 154 | 372 | 58.66 |
| Dec.15.2016 | Clear | −0.2 | 101.87 | 75 | 2 | 86 | 860 | 179.06 |
| Dec.16.2016 | Clear | 0 | 101.37 | 77 | 1.2 | 136 | 1091 | 199.70 |
| Dec.17.2016 | Cloudy | 0 | 100.78 | 81 | 1.1 | 235 | 677 | 120.06 |
| Dec.18.2016 | Cloudy | 0.1 | 101.04 | 83 | 0.8 | 225 | 635 | 105.17 |
| Dec.19.2016 | Cloudy | 0 | 101.14 | 87 | 1.4 | 212 | 645 | 114.64 |
| Dec.20.2016 | R or S | −1.7 | 101.45 | 95 | 1.2 | 185 | 376 | 53.67 |
| Dec.21.2016 | Cloudy | 2.8 | 101.22 | 96 | 1.1 | 217 | 212 | 30.85 |
| Dec.22.2016 | Clear | 5.7 | 100.97 | 61 | 2.6 | 45 | 1145 | 229.62 |
| Dec.23.2016 | Cloudy | 0.1 | 101.6 | 67 | 2 | 83 | 608 | 120.08 |
| Dec.24.2016 | Cloudy | −0.3 | 101.58 | 80 | 1.4 | 82 | 382 | 59.82 |
| Dec.25.2016 | R or S | 0.9 | 101.47 | 90 | 1.5 | 67 | 217 | 17.42 |
| Dec.27.2016 | Clear | −1.7 | 102.07 | 89 | 2.3 | 182 | 902 | 179.27 |
| Dec.28.2016 | Cloudy | −2.1 | 101.87 | 89 | 1.8 | 259 | 684 | 114.12 |
| Dec.29.2016 | Clear | −2.4 | 102.14 | 77 | 2.2 | 89 | 899 | 179.25 |
| Dec.30.2016 | Cloudy | −2 | 101.54 | 85 | 1.1 | 122 | 646 | 118.11 |
| Dec.31.2016 | Cloudy | −1.8 | 101.3 | 94 | 1.3 | 108 | 771 | 131.67 |
| Jan.1.2017 | R or S | −2.1 | 101.1 | 99 | 2.4 | 92 | 175 | 25.66 |
| Jan.2.2017 | Clear | −0.6 | 101.25 | 91 | 1.8 | 128 | 891 | 176.30 |
| Jan.3.2017 | Cloudy | −1.7 | 100.94 | 99 | 1.1 | 109 | 370 | 61.80 |
| Jan.4.2017 | Cloudy | −1.5 | 101.14 | 99 | 1.6 | 144 | 329 | 34.55 |
| Jan.5.2017 | R or S | 0.1 | 101.53 | 96 | 2.9 | 247 | 86 | 8.57 |
| Jan.6.2017 | R or S | 2.3 | 101.33 | 92 | 1.2 | 250 | 285 | 30.22 |
| Jan.7.2017 | R or S | 1.9 | 100.97 | 95 | 1.9 | 140 | 75 | 7.01 |
| Jan.8.2017 | Cloudy | 0.1 | 100.94 | 98 | 2.3 | 98 | 455 | 95.71 |
| Jan.9.2017 | Cloudy | 0.2 | 101.26 | 83 | 1.5 | 143 | 824 | 153.38 |
| Jan.10.2017 | Cloudy | −0.6 | 101.52 | 68 | 1.7 | 127 | 786 | 154.87 |
| Jan.11.2017 | Clear | 0.7 | 101.2 | 73 | 2.1 | 241 | 854 | 185.42 |
| Jan.12.2017 | Clear | 3.6 | 100.73 | 40 | 2.2 | 91 | 968 | 223.92 |
| Jan.13.2017 | Clear | 0.4 | 101.07 | 51 | 1.7 | 114 | 867 | 175.80 |
| Jan.14.2017 | Cloudy | −2.3 | 101.75 | 65 | 1.4 | 138 | 720 | 122.26 |
| Jan.15.2017 | Cloudy | −2.5 | 101.81 | 64 | 1.5 | 179 | 531 | 90.27 |
| Jan.16.2017 | Cloudy | −2.3 | 101.66 | 74 | 2.3 | 211 | 572 | 69.70 |
| Jan.17.2017 | Cloudy | −2.5 | 101.64 | 77 | 1.3 | 275 | 575 | 114.43 |
| Jan.18.2017 | R or S | −2.2 | 101.89 | 82 | 1.1 | 356 | 126 | 18.41 |
| Jan.19.2017 | Clear | −1.2 | 101.62 | 53 | 3.7 | 215 | 1186 | 229.56 |
| Jan.20.2017 | Clear | −4 | 102 | 38 | 2.8 | 116 | 1013 | 213.61 |
| Jan.21.2017 | Clear | −2.7 | 101.57 | 45 | 1.4 | 190 | 975 | 194.99 |
| Jan.22.2017 | Clear | −3.9 | 102.08 | 41 | 1.4 | 109 | 900 | 180.35 |
| Jan.23.2017 | Cloudy | −3.7 | 101.99 | 55 | 1.7 | 264 | 776 | 140.14 |
| Jan.24.2017 | Cloudy | −2.2 | 102.21 | 45 | 2 | 251 | 679 | 118.29 |
| Jan.25.2017 | Cloudy | −2.5 | 101.78 | 62 | 1.4 | 324 | 682 | 116.38 |
| Jan.26.2017 | Cloudy | 0.3 | 100.92 | 64 | 1.5 | 409 | 565 | 86.72 |
| Jan.28.2017 | Cloudy | 0.7 | 100.66 | 47 | 1.1 | 349 | 413 | 64.13 |
| Jan.29.2017 | Cloudy | −0.1 | 101.36 | 41 | 3 | 196 | 720 | 96.10 |
| Jan.30.2017 | Clear | −4.1 | 102.35 | 37 | 1.6 | 64 | 1080 | 226.64 |
| Jan.31.2017 | Cloudy | 0.2 | 101.53 | 31 | 1.6 | 139 | 798 | 146.80 |
| Nov.2.2017 | Clear | 13.2 | 100.31 | 68 | 1.9 | 119 | 1187 | 227.75 |
| Nov.5.2017 | Clear | 9.4 | 100.92 | 75 | 1.7 | 61 | 1119 | 202.59 |
| Nov.6.2017 | Clear | 10.2 | 100.44 | 80 | 0.7 | 151 | 1023 | 173.67 |
| Nov.7.2017 | Clear | 14.7 | 100.59 | 57 | 2.8 | 65 | 1248 | 245.59 |
| Nov.8.2017 | Clear | 10.9 | 101 | 56 | 2.5 | 94 | 918 | 157.07 |
| Nov.10.2017 | Clear | 12.3 | 101.09 | 26 | 2.7 | 20 | 1209 | 254.84 |
| Nov.11.2017 | Clear | 5.6 | 101.22 | 50 | 1.9 | 44 | 1185 | 239.73 |
| Nov.12.2017 | Cloudy | 5.8 | 100.36 | 66 | 1.2 | 100 | 605 | 73.47 |
| Nov.14.2017 | Clear | 4.6 | 101.07 | 38 | 1.4 | 38 | 1213 | 245.78 |
| Nov.15.2017 | Clear | 3.1 | 101.08 | 50 | 1.6 | 48 | 1168 | 224.78 |
| Nov.16.2017 | Clear | 3.3 | 100.75 | 52 | 1.2 | 95 | 844 | 176.55 |
| Nov.17.2017 | Cloudy | 4 | 101.16 | 48 | 2.3 | 71 | 832 | 151.65 |
| Nov.18.2017 | Clear | −0.5 | 102 | 37 | 1.9 | 57 | 1179 | 243.87 |
| Nov.19.2017 | Cloudy | −0.3 | 101.43 | 52 | 1.3 | 128 | 436 | 66.00 |
| Nov.20.2017 | Clear | 3.3 | 101.4 | 49 | 2.4 | 143 | 1113 | 213.70 |
| Nov.21.2017 | Clear | 5.6 | 100.78 | 57 | 2.6 | 104 | 1085 | 199.50 |
| Nov.22.2017 | Clear | 8.1 | 101.24 | 18 | 4.1 | 16 | 1194 | 232.54 |
| Nov.23.2017 | Clear | 3.1 | 101.17 | 39 | 1.3 | 60 | 1119 | 217.04 |
| Nov.24.2017 | Clear | 2.2 | 101.24 | 39 | 2.6 | 40 | 1078 | 216.00 |
| Nov.25.2017 | Clear | 5 | 100.55 | 42 | 3.1 | 68 | 1063 | 204.74 |
| Nov.26.2017 | Clear | 3 | 101.52 | 44 | 2.3 | 64 | 995 | 187.32 |
| Nov.27.2017 | Cloudy | 1.2 | 100.7 | 60 | 2 | 122 | 655 | 119.84 |
| Nov.28.2017 | Clear | 3.1 | 100.94 | 55 | 2.1 | 133 | 843 | 165.24 |
| Nov.29.2017 | Cloudy | −0.4 | 102.07 | 31 | 1.5 | 31 | 467 | 73.71 |
| Date | Classification 1 | Temperature (°C) | Atmospheric Pressure (kPa) | Relative Humidity (%) | Wind Speed (m/s) | PM2.5 (μg/m3) | Radiant Exposure (0.01 MJ/m2) | Daily Power Generation (MWh) |
|---|---|---|---|---|---|---|---|---|
| Nov.1.2018 | Clear | 10.4 | 101.36 | 64 | 1.6 | 120 | 834 | 162.03 |
| Nov.2.2018 | Clear | 11.1 | 101.15 | 69 | 1.9 | 131 | 822 | 160.79 |
| Nov.3.2018 | Clear | 12.4 | 100.79 | 65 | 2.9 | 76 | 995 | 189.85 |
| Nov.4.2018 | R or S | 11.9 | 100.92 | 75 | 3.1 | 164 | 471 | 61.23 |
| Nov.5.2018 | R or S | 7.9 | 101.69 | 78 | 2.3 | 35 | 354 | 40.19 |
| Nov.6.2018 | R or S | 6.5 | 101.83 | 72 | 1.1 | 43 | 425 | 57.88 |
| Nov.7.2018 | Cloudy | 7.8 | 101.44 | 58 | 1.6 | 51 | 781 | 149.91 |
| Nov.8.2018 | Clear | 9.4 | 100.44 | 66 | 2.9 | 63 | 993 | 190.32 |
| Nov.9.2018 | Clear | 8.5 | 100.54 | 67 | 1.9 | 88 | 1135 | 217.15 |
| Nov.11.2018 | Clear | 8.4 | 101.11 | 76 | 1.3 | 75 | 1045 | 194.27 |
| Nov.12.2018 | Clear | 7.4 | 100.9 | 82 | 1.6 | 149 | 1037 | 183.15 |
| Nov.13.2018 | Cloudy | 6.1 | 100.79 | 93 | 1.4 | 193 | 760 | 127.50 |
| Nov.14.2018 | Cloudy | 8.7 | 100.89 | 93 | 1.6 | 167 | 581 | 100.38 |
| Nov.15.2018 | R or S | 8.2 | 101.22 | 85 | 2.2 | 210 | 227 | 28.82 |
| Nov.16.2018 | Cloudy | 6.1 | 101.75 | 52 | 1.9 | 32 | 789 | 152.87 |
| Nov.17.2018 | Cloudy | 6.5 | 101.22 | 69 | 2.2 | 78 | 828 | 157.07 |
| Nov.18.2018 | Clear | 8.5 | 100.93 | 45 | 1.6 | 41 | 921 | 175.82 |
| Nov.19.2018 | Clear | 6 | 100.78 | 54 | 2 | 65 | 1154 | 220.41 |
| Nov.20.2018 | Cloudy | 6.1 | 100.87 | 63 | 1.9 | 141 | 859 | 157.33 |
| Nov.21.2018 | Clear | 6.6 | 101.4 | 51 | 2.6 | 88 | 1187 | 231.79 |
| Nov.22.2018 | Clear | 3.8 | 101.31 | 54 | 1.7 | 51 | 1195 | 233.79 |
| Nov.23.2018 | Cloudy | 4 | 100.71 | 57 | 2.5 | 150 | 828 | 156.58 |
| Nov.24.2018 | Clear | 3.7 | 101.09 | 68 | 1.9 | 153 | 854 | 168.88 |
| Nov.25.2018 | Clear | 5 | 100.78 | 67 | 1.7 | 179 | 970 | 191.59 |
| Nov.26.2018 | Cloudy | 4.4 | 100.61 | 80 | 2 | 353 | 769 | 126.30 |
| Nov.27.2018 | Cloudy | 9.4 | 101.14 | 39 | 2.1 | 118 | 722 | 115.87 |
| Nov.28.2018 | Cloudy | 5.1 | 101 | 45 | 2 | 127 | 779 | 134.24 |
| Nov.29.2018 | Cloudy | 3.5 | 101.49 | 62 | 1.6 | 106 | 867 | 155.80 |
| Nov.30.2018 | Cloudy | 2.9 | 101.21 | 80 | 1.1 | 133 | 581 | 106.35 |
| Dec.1.2018 | R or S | 3.2 | 101.17 | 85 | 1.5 | 167 | 454 | 61.33 |
| Dec.2.2018 | R or S | 5.2 | 100.42 | 94 | 1.2 | 194 | 236 | 28.82 |
| Dec.3.2018 | R or S | 5.2 | 100.95 | 73 | 1.7 | 151 | 483 | 60.99 |
| Dec.4.2018 | Clear | 2 | 101.64 | 42 | 2.1 | 55 | 1001 | 194.41 |
| Dec.6.2018 | Cloudy | −1.4 | 101.98 | 82 | 2.4 | 94 | 610 | 115.10 |
| Dec.7.2018 | Clear | −5.4 | 102.61 | 54 | 2 | 44 | 891 | 175.14 |
| Dec.8.2018 | Clear | −6.7 | 102.7 | 41 | 1.5 | 46 | 928 | 185.19 |
| Dec.9.2018 | Cloudy | −4.2 | 102.17 | 44 | 1.5 | 68 | 734 | 123.02 |
| Dec.10.2018 | Cloudy | −4.4 | 102.05 | 56 | 1.1 | 129 | 629 | 117.17 |
| Dec.13.2018 | Cloudy | −1.7 | 102.16 | 44 | 1.8 | 95 | 858 | 158.11 |
| Dec.18.2018 | Clear | 2.7 | 100.53 | 46 | 1.4 | 98 | 879 | 177.99 |
| Dec.20.2018 | R or S | 0.9 | 100.85 | 56 | 1.6 | 126 | 565 | 56.21 |
| Dec.21.2018 | Cloudy | 4.3 | 100.98 | 45 | 1.6 | 113 | 629 | 117.28 |
| Dec.22.2018 | R or S | 4.4 | 101.37 | 43 | 1.4 | 146 | 585 | 57.68 |
| Dec.24.2018 | Clear | −3.7 | 101.24 | 56 | 1.3 | 84 | 848 | 168.05 |
| Dec.25.2018 | Cloudy | −0.2 | 101.06 | 45 | 1.5 | 159 | 600 | 103.45 |
| Dec.27.2018 | R or S | −6.7 | 102.63 | 76 | 2.6 | 49 | 191 | 12.78 |
| Dec.28.2018 | Cloudy | −8.4 | 102.98 | 58 | 1.9 | 93 | 784 | 141.91 |
| Dec.29.2018 | Clear | −7.7 | 102.91 | 52 | 1.7 | 33 | 865 | 173.72 |
| Dec.30.2018 | Clear | −7.9 | 102.91 | 50 | 1.9 | 65 | 912 | 182.20 |
| Dec.31.2018 | Cloudy | −5.9 | 102.75 | 58 | 2 | 106 | 694 | 132.52 |
| Code | Date | Real Value | Forecasting Result 1 | ||
|---|---|---|---|---|---|
| SVR | EN | GBDT | |||
| 1 | Nov.01 | 162.03 | 171.01 | 160.33 | 159.45 |
| 2 | Nov.02 | 160.79 | 168.14 | 155.81 | 154.38 |
| 3 | Nov.03 | 189.85 | 198.04 | 187.03 | 185.39 |
| 4 | Nov.04 | 61.23 | 67.74 | 60.73 | 58.08 |
| 5 | Nov.05 | 40.19 | 47.84 | 41.92 | 57.86 |
| 6 | Nov.06 | 57.88 | 58.83 | 53.37 | 56.02 |
| 7 | Nov.07 | 149.91 | 142.84 | 137.60 | 142.75 |
| 8 | Nov.08 | 190.32 | 197.99 | 188.93 | 184.76 |
| 9 | Nov.09 | 217.15 | 220.35 | 214.86 | 218.87 |
| 10 | Nov.11 | 194.27 | 204.90 | 196.73 | 200.91 |
| 11 | Nov.12 | 183.15 | 201.07 | 193.50 | 178.80 |
| 12 | Nov.13 | 127.50 | 135.87 | 134.44 | 131.76 |
| 13 | Nov.14 | 100.38 | 102.53 | 101.12 | 106.45 |
| 14 | Nov.15 | 28.82 | 31.30 | 22.52 | 18.52 |
| 15 | Nov.16 | 152.87 | 144.70 | 138.88 | 147.24 |
| 16 | Nov.17 | 157.07 | 151.33 | 146.71 | 151.88 |
| 17 | Nov.18 | 175.82 | 189.52 | 183.71 | 165.61 |
| 18 | Nov.19 | 220.41 | 224.09 | 222.86 | 225.36 |
| 19 | Nov.20 | 157.33 | 155.34 | 150.72 | 148.71 |
| 20 | Nov.21 | 231.79 | 230.87 | 230.98 | 236.91 |
| 21 | Nov.22 | 233.79 | 232.78 | 234.45 | 235.77 |
| 22 | Nov.23 | 156.58 | 148.98 | 143.68 | 149.35 |
| 23 | Nov.24 | 168.88 | 173.14 | 168.10 | 176.83 |
| 24 | Nov.25 | 191.59 | 191.44 | 187.63 | 199.46 |
| 25 | Nov.26 | 126.30 | 132.78 | 131.55 | 136.04 |
| 26 | Nov.27 | 115.87 | 129.29 | 122.90 | 101.47 |
| 27 | Nov.28 | 134.24 | 139.97 | 134.02 | 144.52 |
| 28 | Nov.29 | 155.80 | 157.74 | 153.28 | 150.61 |
| 29 | Nov.30 | 106.35 | 102.99 | 100.75 | 103.71 |
| 30 | Dec.01 | 61.33 | 65.26 | 62.93 | 56.51 |
| 31 | Dec.02 | 28.82 | 32.39 | 24.32 | 24.50 |
| 32 | Dec.03 | 60.99 | 69.44 | 67.71 | 58.08 |
| 33 | Dec.04 | 194.41 | 202.75 | 204.88 | 200.24 |
| 34 | Dec.06 | 115.10 | 109.56 | 107.01 | 119.16 |
| 35 | Dec.07 | 175.14 | 183.88 | 188.88 | 185.28 |
| 36 | Dec.08 | 185.19 | 191.53 | 200.60 | 188.96 |
| 37 | Dec.09 | 123.02 | 132.78 | 127.39 | 122.34 |
| 38 | Dec.10 | 117.17 | 111.43 | 107.87 | 109.55 |
| 39 | Dec.13 | 158.11 | 155.71 | 150.20 | 148.44 |
| 40 | Dec.18 | 177.99 | 181.35 | 180.21 | 177.09 |
| 41 | Dec.20 | 56.21 | 81.67 | 88.52 | 57.07 |
| 42 | Dec.21 | 117.28 | 111.78 | 106.13 | 118.41 |
| 43 | Dec.22 | 57.68 | 85.06 | 89.13 | 56.02 |
| 44 | Dec.24 | 168.05 | 175.61 | 177.95 | 179.12 |
| 45 | Dec.25 | 103.45 | 104.88 | 99.89 | 105.10 |
| 46 | Dec.27 | 12.78 | 23.40 | 33.43 | 18.12 |
| 47 | Dec.28 | 141.91 | 141.93 | 138.20 | 148.29 |
| 48 | Dec.29 | 173.72 | 180.26 | 187.17 | 185.04 |
| 49 | Dec.30 | 182.20 | 187.36 | 196.01 | 189.67 |
| 50 | Dec.31 | 132.52 | 124.47 | 120.80 | 120.92 |
References
- Zhao, J. The Physical Geography of China (in Chinese), 3rd ed.; Higher Education Press: Beijing, China, 1995; p. 203. [Google Scholar]
- National Bureau of Statistics. China Statistical Yearbook 2019 (in Chinese); China Statistics Press: Beijing, China, 2019; pp. 34–35, 69–71.
- China Electricity Council. Annual Development Report of China’s Power Industry 2018 (in Chinese); China Electricity Council: Beijing, China, 2018. [Google Scholar]
- Pei, Z.; Wang, C.; He, Q.; Wang, Y.; Fan, G. Analysis and suggestions on renewable energy integration problems in China (in Chinese). Electr. Power 2016, 11, 1–7. [Google Scholar] [CrossRef]
- Ministry of Ecology and Environment. Bulletin of China’s Ecological Environment (in Chinese). Available online: http://www.mee.gov.cn/hjzl/zghjzkgb/lnzghjzkgb/201905/P020190619587632630618.pdf (accessed on 10 January 2020).
- Wang, L.; Li, P.; Yu, S.; Mehmood, K.; Li, Z. Predicted impact of thermal power generation emission control measures in the Beijing-Tianjin-Hebei region on air pollution over Beijing, China. Sci. Rep. 2018, 8, 934. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Sun, F.; Xu, Y. Does winter heating cause smog? Evidence from a city panel in North China (in Chinese). Nankai Econ. Stud. 2017, 4, 25–40. [Google Scholar] [CrossRef]
- China Meteorological Administration. Annual Bulletin of China’s Wind and Solar Energy Resources in 2018 (in Chinese); China Meteorological Administration: Beijing, China, 2019.
- National Energy Bureau of China. The 13th Five Year Plan for Solar Energy Development (in Chinese); National Energy Bureau of China: Beijing, China. Available online: http://zfxxgk.nea.gov.cn/auto87/201612/t20161216_2358.htm (accessed on 10 January 2020).
- Jin, D.; Olama, M.M.; Kuruganti, T.; Melin, A.M.; Djouadi, S.M.; Zhang, Y.; Xue, Y. Novel stochastic methods to predict short-term solar radiation and photovoltaic power. Renew. Energy 2020, 145, 333–346. [Google Scholar] [CrossRef]
- National Development and Reform Commission of the People’s Republic of China. National Energy Bureau of China. Clean Energy Consumption Plan 2018–2020 (in Chinese). Available online: http://zjb.nea.gov.cn/article/zygg/d1/201812/3022.htm (accessed on 10 January 2020).
- Kushwaha, V.; Pindoriya, N.M. A SARIMA-RVFL hybrid model assisted by wavelet decomposition for very short-term solar PV power generation forecast. Renew. Energy 2019, 140, 124–139. [Google Scholar] [CrossRef]
- Yang, M.; Meng, L. Short-term photovoltaic power dynamic weighted combination forecasting based on least squares method. Ieej Trans. Electr. Electron. Eng. 2019, 14, 1739–1746. [Google Scholar] [CrossRef]
- Alanazi, M.; Alanazi, A.; Khodaei, A. Long-term solar generation forecasting. In Proceedings of the IEEE/PES Transmission and Distribution Conference and Exposition (T&D), Dallas, TX, USA, 3–5 May 2016. [Google Scholar] [CrossRef]
- Ostrometzky, J.; Bernstein, A.; Zussman, G. Irradiance field reconstruction from partial observability of solar radiation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1698–1702. [Google Scholar] [CrossRef]
- Larson, D.P.; Nonnenmacher, L.; Coimbra, C.F.M. Day-ahead forecasting of solar power output from photovoltaic plants in the American Southwest. Renew. Energy 2016, 91, 11–20. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, F.; Zhang, C.; Ge, L.; Yuan, X. Photovoltaic power generation short-term power forecasting based on adaptive fuzzy time sequence method (in Chinese). J. Nanjing Inst. Technol. (Nat. Sci. Ed.) 2014, 1, 6–13. [Google Scholar] [CrossRef]
- Meng, M.; Niu, D.; Shang, W. A small-sample hybrid model for forecasting energy-related CO2 emissions. Energy 2014, 64, 673–677. [Google Scholar] [CrossRef]
- Chaouachi, A.; Kamel, R.M.; Nagasaka, K. Neural network ensemble-based solar power generation short-term forecasting. J. Adv. Comput. Intell. Intell. Inform. 2010, 14, 69–75. [Google Scholar] [CrossRef]
- Yang, Z.; Cao, Y.; Xiu, J. Power generation forecasting model for photovoltaic array based on generic algorithm and BP neural network. In Proceedings of the 2014 IEEE 3rd International Conference on Cloud Computing and Intelligence Systems, Shenzhen, China, 27–29 November 2014. [Google Scholar] [CrossRef]
- Behrens, C.; Pierdzioch, C.; Risse, M. Testing the optimality of inflation forecasts under flexible loss with random forests. Econ. Model. 2018, 72, 270–277. [Google Scholar] [CrossRef]
- Lei, C.; Deng, J.; Cao, K.; Ma, L.; Xiao, Y.; Ren, L. A random forest approach for predicting coal spontaneous combustion. Fuel 2018, 223, 63–73. [Google Scholar] [CrossRef]
- Huang, J.; Troccoli, A.; Coppin, P. An analytical comparison of four approaches to modelling the daily variability of solar irradiance using meteorological records. Renew. Energy 2014, 72, 195–202. [Google Scholar] [CrossRef]
- Liu, J.; Cao, M.; Gao, Z.; Xu, K. A solar radiation prediction model based on random forest (in Chinese). Control. Eng. China 2017, 24, 2472–2477. [Google Scholar] [CrossRef]
- Ahmad, M.W.; Mourshed, M.; Rezgui, Y. Tree-based ensemble methods for predicting PV power generation and their comparison with support vector regression. Energy 2018, 164, 465–474. [Google Scholar] [CrossRef]
- Mohammed, A.A.; Yaqub, W.; Aung, Z. Probabilistic Forecasting of Solar Power: An Ensemble Learning Approach. Smart Innovation, Systems and Technologies; Neves-Silva, R., Jain, L., Howlett, R., Eds.; Springer: Cham, Switzerland, 2015; Volume 39, pp. 449–458. ISBN 978-3-319-19856-9. [Google Scholar]
- Zamo, M.; Mestre, O.; Arbogast, P.; Pannekoucke, O. A benchmark of statistical regression methods for short-term forecasting of photovoltaic electricity production, part I: Deterministic forecast of hourly production. Sol. Energy 2014, 105, 792–803. [Google Scholar] [CrossRef]
- Kim, S.G.; Jung, J.Y.; Sim, M.K. A two-step approach to solar power generation prediction based on weather data using machine learning. Sustainability 2019, 11, 1501. [Google Scholar] [CrossRef]
- Chernokulsky, A.; Mokhov, I.I.; Nikitina, N. Winter cloudiness variability over Northern Eurasia related to the Siberian High during 1966–2010. Environ. Res. Lett. 2013, 8, 045012. [Google Scholar] [CrossRef]
- Chang, C.; Lu, M. Intraseasonal predictability of Siberian High and East Asian Winter Monsoon and Its Interdecadal Variability (in Chinese). J. Clim. 2012, 25, 1773–1778. [Google Scholar] [CrossRef]
- Ren, J.; Chen, T.; Xu, Z.; Wu, C.; Zhao, C. Mechanism analysis and experimental study on the influence of haze on photovoltaic power generation (in Chinese). Res. Explor. Lab. 2019, 38, 42–46. [Google Scholar] [CrossRef]
- China Meteorological Administration. Public Meteorological Service—Weather Graphic Symbols (in Chinese); China Meteorological Administration: Beijing, China, 2017.
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Jiang, R.; Tang, W.; Wu, X.; Fu, W. A random forest approach to the detection of epistatic interactions in case-control studies. BMC Bioinform. 2009, 10, S65. [Google Scholar] [CrossRef]
- Feng, W.; Dauphin, G.; Huang, W.; Quan, Y.; Liao, W. New margin-based subsampling iterative technique in modified random forests for classification. Knowl. Based Syst. 2019, 182, 104845. [Google Scholar] [CrossRef]
- Scikit-learn, Random Forest Regressor. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestRegressor.html (accessed on 2 December 2019).
- Paulescu, M.; Paulescu, E. Short-term forecasting of solar irradiance. Renew. Energy 2019, 143, 985–994. [Google Scholar] [CrossRef]
- Zarzo, M.; Martí, P. Modeling the variability of solar radiation data among weather stations by means of principal components analysis. Appl. Energy 2011, 88, 2775–2784. [Google Scholar] [CrossRef]
- Cui, Y.; Sun, Y.; Chang, Z. A review of short-term solar photovoltaic power generation prediction methods (in Chinese). Resour. Sci. 2013, 35, 1474–1481. [Google Scholar]

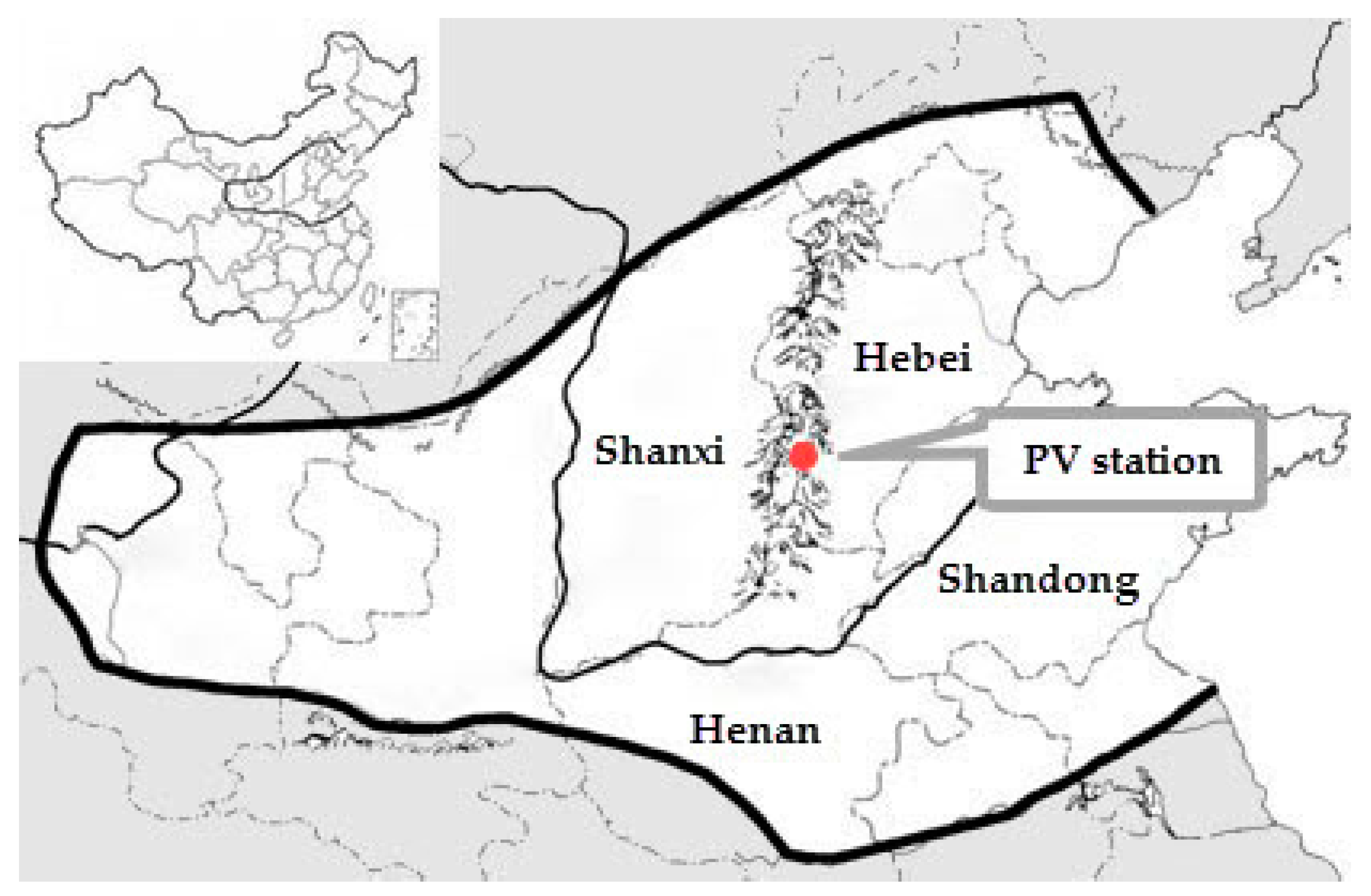

| Data Set | Indicator | Range |
|---|---|---|
| Training samples | Temperature (°C) | −4.1–14.7 |
| Atmospheric pressure (kPa) | 99.91–102.35 | |
| Relative humidity (%) | 18–99 | |
| Wind speed (m/s) | 0.7–4.6 | |
| PM2.5 (μg/m3) | 16–409.15 | |
| Total solar radiation (0.01 MJ/m2) 1 | 54–1376 | |
| Testing samples | Temperature (°C) | −8.4–12.4 |
| Atmospheric pressure (kPa) | 100.42–102.98 | |
| Relative humidity (%) | 39–94 | |
| Wind speed (m/s) | 1.1–3.1 | |
| PM2.5 (μg/m3) | 31.67–353.33 | |
| Total solar radiation (0.01 MJ/m2) 1 | 191–1195 |
| Weather Classification | N Estimators | Criterion | Max Features |
|---|---|---|---|
| Clear days | 900 | MAE | auto |
| Cloudy days | 800 | MAE | auto |
| Rainy or snowy days | 500 | MSE | auto |
| Code | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Date | Nov.1 | Nov.2 | Nov.3 | Nov.4 | Nov.5 | Nov.6 | Nov.7 | Nov.8 | Nov.9 |
| Classification 1 | Clear | Clear | Clear | R or S | R or S | R or S | Cloudy | Clear | Clear |
| Real value 2 | 162.03 | 160.79 | 189.85 | 61.23 | 40.19 | 57.88 | 149.91 | 190.32 | 217.15 |
| Forecasting result 2 | 170.98 | 167.27 | 191.68 | 57.86 | 57.91 | 56.21 | 144.53 | 190.85 | 215.87 |
| Code | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| Date | Nov.11 | Nov.12 | Nov.13 | Nov.14 | Nov.15 | Nov.16 | Nov.17 | Nov.18 | Nov.19 |
| Classification 1 | Clear | Clear | Cloudy | Cloudy | R or S | Cloudy | Cloudy | Clear | Clear |
| Real value 2 | 194.27 | 183.15 | 127.50 | 100.38 | 28.82 | 152.87 | 157.07 | 175.82 | 220.41 |
| Forecasting result 2 | 202.29 | 197.10 | 132.65 | 105.59 | 18.53 | 149.32 | 151.11 | 169.59 | 218.26 |
| Code | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| Date | Nov.20 | Nov.21 | Nov.22 | Nov.23 | Nov.24 | Nov.25 | Nov.26 | Nov.27 | Nov.28 |
| Classification 1 | Cloudy | Clear | Clear | Cloudy | Clear | Clear | Cloudy | Cloudy | Cloudy |
| Real value 2 | 157.33 | 231.79 | 233.79 | 156.58 | 168.88 | 191.59 | 126.30 | 115.87 | 134.24 |
| Forecasting result 2 | 149.50 | 233.37 | 233.30 | 149.43 | 175.86 | 197.06 | 136.88 | 109.43 | 144.84 |
| Code | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| Date | Nov.29 | Nov.30 | Dec.1 | Dec.2 | Dec.3 | Dec.4 | Dec.6 | Dec.7 | Dec.8 |
| Classification 1 | Cloudy | Cloudy | R or S | R or S | R or S | Clear | Cloudy | Clear | Clear |
| Real value 2 | 155.80 | 106.35 | 61.33 | 28.82 | 60.99 | 194.41 | 115.10 | 175.14 | 185.19 |
| Forecasting result 2 | 150.18 | 104.67 | 57.06 | 29.50 | 57.86 | 202.94 | 113.08 | 182.08 | 185.39 |
| Code | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 |
| Date | Dec.9 | Dec.10 | Dec.13 | Dec.18 | Dec.20 | Dec.21 | Dec.22 | Dec.24 | Dec.25 |
| Classification 1 | Cloudy | Cloudy | Cloudy | Clear | R or S | Cloudy | R or S | Clear | Cloudy |
| Real value 2 | 123.02 | 117.17 | 158.11 | 177.99 | 56.21 | 117.28 | 57.68 | 168.05 | 103.45 |
| Forecasting result 2 | 115.28 | 115.71 | 148.22 | 175.68 | 56.99 | 115.22 | 56.21 | 175.99 | 101.67 |
| Code | 46 | 47 | 48 | 49 | 50 | ||||
| Date | Dec.27 | Dec.28 | Dec.29 | Dec.30 | Dec.31 | ||||
| Classification 1 | R or S | Cloudy | Clear | Clear | Cloudy | ||||
| Real value 2 | 12.78 | 141.91 | 173.72 | 182.20 | 132.52 | ||||
| Forecasting result 2 | 17.42 | 139.03 | 181.70 | 185.84 | 134.14 |
| Weather | Algorithm | MAE (MWh) | MAPE (%) | RMSE(MWh) | EV |
|---|---|---|---|---|---|
| Clear | RF | 5.07 | 2.83 | 6.23 | 0.95 |
| SVR | 6.69 | 3.69 | 7.91 | 0.95 | |
| EN | 6.08 | 3.36 | 7.91 | 0.90 | |
| GBDT | 6.02 | 3.30 | 6.73 | 0.91 | |
| Cloudy | RF | 5.23 | 3.89 | 6.02 | 0.91 |
| SVR | 5.52 | 4.26 | 6.39 | 0.89 | |
| EN | 7.21 | 5.39 | 8.22 | 0.88 | |
| GBDT | 6.46 | 4.87 | 7.35 | 0.87 | |
| Rainy or snowy | RF | 4.80 | 14.29 | 6.98 | 0.83 |
| SVR | 9.70 | 24.84 | 13.11 | 0.72 | |
| EN | 11.03 | 33.76 | 16.10 | 0.30 | |
| GBDT | 5.29 | 16.19 | 7.17 | 0.82 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, M.; Song, C. Daily Photovoltaic Power Generation Forecasting Model Based on Random Forest Algorithm for North China in Winter. Sustainability 2020, 12, 2247. https://doi.org/10.3390/su12062247
Meng M, Song C. Daily Photovoltaic Power Generation Forecasting Model Based on Random Forest Algorithm for North China in Winter. Sustainability. 2020; 12(6):2247. https://doi.org/10.3390/su12062247
Chicago/Turabian StyleMeng, Ming, and Chenge Song. 2020. "Daily Photovoltaic Power Generation Forecasting Model Based on Random Forest Algorithm for North China in Winter" Sustainability 12, no. 6: 2247. https://doi.org/10.3390/su12062247
APA StyleMeng, M., & Song, C. (2020). Daily Photovoltaic Power Generation Forecasting Model Based on Random Forest Algorithm for North China in Winter. Sustainability, 12(6), 2247. https://doi.org/10.3390/su12062247





