An Optimization Management Model for Countries with Mutually Competitive Regions
Abstract
:1. Introduction
2. The Multi-Competitive-Region Model
2.1. Decomposed Model
2.2. The Game Model
2.3. Numerical Algorithm
2.3.1. Numerical Algorithm for the Multi-Competitive-Region Model
2.3.2. Numerical Algorithm for the Multi-Regional Game Model
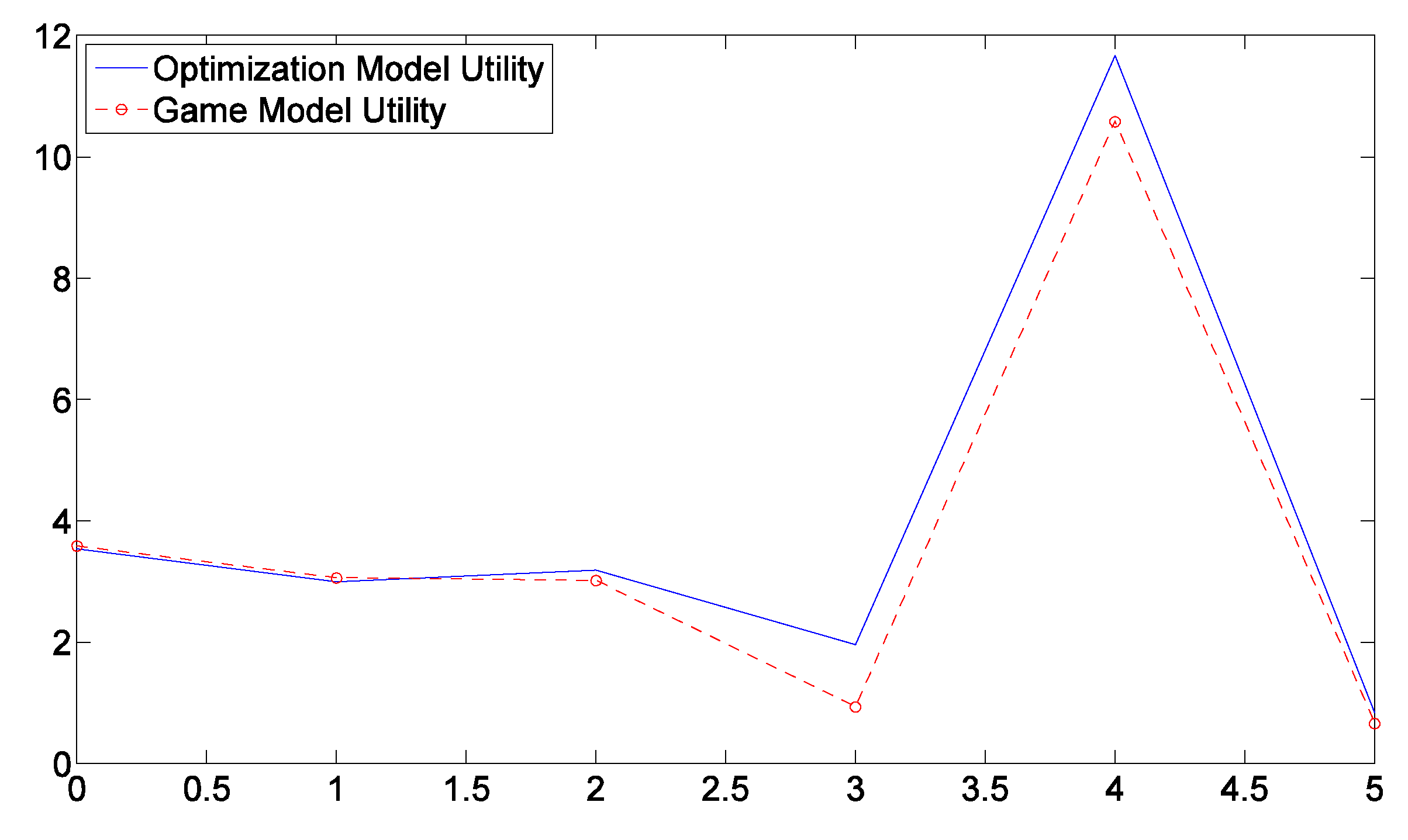
3. Model Experiments
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nash, J. Non-Cooperative Games. Ann. Math. 1951, 54, 286–295. [Google Scholar] [CrossRef]
- Gale, D.; Shapley, L.S. College admissions and the stability of marriage. Am. Math. Mon. 1962, 69, 9–15. [Google Scholar] [CrossRef]
- Nordhaus, W.D. The Cost of Slowing Climate Change: A Survey. Energy J. 1991, 12, 37–66. [Google Scholar] [CrossRef]
- Nordhaus, W.D. Managing the Global Commons: The Economics of Climate Change; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Zhang, A.L.; Zheng, H.; He, J.K. Economy, resource, environment model for the Chinese situation system. J. Tsinghua Univ. Sci. Technol. 2002, 42, 1616–1620. (In Chinese) [Google Scholar]
- Forster, B.A. Optimal Resource Use in a Polluted Environment. J. Environ. Econ. Manag. 1980, 7, 321–333. [Google Scholar] [CrossRef]
- Chiang, A.C. Elements of Dynamic of Optimization; Mc-Graw Hill Inc.: New York, NY, USA, 1992. [Google Scholar]
- Zhong, X.H.; Li, Z.N. A macroeconomic model on climate change (In Chinese). Syst. Eng. Theory Pract. 2002, 3, 20–25. [Google Scholar]
- Yang, Y.H.; Zhu, D.J.; Wang, C.; Song, J. The relations between resource consumption and environment from economic view. Resour. Environ. Eng. 2007, 21, 71–74. [Google Scholar]
- Aaheim, A. The determination of optimal climate policy. Ecol. Econ. 2010, 69, 562–568. [Google Scholar] [CrossRef]
- Leimbach, M.; Eisenack, K. A trade algorithm for multi-regional models subject to spillover externalities. Comput. Econ. 2009, 33, 107–130. [Google Scholar] [CrossRef]
- Li, P.; Zhong, W.Z. Optimization Macroeconomic Model on Energy resource development in Multi-regional Country. Chin. J. Eng. Math. 2012, 29, 317–324. (In Chinese) [Google Scholar]
- Li, P. Pricing weather derivatives with partial differential equations of the Ornstein-Uhlenbeck process. Comput. Math. Appl. 2018, 75, 1044–1059. [Google Scholar] [CrossRef]
- Chevé, M. Irreversibility of pollution accumulation. Environ. Resour. Econ. 2000, 16, 93–104. [Google Scholar] [CrossRef]
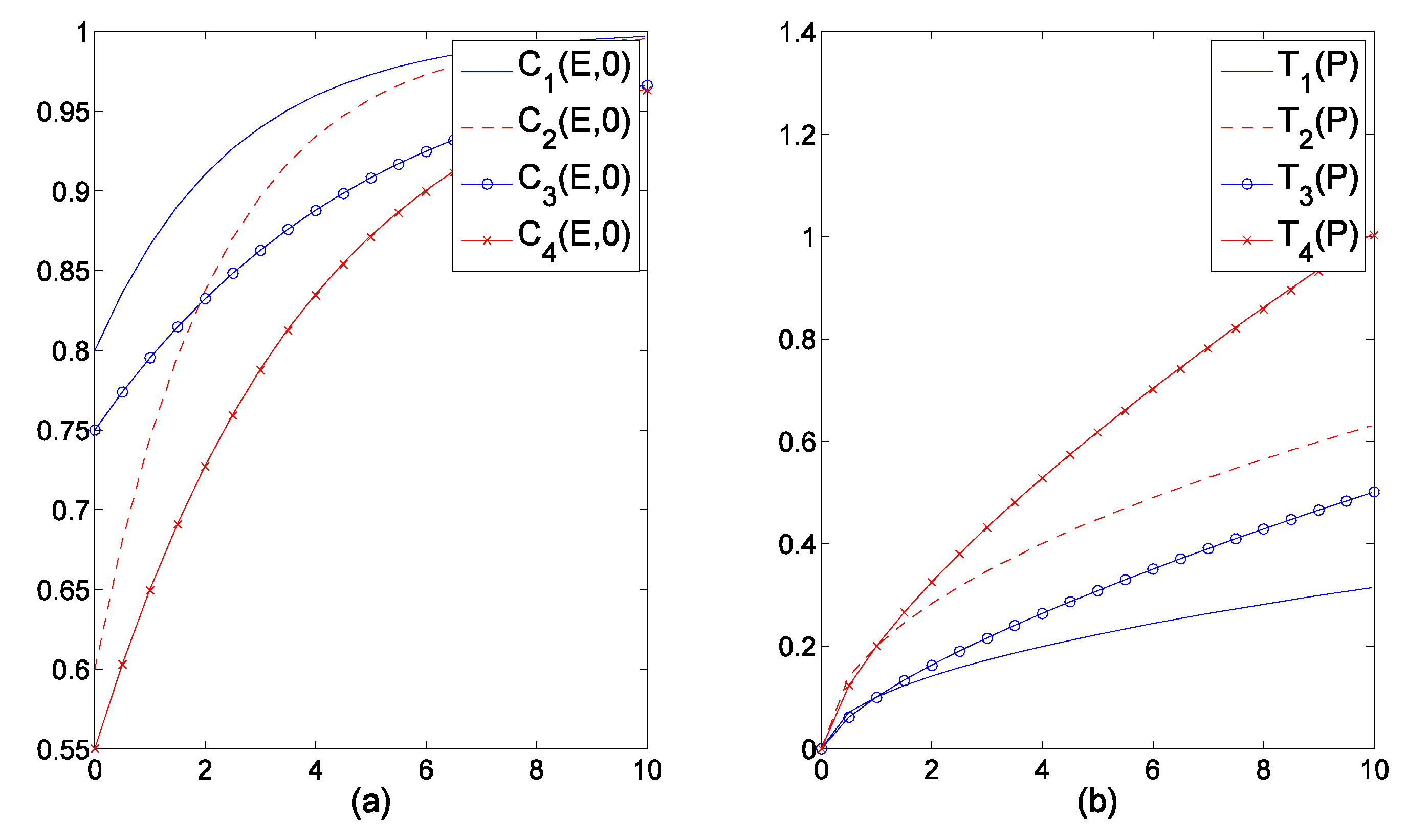
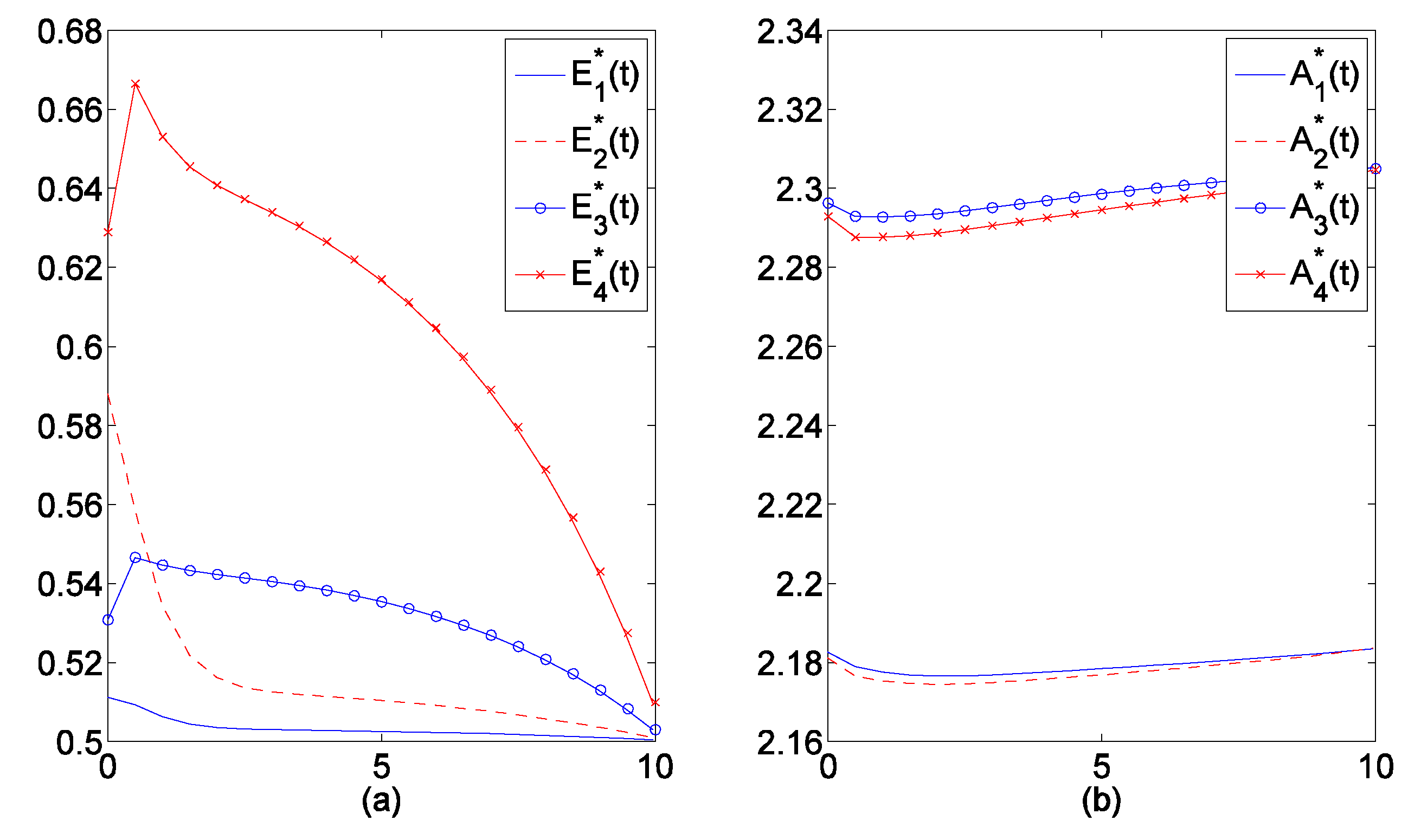
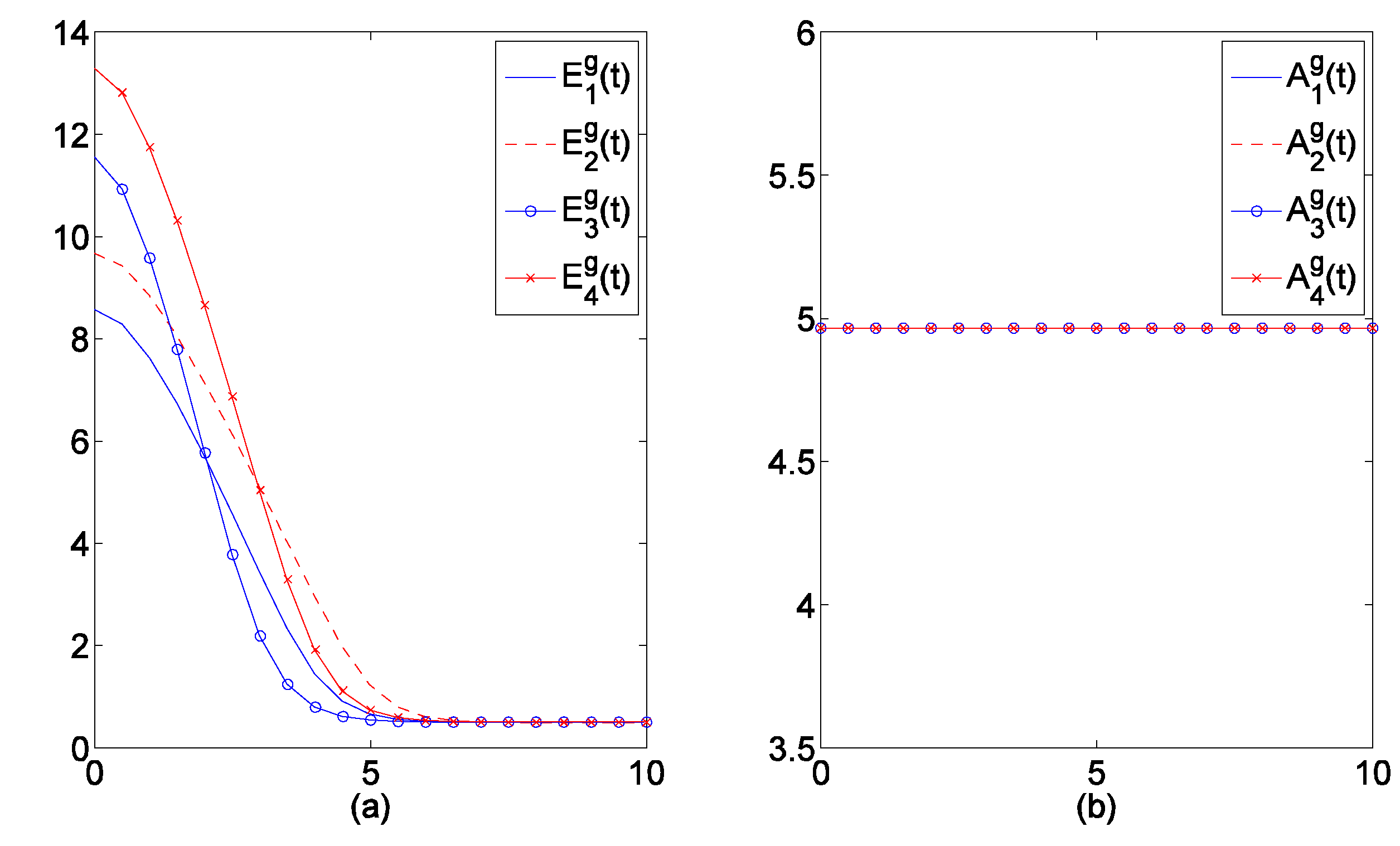
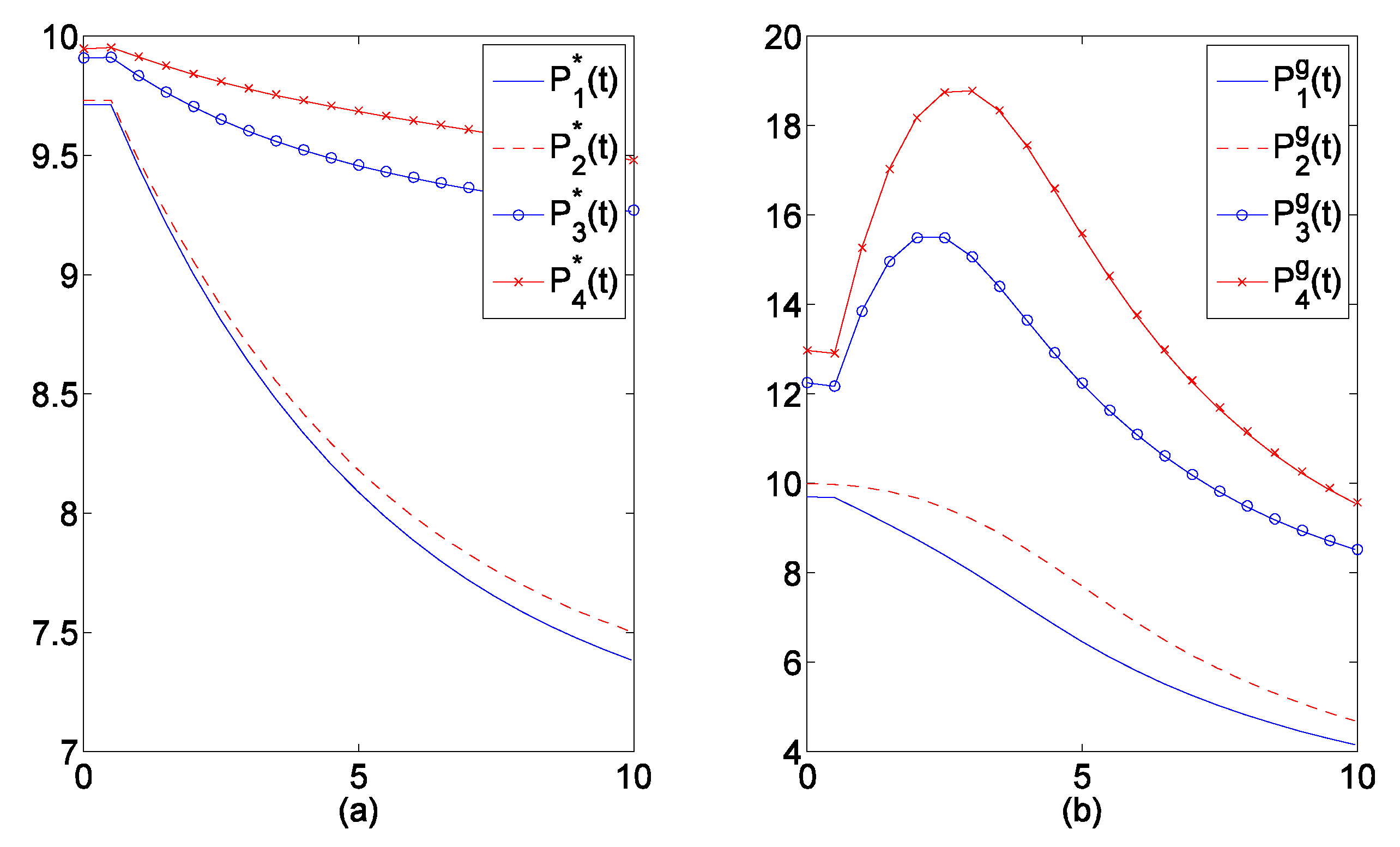
| District | Part 1 | Part 2 | Part 3 | Part 4 | Linear Sum | Total Utility | |
|---|---|---|---|---|---|---|---|
| Model | |||||||
| The Multi-Competitive-Region Model | 35.3412 | 29.9111 | 31.8633 | 19.5866 | 116.7022 | 0.8393 | |
| The Game Model | 35.8356 | 30.5493 | 30.1154 | 9.2892 | 105.7894 | 0.6571 | |
| Difference between the two models | −0.4944 | −0.6382 | 1.7479 | 10.2974 | 10.9128 | 0.1822 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Zhong, W. An Optimization Management Model for Countries with Mutually Competitive Regions. Sustainability 2020, 12, 2326. https://doi.org/10.3390/su12062326
Li P, Zhong W. An Optimization Management Model for Countries with Mutually Competitive Regions. Sustainability. 2020; 12(6):2326. https://doi.org/10.3390/su12062326
Chicago/Turabian StyleLi, Peng, and Weizhou Zhong. 2020. "An Optimization Management Model for Countries with Mutually Competitive Regions" Sustainability 12, no. 6: 2326. https://doi.org/10.3390/su12062326
APA StyleLi, P., & Zhong, W. (2020). An Optimization Management Model for Countries with Mutually Competitive Regions. Sustainability, 12(6), 2326. https://doi.org/10.3390/su12062326




