Investigating a Serious Challenge in the Sustainable Development Process: Analysis of Confirmed cases of COVID-19 (New Type of Coronavirus) Through a Binary Classification Using Artificial Intelligence and Regression Analysis
Abstract
:1. Introduction
2. Materials and Methods
- The possible correlations among the trends of confirmed cases in different case studies were investigated, and then a binary classification model was constructed to predict and classify using the group method of data handling (GMDH) algorithm based upon some critical factors; maximum, minimum, and average temperature, the density of a city, relative humidity, and wind speed were considered as the input dataset and the number of confirmed cases was selected as the output dataset for 30 days.
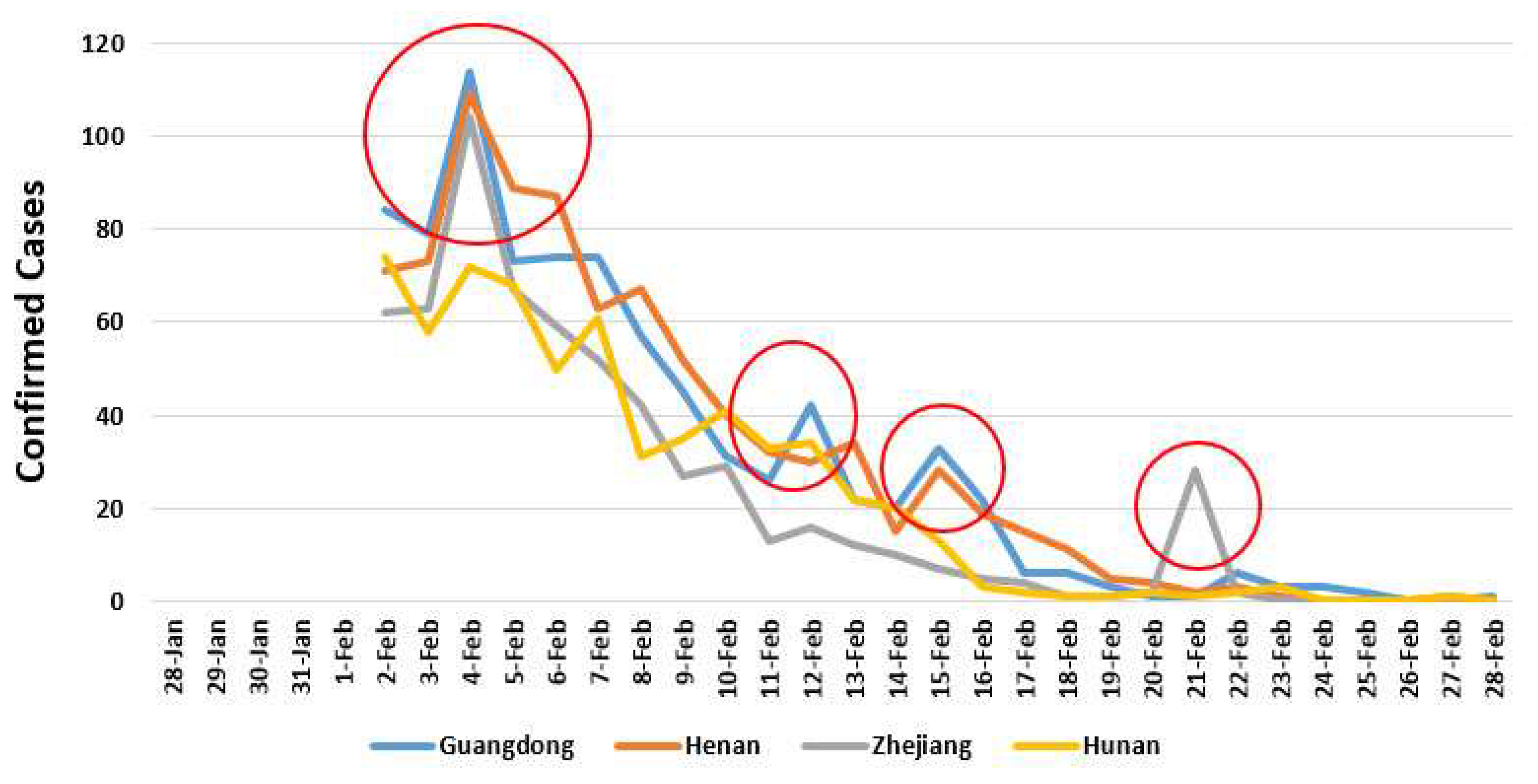
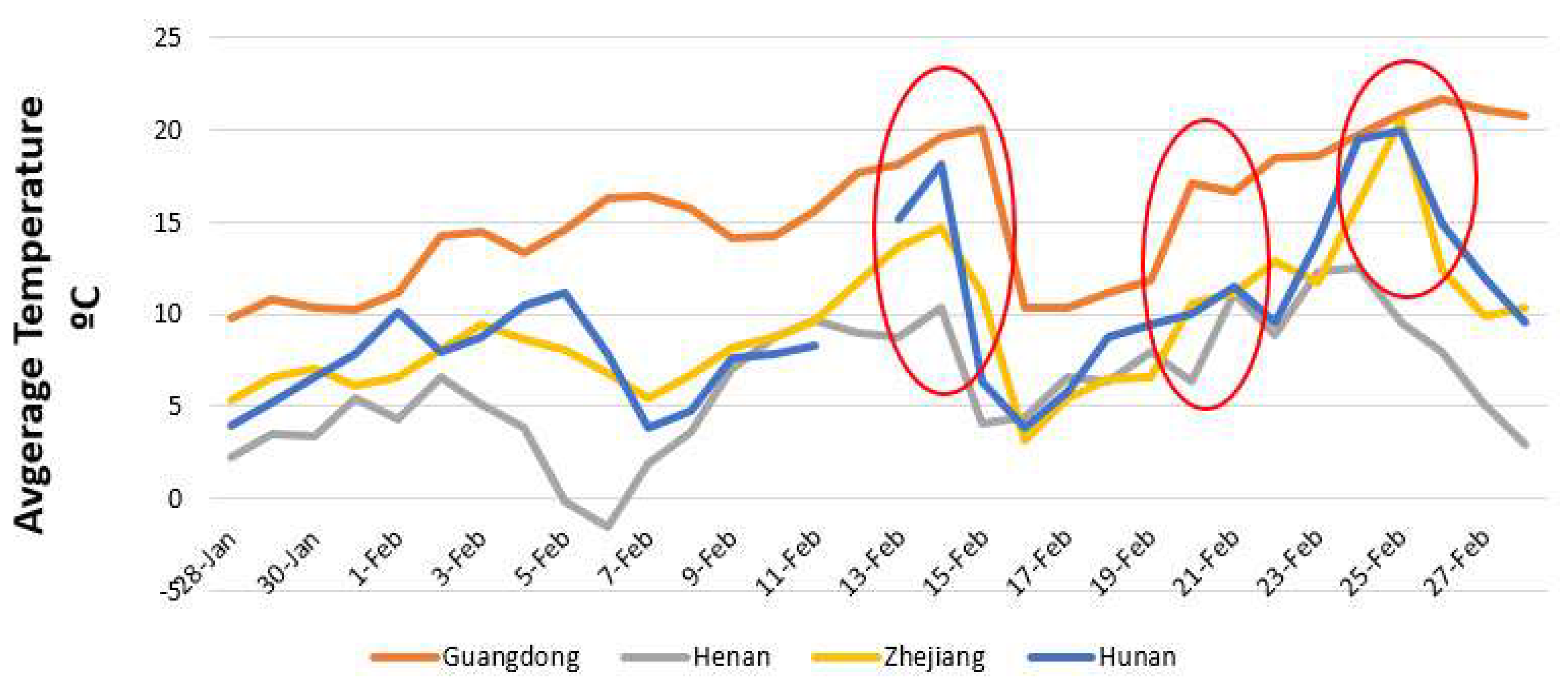
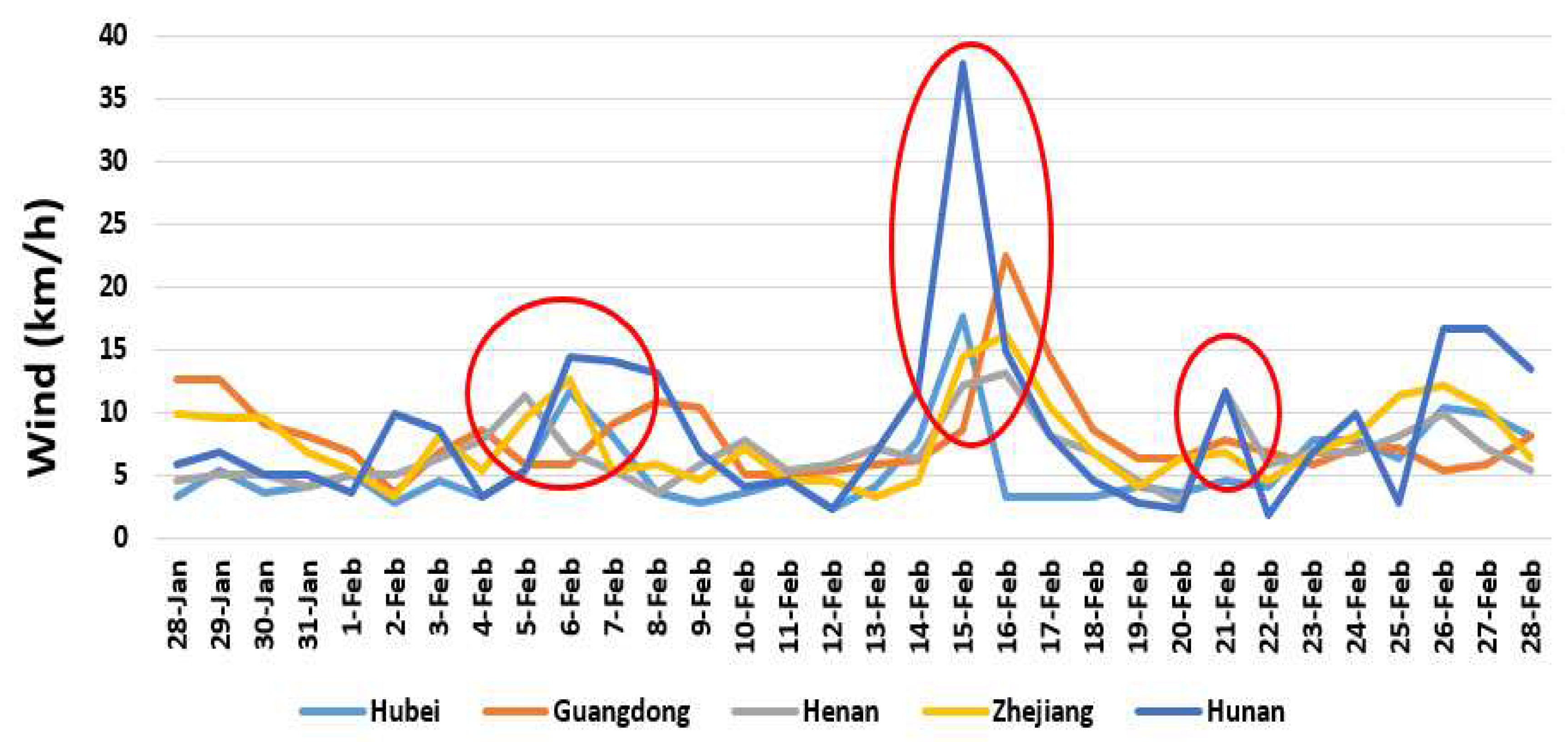
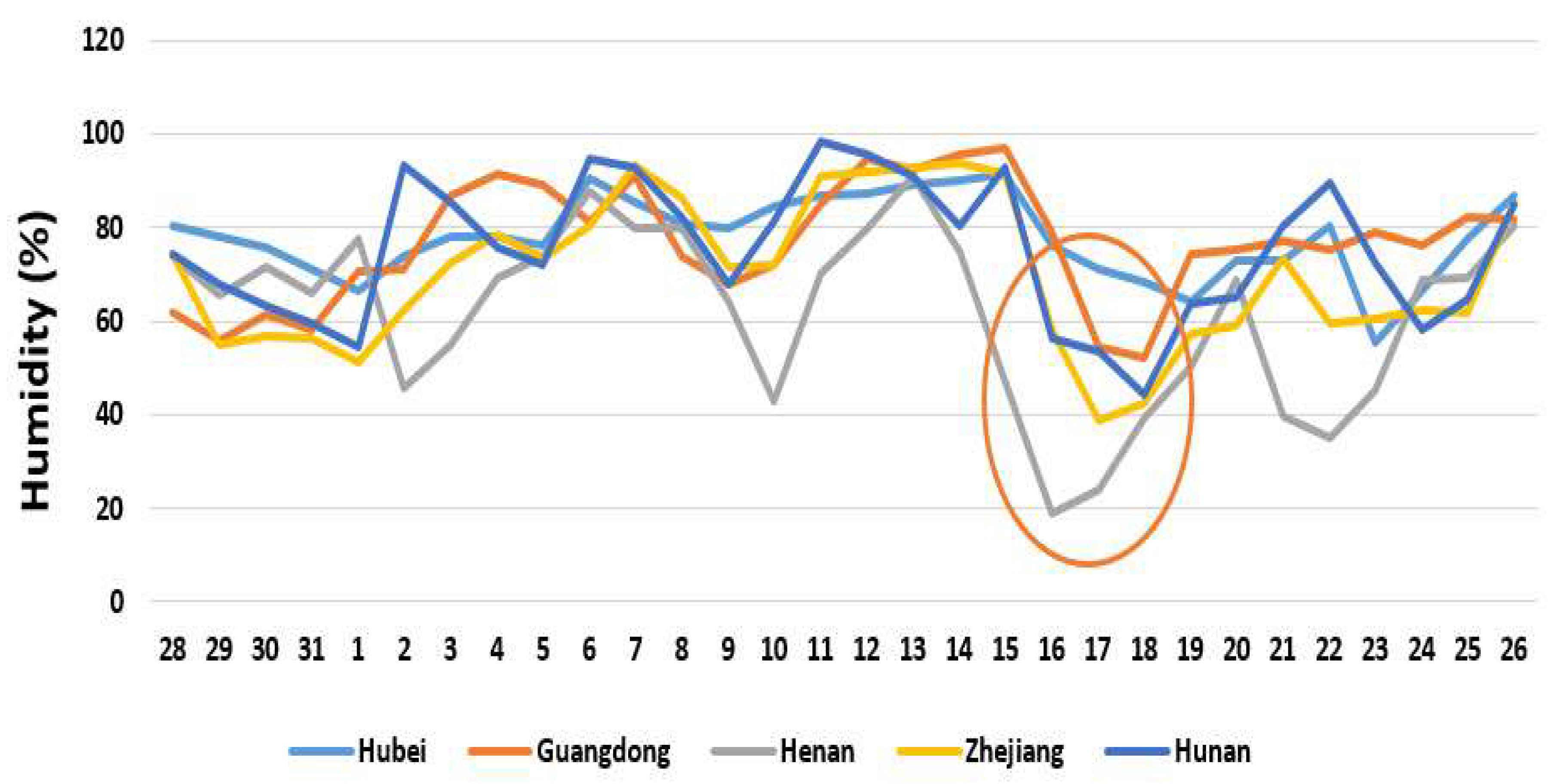
- Regression analysis was used, and a trend of the confirmed cases of COVID-19 analyzed in the five provinces with the highest confirmed cases, including Hubei, Guangdong, Henan, Zhejiang, and Hunan, and the daily fluctuations of confirmed cases were compared with fluctuations of weather parameters.
- The environmental and urban parameters in the analysis included density, sex ratio, average age, elevation, maximum, minimum, and average temperature, relative humidity, and wind.
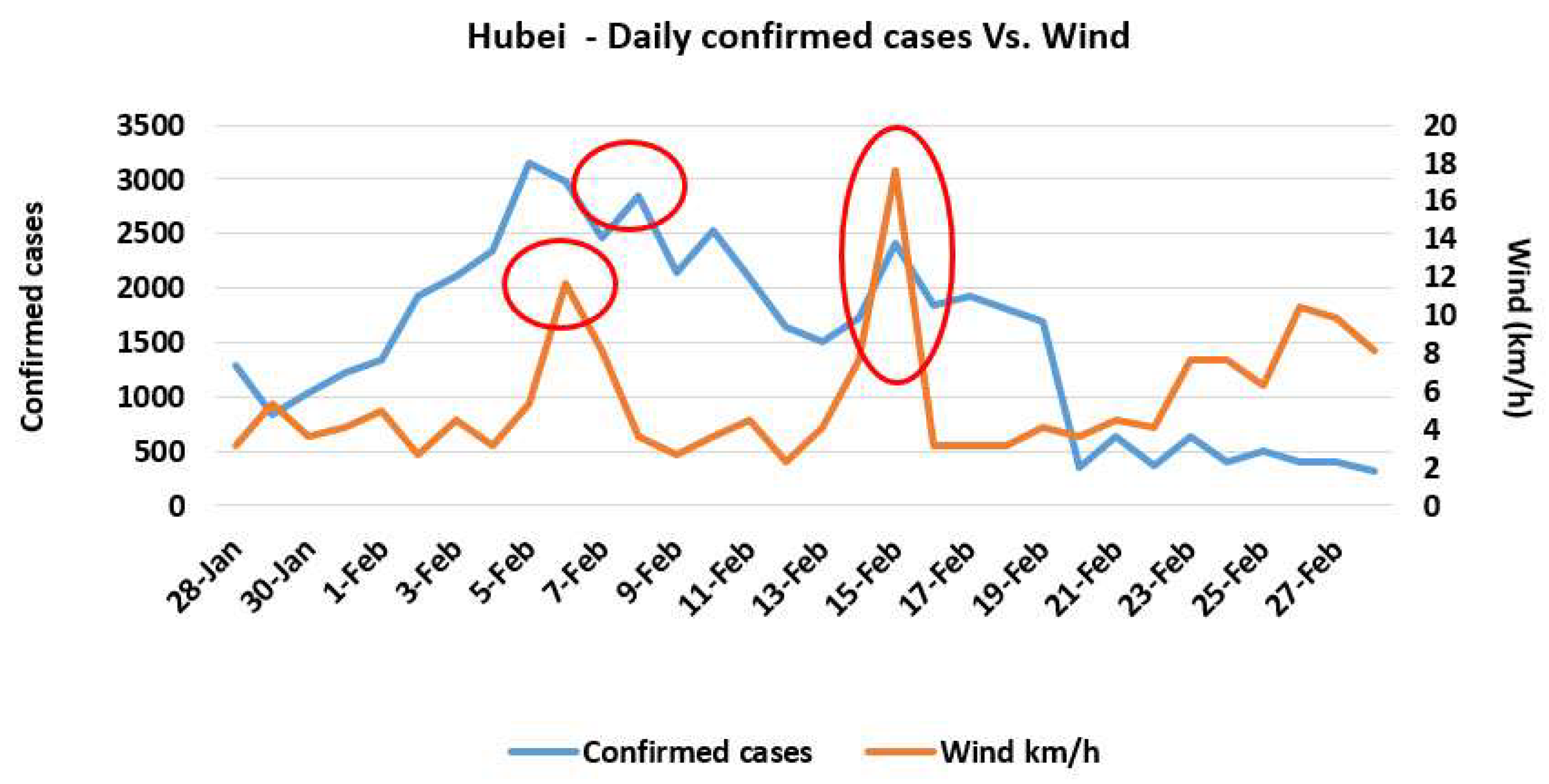
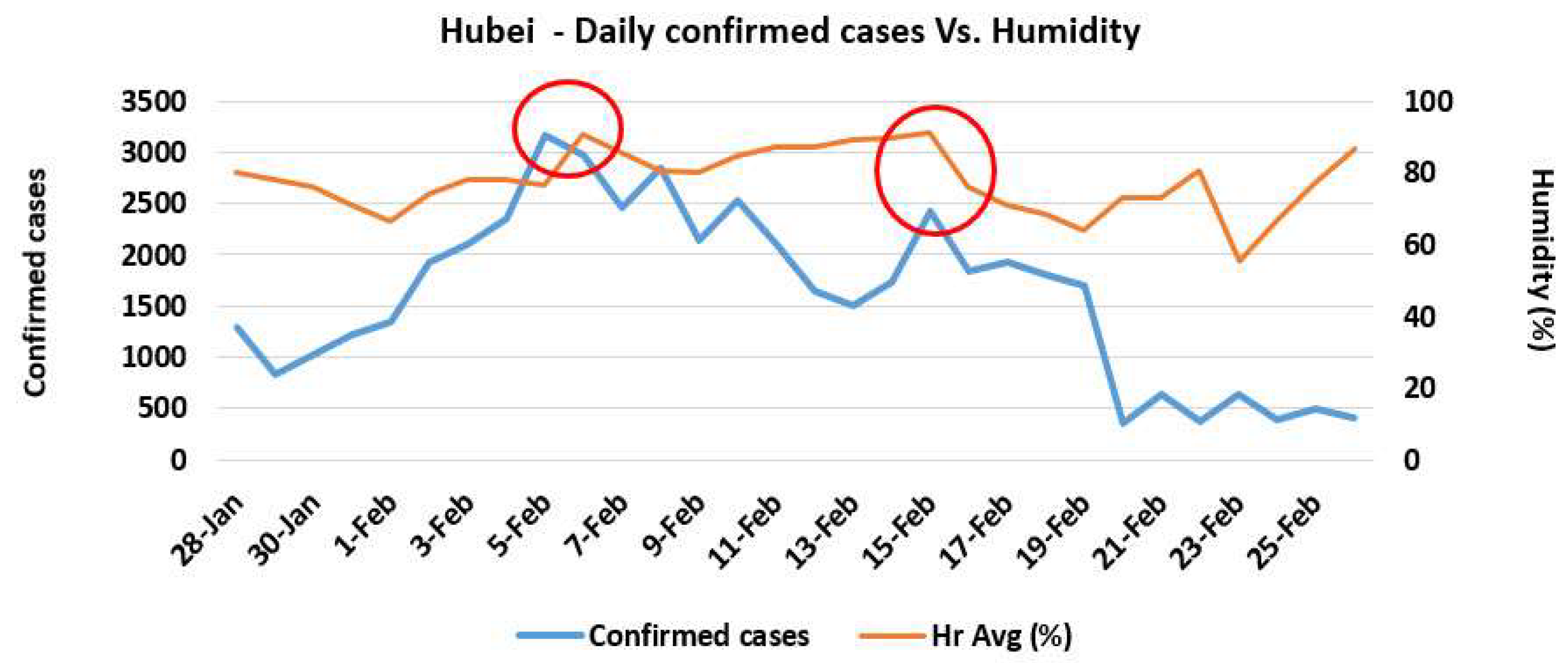
- For daily analysis of the possible trend between confirmed cases of COVID-19 and environmental factors, the data of Hubei province was used.
- The climate data is based on the stations situated in the capital of the provinces or regions because the population is generally higher in these areas.
- The analysis period was from 28 January 2020 to 26 February 2020 (30 days).
- The analysis of the possible correlations about trends of confirmed cases in different case studies was based on the average values in one month.
2.1. Case Study
2.2. Group Method of Data Handling (GMDH)
3. Results
3.1. Binary Classification Modelling Using GMDH
3.2. Regression Analysis
3.3. The Correlations among the Trends of Confirmed Cases and Weather Parameters
4. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Country | Province | Properties | February, 2020 | COVID-19 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Population | Density, Population/km2 | Gender Ratio | Average Age | Elevation, m | Max T °C | Min T °C | Average Temperature °C | Humidity % | Wind km/h | Confirmed Cases | Deaths | ||
| China | Hubei | 59,170,000 | 318 | 1.06 | 38.4 | 37 | 15.4 | 1.4 | 8.3 | 77.9 | 5.4 | 64786 | 2563 |
| Guangdong | 113,460,000 | 630 | 1.06 | 38.4 | 21 | 21.0 | 10.3 | 15.1 | 76.8 | 8.2 | 1347 | 7 | |
| Henan | 96,050,000 | 575 | 1.06 | 38.4 | 104 | 13.7 | −0.1 | 6.3 | 61.9 | 6.8 | 1271 | 19 | |
| Zhejiang | 57,370,000 | 562 | 1.06 | 38.4 | 19 | 15.1 | 4.5 | 9.3 | 70.1 | 7.6 | 1205 | 1 | |
| Hunan | 68,990,000 | 329 | 1.06 | 38.4 | 63 | 16.2 | 4.4 | 9.6 | 75.2 | 8.4 | 1016 | 4 | |
| Anhui | 63,240,000 | 454 | 1.06 | 38.4 | 37 | 14.4 | 0.1 | 7.1 | 76.9 | 9.6 | 989 | 6 | |
| Jiangxi | 46,480,000 | 278 | 1.06 | 38.4 | 37 | 16.6 | 5.9 | 10.5 | 73.4 | 5.3 | 934 | 1 | |
| Shandong | 100,470,000 | 653 | 1.06 | 38.4 | 23 | 11.6 | 0.2 | 5.4 | 56.0 | 8.3 | 755 | 6 | |
| Jiangsu | 80,510,000 | 785 | 1.06 | 38.4 | 15 | 14.2 | 2.4 | 7.8 | 73.0 | 9.0 | 631 | 0 | |
| Chongqing | 31,020,000 | 377 | 1.06 | 38.4 | 244 | 14.3 | 8.0 | 10.7 | 78.3 | 3.4 | 576 | 6 | |
| Sichuan | 83,410,000 | 172 | 1.06 | 38.4 | 500 | 14.9 | 5.4 | 9.75 | 65.50 | 6.10 | 529 | 3 | |
| Heilongjiang | 37,730,000 | 83 | 1.06 | 38.4 | 126 | −5.8 | −20.6 | −12.7 | 69.9 | 9.9 | 480 | 12 | |
| Beijing | 21,540,000 | 1313 | 1.06 | 38.4 | 43.5 | 7.8 | −4.8 | 1.0 | 55.7 | 7.2 | 400 | 4 | |
| Shanghai | 24,240,000 | 3823 | 1.06 | 38.4 | 4 | 14.1 | 2.4 | 8.1 | 72.8 | 9.1 | 335 | 3 | |
| Hebei | 75,560,000 | 403 | 1.06 | 38.4 | 83 | 10.6 | −1.5 | 4.1 | 54.6 | 8.5 | 311 | 6 | |
| Fujian | 39,410,000 | 324 | 1.06 | 38.4 | 14 | 18.4 | 8.3 | 12.7 | 70.6 | 7.4 | 294 | 1 | |
| Guangxi | 49,260,000 | 209 | 1.06 | 38.4 | 499 | 20.4 | 11.5 | 15.5 | 74.4 | 9.6 | 252 | 2 | |
| Shaanxi | 38,640,000 | 247 | 1.06 | 38.4 | 405 | 14.5 | 2.3 | 7.8 | 62.4 | 3.9 | 245 | 1 | |
| Yunnan | 48,300,000 | 123 | 1.06 | 38.4 | 1892 | 18.0 | 3.4 | 10.6 | 64.1 | 9.0 | 174 | 2 | |
| Hainan | 9,340,000 | 275 | 1.06 | 38.4 | 222 | 24.5 | 16.8 | 19.9 | 81.1 | 11.3 | 168 | 5 | |
| Guizhou | 36,000,000 | 205 | 1.06 | 38.4 | 1275 | 12.5 | 3.9 | 7.6 | 82.0 | 8.5 | 146 | 2 | |
| Tianjin | 15,600,000 | 1380 | 1.06 | 38.4 | 1078 | 8.6 | −4.0 | 1.8 | 61.8 | 9.3 | 135 | 3 | |
| Shanxi | 37,180,000 | 181 | 1.06 | 38.4 | 800 | 10.0 | −7.1 | 0.6 | 52.6 | 7.0 | 133 | 0 | |
| Liaoning | 43,590,000 | 299 | 1.06 | 38.4 | 55 | 2.0 | −12.6 | −5.36 | 64.22 | 8.26 | 121 | 1 | |
| Jilin | 27,040,000 | 2704 | 1.06 | 38.4 | 202 | −2.4 | −15.7 | −8.96 | 66.52 | 9.60 | 93 | 1 | |
| South Korea | Seoul | 10,010,983 | 16541 | 1 | 43.2 | 38 | 7.2 | −1.1 | 2.6 | 56.1 | 9.1 | 4 | 0 |
| Daejeon | 1,493,979 | 2767 | 1 | 43.2 | 94 | 9.2 | −0.8 | 3.6 | 67.3 | 5.1 | 49 | 0 | |
| Gyeonggi | 13,653,984 | 1341 | 1 | 43.2 | 87 | 7.4 | −1.8 | 2.5 | 79.3 | 7.1 | 2 | 0 | |
| South Gyeongsang | 3,438,676 | 326 | 1 | 43.2 | 2 | 12.0 | 4.5 | 8.0 | 67.0 | 10.3 | 922 | 10 | |
| Italy | Lazio | 5,879,082 | 341 | 0.93 | 44.6 | 13 | 15.9 | 6.5 | 11 | 71 | 9 | 3 | 0 |
| Veneto | 4,905,854 | 272 | 0.96 | 45.1 | 1 | 11.3 | 3.1 | 7 | 83 | 7 | 42 | 1 | |
| Emilia−Romagna | 4,459,477 | 199 | 0.95 | 45.7 | 54 | 14.5 | 3.1 | 8 | 72 | 7 | 23 | 0 | |
| Lombardy | 10,060,574 | 422 | 0.94 | 44.8 | 120 | 15.2 | 0.1 | 7 | 69 | 8 | 240 | 9 | |
| Japan | Tokyo | 13,929,286 | 6349 | 0.95 | 48.6 | 40 | 13.5 | 4.3 | 8 | 58 | 10 | 14 | 0 |
| Kanagawa Prefecture | 9,058,094 | 3770 | 0.95 | 48.6 | 500 | 13.3 | 5.5 | 9.1 | 56.3 | 13.9 | 1 | 0 | |
| Aichi Prefecture | 7,552,873 | 1500 | 0.95 | 48.6 | 56 | 12.1 | 3.6 | 7 | 65 | 12 | 2 | 0 | |
| Nara Prefecture | 1,348,930 | 365 | 0.95 | 48.6 | 56.4 | 11.6 | 2.9 | 6.6 | 71.5 | 7.7 | 1 | 0 | |
| Kansai region | 22,757,897 | 690 | 0.95 | 48.6 | 50 | 11.8 | 3.8 | 7.2 | 68.3 | 7.5 | 1 | 0 | |
| Tokushima Prefecture | 728,633 | 180 | 0.95 | 48.6 | 11 | 12.6 | 5.2 | 8.59 | 64.02 | 11.94 | 831 | 5 | |
Appendix B
| Hubei (Wuhan) | Date | Max T °C | Min T °C | T Avg °C | Hr Avg (%) | Wind km/h | Confirmed Cases |
|---|---|---|---|---|---|---|---|
| Jan 28 | 28 | 8.3 | −1.6 | 3.5 | 80.3 | 3.2 | 1291 |
| Jan 29 | 29 | 12.2 | −2.7 | 4.1 | 78.2 | 5.4 | 840 |
| Jan 30 | 30 | 14 | −2.7 | 5 | 75.9 | 3.6 | 1032 |
| Ian 31 | 31 | 14 | −2.2 | 4.7 | 71.2 | 4.1 | 1220 |
| Feb 1 | 1 | 14.1 | −2.2 | 7.1 | 66.6 | 5 | 1347 |
| Feb 2 | 2 | 14.1 | 0.1 | 9.3 | 74.1 | 2.7 | 1921 |
| Feb 3 | 3 | 14 | 1.8 | 7.9 | 78.1 | 4.5 | 2103 |
| Feb 4 | 4 | 16.2 | −0.6 | 6.4 | 78.2 | 3.2 | 2345 |
| Feb 5 | 5 | 16.2 | −0.6 | 6.8 | 76.4 | 5.4 | 3156 |
| Feb 6 | 6 | 15.4 | 0.6 | 6.2 | 90.6 | 11.7 | 2977 |
| Feb 7 | 7 | 8.2 | 3.3 | 4.3 | 85.6 | 8.1 | 2457 |
| Feb 8 | 8 | 9.4 | 3.3 | 6 | 80.6 | 3.6 | 2841 |
| Feb 9 | 9 | 14.7 | −1.2 | 6 | 80.1 | 2.7 | 2147 |
| Feb 10 | 10 | 14.7 | −1.2 | 7.6 | 84.5 | 3.6 | 2531 |
| Feb 11 | 11 | 11.8 | 2.8 | 9.8 | 86.9 | 4.5 | 2097 |
| Feb 12 | 12 | 14.1 | 7.4 | 11 | 87.1 | 2.3 | 1638 |
| Feb 13 | 13 | 18.7 | 4.1 | 10.8 | 89.3 | 4.1 | 1508 |
| Feb 14 | 14 | 18.7 | 4.1 | 14.2 | 89.9 | 7.7 | 1728 |
| Feb 15 | 15 | 16.8 | −0.2 | 4.6 | 91.3 | 17.6 | 2420 |
| Feb 16 | 16 | 8.4 | −1.3 | 2.2 | 76 | 3.2 | 1843 |
| Feb 17 | 17 | 12.7 | −2.7 | 3.7 | 70.9 | 3.2 | 1933 |
| Feb 18 | 18 | 13 | −2.7 | 5.2 | 68.5 | 3.2 | 1807 |
| Feb 19 | 19 | 15 | −2.5 | 10.1 | 64 | 4.1 | 1693 |
| Feb 20 | 20 | 18 | 0.5 | 7.9 | 73 | 3.6 | 349 |
| Feb 21 | 21 | 18 | 0.5 | 11.1 | 72.9 | 4.5 | 631 |
| Feb 22 | 22 | 17.9 | 2.9 | 10.1 | 80.5 | 4.1 | 366 |
| Feb 23 | 23 | 20.1 | 2.9 | 15.2 | 55.5 | 7.7 | 630 |
| Feb 24 | 24 | 24.9 | 10.6 | 17.9 | 66.7 | 7.7 | 398 |
| Feb 25 | 25 | 24.9 | 10.6 | 18.1 | 77.4 | 6.3 | 499 |
| Feb 26 | 26 | 22.8 | 10.6 | 12.5 | 86.7 | 10.4 | 401 |
References
- Andrijevic, M.; Crespo Cuaresma, J.; Muttarak, R.; Schleussner, C.F. Governance in socioeconomic pathways and its role for future adaptive capacity. Nat. Sustain. 2020, 3, 35–41. [Google Scholar] [CrossRef]
- Pirouz, B.; Arcuri, N.; Pirouz, B.; Palermo, S.A.; Turco, M.; Maiolo, M. Development of an assessment method for evaluation of sustainable factories. Sustainability 2020, 12, 1841. [Google Scholar] [CrossRef] [Green Version]
- Pirouz, B.; Arcuri, N.; Maiolo, M.; Talarico, V.C.; Piro, P. A new multi-objective dynamic model to close the gaps in sustainable development of industrial sector. IOP Conf. Ser. Earth Environ. Sci. 2020, 410, 012074. [Google Scholar] [CrossRef] [Green Version]
- Shen, M.; Peng, Z.; Guo, Y.; Xiao, Y.; Zhang, L. Lockdown may partially halt the spread of 2019 novel coronavirus in Hubei province, China. medRxiv 2020. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Sun, X.; Solvang, W.; Zhao, X. Reverse logistics network design for effective management of medical waste in epidemic outbreak: Insights from the Coronavirus Disease 2019 (COVID-19) in Wuhan. Int. J. Environ. Res. Public Health 2020, 17, 1770. [Google Scholar] [CrossRef] [Green Version]
- Phan, L.T.; Nguyen, T.V.; Luong, Q.C.; Nguyen, T.V.; Nguyen, H.T.; Le, H.Q.; Nguyen, T.T.; Cao, T.M.; Pham, Q.D. Importation and human-to-human transmission of a novel coronavirus in Vietnam. N. Engl. J. Med. 2020, 382, 872–874. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- World Health Organization (WHO). Laboratory Biosafety Guidance Related to Coronavirus Disease 2019 (COVID-19). Available online: https://apps.who.int/iris/bitstream/handle/10665/331138/WHO-WPE-GIH-2020.1-eng.pdf (accessed on 21 February 2020).
- Kampf, G.; Todt, D.; Pfaender, S.; Steinmann, E. Persistence of coronaviruses on inanimate surfaces and its inactivation with biocidal agents. J. Hosp. Infect. 2020, 104, 246–251. [Google Scholar] [CrossRef] [Green Version]
- Lai, C.-C.; Shih, T.-P.; Ko, W.-C.; Tang, H.-J.; Hsueh, P.-R. Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and coronavirus disease-2019 (COVID-19): The epidemic and the challenges. Int. J. Antimicrob. Agents 2020, 55, 105924. [Google Scholar] [CrossRef]
- Kampf, G. Potential role of inanimate surfaces for the spread of coronaviruses and their inactivation with disinfectant agents. Infect. Prev. Pract. 2020, 2, 100044. [Google Scholar] [CrossRef]
- Telles, C.R. COVID-19, an overview about the epidemic virus behavior. MediArXiv 2020. [Google Scholar] [CrossRef]
- Wen, J.; Aston, J.; Liu, X.; Ying, T. Effects of misleading media coverage on public health crisis: A case of the 2019 novel coronavirus outbreak in China. Anatolia 2020. [Google Scholar] [CrossRef]
- Chen, Y.C.; Lu, P.E.; Chang, C.S. A time-dependent SIR model for COVID-19. arXiv 2020, arXiv:2003.00122. [Google Scholar]
- Li, Q.; Feng, W. Trend and forecasting of the COVID-19 outbreak in China. arXiv 2020, arXiv:2002.05866. [Google Scholar] [CrossRef] [Green Version]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Viboud, C. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020. [Google Scholar] [CrossRef] [Green Version]
- Lowen, A.C.; Mubareka, S.; Steel, J.; Palese, P. Influenza virus transmission is dependent on relative humidity and temperature. PLoS Pathog. 2007, 3, 1470–1476. [Google Scholar] [CrossRef]
- Price, R.H.M.; Graham, C.; Ramalingam, S. Association between viral seasonality and meteorological factors. Sci. Rep. 2019. [Google Scholar] [CrossRef]
- Altamimi, A.; Ahmed, A.E. Climate factors and incidence of Middle East respiratory syndrome coronavirus. J. Infect. Public Health 2019. [Google Scholar] [CrossRef]
- 2019–20 Coronavirus Outbreak. Available online: https://en.wikipedia.org/wiki/2019–20_coronavirus_outbreak (accessed on 21 February 2020).
- WHO. Coronavirus Disease (COVID-2019) Situation Reports. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/ (accessed on 21 February 2020).
- AdminStat. Maps, Analysis and Statistics about the Resident Population. Available online: https://ugeo.urbistat.com/AdminStat/en/it/demografia/dati-sintesi/milano/15/3 (accessed on 21 February 2020).
- South Korea: Cities. Available online: https://www.citypopulation.de/en/southkorea/cities/ (accessed on 21 February 2020).
- World Population Review. Available online: http://worldpopulationreview.com/countries/ (accessed on 21 February 2020).
- List of Countries and Dependencies by Population Density. Available online: https://en.wikipedia.org/wiki/List_of_countries_and_dependencies_by_population_density (accessed on 21 February 2020).
- Regions of Italy. Available online: https://en.wikipedia.org/wiki/Regions_of_Italy (accessed on 21 February 2020).
- Area of Provinces of China. Available online: https://en.wikipedia.org/wiki/Provinces_of_China (accessed on 21 February 2020).
- Gyeonggi Province. Available online: https://en.wikipedia.org/wiki/Gyeonggi_Province (accessed on 21 February 2020).
- Busan Province. Available online: https://en.wikipedia.org/wiki/Busan (accessed on 21 February 2020).
- Seoul. Available online: https://en.wikipedia.org/wiki/Seoul (accessed on 21 February 2020).
- Ulsan. Available online: https://en.wikipedia.org/wiki/Ulsan (accessed on 21 February 2020).
- Daegu. Available online: https://en.wikipedia.org/wiki/Daegu (accessed on 21 February 2020).
- Incheon. Available online: https://en.wikipedia.org/wiki/Incheon (accessed on 21 February 2020).
- Daejeon. Available online: https://en.wikipedia.org/wiki/Daejeon (accessed on 21 February 2020).
- List of Countries by Sex Ratio. Available online: https://en.wikipedia.org/wiki/List_of_countries_by_sex_ratio (accessed on 22 February 2020).
- Countries by Sex Ratio. Available online: http://statisticstimes.com/demographics/countries-by-sex-ratio.php (accessed on 22 February 2020).
- The World Fact Book. Available online: https://www.cia.gov/library/publications/resources/the-world-factbook/fields/343rank (accessed on 22 February 2020).
- List of Countries by Median Age. Available online: https://en.wikipedia.org/wiki/List_of_countries_by_median_age (accessed on 22 February 2020).
- Topographic Maps. Available online: https://en-nz.topographic-map.com/places/stp (accessed on 22 February 2020).
- Coronavirus COVID-19 Outbreak: Latest News, Information and Updates. Available online: https://www.pharmaceutical-technology.com/special-focus/covid-19/coronavirus-covid-19-outbreak-latest-information-news-and-updates/ (accessed on 22 February 2020).
- Pirouz, B.; Khorram, E. A computational approach based on the ε-constraint method in multi-objective optimization problems. Adv. Appl. Stat. 2016, 49, 453. [Google Scholar] [CrossRef]
- Rad, M.Y.; Haghshenas, S.S.; Kanafi, P.R.; Haghshenas, S.S. Analysis of protection of body slope in the rockfill reservoir dams on the basis of fuzzy logic. In Proceedings of the 4th International Joint Conference on Computational Intelligence, Barcelona, Spain, 5–7 October 2012. [Google Scholar]
- Rad, M.Y.; Haghshenas, S.S.; Haghshenas, S.S. Mechanostratigraphy of cretaceous rocks by fuzzy logic in East Arak, Iran. In Proceedings of the 4th International Workshop on Computer Science and Engineering—Summer, Dubai, UAE, 22–23 August 2014. [Google Scholar]
- Petrudi, S.H.J.; Pirouz, M.; Pirouz, B. Application of fuzzy logic for performance evaluation of academic students. In Proceedings of the 13th Iranian Conference on Fuzzy Systems (IFSC), Qazvin, Iran, 27–29 August 2013; pp. 1–5. [Google Scholar]
- Naderpour, H.; Nagai, K.; Haji, M.; Mirrashid, M. Adaptive neuro-fuzzy inference modelling and sensitivity analysis for capacity estimation of fiber reinforced polymer-strengthened circular reinforced concrete columns. Expert Syst. 2019, 36, e12410. [Google Scholar] [CrossRef]
- Haghshenas, S.S.; Ozcelik, Y.; Haghshenas, S.S.; Mikaeil, R.; Moghadam, P.S. Ranking and assessment of tunneling projects risks using fuzzy MCDM (Case study: Toyserkan doolayi tunnel). In Proceedings of the 25th International Mining Congress and Exhibition of Turkey, Antalya, Turkey, 11–14 April 2017. [Google Scholar]
- Pirouz, B.; Palermo, S.A.; Turco, M.; Piro, P. New Mathematical Optimization Approaches for LID Systems; University of Calabria: Rende, Italy, 2020; ISBN 978-3-030-39080-8. [Google Scholar]
- Fairchild, G.; Polgreen, P.M.; Foster, E.; Rushton, G.; Segre, A.M. How many suffice? A computational framework for sizing sentinel surveillance networks. Int. J. Health Geogr. 2013, 12, 56. [Google Scholar] [CrossRef] [Green Version]
- De Pretis, F. A Quantitative Approach for Modeling Interacting Systems Starting from Empirical Data: The Point of View of Statistical Mechanics and a Case Study from the Social Sciences. Ph.D. Thesis, Università degli Studi di Modena e Reggio Emilia, Modena, Italy, 2014. [Google Scholar]
- Fairchild, G.; Hickmann, K.S.; Mniszewski, S.M.; Del Valle, S.Y.; Hyman, J.M. Optimizing human activity patterns using global sensitivity analysis. Comput. Math. Organ. Theory 2014, 20, 394–416. [Google Scholar] [CrossRef] [Green Version]
- Mikaeil, R.; Shaffiee Haghshenas, S.; Sedaghati, Z. Geotechnical risk evaluation of tunneling projects using optimization techniques (Case study: The second part of Emamzade Hashem tunnel). Nat. Hazards 2019, 97, 1099–1113. [Google Scholar] [CrossRef]
- Palermo, S.A.; Talarico, V.C.; Pirouz, B. Optimizing Rainwater Harvesting Systems for Non-Potable Water Uses and Surface Runoff Mitigation; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-030-39080-8. [Google Scholar]
- Dormishi, A.; Ataei, M.; Mikaeil, R.; Khalokakaei, R.; Haghshenas, S.S. Evaluation of gang saws’ performance in the carbonate rock cutting process using feasibility of intelligent approaches. Eng. Sci. Technol. Int. J. 2019, 22, 990–1000. [Google Scholar] [CrossRef]
- Kidando, E.; Moses, R.; Sando, T.; Ozguven, E.E. An application of Bayesian multilevel model to evaluate variations in stochastic and dynamic transition of traffic conditions. J. Mod. Transp. 2019, 27, 235–249. [Google Scholar] [CrossRef] [Green Version]
- Behnood, A.; Golafshani, E.M. Machine learning study of the mechanical properties of concretes containing waste foundry sand. Constr. Build. Mater. 2020, 243, 118152. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Behnood, A.; Arashpour, M. Predicting the compressive strength of normal and high-performance concretes using ANN and ANFIS hybridized with grey wolf optimizer. Constr. Build. Mater. 2020, 232, 117266. [Google Scholar] [CrossRef]
- Mehdi Hosseini, S.; Ataei, M.; Khalokakaei, R.; Mikaeil, R.; Shaffiee Haghshenas, S. Study of the effect of the cooling and lubricant fluid on the cutting performance of dimension stone through artificial intelligence models. Eng. Sci. Technol. Int. J. 2019, 23, 71–81. [Google Scholar] [CrossRef]
- Shaffiee Haghshenas, S.; Shirani Faradonbeh, R.; Mikaeil, R.; Haghshenas, S.S.; Taheri, A.; Saghatforoush, A.; Dormishi, A. A new conventional criterion for the performance evaluation of gang saw machines. Meas. J. Int. Meas. Confed. 2019, 146, 159–170. [Google Scholar] [CrossRef]
- Mikaeil, R.; Haghshenas, S.S.; Haghshenas, S.S.; Ataei, M. Performance prediction of circular saw machine using imperialist competitive algorithm and fuzzy clustering technique. Neural Comput. Appl. 2018, 29, 283–292. [Google Scholar] [CrossRef]
- Mikaeil, R.; Haghshenas, S.S.; Hoseinie, S.H. Rock penetrability classification using Artificial Bee Colony (ABC) algorithm and self-organizing map. Geotech. Geol. Eng. 2018, 36, 1309–1318. [Google Scholar] [CrossRef]
- Salemi, A.; Mikaeil, R.; Haghshenas, S.S. Integration of finite difference method and genetic algorithm to seismic analysis of circular shallow tunnels (Case study: Tabriz urban railway tunnels). KSCE J. Civ. Eng. 2018, 22, 1978–1990. [Google Scholar] [CrossRef]
- Aryafar, A.; Mikaeil, R.; Haghshenas, S.S.; Haghshenas, S.S. Application of metaheuristic algorithms to optimal clustering of sawing machine vibration. Meas. J. Int. Meas. Confed. 2018, 124, 20–31. [Google Scholar] [CrossRef]
- Shirani Faradonbeh, R.; Shaffiee Haghshenas, S.; Taheri, A.; Mikaeil, R. Application of self-organizing map and fuzzy c-mean techniques for rockburst clustering in deep underground projects. Neural Comput. Appl. 2019. [Google Scholar] [CrossRef]
- Ivakhnenko, A.G. Self-Organizing Methods in Modelling and Clustering: GMDH Type Algorithms; Springer: Berlin/Heidelberg, Germany, 1988; ISBN 978-0-387-97091-2. [Google Scholar]
- Ivakhnenko, A.G. Polynomial theory of complex systems. IEEE Trans. Syst. Man Cybern. 1971, 4, 364–378. [Google Scholar] [CrossRef] [Green Version]
- Ikeda, S.; Sawaragi, Y.; Ochiai, M. Sequential GMDH algorithm and its application to river flow prediction. IEEE Trans. Syst. Man Cybern. 1976, 7, 473–479. [Google Scholar] [CrossRef]
- Dag, O.; Karabulut, E.; Alpar, R. GMDH2: Binary classification via GMDH-type neural network algorithms—R package and web-based tool. Int. J. Comput. Intell. Syst. 2019, 12, 649–660. [Google Scholar] [CrossRef] [Green Version]
- Mikaeil, R.; Haghshenas, S.S.; Ozcelik, Y.; Gharehgheshlagh, H.H. Performance evaluation of adaptive neuro-fuzzy inference system and group method of data handling-type neural network for estimating wear rate of diamond wire saw. Geotech. Geol. Eng. 2018, 36, 3779–3791. [Google Scholar] [CrossRef]
- Park, D.; Cha, J.; Kim, M.; Go, J.S. Multi-objective optimization and comparison of surrogate models for separation performances of cyclone separator based on CFD, RSM, GMDH-neural network, back propagation-ANN and genetic algorithm. Eng. Appl. Comput. Fluid Mech. 2020, 14, 180–201. [Google Scholar] [CrossRef]
- Naderpour, H.; Fakharian, P.; Rafiean, A.H.; Yourtchi, E. Estimation of the shear strength capacity of masonry walls improved with Fiber Reinforced Mortars (FRM) using ANN-GMDH approach. J. Concr. Struct. Mater. 2016, 1, 47–59. [Google Scholar] [CrossRef]
- Shaffiee Haghshenas, S.; Shaffiee Haghshenas, S.; Mikaeil, R.; Sirati Moghadam, P.; Shafiee Haghshenas, A. A New model for evaluating the geological risk based on geomechanical properties—Case study: The second part of emamzade hashem tunnel. Electron. J. Geotech. Eng. 2017, 22, 309–320. [Google Scholar]
- Mohammadi, J.; Ataei, M.; Khalo Kakaei, R.; Mikaeil, R.; Shaffiee Haghshenas, S. Prediction of the production rate of chain saw machine using the Multilayer Perceptron (MLP) neural network. Civ. Eng. J. 2018, 4, 1575–1583. [Google Scholar] [CrossRef] [Green Version]
- Dormishi, A.; Ataei, M.; Khaloo Kakaie, R.; Mikaeil, R.; Shaffiee Haghshenas, S. Performance evaluation of gang saw using hybrid ANFIS-DE and hybrid ANFIS-PSO algorithms. J. Min. Environ. 2018, 10, 543–557. [Google Scholar] [CrossRef]
- Noori, A.M.; Mikaeil, R.; Mokhtarian, M.; Haghshenas, S.S.; Foroughi, M. Feasibility of intelligent models for prediction of utilization factor of TBM. Geotech. Geol. Eng. 2020. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Ataei, M.; Khalokakaei, R.; Mikaeil, R.; Haghshenas, S.S. Investigating the role of coolant and lubricant fluids on the performance of cutting disks (Case study: Hard rocks). Rud. Geol. Naft. Zb. 2019, 34, 13–24. [Google Scholar] [CrossRef]
- Mikaeil, R.; Beigmohammadi, M.; Bakhtavar, E.; Haghshenas, S.S. Assessment of risks of tunneling project in Iran using artificial bee colony algorithm. SN Appl. Sci. 2019, 1, 1711. [Google Scholar] [CrossRef] [Green Version]
- Mikaeil, R.; Bakhshinezhad, H.; Haghshenas, S.S.; Ataei, M. Stability analysis of tunnel support systems using numerical and intelligent simulations (Case study: Kouhin tunnel of qazvin-rasht railway). Rud. Geol. Naft. Zb. 2019, 34, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Looney, C.G. Advances in feedforward neural networks: Demystifying knowledge acquiring black boxes. IEEE Trans. Knowl. Data Eng. 1996, 8, 211–226. [Google Scholar] [CrossRef]
- Zorlu, K.; Gokceoglu, C.; Ocakoglu, F.; Nefeslioglu, H.A.; Acikalin, S. Prediction of uniaxial compressive strength of sandstones using petrography-based models. Eng. Geol. 2008, 96, 141–158. [Google Scholar] [CrossRef]
- New Coronavirus Cases in China. Available online: https://www.timesleader.com/interactives/774260/new-coronavirus-cases-in-china (accessed on 22 February 2020).
- Meteorological Conditions in the World. Available online: https://www.ogimet.com/ranking.phtml.en (accessed on 22 February 2020).
- Guangzhou January Weather. Available online: https://www.accuweather.com/it/cn/guangzhou/102255/january-weather/102255?year=2020 (accessed on 22 February 2020).
- Guangzhou Extended Forecast with High and Low Temperatures. Available online: https://www.timeanddate.com/weather/china/guangzhou/ext (accessed on 22 February 2020).
- Average Weather in February in Hubei. Available online: https://weatherspark.com/m/125701/2/Average-Weather-in-February-in-Hubei-China#Sections-Rain (accessed on 22 February 2020).
- Guangzhou Weather February. Available online: https://www.weather-atlas.com/en/china/guangzhou-weather-february (accessed on 22 February 2020).
- Climate-data. Available online: https://en.climate-data.org/asia/china/gansu/xizang-855625/ (accessed on 22 February 2020).
- Wuhan January Weather. Available online: https://www.accuweather.com/it/cn/wuhan/103847/january-weather/103847?year=2020 (accessed on 22 February 2020).
- Past Weather in Wuhan—Graph. Available online: https://www.timeanddate.com/weather/china/wuhan/historic (accessed on 22 February 2020).
- Annual Weather Averages near Wuhan. Available online: https://www.timeanddate.com/weather/china/wuhan/climate (accessed on 22 February 2020).
- Hubei Climate. Available online: http://en.hubei.gov.cn/hubei_info/climate/201305/t20130521_449918.shtml (accessed on 22 February 2020).







| Country | Province/ Region | Capital | Population [21,22,23] | Density, Population/km2 [22,24,25,26,27,28,29,30,31,32,33] | Gender Ratio [34,35] | Average Age, years [36,37] | Elevation, m [38] |
|---|---|---|---|---|---|---|---|
| China | Hubei | Wuhan | 59,170,000 | 318 | 1.06 | 38.4 | 37 |
| Guangdong | Canton (Guangzhou) | 113,460,000 | 630 | 1.06 | 38.4 | 21 | |
| Henan | Zhengzhou | 96,050,000 | 575 | 1.06 | 38.4 | 104 | |
| Zhejiang | Hangzhou | 57,370,000 | 562 | 1.06 | 38.4 | 19 | |
| Hunan | Changsha | 68,990,000 | 329 | 1.06 | 38.4 | 63 | |
| Anhui | Hefei | 63,240,000 | 454 | 1.06 | 38.4 | 37 | |
| Jiangxi | Nanchang | 46,480,000 | 278 | 1.06 | 38.4 | 37 | |
| Shandong | Jinan | 100,470,000 | 653 | 1.06 | 38.4 | 23 | |
| Jiangsu | Nanchino | 80,510,000 | 785 | 1.06 | 38.4 | 15 | |
| Chongqing | Chongqing | 31,020,000 | 377 | 1.06 | 38.4 | 244 | |
| Sichuan | Chengdu | 83,410,000 | 172 | 1.06 | 38.4 | 500 | |
| Heilongjiang | Harbin | 37,730,000 | 83 | 1.06 | 38.4 | 126 | |
| Beijing | Beijing | 21,540,000 | 1313 | 1.06 | 38.4 | 43.5 | |
| Shanghai | Shanghai | 24,240,000 | 3823 | 1.06 | 38.4 | 4 | |
| Hebei | Shijiazhuang | 75,560,000 | 403 | 1.06 | 38.4 | 83 | |
| Fujian | Fuzhou | 39,410,000 | 324 | 1.06 | 38.4 | 14 | |
| Guangxi | Nanning | 49,260,000 | 209 | 1.06 | 38.4 | 499 | |
| Shaanxi | Xi’an | 38,640,000 | 247 | 1.06 | 38.4 | 405 | |
| Yunnan | Kunming | 48,300,000 | 123 | 1.06 | 38.4 | 1892 | |
| Hainan | Haikou | 9,340,000 | 275 | 1.06 | 38.4 | 222 | |
| Guizhou | Guiyang | 36,000,000 | 205 | 1.06 | 38.4 | 1275 | |
| Tianjin | Tianjin | 15,600,000 | 1380 | 1.06 | 38.4 | 1078 | |
| Shanxi | Taiyuan | 37,180,000 | 181 | 1.06 | 38.4 | 800 | |
| Liaoning | Shenyang | 43,590,000 | 299 | 1.06 | 38.4 | 55 | |
| Jilin | Changchun | 27,040,000 | 2704 | 1.06 | 38.4 | 202 | |
| South Korea | Seoul | Seoul | 10,010,983 | 16541 | 1 | 43.2 | 38 |
| Daejeon | Daejeon | 1,493,979 | 2767 | 1 | 43.2 | 94 | |
| Gyeonggi | Suwon | 13,653,984 | 1341 | 1 | 43.2 | 87 | |
| South Gyeongsang | Changwon | 3,438,676 | 326 | 1 | 43.2 | 2 | |
| Italy | Lazio | Rome | 5,879,082 | 341 | 0.93 | 44.6 | 13 |
| Veneto | Venice | 4,905,854 | 272 | 0.96 | 45.1 | 1 | |
| Emilia-Romagna | Bologna | 4,459,477 | 199 | 0.95 | 45.7 | 54 | |
| Lombardy | Milan | 10,060,574 | 422 | 0.94 | 44.8 | 120 | |
| Japan | Tokyo | Tokyo | 13,929,286 | 6349 | 0.95 | 48.6 | 40 |
| Kanagawa Prefecture | Yokohama | 9,058,094 | 3770 | 0.95 | 48.6 | 500 | |
| Aichi Prefecture | Nagoya | 7,552,873 | 1500 | 0.95 | 48.6 | 56 | |
| Nara Prefecture | Nara | 1,348,930 | 365 | 0.95 | 48.6 | 56.4 | |
| Kansai region | Kyoto | 22,757,897 | 690 | 0.95 | 48.6 | 50 | |
| Tokushima Prefecture | Tokushima | 728,633 | 180 | 0.95 | 48.6 | 11 |
| Environmental Factors | Maximum Temperature °C | Minimum Temperature °C | Average Temperature °C | Relative Humidity % | Wind Speed km/h |
|---|---|---|---|---|---|
| Maximum Temperature | 1 | 0.63 | 0.83 | −0.11 | 0.35 |
| Minimum Temperature | 0.63 | 1 | 0.78 | 0.24 | 0.28 |
| Average Temperature | 0.83 | 0.78 | 1 | −0.14 | 0.15 |
| Relative Humidity | −0.11 | 0.24 | −0.14 | 1 | 0.33 |
| Wind Speed | 0.35 | 0.28 | 0.15 | 0.33 | 1 |
| Models No. | SP | Maximum Number of Layers | Maximum Number of Neurons in a Layer | Accuracy of Training (%) | Accuracy of Testing (%) |
|---|---|---|---|---|---|
| 1 | 0.6 | 5 | 5 | 73.9 | 71.4 |
| 2 | 0.6 | 5 | 10 | 91.3 | 71.4 |
| 3 | 0.6 | 5 | 15 | 95.7 | 85.7 |
| 4 | 0.6 | 5 | 20 | 80.5 | 42.9 |
| 5 | 0.6 | 5 | 25 | 91.3 | 71.4 |
| 6 | 0.6 | 10 | 5 | 95.7 | 71.4 |
| 7 | 0.6 | 10 | 10 | 73.9 | 71.4 |
| 8 | 0.6 | 10 | 15 | 82.6 | 71.4 |
| 9 | 0.6 | 10 | 20 | 95.7 | 57.1 |
| 10 | 0.6 | 10 | 25 | 87 | 71.4 |
| 11 | 0.6 | 15 | 5 | 82.6 | 71.4 |
| 12 | 0.6 | 15 | 10 | 91.3 | 71.4 |
| 13 | 0.6 | 15 | 15 | 87 | 71.4 |
| 14 | 0.6 | 15 | 20 | 91.3 | 71.4 |
| 15 | 0.6 | 15 | 25 | 87 | 85.7 |
| 16 | 0.6 | 20 | 5 | 91.3 | 85.7 |
| 17 | 0.6 | 20 | 10 | 95.7 | 42.9 |
| 18 | 0.6 | 20 | 15 | 91.3 | 42.9 |
| 19 | 0.6 | 20 | 20 | 82.6 | 85.7 |
| 20 | 0.6 | 20 | 25 | 95.7 | 71.4 |
| Models No. | SP | Maximum Number of Layers | Maximum Number of Neurons in a Layer | Ranking for Accuracy of Training | Ranking for Accuracy of Testing | Total Rank |
|---|---|---|---|---|---|---|
| 1 | 0.6 | 5 | 5 | 15 | 19 | 34 |
| 2 | 0.6 | 5 | 10 | 19 | 19 | 38 |
| 3 | 0.6 | 5 | 15 | 20 | 20 | 40 |
| 4 | 0.6 | 5 | 20 | 16 | 18 | 33 |
| 5 | 0.6 | 5 | 25 | 19 | 19 | 38 |
| 6 | 0.6 | 10 | 5 | 20 | 19 | 39 |
| 7 | 0.6 | 10 | 10 | 15 | 19 | 34 |
| 8 | 0.6 | 10 | 15 | 17 | 19 | 36 |
| 9 | 0.6 | 10 | 20 | 20 | 18 | 38 |
| 10 | 0.6 | 10 | 25 | 18 | 19 | 37 |
| 11 | 0.6 | 15 | 5 | 17 | 19 | 36 |
| 12 | 0.6 | 15 | 10 | 19 | 19 | 38 |
| 13 | 0.6 | 15 | 15 | 18 | 19 | 37 |
| 14 | 0.6 | 15 | 20 | 19 | 19 | 38 |
| 15 | 0.6 | 15 | 25 | 18 | 20 | 38 |
| 16 | 0.6 | 20 | 5 | 19 | 20 | 39 |
| 17 | 0.6 | 20 | 10 | 20 | 17 | 37 |
| 18 | 0.6 | 20 | 15 | 19 | 17 | 36 |
| 19 | 0.6 | 20 | 20 | 17 | 20 | 37 |
| 20 | 0.6 | 20 | 25 | 20 | 19 | 39 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirouz, B.; Shaffiee Haghshenas, S.; Shaffiee Haghshenas, S.; Piro, P. Investigating a Serious Challenge in the Sustainable Development Process: Analysis of Confirmed cases of COVID-19 (New Type of Coronavirus) Through a Binary Classification Using Artificial Intelligence and Regression Analysis. Sustainability 2020, 12, 2427. https://doi.org/10.3390/su12062427
Pirouz B, Shaffiee Haghshenas S, Shaffiee Haghshenas S, Piro P. Investigating a Serious Challenge in the Sustainable Development Process: Analysis of Confirmed cases of COVID-19 (New Type of Coronavirus) Through a Binary Classification Using Artificial Intelligence and Regression Analysis. Sustainability. 2020; 12(6):2427. https://doi.org/10.3390/su12062427
Chicago/Turabian StylePirouz, Behrouz, Sina Shaffiee Haghshenas, Sami Shaffiee Haghshenas, and Patrizia Piro. 2020. "Investigating a Serious Challenge in the Sustainable Development Process: Analysis of Confirmed cases of COVID-19 (New Type of Coronavirus) Through a Binary Classification Using Artificial Intelligence and Regression Analysis" Sustainability 12, no. 6: 2427. https://doi.org/10.3390/su12062427
APA StylePirouz, B., Shaffiee Haghshenas, S., Shaffiee Haghshenas, S., & Piro, P. (2020). Investigating a Serious Challenge in the Sustainable Development Process: Analysis of Confirmed cases of COVID-19 (New Type of Coronavirus) Through a Binary Classification Using Artificial Intelligence and Regression Analysis. Sustainability, 12(6), 2427. https://doi.org/10.3390/su12062427








