1. Introduction
The ancient water conservancy projects, such as the control project of Nel-Hammurabi on the Euphrates River built by the Babylon Kingdom, the manmade canals constructed by the ancient Roman Empire [
1], and the agricultural irrigation systems dating back to the 1st-6th centuries in Israel [
2] have long fallen into disuse. However, there are some old irrigation structures that are still in operation, such as the irrigation in sediment-laden rivers developed in ancient Peru [
3]. Moreover, the qanat system, a subterranean aqueduct used to convey water for irrigation and domestic consumption, originated in Iran as early as the 7th century BCE [
4], was brought to Spain in the 8th century, and then to the New World in the 16th century [
5,
6]. This system still irrigates farmlands in Iran at the present day.
The Dujiangyan Irrigation System (DIS) is one of the ancient irrigation systems which are still in operation. This system began in the 3rd century BCE, is characterized by the non-dam intake project and is still discharging its functions perfectly [
1]. It was listed as a World Cultural Heritage Site in 2000 and a World Heritage Irrigation Structure in 2018. The main headworks of the DIS are located in the transitional region, where the river flows from a gorge to an alluvial plain. The location has a 50 km distance and 273 m elevation difference from Chengdu City, China (
Figure 1). This is on the commanding point of the alluvial plain so as to prevent floodwater flowing directly to the Chengdu Plain [
7]. Natural topographical and hydrological features are used to exclude sediment and divert water for irrigation without the use of dams. The system has produced benefits in flood prevention, agricultural irrigation, and water consumption for many years [
8].
Recently, a dam was constructed upstream of the DIS (about 4 km from the Fish Mouth). The reservoir of the dam can be seen in
Figure 1. The dam construction was completed in 2006, and since then, it has provided a more stable water supply to the Dujiangyan areas during the dry season, and also reduced the peak flow discharge of the river during the flood season. Since this dam is a relatively new structure and the focus of the present study is on the historical performance of the DIS based on its natural and topographical characteristics during the past 2000 years, the effect of the dam is not taken into consideration in this study.
The headworks of the DIS are composed of three primary components: (1) The Fish Mouth (the front end looks like a fish mouth), a diversion embankment dividing the Minjiang River into the Inner River, primarily for irrigation, and the Outer River, mainly for flood and sediment discharge; (2) Feishayan, a low spillway dam removing sediment and excess water from the Inner River into the Outer River; and (3) Baopingkou (bottle-neck channel), a water intake automatically controlling intake discharge from the Inner River (
Figure 2).
The need to understand how the DIS has preserved its functionality for more than 2000 years and the need for protecting it have urged researchers and engineers to investigate the hydrodynamics of the system, such as flow motion, sediment transport, and riverbed evolution. They have been conducting research in the last few decades on the mechanisms of water and sediment diversion under different discharge conditions in order to improve the methods of protecting the system. Since the first physical model experiment of the DIS conducted in 1941 [
9], scholars have studied the characteristics of the water and sediment transport by using the prototype survey [
10,
11], physical hydraulics model [
12], and numerical model [
13,
14,
15]. As for the dynamic water diversion process, based on the ancients’ experience, more than 60% of the Minjiang River typically goes into the Inner River for the use of the Chengdu Plain during the low discharge period, while in the flood period, this ratio can reduce to less than 40% [
16]. The analysis of the prototype data carried out by Sun et al. suggested that after the construction of the check gate across the Outer River in 1974, the water distribution into the Inner River was close to 75% in spring time and only 37.5% in the flood season [
10]. Later, as a complement to the laboratory experiments conducted in Sichuan University [
12], a two-dimensional (2D) numerical model has been used to study the performance of the system under different inflow conditions [
13].
Many irrigation projects in history were abandoned due to sedimentation. The long-term vitality of the DIS project is linked to the fact that sediment is automatically excluded by natural characteristics of the system. Sediment deposition is primarily formed by the moving bed load from May to October [
11]. Based on the distorted movable model, the amount of bed load entering the Inner River through the Fish Mouth is only about 29% of the total load in the Minjiang River [
17]; and that is 26% based on the results of the prototype observations [
18]. The Feishayan begins to discharge sediment to the Outer River when the flow rate of the Inner River is over 500 m
3/s [
12]. The larger the flood discharge is, the higher is the discharge diversion ratio at the Feishayan and the more efficient is the system in discharging sediment from the Inner River. Under the function of the Feishayan, over 90% of the bed load carried into the Inner River can be discharged to the downstream area of the Outer River [
19]. In addition, the V-Shaped Dike Spillway, an auxiliary project of the DIS, also diverts sediment and excess water during periods of flood [
20]. Finally, less than 8% of the total sediment of the Minjiang River can reach the Baopingkou, ensuring that the irrigation lands receive clear water [
17]. It is notable that there have also been small amounts of sediment deposition in the Inner River section which have been dredged annually (probably since the irrigation system was first constructed).
At present, the prototype observations and model experiments can only explain the basics of the sediment discharge process in the DIS. On the other hand, the one-dimensional (1D) [
14] and 2D [
15] numerical models used for simulating riverbed evolution in the DIS have difficulty in describing the ‘dynamic’ sediment diversion, which has a key role in the understanding of the dynamics of the sediment discharge processes in the system. For 1D models, this is due to the one dimensionality of the model being able to describe the bed load movement process only in one channel while ignoring it in the other DIS channels. For 2D models, when considering only the continuity of the bed load, there is often a large time scale difference between flow and sediment motion, which results in non-accurate estimation of riverbed morphology. In addition, the grid-based models, due to the Eulerian description of the sediment medium, are unable to provide details of the motion of sediment particles between different channels.
In this study, to tackle these difficulties, the fluid flow in the DIS is simulated by solving the Shallow Water Equations (SWEs), which can effectively deal with the large scale of the study area, coupled with a newly proposed Sediment Mass (SM) model for the bed load transport. The fluid model is based on the coupled explicit-implicit solution algorithms of the SWEs and the SM model is developed from the Lagrangian particle modeling concept, considering the orderly movement (in the form of bed load transport belt) of large amounts of sediment. With the SM model, due to its Lagrangian framework, we can understand how sediment particles move from one channel to another, i.e., ‘dynamic’ sediment diversion. Examples of such particle modeling approaches in fluid flow simulation and sediment transport process were developed by Pu et al. [
21], Ran et al. [
22], and Zheng et al. [
23].
The developed coupled model is used to simulate the sediment motion in the DIS under different flow conditions; and the results are discussed to explain why the DIS has operated for 2300 years and is still functioning well.
2. Fluid Flow Model
The 2D Shallow Water Equations (Equations (1) and (2)) are solved for the fluid flow:
where:
η = water surface;
t = time;
h = flow depth;
u = the velocity vector with the longitudinal and transversal components of
u and
v, respectively;
AH = the horizontal eddy viscosity coefficient;
= gravitational acceleration; and
μ = the bed roughness coefficient.
The solution is based on the method used in Zheng et al. [
24]. The water level and flow velocity are calculated by the implicit Eulerian-Lagrangian method (ELM), i.e., the quantities at time
t +
dt are updated using those at time
t, implicitly, where
dt is the time step size in the flow model; and then the temporary ELM traced lines are corrected explicitly by using the Characteristics-based Splitting method, i.e., the intermediate values between times
t and
t +
dt are explicitly computed. This leads to the enhancement of the computational efficiency of the model as the detailed flow information lost in the implicit computation can be recovered by increasing the number of explicit intermediate computational steps. In fact, the coupled method merges the merits of the high computational accuracy from the explicit scheme with the high numerical efficiency and stability from the implicit scheme.
For the ELM computations, the computational domain is discretized by triangular mesh elements, and the governing equations are solved by using the Finite Element Method. For the boundary conditions, three types of boundaries are considered:
(1) an open boundary applied in the flow inlet and outlet;
(2) a land boundary satisfying slip and non-penetration conditions; and
(3) a moving boundary relating to the continuous changes of flow and sediment transport. More details on the numerical discretization and boundary conditions can be found in Zheng et al. [
24] and Chen et al. [
25].
The model has previously been used for a few applications including dam-break flow [
24], long-term river meandering process [
24], and unsteady flow propagation [
26].
Due to the bending section of the Minjiang River and the diversion of flow at the Fish Mouth, the effect of secondary flow is not negligible in the present application, an effect which is often neglected in 2D SWE models. To include the secondary flow effect in the present model, a transversal velocity
vr is computed at the nodes of the computational domain by using the Rozovskii formula (Equation (3), [
27]), and added to the transversal component of
u (i.e.,
v) with the magnitude of velocity |
u|being unchanged. This applies a modification to the direction of the velocity vector, while its magnitude remains unchanged.
where:
κ = von Karman constant (~0.4);
R = radius of curvature;
λ = normalized vertical co-ordinate (which is set to 0.3 here);
; and
.
3. Sediment Transport Model
In the present study, bed load is considered as the dominant form of sediment transport, and a particle-based SM model is proposed to model the convection motion of bed load in a disk-like form, considering sediment as a discrete medium and bed load as a motion of a group of sediment grains. In the following, a description of the SM model is presented.
Taking only the convective motion into account, in order to minimize the error caused by the omission of the sediment diffusion, a time step size smaller than the one used in the flow model is set for the calculation of sediment motion, i.e., ΔT = dt/N, where N is the number of segments determined based on the velocity gradient (set to 2~10 in this study). Disks, representing SMs, are used to discretize the sediment domain. Each disk contains a number of sediment particles virtually, with a circular bottom area defining the influence domain of the SM, and a height (thickness) equal to the multiplication of the porosity of sediment medium by the mean diameter of the sediment grains within the disk influence area. The disks can overlap each other and move over the fluid domain based on their velocity, which is determined as follows.
Firstly, in each sub-step Δ
T, the velocity of a virtual sediment particle is calculated as follows:
where:
ut and
ut+ΔT = the sediment particle velocity vector at times
t and
t+Δ
T, respectively; and
ua = the increase in the velocity of the sediment particle during Δ
T. The magnitude of
ua, i.e.,
ua, is calculated by Equation (5); and its direction is determined by considering a normal distribution for the angle between it and the streamline (as depicted in
Figure 3a) based on the assumption that the direction of
ua is random due to the randomness of sediment particle collisions during bed load transport:
where
uc = critical incipient velocity computed by the Sharmove formula [
28]:
and
uw = mean flow velocity at the center of the SM, calculated as the arithmetic average of flow velocity at the nodes located inside the influence area of the disk. In addition,
β = correction coefficient (which is set to 0.1 in the present simulations),
γs = specific weigh of sediment grains (= 26.5 kN/m
3 here),
γ = specific weigh of flow (= 10 kN/m
3 for water), and
D = diameter of sediment grains.
To determine the direction of the velocity vector
ua a normal distribution is considered for the angle between the streamline and the direction of the
ua vector (as depicted in
Figure 3a). Then, the velocity of the SM is calculated as
uSM =
ut+ΔT ×
P, where the Einstein bed load theory is used to estimate the incipient probability
P:
in which
and
J = the bed slope. The displacement of the SM in each sub-step is then evaluated as Δ
x =
uSM × Δ
T.
Figure 3 shows the resultant velocity of a sediment particle and the motion of an SM according to its velocity.
After the position of the SM disks is updated, the calculated properties of the sediment domain are transported to the fluid domain. For this, the velocity and thickness of each disk is converted to the flow domain nodes that are located inside the influence domain of the disk using a weighting function (Spline here), and then the converted values at each node are summed up. This yields the average thickness
hs and velocity
us of the sediment layer at the position of the nodes. Then, the bed load transport rate
qb is estimated using Equation (8), and the change of the riverbed elevation from
t to
t + Δ
T is computed by using Equation (9):
where
ξ = porosity; and
zb = thickness of the movable bed layer.
Then, the fluid model equations are solved in the next sub-step, and this process is repeated until the number of sub-steps reaches N. Then, for the next time step, i.e., at t + dt, SMs are regenerated instead of turning the node information back to them. This will reduce the error related to the diffusion effect without increasing extra calculation.
5. Discussion
Three key components of the DIS (i.e., the Fish Mouth, the Feishayan, and the Baopingkou) combining with ancillary embankments and watercourses ensure there is efficient sediment diversion and regular water supply for the Chengdu Plain. The reason behind that the DIS is still performing designated functions today is that the sediment is automatically transported in an orderly manner without causing adverse effects on the system. A summary of the operation of the DIS is the 6-character maxim “deeply clearing channel (specially meaning the channel at the Fengqiwo Section), building low dike” [
1].
The purpose of a “deeply clearing channel” is to keep the sediment transport in an equilibrium state during a year, namely, the equilibrium of erosion and deposition in the Inner River. This requires the longitudinal profile of the riverbed to reach the balanced section. Therefore, annual dredging is necessary. Also, the dredging level needs to reach the iron bar markers (the position of the riverbed balanced section) buried in the Fengqiwo Section. If the dredging depth is shallower than the iron bar markers, the sediment will further deposit, which is an adverse effect to the sediment diversion and the water intake of irrigation areas. If the dredging depth exceeds the iron bar markers (equivalent to the reduction of the erosional basis), then the erosion will strengthen and cause the non-equilibrium of the sediment supply and transport. The DIS is a successful case where the theory of riverbed balanced section can be applied to the water conservancy project [
30].
“Building low dike” means that the height of the Feishayan should be low, which is conducive to discharge water and sediment in the flood period. It shows that floods have been a key factor in designing the DIS. If a hydraulic system is designed without taking floods into consideration, it is unlikely that it can remain in working condition. There are numerous examples of hydraulic works built in which usage for irrigation and the hydraulic profile for the flood period have been combined. A few examples are the spate irrigation system in Africa [
31,
32,
33,
34] and the ancient irrigation system in the Central Negev desert [
35].
Principles of the DIS are still valuable references in modern diversion project design, including: making full use of the natural bend flow to discharge water and sediment; annual well-organized maintenance to dredge a specific river section; and coexistence of water intake and flood control. This is a good example of comprehensively utilizing natural water resources and realizing harmonious coordination between humans and the nature.
6. Conclusions
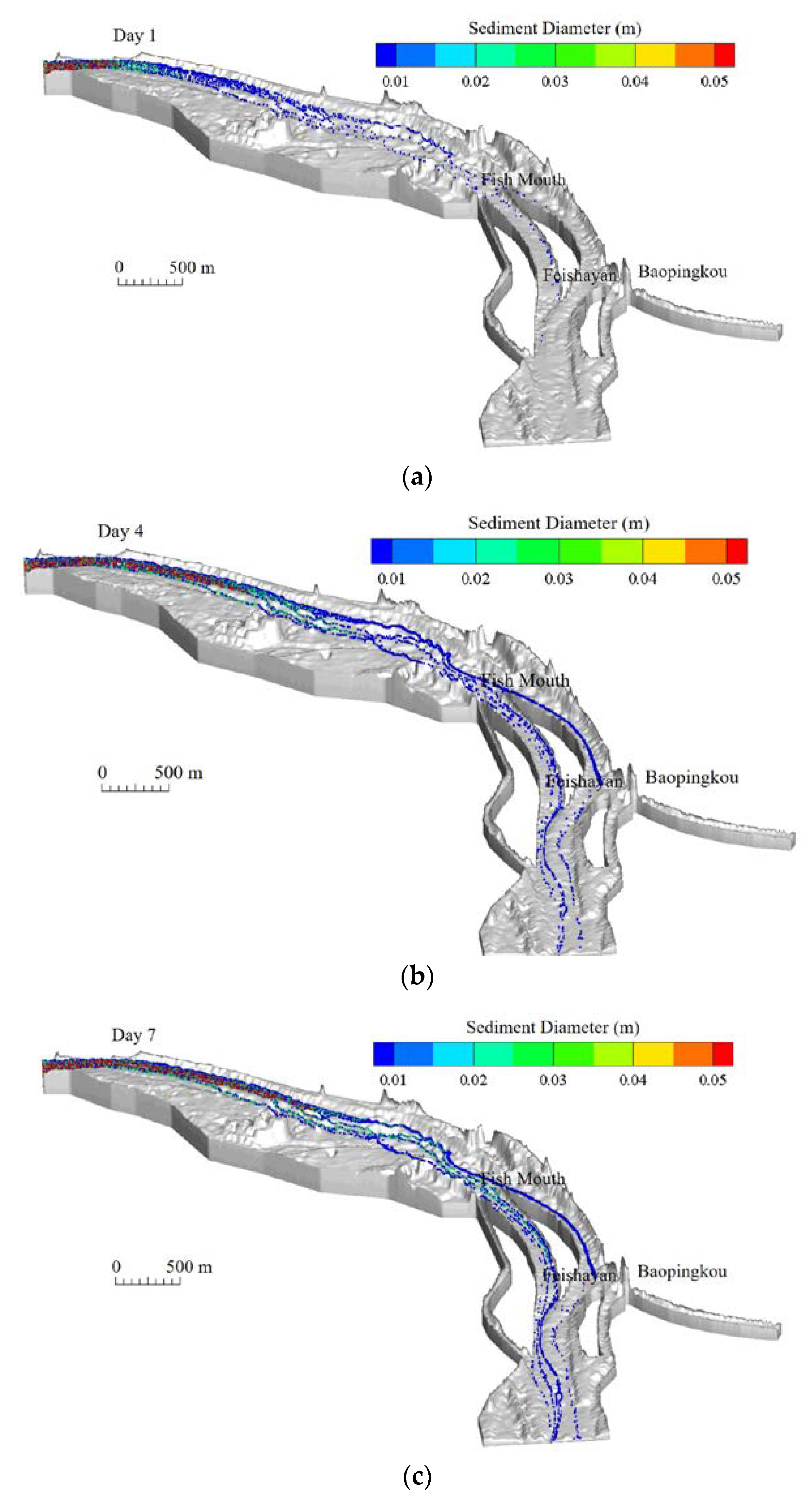
The DIS, both naturally and with the aid of man-made structures, has been functioning for 2300 years, excluding sediment, preventing flood, and diverting water for irrigation in the Chengdu plain. To better understand the hydrodynamics and sediment transport processes in the system, numerical modeling approaches were used in this study. A coupled explicit-implicit numerical scheme was applied to simulate the fluid flow, coupled with an SM model for the sediment transport. The simulations were carried out for three different flow regimes: low, medium, and high (based on the 1000-year flood event) discharges; and the water and sediment diversions at the Fish Mouth, Feishayan, and V-shaped Dike Spillway were investigated in detail.
According to the model results, (1) under the low discharge condition, the system mainly diverts the water flow at the Fish Mouth for irrigation; (2) under the medium discharge condition, the current carries more bed load flowing into the Inner River, which is then discharged through the Feishayan to the Outer River; and (3) under the high discharge condition, the main current flows straight into the Outer River, thus the bed load is discharged directly through that channel. The model was able to demonstrate these processes numerically and complement the findings of the previous studies. The processes are mainly attributed to the central shoal located upstream of the Fish Mouth and the bending channel, i.e., at low discharges, the shoal is unsubmerged, thus it diverts more water into the Inner River; and when coming to the high discharge conditions, the shoal is submerged and the water flows straight into the Outer River.
In summary, the water flow and sediment diversion project (Fish Mouth), the discharge projects (Feishayan and V-shaped Dike Spillway) and the intake project (Baopingkou) make full use of the flow dynamics and topographical characteristics (e.g., the bending channel and the elevation differences between these components) to effectively discharge excess floodwater and provide a reliable water supply to the irrigation areas. The results and discussions in this study clearly explain why the DIS has operated for thousands of years, and provide useful references for the engineering design of such systems. The proposed numerical models, however, still need rigorous and comprehensive validations based on benchmark tests of flow and sediment transport, different channel geometries, and various flow conditions. These are considered as future study areas.