Grain Area Yield Index Insurance Ratemaking Based on Time–Space Risk Adjustment in China
Abstract
:1. Introduction
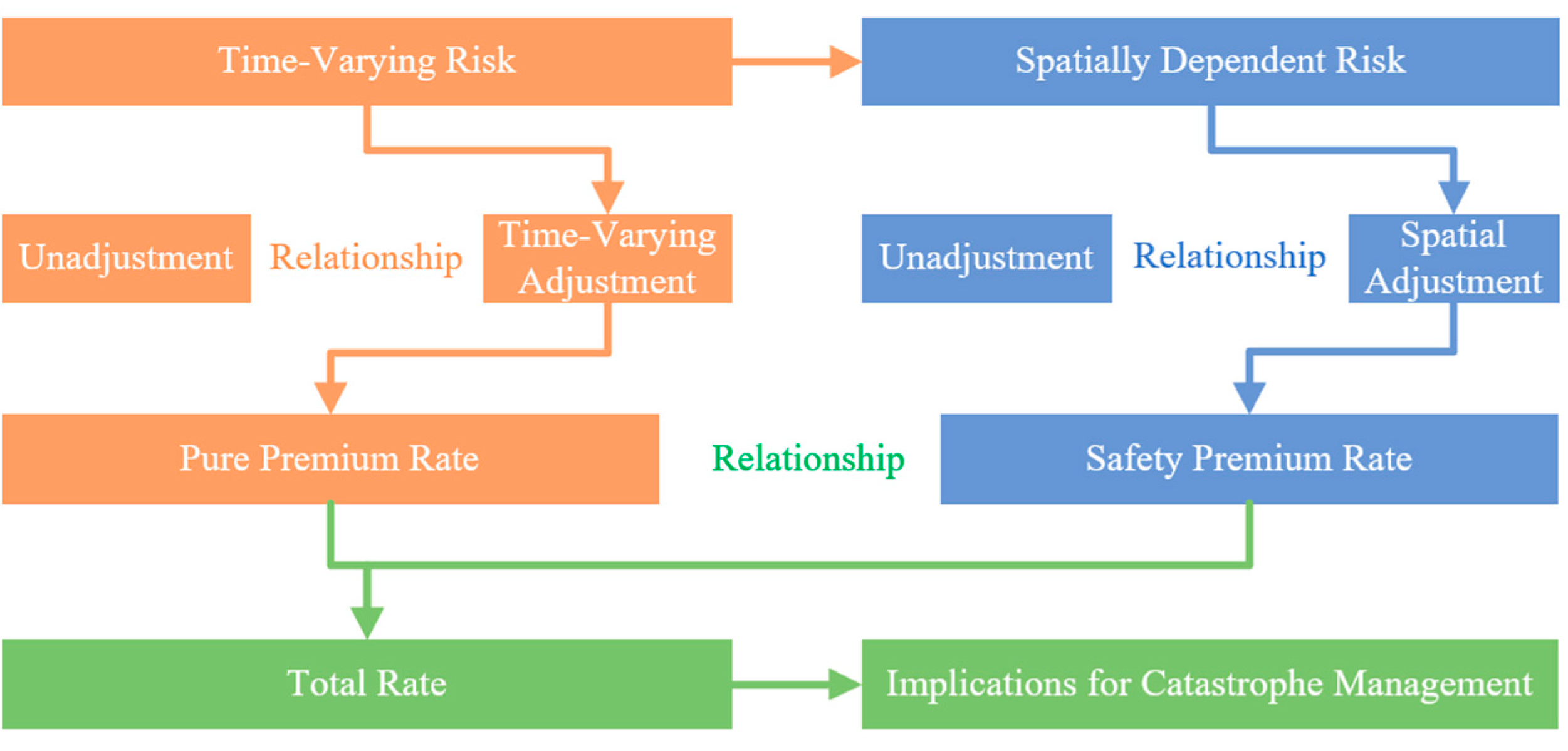
2. Methodology
2.1. Pure Premium Ratemaking Based on Time-Varying Risk Adjustment
2.2. Safety Premium Ratemaking Based on Spatially Dependent Risk Adjustment
2.3. Study Area and Data Collection
3. Results
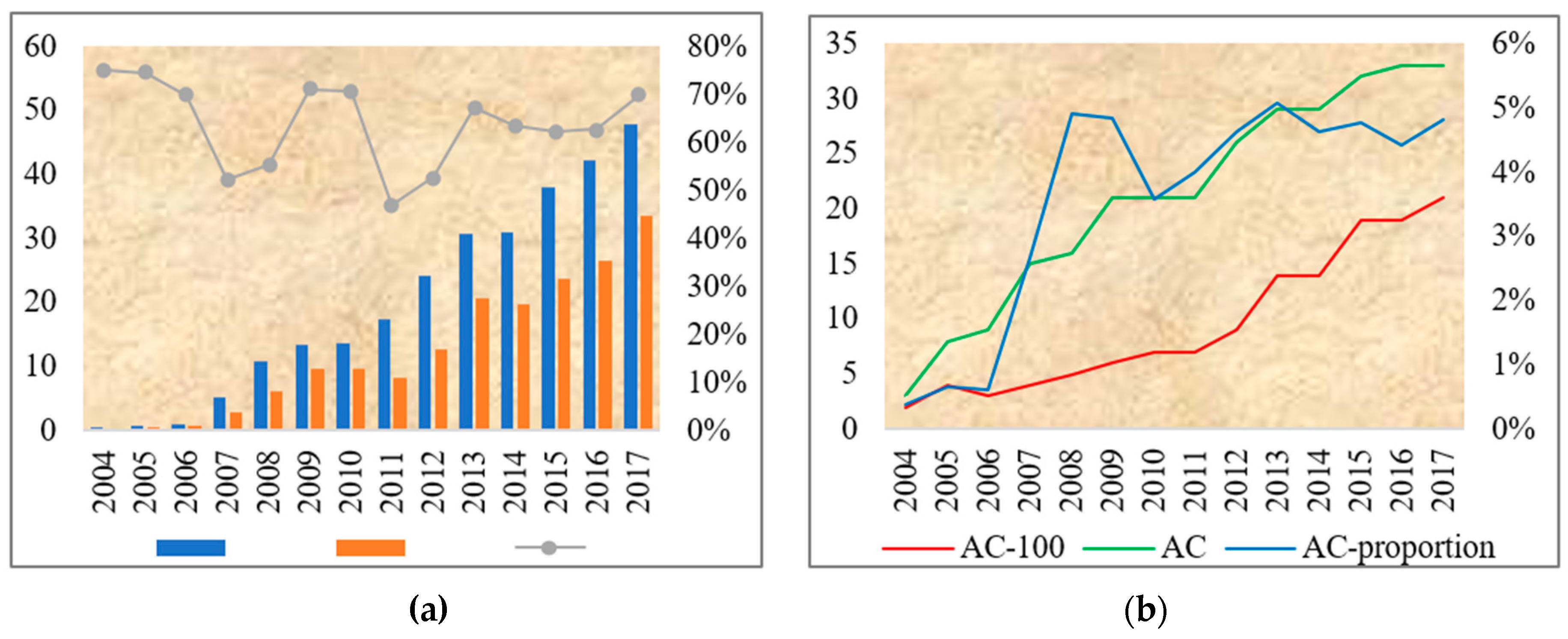
3.1. Estimated Results of Time-Varying Risk Adjustment Coefficients and Pure Premium Ratemaking
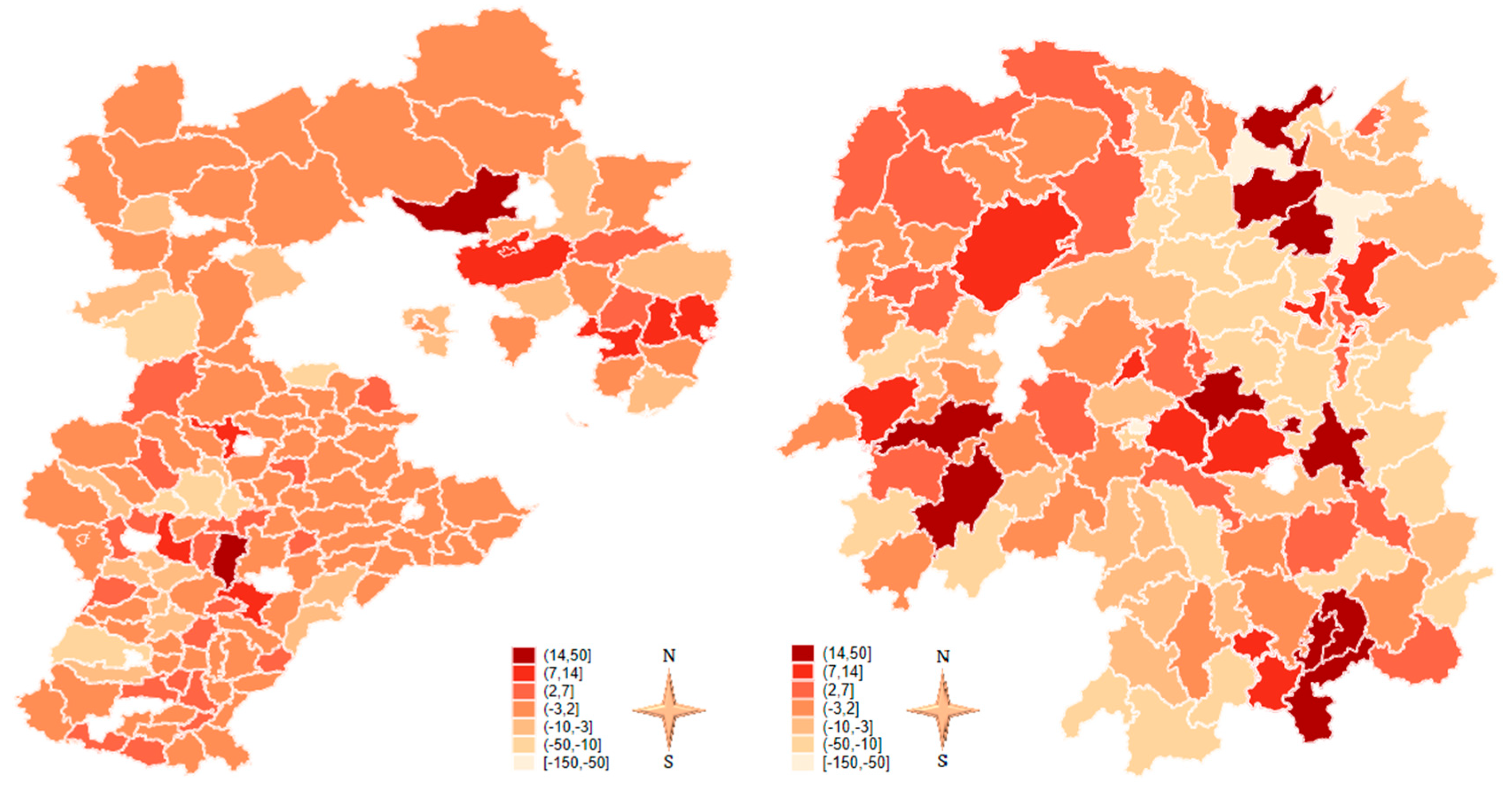
3.2. Loading Factor and Safety Premium Ratemaking
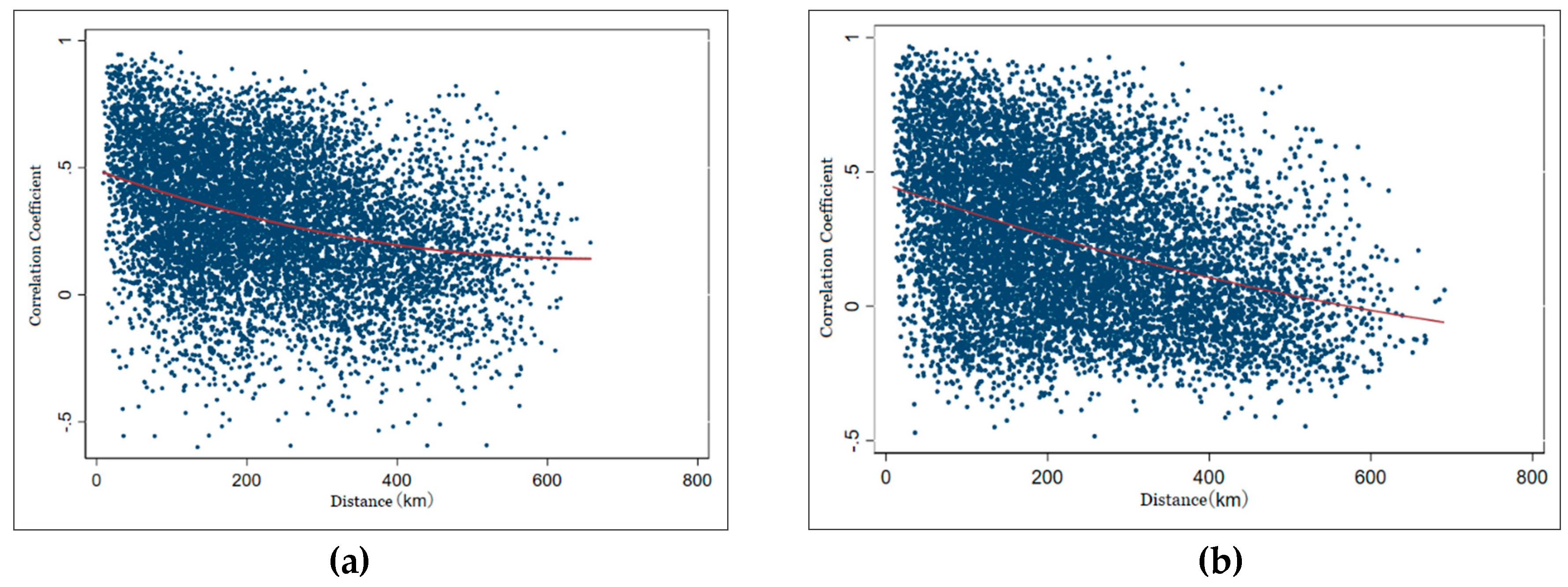
3.3. Robustness Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Tuo, G.; Li, H. Some Thoughts on Improving China′s Agricultural Insurance System. China Insur. 2019, 8–17. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, K.; Li, Y.; Wang, Y. On the Current situation and Problems of Risk Protection of Agricultural Insurance in China and Relevant Suggestions. Insur. Stud. 2019, 3–18. [Google Scholar] [CrossRef]
- Ministry of Finance of the People′s Republic of China. Notice on Printing and Distributing the Guiding Opinions on Accelerating the High-quality Development of Agricultural Insurance. 2019. Available online: http://www.mof.gov.cn/mofhome/jinrongsi/zhengwuxinxi/zhengcefabu/201910/t20191012_3400537.html (accessed on 18 January 2020).
- Tuo, G.; Zhu, J. Several Issues to be Solved for Improving on the Agricultural Insurance System in China. Insur. Stud. 2014, 44–53. [Google Scholar] [CrossRef]
- Miranda, M.J.; Glauber, J.W. Systemic Risk, Reinsurance, and the Failure of Crop Insurance Markets. Am. J. Agr. Econ. 1997, 79, 206–215. [Google Scholar] [CrossRef]
- Ye, T.; Hu, W.; Barnett, B.J.; Wang, J.; Gao, Y. Area Yield Index Insurance or Farm Yield Crop Insurance? Chinese Perspectives on Farmers′ Welfare and Government Subsidy Effectiveness. J. Agr. Econ. 2019, 71, 144–164. [Google Scholar] [CrossRef] [Green Version]
- Bao, L.; Jiang, S. A Research on the Mechanism of Agricultural Insurance Catastrophe Risk Dispersion. Insur. Stud. 2019, 36–51. [Google Scholar] [CrossRef]
- He, X.; Wang, K. Justification and Path Selection for Public Finance to Support the Risk Diversification Mechanism of Agriculture Insurance. Issues Agric. Econ. 2013, 34, 36–40. [Google Scholar] [CrossRef]
- Ouyang, Y.; Li, Z. Adverse Selection, Systematic Risks and Sustainable Development of Policy Agricultural Insurance. Insur. Stud. 2010, 4, 66–71. [Google Scholar] [CrossRef]
- Coble, K.H.; Knight, T.O.; Pope, R.D.; Williams, J.R. Modeling Farm-Level Crop Insurance Demand with Panel Data. Am. J. Agr. Econ. 1996, 78, 439–447. [Google Scholar] [CrossRef]
- The People′s Republic of China. National Climate Change Adaptation Strategy. Available online: http://www.gov.cn/gongbao/content/2014/content_2620283.htm (accessed on 2 January 2020).
- Zhu, Y.; Goodwin, B.K.; Ghosh, S.K. Modeling Yield Risk under Technological Change: Dynamic Yield Distributions and the U.S. Crop Insurance Program. J. Agric. Resour. Econ. 2011, 36, 192–210. [Google Scholar]
- Weng, C.; Porth, L.; Tan, K.S.; Samaratunga, R. Modelling the Sustainability of the Canadian Crop Insurance Program: A Reserve Fund Process Under a Public–Private Partnership Model. Geneva Papers Risk Insur. Issues Pract. 2017, 42, 226–246. [Google Scholar] [CrossRef]
- Liu, B.; Mei, X. Theory and Practice of Agricultural Insurance; Science Press: Beijing, China, 2010; pp. 189–193. [Google Scholar]
- Goodwin, B.K. Problems with Market Insurance in Agriculture. Am. J. Agr. Econ. 2001, 83, 643–649. [Google Scholar] [CrossRef]
- Tack, J.B.; Ubilava, D. Climate and Agricultural Risk: Measuring the Effect of ENSO on U.S. Crop Insurance. Agr. Econ. Blackwell 2015, 46, 245–257. [Google Scholar] [CrossRef]
- Shen, Z.; Odening, M. Coping with Systemic Risk in Index-Based Crop Insurance. Agr. Econ. Blackwell 2013, 44, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Thomä, J.; Dupré, S.; Hayne, M. A Taxonomy of Climate Accounting Principles for Financial Portfolios. Sustain. Basel 2018, 10, 328. [Google Scholar] [CrossRef] [Green Version]
- Skees, J.R.; Black, J.R.; Barnett, B.J. Designing and Rating an Area Yield Crop Insurance Contract. Am. J. Agr. Econ. 1997, 79, 430–438. [Google Scholar] [CrossRef]
- Alan, P.K.; Keith, C. Modeling Conditional Yield Densities. Am. J. Agr. Econ. 2003, 85, 291–304. [Google Scholar] [CrossRef]
- Goodwin, B.K.; Ker, A.P. Nonparametric Estimation of Crop Yield Distributions: Implications for Rating Group-Risk Crop Insurance Contracts. Am. J. Agr. Econ. 1998, 80, 139–153. [Google Scholar] [CrossRef]
- Park, E.; Brorsen, B.W.; Harri, A. Using Bayesian Kriging for Spatial Smoothing in Crop Insurance Rating. Am. J. Agr. Econ. 2018, 101, 330–351. [Google Scholar] [CrossRef]
- Ren, J.; Li, S. Estimation of the Risk of Crop Disaster Losses in China: Method Selection and Improvement. Insur. Stud. 2017, 75–84. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, K. Integrated Agricultural Risk Management in China; China Agricultural Science and Technology Press: Beijing, China, 2015; pp. 75–82. [Google Scholar]
- Liang, L. A Comparison and Choice on the Pure Rate-making Methods of Grain Insurance in China. J. Quant. Tech. Econ. 2011, 28, 124–134. [Google Scholar] [CrossRef]
- Urban, D.W.; Sheffield, J.; Lobell, D.B. The Impacts of Future Climate and Carbon Dioxide Changes on the Average and Variability of US Maize Yields under Two Emission Scenarios. Environ. Res. Lett. 2015, 10. [Google Scholar] [CrossRef]
- Mar, S.; Nomura, H.; Takahashi, Y.; Ogata, K.; Yabe, M. Impact of Erratic Rainfall from Climate Change on Pulse Production Efficiency in Lower Myanmar. Sustain. Basel 2018, 10, 402. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Y. Research on Actuarial Models in Agricultural Insurance; Tsinghua University Press: Beijing, China, 2018; pp. 25–26. [Google Scholar]
- Harri, A.; Coble, K.H.; Ker, A.P.; Goodwin, B.J. Relaxing Heteroscedasticity Assumptions in Area-Yield Crop Insurance Rating. Am. J. Agr. Econ. 2011, 93, 707–717. [Google Scholar] [CrossRef]
- Ker, A.P.; Tolhurst, T.N. On the Treatment of Heteroscedasticity in Crop Yield Data. Am. J. Agr. Econ. 2019, 101, 1247–1261. [Google Scholar] [CrossRef]
- Wang, H.H.; Zhang, H. On the Possibility of a Private Crop Insurance Market: A Spatial Statistics Approach. J. Risk Insur. 2003, 70, 111–124. [Google Scholar] [CrossRef]
- Okhrin, O.; Odening, M.; Xu, W. Systemic Weather Risk and Crop Insurance: The Case of China. J. Risk Insur. 2013, 80, 351–372. [Google Scholar] [CrossRef] [Green Version]
- Cao, N.; Yang, R.; Luo, S. A Study on Estimation of Premium for Cotton Revenue Insurance based on Clayton Copula Function. Stat. Res. 2017, 34, 92–99. [Google Scholar] [CrossRef]
- Paudel, Y. A Comparative Study of Public—Private Catastrophe Insurance Systems: Lessons from Current Practices. Geneva Pap. 2012, 37, 257–285. [Google Scholar] [CrossRef] [Green Version]
- Guyon, X. Random Fields on a Network: Modeling, Statistics and Applications; Springer: New York, NY, USA, 1995. [Google Scholar]
- Kaas, R.; Goovaerts, M.; Dhaene, J.; Denuit, M. Modern Actuarial Risk Theory Using R; Springer: New York, NY, USA, 2008; pp. 30–36. [Google Scholar]
- Huang, J.; Wang, Y.; Wang, J. Farmers′ Adaptation to Extreme Weather Events through Farm Management and Its Impacts on the Mean and Risk of Rice Yield in China. Am. J. Agr. Econ. 2014, 97, 602–617. [Google Scholar] [CrossRef]
- Chen, S.; Chen, X.; Xu, J. Impacts of Climate Change on Agriculture: Evidence from China. J. Environ. Econ. Manag. 2016, 76, 105–124. [Google Scholar] [CrossRef]
- Ren, J.; Li, X. The Impact of Crop Unit Yield Risk Distribution based on Heteroscedasticity Adjustment on Premium Rates. Insur. Stud. 2019, 74–87. [Google Scholar] [CrossRef]
- Ding, S.; Li, Z. Urgency and Development Path of Establishing Agricultural Insurance Catastrophe Risk Decentralization Mechanism. China Insur. 2019, 23–29. [Google Scholar] [CrossRef]
- Feng, W. Market Failure and Institution Supply of Agriculture Insurance in China. J. Financ. Res. 2004, 4, 124–129. [Google Scholar]
- Yang, R.; Sun, J. Agricultural Insurance Catastrophe Threshold Point and Risk Stratification Calculation. Stat. Decis. 2018, 34, 28–32. [Google Scholar] [CrossRef]
- Stohs, S.; LaFrance, J. A Learning Rule for Inferring Local Distributions over Space and Time. In Proceedings of the 2nd Annual Advanced in Econometrics Conference, Louisiana State University, Baton Rouge, LA, USA, 7–9 November 2003. [Google Scholar]


| Province | Counties (n) | Area (10,000 km2) | Yield Per Unit Area (kg/Ha) | ||
|---|---|---|---|---|---|
| Average | Max | Min | |||
| Henan | 108 | 16.70 | 5281.32 | 7714.33 | 2880.42 |
| Hebei | 135 | 18.88 | 4795.66 | 7675.55 | 1185.47 |
| Shanxi | 112 | 15.67 | 3642.67 | 7258.71 | 1029.40 |
| Hunan | 117 | 21.18 | 5613.70 | 7348.39 | 3163.69 |
| Jilin | 40 | 18.74 | 6052.16 | 9992.24 | 2859.93 |
| Zhejiang | 55 | 10.18 | 5400.06 | 6626.36 | 3757.63 |
| Fujian | 58 | 12.40 | 4973.71 | 6265.97 | 3950.41 |
| All | 625 | 113.75 | 4976.23 | 9992.24 | 1029.40 |
| Province | Sig-num 2 | Ratio 3 | Total- | Sig- | ||
|---|---|---|---|---|---|---|
| n | > 2 | < 2 | ||||
| Henan | 34 | 1 | 33 | 31.48% | −6.444 | −9.002 |
| Hebei | 23 | 9 | 14 | 17.04% | −0.300 | 0.051 |
| Shanxi | 36 | 4 | 32 | 32.14% | −3.297 | −6.473 |
| Hunan | 22 | 9 | 13 | 18.80% | −4.180 | −11.806 |
| Jilin | 11 | 3 | 8 | 27.50% | −4.068 | −5.531 |
| Zhejiang | 9 | 6 | 3 | 16.36% | 0.595 | 1.211 |
| Fujian | 11 | 1 | 10 | 18.97% | −4.398 | −20.781 |
| All | 146 | 33 | 113 | 23.36% | −3.163 | −7.371 |
| Rate Styles | Pv-1 1 | Pv-2 | Pv-3 | Pv-4 | Pv-5 | Pv-6 | Pv-7 | Average Diff 2 |
|---|---|---|---|---|---|---|---|---|
| Pure premium rate 3 | 2.854 | 3.588 | 4.322 | 3.792 | 3.996 | 3.776 | 3.601 | 0.568 |
| Adj 4-pure premium rate | 2.289 | 3.114 | 3.626 | 3.230 | 3.382 | 3.229 | 3.083 | |
| Loading factor | 1.659 | 1.204 | 0.954 | 0.842 | 0.787 | 0.747 | 0.735 | 0.029 |
| Adj-safety factor | 1.742 | 1.180 | 0.912 | 0.790 | 0.734 | 0.689 | 0.680 | |
| Safety premium rate | 4.735 | 4.321 | 4.123 | 3.191 | 3.146 | 2.822 | 2.647 | 0.665 |
| Adj-safety premium rate | 3.987 | 3.676 | 3.307 | 2.552 | 2.482 | 2.227 | 2.097 | |
| Total rate | 7.588 | 7.909 | 8.446 | 6.983 | 7.141 | 6.598 | 6.248 | 1.233 |
| Adj-total rate | 6.276 | 6.790 | 6.933 | 5.781 | 5.864 | 5.456 | 5.180 | |
| Total rate diff | 1.312 | 1.119 | 1.513 | 1.202 | 1.277 | 1.142 | 1.068 | 1.233 |
| Detrending Model (Significant Level) | Sig-num | Insig-num 1 | Total- | Sig- | ||||
|---|---|---|---|---|---|---|---|---|
| num | > 2 | < 2 | Ratio | num | Ratio | |||
| Quadratic (5%) | 146 | 29 | 117 | 23.36% | 479 | 76.64% | −3.163 | −7.371 |
| Lowess 2 (5%) | 180 | 28 | 152 | 28.80% | 445 | 71.20% | −4.437 | −9.045 |
| Consistency 3 (5%) | 68.49% | 55.17% | 71.80% | — | 83.3% | — | — | — |
| Quadratic (10%) | 194 | 45 | 149 | 31.04% | 431 | 68.96% | −3.163 | −6.035 |
| Lowess (10%) | 232 | 41 | 191 | 37.12% | 393 | 62.88% | −4.437 | −8.137 |
| Consistency (10%) | 73.20% | 57.78 | 77.85% | — | 79.1% | — | — | — |
| Unadjust 1-“θ = 2” | Unadjust-“” | “θ = 2”-“” | |
|---|---|---|---|
| All counties (625) | 0 | 0.016*** 2 | 0.017*** |
| Sig counties (146) | 0 | 0.027*** | 0.027*** |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Ren, J.; Niu, B.; Wu, H. Grain Area Yield Index Insurance Ratemaking Based on Time–Space Risk Adjustment in China. Sustainability 2020, 12, 2491. https://doi.org/10.3390/su12062491
Li X, Ren J, Niu B, Wu H. Grain Area Yield Index Insurance Ratemaking Based on Time–Space Risk Adjustment in China. Sustainability. 2020; 12(6):2491. https://doi.org/10.3390/su12062491
Chicago/Turabian StyleLi, Xiaotao, Jinzheng Ren, Beibei Niu, and Haiping Wu. 2020. "Grain Area Yield Index Insurance Ratemaking Based on Time–Space Risk Adjustment in China" Sustainability 12, no. 6: 2491. https://doi.org/10.3390/su12062491




