A Comparative Assessment of Analytical Fate and Transport Models of Organic Contaminants in Unsaturated Soils

Abstract

Analytical models for the simulation of contaminants’ fate and transport in the unsaturated zone are used in many engineering applications concerning groundwater resource management and risk assessment. As a consequence, several scientific studies dealing with the development and application of analytical solutions have been carried out. Six models have been selected and compared based on common characteristics to identify pros and cons as well as to highlight any difference in the final output. The analyzed models have been clustered into three groups according to the assumptions on contaminant source and physico-chemical mechanisms occurring during the transport. Comparative simulations were carried out with five target contaminants (Benzene, Benzo(a)pyrene, Vinyl Chloride, Trichloroethylene and Aldrin) with different decay’s coefficient, three types of soil (sand, loam and clay) and three different thicknesses of the contaminant source. The calculated concentration at a given depth in the soil for the same contamination scenario varied greatly among the models. A significant variability of the concentrations was shown due to the variation of contaminant and soil characteristics. As a general finding, the more advanced is the model, the lower the predicted concentrations; thus, models that are too simplified could lead to outcomes of some orders of magnitude greater than the advanced one.

1. Introduction

The release of organic contaminants into the environment represents a growing threat for groundwater and human health, as evidenced by the concentrations measured in several groundwater bodies [1,2,3,4,5]. Groundwater contamination is a significant environmental issue because it can damage potable water supply, endangering human health [6,7], and can affect aquatic ecosystems [8,9]. Organic contaminants moving in groundwater come from both point sources (solid waste tips, landfills, leaking storage tanks and leaking sewers) and diffuse sources (agricultural activities and farmyard drainage) [10]. Most of the fate and transport processes take place into the unsaturated zone [11], commonly known as vadose zone, posing a great concern in terms of environmental preservation and protection [12].

Due to the increasing interest in groundwater protection, models for simulating contaminants fate and transport in the unsaturated zone are a valuable and useful tool in many scientific and engineering applications [13,14,15,16,17]. They allow to evaluate the concentration of the chemicals at the point of exposure on the basis of source concentration [18] or they are useful in the assessment of the best technical solution in remediation practices [19,20,21,22,23].

The modelling of transport processes in the vadose zone is a challenging task [24], more complex than the modelling of fate and transport of contaminants in water bodies [25]. On one hand, a wide range of chemicals with variable physical-chemical properties can migrate through the unsaturated zone and interact between them and with soil; on the other hand, different transport mechanisms (advection; dispersion-diffusion) and reaction processes (sorption; abiotic transformation; biodegradation) can act simultaneously in two coupled phases (air and water) [26,27]. Several modelling approaches are available in the scientific literature, ranging from models that solve a single equation (solute transport) [28,29,30] to more complex models that solve a set of governing equations (e.g., groundwater flow, solute transport, heat movement, etc.) [31,32]. Models can be classified as analytical or numerical [33]. Numerical models allow simulating contaminant transport for both steady-state and transient groundwater flow, in three-dimensional, heterogeneous and anisotropic media with complex initial and boundary conditions, for multi-contaminant systems with different types of reactions. However, this high complexity requires a large number of input parameters, which may affect the reliability and accuracy of the prediction. This makes them unsuitable for many applications [34]. Analytical models are based on closed form solutions of governing equations; thus, they require a high level of simplification of the hydrogeological setting. Usually, they assume homogeneous soils, simple geometries, constant or highly simplified initial and boundary conditions and the transport of a single component [35]. Hence, they are characterized by ease of use and a limited number of input parameters. These peculiarities make them especially suitable for Tier II risk assessment [34,36].

Different reviews discussing many aspects of organic contaminant fate and transport models in unsaturated zone are presented in literature. In [37] models dealing with solute transport in heterogeneous media are discussed, by presenting their theoretical aspects and related applications. Vanclooster and co-workers [38] focus upon solute transport mechanisms at core scale and field scale and describe some modelling approaches. In [26] and [39] the authors analyze fate and transport of volatile organic compounds (VOCs), with experimental and modelling studies [39], providing a wide list of models [26]. Šimůnek [40] describes several models reproducing mechanisms of preferential and non-equilibrium flow and transport. Finally, Nolan and co-workers [41] tested seven transport models for pesticides with the data sets of two test sites.

None of the existing reviews focus exclusively on a comparison of analytical models. Furthermore, in the available reviews, analytical models are often described in qualitative terms neglecting their comparison in terms of numerical outputs. In order to fill this gap, a review of analytical models from a quantitative point of view is proposed in this paper. Pros and cons as well as differences in the outcomes of the different models are finally reported as result of this comparison. Six models have been selected among several unsaturated zone models existing in the scientific literature. They are presented in ASTM [42], Troldborg and co-workers (2009) [43] and (2008) [44], Verginelli and Baciocchi [45], Enfield and co-workers [46], Spence and Walden [47] and later discussed in Section 2. They model the fate and transport of organic contaminants dissolved in the aqueous phase from unsaturated zone to groundwater, assuming steady-state flow and constant parameters over the time. Comparative simulations have been carried out by using five target contaminants (Benzene, Benzo(a)pyrene, Vinyl Chloride, Trichloroethylene, Aldrin) widespread in contaminated sites and characterized by different physico-chemical properties (e.g., density, solubility, biodegradation rates), three types of soils (sand, loam and clay) and three different thickness L₁ of the contaminant source, as discussed in Section 3.

2. Models Description

Analytical solutions of the selected models, named as I, II, III, IV, V and VI are listed in

Table 1. Analytical solutions of the selected models.

Group	Model	Boundary and Initial Conditions	Solution	Reference
1	I	(-)	$C_w\left(\mathrm{z}=L_f\right)=SAM·C_{w0}$        $SAM=\frac{L_1}{L_f+L_1}$	ASTM, 2000 [42]
	II	$C_w\left(z,x,y,0\right)=0$ $0<z<\infty -\infty <x<\infty$ $-\infty <y<\infty$ $C_w\left(0,x,y,t\right)=\{\begin{array}{cc}{C}_{w0}& -\frac{X}{2}<x<\frac{X}{2},-\frac{Y}{2}<y<\frac{Y}{2}\\ 0& otherwise\end{array}$	$C_w\left(z,x,y,t\right)=\frac{C_{w0}}{8}\underset{\tau =0}{\overset{\tau =t}{{\displaystyle \int }}}{f^{\prime }}_z\left(z,\tau \right){f^{\prime }}_x\left(x,\tau \right){f^{\prime }}_y\left(y,\tau \right)d\tau$ ${f^{\prime }}_z\left(z,\tau \right)=\frac{z}{\sqrt{\pi {D^{\prime }}_z}}exp\left(\frac{v^{\prime }z}{2{D^{\prime }}_z}\right)·exp\left[-\tau \left(\frac{{\left(v^{\prime }\right)}^2}{4{D^{\prime }}_z}+{\lambda }^{\prime }\right)-\frac{z^2}{4{D^{\prime }}_z\tau }\right]·{\tau }^{-\raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$ ${f^{\prime }}_x\left(x,\tau \right)=\left\{erf\left[\frac{x+\frac{X}{2}}{2\sqrt{{D^{\prime }}_x\tau }}\right]-erf\left[\frac{x-\frac{X}{2}}{2\sqrt{{D^{\prime }}_x\tau }}\right]\right\}$ ${f^{\prime }}_y\left(y,\tau \right)=\left\{erf\left[\frac{y+\frac{Y}{2}}{2\sqrt{{D^{\prime }}_y\tau }}\right]-erf\left[\frac{y-\frac{Y}{2}}{2\sqrt{{D^{\prime }}_y\tau }}\right]\right\}$	Troldborg et al., 2009 [43]
2	III	(-)	$C_w\left(t\right)=C_{w0}\exp \left(-{\mu }_{1}t\right)$ ${\mu }_1=\frac{{\theta }_W}{{\theta }_W+{\rho }_b{K}_d+H{\theta }_a}\left(\frac{I_{eff}}{L_2{\theta }_W}+\lambda \right)$	Troldborg et al., 2008 [44]
	IV	$C_w\left(z=0\right)=C_{w0}$ $\frac{d^2{C}_w}{d{z}^2}\left(z=L_f\right)=0$	$C_w\left(\mathrm{z},t\right)=C_{w0}·{\alpha }_{dep}\left(t\right)·{\alpha }_{leach}$ ${\alpha }_{dep}\left(t\right)=\exp \left(-{\mu }_2·t\right)$ ${\mu }_2=\frac{I_{eff}·K_{sw}}{R·L_1·{\rho }_s}+\frac{{\lambda }_{source}·{\theta }_w·K_{sw}}{{\rho }_s}$       ${\alpha }_{leach}=\frac{\sigma ·\exp \left(k·z\right)}{k·\sinh \left(\sigma ·z\right)+\sigma ·\cosh \left(\sigma ·z\right)}$     $k=\frac{z}{2·D·t_{leach}}$    $\sigma =\sqrt{k^2+\frac{\lambda ·{\theta }_w}{D}}$	Verginelli and Baciocchi, 2013 [45]
3	V	$C_w\left(z,t=0\right)=\{\begin{array}{cc}0& -\infty <z<-z_0\\ C_{w0}& -z_0<z<0\\ 0& 0<z<\infty \end{array}$ $\underset{z\to \infty }{\lim }\frac{\partial C_w}{\partial z}=0$	$C_w\left(z,t\right)=\frac{C_{w0}}{2}\exp \left(-\lambda t\right)\left\{erf\left[\frac{z+z_0-\frac{vt}{R}}{2\sqrt{\frac{Dt}{R}}}\right]-erf\left[\frac{z-\frac{vt}{R}}{2\sqrt{\frac{Dt}{R}}}\right]\right\}$	Enfield et al., 1982 [46]
	VI	$C_w\left(z,0\right)=0$ $C_w\left(0,t\right)=C_{w0}\exp \left(-{\mu }_{3}t\right)$ $\frac{\partial C_w}{\partial z}\left(\infty ,t\right)=0$	$C_w\left(z,t\right)=C_{w0}\exp \left(-{\mu }_{3}t\right)\frac{1}{2}exp\left[\frac{\left(v-w\right)z}{2D_z}\right]erfc\left[\frac{zR-wt}{2\sqrt{D_{z}Rt}}\right]+\frac{1}{2}exp\left[\frac{\left(v+w\right)z}{2D_z}\right]erfc\left[\frac{zR+wt}{2\sqrt{D_{z}Rt}}\right]$ $w=\overline{v}\sqrt{1+\frac{4D_{z}R}{v^2}\left[\lambda -{\mu }_3\right]}$ ${\mu }_3=\frac{I_{eff}{K}_{sw}}{L_1{\rho }_b}+\frac{D_{eff}H}{{\rho }_b{L}_1{L}_d}$	Spence & Walden, 2001 [47]

.

They share the following common features: (i) the assessment of the concentration of a single contaminant dissolved in aqueous phase that moves from a source located in the unsaturated zone to the water table; (ii) the negligible effect related to the movement of substances in the non-aqueous phase; (iii) the small number of geometrical, hydrogeological and chemical input data; (iv) the use of a set of simplifying assumptions that allows to obtain analytical solutions. These characteristics make them straightforward tools in many applications such as the analysis of groundwater vulnerability to pesticides contamination as well as the risk assessment of contaminated sites [48,49,50,51]. They differ mainly in their assumptions on the source and in the physico-chemical mechanisms as highlighted in

Table 2. Features of the selected models.

Group	Model	Source					Chemical-Physical Mechanisms during the Transport					Solve Transport Equation
		On Ground Surface	Inner Domain	Continuous	Time-Varying	Residual NAPL Phase	Advection	Dispersion-Diffusion in Water	Diffusion in Gas	Sorption	Degradation
1	I		x	x			x			x
	II		x	x			x	x (3D)	x (3D)	x	x	x
2	III		x		x	x	x
	IV		x		x	x	x	x (1D)		x	x	x (steady state)
3	V	x			x		x	x (1D)		x	x	x
	VI		x		x	x	x	x (1D)		x	x	x

.

The reference spatial domain assumed by the models is depicted in Figure 1. It consists of an unsaturated layer, lower bounded by an aquifer. The contaminant source, located in the upper region, is a parallelepiped shape with edges L₁ (thickness), X and Y. Upper and lower positions of the source along the z-axis are given by L_f and L₂, respectively, with reference to the water table and by L_d with reference to the ground surface. The unsaturated zone is characterized by fixed homogeneous and isotropic hydrogeological properties θ, θ_w, θ_a, ρ_b, K_sat, f_oc, I_eff, according to the hypotheses of the models. The physical-chemical characteristics of the contaminants are indicated by H, D_a⁰, D_w⁰, S, K_oc. The selected models, except Model I, consider the degradation processes of the contaminant in water phase using a first-order kinetic formulation, where λ is the degradation constant.

The total concentration of the contaminant is expressed by Equation (1):

$${\mathrm{C}}_{\mathrm{tot}}=\frac{{\mathrm{M}}_{\mathrm{tot}}}{{\mathsf{\rho }}_{\mathrm{b}}\mathrm{V}},$$

(1)

whereas the concentration of the contaminant in the different phases (water; solid and air) is expressed by Equation (2):

$${\mathrm{C}}_{\mathrm{w}}=\frac{{\mathrm{M}}_{\mathrm{w}}}{{\mathsf{\theta }}_{\mathrm{w}}\mathrm{V}}$$

(2)

The mass of the contaminant sorbed by the soil fraction upon the mass of the affected soil C_s and the mass of contaminant in vapor phase upon the volume of pore air C_a are given by Equations (3) and (4), respectively:

$${\mathrm{C}}_{\mathrm{s}}=\frac{{\mathrm{M}}_{\mathrm{s}}}{{\mathsf{\rho }}_{\mathrm{b}}\mathrm{V}},$$

(3)

$${\mathrm{C}}_{\mathrm{a}}=\frac{{\mathrm{M}}_{\mathrm{a}}}{{\mathsf{\theta }}_{\mathrm{a}}\mathrm{V}}.$$

(4)

In all models, the partitioning of the chemicals among these three different phases is expressed by instantaneous linear equilibrium.

When low solute concentration occurs, a linear adsorption isotherm can be assumed [52]. Thus, the ratio between C_s and C_w is constant and equal to K_d:

$${\mathrm{C}}_{\mathrm{s}}{=\mathrm{K}}_{\mathrm{d}}·{\mathrm{C}}_{\mathrm{w}},$$

(5)

where

$${\mathrm{K}}_{\mathrm{d}}{=\mathrm{f}}_{\mathrm{oc}}·{\mathrm{K}}_{\mathrm{oc}}$$

(6)

The liquid-vapor partition is evaluated through Henry’s Law:

$${\mathrm{C}}_{\mathrm{a}}=\mathrm{H}·{\mathrm{C}}_{\mathrm{w}}$$

(7)

On the basis of Equation (7), the dissolved concentration in pore water C_w can be evaluated from C_tot:

$${\mathrm{C}}_{\mathrm{w}}{=\mathrm{K}}_{\mathrm{SW}}·{\mathrm{C}}_{\mathrm{tot}}$$

(8)

where K_sw is expressed by Equation (9)

$${\mathrm{K}}_{\mathrm{SW}}=\frac{{\mathsf{\rho }}_{\mathrm{b}}}{{\mathsf{\theta }}_{\mathrm{W}}{+\mathsf{\rho }}_{\mathrm{b}}{\mathrm{K}}_{\mathrm{d}}{+\mathrm{H}\mathsf{\theta }}_{\mathrm{a}}},$$

(9)

representing the dissolution of soil contaminants into infiltrating rainwater, according to the hypothesis of instantaneous and linear equilibrium.

The maximum value of C_w is the solubility (S) of the contaminant. Therefore, taking into account air, water and solid phases, the maximum C_tot is

$${\mathrm{C}}_{\mathrm{tot};\mathrm{sat}}=\frac{\mathrm{S}}{{\mathrm{K}}_{\mathrm{SW}}}.$$

(10)

Some of the selected models (Models III, IV, VI; Table 1) take into account the presence of a residual NAPL (Non-Aqueous Phase Liquid) in the source. This allows to consider an initial C_tot higher than C_tot;sat. For these models, when the measured C_tot is higher than C_tot;sat it is possible to consider C_tot as a sum of two components:

$${\mathrm{C}}_{\mathrm{tot}}{=\mathrm{C}}_{\mathrm{tot};\mathrm{sat}}{+\mathrm{C}}_{\mathrm{NAPL}}$$

(11)

where C_NAPL is the concentration of the contaminant in non-aqueous phase.

The initial dissolved concentration in pore water at the source C_w0 can be evaluated as follows:

$${\mathrm{C}}_{\mathrm{w}0}{=\mathrm{K}}_{\mathrm{SW}}·{\mathrm{C}}_{\mathrm{tot}}{\mathrm{in}\mathrm{case}\mathrm{of}\mathrm{C}}_{\mathrm{tot}}{<\mathrm{C}}_{\mathrm{tot};\mathrm{sat}}$$

(12)

$${\mathrm{C}}_{\mathrm{w}0}=\mathrm{S}\mathrm{otherwise}$$

(13)

In all the analyses here developed, C_tot is assumed less than C_tot;sat in order to use the same initial C_tot for all the simulations.

Based on the common characteristics, the models were organized into three groups. The first group is composed by models with a continuous source (Models I and II), leading to a constant concentration after a certain period of time. The second group considers a decaying source. In this case, the transport equation is not solved (Models III), or it is solved for a steady state condition (Model IV). Finally, the third group considers a decaying source and a solution of the transport equation in transient conditions (Models V and VI). Specific features of the models will be carefully described in the following sections.

2.1. Model I

Model I was developed by ASTM (American Society for Testing and Materials) and described in Appendix 3 of the Standard Guide for Risk-Based Corrective Action [42]. It provides a very basic approach to estimate the dissolved concentration of contaminant in the water table. The model is based on the determination of the contaminant LF, which represents the steady ratio between the contaminant concentration in the soil source and the resultant concentration in groundwater. This approach may be applied both to organic and inorganic contaminants and it is adopted by various software for risk assessment, e.g., Risk-Based Corrective Action (RBCA) Tool Kit for Chemical Releases [53]. Its widespread use is related to its simplicity and a limited number of input parameters. The source is assumed uniform and constant, the only considered transport mechanism is the steady leaching from the source to the groundwater table.

The LF is composed by three coefficients: K_SW (see Equation (9)) SAM and LDF. SAM, introduced by [53], represents the attenuation of contaminant concentration caused by its sorption related to the leaching through the clean soil. This coefficient is derived from the principle of mass conservation and it depends only on the geometry of the scheme. In fact, it is defined as the source thickness L₁ and the distance between the top of the source and the water table L₂, ratio. Thus, it is possible to obtain C_w at the water table as reported in Table 1-Model I. LDF evaluates the uniform dilution of the contaminant in groundwater, but this mechanism has not been taken into account.

2.2. Model II

Model II differs from the others as it considers combined gas and water phase diffusion in three dimensions [43]. For this reason, the model is particularly suitable to be applied when gas phase transport may be prevalent as for VOCs. It assumes mono-dimensional advection in water phase and three-dimensional diffusion in gas and water phases. In addition, it considers uniform and constant concentration of the contaminant in the source, neglecting the attenuation processes. Furthermore, soil sorption and first-order degradation take place in the unsaturated zone.

The starting point of the transport equations for water and gas phases is

$$\{\begin{array}{c}\frac{\partial {\mathrm{R}\mathsf{\theta }}_{\mathrm{w}}{\mathrm{C}}_{\mathrm{w}}}{\partial \mathrm{t}}=\left[\nabla ·\left({\mathsf{\theta }}_{\mathrm{w}}{\mathrm{D}}_{\mathrm{w}}\right)\right]·\nabla {\mathrm{C}}_{\mathrm{w}}-{\mathrm{I}}_{\mathrm{eff}}\frac{\partial {\mathrm{C}}_{\mathrm{w}}}{\partial \mathrm{z}}-{\mathsf{\lambda }\mathsf{\theta }}_{\mathrm{w}}{\mathrm{C}}_{\mathrm{w}}\\ \frac{\partial {\mathsf{\theta }}_{\mathrm{a}}{\mathrm{C}}_{\mathrm{a}}}{\partial \mathrm{t}}=\left[\nabla ·\left({\mathsf{\theta }}_{\mathrm{a}}{\mathrm{D}}_{\mathrm{a}}\right)\right]·\nabla {\mathrm{C}}_{\mathrm{a}}\end{array}$$

(14)

where R is assumed as follows:

$$\mathrm{R}=1+\frac{{\mathsf{\rho }}_{\mathrm{B}}}{{\mathsf{\theta }}_{\mathrm{w}}}{\mathrm{K}}_{\mathrm{d}}.$$

(15)

Troldborg and co-workers [44] obtained the following Equation (16)

$$\frac{\partial {\mathrm{C}}_{\mathrm{w}}}{\partial \mathrm{t}}+{\mathrm{v}}^{\prime }\frac{\partial {\mathrm{C}}_{\mathrm{w}}}{\partial \mathrm{z}}-\nabla {\mathrm{D}}^{\prime }·\nabla {\mathrm{C}}_{\mathrm{w}}+{\mathsf{\lambda }}^{\prime }{\mathrm{C}}_{\mathrm{w}}=0.$$

(16)

where

$${\mathrm{v}}^{\prime }=\frac{{\mathrm{I}}_{\mathrm{eff}}}{{\mathrm{R}}^{\prime }}$$

(17)

$${\mathrm{D}}^{\prime }=\left(\begin{array}{ccc}{\mathrm{D}}_{\mathrm{x}}^{\prime }& 0& 0\\ 0& {\mathrm{D}}_{\mathrm{y}}^{\prime }& 0\\ 0& 0& {\mathrm{D}}_{\mathrm{z}}^{\prime }\end{array}\right)$$

(18)

$${\mathsf{\lambda }}^{\prime }=\frac{{\mathsf{\theta }}_{\mathrm{w}}\mathsf{\lambda }}{{\mathrm{R}}^{\prime }}$$

(19)

where

$${\mathrm{R}}^{\prime }={\mathrm{R}\mathsf{\theta }}_{\mathrm{w}}+{\mathrm{H}\mathsf{\theta }}_{\mathrm{a}}.$$

(20)

The dispersion coefficients of the diagonal tensor D’, appearing in the matrix representation (18), are given by

$${\mathrm{D}}_{\mathrm{x}}^{\prime }={\mathrm{D}}_{\mathrm{y}}^{\prime }=\frac{{\mathsf{\theta }}_{\mathrm{w}}{\mathrm{D}}_{\mathrm{w}}^{\mathrm{e}}+{\mathsf{\theta }}_{\mathrm{w}}{\mathsf{\alpha }}_{\mathrm{t}}\mathrm{v}+\mathrm{H}{\mathsf{\theta }}_{\mathrm{a}}{\mathrm{D}}_{\mathrm{a}}^{\mathrm{e}}}{{\mathrm{R}}^{\prime }},$$

(21)

$${\mathrm{D}}_{\mathrm{z}}^{\prime }=\frac{{\mathsf{\theta }}_{\mathrm{w}}{\mathrm{D}}_{\mathrm{w}}^{\mathrm{e}}+{\mathsf{\theta }}_{\mathrm{w}}{\mathsf{\alpha }}_1\mathrm{v}+\mathrm{H}{\mathsf{\theta }}_{\mathrm{a}}{\mathrm{D}}_{\mathrm{a}}^{\mathrm{e}}}{{\mathrm{R}}^{\prime }},$$

(22)

where D_w^e and D_a^e are estimated according to [54] whereas v is calculated by means of the following equation:

$$\mathrm{v}=\frac{{\mathrm{I}}_{\mathrm{eff}}}{{\mathsf{\theta }}_{\mathrm{w}}}$$

(23)

The set of initial and boundary conditions is shown in Table 1-Model II. The solution of Equation (16) was developed by Sagar [55] and Wexler [56] and has been reported in Table 1-Model II as well.

Troldborg [43] pointed out that the evaluation of the contaminant dilution in groundwater is more difficult using a three-dimensional model because the contaminated area at the water table is bigger than the source area. Therefore, the water dilution volume has to be evaluated since the concentrations are not spatially constant within this area.

2.3. Model III

Model III consists of a subset module of a large model named CatchRisk [44]. This model evaluates the contaminant transport from a point source to the groundwater. In Model III, the unsaturated zone is designed like a reactor where the mass flux is governed only by water advection and the other transport mechanisms are neglected; the transport equation is not solved as in the Model I. On the contrary, Model III assumes that the dissolved concentration is constant along the depth.

The decay of the source concentration is taken into account. The mass of contaminant within the compartment decreases due to both leaching through the unsaturated zone and degradation of the contaminant in water phase. The dissolved concentration over the time can be obtained solving a mass balance. The variation of the chemical mass over the time is equal to the rate of mass depletion due to leaching and degradation. The solution of this mass balance is shown in Table 1-Model III.

Furthermore, the model considers the residual non-aqueous phase concentration in the source. If the mass of contaminant is higher than the equilibrium mass, a separate phase is present. At the initial time, C_tot and C_w0 are described by Equations (11) and (13), respectively, and the total contaminant mass is equal to

$${\mathrm{M}}_{\mathrm{tot}}{=\mathrm{C}}_{\mathrm{tot}}{\mathsf{\rho }}_{\mathrm{b}}\mathrm{V}$$

(24)

The mass flux J, Equation (25), leaving the unsaturated zone is constant on time until the contaminant mass is equal to the mass equivalent to the saturation conditions M_sat, Equation (26);

$${\mathrm{J}=\mathrm{S}\mathrm{X}\mathrm{Y}\mathrm{I}}_{\mathrm{eff}},$$

(25)

$${\mathrm{M}}_{\mathrm{sat}}=\frac{\mathrm{S}}{{\mathrm{K}}_{\mathrm{sw}}}{\mathsf{\rho }}_{\mathrm{b}}\mathrm{V}.$$

(26)

When M_tot is equal to M_sat, C_w can be calculated through the solution shown in Table 1-Model III.

2.4. Model IV

Model IV is composed of three terms: α_dep(t), α_leach and LDF [45]. α_dep(t) considers the source depletion caused by leaching and biodegradation. α_leach describes the transport phenomena taking into account the mechanisms of advection, dispersion-diffusion, sorption and biodegradation. LDF evaluates the dilution of the contaminant in groundwater; however, this mechanism has not been taken into account.

The term α_dep(t) is defined by an exponential law, obtained from a mass balance that includes the mass losses caused by leaching and biodegradation, reported in Table 1-Model IV.

Furthermore, the model includes the presence of a residual phase in the source. In this case, the dissolved concentration in the source over the time is equal to

$${\mathrm{C}}_{\mathrm{w}}\left(\mathrm{t}\right)=\{\begin{array}{cc}{\mathrm{C}}_{\mathrm{w}0}{\mathsf{\alpha }}_{\mathrm{dep}}\left(\mathrm{t}\right)& {\mathrm{for}\mathrm{t}}^{*}\le 0\\ {\mathrm{S}\mathsf{\alpha }}_{\mathrm{dep}}\left(\mathrm{t}\right)& {\mathrm{for}\mathrm{t}}^{*}>0\end{array}$$

(27)

where

$${\mathsf{\alpha }}_{\mathrm{dep}}\left(\mathrm{t}\right)=\{\begin{array}{cc}\exp \left(-{\mathsf{\mu }}_2\mathrm{t}\right)& {\mathrm{for}\mathrm{t}}^{*}\le 0\\ \exp \left(-{\mathsf{\mu }}_2\left(\mathrm{t}-{\mathrm{t}}^{*}\right)\right)& {\mathrm{t}}^{*}>0;\mathrm{for}\mathrm{t}>{\mathrm{t}}^{*}\\ 1& {\mathrm{t}}^{*}>0;\mathrm{for}0<\mathrm{t}\le {\mathrm{t}}^{*}\end{array}$$

(28)

and t* is the time when the initial source concentration reaches the saturation conditions, defined as

$${\mathrm{t}}^{*}=\frac{{\mathrm{C}}_{\mathrm{tot}}-{\mathrm{C}}_{\mathrm{tot};\mathrm{sat}}}{{\mathrm{C}}_{\mathrm{tot};\mathrm{sat}}{\mathsf{\mu }}_2}.$$

(29)

The term α_leach is obtained solving the advection-diffusion differential equation for the steady state:

$${\mathrm{D}}_{\mathrm{z}}\frac{{\mathrm{d}}^2{\mathrm{C}}_{\mathrm{w}}}{{\mathrm{d}}^2\mathrm{z}}-{\mathrm{v}}_{\mathrm{leach}}\frac{{\mathrm{dC}}_{\mathrm{w}}}{\mathrm{dz}}-{\mathsf{\lambda }\mathsf{\theta }}_{\mathrm{w}}{\mathrm{C}}_{\mathrm{w}}=0.$$

(30)

The dispersion-diffusion coefficient D_z is calculated as

$${\mathrm{D}}_{\mathrm{z}}{=\mathsf{\alpha }}_{\mathrm{l}}{\mathrm{v}}_{\mathrm{leach}}{+\mathrm{D}}_{\mathrm{w}}^{\mathrm{e}}$$

(31)

where D_w^e is calculated as:

$${\mathrm{D}}_{\mathrm{w}}^{\mathrm{e}}{=\mathrm{D}}_{\mathrm{w}}^0\frac{{\mathsf{\theta }}_{\mathrm{w}}^{10/3}}{{\mathsf{\theta }}^2}.$$

(32)

Unlike other models, the seepage velocity is not obtained from the effective infiltration, but from the time required by the contaminant to reach the underlying water table t_leach. The latter is calculated as a linear function of the time required to the infiltrating water to reach the water table t_w, by means of the retardation coefficient of the contaminant R:

$${\mathrm{t}}_{\mathrm{leach}}{=\mathrm{R}\mathrm{t}}_{\mathrm{w}}$$

(33)

R is calculated according to the following equation:

$$\mathrm{R}=1+\frac{{\mathsf{\rho }}_{\mathrm{b}}{\mathrm{K}}_{\mathrm{sw}}}{\mathsf{\theta }}.$$

(34)

The time t_w is calculated using the Green and Ampt equation [57]:

$${\mathrm{t}}_{\mathrm{w}}=\frac{{\mathsf{\theta }}_{\mathrm{a}}}{{\mathrm{K}}_{\mathrm{sat}}}\left[{\mathrm{L}}_{\mathrm{f}}-\left({\mathrm{H}}_{\mathrm{w}}-{\mathrm{h}}_{\mathrm{cr}}\right)\ln \left(\frac{{\mathrm{H}}_{\mathrm{w}}{+\mathrm{L}}_{\mathrm{f}}-{\mathrm{h}}_{\mathrm{cr}}}{{\mathrm{H}}_{\mathrm{w}}-{\mathrm{h}}_{\mathrm{cr}}}\right)\right]$$

(35)

where H_w is the ponding depth of water surface and h_cr the wetting front suction head.

The set of initial and boundary conditions to be given to the differential equation (30) is reported in Table 1-Model IV.

2.5. Model V

PESTAN (PESTicide ANalytical) is a software developed by the U.S. EPA (Environmental Protection Agency of United States) to assess the transport of organic contaminants, mainly pesticides [58]. The theoretical model underlying the software PESTAN was published in [46]. It differs from the others mainly due to the conceptualization of the source. The source is considered a mass of granular solid contaminant located on the ground surface which dissolves in a “slug” of contaminated water infiltrating into the soil. The thickness of the slug z₀ is the equivalent depth of the pore water required to dissolve the total mass of the solid chemical in water.

In order to compare the model with the others, the reference scheme presented above was adopted and z₀ was assumed equal to the equivalent depth of the pore water contained in the source (Equation (36)).

$${\mathrm{z}}_0{=\mathsf{\theta }}_{\mathrm{w}}{\mathrm{L}}_1$$

(36)

The differential equation underlying the model (Equation (37)) takes into account the following mechanisms: advection and dispersion in the vertical dimension, sorption and biochemical degradation described according to a first order kinetic.

$$\mathrm{R}\frac{\partial {\mathrm{C}}_{\mathrm{w}}}{\partial \mathrm{t}}=\mathrm{D}\frac{{\partial }^2{\mathrm{C}}_{\mathrm{w}}}{\partial {\mathrm{z}}^2}-\mathrm{v}\frac{\partial {\mathrm{C}}_{\mathrm{w}}}{\partial \mathrm{z}}-{\mathsf{\lambda }\mathrm{C}}_{\mathrm{w}}$$

(37)

where R is given in Equation (34). The term D is evaluated through the relationship of Biggar and Nielsen [59]

$${\mathrm{D}=\mathrm{D}}_{\mathrm{w}}^{\mathrm{e}}+2.93{\mathrm{v}}^{1.11}$$

(38)

where D and D_w^e are expressed in cm² day⁻¹ and v in cm day⁻¹.

The initial and boundary condition for the Equation (37) and the proposed analytical solution are given in Table 1-Model V.

2.6. Model VI

Model VI was first implemented in the risk assessment software RISC₄ [47], then upgraded to the newer version RISC₅, which incorporates the approach developed in [60]. In this model, the source depletes with time due to the simultaneous effect of leaching and volatilization of VOCs. Unlike the previous model, biological degradation is neglected. The presence of a residual phase in the source is considered as described above.

The leachate concentration in the source decays exponentially with time. The exponential law is obtained from a mass balance where the variation over the time of the contaminant mass is equal to the rate of mass depletion due to leaching and volatilization. The source depletion law is

$${\mathrm{C}}_{\mathrm{w}}\left(\mathrm{t}\right){=\mathrm{C}}_{\mathrm{w}0}\exp (-{\mathsf{\mu }}_3\mathrm{t}).$$

(39)

The coefficient μ₃ is described by the following equation:

$${\mathsf{\mu }}_3=\frac{{\mathrm{I}}_{\mathrm{eff}}{\mathrm{K}}_{\mathrm{sw}}}{{\mathrm{L}}_1{\mathsf{\rho }}_{\mathrm{b}}}+\frac{{\mathrm{D}}_{\mathrm{eff}}\mathrm{H}}{{\mathsf{\rho }}_{\mathrm{b}}{\mathrm{L}}_1{\mathrm{L}}_{\mathrm{d}}}$$

(40)

where D_eff is the effective diffusion coefficient in soil estimated using the Millington–Quirk relationships [61]

$${\mathrm{D}}_{\mathrm{eff}}{=\mathrm{D}}_{\mathrm{w}}^0\left(\frac{{\mathsf{\theta }}_{\mathrm{w}}^{10/3}}{{\mathsf{\theta }}^2}\right){+\mathrm{D}}_{\mathrm{a}}^0\frac{1}{\mathrm{H}}\left(\frac{{\mathsf{\theta }}_{\mathrm{a}}^{10/3}}{{\mathsf{\theta }}^2}\right)$$

(41)

and L_d is the distance from the ground surface to the center of the source. Model VI is ruled by the same differential equation of Model V (Equation (37)). The dispersion coefficient is assumed as a linear function of the seepage velocity (Equation (42)) because the mechanism of molecular diffusion is neglected,

$${\mathrm{D}}_{\mathrm{z}}{=\mathsf{\alpha }}_{\mathrm{l}}\mathrm{v}$$

(42)

where α_l is calculated using the Gelhar relationship [62]:

$${\ln \mathsf{\alpha }}_{\mathrm{l}}=-4.933+3.811{\mathrm{lnz}}_{\mathrm{m}}\mathrm{in}\mathrm{case}\mathrm{of}{\mathrm{z}}_{\mathrm{m}}\le 2$$

(43)

$$\ln {\mathsf{\alpha }}_l=-2.727+0.584\ln {\mathrm{z}}_{\mathrm{m}}\mathrm{otherwise}$$

(44)

being z_m the distance from the source to the observation location.

The set of initial and boundary condition and the solution to be given are reported in Table 1-Model VI.

3. Methodology

The analysis has been carried out by comparing the solutions of the models with reference to the same scenario (Figure 1) and varying soils, contaminants and thickness of the source L₁. As one can expect, the models do not respond the same way to the variation of the parameters because of the different assumptions about the source and transport mechanisms.

The values of the geometrical parameters are reported in

Table 3. Values of the geometrical parameters.

Parameter *	Value
L1	1-2-4 m
X	4 m
Y	4 m
Lf	5 m

* See nomenclature list.

.

Three types of soils, differing mainly in water content and hydraulic conductivity, have been chosen: sand, loam and clay. Furthermore, five organic contaminants have been selected according to their different mobility and biodegradability characteristics in order to explore a wide range of fate and transport mechanisms.

The soil parameter values are derived from [63,64] and listed in

Table 4. Soil parameters values.

Parameter *	Measurement Unit	Sand	Loam	Clay
ρb	kg/m3	1700	1700	1700
θ	-	0.385	0.352	0.312
θw	-	0.130	0.200	0.304
θa	-	0.300	0.230	0.076
hcr	m	−0.0164	−0.178	−0.269
Ief	m/s	5.708 × 10−9	2.854 × 10−9	5.708 × 10−10
Ksat	m/s	8.250 × 10−5	2.889 × 10−6	5.556 × 10−7
foc	-	0.001	0.001	0.001

* See nomenclature list.

.

Chemical properties of the contaminants have been derived by USEPA 1996 [65], except for the first order degradation constant λ, taken from the handbook of Howard [66]. The C_w0 has been chosen according to the literature focusing on contaminated sites [43,67,68,69,70]. The physico-chemical properties of the selected contaminants are reported in

Table 5. Physico-chemical properties values of the selected contaminants.

Parameter *	Measurement Unit	Contaminant
		Benzene	Benzo(a)pyrene	Vinyl Chloride	Trichloroethylene	Aldrin
H	-	2.280 × 10−1	4.630 × 10−5	1.110	4.220 × 10−1	6.970 × 10−3
S	kg/m3	1.750	1.620 × 10−6	2.760	1.100	1.800 × 10−4
Da	m2/s	8.800 × 10−6	4.300 × 10−6	1.060 × 10−5	7.900 × 10−6	1.320 × 10−4
Dw	m2/s	9.800 × 10−10	9.000 × 10−10	1.230 × 10−10	9.100 × 10−10	4.860 × 10−10
Koc	m3/kg	6.170 × 10−2	9.690 × 102	1.860 × 10−2	9.430 × 10−2	4.870 × 101
λ	1/s	1.114 × 10−8	7.567 × 10−9	2.790 × 10−9	4.852 × 10−9	6.778 × 10−9
Cw0	μg/dm3	100	1	100	100	10

* See nomenclature list.

.

4. Results and Discussion

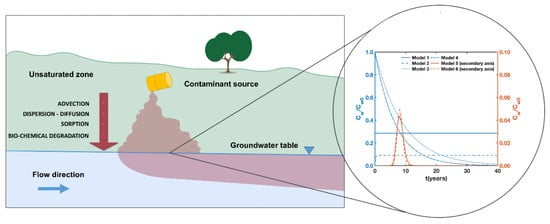
4.1. Predicted Concentration over the Time According to the Different Models

In order to evaluate the differences among the solutions of Models I-VI, the dimensionless concentrations C_w/C_w0 have been calculated at a certain spatial location (z = 5 m) as a function of time, fixing a single contaminant, Trichloroethylene (TCE), soil type (sand), source thickness (L₁ = 2 m). The results of the ratio between C_w/C_w0 are sketched in Figure 2.

As shown in Figure 2, the value of the initial dimensionless concentration and the shape of the curve are influenced by source hypotheses and transport mechanisms. According to these results, models belonging to group 1 (Model I and II) show a constant concentration over the time (with the exception of an initial transient phase for Model II); models belonging to group 2 (Model III and IV) show a decreasing exponential trend whereas models belonging to group 3 (Model V and VI) exhibit a temporal trend represented by a bell-shaped curve.

Model I is the most basic, as it neglects fate and transport mechanisms over time. Therefore, the dimensionless concentration C_w/C_w0 is constant. Conversely, Model II solves the transport equation, and it considers a constant source; therefore, at the initial time t = 0 the value of C_w/C_w0 is zero and after a transient phase reaches a constant value. Although both models showed a similar trend over the time, Model II depends on the spatial coordinates x, y, and z. The models belonging to group 1 can be used when the reduction processes of the source, like leaching and volatilization losses or biodegradation, are negligible, so the source can be modelled as constant. Pascuzzi et al. [71] used the model I for evaluating the risk for human health assuming a steady redeposition on the soil of pollutants in the selected site. The C_W/C_W0 was equal to 3.33 × 10⁻², while according to our results the C_W/C_W0 calculated through the application of the SAM coefficient ranges between 0.167 and 0.444. These different values are related to the differences in the adopted reference schemes, which cause a stronger attenuation process in the scheme presented by Pascuzzi et al. They consider a source thickness L₁ of 0.2 m and a distance between the bottom of the source and the water table L_f equal to 6m, while in our case L₁ ranges between 1 m and 4 m and L_f is 5 m.

Di Gianfilippo et al. [51] used Model I to reproduce the transport of leaching substances from alkaline waste material assuming a constant source. They carried out a Monte Carlo analysis to evaluate a wide range of scenario conditions, varying the input parameters within selected intervals. The SAM value was estimated using a value of L₁ varying from 0.1 m to 1 m and a value of L_f from 5 to 10 m, thus obtaining a value of C_W/C_W0 ranging between 9.9 × 10⁻³ and 0.167. These concentrations are slightly lower than those calculated in this work because of the different geometrical conditions, as in the previous case.

The solutions of the group 2 consist of exponential laws, describing the depletion processes of the source. Model III assumes instantaneous mixing in the unsaturated zone, and it does not consider transport mechanisms. Therefore, C_w/C_w0 is spatially constant along the vertical axis, and it decreases over time. In Model IV the exponential law is multiplied by α_leach. In this scenario, the value of α_leach is approximately equal to 1, because of the selected type of soil and the contaminant. In consequence, the exponential part is dominant. The depletion coefficients μ₁ and μ₂ are equal to 3.469 × 10⁻⁹ s⁻¹ and 4.800 × 10⁻⁹ s⁻¹, respectively. They are indicators of the depletion rate of the contaminant and differ only for the retardation coefficient. Therefore, in these conditions, the results of the two models are very similar. For group 2, the source depletion processes (bio-chemical degradation and leaching losses) are predominant, while the transport mechanisms are less relevant.

Models V and VI can be considered as the more advanced ones as they consider both the source depletion and a transient transport equation. This causes the distinctive bell-shape, yielding a dimensionless concentration peak lower than the other models I-IV. The solutions contain two parts: a time-dependent exponential law and the space- and time-dependent solution of the transport equation. For Model V the first part takes into account only the biochemical degradation, while for Model VI, it considers leaching and volatilization losses. The second part of the solution is different due to the initial and boundary conditions of the transport equation. For these reasons, the peaks of the solutions differ between the Models V and VI. In this scenario, for Model V the maximum of the normalized concentration is 4.338 × 10⁻² at 8.17 y, while in Model VI, the maximum of the normalized concentration corresponds to 4.920 × 10⁻² at 8.08 y. These models allow to describe the fate and transport mechanisms more thoroughly than the other models. In this case, the predicted concentrations are approximately an order of magnitude lower than those obtained by using the other models.

For these reasons, in some applications, the models of these groups are preferable. Di Sante et al. [72] used Model VI to assess the sanitary and environmental risk of a disused industrial plant contaminated with polycyclic aromatic hydrocarbons, heavy hydrocarbons and polychlorinated biphenyls. Although the Italian guidelines [73] consider adequate a steady-state model to reproduce leaching phenomena, the authors suggest the use of a transient model for contaminants with high experimental leaching value, because they are more suitable to reproduce real conditions. They evaluated concentrations of aromatic fraction of heavy hydrocarbons and benzo(a)pyrene after 20 years roughly equal to 0.40 mg/L e 1 × 10⁻⁶ mg/L, respectively. Their results consider not only the leaching process but also the uniform dilution in groundwater, which is not considered by this paper. Furthermore, their results cannot be expressed as a dimensionless quantity. For these reasons, a direct comparison with the results of this work is not possible.

The different output concentrations of the models lead to different amounts of contaminant reaching the water table. In order to determine and compare the mass value reaching the groundwater for the different models, the mass flux (J) from unsaturated zone to groundwater is integrated over the time. J is governed only by water phase advection, and it is evaluated as suggested in [43]:

$${\mathrm{J}=\mathrm{C}}_{\mathrm{w}}{\mathrm{A}}_{\mathrm{uz-gw}}{\mathrm{v}}_{\mathrm{leach}}$$

(45)

where A_uz-gw is the exchange area between the two zones.

For all the models but Model II, A_uz-gw is equal to A, and the dissolved concentration C_w is constant over the area. In the paper describing Model II [43], A_uz-gw is bigger than A, and the concentration is variable in space; hence, it is necessary to integrate C(x,y,t) over space and time.

For the considered contaminant, soil type and source thickness, the mass reaching the water table, considering a period of twenty years and forty years, has been calculated starting from an initial source concentration C_w0 (100 μg/dm³); see

Table 6. Mass of Trichloroethylene (TCE) at the water table in twenty and forty years.

Group	Model	Mw (kg) in 20 years	Mw (kg) in 40 years
1	I	1.272 × 10−2	2.534 × 10−2
	II	2.201 × 10−2	4.443 × 10−2
2	III	1.798 × 10−2	2.000 × 10−2
	IV	1.393 × 10−3	1.460 × 10−2
3	V	2.599 × 10−4	2.599 × 10−4
	VI	2.391 × 10−4	2.391 × 10−4

. As can be noted, the third group of models returns a lower contaminant mass than the others. After 20 years, the exponential models belonging to group 2 exhibit the highest values, while extending the period of time to 40 years Model I exhibits the maximum value of J.

4.2. Predicted Concentration of Different Contaminants over Time

The physico-chemical characteristics of the contaminant, e.g., the volatility and the degradation rate [52,74], strongly affect its mobility through the unsaturated zone as well as its fate in time. The selected models are solved using the contaminants properties listed in Table 5, fixing the thickness of the source L₁ = 2 m and a sand soil.

The transport time ranges between some orders of magnitude according to the contaminant mobility. Hence, in order to overcome this discrepancy and compare the results consistently, the dimensionless concentration has been plotted versus a dimensionless time τ, calculated as the ratio between the physical time and a reference time t_ref. This criterion has not been used for Model I because the results are not depended by time and contaminant properties. In this case, t_ref has not been considered, and the dimensionless concentration is plotted versus physical time. The value of the t_ref cannot be evaluated the same way for all the models. For models belonging to the groups 2 and 3, the dimensionless concentration goes to zero after a certain period of time, depending on contaminants and medium properties. Therefore, the value of t_ref has been set equal to the time when C_w/C_w0 reaches the residual value of 0.1%. For model II, the value of t_ref has been calculated with a different criterion, as in this case C_w/C_w0 tends to a horizontal asymptote: It is set equal to the time when the variation of the concentration is negligible (<0.01 μg/dm³). As one can perceive, in this case the value of t_ref depends on the temporal discretization, which has been set equal to 1 month for Benzene, Vinyl chloride and Trichloroethylene and 1 year for Benzo(a)pyrene and Aldrin.

The values of t_ref are listed in

Table 7. Reference time evaluated for different contaminants and models.

Group	Model	tref (year)
		Benzene	Benzo(a)pyrene	Vinyl Chloride	Trichloroethylene	Aldrin
1	I	-	-	-	-	-
	II	1.75	7.00	1.17	1.67	1.00 × 101
2	III	2.93 × 101	2.00 × 105	9.19 × 101	6.33 × 101	1.07 × 104
	IV	2.18 × 101	4.03 × 104	6.72 × 101	4.57 × 101	2.29 × 103
3	V	8.67	-	6.83	1.16 × 101	-
	VI	9.0	1.58 × 105	5.75	1.09 × 101	7.73 × 103

. It can be observed that Model III has the highest t_ref for all the contaminants. More generally, the models belonging to group 2 exhibit a higher t_ref than the other models for the contaminants characterized by a greater mobility (Benzene, Vinyl Chloride, and Trichloroethylene). For Benzo(a)pyrene and Aldrin, the reference time t_ref of Model V is not reported because C_w is negligible.

For the Model II (Figure 3b), it is possible to observe a marked distinction in the trend concentration between contaminants characterized by a less mobility (Benzo(a)pyrene and Aldrin) and the others (Benzene, Vinyl chloride, Trichloroethylene). The first group of contaminants reaches a steady-state concentration higher than the others: the C_w/C_w0 ratio is equal to 0.443 for Benzo(a)pyrene and 0.358 for Aldrin. The second group reaches lower values, the C_w/C_w0 ratio is about equal to 0.090 for the three contaminants. These results are in accordance with the application of the model presented by Locatelli et al. [75], considering the different hydrogeological setting of the simulated site. Locatelli et al. [75] used the model II to simulate leaching of benzene and toluene in a simulated contamination scenario; at 5 meters, they obtain a C_w/C_w0 ratio corresponding to 0.01 for benzene and 0.04 for toluene. The lower value compared to the obtained value in this paper can be attributed to the different hydrogeological setting and the different assessment of some parameters, like the degradation constant.

The C_w/C_w0 ratios for Benzo(a)pyrene and Aldrin in the Model II are higher than in Model I (C_w/C_w0 = 0.286). This proves that in some circumstances, the Model I is not the most conservative approach, as it is typically considered (ASTM, 2000). This result can be related to the fact that in Model I the SAM is assumed simplistically constant for all the contaminants.

In Model III, as can be seen from Figure 3c, the results collapse on the same curve as consequence of the use of the dimensionless time τ. This occurs in Model IV to some extent. In fact, as previously explained, Model IV consists of two terms: α_dep and α_leach. The former is characterized by scale invariance while the latter is approximately equal to one for all the contaminants. The minimum value of α_leach corresponding to 0.930 has been obtained for Benzo(a)pyrene.

In Model V the concentrations of contaminants with low mobility (Benzo(a)pyrene and Aldrin) is closed to zero during the whole considered range of time (10⁴–10⁵ years) because of the exponential part of the solution. Therefore, the results of this model (Figure 3e) are shown only for the three contaminants Benzene, Vinyl Chloride and Trichloroethylene. In Figure 3f. sketching the results of Model VI, it is possible to identify two groups of contaminants, characterized by low and high mobility, respectively. The concentration of contaminants belonging to the first group reach a maximum value earlier than the second group.

Comparison between Different Degradation Constants

The contaminant degradation into the environment, λ, simulated through a first order kinetics, takes into account both chemical mechanisms (hydrolysis, redox reductions and photodegradations) and biodegradation. Several mechanisms are involved, and each of them can be affected by many environmental variables, making the assessments of these coefficients highly uncertain [76,77]. The λ values can vary by more than one order of magnitude for each contaminant in a natural porous media [15,78]. For these reasons, a sensitivity analysis based on the variation of λ has been carried out. The comparison is developed with respect to the Trichloroethylene compound, in the same conditions of the previous sections: depth equal to z = 5 m, source thickness L₁ equal to 2 m and the unsaturated zone composed by sand. In Howard [66], the values of λ for Trichloroethylene in groundwater range from 4.852 × 10⁻⁹ s⁻¹ to 2.499 × 10⁻⁸ s⁻¹. Three values have then been chosen for the comparison: the first λ₁ is the minimum value (4.852 × 10⁻⁹ s⁻¹), the second λ₂ is the mean of logarithms of the two extremes (1.101 × 10⁻⁹ s⁻¹), and the third λ₃ is the maximum value (2.499 × 10⁻⁸ s⁻¹). The results of the comparison are shown in Figure 4.

As already highlighted, Model I is independent of contaminant properties; therefore, the ratio C_w/C_w0 is constant, equal to 0.286 for all the values of λ. In Model II (Figure 4b), little differences related to the decay coefficients can be noted. The obtained C_w/C_w0, equal to 0.0901, 0.0884 and 0.0848 for λ₁, λ₂ and λ₃, respectively, present similar values, reaching the steady state conditions in a small period of time.

In the Models III and IV (Figure 4c,d), the λ coefficients play the same role, affecting the depletion coefficients μ₁ and μ₂, see Table 1.

The variation of λ affects Model V more than Model VI (Figure 4e,f). In particular, it influences the C_w/C_w0 peak (maximum concentration) as well as the time when it occurs. In both models, the higher is the value of λ, the earlier and lower is the peak. In Model V, C_w/C_w0 peaks correspond to 0.0438 at 8 y, 0.0094 at 7.83 y, 0.00033 at 7.42 y for the three values of λ considered, respectively, whereas in Model VI the C_w/C_w0 are equal to 0.0492 at 8.08 y, 0.0247 at 7.92 y and 0.0053 at 7.83 y.

4.3. Comparison between Different Soils

The physical properties of soil represent a further element that influences the fate and transport mechanisms of the contaminants. Simulations with three different soils (sand, loam, clay) have been carried out, in order to evaluate the corresponding differences in the models. Again, the comparison has been developed with respect to the Trichloroethylene compound in the same conditions depicted in the previous section. The three types of soils are characterized by the same organic carbon fraction, whereas they differ in grain size, water content, hydraulic conductivity and infiltration rate. The soil parameters values are listed in Table 4.

It is worth noting that the analyzed models consider the sorption process only through the soil-water partition coefficient, which is a synthetic parameter considering the characteristics of the soil, the contaminant and their interaction. This parameter should be assessed experimentally with reference to the specific soil-contaminant complex. In this analysis, it has been chosen to evaluate the partition coefficient referring only to the contaminant characteristics. For this reason, the obtained results for the different types of soils are affected only by the difference between hydrological characteristics of the soils, while the differences related to the sorption capacity are neglected. This assumption has resulted in a lower partition coefficient value of the clays than the experimental values in these soils and, consequently, a higher value of the simulated contaminant concentration. Clay soils have, in fact, a higher sorption behavior than the other soils because of the high surface area and negative charged sites of the soils particles.

As previously seen, Model I is independent by the soil parameters (Figure 5a). Model II (Figure 5b) shows a similar behavior for sand and loam, reaching the steady state C_w/C_w0 ratios corresponding to 0.0902 and 0.0836, at 1.67 y and 2.42 y respectively. A lower mobility could be observed for clay. In this case the steady concentration, C_w/C_w0 equal to 0.0538, is reached at t = 7.67 y. Hence, the leaching velocity has a greater impact compared to the sorption capacity.

Model III and IV give similar trends as shown in Figure 5c,d, respectively. In Model III, the time needed to reach the 0.1% of the initial concentration, is equal to 63.17 y, 72.67 y, 69.83 y whereas, in Model IV the time needed to reach the 0.1% of the initial concentration is equal to 45.67 y, 63.00 y and 68.58 y for sand, clay and loam, respectively.

Models V and VI are most influenced by soil parameters, which affect both the time at which the maximum concentration occurs at z = 5 m and the related values. The transport mechanism lasts very long when Model V is applied for clay. Hence the concentration is so extremely low and therefore undetectable. The C_w/C_w0 peaks are equal to 4.380 × 10⁻² at 8 y and 8.651 × 10⁻³ at 18.67 y in sand and loam, respectively. In Model VI the peaks are of the same order of magnitude for sand and loam, whereas it is negligible for clay. In this case, the C_w/C_w0 ratios are equal to 4.920 × 10⁻² at 8.08 y and 1.509 × 10⁻² at 19.75 y for sand and loam, respectively.

4.4. Comparison between Different Source Thickness

As can be seen in Table 1, the thickness of the source L₁ determines the soil attenuation of the contaminant in the Model I, and the time needed to deplete the source in the models composed of an exponential part (Models III to VI). Model II is not influenced by the change of source thickness because it does not take into account the source depletion and soil attenuation. The simulations have been carried out taking into account the scheme depicted in Figure 1, with three different source depths: L₁ = 1 m, 2 m and 4 m, using sand as type of soil and Trichloroethylene as contaminant. Again, the dimensionless concentration C_w/C_w0 has been calculated at the depth z = 5 m. The concentrations calculated with Model I (Figure 6a) shows a significant variation in relation to the source thickness, being equal to 0.167, 0.286 and 0.444, for L₁ equal to 1 m, 2 m, 4 m respectively.

In the exponential Models III and IV (Figure 6c,d), the source thickness has a different effect. The depletion coefficients μ₁ and μ₂ (Table 1) may be used as indicators of the contaminant depletion velocity. The time needed to reach the 0.1% of the initial concentration increases with thickness, reaching the values of 58, 64 and 73 years in the Model III. In Model IV the time needed to reach the 0.1% of the initial concentration is equal to 27, 46 and 70 years for the three values of L₁.

In the Model V, an increased thickness of the source determines delayed and higher peaks. The C_w/C_w0 ratios are 2.25 × 10⁻² (t = 7.92 y), 4.38 × 10⁻² (t = 8.00 y) and 8.24 × 10⁻² (t = 8.25 y) for L₁ equal to 1 m, 2 m, 4 m respectively.

In the Model VI, the increasing of the source thickness lead to higher but earlier peaks. The C_w/C_w0 ratios are equal to 3.19 × 10⁻² (t = 8.08 y), 4.92 × 10⁻² (t = 8.08 y) and 7.93 × 10⁻² (t = 8.00 y), for L₁ equal to 1 m, 2 m, 4 m respectively.

5. Conclusions

The use of fate and transport models may give a considerable support to tackle with environmental problems involving chemical leaching in the vadose zone. Unlike numerical based approaches, analytical models are used especially in the risk assessment of contaminants due to their straightforward application and simplicity. Six analytical models, reproducing contaminant fate and transport from a source located in the unsaturated zone to the groundwater were described and compared with the aim of giving some insights about their use.

On the basis of their characteristics three groups were identified. The first one is suited for contamination scenarios where the source may be assumed constant, e.g. in the case of continuous chemicals leakage. The second group is particularly appropriate when the depletion processes are predominant and the travel distance of the chemical is low, e.g. a localized spill of biodegradable organic contaminant near the water table. The third group describes more comprehensively all the processes occurring during the transport.

Simulations being carried out, showed that models belonging to the third group yielded lowest values of contaminant concentration with respect to the other models, giving the less conservative results. When a more conservative approach is needed, Models I to IV should be preferred instead.

Future research could be addressed to either enhance the existing analytical models or to propose new advanced ones, while preserving their suitability for engineering applications, in order to obtain a more realistic representation of contaminant fate and transport in the unsaturated zone.