Optimal Placement and Sizing of Wind Generators in AC Grids Considering Reactive Power Capability and Wind Speed Curves
Abstract
:1. Introduction
- A methodology for optimal placement and sizing of wind power generators considering reactive power capability and wind speed curves is described. In addition, the methodology also takes into account demand curves over a 24-h period.
- The proposed methodology is focused on minimizing power losses, which can be applied to radial and mesh networks.
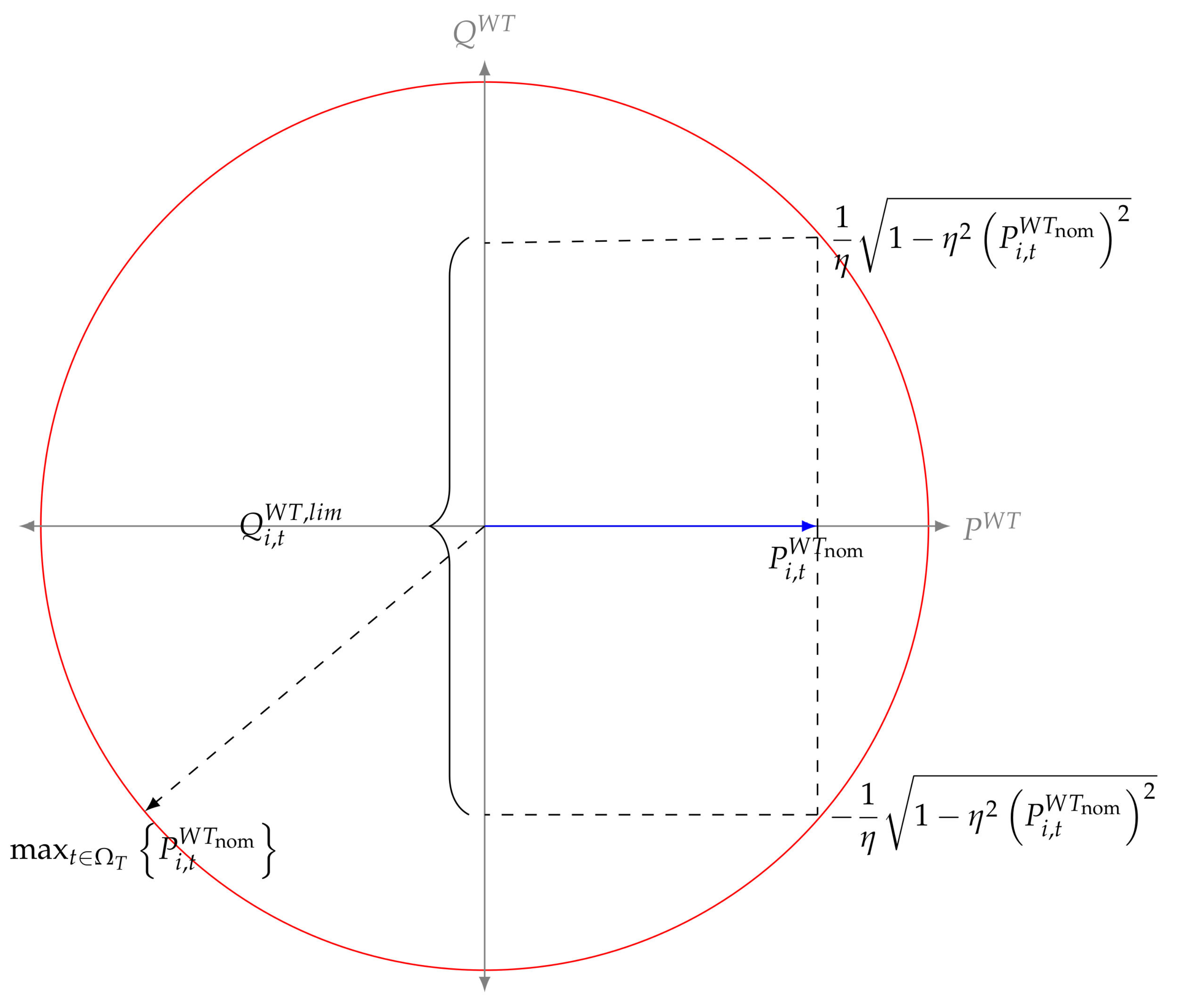
- A chargeability factor is proposed to represent the capacity to support the reactive power of a wind power system.
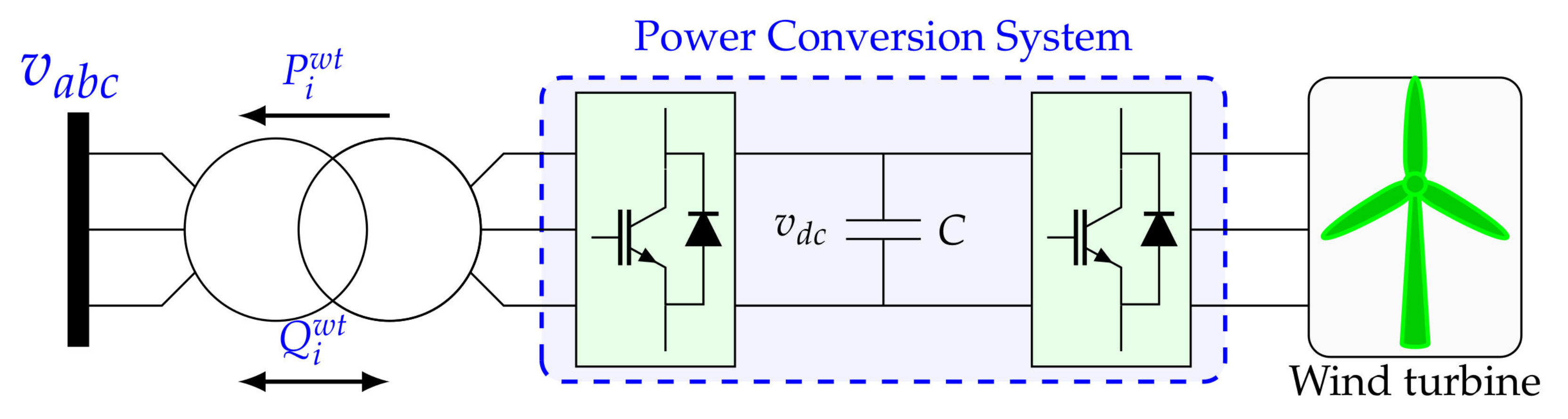
2. Mathematical Modeling
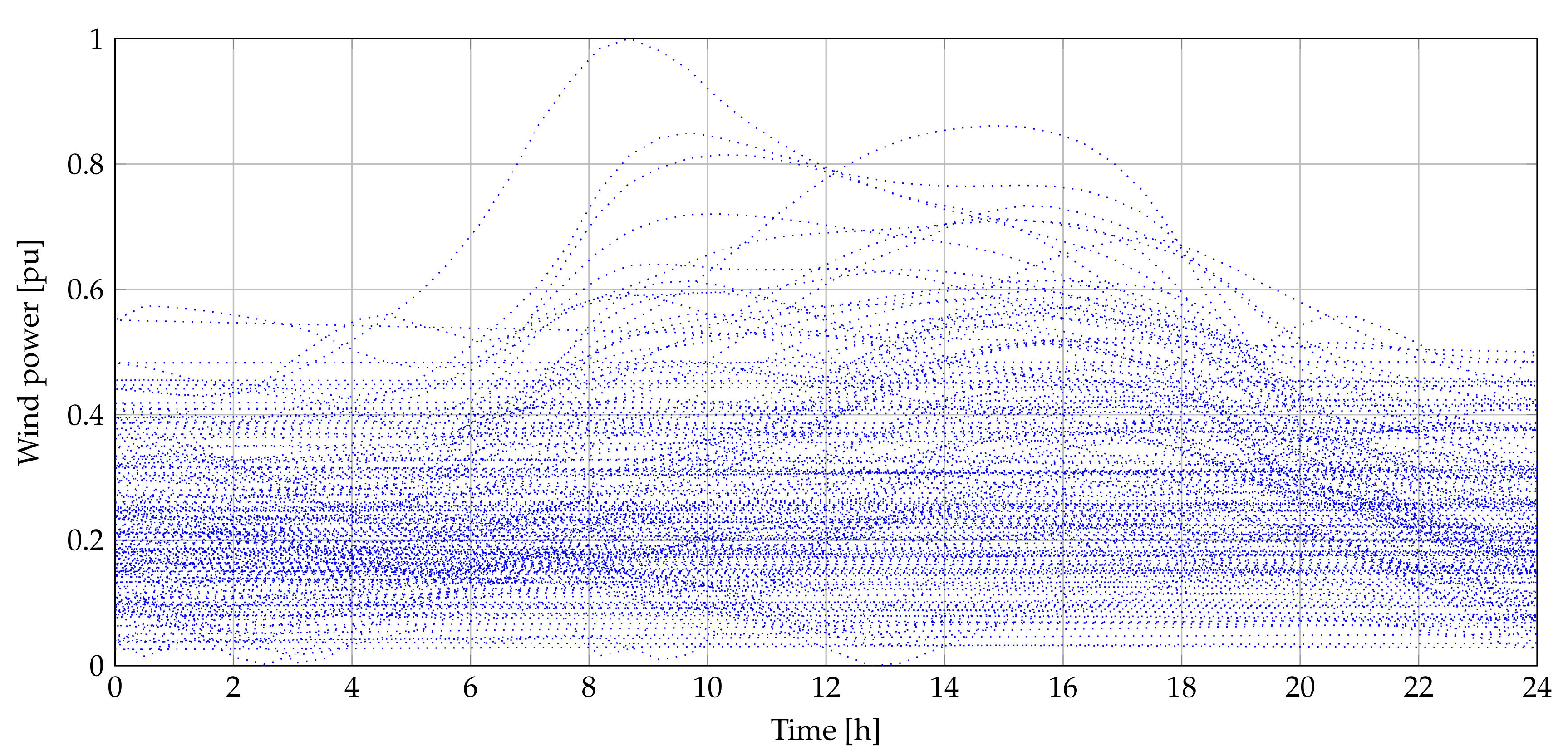
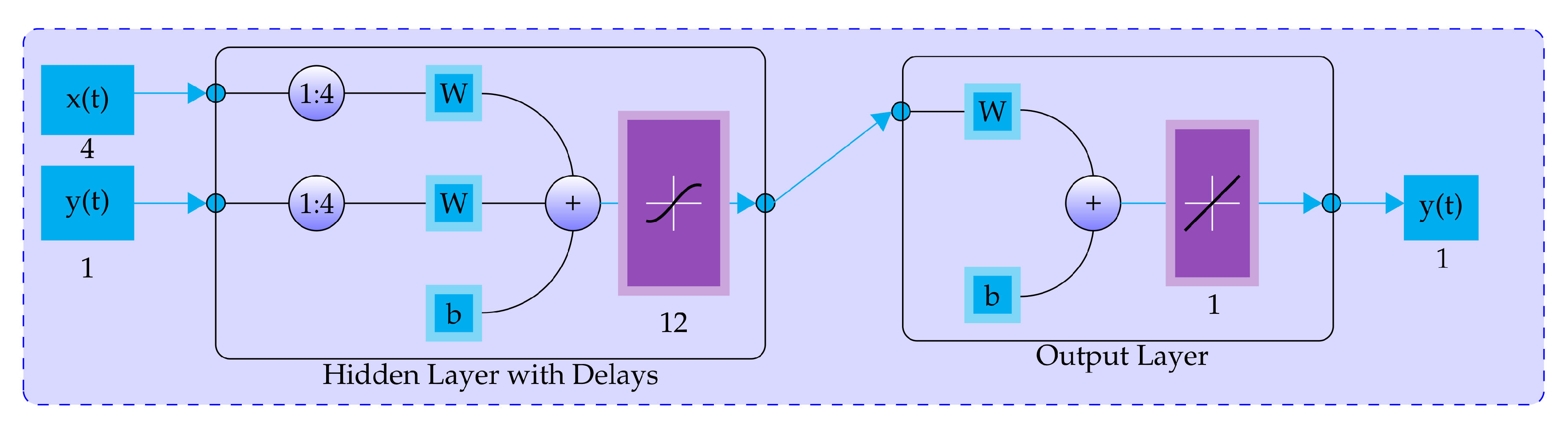
3. Wind Power Forecasting
Artificial Neural Network
4. Solution Methodology
- ✔
- Representation of the mathematical models by sets, which generates a compact formulation.
- ✔
- ✔
- This optimization software allows solving multiple optimization problems, such as linear programming, discrete models, and general non-convex formulations.
- ✔
- Availability of a free version for demonstration, useful to introduce undergraduate students with mathematical optimization.
- ✔
- Non-advanced programming skills are required for using GAMS, since it has an intuitive manner to implement a mathematical model using a basic plain text interface.
| Algorithm 1: Main features for implementing a mathematical optimization model in GAMS |
Data: Define the nature of the optimization problem and select the test system. Sets Definition of sets, parameters (constant vectors), scalars (constant number), and tables (constant matrices). Variables: Determine the type of variables, e.g., integer, continuous or binary. Solution: Select a MINLP solver to reach the solution via minimization of the objective function. Visualization: Extract the variables of interest, i.e., location of the generators and their sizes, the value of the objective function, etc. Result: Optimal location and sizing of wind turbines in AC distribution networks under daily operative scenarios. |
5. Test Systems
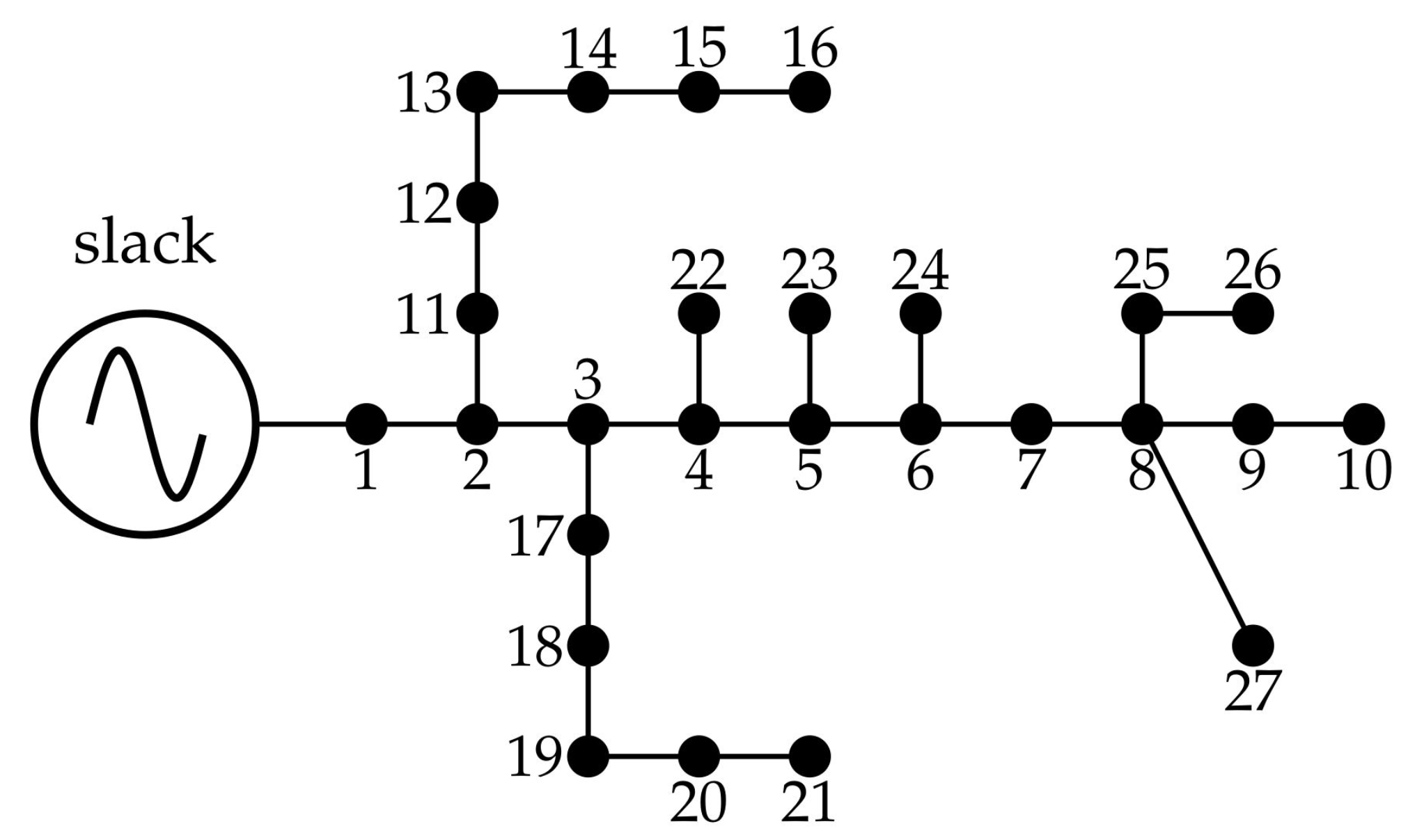
5.1. 27-Node Test System
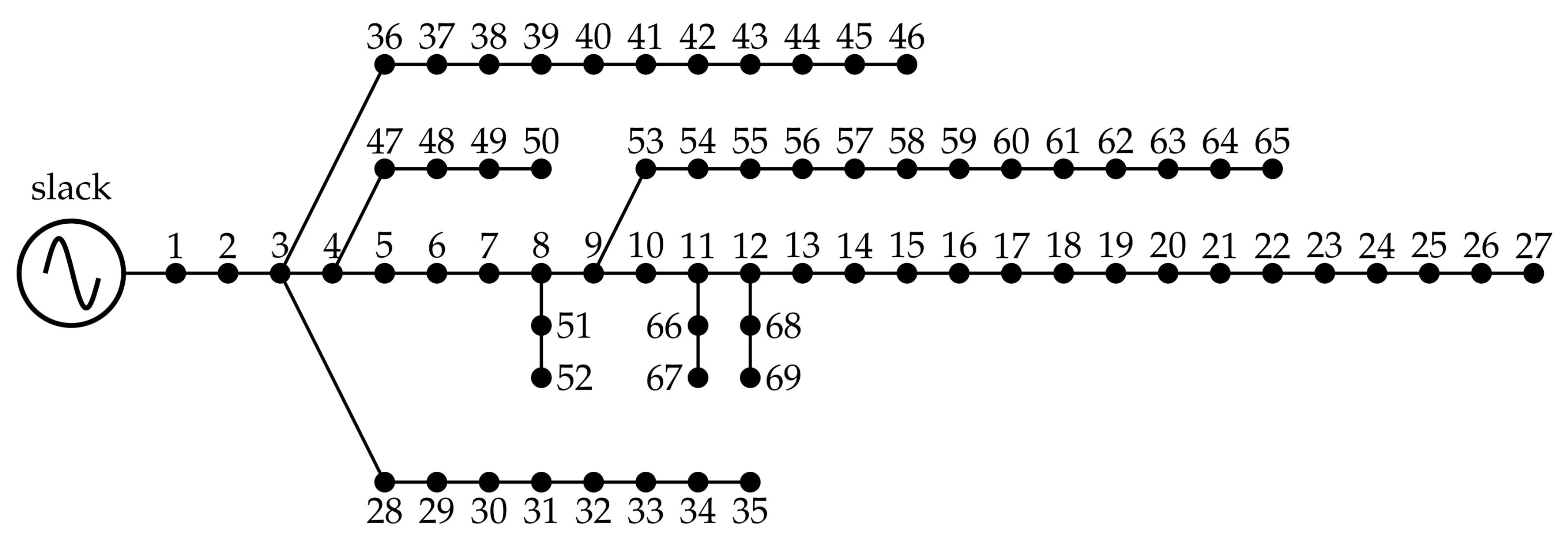
5.2. 69-Node Test Feeder
6. Computational Validation
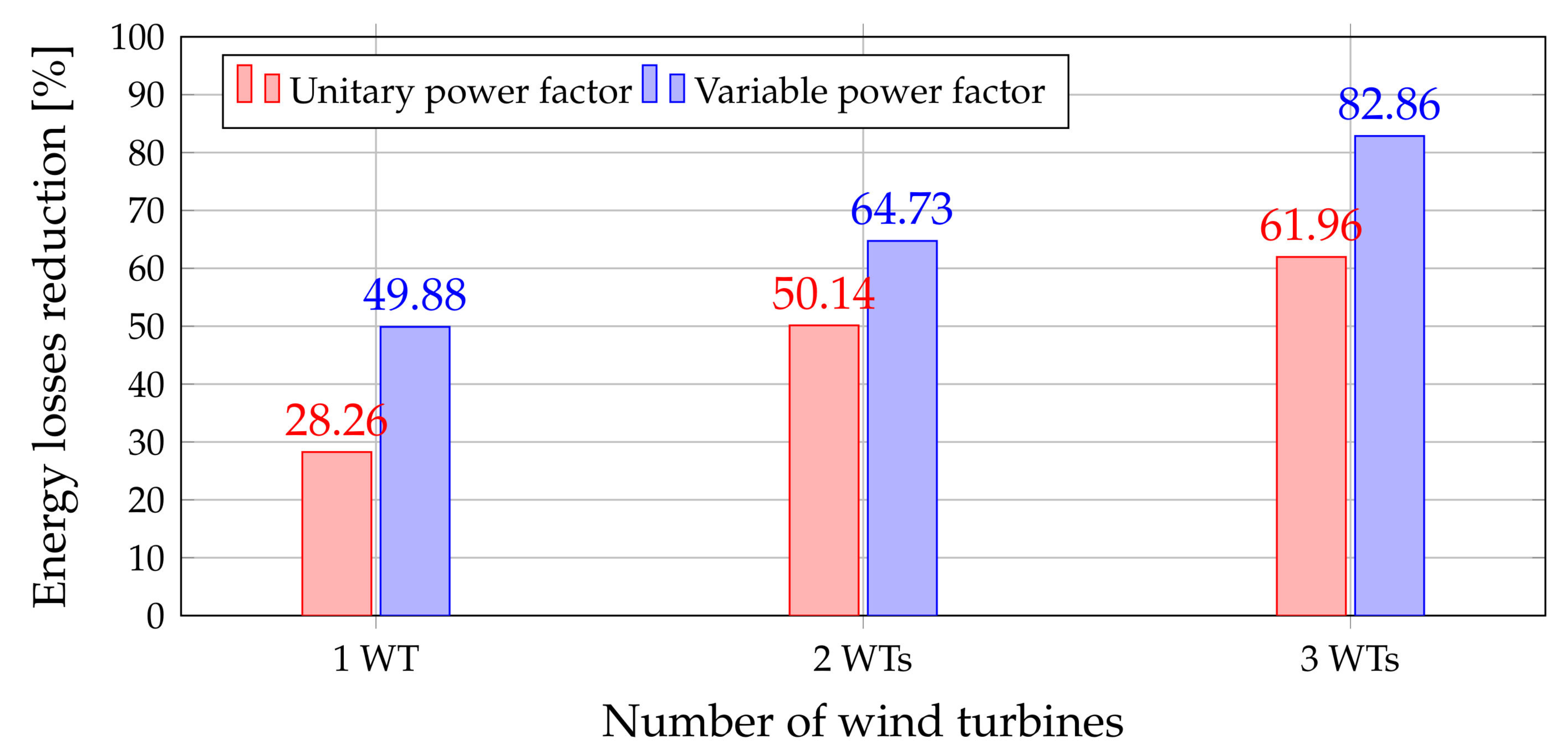
6.1. 27-Node Test Feeder
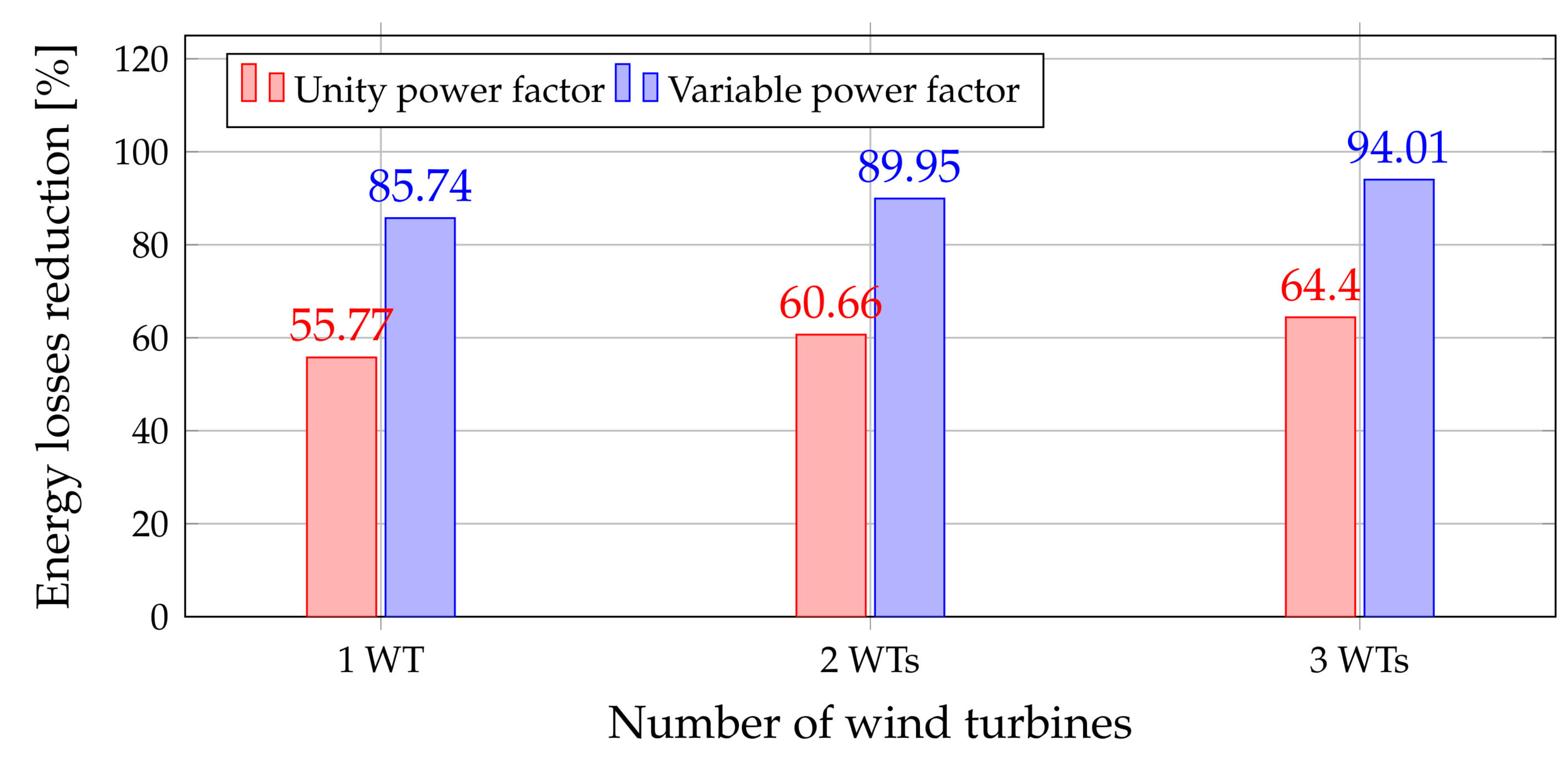
6.2. 69-Node Test Feeder
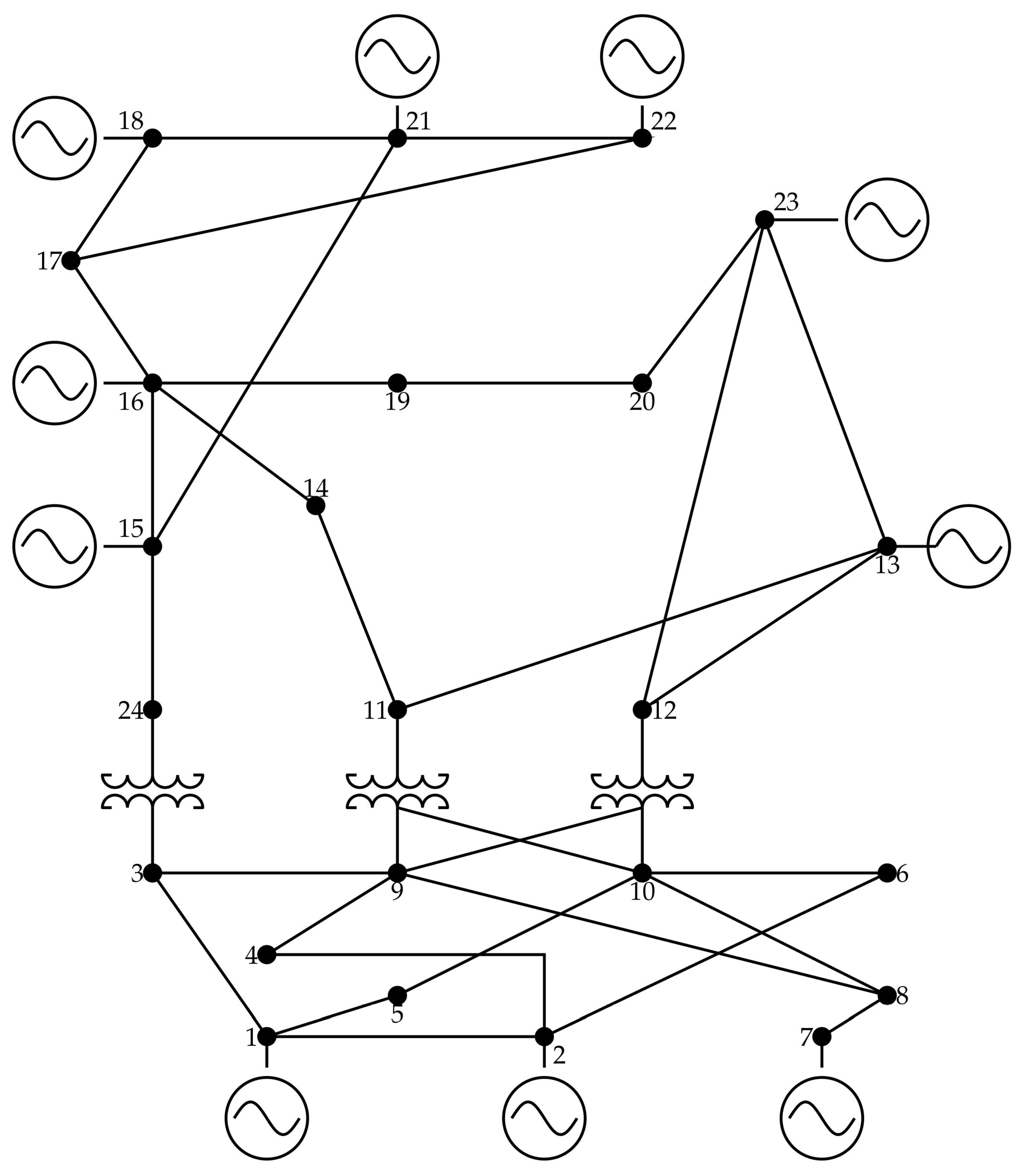
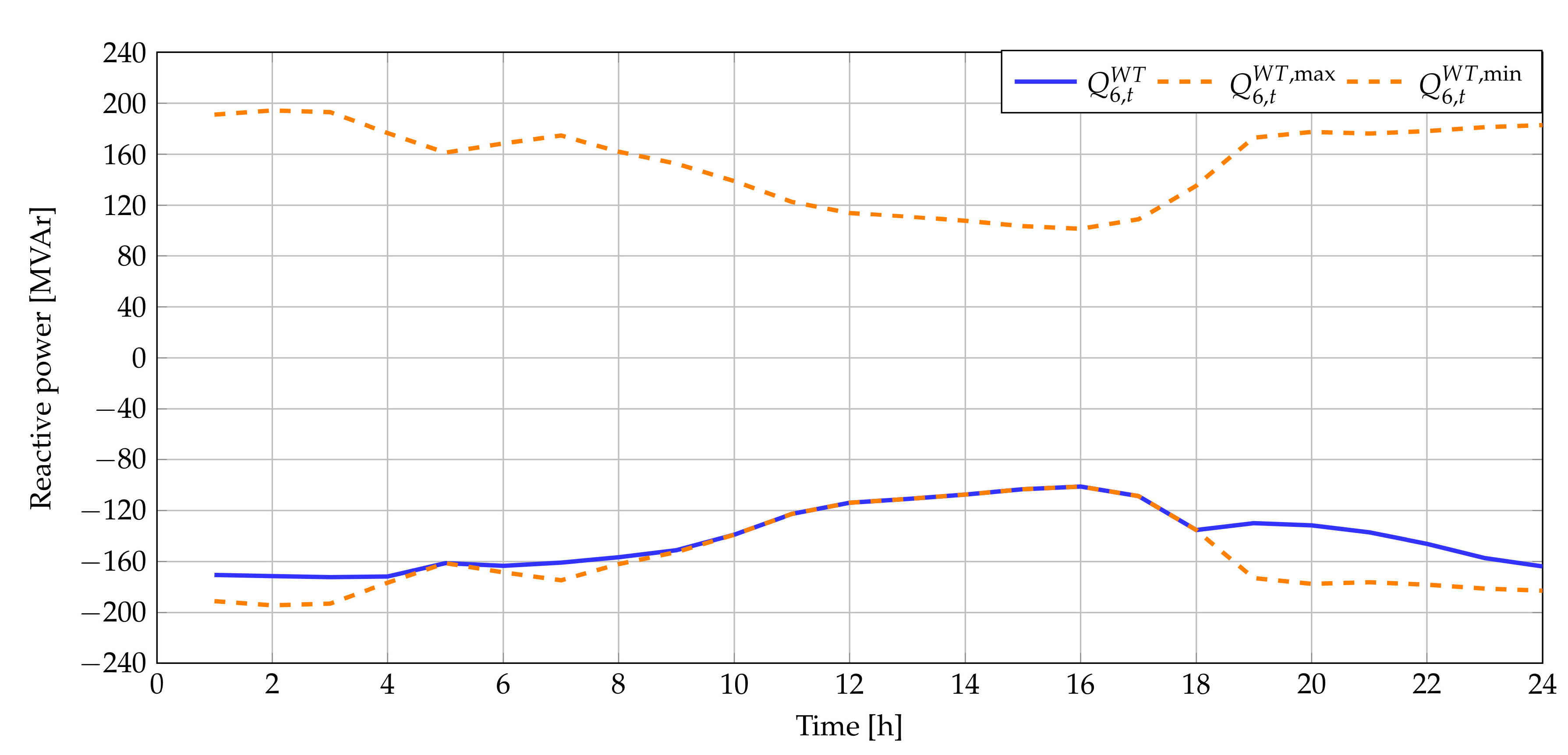
6.3. Large-Scale Power System Evaluation
- To reach a total daily energy losses reduction of about % it is required to install a WT at node 6 with a nominal rate of MW; and to increase the daily energy reduction by %, MW is required to be installed, which implies more than of additional power injection. This result implies that energy losses formulated in (1) have a strong nonlinear relation between the amount of power injection by renewable energy resources and their location in regards with the objective function minimization. Note that this behavior was also observed in both radial test feeders previously reported.
- The proposed mathematical model is suitable to be applied for both radial medium voltage and high-voltage meshed networks, which confirms that it is general and scalable for multiple grid topologies.
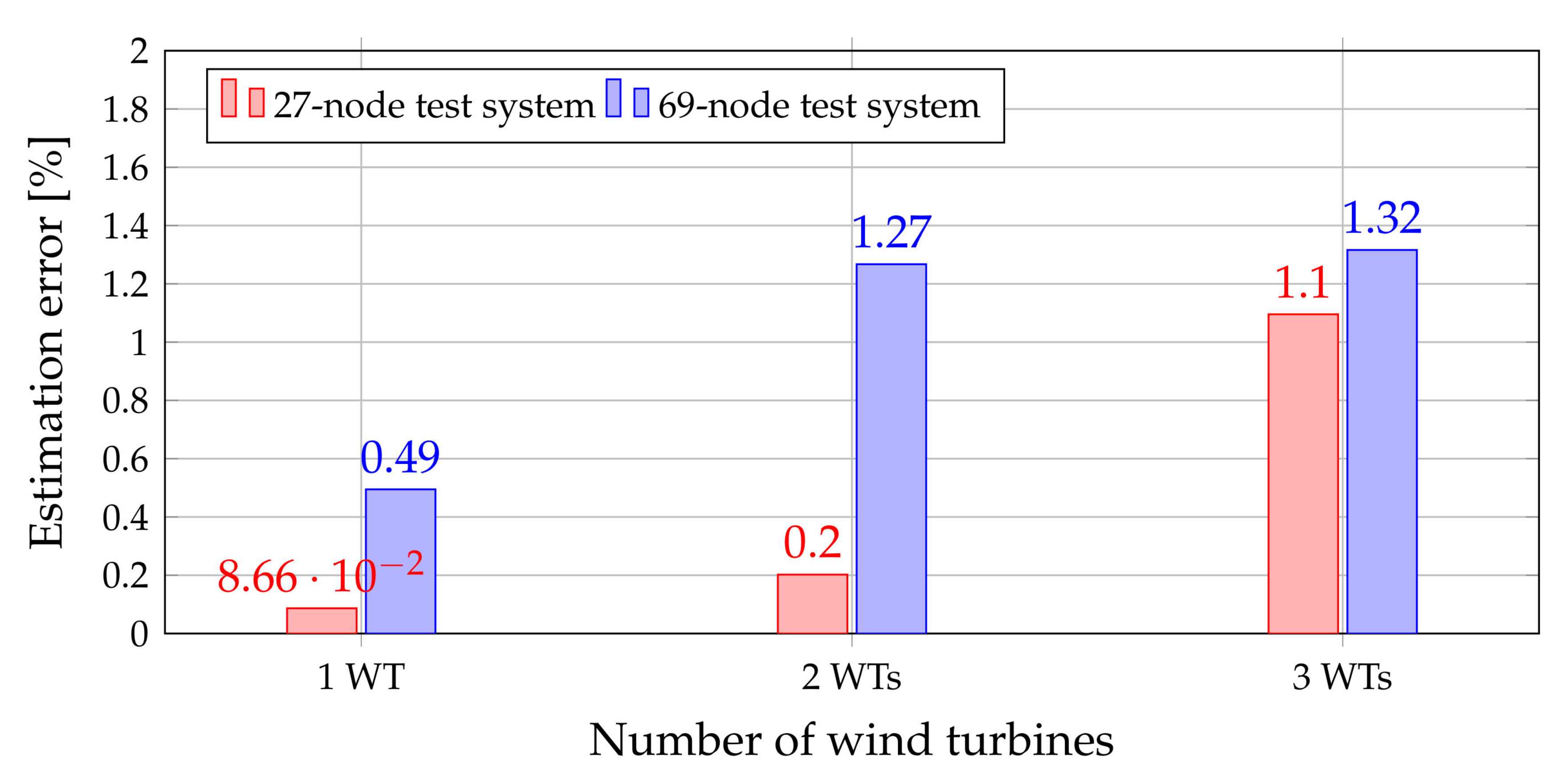
6.4. Assessment of ANN Performance
7. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Mazhari, S.M.; Monsef, H.; Romero, R. A multi-objective distribution system expansion planning incorporating customer choices on reliability. IEEE Trans. Power Syst. 2015, 31, 1330–1340. [Google Scholar] [CrossRef]
- Essallah, S.; Khedher, A.; Bouallegue, A. Integration of distributed generation in electrical grid: Optimal placement and sizing under different load conditions. Comput. Electr. Eng. 2019, 79, 106461. [Google Scholar] [CrossRef]
- Mohseni-Bonab, S.M.; Rabiee, A. Optimal reactive power dispatch: A review, and a new stochastic voltage stability constrained multi-objective model at the presence of uncertain wind power generation. IET Gener. Transm. Distrib. 2017, 11, 815–829. [Google Scholar] [CrossRef]
- Strunz, K.; Abbasi, E.; Huu, D.N. DC microgrid for wind and solar power integration. IEEE Trans. Emerg. Sel. Top. Power Electron. 2013, 2, 115–126. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grisales-Noreña, L.F.; Gil-González, W.; Alcalá, G.; Hernandez-Escobedo, Q. Optimal Location and Sizing of PV Sources in DC Networks for Minimizing Greenhouse Emissions in Diesel Generators. Symmetry 2020, 12, 322. [Google Scholar] [CrossRef] [Green Version]
- Kaur, S.; Kumbhar, G.; Sharma, J. A MINLP technique for optimal placement of multiple DG units in distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 609–617. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghoshal, S.P.; Ghosh, S. Optimal sizing and placement of distributed generation in a network system. Int. J. Electr. Power Energy Syst. 2010, 32, 849–856. [Google Scholar] [CrossRef]
- Manikanta, G.; Mani, A.; Singh, H.; Chaturvedi, D. Placing distributed generators in distribution system using adaptive quantum inspired evolutionary algorithm. In Proceedings of the Second International Conference on Research in Computational Intelligence and Communication Networks (ICRCICN), Kolkata, India, 23–25 September 2016; pp. 157–162. [Google Scholar]
- Babu, P.V.; Singh, S. Optimal Placement of DG in Distribution network for Power loss minimization using NLP & PLS Technique. Energy Procedia 2016, 90, 441–454. [Google Scholar]
- Meena, N.K.; Swarnkar, A.; Gupta, N.; Niazi, K. Wind Power Generation Planning by Utilizing the Reactive Power Capabilities of Generators. In Proceedings of the Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 24–26 October 2017; pp. 1–6. [Google Scholar]
- Prabha, D.R.; Jayabarathi, T. Optimal placement and sizing of multiple distributed generating units in distribution networks by invasive weed optimization algorithm. Ain Shams Eng. J. 2016, 7, 683–694. [Google Scholar] [CrossRef] [Green Version]
- Jamil, M.; Anees, A.S. Optimal sizing and location of SPV (solar photovoltaic) based MLDG (multiple location distributed generator) in distribution system for loss reduction, voltage profile improvement with economical benefits. Energy 2016, 103, 231–239. [Google Scholar] [CrossRef]
- Das, B.; Mukherjee, V.; Das, D. DG placement in radial distribution network by symbiotic organisms search algorithm for real power loss minimization. Appl. Soft Comput. 2016, 49, 920–936. [Google Scholar] [CrossRef]
- Parizad, A.; Khazali, A.H.; Kalantar, M. Sitting and sizing of distributed generation through Harmony Search Algorithm for improve voltage profile and reducuction of THD and losses. In Proceedings of the CCECE 2010, Calgary, AB, Canada, 2–5 May 2010; pp. 1–7. [Google Scholar]
- Abu-Mouti, F.S.; El-Hawary, M. Optimal distributed generation allocation and sizing in distribution systems via artificial bee colony algorithm. IEEE Trans. Power Deliv. 2011, 26, 2090–2101. [Google Scholar] [CrossRef]
- García, J.A.M.; Mena, A.J.G. Optimal distributed generation location and size using a modified teaching–learning based optimization algorithm. Int. J. Electr. Power Energy Syst. 2013, 50, 65–75. [Google Scholar] [CrossRef]
- Cheng, S.; Chen, M.Y.; Fleming, P.J. Improved multi-objective particle swarm optimization with preference strategy for optimal DG integration into the distribution system. Neurocomputing 2015, 148, 23–29. [Google Scholar] [CrossRef]
- Tolabi, H.B.; Ali, M.H.; Rizwan, M. Simultaneous reconfiguration, optimal placement of DSTATCOM, and photovoltaic array in a distribution system based on fuzzy-ACO approach. IEEE Trans. Sustain. Energy 2014, 6, 210–218. [Google Scholar] [CrossRef]
- Muthukumar, K.; Jayalalitha, S. Optimal placement and sizing of distributed generators and shunt capacitors for power loss minimization in radial distribution networks using hybrid heuristic search optimization technique. Int. J. Electr. Power Energy Syst. 2016, 78, 299–319. [Google Scholar] [CrossRef]
- Kefayat, M.; Ara, A.L.; Niaki, S.N. A hybrid of ant colony optimization and artificial bee colony algorithm for probabilistic optimal placement and sizing of distributed energy resources. Energy Convers. Manag. 2015, 92, 149–161. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Gonzalez Montoya, D.; Ramos-Paja, C.A. Optimal sizing and location of distributed generators based on PBIL and PSO techniques. Energies 2018, 11, 1018. [Google Scholar] [CrossRef] [Green Version]
- Martinez-Rojas, M.; Sumper, A.; Gomis-Bellmunt, O.; Sudrià-Andreu, A. Reactive power dispatch in wind farms using particle swarm optimization technique and feasible solutions search. Appl. Energy 2011, 88, 4678–4686. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.; Orozco-Henao, C.; Serra, F. Economic Dispatch of BESS and Renewable Generators in DC Microgrids Using Voltage-Dependent Load Models. Energies 2019, 12, 4494. [Google Scholar] [CrossRef] [Green Version]
- Cisneros, R.; Mancilla-David, F.; Ortega, R. Passivity-Based Control of a Grid-Connected Small-Scale Windmill With Limited Control Authority. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 1, 247–259. [Google Scholar] [CrossRef]
- Namazi, M.M.; Nejad, S.M.S.; Tabesh, A.; Rashidi, A.; Liserre, M. Passivity-Based Control of Switched Reluctance-Based Wind System Supplying Constant Power Load. IEEE Trans. Ind. Electron. 2018, 65, 9550–9560. [Google Scholar] [CrossRef] [Green Version]
- Barambones, O. Sliding Mode Control Strategy for Wind Turbine Power Maximization. Energies 2012, 5, 2310–2330. [Google Scholar] [CrossRef]
- Lee, S.W.; Chun, K.H. Adaptive Sliding Mode Control for PMSG Wind Turbine Systems. Energies 2019, 12, 595. [Google Scholar] [CrossRef] [Green Version]
- Alrifai, M.; Zribi, M.; Rayan, M. Feedback Linearization Controller for a Wind Energy Power System. Energies 2016, 9, 771. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Wang, J.; Xiong, L.; Wu, F. Nonlinear Controllers Based on Exact Feedback Linearization for Series-Compensated DFIG-Based Wind Parks to Mitigate Sub-Synchronous Control Interaction. Energies 2017, 10, 1182. [Google Scholar] [CrossRef] [Green Version]
- Salgado-Herrera, N.M.; Medina-Ríos, A.; Tapia-Sánchez, R.; Anaya-Lara, O. Reactive power compensation through active back to back converter in type-4 wind turbine. In Proceedings of the IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 9–11 November 2016; pp. 1–6. [Google Scholar]
- Murillo-Yarce, D.; Garcés-Ruiz, A.; Escobar-Mejía, A. Passivity-Based Control for DC-Microgrids with Constant Power Terminals in Island Mode Operation. Revista Facultad de Ingeniería Universidad de Antioquia 2018, 86, 32–39. [Google Scholar] [CrossRef]
- Choi, Y.H.; Cho, Y.S. Multiple-Point Voltage Control to Minimize Interaction Effects in Power Systems. Energies 2019, 12, 274. [Google Scholar] [CrossRef] [Green Version]
- Gil-González, W.; Montoya, O.D.; Holguín, E.; Garces, A.; Grisales-Noreña, L.F. Economic dispatch of energy storage systems in dc microgrids employing a semidefinite programming model. J. Energy Storage 2019, 21, 1–8. [Google Scholar] [CrossRef]
- Data, S.S.R. Time Series of Solar Radiation Data. Available online: http://www.soda-pro.com/ (accessed on 5 July 2019).
- Koo, J.; Han, G.D.; Choi, H.J.; Shim, J.H. Wind-speed prediction and analysis based on geological and distance variables using an artificial neural network: A case study in South Korea. Energy 2015, 93, 1296–1302. [Google Scholar] [CrossRef]
- Demuth, H.B.; Beale, M.H.; De Jess, O.; Hagan, M.T. Neural Network Design, 2nd ed.; Martin Hagan: Stillwater, OK, USA, 2014. [Google Scholar]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L. An exact MINLP model for optimal location and sizing of DGs in distribution networks: A general algebraic modeling system approach. Ain Shams Eng. J. 2019. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grajales, A.; Garces, A.; Castro, C.A. Distribution Systems Operation Considering Energy Storage Devices and Distributed Generation. IEEE Lat. Am. Trans. 2017, 15, 890–900. [Google Scholar] [CrossRef]
- Tartibu, L.; Sun, B.; Kaunda, M. Multi-objective optimization of the stack of a thermoacoustic engine using GAMS. Appl. Soft Comput. 2015, 28, 30–43. [Google Scholar] [CrossRef]
- Skworcow, P.; Paluszczyszyn, D.; Ulanicki, B.; Rudek, R.; Belrain, T. Optimisation of Pump and Valve Schedules in Complex Large-scale Water Distribution Systems Using GAMS Modelling Language. Procedia Eng. 2014, 70, 1566–1574. [Google Scholar] [CrossRef] [Green Version]
- Giraldo, O.D.M. Solving a Classical Optimization Problem Using GAMS Optimizer Package: Economic Dispatch Problem Implementation. Ing. Y Cienc. 2017, 13, 39–63. [Google Scholar] [CrossRef] [Green Version]
- Soroudi, A. Power System Optimization Modeling in GAMS; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Martínez-Lacañina, P.J.; Marcolini, A.M.; Martínez-Ramos, J.L. DCOPF contingency analysis including phase shifting transformers. In Proceedings of the Power Systems Computation Conference, Wroclaw, Poland, 18–22 August 2014; pp. 1–7. [Google Scholar]

| Node | Node | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| i | j | [] | [] | [kW] | [kW] | i | j | [] | [] | [kW] | [kW] |
| 1 | 2 | 0.15208 | 0.19855 | 0 | 0 | 14 | 15 | 0.87630 | 0.41330 | 106.3 | 65.8 |
| 2 | 3 | 0.65805 | 0.59745 | 0 | 0 | 15 | 16 | 0.87630 | 0.41330 | 25 | 158 |
| 3 | 4 | 0.19742 | 0.17924 | 297.5 | 184.4 | 3 | 17 | 0.87630 | 0.41330 | 255 | 158 |
| 4 | 5 | 0.43848 | 0.26038 | 0 | 0 | 17 | 18 | 0.52578 | 0.24798 | 127.5 | 79 |
| 5 | 6 | 0.48720 | 0.28931 | 255 | 158 | 18 | 19 | 0.78867 | 0.37197 | 297.5 | 184.4 |
| 6 | 7 | 0.48197 | 0.22732 | 0 | 0 | 19 | 20 | 0.83248 | 0.39263 | 340 | 210.7 |
| 7 | 8 | 0.87630 | 0.41330 | 212.5 | 131.7 | 20 | 21 | 0.87630 | 0.41330 | 85 | 52.7 |
| 8 | 9 | 1.09540 | 0.51663 | 0 | 0 | 4 | 22 | 0.87630 | 0.41330 | 106.3 | 65.8 |
| 9 | 10 | 0.87630 | 0.41330 | 266.1 | 164.9 | 5 | 23 | 0.87630 | 0.41330 | 55.3 | 34.2 |
| 2 | 11 | 0.87630 | 0.41330 | 85 | 52.7 | 6 | 24 | 0.35052 | 0.16532 | 69.7 | 43.2 |
| 11 | 12 | 1.07780 | 0.50836 | 340 | 210.7 | 8 | 25 | 0.52578 | 0.24798 | 256 | 158 |
| 12 | 13 | 0.65722 | 0.30998 | 297.5 | 184.4 | 8 | 26 | 0.52578 | 0.24798 | 63.8 | 39.5 |
| 13 | 14 | 0.49073 | 0.23145 | 191.3 | 118.5 | 26 | 27 | 0.70104 | 0.33064 | 170 | 105.4 |
| Node | Node | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| i | j | [] | [] | [kW] | [kW] | i | j | [] | [] | [kW] | [kW] |
| 1 | 2 | 0.0005 | 0.0012 | 0 | 0 | 3 | 36 | 0.0044 | 0.0108 | 26 | 18.55 |
| 2 | 3 | 0.0005 | 0.0012 | 0 | 0 | 36 | 37 | 0.0640 | 0.1565 | 26 | 18.55 |
| 3 | 4 | 0.0015 | 0.0036 | 0 | 0 | 37 | 38 | 0.1053 | 0.1230 | 0 | 0 |
| 4 | 5 | 0.0251 | 0.0294 | 0 | 0 | 38 | 39 | 0.0304 | 0.0355 | 24 | 17 |
| 5 | 6 | 0.3660 | 0.1864 | 2.6 | 2.2 | 39 | 40 | 0.0018 | 0.0021 | 24 | 17 |
| 6 | 7 | 0.3811 | 0.1941 | 40.4 | 30 | 40 | 41 | 0.7283 | 0.8509 | 102 | 1 |
| 7 | 8 | 0.0922 | 0.0470 | 75 | 54 | 41 | 42 | 0.3100 | 0.3623 | 0 | 0 |
| 8 | 9 | 0.0493 | 0.0251 | 30 | 22 | 42 | 43 | 0.0410 | 0.0478 | 6 | 4.3 |
| 9 | 10 | 0.8190 | 0.2707 | 28 | 19 | 43 | 44 | 0.0092 | 0.0116 | 0 | 0 |
| 10 | 11 | 0.1872 | 0.0619 | 145 | 104 | 44 | 45 | 0.1089 | 0.1373 | 39.22 | 26.3 |
| 11 | 12 | 0.7114 | 0.2351 | 145 | 104 | 45 | 46 | 0.0009 | 0.0012 | 39.22 | 26.3 |
| 12 | 13 | 1.0300 | 0.3400 | 8 | 5 | 4 | 47 | 0.0034 | 0.0084 | 0 | 0 |
| 13 | 14 | 1.0440 | 0.3450 | 8 | 5 | 47 | 48 | 0.0851 | 0.2083 | 79 | 56.4 |
| 14 | 15 | 1.0580 | 0.3496 | 0 | 0 | 48 | 49 | 0.2898 | 0.7091 | 384.7 | 274.5 |
| 15 | 16 | 0.1966 | 0.0650 | 45 | 30 | 49 | 50 | 0.0822 | 0.2011 | 384.7 | 274.5 |
| 16 | 17 | 0.3744 | 0.1238 | 60 | 35 | 8 | 51 | 0.0928 | 0.0473 | 40.5 | 28.3 |
| 17 | 18 | 0.0047 | 0.0016 | 60 | 35 | 51 | 52 | 0.3319 | 0.1140 | 3.6 | 2.7 |
| 18 | 19 | 0.3276 | 0.1083 | 0 | 0 | 9 | 53 | 0.1740 | 0.0886 | 4.35 | 3.5 |
| 19 | 20 | 0.2106 | 0.0690 | 1 | 0.6 | 53 | 54 | 0.2030 | 0.1034 | 26.4 | 19 |
| 20 | 21 | 0.3416 | 0.1129 | 114 | 81 | 54 | 55 | 0.2842 | 0.1447 | 24 | 17.2 |
| 21 | 22 | 0.0140 | 0.0046 | 5 | 3.5 | 55 | 56 | 0.2813 | 0.1433 | 0 | 0 |
| 22 | 23 | 0.1591 | 0.0526 | 0 | 0 | 56 | 57 | 1.5900 | 0.5337 | 0 | 0 |
| 23 | 24 | 0.3463 | 0.1145 | 28 | 20 | 57 | 58 | 0.7837 | 0.2630 | 0 | 0 |
| 24 | 25 | 0.7488 | 0.2475 | 0 | 0 | 58 | 59 | 0.3042 | 0.1006 | 100 | 72 |
| 25 | 26 | 0.3089 | 0.1021 | 14 | 10 | 59 | 60 | 0.3861 | 0.1172 | 0 | 0 |
| 26 | 27 | 0.1732 | 0.0572 | 14 | 10 | 60 | 61 | 0.5075 | 0.2585 | 1244 | 888 |
| 3 | 28 | 0.0044 | 0.0108 | 26 | 18.6 | 61 | 62 | 0.0974 | 0.0496 | 32 | 23 |
| 28 | 29 | 0.0640 | 0.1565 | 26 | 18.6 | 62 | 63 | 0.1450 | 0.0738 | 0 | 0 |
| 29 | 30 | 0.3978 | 0.1315 | 0 | 0 | 63 | 64 | 0.7105 | 0.3619 | 227 | 162 |
| 30 | 31 | 0.0702 | 0.0232 | 0 | 0 | 64 | 65 | 1.0410 | 0.5302 | 59 | 42 |
| 31 | 32 | 0.3510 | 0.1160 | 0 | 0 | 11 | 66 | 0.2012 | 0.0611 | 18 | 13 |
| 32 | 33 | 0.8390 | 0.2816 | 10 | 10 | 66 | 67 | 0.0047 | 0.0014 | 18 | 13 |
| 33 | 34 | 1.7080 | 0.5646 | 14 | 14 | 12 | 68 | 0.7394 | 0.2444 | 28 | 20 |
| 34 | 35 | 1.4740 | 0.4873 | 4 | 4 | 68 | 69 | 0.0047 | 0.0016 | 28 | 20 |
| Number of WTs | Location [Node] | Size [kW] | Energy Losses [kWh/Day] |
|---|---|---|---|
| 1 | 18 | 1547.17725 | 1185.164 |
| 2 | 823.6474 | ||
| 3 | 628.4598 |
| Number of WTs | Location [Node] | Size [kW] | Energy Losses [kWh/Day] |
|---|---|---|---|
| 1 | 8 | 1432.89260 | 827.9621 |
| 2 | 582.6569 | ||
| 3 | 283.1916 |
| Number of WTs | Location [Node] | Size [kW] | Energy Losses [kWh/Day] |
|---|---|---|---|
| 1 | 60 | 1639.2766 | 1179.3480 |
| 2 | 1048.7920 | ||
| 3 | 949.2134 |
| Number of WTs | Location [Node] | Size [kW] | Energy Losses [kWh/Day] |
|---|---|---|---|
| 1 | 62 | 1597.3204 | 380.2232 |
| 2 | 268.0452 | ||
| 3 | 159.6235 |
| Node | Node | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.500 | 2.500 | −0.750 | 0.750 | 16 | 0.150 | 1.350 | −0.500 | 0.750 |
| 2 | 0.250 | 1.850 | −0.900 | 0.700 | 16 | 0.150 | 1.350 | −0.500 | 0.750 |
| 7 | 0.400 | 3.000 | −0.800 | 1.200 | 18 | 0.500 | 4.000 | −1.850 | 2.000 |
| 13 | 0.000 | 6.000 | −5.000 | 5.000 | 21 | 0.450 | 4.500 | −1.500 | 1.500 |
| 14 | 0.000 | 0.000 | −1.500 | 1.500 | 22 | 0.250 | 2.800 | −1.000 | 1.000 |
| 15 | 0.250 | 1.500 | −0.750 | 0.800 | 23 | 0.750 | 6.000 | −1.650 | 1.750 |
| Node | Node | Node | Node | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.080 | 0.220 | 7 | 1.250 | 0.250 | 13 | 2.650 | 0.540 | 19 | 1.810 | 0.370 |
| 2 | 0.970 | 0.200 | 8 | 1.710 | 0.350 | 14 | 1.940 | 0.390 | 20 | 1.280 | 0.260 |
| 3 | 1.800 | 0.370 | 9 | 1.750 | 0.360 | 15 | 3.170 | 0.640 | 21 | 0.000 | 0.000 |
| 4 | 0.740 | 0.150 | 10 | 1.950 | 0.400 | 16 | 1.000 | 0.200 | 22 | 0.000 | 0.000 |
| 5 | 0.710 | 0.140 | 11 | 0.000 | 0.000 | 17 | 0.000 | 0.000 | 23 | 0.000 | 0.000 |
| 6 | 1.360 | 0.280 | 12 | 0.000 | 0.000 | 18 | 3.330 | 0.680 | 24 | 0.000 | 0.000 |
| Node i | Node j | Tap | Node i | Node j | Tap | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.0026 | 0.0139 | 0.4611 | 0 | 12 | 13 | 0.0061 | 0.0476 | 0.0999 | 0 |
| 1 | 3 | 0.0546 | 0.2112 | 0.0572 | 0 | 12 | 23 | 0.0124 | 0.0966 | 0.2030 | 0 |
| 1 | 5 | 0.0218 | 0.0845 | 0.0229 | 0 | 13 | 23 | 0.0111 | 0.0865 | 0.1818 | 0 |
| 2 | 4 | 0.0328 | 0.1267 | 0.0343 | 0 | 14 | 16 | 0.0050 | 0.0389 | 0.0818 | 0 |
| 2 | 6 | 0.0497 | 0.1920 | 0.0520 | 0 | 15 | 16 | 0.0022 | 0.0173 | 0.0364 | 0 |
| 3 | 9 | 0.0308 | 0.1190 | 0.0322 | 0 | 15 | 21 | 0.0063 | 0.0490 | 0.1030 | 0 |
| 3 | 24 | 0.0023 | 0.0839 | 0 | 1.015 | 15 | 21 | 0.0063 | 0.0490 | 0.1030 | 0 |
| 4 | 9 | 0.0268 | 0.1037 | 0.0281 | 0 | 15 | 24 | 0.0067 | 0.0519 | 0.1091 | 0 |
| 5 | 10 | 0.0228 | 0.0883 | 0.0239 | 0 | 16 | 17 | 0.0033 | 0.0259 | 0.0545 | 0 |
| 6 | 10 | 0.0139 | 0.0605 | 2.4590 | 0 | 16 | 19 | 0.0030 | 0.0231 | 0.0485 | 0 |
| 7 | 8 | 0.0159 | 0.0614 | 0.0166 | 0 | 17 | 18 | 0.0018 | 0.0144 | 0.0303 | 0 |
| 8 | 9 | 0.0427 | 0.1651 | 0.0447 | 0 | 17 | 22 | 0.0135 | 0.1053 | 0.2212 | 0 |
| 8 | 10 | 0.0427 | 0.1651 | 0.0447 | 0 | 18 | 21 | 0.0033 | 0.0259 | 0.0545 | 0 |
| 9 | 11 | 0.0023 | 0.0839 | 0 | 1.030 | 18 | 21 | 0.0033 | 0.0259 | 0.0545 | 0 |
| 9 | 12 | 0.0023 | 0.0839 | 0 | 1.030 | 19 | 20 | 0.0051 | 0.0396 | 0.0833 | 0 |
| 10 | 11 | 0.0023 | 0.0839 | 0 | 1.015 | 19 | 20 | 0.0051 | 0.0396 | 0.0833 | 0 |
| 10 | 12 | 0.0023 | 0.0839 | 0 | 1.015 | 20 | 23 | 0.0028 | 0.0216 | 0.0455 | 0 |
| 11 | 13 | 0.0061 | 0.0476 | 0.0999 | 0 | 20 | 23 | 0.0028 | 0.0216 | 0.0455 | 0 |
| 11 | 14 | 0.0054 | 0.0418 | 0.0879 | 0 | 21 | 22 | 0.0087 | 0.0678 | 0.1424 | 0 |
| No. of WTs | Loc. [Node] | Size [MW] | Energy Losses [MWh/Day] | Reduction [%] |
|---|---|---|---|---|
| 1 | 6 | 208.9887 | 225.8110 | 45.0384 |
| 2 | 169.4930 | 58.7460 | ||
| 3 | 131.8012 | 67.9201 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gil-González, W.; Montoya, O.D.; Grisales-Noreña, L.F.; Perea-Moreno, A.-J.; Hernandez-Escobedo, Q. Optimal Placement and Sizing of Wind Generators in AC Grids Considering Reactive Power Capability and Wind Speed Curves. Sustainability 2020, 12, 2983. https://doi.org/10.3390/su12072983
Gil-González W, Montoya OD, Grisales-Noreña LF, Perea-Moreno A-J, Hernandez-Escobedo Q. Optimal Placement and Sizing of Wind Generators in AC Grids Considering Reactive Power Capability and Wind Speed Curves. Sustainability. 2020; 12(7):2983. https://doi.org/10.3390/su12072983
Chicago/Turabian StyleGil-González, Walter, Oscar Danilo Montoya, Luis Fernando Grisales-Noreña, Alberto-Jesus Perea-Moreno, and Quetzalcoatl Hernandez-Escobedo. 2020. "Optimal Placement and Sizing of Wind Generators in AC Grids Considering Reactive Power Capability and Wind Speed Curves" Sustainability 12, no. 7: 2983. https://doi.org/10.3390/su12072983
APA StyleGil-González, W., Montoya, O. D., Grisales-Noreña, L. F., Perea-Moreno, A. -J., & Hernandez-Escobedo, Q. (2020). Optimal Placement and Sizing of Wind Generators in AC Grids Considering Reactive Power Capability and Wind Speed Curves. Sustainability, 12(7), 2983. https://doi.org/10.3390/su12072983









