Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments
Abstract
1. Introduction
2. Problem Description
3. An Uncertain Programming Model
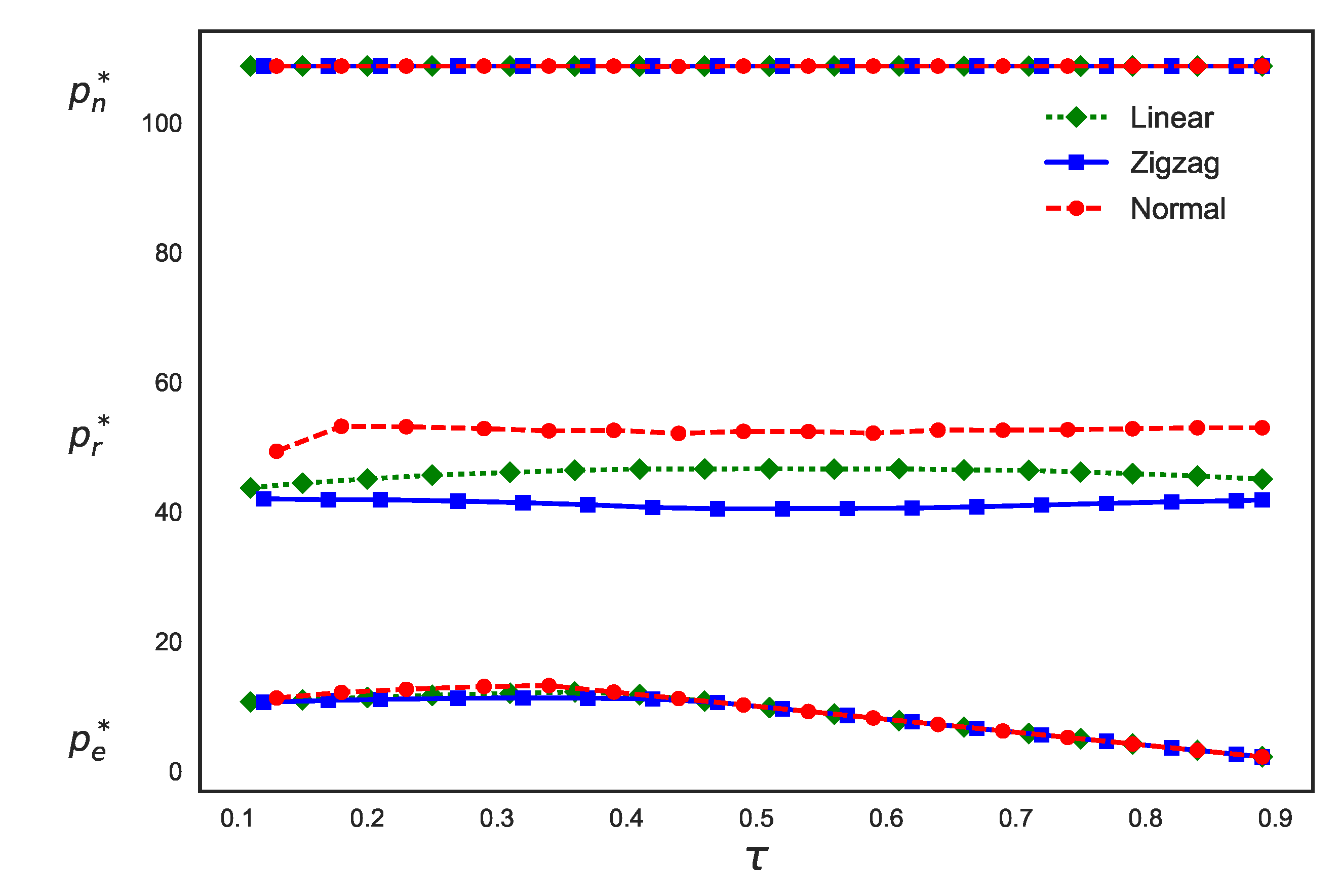
4. Numerical Experiments
5. Conclusions and Future Research
Author Contributions
Funding
Conflicts of Interest
Appendix A. Uncertainty Theory
References
- Rosa, P.; Terzi, S. Improving end of life vehicle’s management practices: An economic assessment through system dynamics. J. Clean. Prod. 2018, 184, 520–536. [Google Scholar] [CrossRef]
- D’Adamo, I.; Rosa, P.; Terzi, S. Challenges in waste electrical and electronic equipment management: A profitability assessment in three European countries. Sustainability 2016, 8, 633. [Google Scholar] [CrossRef]
- D’Adamo, I. Adopting a Circular Economy: Current Practices and Future Perspectives. Soc. Sci. 2019, 8, 328. [Google Scholar] [CrossRef]
- Ferrer, G.; Swaminathan, J.M. Managing new and remanufactured products. Manag. Sci. 2006, 52, 15–26. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Van Wassenhove, L.N. Reverse channel design: The case of competing retailers. Manag. Sci. 2006, 52, 1–14. [Google Scholar] [CrossRef]
- Jun, H.B.; Cusin, M.; Kiritsis, D.; Xirouchakis, P. A multi-objective evolutionary algorithm for end-of-life product recovery optimization: Turbocharger case study. Int. J. Prod. Res. 2007, 45, 4573–4594. [Google Scholar] [CrossRef]
- Gu, Q.; Ji, J.; Gao, T. Pricing management for a closed-loop supply chain. J. Revenue Pricing Manag. 2008, 7, 45–60. [Google Scholar]
- Wei, J.; Zhao, J. Pricing decisions with retail competition in a fuzzy closed-loop supply chain. Expert Syst. Appl. 2011, 38, 11209–11216. [Google Scholar] [CrossRef]
- Wan, H.D.; Krishna Gonnuru, V. Disassembly planning and sequencing for end-of-life products with RFID enriched information. Robot. Comput. Integr. Manuf. 2013, 29, 112–118. [Google Scholar] [CrossRef]
- Gan, S.S.; Pujawan, I.N.; Suparno; Widodo, B. Pricing decision for new and remanufactured product in a closed-loop supply chain with separate sales-channel. Int. J. Prod. Econ. 2017, 190, 120–132. [Google Scholar] [CrossRef]
- Govindan, K.; Beatriz, J.P.; Sergio, R.; María-Azucena, V.M. Marketing issues for remanufactured products. J. Clean. Prod. 2019, 227, 890–899. [Google Scholar] [CrossRef]
- Zhang, W.; He, Y. Optimal policies for new and green remanufactured short-life-cycle products considering consumer behavior. J. Clean. Prod. 2019, 214, 483–505. [Google Scholar] [CrossRef]
- Souza, G. Remanufacturing in closed-loop supply chains. Prod. Invent. Manag. J. 2009, 45, 56–66. [Google Scholar]
- Lund, R.T.; Hauser, W.M. Remanufacturing—An American perspective. In Proceedings of the International Conference on Responsive Manufacturing—Green Manufacturing, Ningbo, China, 11–13 January 2010; pp. 1–6. [Google Scholar]
- Guide, V.D.R.; Van Wassenhove, L.N. Managing product returns for remanufacturing. Prod. Oper. Manag. 2010, 10, 142–155. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, G.; Sha, J. Optimal production and pricing policy for a closed loop system. Resour. Conserv. Recycl. 2011, 55, 639–647. [Google Scholar] [CrossRef]
- Chen, J.M.; Chang, C.I. Dynamic pricing for new and remanufactured products in a closed-loop supply chain. Int. J. Prod. Econ. 2013, 146, 153–160. [Google Scholar] [CrossRef]
- Gan, S.S.; Pujawan, I.N.; Suparno; Widodo, B. Pricing decision model for new and remanufactured short-life cycle products with time-dependent demand. Oper. Res. Pers. 2015, 2, 1–12. [Google Scholar] [CrossRef]
- Meng, K.; Lou, P.; Peng, X.; Prybutok, V. Multi-objective Optimization Decision-making of Quality Dependent Product Recovery for Sustainability. Int. J. Prod. Econ. 2017, 188, 72–85. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Kaur, A.; Amit, R.K. Price optimization of multi-stage remanufacturing in a closed loop supply chain. J. Clean. Prod. 2018, 186, 943–962. [Google Scholar] [CrossRef]
- Modak, N.M.; Modak, N.; Panda, S.; Sana, S.S. Analyzing structure of two-echelon closed-loop supply chain for pricing, quality and recycling management. J. Clean. Prod. 2018, 171, 512–528. [Google Scholar] [CrossRef]
- Tao, F.; Fan, T.; Jia, X.; Lai, K.K. Optimal production strategy for a manufacturing and remanufacturing system with return policy. Oper. Res. 2019, 1–21. [Google Scholar] [CrossRef]
- Ouhimmoua, M.; Nourelfathb, M.; Bouchardb, M.; Brichab, N. Design of robust distribution network under demand uncertainty: A case study in the pulp and paper. Int. J. Prod. Econ. 2019, 218, 96–105. [Google Scholar] [CrossRef]
- Zhao, S.; Zhu, Q. Remanufacturing supply chain coordination under the stochastic remanufacturability rate and the random demand. Ann. Oper. Res. 2017, 257, 661–695. [Google Scholar] [CrossRef]
- Heydari, J.; Govindan, K.; Sadeghi, R. Reverse supply chain coordination under stochastic remanufacturing capacity. Int. J. Prod. Econ. 2018, 202, 1–11. [Google Scholar] [CrossRef]
- Almaraj, I.I.; Trafalis, T.B. An integrated multi-echelon robust closed- loop supply chain under imperfect quality production. Int. J. Prod. Econ. 2019, 218, 212–227. [Google Scholar] [CrossRef]
- Ren, J.; Chen, X.; Hu, J. The effect of production- versus consumption-based emission tax under demand uncertainty. Int. J. Prod. Econ. 2020, 219, 82–98. [Google Scholar] [CrossRef]
- Zhao, J.; Tanga, W.; Wei, J. Pricing decisions for substitutable products with a common retailer in fuzzy environments. Eur. J. Oper. Res. 2012, 216, 409–419. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z. Stackelberg game models between two competitive retailers in fuzzy decision environment. Fuzzy Optim. Decis. Mak. 2014, 13, 33–48. [Google Scholar] [CrossRef]
- Wei, J.; Zhao, J. Pricing decisions for substitutable products with horizontal and vertical competition in fuzzy environments. Ann. Oper. Res. 2016, 242, 505–528. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Liu, B. Some research problems in uncertainty theory. J. Uncertain. Syst. 2009, 3, 3–10. [Google Scholar]
- Zhou, J.; Yang, F.; Wang, K. Multi-objective optimization in uncertain random environments. Fuzzy Optim. Decis. Mak. 2014, 13, 397–413. [Google Scholar] [CrossRef]
- Ke, H.; Wu, Y.; Huang, H.; Chen, Z. Pricing Decision in a Two-Echelon Supply Chain with Competing Retailers Under Uncertain Environment. J. Uncertain. Anal. Appl. 2017, 5, 5. [Google Scholar] [CrossRef]
- Shen, J.; Kai, Z. Uncertain Supply Chain Problem with Price and Effort. Int. J. Fuzzy Syst. 2018, 20, 1145–1158. [Google Scholar] [CrossRef]
- Gao, Y. Uncertain models for single facility location problems on networks. Appl. Math. Model. 2012, 36, 2592–2599. [Google Scholar] [CrossRef]
- Gao, R.; Ralescu, D.A. Elliptic entropy of uncertain set and its applications. Int. J. Intell. Syst. 2018, 33, 836–857. [Google Scholar] [CrossRef]
- Ke, H. A genetic algorithm-based optimizing approach for project time-cost trade-off with uncertain measure. J. Uncertain. Anal. Appl. 2014, 2, 8. [Google Scholar] [CrossRef]
- Wang, L.; Huang, H.; Ke, H. Chance-constrained model for rcpsp with uncertain durations. J. Uncertain. Anal. Appl. 2015, 3, 1–10. [Google Scholar]
- Ma, W.; Che, Y.; Huang, H.; Ke, H. Resource-constrained project scheduling problem with uncertain durations and renewable resources. Int. J. Mach. Learn. Cybern. 2016, 7, 613–621. [Google Scholar] [CrossRef]
- Ning, Y.; Ke, H.; Fu, Z. Triangular entropy of uncertain variables with application to portfolio selection. Soft Comput. 2015, 19, 2203–2209. [Google Scholar] [CrossRef]
- Ke, H.; Su, T.; Ni, Y. Uncertain random multilevel programming with application to production control problem. Soft Comput. 2015, 19, 1739–1746. [Google Scholar] [CrossRef]
- Chen, L.; Peng, J.; Liu, Z.; Zhao, R. Pricing and effort decisions for a supply chain with uncertain information. Int. J. Prod. Res. 2017, 1, 264–284. [Google Scholar] [CrossRef]
- Charter, M.; Gray, C. Remanufacturing and product design. Int. J. Prod. Dev. 2008, 6, 375–392. [Google Scholar] [CrossRef]
- Lee, H.B.; Cho, N.W.; Hong, Y.S. A hierarchical end-of-life decision model for determining the economic levels of remanufacturing and disassembly under environmental regulations. J. Clean. Prod. 2010, 18, 1276–1283. [Google Scholar] [CrossRef]
- Bulmus, S.C.; Zhu, S.X.; Teunter, R. Competition for cores in remanufacturing. Eur. J. Oper. Res. 2014, 233, 105–113. [Google Scholar] [CrossRef]
- Yoo, S.H.; Kim, B.C. Joint pricing of new and refurbished items: A comparison of closed-loop supply chain models. Int. J. Prod. Econ. 2016, 182, 132–143. [Google Scholar] [CrossRef]
- Ding, S. Uncertain multi-product newsboy problem with chance constraint. Appl. Math. Comput. 2013, 223, 139–146. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, J.; Ru, J. Impacts of power structure on supply chains with uncertain demand. Prod. Oper. Manag. 2013, 22, 1232–1249. [Google Scholar] [CrossRef]
- Bakal, I.S.; Akcali, E. Effects of random yield in remanufacturing with price-sensitive supply and demand. Prod. Oper. Manag 2010, 15, 407–420. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Liu, B. Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Yang, X. On comonotonic functions of uncertain variables. Fuzzy Optim. Decis. Mak. 2013, 12, 89–98. [Google Scholar] [CrossRef]
- Liu, Y.; Ha, M. Expected value of function of uncertain variables. J. Uncertain. Syst. 2010, 4, 181–186. [Google Scholar]
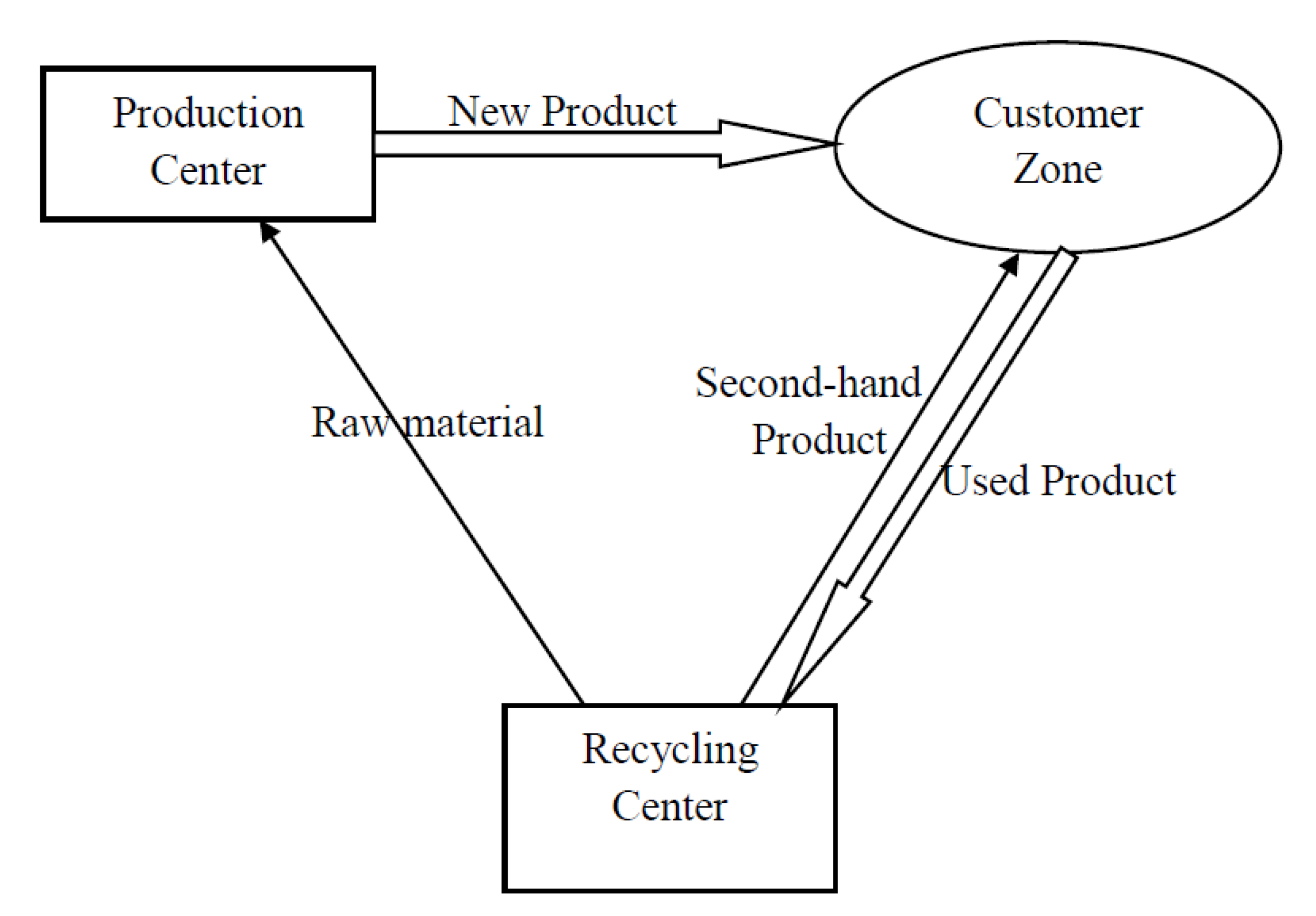

| : | Unit price of a new product, which is a decision variable. |
| : | Unit price of a second-hand product, which is a decision variable. |
| : | Unit price of recycling a used product, which is a decision variable. |
| : | Unit cost for manufacturing a new product with virgin raw materials. |
| : | Unit cost for manufacturing a new product with recycled raw materials. |
| : | Unit cost for renewing a used product in good condition. |
| : | Proportion of the used products that are in good condition, . |
| Parameters | Linear | Zigzag | Normal | Expected Value |
|---|---|---|---|---|
| (5000,10000) | (5000,8000,9000) | (7500,200) | 7500 | |
| (30,50) | (30,40,50) | (40,8) | 40 | |
| (2500,5000) | (2500,3000,6500) | (3750,100) | 3750 | |
| (40,60) | (40,50,60) | (50,4) | 50 | |
| (50,100) | (50,80,90) | (75,6) | 75 | |
| (100,200) | (100,150,200) | (150,9) | 150 | |
| (5000,8000) | (5000,6500,8000) | (6500,120) | 6500 |
| Distribution | ||||
|---|---|---|---|---|
| Linear | 108.7501 | 46.5202 | 11.9011 | 274,767.7100 |
| Zigzag | 108.7503 | 40.8848 | 11.2037 | 272,293.4025 |
| Normal | 108.7498 | 56.1929 | 11.9987 | 282,495.1945 |
| Distribution | ||||||
|---|---|---|---|---|---|---|
| Linear | (31,49) | 27.0000 | 108.7476 | 46.5347 | 11.8987 | 274,767.7138 |
| (30,50) | 33.3333 | 108.7501 | 46.5202 | 11.9011 | 274,767.7120 | |
| (29,51) | 40.3333 | 108.7519 | 46.5380 | 11.9011 | 274,767.7115 | |
| (28,52) | 48.0000 | 108.7531 | 46.5347 | 11.9987 | 274,767.7040 | |
| Zigzag | (31,40,49) | 27.0000 | 108.7564 | 40.8623 | 11.1994 | 272,293.4822 |
| (30,40,50) | 33.3333 | 108.7503 | 40.8848 | 11.2037 | 272,293.4025 | |
| (29,40,51) | 40.3333 | 108.7540 | 40.8680 | 11.1944 | 272,293.3899 | |
| (28,40,52) | 48.0000 | 108.7500 | 40.8653 | 11.1960 | 272,293.3799 | |
| Normal | (40,7) | 49.0000 | 108.7500 | 56.1966 | 11.8987 | 282,495.1944 |
| (40,8) | 64.0000 | 108.7498 | 56.1929 | 11.9987 | 282,495.1945 | |
| (40,9) | 81.0000 | 108.7509 | 56.1928 | 11.9987 | 282,495.1978 | |
| (40,10) | 100.0000 | 108.7494 | 56.1929 | 12.0000 | 282,495.3938 |
| Distribution | ||||||
|---|---|---|---|---|---|---|
| Linear | (51,99) | 192.0000 | 108.7499 | 46.5122 | 11.9890 | 274,764.4382 |
| (50,100) | 208.3333 | 108.7501 | 46.5202 | 11.9011 | 274,767.7120 | |
| (49,101) | 225.3333 | 108.7582 | 46.5330 | 11.9909 | 274,770.9045 | |
| (48,102) | 243.0000 | 108.7662 | 46.5397 | 11.9948 | 274,774.2556 | |
| Zigzag | (51,80,89) | 128.6667 | 108.7498 | 40.8604 | 11.1983 | 272,290.4050 |
| (50,80,90) | 141.6667 | 108.7503 | 40.8848 | 11.2037 | 272,293.4025 | |
| (49,80,91) | 155.3333 | 108.7570 | 40.8944 | 11.2099 | 272,296.5589 | |
| (48,80,92) | 169.6667 | 108.7580 | 40.8967 | 11.2102 | 272,299.6402 | |
| Normal | (75,5) | 25.0000 | 108.7479 | 56.1877 | 11.8999 | 282,486.3327 |
| (75,6) | 36.0000 | 108.7498 | 56.1929 | 11.9987 | 282,495.1945 | |
| (75,7) | 49.0000 | 108.7500 | 56.1980 | 11.9326 | 282,504.0573 | |
| (75,8) | 64.0000 | 108.7501 | 56.2032 | 11.9489 | 282,512.9213 |
| Distribution | ||||||
|---|---|---|---|---|---|---|
| Linear | (5100,7900) | 653,333.3333 | 108.7501 | 46.5200 | 11.9009 | 274,767.7116 |
| (5000,8000) | 750,000.0000 | 108.7501 | 46.5202 | 11.9011 | 274,767.7120 | |
| (4900,8100) | 853,333.3333 | 108.7577 | 46.5347 | 12.0000 | 274,767.7135 | |
| (4800,8200) | 963,333.3333 | 108.7740 | 46.5315 | 12.0000 | 274,767.7235 | |
| Zigzag | (5600,6500,7400) | 653,333.3333 | 108.7487 | 40.8631 | 11.1981 | 272,293.3926 |
| (5100,6500,7900) | 750,000.0000 | 108.7490 | 40.8848 | 11.2037 | 272,293.4025 | |
| (4900,6500,8100) | 853,333.3333 | 108.7490 | 40.8626 | 11.2014 | 272,293.4838 | |
| (4800,6500,8200) | 963,333.3333 | 108.7529 | 40.8660 | 11.1972 | 272,293.4930 | |
| Normal | (6500,110) | 12,100.0000 | 108.7492 | 56.1929 | 11.9999 | 282,495.1942 |
| (6500,120) | 14,400.0000 | 108.7498 | 56.1929 | 11.9987 | 282,495.1945 | |
| (6500,130) | 16,900.0000 | 108.7614 | 56.1928 | 11.9980 | 282,495.1981 | |
| (6500,140) | 19,600.0000 | 108.7500 | 56.1929 | 11.9980 | 282,495.1999 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, G.; Ni, Y.; Yang, X. Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments. Sustainability 2020, 12, 3199. https://doi.org/10.3390/su12083199
Yan G, Ni Y, Yang X. Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments. Sustainability. 2020; 12(8):3199. https://doi.org/10.3390/su12083199
Chicago/Turabian StyleYan, Guangzhou, Yaodong Ni, and Xiangfeng Yang. 2020. "Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments" Sustainability 12, no. 8: 3199. https://doi.org/10.3390/su12083199
APA StyleYan, G., Ni, Y., & Yang, X. (2020). Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments. Sustainability, 12(8), 3199. https://doi.org/10.3390/su12083199




