Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments
Abstract
:1. Introduction
2. Problem Description
3. An Uncertain Programming Model
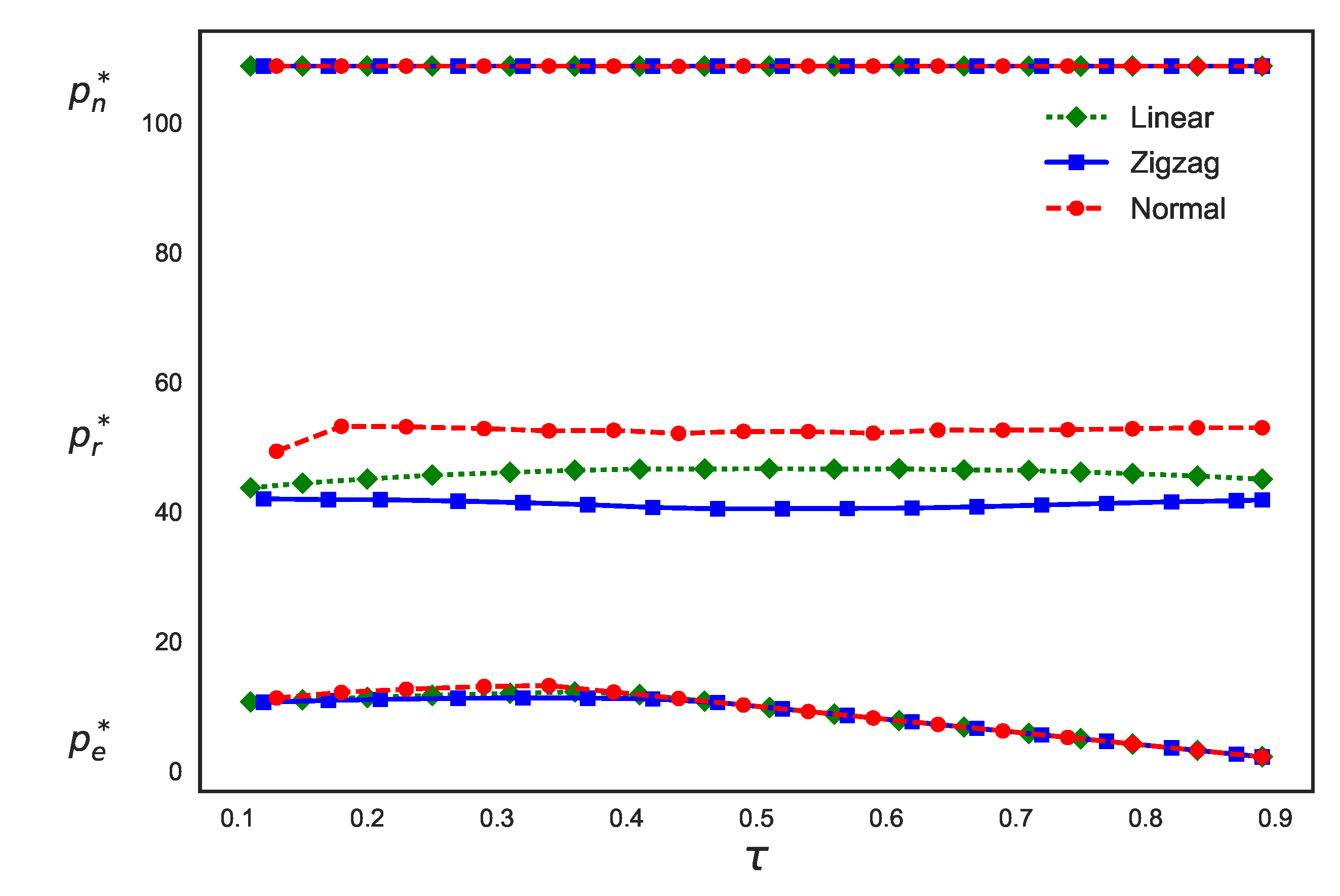
4. Numerical Experiments
5. Conclusions and Future Research
Author Contributions
Funding
Conflicts of Interest
Appendix A. Uncertainty Theory
References
- Rosa, P.; Terzi, S. Improving end of life vehicle’s management practices: An economic assessment through system dynamics. J. Clean. Prod. 2018, 184, 520–536. [Google Scholar] [CrossRef]
- D’Adamo, I.; Rosa, P.; Terzi, S. Challenges in waste electrical and electronic equipment management: A profitability assessment in three European countries. Sustainability 2016, 8, 633. [Google Scholar] [CrossRef] [Green Version]
- D’Adamo, I. Adopting a Circular Economy: Current Practices and Future Perspectives. Soc. Sci. 2019, 8, 328. [Google Scholar] [CrossRef] [Green Version]
- Ferrer, G.; Swaminathan, J.M. Managing new and remanufactured products. Manag. Sci. 2006, 52, 15–26. [Google Scholar] [CrossRef] [Green Version]
- Savaskan, R.C.; Van Wassenhove, L.N. Reverse channel design: The case of competing retailers. Manag. Sci. 2006, 52, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Jun, H.B.; Cusin, M.; Kiritsis, D.; Xirouchakis, P. A multi-objective evolutionary algorithm for end-of-life product recovery optimization: Turbocharger case study. Int. J. Prod. Res. 2007, 45, 4573–4594. [Google Scholar] [CrossRef]
- Gu, Q.; Ji, J.; Gao, T. Pricing management for a closed-loop supply chain. J. Revenue Pricing Manag. 2008, 7, 45–60. [Google Scholar]
- Wei, J.; Zhao, J. Pricing decisions with retail competition in a fuzzy closed-loop supply chain. Expert Syst. Appl. 2011, 38, 11209–11216. [Google Scholar] [CrossRef]
- Wan, H.D.; Krishna Gonnuru, V. Disassembly planning and sequencing for end-of-life products with RFID enriched information. Robot. Comput. Integr. Manuf. 2013, 29, 112–118. [Google Scholar] [CrossRef]
- Gan, S.S.; Pujawan, I.N.; Suparno; Widodo, B. Pricing decision for new and remanufactured product in a closed-loop supply chain with separate sales-channel. Int. J. Prod. Econ. 2017, 190, 120–132. [Google Scholar] [CrossRef] [Green Version]
- Govindan, K.; Beatriz, J.P.; Sergio, R.; María-Azucena, V.M. Marketing issues for remanufactured products. J. Clean. Prod. 2019, 227, 890–899. [Google Scholar] [CrossRef]
- Zhang, W.; He, Y. Optimal policies for new and green remanufactured short-life-cycle products considering consumer behavior. J. Clean. Prod. 2019, 214, 483–505. [Google Scholar] [CrossRef]
- Souza, G. Remanufacturing in closed-loop supply chains. Prod. Invent. Manag. J. 2009, 45, 56–66. [Google Scholar]
- Lund, R.T.; Hauser, W.M. Remanufacturing—An American perspective. In Proceedings of the International Conference on Responsive Manufacturing—Green Manufacturing, Ningbo, China, 11–13 January 2010; pp. 1–6. [Google Scholar]
- Guide, V.D.R.; Van Wassenhove, L.N. Managing product returns for remanufacturing. Prod. Oper. Manag. 2010, 10, 142–155. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, G.; Sha, J. Optimal production and pricing policy for a closed loop system. Resour. Conserv. Recycl. 2011, 55, 639–647. [Google Scholar] [CrossRef]
- Chen, J.M.; Chang, C.I. Dynamic pricing for new and remanufactured products in a closed-loop supply chain. Int. J. Prod. Econ. 2013, 146, 153–160. [Google Scholar] [CrossRef]
- Gan, S.S.; Pujawan, I.N.; Suparno; Widodo, B. Pricing decision model for new and remanufactured short-life cycle products with time-dependent demand. Oper. Res. Pers. 2015, 2, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Meng, K.; Lou, P.; Peng, X.; Prybutok, V. Multi-objective Optimization Decision-making of Quality Dependent Product Recovery for Sustainability. Int. J. Prod. Econ. 2017, 188, 72–85. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Kaur, A.; Amit, R.K. Price optimization of multi-stage remanufacturing in a closed loop supply chain. J. Clean. Prod. 2018, 186, 943–962. [Google Scholar] [CrossRef]
- Modak, N.M.; Modak, N.; Panda, S.; Sana, S.S. Analyzing structure of two-echelon closed-loop supply chain for pricing, quality and recycling management. J. Clean. Prod. 2018, 171, 512–528. [Google Scholar] [CrossRef]
- Tao, F.; Fan, T.; Jia, X.; Lai, K.K. Optimal production strategy for a manufacturing and remanufacturing system with return policy. Oper. Res. 2019, 1–21. [Google Scholar] [CrossRef]
- Ouhimmoua, M.; Nourelfathb, M.; Bouchardb, M.; Brichab, N. Design of robust distribution network under demand uncertainty: A case study in the pulp and paper. Int. J. Prod. Econ. 2019, 218, 96–105. [Google Scholar] [CrossRef]
- Zhao, S.; Zhu, Q. Remanufacturing supply chain coordination under the stochastic remanufacturability rate and the random demand. Ann. Oper. Res. 2017, 257, 661–695. [Google Scholar] [CrossRef]
- Heydari, J.; Govindan, K.; Sadeghi, R. Reverse supply chain coordination under stochastic remanufacturing capacity. Int. J. Prod. Econ. 2018, 202, 1–11. [Google Scholar] [CrossRef]
- Almaraj, I.I.; Trafalis, T.B. An integrated multi-echelon robust closed- loop supply chain under imperfect quality production. Int. J. Prod. Econ. 2019, 218, 212–227. [Google Scholar] [CrossRef]
- Ren, J.; Chen, X.; Hu, J. The effect of production- versus consumption-based emission tax under demand uncertainty. Int. J. Prod. Econ. 2020, 219, 82–98. [Google Scholar] [CrossRef]
- Zhao, J.; Tanga, W.; Wei, J. Pricing decisions for substitutable products with a common retailer in fuzzy environments. Eur. J. Oper. Res. 2012, 216, 409–419. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z. Stackelberg game models between two competitive retailers in fuzzy decision environment. Fuzzy Optim. Decis. Mak. 2014, 13, 33–48. [Google Scholar] [CrossRef]
- Wei, J.; Zhao, J. Pricing decisions for substitutable products with horizontal and vertical competition in fuzzy environments. Ann. Oper. Res. 2016, 242, 505–528. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Liu, B. Some research problems in uncertainty theory. J. Uncertain. Syst. 2009, 3, 3–10. [Google Scholar]
- Zhou, J.; Yang, F.; Wang, K. Multi-objective optimization in uncertain random environments. Fuzzy Optim. Decis. Mak. 2014, 13, 397–413. [Google Scholar] [CrossRef]
- Ke, H.; Wu, Y.; Huang, H.; Chen, Z. Pricing Decision in a Two-Echelon Supply Chain with Competing Retailers Under Uncertain Environment. J. Uncertain. Anal. Appl. 2017, 5, 5. [Google Scholar] [CrossRef] [Green Version]
- Shen, J.; Kai, Z. Uncertain Supply Chain Problem with Price and Effort. Int. J. Fuzzy Syst. 2018, 20, 1145–1158. [Google Scholar] [CrossRef]
- Gao, Y. Uncertain models for single facility location problems on networks. Appl. Math. Model. 2012, 36, 2592–2599. [Google Scholar] [CrossRef]
- Gao, R.; Ralescu, D.A. Elliptic entropy of uncertain set and its applications. Int. J. Intell. Syst. 2018, 33, 836–857. [Google Scholar] [CrossRef]
- Ke, H. A genetic algorithm-based optimizing approach for project time-cost trade-off with uncertain measure. J. Uncertain. Anal. Appl. 2014, 2, 8. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Huang, H.; Ke, H. Chance-constrained model for rcpsp with uncertain durations. J. Uncertain. Anal. Appl. 2015, 3, 1–10. [Google Scholar]
- Ma, W.; Che, Y.; Huang, H.; Ke, H. Resource-constrained project scheduling problem with uncertain durations and renewable resources. Int. J. Mach. Learn. Cybern. 2016, 7, 613–621. [Google Scholar] [CrossRef]
- Ning, Y.; Ke, H.; Fu, Z. Triangular entropy of uncertain variables with application to portfolio selection. Soft Comput. 2015, 19, 2203–2209. [Google Scholar] [CrossRef]
- Ke, H.; Su, T.; Ni, Y. Uncertain random multilevel programming with application to production control problem. Soft Comput. 2015, 19, 1739–1746. [Google Scholar] [CrossRef]
- Chen, L.; Peng, J.; Liu, Z.; Zhao, R. Pricing and effort decisions for a supply chain with uncertain information. Int. J. Prod. Res. 2017, 1, 264–284. [Google Scholar] [CrossRef]
- Charter, M.; Gray, C. Remanufacturing and product design. Int. J. Prod. Dev. 2008, 6, 375–392. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.B.; Cho, N.W.; Hong, Y.S. A hierarchical end-of-life decision model for determining the economic levels of remanufacturing and disassembly under environmental regulations. J. Clean. Prod. 2010, 18, 1276–1283. [Google Scholar] [CrossRef]
- Bulmus, S.C.; Zhu, S.X.; Teunter, R. Competition for cores in remanufacturing. Eur. J. Oper. Res. 2014, 233, 105–113. [Google Scholar] [CrossRef]
- Yoo, S.H.; Kim, B.C. Joint pricing of new and refurbished items: A comparison of closed-loop supply chain models. Int. J. Prod. Econ. 2016, 182, 132–143. [Google Scholar] [CrossRef]
- Ding, S. Uncertain multi-product newsboy problem with chance constraint. Appl. Math. Comput. 2013, 223, 139–146. [Google Scholar] [CrossRef]
- Shi, R.; Zhang, J.; Ru, J. Impacts of power structure on supply chains with uncertain demand. Prod. Oper. Manag. 2013, 22, 1232–1249. [Google Scholar] [CrossRef]
- Bakal, I.S.; Akcali, E. Effects of random yield in remanufacturing with price-sensitive supply and demand. Prod. Oper. Manag 2010, 15, 407–420. [Google Scholar] [CrossRef]
- Liu, B. Uncertainty Theory, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Liu, B. Uncertainty Theory: A Branch of Mathematics for Modeling Human Uncertainty; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Yang, X. On comonotonic functions of uncertain variables. Fuzzy Optim. Decis. Mak. 2013, 12, 89–98. [Google Scholar] [CrossRef]
- Liu, Y.; Ha, M. Expected value of function of uncertain variables. J. Uncertain. Syst. 2010, 4, 181–186. [Google Scholar]
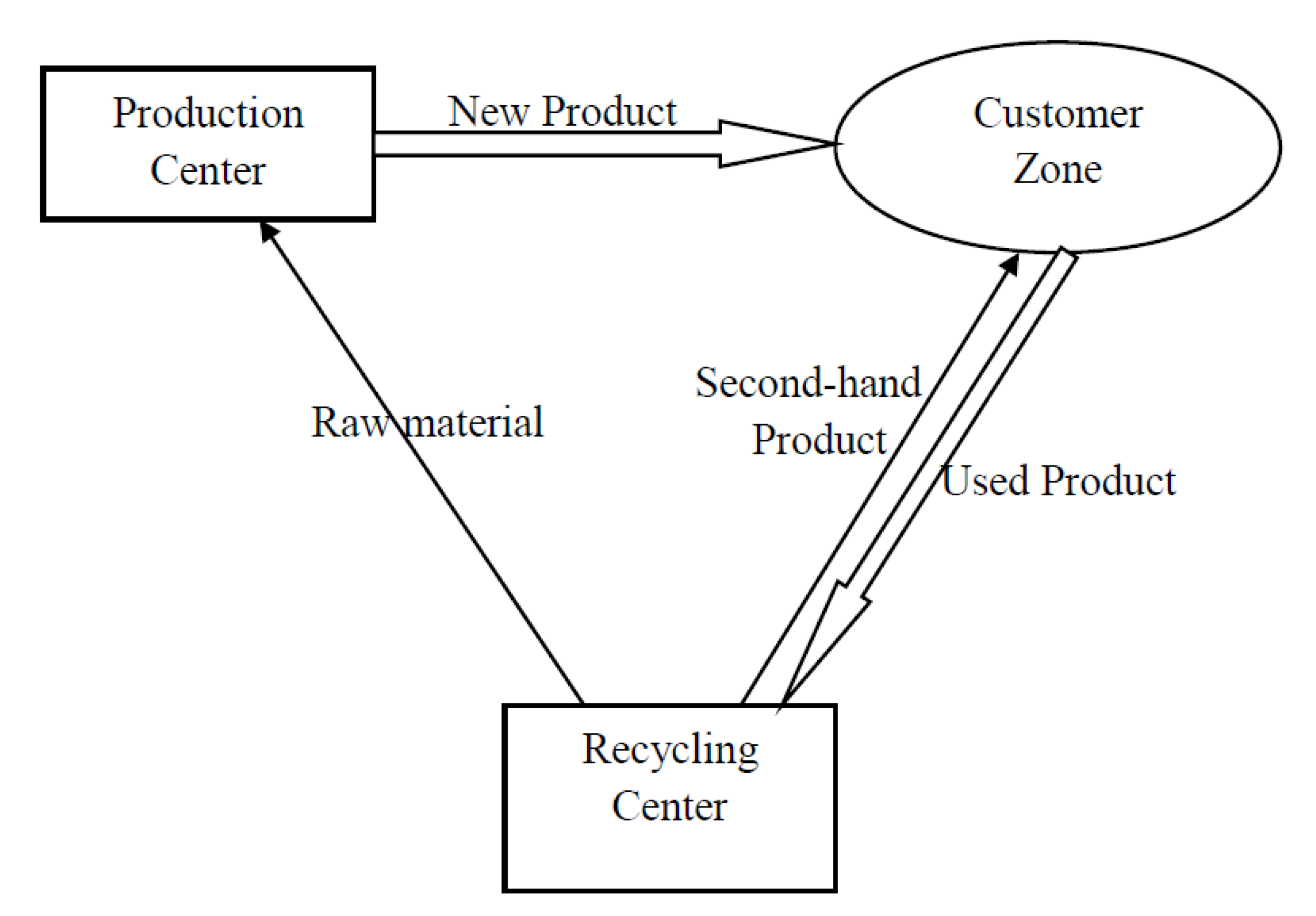

| : | Unit price of a new product, which is a decision variable. |
| : | Unit price of a second-hand product, which is a decision variable. |
| : | Unit price of recycling a used product, which is a decision variable. |
| : | Unit cost for manufacturing a new product with virgin raw materials. |
| : | Unit cost for manufacturing a new product with recycled raw materials. |
| : | Unit cost for renewing a used product in good condition. |
| : | Proportion of the used products that are in good condition, . |
| Parameters | Linear | Zigzag | Normal | Expected Value |
|---|---|---|---|---|
| (5000,10000) | (5000,8000,9000) | (7500,200) | 7500 | |
| (30,50) | (30,40,50) | (40,8) | 40 | |
| (2500,5000) | (2500,3000,6500) | (3750,100) | 3750 | |
| (40,60) | (40,50,60) | (50,4) | 50 | |
| (50,100) | (50,80,90) | (75,6) | 75 | |
| (100,200) | (100,150,200) | (150,9) | 150 | |
| (5000,8000) | (5000,6500,8000) | (6500,120) | 6500 |
| Distribution | ||||
|---|---|---|---|---|
| Linear | 108.7501 | 46.5202 | 11.9011 | 274,767.7100 |
| Zigzag | 108.7503 | 40.8848 | 11.2037 | 272,293.4025 |
| Normal | 108.7498 | 56.1929 | 11.9987 | 282,495.1945 |
| Distribution | ||||||
|---|---|---|---|---|---|---|
| Linear | (31,49) | 27.0000 | 108.7476 | 46.5347 | 11.8987 | 274,767.7138 |
| (30,50) | 33.3333 | 108.7501 | 46.5202 | 11.9011 | 274,767.7120 | |
| (29,51) | 40.3333 | 108.7519 | 46.5380 | 11.9011 | 274,767.7115 | |
| (28,52) | 48.0000 | 108.7531 | 46.5347 | 11.9987 | 274,767.7040 | |
| Zigzag | (31,40,49) | 27.0000 | 108.7564 | 40.8623 | 11.1994 | 272,293.4822 |
| (30,40,50) | 33.3333 | 108.7503 | 40.8848 | 11.2037 | 272,293.4025 | |
| (29,40,51) | 40.3333 | 108.7540 | 40.8680 | 11.1944 | 272,293.3899 | |
| (28,40,52) | 48.0000 | 108.7500 | 40.8653 | 11.1960 | 272,293.3799 | |
| Normal | (40,7) | 49.0000 | 108.7500 | 56.1966 | 11.8987 | 282,495.1944 |
| (40,8) | 64.0000 | 108.7498 | 56.1929 | 11.9987 | 282,495.1945 | |
| (40,9) | 81.0000 | 108.7509 | 56.1928 | 11.9987 | 282,495.1978 | |
| (40,10) | 100.0000 | 108.7494 | 56.1929 | 12.0000 | 282,495.3938 |
| Distribution | ||||||
|---|---|---|---|---|---|---|
| Linear | (51,99) | 192.0000 | 108.7499 | 46.5122 | 11.9890 | 274,764.4382 |
| (50,100) | 208.3333 | 108.7501 | 46.5202 | 11.9011 | 274,767.7120 | |
| (49,101) | 225.3333 | 108.7582 | 46.5330 | 11.9909 | 274,770.9045 | |
| (48,102) | 243.0000 | 108.7662 | 46.5397 | 11.9948 | 274,774.2556 | |
| Zigzag | (51,80,89) | 128.6667 | 108.7498 | 40.8604 | 11.1983 | 272,290.4050 |
| (50,80,90) | 141.6667 | 108.7503 | 40.8848 | 11.2037 | 272,293.4025 | |
| (49,80,91) | 155.3333 | 108.7570 | 40.8944 | 11.2099 | 272,296.5589 | |
| (48,80,92) | 169.6667 | 108.7580 | 40.8967 | 11.2102 | 272,299.6402 | |
| Normal | (75,5) | 25.0000 | 108.7479 | 56.1877 | 11.8999 | 282,486.3327 |
| (75,6) | 36.0000 | 108.7498 | 56.1929 | 11.9987 | 282,495.1945 | |
| (75,7) | 49.0000 | 108.7500 | 56.1980 | 11.9326 | 282,504.0573 | |
| (75,8) | 64.0000 | 108.7501 | 56.2032 | 11.9489 | 282,512.9213 |
| Distribution | ||||||
|---|---|---|---|---|---|---|
| Linear | (5100,7900) | 653,333.3333 | 108.7501 | 46.5200 | 11.9009 | 274,767.7116 |
| (5000,8000) | 750,000.0000 | 108.7501 | 46.5202 | 11.9011 | 274,767.7120 | |
| (4900,8100) | 853,333.3333 | 108.7577 | 46.5347 | 12.0000 | 274,767.7135 | |
| (4800,8200) | 963,333.3333 | 108.7740 | 46.5315 | 12.0000 | 274,767.7235 | |
| Zigzag | (5600,6500,7400) | 653,333.3333 | 108.7487 | 40.8631 | 11.1981 | 272,293.3926 |
| (5100,6500,7900) | 750,000.0000 | 108.7490 | 40.8848 | 11.2037 | 272,293.4025 | |
| (4900,6500,8100) | 853,333.3333 | 108.7490 | 40.8626 | 11.2014 | 272,293.4838 | |
| (4800,6500,8200) | 963,333.3333 | 108.7529 | 40.8660 | 11.1972 | 272,293.4930 | |
| Normal | (6500,110) | 12,100.0000 | 108.7492 | 56.1929 | 11.9999 | 282,495.1942 |
| (6500,120) | 14,400.0000 | 108.7498 | 56.1929 | 11.9987 | 282,495.1945 | |
| (6500,130) | 16,900.0000 | 108.7614 | 56.1928 | 11.9980 | 282,495.1981 | |
| (6500,140) | 19,600.0000 | 108.7500 | 56.1929 | 11.9980 | 282,495.1999 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, G.; Ni, Y.; Yang, X. Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments. Sustainability 2020, 12, 3199. https://doi.org/10.3390/su12083199
Yan G, Ni Y, Yang X. Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments. Sustainability. 2020; 12(8):3199. https://doi.org/10.3390/su12083199
Chicago/Turabian StyleYan, Guangzhou, Yaodong Ni, and Xiangfeng Yang. 2020. "Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments" Sustainability 12, no. 8: 3199. https://doi.org/10.3390/su12083199
APA StyleYan, G., Ni, Y., & Yang, X. (2020). Optimal Pricing in Recycling and Remanufacturing in Uncertain Environments. Sustainability, 12(8), 3199. https://doi.org/10.3390/su12083199




