Can China’s Aging Population Sustain Its Entrepreneurship? Evidence of Nonlinear Effects
Abstract
:1. Introduction
2. Literature Review
2.1. Nonlinear Effects of Age on Entrepreneurship at the Micro Level
2.2. Nonlinear Effects of Aging on Entrepreneurship at the Macro Level
3. Model
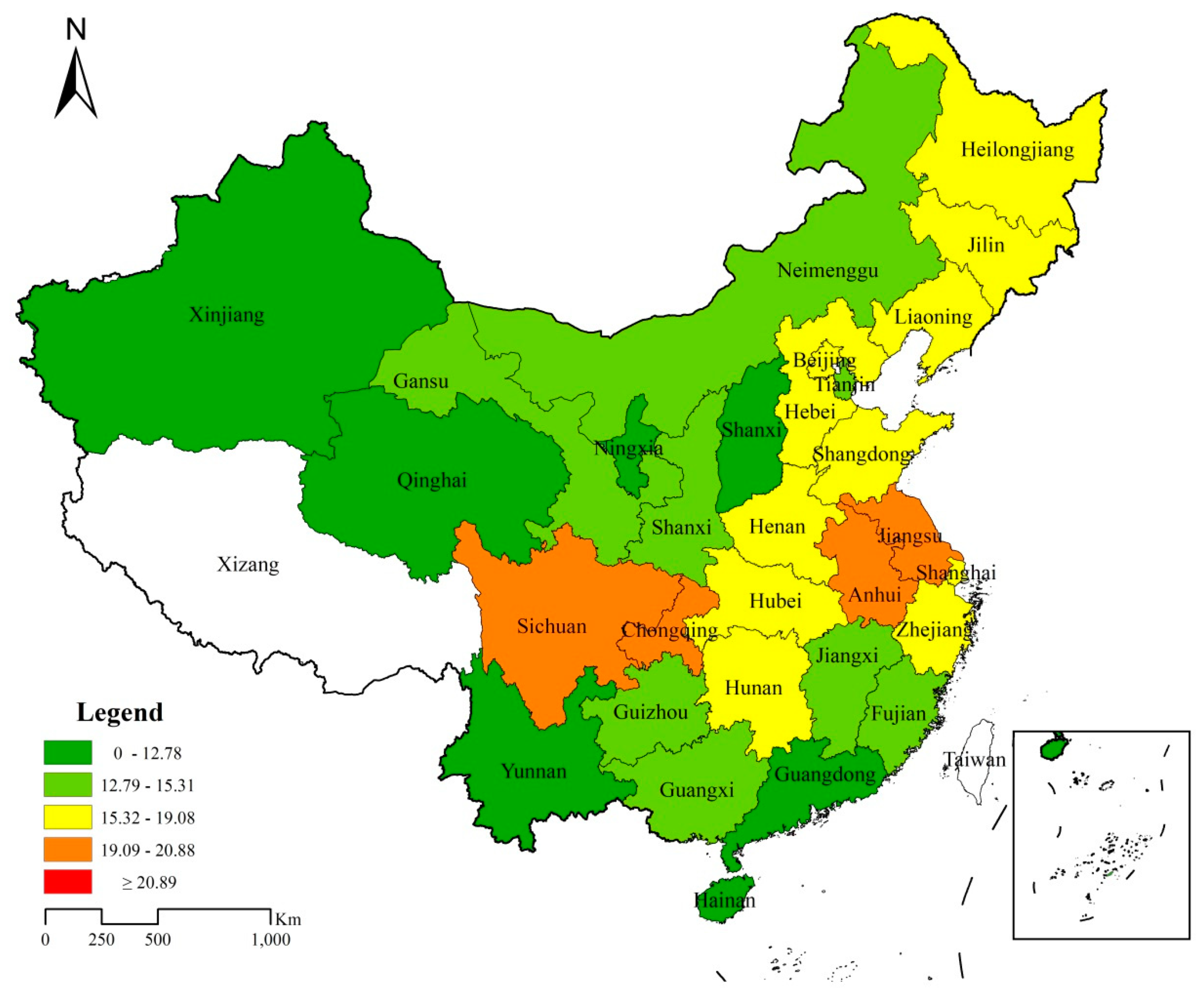
3.1. Data Collection
3.2. Variables
3.3. Empirical Model
4. Results
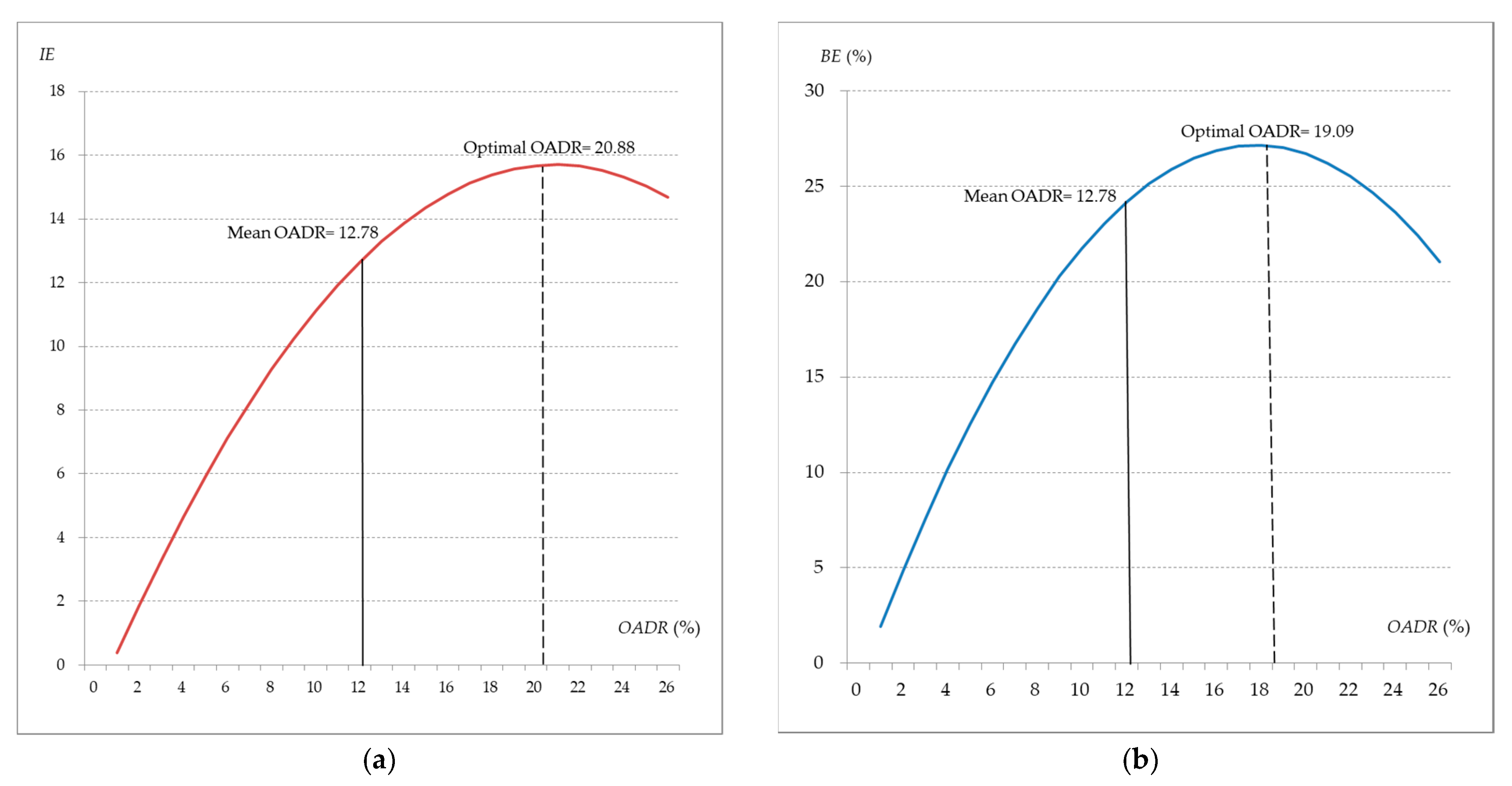
4.1. Linear and Nonlinear Effects Analysis
4.2. Robustness Check
5. Discussion, Conclusion and Implications
5.1. Discussion and Conclusion
5.2. Managerial Implications
6. Limitations and Future Research
Author Contributions
Funding
Conflicts of Interest
References
- Ireland, R.D.; Hitt, M.A.; Sirmon, D.G. A model of strategic entrepreneurship: The construct and its dimensions. J. Manag. 2003, 29, 963–989. [Google Scholar]
- Zahra, S.; Wright, M. Entrepreneurship’s next act. Acad. Manag. Perspect. 2011, 25, 67–83. [Google Scholar] [CrossRef] [Green Version]
- Bönte, W.; Falck, O.; Heblich, S. The impact of regional age structure on entrepreneurship. Econ. Geogr. 2009, 85, 269–287. [Google Scholar] [CrossRef]
- Maritz, A. Senior entrepreneurship in Australia: An exploratory approach. Int. J. Org. Innov. 2015, 7, 6–23. [Google Scholar]
- United Nations (UN). World Population Ageing 2017—Highlights. Available online: https://www.un.org/en/development/desa/population/publications/pdf/ageing/WPA2017_Highlights.pdf (accessed on 20 March 2020).
- Kurek, S.; Rachwał, T. Development of entrepreneurship in ageing populations of the European Union. Procd. Soc. Behv. 2011, 19, 397–405. [Google Scholar] [CrossRef] [Green Version]
- Stangler, D.; Spulber, D.F. The Age of the Entrepreneur: Demographics and Entrepreneurship. Available online: http://iiij.org/wp–content/uploads/2013/05/i4jDaneStanglerDemographicsandEntrepreneurship–1.pdf (accessed on 20 March 2020).
- World Bank. Age Dependency Ratio (% of working-age population). Available online: https://data.worldbank.org/indicator/SP.POP.DPND?view=chart (accessed on 20 March 2020).
- Bosma, N.; Kelley, D. GEM Global Entrepreneurship Monitor _ GEM 2018 / 2019 GLOBAL REPORT. Available online: https://www.gemconsortium.org/report/gem–2018–2019–global–report (accessed on 20 March 2020).
- Qiao, H. Will China Grow Old Before Getting Rich; Global Economics Paper No. 138; Goldman Sachs: New York, NY, USA, 2006. [Google Scholar]
- Hall, J.K.; Daneke, G.A.; Lenox, M.J. Sustainable development and entrepreneurship: Past contributions and future directions. J. Bus. Ventur. 2010, 25, 439–448. [Google Scholar] [CrossRef]
- Guo, K.; Yu, J.; Gong, L. Demographic transition, entrepreneurship and growth. China Econ. Quart. 2016, 15, 989–1010. (In Chinese) [Google Scholar]
- Liang, J.; Wang, H.; Lazear, E.P. Demographics and entrepreneurship. J. Political Econ. 2018, 126, 140–196. [Google Scholar] [CrossRef] [Green Version]
- Kautonen, T.; Tornikoski, E.T.; Kibler, E. Entrepreneurial intentions in the third age: Impact of perceived age norms. Small Bus. Econ. 2011, 37, 219–234. [Google Scholar] [CrossRef]
- Organization for Economic Cooperation and Development/European Union (OECD/EU). The Missing Entrepreneurs 2019: Policies for Inclusive Entrepreneurship. Available online: https://doi.org/10.1787/3ed84801–en (accessed on 20 March 2020).
- Knight, F.H. Risk, Uncertainty, and Profit, 3rd ed.; Hart, Schaffner & Marx: Boston, MA, USA, 1921; pp. 22–50. [Google Scholar]
- Hatak, I.; Kautonen, T.; Fink, M. Senior-unternehmertum. Empirische Evidenz Aus 2013, 27, 7–26. (In German) [Google Scholar]
- Evans, D.S.; Jovanovic, B. An estimated model of entrepreneurial choice under liquidity constraints. J. Political Econ. 1989, 97, 808–827. [Google Scholar] [CrossRef]
- Schumpeter, J.A. The Theory of Economic Development; an Inquiry into Profits, Capital Credit, Interest and the Business Cycle, 6th ed.; Oxford University Press: London, UK, 1934; pp. 95–156. [Google Scholar]
- Rosen, B.; Jerdee, T.H. The influence of age stereotypes on managerial decisions. J. Appl. Psychol. 1976, 61, 428. [Google Scholar] [CrossRef]
- Lévesque, M.; Minniti, M. The effect of aging on entrepreneurial behavior. J. Bus. Ventur. 2006, 21, 177–194. [Google Scholar] [CrossRef]
- Parker, S.C. The Economics of Self–Employment and Entrepreneurship, 1st ed.; Cambridge University Press: Cambridge, UK, 2004; pp. 266–271. [Google Scholar]
- Mueller, P. Entrepreneurship in the region: Breeding ground for nascent entrepreneurs? Smal. Bus. Econ. 2006, 27, 41–58. [Google Scholar] [CrossRef]
- Sanderson, W.C.; Scherbov, S. The characteristics approach to the measurement of population aging. Popul. Dev. Rev. 2013, 39, 673–685. [Google Scholar] [CrossRef] [Green Version]
- Metcalfe, S.; Ramlogan, R. Innovation systems and the competitive process in developing economies. Q. Rev. Econ. Financ. 2008, 48, 433–446. [Google Scholar] [CrossRef]
- Hsiao, C. Panel data analysis—Advantages and challenges. Test 2007, 16, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Vergeer, R.; Kleinknecht, A. Do flexible labor markets indeed reduce unemployment? A robustness check. Rev. Soc. Econ. 2012, 70, 451–467. [Google Scholar] [CrossRef]
- Roodman, D. How to do xtabond2: An introduction to difference and system GMM in Stata. Stata. J. 2009, 9, 86–136. [Google Scholar] [CrossRef] [Green Version]
- World Health Organization (WHO). Active ageing: A Policy Framework. Available online: https://apps.who.int/iris/bitstream/handle/10665/67215/WHO_NMH_NPH_02.8.pdf (accessed on 20 March 2020).


| Variables | Definition | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| OADR | Old Age Dependency Ratio, population ages 65+ to working age | 12.78 | 2.630 | 7.440 | 21.88 |
| OADR2 | OADR squared | 170.3 | 72.04 | 55.35 | 478.7 |
| IE | Innovation in Entrepreneurship, log of patent license number | 8.980 | 1.650 | 4.250 | 12.51 |
| BE | Business for Entrepreneurs, self-employed/employed in private enterprises of total employment | 41.88 | 10.36 | 16.53 | 69.41 |
| HC | Human Capital, log of average years of education | 2.170 | 0.110 | 1.830 | 2.550 |
| FD | Financial Development, year-end loan balance to GDP | 1.170 | 0.410 | 0.540 | 2.580 |
| FO | Financial Openness, Foreign Direct Investment in CNY to GDP, inverse indicator | 0.020 | 0.020 | 0.000 | 0.080 |
| MKT | Marketization, added value of state-owned enterprises to that of the second industry, inverse indicator | 0.400 | 0.190 | 0.070 | 0.840 |
| ST | Science and Technology, Government Science and Technology of total government expenditure | 1.570 | 1.320 | 0.220 | 7.200 |
| GI | Government Intervention, government spending to GDP | 0.210 | 0.090 | 0.080 | 0.630 |
| OPR | Older Population Rate, population ages 65+ of total population | 9.360 | 1.920 | 5.430 | 16.38 |
| OPR2 | OPR squared | 91.34 | 38.31 | 29.48 | 268.3 |
| Variables | Linear Effects | Nonlinear Effects | ||||
|---|---|---|---|---|---|---|
| OLS-IE | OLS-BE | FE-IE | FE-BE | FE-IE | FE-BE | |
| OADR | 0.188 *** | 0.702 *** | 0.0701 *** | 0.852 *** | 0.162 ** | 3.195 *** |
| (10.63) | (4.58) | (4.74) | (4.74) | (2.44) | (3.26) | |
| OADR2 | −0.00388 * | −0.0837 ** | ||||
| (−1.68) | (−2.46) | |||||
| HC | 7.457 *** | 65.87 *** | ||||
| (17.82) | (11.26) | |||||
| FD | −0.236 * | 0.847 | 1.414 *** | 6.745 *** | 0.615 *** | 2.874 * |
| (−1.89) | (0.83) | (11.52) | (3.82) | (5.99) | (1.81) | |
| FO | −14.64 *** | −0.232 | −4.213 * | 11.05 | −0.842 | 44.56 * |
| (−5.69) | (−0.01) | (−1.83) | (0.39) | (−0.48) | (1.78) | |
| MKT | −3.529 *** | −32.96 *** | −4.230 *** | −39.26 *** | −2.109 *** | −24.81 *** |
| (−13.01) | (−14.80) | (−15.88) | (−9.80) | (−8.91) | (−6.63) | |
| ST | 0.661 *** | 0.397 *** | 0.238 *** | |||
| (15.95) | (15.33) | (11.08) | ||||
| GI | 52.62 *** | 23.74 ** | −13.72 | |||
| (10.78) | (2.49) | (−1.50) | ||||
| Cons | 7.572 *** | 34.16 *** | 7.612 *** | 33.68 *** | −8.835 *** | −119.2 *** |
| (25.68) | (13.04) | (24.34) | (8.18) | (−8.20) | (−7.74) | |
| Obs | 450 | 450 | 450 | 450 | 450 | 450 |
| N | 30 | 30 | 30 | 30 | ||
| R2 | 0.720 | 0.471 | 0.790 | 0.570 | 0.881 | 0.670 |
| F | 232.2 | 80.94 | 345.5 | 125.9 | 480.6 | 135.1 |
| F-Statistic | 50.41 (p = 0) | 17.75 (p = 0) | 86.45 (p = 0) | 25.49 (p = 0) | ||
| Variables | Linear Effects | Nonlinear Effects | ||||
|---|---|---|---|---|---|---|
| OLS-IE | OLS-BE | FE-IE | FE-BE | FE-IE | FE-BE | |
| OPR | 0.303 *** | 1.163 *** | 0.125 *** | 1.486 *** | 0.360 *** | 6.106 *** |
| (12.46) | (5.33) | (5.70) | (5.52) | (3.71) | (4.21) | |
| OPR2 | −0.0134 *** | −0.228 *** | ||||
| (−2.96) | (−3.38) | |||||
| HC | 7.304 *** | 63.10 *** | ||||
| (17.55) | (11.01) | |||||
| FD | −0.277 ** | 0.216 | 1.394 *** | 6.792 *** | 0.621 *** | 3.418 ** |
| (−2.29) | (0.21) | (11.48) | (3.90) | (6.10) | (2.17) | |
| FO | −17.39 *** | −9.450 | −4.392 * | 9.117 | −1.313 | 37.84 |
| (−6.92) | (−0.40) | (−1.93) | (0.33) | (−0.75) | (1.51) | |
| MKT | −3.513 *** | −32.62 *** | −4.040 *** | −37.77 *** | −2.015 *** | −24.33 *** |
| (−13.60) | (−14.84) | (−14.94) | (−9.43) | (−8.47) | (−6.54) | |
| ST | 0.618 *** | 0.395 *** | 0.232 *** | |||
| (15.49) | (15.48) | (10.81) | ||||
| GI | 54.57 *** | 21.02 ** | −18.91 ** | |||
| (11.18) | (2.22) | (−2.05) | ||||
| Cons | 7.316 *** | 32.65 *** | 7.293 *** | 30.61 *** | −9.268 *** | −122.6 *** |
| (26.21) | (12.57) | (22.43) | (7.25) | (−8.80) | (−8.20) | |
| Obs | 450 | 450 | 450 | 450 | 450 | 450 |
| N | 30 | 30 | 30 | 30 | ||
| R2 | 0.740 | 0.479 | 0.795 | 0.578 | 0.882 | 0.674 |
| F | 256.5 | 83.64 | 355.3 | 129.8 | 486.7 | 137.9 |
| F-Statistic | 47.23 (p = 0) | 17.83 (p = 0) | 82.57 (p = 0) | 26.35 (p = 0) | ||
| SYSGMM-IE | SYSGMM-BE | |||
|---|---|---|---|---|
| Coefficient | Standard Errors | Coefficient | Standard Errors | |
| OADR | 0.1165 ** | 0.0546 | 0.1817 | 0.7310 |
| OADR2 | −0.0043 *** | 0.0016 | −0.0049 | 0.0266 |
| IEt-1 | 0.9454 *** | 0.0710 | ||
| BEt-1 | 0.9597 *** | 0.0880 | ||
| OPR(1)-p | 0.002 | 0.001 | ||
| OPR(2)-p | 0.749 | 0.586 | ||
| Wald test | 75,354.70 (p = 0) | 4118.43 (p = 0) | ||
| Hansen-p | 0.00 | 0.06 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Yu, J.; Su, C.-H.; Chen, M.-H.; Zhou, D. Can China’s Aging Population Sustain Its Entrepreneurship? Evidence of Nonlinear Effects. Sustainability 2020, 12, 3434. https://doi.org/10.3390/su12083434
Yang H, Yu J, Su C-H, Chen M-H, Zhou D. Can China’s Aging Population Sustain Its Entrepreneurship? Evidence of Nonlinear Effects. Sustainability. 2020; 12(8):3434. https://doi.org/10.3390/su12083434
Chicago/Turabian StyleYang, Hongying, Jin Yu, Ching-Hui (Joan) Su, Ming-Hsiang Chen, and Dahui Zhou. 2020. "Can China’s Aging Population Sustain Its Entrepreneurship? Evidence of Nonlinear Effects" Sustainability 12, no. 8: 3434. https://doi.org/10.3390/su12083434
APA StyleYang, H., Yu, J., Su, C.-H., Chen, M.-H., & Zhou, D. (2020). Can China’s Aging Population Sustain Its Entrepreneurship? Evidence of Nonlinear Effects. Sustainability, 12(8), 3434. https://doi.org/10.3390/su12083434





