Multi-Technical Flexibility Retrofit Planning of Thermal Power Units Considering High Penetration Variable Renewable Energy: The Case of China
Abstract
:1. Introduction
- A multi-technical FRP model is proposed to minimize the overall investment and operational costs of the system. This model takes into account various feasible retrofit options and changes in multiple operating parameters of TPUs after retrofitting, providing assistance to planning departments and power generation companies.
- A linear formulating method is proposed to solve the coupling problems of decision-making on retrofitting and operating, and a mixed integer programming model is established to facilitate the use of commercial solvers such as cplex or gurobi.
- The effectiveness of the proposed approach is verified through a modified IEEE-30 bus system. Furthermore, the correctness and sensitivity of the model under several scenarios are analyzed and discussed.
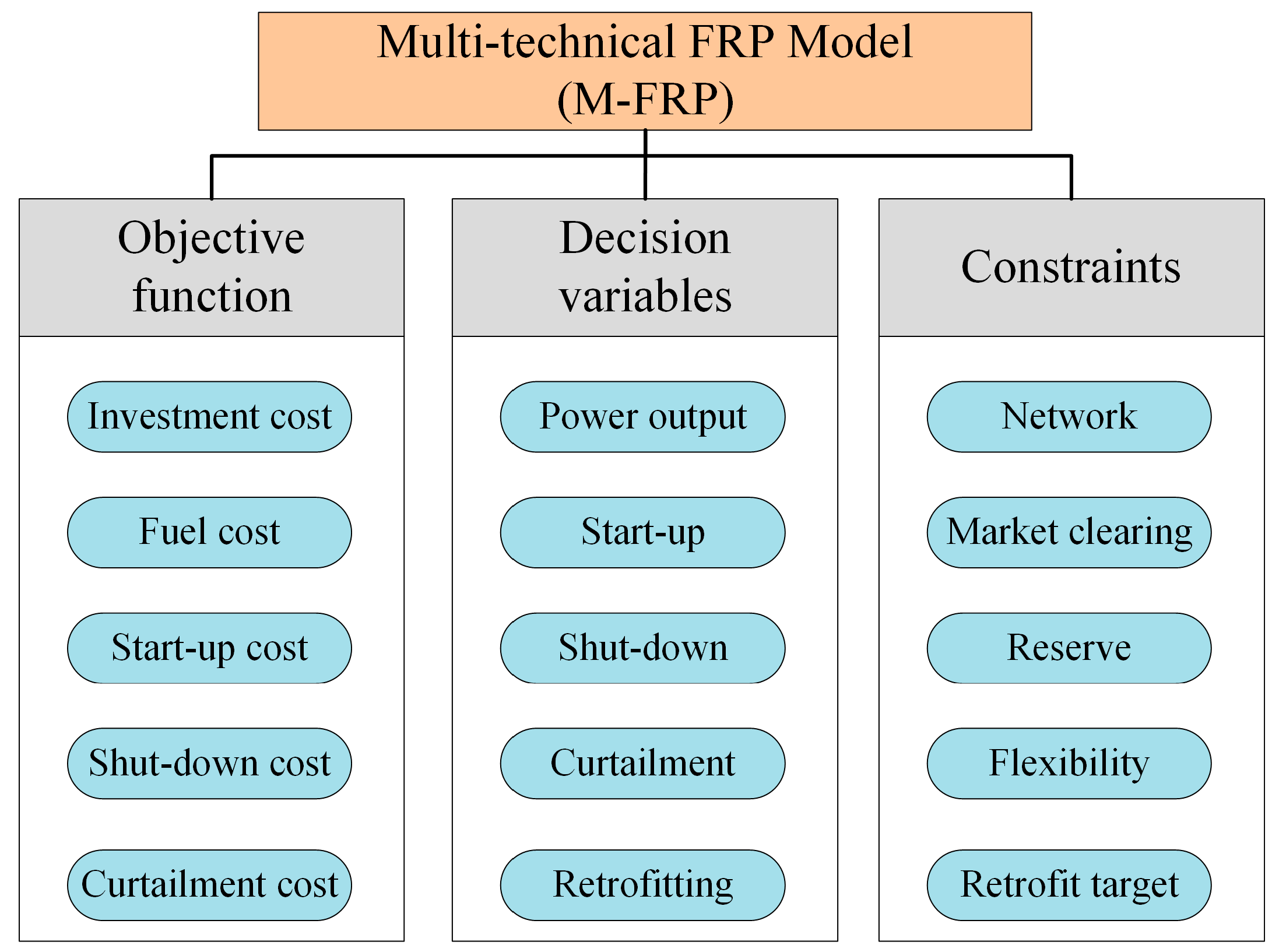
2. Flexibility Retrofit Options of TPUs
3. Multi-Technical FRP Model
3.1. Objective Function
3.2. Constraints
4. Case Study
4.1. Dataset
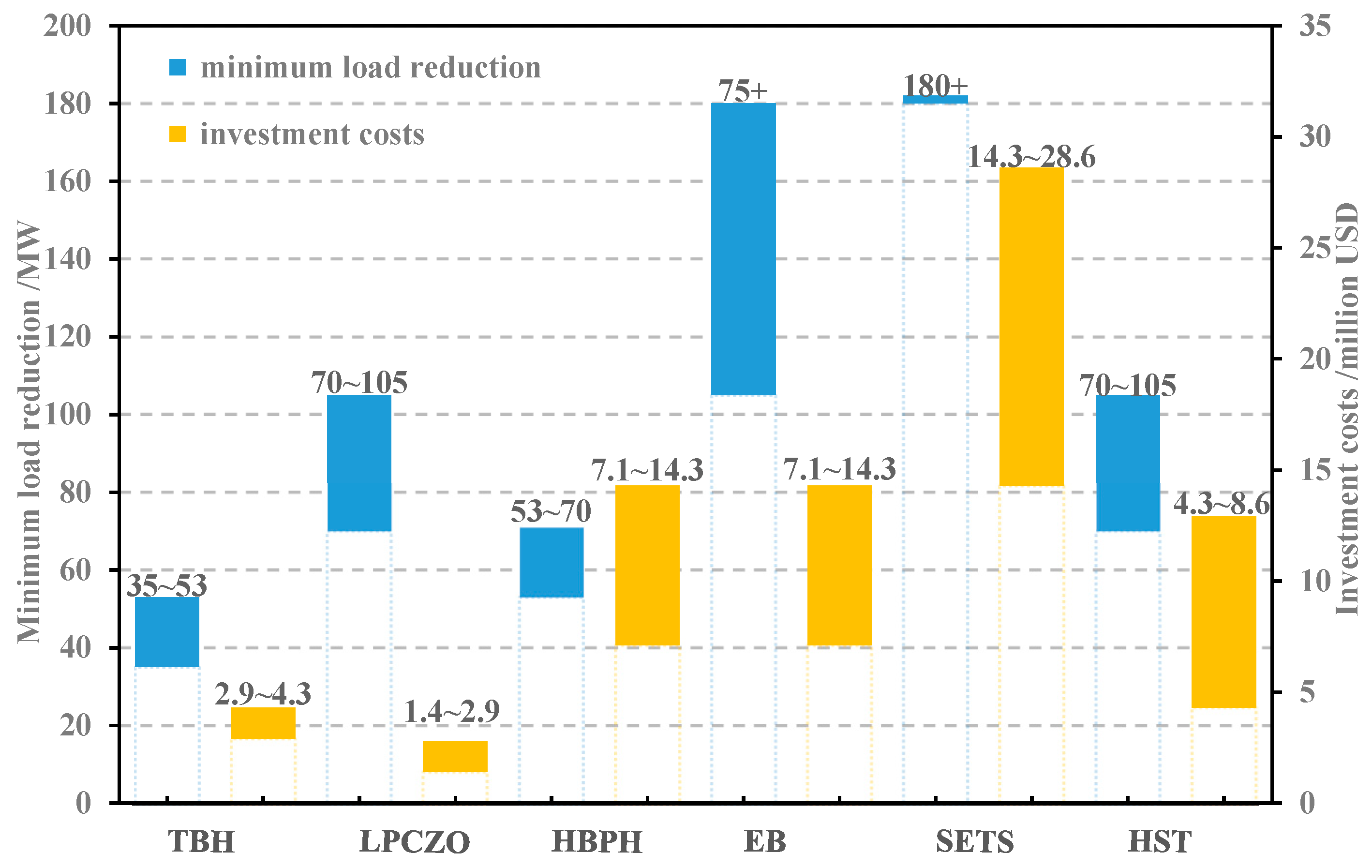
4.2. The Impact of Multiple Technical Retrofit Options
4.2.1. Comparison of Retrofit Decisions
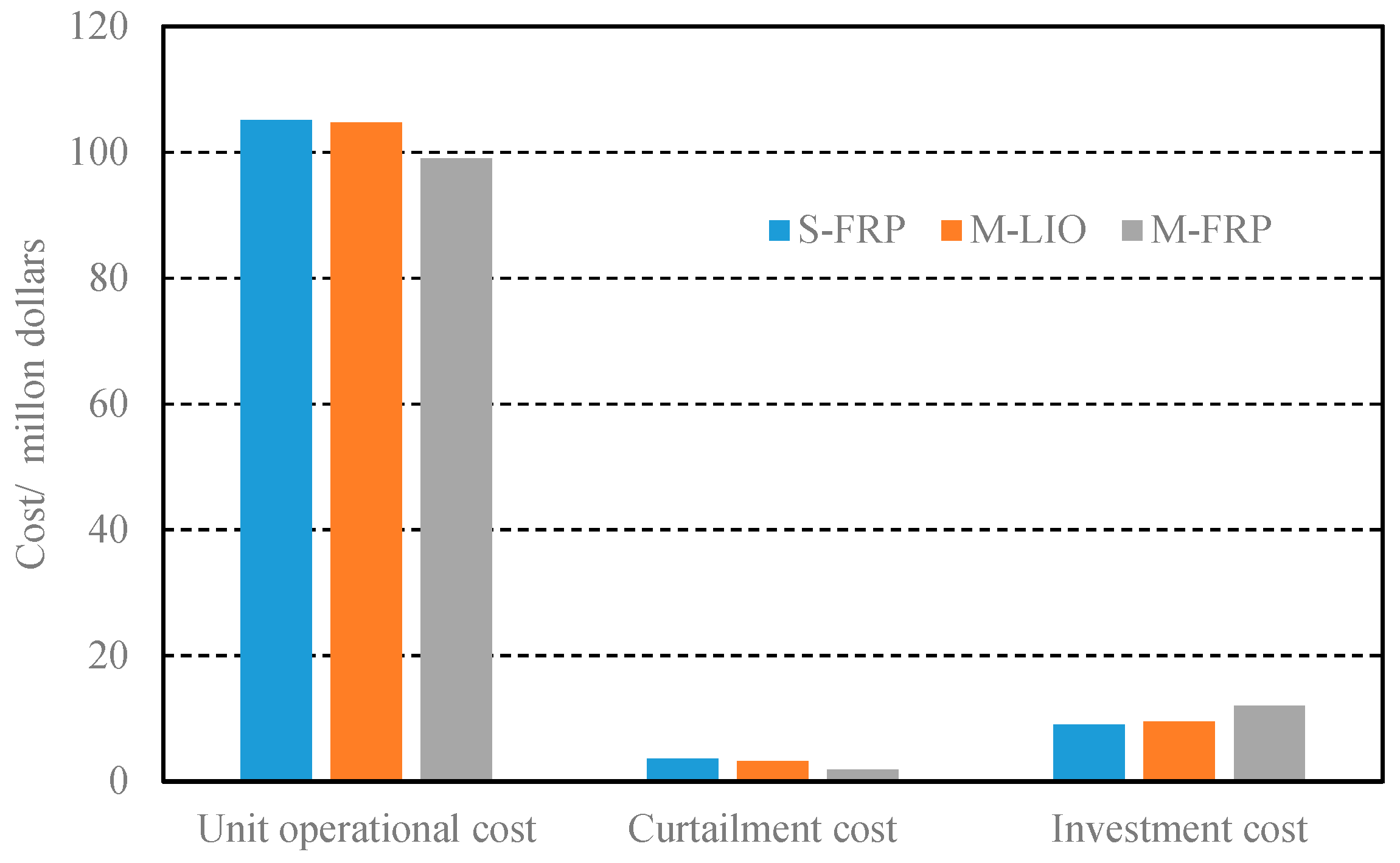
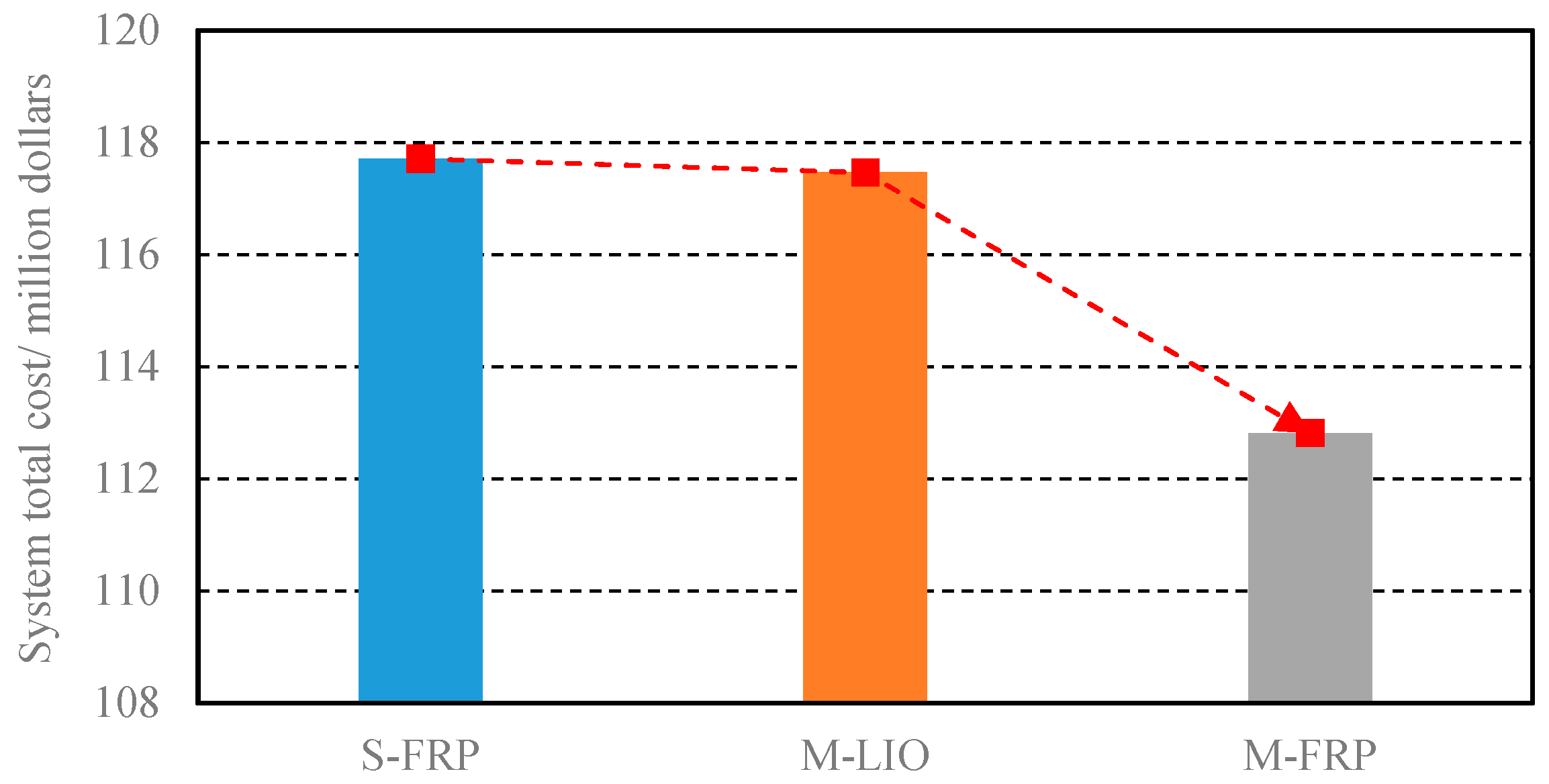
4.2.2. Comparison of System Costs
4.3. The Impact of Quota System for Retrofits Deployment
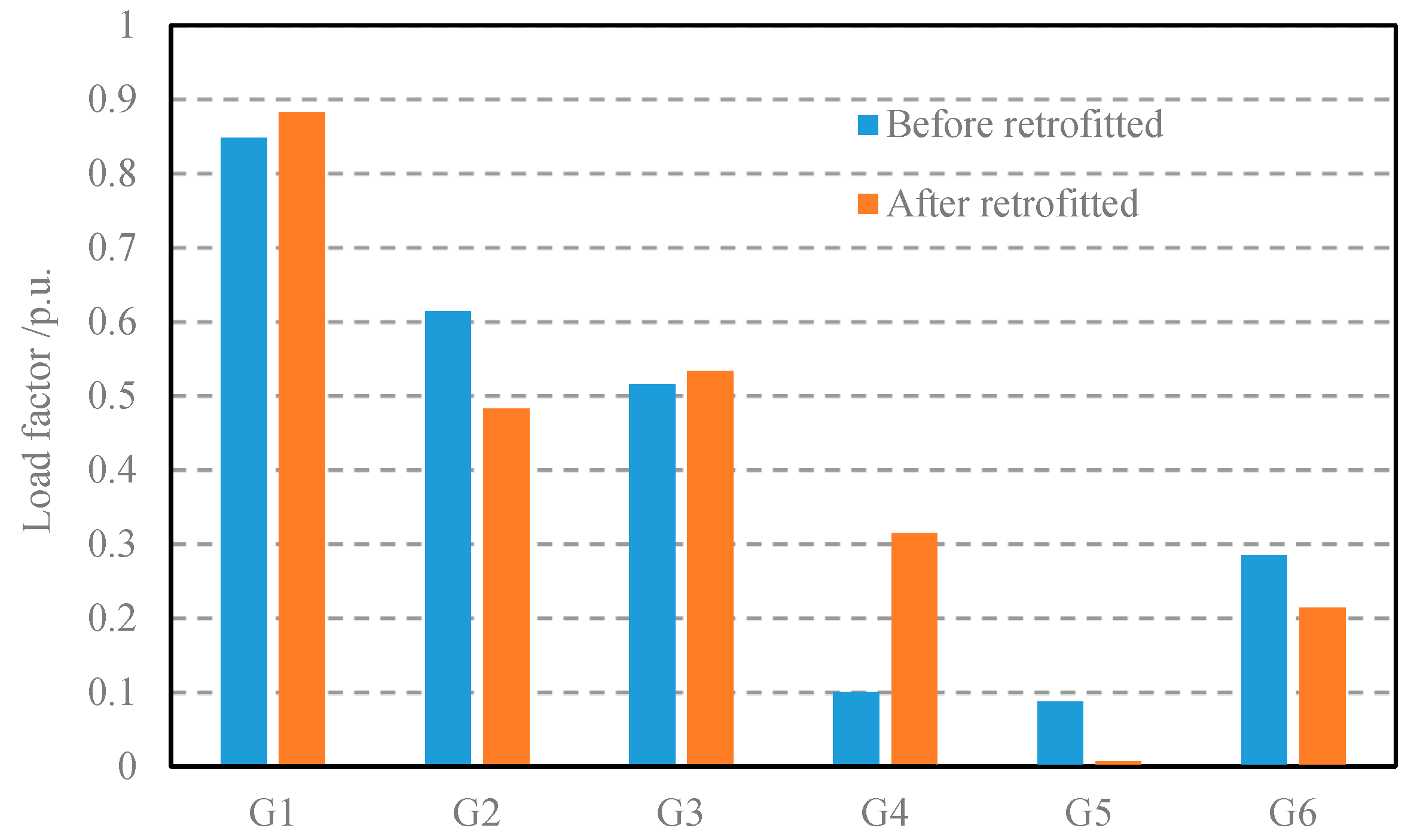
4.4. Comparison before and after Retrofitting
5. Conclusions
- Compared with single-option retrofit deployment, considering multiple technical retrofit options can reduce the system total cost and increase the accommodation of VRE. In addition, the planners need to comprehensively evaluate the complementarity of multiple technologies between units and reasonably set retrofitted target.
- Multiple parameter changes may affect the retrofit decision. Among them, the minimum output and ramping rate parameters may be the dominant factors affecting the retrofit deployment.
- When a unit is retrofitted, the roles of all the units in the system may be changed. Therefore, in order to ensure that the plan can be implemented, it is essential to ensure that the subsidies for the retrofitted units are sufficient.
- The proposed linear formulating method, which solved the coupling problems of decision-making on retrofitting and operating, could be integrated in other countries’ CExMs to provide guidance on the investment of various flexible resources to assist the VRE integration.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Unit | Option | MUT/MDT | RU/RD | SUC | SDC | NC | MC | SU/SD | Investment Cost ($) | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (h) | (MW/h) | ($) | ($) | ($) | ($/MW) | (MW/h) | |||||
| G1 | 1 | 600 | 240 | 10 | 150 | 37,403 | 18,702 | 765.8 | 36.92 | 450 | 21,000,000 |
| G1 | 2 | 600 | 180 | 9 | 200 | 35,434 | 17,717 | 725.11 | 34.2 | 460 | 30,000,000 |
| G2 | 1 | 350 | 170 | 8 | 70 | 25,000 | 12,500 | 909.32 | 40.2 | 270 | 2,000,000 |
| G2 | 2 | 350 | 135 | 8 | 90 | 25,000 | 12,500 | 957.18 | 42.32 | 265 | 6,000,000 |
| G2 | 3 | 350 | 0 | 8 | 110 | 25,000 | 12,500 | 957.18 | 42.32 | 265 | 20,000,000 |
| G3 | 1 | 350 | 180 | 8 | 90 | 25,000 | 12,500 | 1056.06 | 40.42 | 265 | 4,000,000 |
| G3 | 2 | 350 | 140 | 8 | 100 | 25,000 | 12,500 | 1010.26 | 38.42 | 280 | 2,500,000 |
| G4 | 1 | 200 | 60 | 6 | 50 | 20,000 | 10,000 | 1251.2 | 44.35 | 160 | 5,000,000 |
| G4 | 2 | 200 | 0 | 6 | 50 | 20,000 | 10,000 | 1251.2 | 44.35 | 160 | 10,000,000 |
| G4 | 3 | 200 | 80 | 6 | 50 | 20,000 | 10,000 | 1251.2 | 44.35 | 160 | 3,500,000 |
| G5 | 1 | 200 | 55 | 6 | 70 | 20,000 | 10,000 | 1362.2 | 43.34 | 160 | 4,000,000 |
| G5 | 2 | 200 | 0 | 6 | 70 | 20,000 | 10,000 | 1362.2 | 43.34 | 160 | 8,000,000 |
| G5 | 3 | 200 | 85 | 6 | 70 | 20,000 | 10,000 | 1362.2 | 43.34 | 160 | 4,500,000 |
| G6 | 1 | 150 | 60 | 4 | 60 | 10,000 | 5000 | 1360.49 | 44.28 | 120 | 1,500,000 |
| G6 | 2 | 150 | 45 | 4 | 60 | 10,000 | 5000 | 1292.56 | 42.06 | 130 | 1,000,000 |


References
- International Energy Agency. Harnessing Variable Renewables; International Energy Agency: Paris, France, 2011; pp. 43–50. [Google Scholar]
- Ahmadi-Khatir, A.; Conejo, J.; Cherkaoui, R. Multi-area energy and reserve dispatch under wind uncertainty and equipment failures. IEEE Trans. Power Syst. 2013, 28, 4373–4383. [Google Scholar] [CrossRef]
- Wang, F.; Li, K.; Liu, C.; Mi, Z.; Shafie-Khah, M.; Catalão, J. Synchronous pattern matching principle-based residential demand response baseline estimation: Mechanism analysis and approach description. IEEE Trans. Smart Grid 2018, 9, 6972–6985. [Google Scholar] [CrossRef]
- Raventós, O.; Bartels, J. Evaluation of temporal complexity reduction techniques applied to storage expansion planning in power system models. Energies 2020, 13, 988. [Google Scholar] [CrossRef] [Green Version]
- Na, C.; Pan, H.; Zhu, Y.; Yuan, J.; Ding, L.; Yu, J. The Flexible Operation of Coal Power and Its Renewable Integration Potential in China. Sustainability 2019, 11, 4424. [Google Scholar] [CrossRef] [Green Version]
- Na, C.; Yuan, J.; Zhu, Y.; Xue, L. Economic Decision-Making for Coal Power Flexibility Retrofitting and Compensation in China. Sustainability 2018, 10, 348. [Google Scholar] [CrossRef] [Green Version]
- Agora Energiewende. Flexibility in Thermal Power Plants—With a Focus on Existing Coal-Fired Power Plants; Agora Energiewende: Berlin, Germany, 2017. [Google Scholar]
- Gong, X.; Li, F.; Sun, B.; Liu, D. Collaborative optimization of multi-energy complementary combined cooling, heating, and power systems considering schedulable loads. Energies 2020, 13, 918. [Google Scholar] [CrossRef] [Green Version]
- Teng, Y.; Sun, P.; Leng, O.; Chen, Z.; Zhou, G. Optimal operation strategy for combined heat and power system based on solid electric thermal storage boiler and thermal inertia. IEEE Access 2019, 7, 180761–180770. [Google Scholar] [CrossRef]
- Yin, C.; Yan, J. Oxy-fuel combustion of pulverized fuels: Combustion fundamentals and modeling. Appl. Energy 2016, 162, 742–762. [Google Scholar] [CrossRef]
- Nerijus, S.; Andrius, T.; Liutauras, M.; Rolandas, P.; Kęstutis, Z.; Raminta, S. A sustainable approach for plasma reforming of tail biogas for onsite syngas production during lean combustion operation. Energy Convers. Manag. 2020, 209, 112617. [Google Scholar]
- National Renewable Energy Laboratory. Cost-Benefit Analysis of Flexibility Retrofits for Coal and Gas-Fueled Power Plants; National Renewable Energy Laboratory: Golden, CO, USA, 2013.
- Barbara, G.; Reinhard, M. Evaluating the enhanced flexibility of lignite-fired power plants: A real options analysis. Energy Convers. Manag. 2018, 177, 737–749. [Google Scholar]
- Jonghe, C.; Delarue, E.; Belmans, R. Determining optimal electricity technology mix with high level of wind power penetration. Appl. Energy 2011, 88, 2231–2238. [Google Scholar] [CrossRef] [Green Version]
- Steven, S. Power System Economics: Designing Markets for Electricity; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Poncelet, K.; Delarue, E.; Six, D. Impact of the level of temporal and operational detail in energy-system planning models. Appl. Energy 2016, 162, 631–643. [Google Scholar] [CrossRef] [Green Version]
- Palmintier, B.S.; Webster, M.D. Heterogeneous unit clustering for efficient operational flexibility modeling. IEEE Trans. Power Syst. 2014, 29, 1089–1098. [Google Scholar] [CrossRef]
- Meus, J.; Poncelet, K.; Delarue, E. Applicability of a clustered unit commitment model in power system modeling. IEEE Trans. Power Syst. 2017, 33, 2195–2204. [Google Scholar] [CrossRef] [Green Version]
- MA, J.; Silva, V.; Belhomme, R. Evaluating and planning flexibility in sustainable power systems. IEEE Trans. Sustain. Energy 2013, 4, 200–209. [Google Scholar] [CrossRef] [Green Version]
- Belderbos, A.; Delarue, E. Accounting for flexibility in power system planning with renewables. Int. J. Electr. Power Energy Syst. 2015, 71, 33–41. [Google Scholar] [CrossRef] [Green Version]
- International Energy Agency. The Power of Transformation: Wind, Sun and the Economics of Flexible Power Systems; International Energy Agency: Paris, France, 2014. [Google Scholar]
- International Energy Agency. Status of Power System Transformation 2018; International Energy Agency: Paris, France, 2018. [Google Scholar]
- Xingmei, L.; Zhiming, Z.; Jie, Y. Flexibility reformation planning of thermal power units with large-scale integration of wind power. Autom. Electr. Power Syst. 2019, 43, 51–57. [Google Scholar]
- National Development and Reform Commission (NDRC). China 13th Renewable Energy Development Five-Year Plan (2016–2020); NDRC: Beijing, China, 2016.
- IEA Clean Coal Centre. Increasing the Flexibility of Coal-Fired Power Plants; IEA Clean Coal Centre: London, UK, 2014. [Google Scholar]
- Carrion, M.; Arroyo, J.A. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans. Power Syst. 2006, 21, 1371–1378. [Google Scholar] [CrossRef]
- Frangioni, A.; Gentile, C.; Lacalandra, F. Tighter approximated MILP formulations for unit commitment problems. IEEE Trans Power Syst. 2008, 24, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Elisa, L.; Lorenzo, P. Cycles optimization: The equivalent annuity and the NPV approaches. Int. J. Prod. Econ. 2001, 69, 65–83. [Google Scholar]
- Morales-Espana, G.; Ramos, A.; Garcia-Gonzalez, J. An MIP Formulation for joint market-clearing of energy and reserves based on ramp scheduling. IEEE Trans. Power Syst. 2014, 29, 476–488. [Google Scholar] [CrossRef]
- Bahrami, S.; Wong, V. Security-constrained unit commitment for AC-DC grids with generation and load uncertainty. IEEE Trans. Power Syst. 2018, 33, 2717–2731. [Google Scholar] [CrossRef]
- Liu, Y.; Sioshansi, R.; Conejo, A.J. Hierarchical clustering to find representative operating periods for capacity-expansion modeling. IEEE Trans. Power Syst. 2018, 33, 3029–3039. [Google Scholar] [CrossRef]




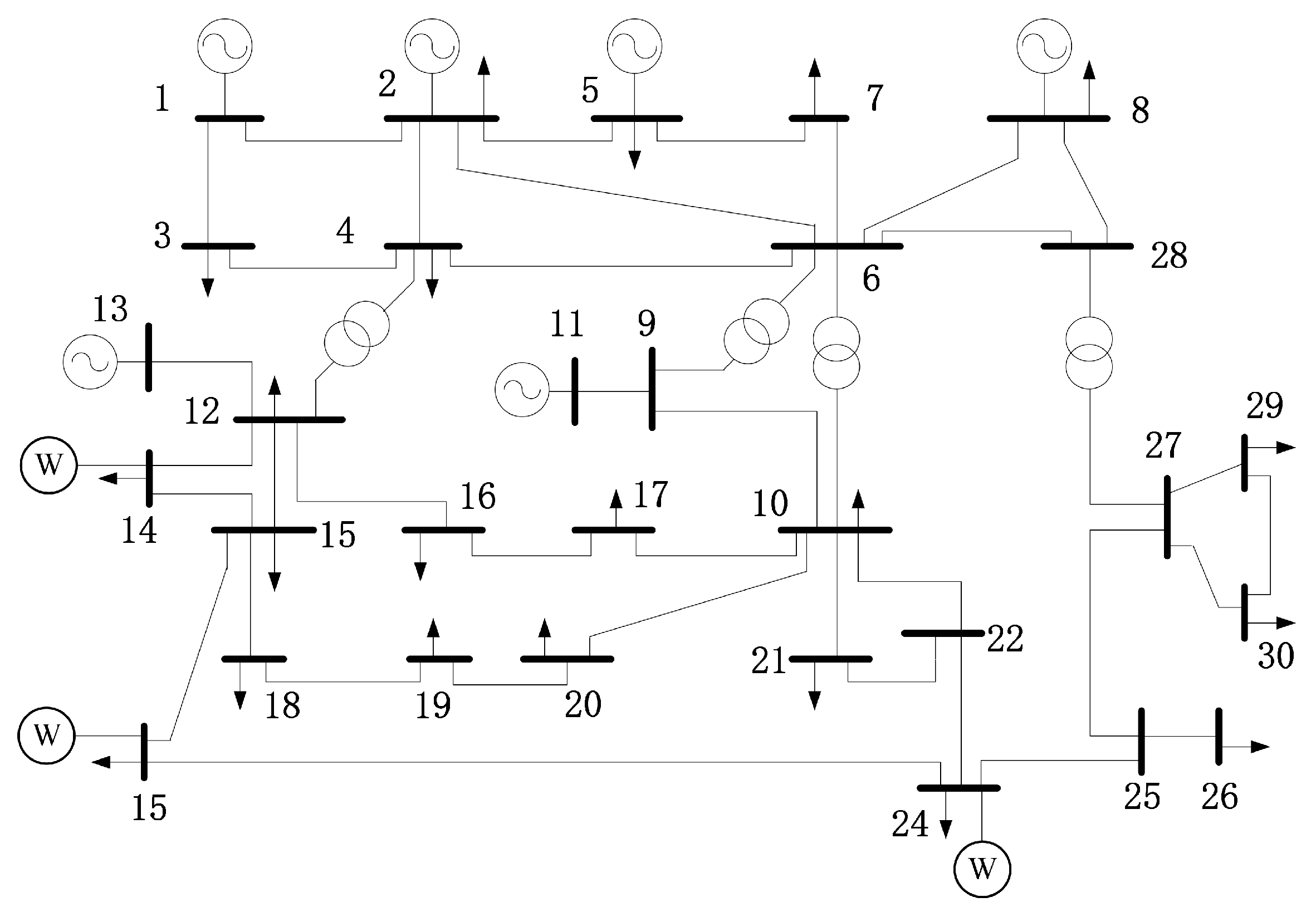
| Unit Name | Bus No. | PGCs | (MW) | (MW) | MUT/MDT 1 (h) | RU/RD (MW/h) | SUC ($) | SDC ($) | NC ($) | MC ($/MW) | SU/SD (MW/h) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | 1 | C1 | 600 | 380 | 10 | 120 | 39,372 | 19,686 | 806.11 | 38.87 | 440 |
| G2 | 2 | C2 | 350 | 200 | 8 | 70 | 25,000 | 12,500 | 957.18 | 42.32 | 265 |
| G3 | 5 | C3 | 350 | 180 | 8 | 80 | 25,000 | 12,500 | 1056.06 | 40.42 | 265 |
| G4 | 8 | C2 | 200 | 120 | 6 | 50 | 20,000 | 10,000 | 1251.2 | 44.35 | 160 |
| G5 | 11 | C3 | 200 | 150 | 6 | 70 | 20,000 | 10,000 | 1362.2 | 43.34 | 160 |
| G6 | 13 | C1 | 150 | 100 | 4 | 40 | 10,000 | 5000 | 1360.49 | 44.28 | 120 |
| Unit Name | G1 | G2 | G3 | G4 | G5 | G6 |
|---|---|---|---|---|---|---|
| Option No. | 1 | 1 | 2 | 3 | 1 | 2 |
| Strategies | G1 | G2 | G3 | G4 | G5 | G6 |
|---|---|---|---|---|---|---|
| S_FRP | 0 1 | 1 | 2 | 3 | 0 | 2 |
| M_LIO | 0 | 1 | 2 | 0 | 1 | 2 |
| M-FRP | 0 | 0 | 2 | 0 | 2 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Guo, T.; Wang, Y.; Li, Y.; Xu, S. Multi-Technical Flexibility Retrofit Planning of Thermal Power Units Considering High Penetration Variable Renewable Energy: The Case of China. Sustainability 2020, 12, 3543. https://doi.org/10.3390/su12093543
Liu J, Guo T, Wang Y, Li Y, Xu S. Multi-Technical Flexibility Retrofit Planning of Thermal Power Units Considering High Penetration Variable Renewable Energy: The Case of China. Sustainability. 2020; 12(9):3543. https://doi.org/10.3390/su12093543
Chicago/Turabian StyleLiu, Jiaomin, Tong Guo, Yue Wang, Yonggang Li, and Shanshan Xu. 2020. "Multi-Technical Flexibility Retrofit Planning of Thermal Power Units Considering High Penetration Variable Renewable Energy: The Case of China" Sustainability 12, no. 9: 3543. https://doi.org/10.3390/su12093543
APA StyleLiu, J., Guo, T., Wang, Y., Li, Y., & Xu, S. (2020). Multi-Technical Flexibility Retrofit Planning of Thermal Power Units Considering High Penetration Variable Renewable Energy: The Case of China. Sustainability, 12(9), 3543. https://doi.org/10.3390/su12093543




