Parametric Assessment of Trend Test Power in a Changing Environment
Abstract
:1. Introduction
2. Methodologies
2.1. The Akaike Information Criteria Based Test
- Generate a certain number of samples (e.g., 10,000) from an assigned stationary model, assumed as the null hypothesis of the test;
- Compute AICΔ for all samples and determine its empirical probability distribution;
- Evaluate the threshold value AICΔ,α corresponding to an assigned level of significance (here set to 0.05), that will be used for accepting or rejecting the null hypothesis of stationarity of point 1.
2.2. Rescaled GEV Distribution
| First-order (Mean) | (4) | ||
| Second-order | (5) | ||
| L-CV | (6) | ||
| L-Skewness | (7) | ||
| L-Kurtosis | (8) |
| First-order (Mean) | (15) | ||
| Second-order | (16) |
| L-CV | (18) |
2.3. Power Evaluation and Sensitivity Analysis
3. Literature Parameter Range of Extreme Rainfall, Flow Peak, and Wind Speed
3.1. Literature Studies on Extreme Rainfall
3.2. Literature Studies on Extreme Flow Peak
3.3. Literature Studies on Extreme Wind Speed
4. Results and Discussion
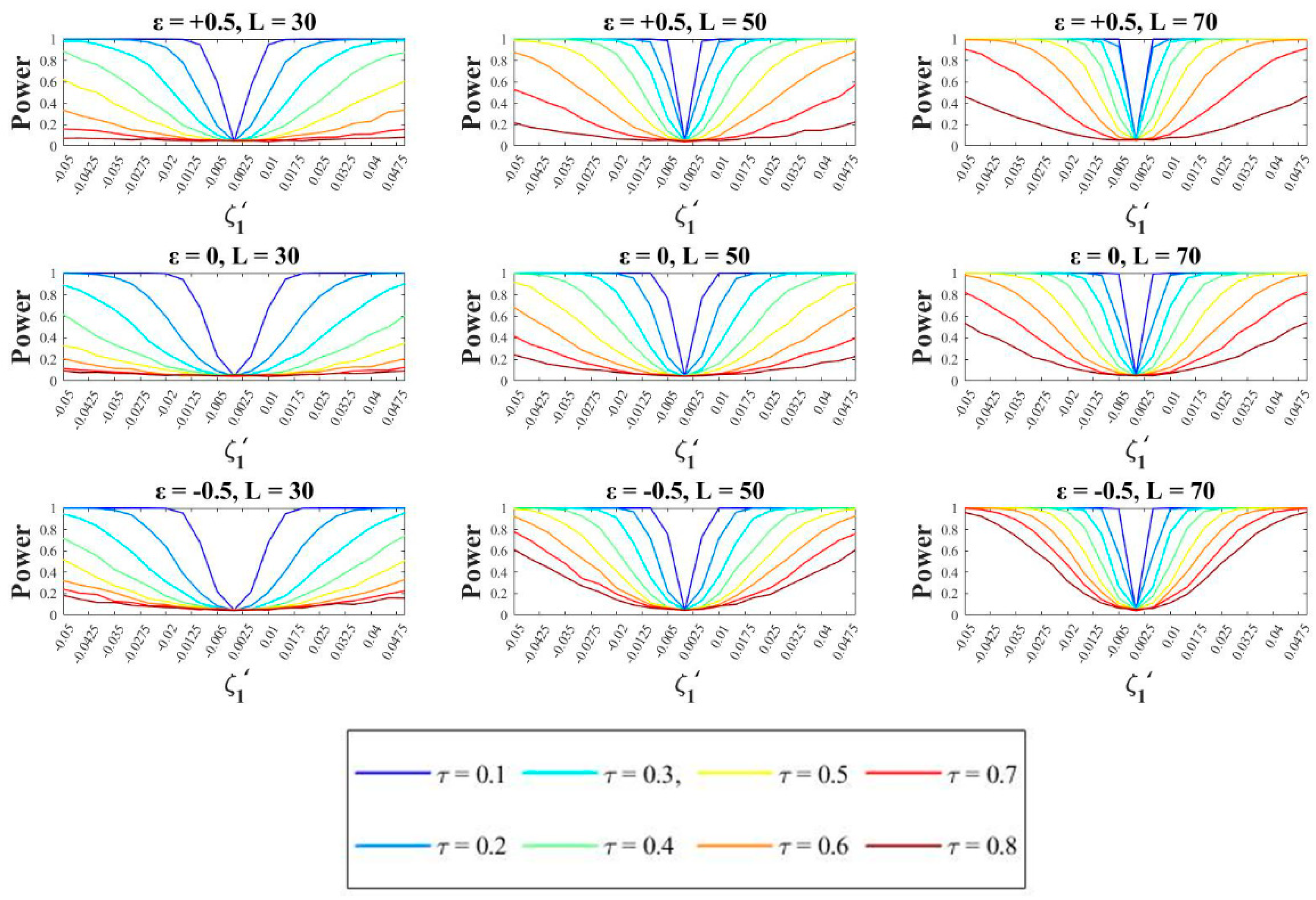
4.1. Power of AICΔ and MK Tests for Different Values of ε and L-CV.
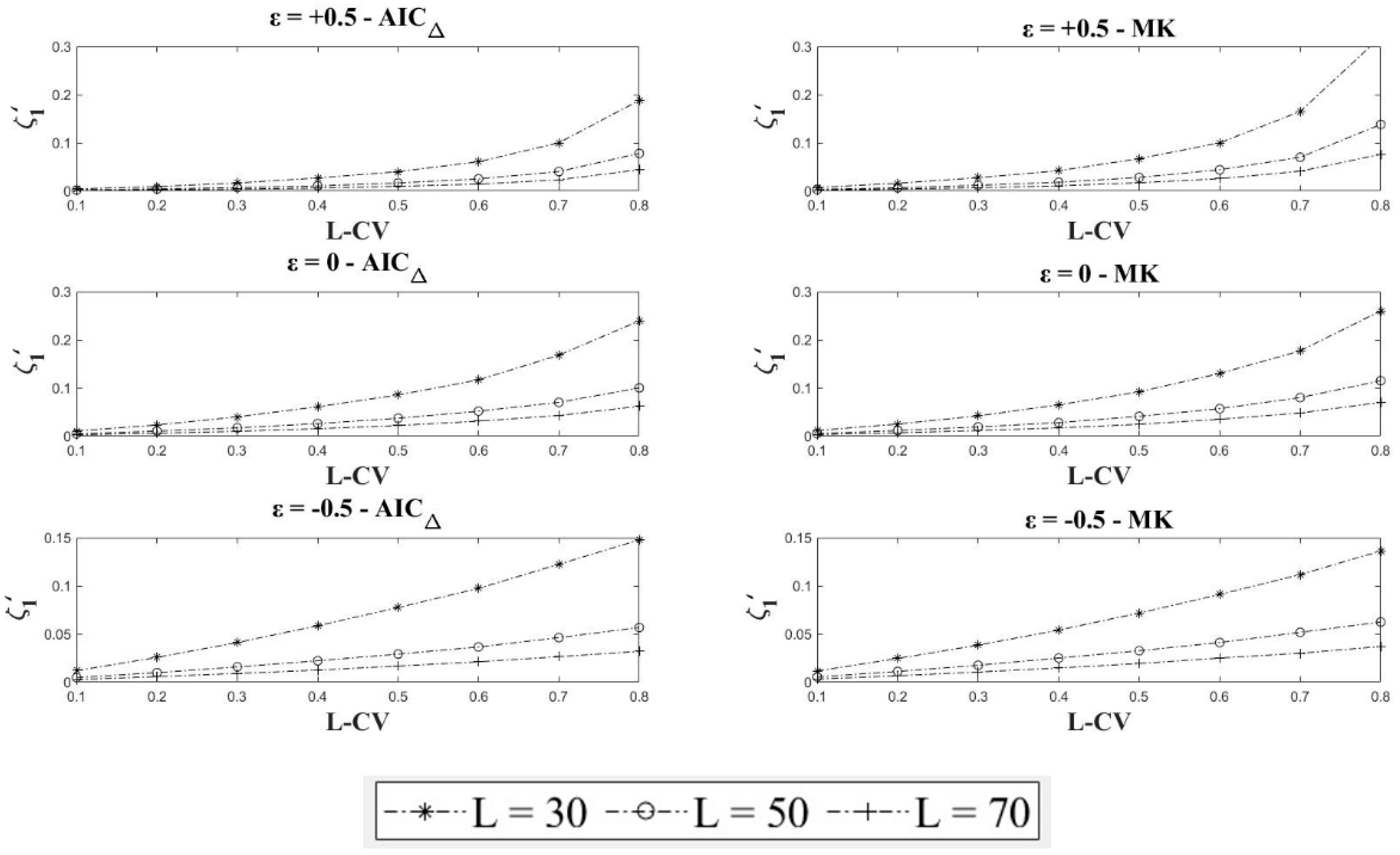
4.2. Sampling Variance of
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
List of Acronyms
| Acronym | Explanation |
| AIC | Akaike Information Criterion |
| ASA | American Statistical Association |
| EV1 | Extreme Value Type 1 |
| EV2 | Extreme Value Type 2 |
| EV3 | Extreme Value Type 3 |
| GEV | Generalized Extreme Value |
| L-CV | L-Coefficient of Variation |
| MK | Mann–Kendall |
| ML | Maximum Likelihood |
| NHST | Null-Hypothesis Statistical Tests |
Appendix A
References
- Murphy, B.L. From interdisciplinary to inter-epistemological approaches: Confronting the challenges of integrated climate change research. Can. Geogr. 2011, 55, 490–509. [Google Scholar] [CrossRef]
- Rineau, F.; Malina, R.; Beenaerts, N.; Arnauts, N.; Bardgett, R.D.; Berg, M.P.; Boerema, A.; Bruckers, L.; Clerinx, J.; Davin, E.L.; et al. Towards more predictive and interdisciplinary climate change ecosystem experiments. Nat. Clim. Chang. 2019, 9, 809–816. [Google Scholar] [CrossRef]
- Metzger, M.J.; Leemans, R.; Schröter, D. A multidisciplinary multi-scale framework for assessing vulnerabilities to global change. Int. J. Appl. Earth Obs. Geoinf. 2005, 7, 253–267. [Google Scholar] [CrossRef]
- Cagle, L.E.; Tillery, D. Climate change research across disciplines: The value and uses of multidisciplinary research reviews for technical communication. Tech. Commun. Q. 2015, 24, 147–163. [Google Scholar] [CrossRef]
- Blöschl, G.; Montanari, A. Climate change impacts-throwing the dice? Hydrol. Process. 2010, 24, 374–381. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’ s dry and wet regions. Nat. Clim. Chang. 2016, 6, 508–513. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Robson, A.J. Change detection in hydrological records—A review of the methodology. Hydrol. Sci. J. 2004, 49, 7–19. [Google Scholar] [CrossRef]
- Cohen, J. The earth is round (p < 0.05). Am. Psychol. 1994. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G.; Lombardo, F. Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology. Adv. Water Resour. 2018, 111, 132–155. [Google Scholar] [CrossRef]
- Vogel, R.M.; Rosner, A.; Kirshen, P.H. Brief Communication: Likelihood of societal preparedness for global change: Trend detection. Nat. Hazards Earth Syst. Sci. 2013, 13, 1773–1778. [Google Scholar] [CrossRef] [Green Version]
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J.; Dettinger, M.D.; Krysanova, V. On Critiques of “stationarity is Dead: Whither Water Management?”. Water Resour. Res. 2015, 7785–7789. [Google Scholar] [CrossRef] [Green Version]
- Beven, K. Facets of uncertainty: Epistemic uncertainty, non-stationarity, likelihood, hypothesis testing, and communication. Hydrol. Sci. J. 2016, 61, 1652–1665. [Google Scholar] [CrossRef] [Green Version]
- Wasserstein, R.L.; Schirm, A.L.; Lazar, N.A. Moving to a World Beyond “p < 0.05.”. Am. Stat. 2019, 73, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Totaro, V.; Gioia, A.; Iacobellis, V. Numerical investigation on the power of parametric and nonparametric tests for trend detection in annual maximum series. Hydrol. Earth Syst. Sci. 2020, 24, 473–488. [Google Scholar] [CrossRef] [Green Version]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Wang, F.; Shao, W.; Yu, H.; Kan, G.; He, X.; Zhang, D.; Ren, M.; Wang, G. Re-evaluation of the Power of the Mann-Kendall Test for Detecting Monotonic Trends in Hydrometeorological Time Series. Front. Earth Sci. 2020, 8. [Google Scholar] [CrossRef]
- Montanari, A.; Koutsoyiannis, D. Modeling and mitigating natural hazards: Stationarity is immortal! Water Resour. Res. 2014, 50, 9748–9756. [Google Scholar] [CrossRef]
- Serinaldi, F.; Kilsby, C.G. Stationarity is undead: Uncertainty dominates the distribution of extremes. Adv. Water Resour. 2015, 77, 17–36. [Google Scholar] [CrossRef] [Green Version]
- Salas, J.D.; Obeysekera, J. Revisiting the Concepts of Return Period and Risk for Nonstationary Hydrologic Extreme Events. J. Hydrol. Eng. 2014, 19, 554–568. [Google Scholar] [CrossRef] [Green Version]
- Yohe, G.W.; Lasco, R.D.; Ahmad, Q.K.; Arnell, N.W.; Cohen, S.J.; Hope, C.; Janetos, A.C.; Perez, R.T. Perspectives on climate change and sustainability. Climate Change 2007: Impacts, Adaptation and Vulnerability. Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Parry, M.L., Canziani, O.F., Palutikof, J.P., van der Linden, P.J., Hanson, C.E., Eds.; Cambridge University Press: Cambridge, UK, 2007; pp. 811–841. [Google Scholar]
- Stedinger, J.R.; Vogel, R.M.; Foufoula-Georgiou, E. Frequency analysis of extreme events. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993; pp. 18.1–18.68. [Google Scholar]
- Lieber, R.L. Statistical significance and statistical power in hypothesis testing. J. Orthop. Res. 1990, 8, 304–309. [Google Scholar] [CrossRef]
- Cohen, J. A power primer. Psychol. Bull. 1992, 112, 155–159. [Google Scholar] [CrossRef] [PubMed]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. Ser. B 1990, 52, 105–124. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975; ISBN 978-0-85264-199-6. [Google Scholar]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Laio, F.; Di Baldassarre, G.; Montanari, A. Model selection techniques for the frequency analysis of hydrological extremes. Water Resour. Res. 2009. [Google Scholar] [CrossRef]
- Iacobellis, V.; Fiorentino, M.; Gioia, A.; Manfreda, S. Best fit and selection of theoretical flood frequency distributions based on different runoff generation mechanisms. Water (Switzerland) 2010, 2, 239–256. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R.; Huyvaert, K.P. AIC model selection and multimodel inference in behavioral ecology: Some background, observations, and comparisons. Behav. Ecol. Sociobiol. 2011, 65, 23–35. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Gilleland, E.; Katz, R.W. ExtRemes 2.0: An extreme value analysis package in R. J. Stat. Softw. 2016, 72, 1–39. [Google Scholar] [CrossRef] [Green Version]
- Fowler, H.J.; Kilsby, C.G. A regional frequency analysis of United Kingdom extreme rainfall from 1961 to 2000. Int. J. Climatol. 2003, 23, 1313–1334. [Google Scholar] [CrossRef]
- Lee, S.H.; Maeng, S.J. Frequency analysis of extreme rainfall using L-moment. Irrig. Drain. 2003, 52, 219–230. [Google Scholar] [CrossRef]
- Ngongondo, C.S.; Xu, C.Y.; Tallaksen, L.M.; Alemaw, B.; Chirwa, T. Regional frequency analysis of rainfall extremes in Southern Malawi using the index rainfall and L-moments approaches. Stoch. Environ. Res. Risk Assess. 2011, 25, 939–955. [Google Scholar] [CrossRef] [Green Version]
- Wan Zin, W.Z.; Jemain, A.A.; Ibrahim, K. The best fitting distribution of annual maximum rainfall in Peninsular Malaysia based on methods of L-moment and LQ-moment. Theor. Appl. Climatol. 2009, 96, 337–344. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Battle of extreme value distributions: A global survey on extreme daily rainfall. Water Resour. Res. 2013, 49, 187–201. [Google Scholar] [CrossRef]
- Abolverdi, J.; Khalili, D. Development of Regional Rainfall Annual Maxima for Southwestern Iran by L-Moments. Water Resour. Manag. 2010, 24, 2501–2526. [Google Scholar] [CrossRef]
- Alahmadi, F.S. Regional Rainfall Frequency Analysis By L-Moments Approach For Madina Region, Saudi Arabia. Int. J. Eng. Res. Dev. 2017, 13, 39–48. [Google Scholar]
- Yurekli, K.; Modarres, R.; Ozturk, F. Regional daily maximum rainfall estimation for Cekerek Watershed by L-moments. Meteorol. Appl. 2009, 16, 435–444. [Google Scholar] [CrossRef]
- Shahzadi, A.; Akhter, A.S.; Saf, B. Regional frequency analysis of annual maximum rainfall in monsoon region of pakistan using L-moments. Pak. J. Stat. Oper. Res. 2013, 9, 111–136. [Google Scholar] [CrossRef] [Green Version]
- Zakaria, Z.A.; Shabri, A.; Ahmad, U.N. Regional Frequency Analysis of Extreme Rainfalls in the West Coast of Peninsular Malaysia using Partial L-Moments. Water Resour. Manag. 2012, 26, 4417–4433. [Google Scholar] [CrossRef]
- Forestieri, A.; Lo Conti, F.; Blenkinsop, S.; Cannarozzo, M.; Fowler, H.J.; Noto, L.V. Regional frequency analysis of extreme rainfall in Sicily (Italy). Int. J. Climatol. 2018, 38, e698–e716. [Google Scholar] [CrossRef]
- Abida, H.; Ellouze, M. Probability distribution of flood flows in Tunisia. Hydrol. Earth Syst. Sci. 2008, 12, 703–714. [Google Scholar] [CrossRef] [Green Version]
- Glaves, R.; Waylen, P.R. Regional flood frequency analysis in Southern Ontario using L-moments. Can. Geogr. 1997, 41, 178–193. [Google Scholar] [CrossRef]
- Salinas, J.L.; Castellarin, A.; Viglione, A.; Kohnová, S.; Kjeldsen, T.R. Regional parent flood frequency distributions in Europe—Part 1: Is the GEV model suitable as a pan-European parent? Hydrol. Earth Syst. Sci. 2014, 18, 4381–4389. [Google Scholar] [CrossRef] [Green Version]
- Vogel, R.M.; Thomas, W.O.; McMahon, T.A. Flood-flow frequency model selection in southwestern United States. J. Water Resour. Plan. Manag. 1993, 119, 353–366. [Google Scholar] [CrossRef] [Green Version]
- Drissia, T.K.; Jothiprakash, V.; Anitha, A.B. Flood Frequency Analysis Using L Moments: A Comparison between At-Site and Regional Approach. Water Resour. Manag. 2019, 33, 1013–1037. [Google Scholar] [CrossRef]
- Hussain, Z.; Pasha, G.R. Regional flood frequency analysis of the seven sites of Punjab, Pakistan, using L-moments. Water Resour. Manag. 2009, 23, 1917–1933. [Google Scholar] [CrossRef]
- Meshgi, A.; Khalili, D. Comprehensive evaluation of regional flood frequency analysis by L- and LH-moments. I. A re-visit to regional homogeneity. Stoch. Environ. Res. Risk Assess. 2009, 23, 119–135. [Google Scholar] [CrossRef]
- Noto, L.V.; La Loggia, G. Use of L-moments approach for regional flood frequency analysis in Sicily, Italy. Water Resour. Manag. 2009, 23, 2207–2229. [Google Scholar] [CrossRef]
- Pearson, C.P. New Zealand regional flood frequency analysis using L-moments. J. Hydrol. (N. Z.) 1991, 30, 53–64. [Google Scholar]
- Salinas, J.L.; Castellarin, A.; Kohnová, S.; Kjeldsen, T.R. Regional parent flood frequency distributions in Europe—Part 2: Climate and scale controls. Hydrol. Earth Syst. Sci. 2014, 18, 4391–4401. [Google Scholar] [CrossRef] [Green Version]
- Seckin, N.; Haktanir, T.; Yurtal, R. Flood frequency analysis of Turkey using L-moments method. Hydrol. Process. 2011, 25, 3499–3505. [Google Scholar] [CrossRef]
- Vogel, R.M.; McMahon, T.A.; Chiew, F.H.S. Floodflow frequency model selection in Australia. J. Hydrol. 1993, 146, 421–449. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Wind speed distribution selection—A review of recent development and progress. Renew. Sustain. Energy Rev. 2019, 114, 109290. [Google Scholar] [CrossRef]
- Morgan, E.C.; Lackner, M.; Vogel, R.M.; Baise, L.G. Probability distributions for offshore wind speeds. Energy Convers. Manag. 2011, 52, 15–26. [Google Scholar] [CrossRef]
- Palutikof, J.P.; Brabson, B.B.; Lister, D.H.; Adcock, S.T. A review of methods to calculate extreme wind speeds. Meteorol. Appl. 1999, 6, 119–132. [Google Scholar] [CrossRef]
- Fawad, M.; Yan, T.; Chen, L.; Huang, K.; Singh, V.P. Multiparameter probability distributions for at-site frequency analysis of annual maximum wind speed with L-Moments for parameter estimation. Energy 2019, 181, 724–737. [Google Scholar] [CrossRef]
- Goel, N.K.; Burn, D.H.; Pandey, M.D.; An, Y. Wind quantile estimation using a pooled frequency analysis approach. J. Wind Eng. Ind. Aerodyn. 2004, 92, 509–528. [Google Scholar] [CrossRef]
- Hong, H.P.; Ye, W. Estimating extreme wind speed based on regional frequency analysis. Struct. Saf. 2014, 47, 67–77. [Google Scholar] [CrossRef]
- MacKenzie, C.A.; Winterstein, S.R. Comparing L-moments and conventional moments to model current speeds in the North Sea. In Proceedings of the 61st Annual IIE Conference and Expo Proceedings, Reno, NV, USA, 24 May 2011. [Google Scholar]
- Pandey, M.D.; Van Gelder, P.H.A.J.M.; Vrijling, J.K. The estimation of extreme quantiles of wind velocity using L-moments in the peaks-over-threshold approach. Struct. Saf. 2001, 23, 179–192. [Google Scholar] [CrossRef]
- Hundecha, Y.; St-Hilaire, A.; Ouarda, T.B.M.J.; El Adlouni, S.; Gachon, P. A nonstationary extreme value analysis for the assessment of changes in extreme annual wind speed over the gulf of St. Lawrence Canada. J. Appl. Meteorol. Climatol. 2008, 47, 2745–2759. [Google Scholar] [CrossRef]
- Fawad, M.; Ahmad, I.; Nadeem, F.A.; Yan, T.; Abbas, A. Estimation of wind speed using regional frequency analysis based on linear-moments. Int. J. Climatol. 2018, 38, 4431–4444. [Google Scholar] [CrossRef]
- Modarres, R. Regional maximum wind speed frequency analysis for the arid and semi-arid regions of Iran. J. Arid Environ. 2008, 72, 1329–1342. [Google Scholar] [CrossRef]
- Olsen, J.R.; Lambert, J.H.; Haimes, Y.Y. Risk of extreme events under nonstationary conditions. Risk Anal. 1998, 18, 497–510. [Google Scholar] [CrossRef]
- Du, T.; Xiong, L.; Xu, C.Y.; Gippel, C.J.; Guo, S.; Liu, P. Return period and risk analysis of nonstationary low-flow series under climate change. J. Hydrol. 2015, 527, 234–250. [Google Scholar] [CrossRef] [Green Version]
- Do, H.X.; Westra, S.; Leonard, M. A global-scale investigation of trends in annual maximum streamflow. J. Hydrol. 2017, 552, 28–43. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Kanae, S.; Seneviratne, S.I.; Handmer, J.; Nicholls, N.; Peduzzi, P.; Mechler, R.; Bouwer, L.M.; Arnell, N.; Mach, K.; et al. Flood risk and climate change: Global and regional perspectives. Hydrol. Sci. J. 2014, 59, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Wallemacq, P.; Below, R. The Human Cost of Natural Disasters: A Global Perspective; Centre for Research on the Epidemiology of Disaster: Brussels, Belgium, 2015. [Google Scholar]
- Formetta, G.; Feyen, L. Empirical evidence of declining global vulnerability to climate-related hazards. Glob. Environ. Chang. 2019, 57. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Forzieri, G.; Bianchi, A.; Silva, F.P.; Herrerad, M.A.M.; Lebloise, A.; Lavallec, C.; Jeroen, C.J.H.; Aertsf, J.C.J.H.; Feyenh, L. Escalating impacts of climate extremes on critical infrastructures in Europe. Glob. Environ. Chang. 2018, 48, 97–107. [Google Scholar] [CrossRef]
- Gill, J.C.; Malamud, B.D. Hazard interactions and interaction networks (cascades) within multi-hazard methodologies. Earth Syst. Dyn. 2016, 7. [Google Scholar] [CrossRef] [Green Version]
- Krausmann, E.; Cruz, A.M.; Salzano, E. Natech Risk Assessment and Management: Reducing the Risk of Natural-Hazard Impact on Hazardous Installations; Elsevier: Amsterdam, The Netherlands, 2016; ISBN 9780128038796. [Google Scholar]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]



| Location | Sites | L-CV | L-Skewness | L-Kurtosis | Length | Reference |
|---|---|---|---|---|---|---|
| Iran (southwestern) | 154 | 0.130–0.600 | −0.180–0.750 | 0.050–0.700 | 10–52 | [41] |
| World | 15,137 | N.A. | −0.160–0.760 | −0.060–0.730 | 40–163 | [40] |
| Saudi Arabia (Medina Region) | 20 | 0.294–0.442 | 0.118–0.376 | 0.033–0.338 | 28–50 | [42] |
| Turkey (Cekerek watershed) | 17 | 0.133–0.205 | −0.083–0.468 | −0.029–0.453 | 11–76 | [43] |
| Pakistan (east-northeast) | 23 | 0.168–0.429 | 0.095–0.487 | 0.043–0.381 | 24–60 | [44] |
| Malaysia (West Coast) | 30 | 0.142–0.267 | 0.046–0.447 | 0.096–0.382 | 33–38 | [45] |
| Italy (Sicily) | 124 | 0.240 | 0.244 | 0.168 | >20 | [46] |
| Location(s) | Sites | L-CV | L-Skewness | L-Kurtosis | Length | Reference |
|---|---|---|---|---|---|---|
| India (Kerala) | 43 | 0.125–0.530 | −0.013–0.581 | 0.003–0.400 | 13–47 | [51] |
| Pakistan (Punjab) | 7 | 0.351–0.453 | 0.242–0.457 | 0.063–0.355 | 36–85 | [52] |
| Iran (Karkheh watershed) | 42 | 0.272–0.501 | 0.001–0.575 | −0.048–0.381 | 13–43 | [53] |
| Italia (Sicily) | 55 | 0.202–0.871 | −0.169–0.854 | −0.010–0.818 | 10–64 | [54] |
| New Zealand (South Canterbury and West Coast) | 20 | 0.081–0.560 | −0.171–0.640 | −0.065–0.511 | 11–52 | [55] |
| Italy, Austria, Slovakia | 1132 | 0.015–0.769 | −0.121–0.773 | −0.158–0.713 | 9–182 | [56] |
| Turkey | 543 | 0.100–0.600 | −0.050–0.600 | 0.000–0.400 | 15–57 | [57] |
| Australia | 61 | 0.160–0.646 | −0.192–0.586 | −0.058–0.536 | 21–72 | [58] |
| Location | Sites | L-CV | L-Skew | L-Kurtosis | Length | Reference |
|---|---|---|---|---|---|---|
| Pakistan | 9 | 0.061–0.145 | −0.250–0.283 | 0.080–0.326 | 7–25 | [68] |
| Iran | 19 | 0.100–0.320 | 0.030–0.700 | 0.080–0.660 | 17–53 | [69] |
| United States | 6 | 0.0958–0.1821 | 0.0406–0.5107 | 0.0838–0.3150 | 19–35 | [33] |
| Canada | 235 | 0.030–0.160 | −0.220–0.350 | −0.040–0.400 | >17 | [64] |
| L-CV | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | ||
| ε | −0.5 | 0.201 | 0.422 | 0.655 | 0.934 | 1.233 | 1.568 | 1.945 | 2.373 |
| 0 | 0.157 | 0.341 | 0.577 | 0.865 | 1.236 | 1.730 | 2.421 | 3.457 | |
| +0.5 | 0.076 | 0.172 | 0.298 | 0.470 | 0.718 | 1.108 | 1.809 | 3.442 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gioia, A.; Bruno, M.F.; Totaro, V.; Iacobellis, V. Parametric Assessment of Trend Test Power in a Changing Environment. Sustainability 2020, 12, 3889. https://doi.org/10.3390/su12093889
Gioia A, Bruno MF, Totaro V, Iacobellis V. Parametric Assessment of Trend Test Power in a Changing Environment. Sustainability. 2020; 12(9):3889. https://doi.org/10.3390/su12093889
Chicago/Turabian StyleGioia, Andrea, Maria Francesca Bruno, Vincenzo Totaro, and Vito Iacobellis. 2020. "Parametric Assessment of Trend Test Power in a Changing Environment" Sustainability 12, no. 9: 3889. https://doi.org/10.3390/su12093889
APA StyleGioia, A., Bruno, M. F., Totaro, V., & Iacobellis, V. (2020). Parametric Assessment of Trend Test Power in a Changing Environment. Sustainability, 12(9), 3889. https://doi.org/10.3390/su12093889







