Experiments on Fiber Concrete Foundation Slabs in Interaction with the Subsoil

Abstract

This article focuses on researching the interactions of fiber concrete slabs with subsoil. The experimental series includes four slabs made of fiber concrete with different dosages of fibers, from 0 to 75 kg/m³. The slabs were exposed to a loading test on a specialized loading frame. The laboratory tests for detailed descriptions of the fiber concrete’s mechanical properties were also an integral part of the experiments, including tests of the compressive strength, the modulus of elasticity, and split and bending tensile strength. Each slab’s deformation in a particular load step was evaluated in two-dimensional (2D) sections based on data measured with displacement sensors and in three-dimensional (3D) charts with the use of interpolation.

1. Introduction

Sustainable development in structural engineering goes hand in hand with investigations into new structural arrangements and the utilization of innovative materials, such as fiber concrete [1,2,3]. Dispersed reinforcement can be meaningful not only for structural serviceability but also for load bearing capacity. Fiber concrete utilization could contribute to higher sustainability with increased structural durability. The optimization of the concrete mixture’s composition and the dispersed reinforcement dosage is very important not only from the perspective of structural reliability but also from an economic point of view. Improved material characteristics enable the optimization of structural element dimensions and an increase in load capacity [4,5].

The common applications of fiber concrete include industrial floors [6,7] and universal slabs exposed to point or linear mechanical loads in interaction with the subsoil, with prospective punching failure [8,9,10] or general shear failure [11,12]. The design of fiber concrete slabs requires comprehensive knowledge of the input parameters [13,14], especially the mechanical properties determined by specialized laboratory tests.

The high number of fiber concrete types leads to a wide variety of mechanical properties and shapes in load–displacement diagrams, as shown in Figure 1. Material properties are influenced by the type, shape, and amount of fibers, as well as by the concrete mixture [15,16,17,18]. The multitude of fiber concrete variants usually necessitates individual structural analyses for particular tasks.

Numerical modelling, especially non-linear analysis with the utilization of a finite element method [19,20,21], is an up-to-date and effective tool for structural design optimization. A wider application of numerical modelling in common structural design is limited by our insufficient knowledge of mechanical properties as input parameters for non-linear material models. From this point of view, material characteristics are very important—not only compressive strength but also the modulus of elasticity and split tensile strength. Specific input parameters also include bending tensile strength, fracture energy, and load–displacement diagrams. These material properties can also be determined on the basis of compressive strength. Nevertheless, the accuracy of material properties determined in this way is often inadequate for non-linear numerical analysis. Laboratory testing of fiber concrete is demanding and frequently involves a wide scatter of measured data. A specific issue is the testing of tensile strength and fracture energy [22,23]. Therefore, in the presented research, we performed an extensive and comprehensive series of laboratory tests (Figure 2).

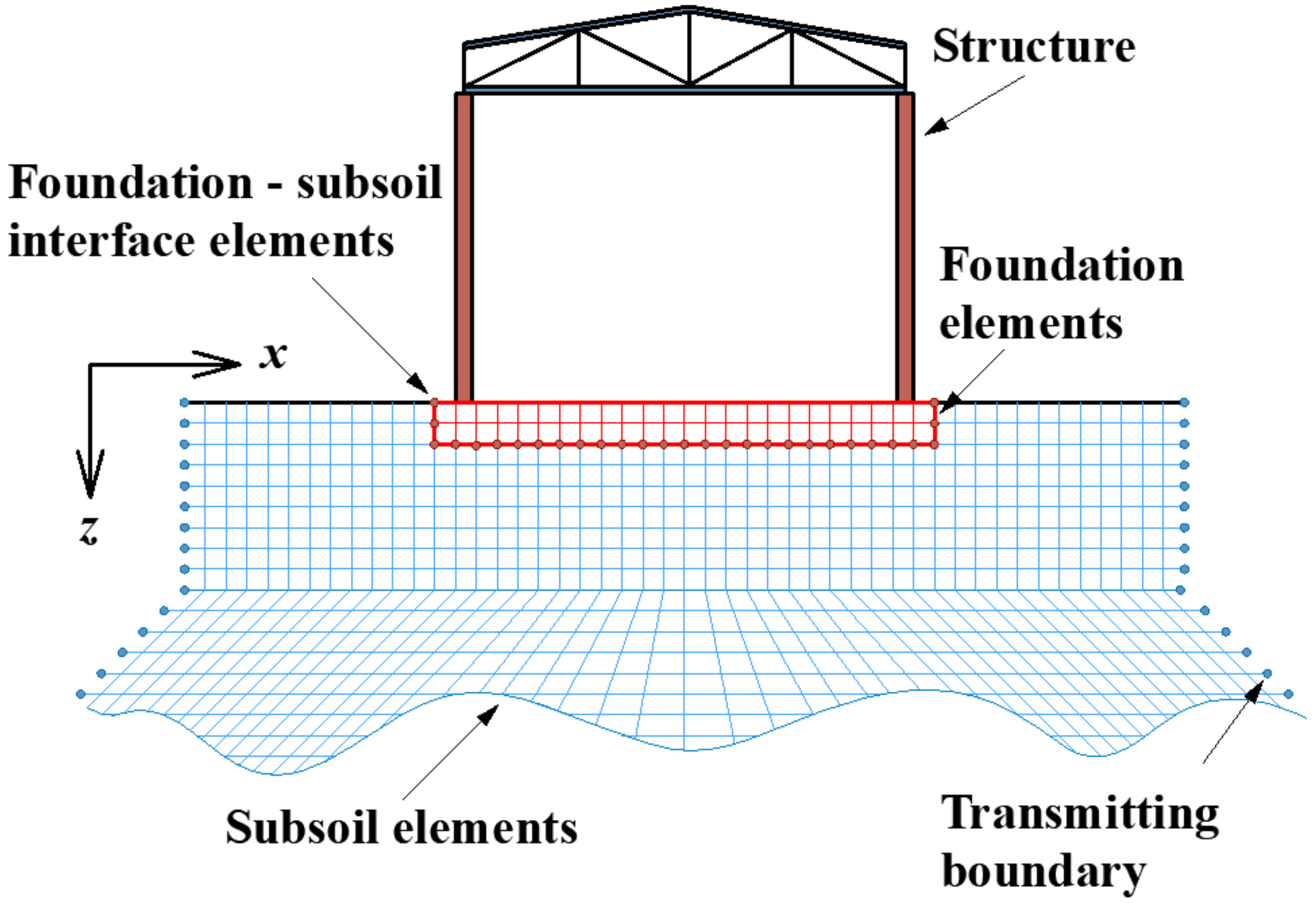
Another aspect of advanced numerical modelling is soil–structure interactions (Figure 3). The interaction model is divided into three parts: Subsoil, foundation structure, and over-ground load-bearing structure. It is necessary to consider the subsoil model and its stiffness [24,25], as well as the modelling of the surface between the subsoil and the foundation’s structure. The interaction of fiber concrete foundation slab with the subsoil connects two disciplines: The design of concrete structures and soil mechanics [26,27,28].

The application of fiber concrete as a load bearing material is still an objective of contemporary research. Previous studies also explore the use of fiber concrete slabs on the ground [29,30]. The design of a foundation slab requires not only its load capacity in bending but also its shear resistance and specific punching [31,32,33] or deformations [34].

Load tests of structural elements or their parts, together with laboratory testing of material characteristics, provide very valuable knowledge about material behaviors in real structures, such as bending and shear load capacity [35,36,37], and can help with numerical analysis specifications (Figure 2).

The aim of this paper is to evaluate the benefits of using fiber concrete in structural slab elements based on interactions with the subsoil. Experimental loading tests of structural elements are complemented with extensive laboratory testing of the material’s mechanical properties. The loading tests of the slabs were performed on specialized testing equipment, and evaluation of the achieved deformation is expressed using three-dimensional (3D) charts. Detailed knowledge of these mechanical properties enables more advanced numerical modelling of the experiment with respect to the non-linear behavioral characteristics of concrete.

2. Fiber Concrete

Within the experimental program, identical types of fiber were used in all test samples: Cold-strained steel fibers (3D DRAMIX 65/60BG) [38] (Figure 4). The fiber dosage was 25 kg/m³, 50 kg/m³, and 75 kg/m³. A reference variant slab without fibers was also made. The same concrete mixture was used for all fiber dosages; the basic parameters are shown in

Table 1. Material composition and properties of the concrete mixture.

Material Composition	Values
Consistency	S3
Cement	CEM I 42.5 R
Maximum aggregate size	16 mm
Minimum content of cement	300 kg
Water–cement ratio: w/c	0.6
Aggregates 0/4 (mined)	870 kg
Aggregates 4/8 (mined)	150 kg
Aggregates 8/16 (mined)	820 kg
Water	189 l
Plasticizer	2.9 l

. The maximum water–cement ratio was w/c = 0.6, and the minimum cement content was 300 kg/m³. CEM I 42.5 R cement was used, with a maximum grain size of 16 mm. The fiber’s material characteristics are provided in

Table 2. Material characteristics of the Dramix 3D 65/60 BG fibers.

Dramix 3D 65/60 BG	Values
Tensile strength: Rm,nom	1.160 N/mm; Tolerances: ±7.5% Avg
Modulus of elasticity:	±210.000 N/mm2
Amounts	3.200 Fibers/kg
Length	60 mm
Diameter	0.9 mm

.

The configuration of each of the tests is shown in Figure 2, and the detailed configuration of the bending tests is shown Figure 5. The selected laboratory tests are commonly performed and are mostly standardized tests. The research program included the following laboratory tests:

• Test of the compressive strength on cubes (150 mm × 150 mm × 150 mm),
• Test of the compressive strength on a cylinder (150 mm × 300 mm),
• Test of the split tensile strength on cubes (150 mm × 150 mm × 150 mm),
• Three-point bending test with a 50 mm notch—3B600 (cross section 150 mm × 150 mm),
• Three-point bending test without a notch—3B500 (cross section 150 mm × 150 mm),
• Four-point bending test without a notch—4B600 (cross section 150 mm × 150 mm),
• Four-point bending test without a notch—4B500 (cross section 150 mm × 150 mm).

Testing the concrete cube and cylinder’s compressive strength was done using basic standard tests made for the material classification and evaluation of increased strength with an increased dosage of fibers. In this loading test of the slab element, the tensile strength is critical, which is why the element was tested carefully. The tensile strength was tested via two types of tests: One for split tensile strength and one for bending tensile strength.

For the bending tensile strength test, a detailed analysis was performed. Three and four-point bending tests were performed. For the three-point bending with notch variant, the notch predicts the place of specimen failure, while the failure of specimens without a notch is located near the midspan in an area with low fiber concentration. The position of the loading forces in the four-point bending test enables evaluation of the bending tensile strength without shear effect.

2.1. Concrete Compressive Strength

The concrete’s compressive strength is one of its basic mechanical properties. Compressive strength was determined on cube specimens with dimensions of 150 × 150 × 150 mm or cylinder specimens with diameters of 150 mm and height 300 mm. In each series, six cube specimens and three cylinder specimens were tested to enable a wider evaluation of the measured values.

Table 3. Compressive strength—cube and cylinder specimens.

Fibers [kg/m3]	Sample Type	Number of Samples	Average Weight [kg]	Average Compressive Strength [MPa]	Standard Deviation [MPa]	Coefficient of Variation [%]
0	Cube	6	7.586	25.11	0.945	3.8
	Cylinder	3	11.586	20.03	0.411	2.1
25	Cube	6	7.744	34.96	1.417	4.1
	Cylinder	3	12.092	29.28	0.846	2.9
50	Cube	6	7.854	31.65	0.942	3.0
	Cylinder	3	11.957	25.27	2.012	8.0
75	Cube	6	7.794	27.87	0.864	3.1
	Cylinder	3	12.289	24.90	1.007	4.0

provides the mean values of the measured compressive strength for the cubes and cylinders. Data are presented with the mean value of the specimen weight.

2.2. Split Tensile Strength of Concrete

Split tensile strength is one of the most widely used methods of concrete tensile strength testing. It is possible to use cube or cylindrical specimens for this test. Considering the capacity and testing equipment of the laboratory, cube specimens were used for the split tensile strength testing. The resulting split tensile strength was determined according to the following formula:

$$f_{ct,sp}=\frac{2.P_{\max }}{\pi .l.d}$$

(1)

where P_max is the maximum load, l is the length of the touch line along the specimen’s body, and d is the selected transverse dimension of the specimen. The resulting evaluations of the tests on split tensile strength are shown in

Table 4. Split tensile strength.

Fibers [kg/m3]	Number of Samples	Average Weight [kg]	Average Split Tensile Strength [MPa]	Standard Deviation [MPa]	Coefficient of Variation [%]
0	6	7.518	2.10	0.281	13.4
25	6	7.818	2.96	0.223	7.5
50	6	7.788	3.12	0.210	6.7
75	6	7.794	3.17	0.593	18.7

.

An increase of about 1 MPa in the split tensile strength of the samples containing fibers is apparent from the test results. This is about a 50% increase compared to the samples without fibers. The increase in the tensile strength of the samples with different amounts of fibers is small. The values of the split tensile strength for the fiber concrete range from 2.96 to 3.17 MPa.

2.3. Three-Point and Four-Point Bending Test

Common tests of tensile strength include three-point and four-point bending tests. There are different configurations for these tests, which mainly differ in the span of supports, the position of the load, and the depth of the notch. In the experimental program, we selected four variants of bending tests, and each test was carried out for two samples. The calculation of the tensile strength is affected by the assumption of stress distribution within the cross section and the nonlinear behavior of the concrete. Concrete plasticization and formation of micro-cracks has to be taken into consideration. The tensile strength of the concrete based on the three-point bending test can be calculated using the following relation:

$$f_{ct,fl,3B}=\frac{3P_{\max }L}{2b{\left(h-a_0\right)}^2}$$

(2)

where P_max is the maximum load, L is the span of the specimen, b and h are the specimen cross-section dimensions, and a₀ is the height of the notch.

Two variants of the tests were carried out. The test of specimens with a nominal size of 150 × 150 × 700 mm, a span of 600 mm, and a notch of 50 mm is indicated as 3B600. In this test, the position failure crack is localized at the notch. The test of the specimen without a notch with a nominal size of 150 × 150 × 600 mm and a span of 500 mm is indicated as 3B500. The failure crack is located near the specimen’s midspan in the place with the weakest strength. The test schemes of the three-point and four-point bending tests are shown in Figure 5. The test results are shown in

Table 5. Bending tensile strength [MPa].

Specification	Position of the Load	Notch a0	Span L	Amount of Fibers [kg/m3]
	[mm]	[mm]	[mm]	0	25	50	75
3B500	250/250	-	500	3.02 ± 0.02	4.04 ± 0.03	4.41 ± 0.10	4.72 ± 0.20
3B600	300/300	50	600	2.89 ± 0.10	3.81 ± 0.14	4.24 ± 0.09	5.16 ± 0.21
4B600	200/200/200	-	600	2.55 ± 0.20	3.10 ± 0.35	3.56 ± 0.13	4.35 ± 0.74
4B500	175/150/175	-	500	2.85 ± 0.04	3.76 ± 0.18	4.06 ± 0.11	4.95 ± 0.10

.

Within the experimental program, two variants of four-point bending tests were carried out. The test indicated as 4B600 was calibrated for the specimen with a nominal size of 150 × 150 × 700 mm, a span between supports of 600 mm, and a distance between the supports and loading forces of 200 mm. The second variant of the four-point bending test, indicated as 4B500, was calibrated for the specimen with a nominal size of 150 × 150 × 600 mm and a span between supports of 500 mm. This test differs from the previous one by the position of the loading forces (Figure 5).

The tensile strength in bending, determined by the 4B600 test, was calculated using Equation (3). The bending tensile strength based on the 4B500 test was calculated according to the more complex Formula (4). The load–displacement diagrams of the bending tests are presented in Figure 6. The test results are presented in Table 5 and Figure 7.

$$f_{ct,fl,4B}=\frac{P_{\max }L}{b{h}^2}$$

(3)

$$f_{ct,fl,4B}=\frac{6P_{\max }e}{2b{h}^2}$$

(4)

where P_max is the maximum load, L is the span of the specimen, b and h are the specimen’s cross-sectional dimensions, and e is the distance between the support and force.

2.4. Concrete Tensile Strength

Testing of the uniaxial tensile strength is demanding, and there is often a large dispersion of the measured values. This test is sensitive to boundary conditions, particularly the fixing and fastening of the tested specimen.

The axial concrete tensile strength f_ct is required as a fundamental input for advanced numerical simulations and analyses. The axial tensile strength is calculated by the split tensile strength and the bending tensile strength according to the known relations, which are verified using many experiments. The split tensile strength uses relation (5), and the bending tensile strength uses Formula (6):

$$f_{ct,sp}=\left(1.1\approx 1.25\right)f_{ct},$$

(5)

$$f_{ct,fl}=\left(1.5\approx 1.75\right)f_{ct}.$$

(6)

For concrete with a lower compressive strength, it is recommended to choose a lower value of particular coefficients. In this paper, coefficient 1.1 was chosen for the calculations based on f_ct,sp and coefficient 1.5 was chosen for f_ct,fl.

Subsequently, it is possible to establish a functional dependence between the amount of wires and the axial tensile strength based on the three-point bending test:

$$f_{ct,3B}=0.0169x+2.0557\left[MPa\right],\left(R^2=0.9694\right).$$

(7)

Similarly, functional dependence is also based on the four-point bending test:

$$f_{ct,4B}=0.0166x+1.8089\left[MPa\right],\left(R^2=0.9816\right).$$

(8)

Using all types of tensile strength tests, it is possible to determine the resulting functional dependence for axial tensile strength (9) (Figure 7):

$$f_{ct}=0.0159x+1.970\left[MPa\right],\left(R^2=0.9686\right).$$

(9)

3. Load Test of the Fiber Concrete Slabs on Subsoil

The experimental program included a load test of four fiber concrete slabs of identical size with different dosages of fibers. The load tests were carried out on a specialized load frame (Figure 8). The slab indicated as G01 was free of fibers (or 0 kg/m³), the slab indicated as G02 was made of fiber concrete with a dosage of 25 kg/m³, the slab indicated as G03 included 50 kg/m³ of fibers, and the slab indicated as G04 included 75 kg/m³ of fibers. The nominal slab dimensions were 2000 × 2000 × 150 mm (see Figure 9). The slabs were placed on the subsoil, which was modified prior to realization of the whole set of load tests. Before the experimental load tests, geotechnical testing was performed to acquire the material properties of the homogenized subsoil. The soil was classified as CI—clay with medium plasticity. From the static load test, the modulus of deformation value E_def = 12.5 MPa was acquired. The box shear test determined the value of consistency c = 9.0 kPa and the internal friction angle φ = 19.3°.

The load was gradually applied through a steel plate with dimensions of 400 × 400 mm in loading steps until slab failure (see Figure 9). The load steps for slab G01 were 25 kN/30 min, and those for slabs G02, G03, and G04 were 75 kN/30 min. In the course of testing, slab deformation was measured by 16 deformation sensors with an accuracy of 0.01 mm. A diagram of the regular arrangement of deformation sensors is shown in Figure 10.

Concrete slab G01 was made of plain concrete, so it was loaded in smaller load steps (25 kN/30 min). The maximum load at the moment of its failure was 345 kN. A load-time diagram of the loading test is provided in Figure 11. The value of the failure/load capacity of the slab is presumed to be the force at which the deformation increases, thereby making the pressure in the hydraulic cylinder drop rapidly (see Figure 11).

All other slabs were loaded with loading steps of 75 kN/30 min. The load diagram shows the apparent effects of the volume of fibers on the total load capacity of the fiber concrete slab. The load capacity of slab G02 is 542 kN, that of slab G03 is 640 kN, and that of slab G04 is 752 kN.

As expected, the maximum load capacity of the slabs gradually increased in dependence according to the dosage of fibers. Using 25 kg/m³ of fibers in the concrete, the total load capacity increased by 200 kN compared with the plain concrete slab—i.e., by nearly 60%. By increasing the fiber content to 50 kg/m³, the load capacity of the concrete slab increased by up to 85% compared with the plain concrete slab. The further addition of fibers (75 kg/m³) increased the load capacity of the concrete slab by nearly 120%.

4. Analysis of Slab Deformation

The diagrams in Figure 12, Figure 13, Figure 14 and Figure 15 show the course of deformations in the cross section of the four slabs, G01 to G04. The measured deformation for the particular load steps of slab G01 made of plain concrete is provided in Figure 12. The course of deformation occurs in the slab section that corresponds to the position of displacement sensors 05 to 08 (see Figure 10a). The maximum measured positive deformation was 16.06 mm (sensor 06), and the maximum negative deformation was 17.72 mm (sensor 05).

The measured deformation for the particular load steps of slab G02 made of fiber concrete with a 25 kg/m³ dosage of fibers is shown in Figure 13. The course of deformation occurs in the slab section that corresponds to the position of displacement sensors 04 to 08 (see Figure 10b). The maximum measured positive deformation was 32.01 mm (sensor 06), and the maximum negative deformation was 11.67 mm (sensor 04).

The measured deformation for particular load steps of slab G03 made of fiber concrete with a 50 kg/m³ dosage of fibers is shown in Figure 14. The course of deformation occurs in the slab section that corresponds to the position of displacement sensors 04 to 08 (see Figure 10b). The maximum measured positive deformation was 31.22 mm (sensor 06), and the maximum negative deformation was 9.43 mm (sensor 04).

The measured deformation for the particular load steps of slab G04 made of fiber concrete with a 75 kg/m³ dosage of fibers is shown in Figure 15. The course of deformation occurs in the slab section that corresponds to the position of displacement sensors 04 to 08 (see Figure 10b). The maximum measured positive deformation was 37.28 mm (sensor 06), and the maximum negative deformation was 5.81 mm (sensor 08).

The following diagrams compare the deformation of all four slabs in each particular load step. The individual diagrams in Figure 16 and Figures 18–20 compare the deformation of the concrete slabs for loading forces of 150 kN, 225 kN, 300 kN, and 450 kN. Deformation is compared in the section that corresponds with the position of the displacement sensors—i.e., for the concrete slab G01, sensors 05, 06, 07, and 08 are indicated in Figure 10a, and for the fiber concrete slabs G02, G03, and G04, sensors 04, 05, 06, 07, and 08 are indicated in Figure 10b.

Figure 16 shows a comparison of the deformation measured in the second load step, which responds to a loading force 150 kN. Here, there are noticeable positive and negative deformations of slab G01 made of plain concrete. Vertical cracks already appeared in this load step, and they progressed gradually from the lower surface to the top (Figure 17). The bending stiffness was reduced significantly. The deformation of the slabs made of fiber concrete (G02, G03, and G04) is very small in this load step. A significant occurrence of cracks was not observed. The specific measured values are ordered in

Table 6. Measured values of slab deformation for specific load steps.

Slab	Load Step [kN]
	150		225		300		375
	Deformation [mm]
	Positive	Negative	Positive	Negative	Positive	Negative	Positive	Negative
G01	5.03	2.95	7.56	4.93	13.25	12.47
G02	1.66		5.93		10.11		13.96	1.10
G03	2.30		4.25		7.11		10.22
G04	1.90		3.72		6.55		9.57

.

Figure 18 provides a comparison of the deformation measured in the third load step, which responds to a loading force of 225 kN. Here, the positive and negative deformations of slab G01 increased. The positive deformation of the slabs made of fiber concrete (G02, G03, and G04) increased in this load step, but there are still zero negative deformations. The specific measured values are ordered in Table 6.

Figure 19 provides a comparison of the deformation measured in the fourth load step, which responds to a loading force 300 kN. Very significant deformations of the slab G01 predict that the load capacity will be exceeded. The trend of deformation development of the slabs G02, G03, and G04 is the same as that in the previous load step, and there are still zero negative deformations. The specific measured values are ordered in Table 6.

Figure 20 shows a comparison of the deformation measured in the fifth load step, which responds to a loading force 450 kN. Positive deformation of the slab G02 produced noticeable values, and small negative deformation appeared. Slabs G03 and G04 retain small positive and zero negative deformations. The specific measured values are ordered in Table 6.

On the basis of the deformation measured with 16 displacement sensors, interpolation of the intermediate values was performed and processed into a 3D deformation chart. Figure 21, Figure 22, Figure 23 and Figure 24 provide charts of 3D deformation for a load force 300 kN (the fourth load step).

Figure 21 provides a 3D model of the G01 slab deformation exposed to a 300 kN load. The maximum positive deformation is 12.99 mm, and the maximum negative deformation is 40.64 mm.

Figure 22 shows a 3D model of the G02 slab deformation exposed to a 300 kN load. The maximum positive deformation is 9.91 mm, and the maximum negative deformation is 4.96 mm.

Figure 23 shows a 3D model of the G03 slab deformation exposed to a 300 kN load. The maximum positive deformation is 7.28 mm, and the maximum negative deformation is 0.85 mm.

Figure 24 shows a 3D model of the G04 slab deformation exposed to a 300 kN load. The maximum positive deformation is 6.46 mm, and negative deformation did not appear in this load step.

The maximum values of the positive deformation in the middle of the slab under particular load steps calculated using interpolation are shown in

Table 7. Loads and interpolated deformations of the slab.

Load [kN]	Interpolated Deformations in the Middle of the Slab [mm]
	G01 (345 kN)	G02 (542 kN)	G03 (640 kN)	G04 (752 kN)
150	4.81	1.58	2.35	1.9
225	7.42	5.55	4.32	3.63
300	11.16	9.55	7.05	6.33
450		18.47	13.1	12.09
Peak load	13.19	25.49	30.89	34.76

.

Figure 25 shows the gradual negative deformation with an increasing value of the loading force. The negative deformation of the slab corners for each slab is expressed with the zero deformation line for a particular load step. For the G01 slab, negative deformation appeared by the second load step (Figure 25a). Negative deformation appeared in the load step 225 kN for the G02 slab (Figure 25b) and in the load step 300 kN for the slab G03 (Figure 25c). For slab G04, negative deformation in the corners did not appear until the load step of 375 kN (Figure 25d).

5. Discussion

The cube and cylindrical compressive strength tests demonstrate the beneficial effect of the fibers. Compressive strength also depends significantly on the orientation of the fibers, and this may be one of the reasons why compressive strength decreases with the amount of fibers in some cases. This problem can also be found in other experimental programs, where the same concrete mix properties were used for a different fiber dosage. The value of the ratio between the cube and the cylindrical strength of 0.83 is in good agreement with the recommendations, which mostly cite a value of 0.85.

The split tensile tests illustrate the influence of the amount of fibers on the growth of tensile strength even when the amount of fibers is only 25 kg/m³. An overall comparison of the test results shows that the fiber concrete used in the experiments included fibers that were evenly distributed over the volume. Nevertheless, with a larger fiber amount, there is increasing dispersion in the measured values of tensile strength, especially for the mixture with a dosage of 75 kg/m³.

Experimental testing of the four slabs on the subsoil also showed the significant influence of fibers on the load capacity of the slabs. As much as 25 kg/m³ of fibers significantly increased the total load capacity of the slab, and the load capacity increased further with higher dosage of fibers.

A higher content of fibers also significantly influenced the total deformations, which are important for the serviceability limit state. The slab deformations apparent from the 3D deformation diagrams and observed during the loading test show a difference in slab deformation even with a load step of 300 kN. Slab G01 made of plain concrete showed especially significant positive and negative deformations. Vertical cracks appeared, which spread from the bottom to the upper surface and decreased the bending stiffness significantly, consequently leading to high negative deformation in the slab corners, gradually losing the entire load capacity. The deformation of the fiber concrete slabs was different. The width of the crack was smaller, and the entirety of the slab was not disrupted by the crack’s appearance, even under a higher load intensity. With a higher load intensity, the deformation increased and the bending stiffness also decreased, but the deformation was lower with a higher dosage of fibers. The dosage benefit of 75 kg/m³ of fibers compared with a dosage of 50 kg/m³ is, in this case, limited with respect to the economy and production technology.

6. Conclusions

This paper presented an integrated research program that focused on the use of fiber concrete for the specific structure of a foundation slab. The experimental program included a series of four in situ loading tests of slabs and a laboratory program for determining the mechanical properties of concrete and fiber concrete. The in situ and laboratory tests were carried out for fiber concrete with a dosage of 0, 25, 50, 75 kg/m³ of fibers. On the basis of the measured deformations, and by using interpolation, we processed illustrative charts of the 3D deformation models. The experiments proved the positive influence of fiber concrete on the increased load capacity and more favorable deformations of the slab on subsoil exposed to a vertical concentrated load.