Prediction of Potential Evapotranspiration Using Temperature-Based Heuristic Approaches

Abstract

The potential or reference evapotranspiration (ET₀) is considered as one of the fundamental variables for irrigation management, agricultural planning, and modeling different hydrological pr°Cesses, and therefore, its accurate prediction is highly essential. The study validates the feasibility of new temperature based heuristic models (i.e., group method of data handling neural network (GMDHNN), multivariate adaptive regression spline (MARS), and M5 model tree (M5Tree)) for estimating monthly ET₀. The outcomes of the newly developed models are compared with empirical formulations including Hargreaves-Samani (HS), calibrated HS, and Stephens-Stewart (SS) models based on mean absolute error (MAE), root mean square error (RMSE), and Nash-Sutcliffe efficiency. Monthly maximum and minimum temperatures (T_max and T_min) observed at two stations in Turkey are utilized as inputs for model development. In the applications, three data division scenarios are utilized and the effect of periodicity component (PC) on models’ accuracies are also examined. By importing PC into the model inputs, the RMSE accuracy of GMDHNN, MARS, and M5Tree models increased by 1.4%, 8%, and 6% in one station, respectively. The GMDHNN model with periodic input provides a superior performance to the other alternatives in both stations. The recommended model reduced the average error of MARS, M5Tree, HS, CHS, and SS models with respect to RMSE by 3.7–6.4%, 10.7–3.9%, 76–75%, 10–35%, and 0.8–17% in estimating monthly ET₀, respectively. The HS model provides the worst accuracy while the calibrated version significantly improves its accuracy. The GMDHNN, MARS, M5Tree, SS, and CHS models are also compared in estimating monthly mean ET₀. The GMDHNN generally gave the best accuracy while the CHS provides considerably over/under-estimations. The study indicated that the only one data splitting scenario may mislead the modeler and for better validation of the heuristic methods, more data splitting scenarios should be applied.

1. Introduction

Reference evapotranspiration (ET₀) is one of the major components in the hydrological cycle [1]. It contributes to a rationale water resources management [2,3], and it is important in agriculture for measuring crop water requirement quantification [4]. In addition, ET₀ is used as inputs for several hydrological models, and adopted for climate change studies [5]. Several empirical and semi-empirical methods have been developed at different time scales for ET₀ prediction. The performance of the methods varies with respect to the meteorological variables included in the methods, ranging from temperature based, radiation based, and combination methods [6]. One of the earliest methodologies, the ET0 calculated using the standards FAO56 Penman-Monteith, has been adopted as a reference approach [7]. However, ET0 can be measured directly using lysimeters [2]. Measurement of ET0 is varied from one region to another and that is totally based on the regional climate characteristics [8]. Hence, empirical formulation is demonstrated as a remarkable limitation on the ET0 estimation. During the last few decades, models based on computer aid capacity indicated a distinguished progress in the hydrology and water resources fields [9,10,11,12,13]. Artificial intelligence (AI) models have been extensively applied as a reliable soft computing technology for ET0 estimation based on the available and measured climatic variables [14,15,16].

A review of the literature indicates that numerous studies have examined the application of several AI models for estimating ET₀ [17,18,19,20,21,22,23,24,25,26,27,28]. In more detailed state-of-the-art, Yin et al. [26] introduced a new hybrid AI model dependent on the hybridization of a genetic algorithm with a kernel model i.e., a support vector machine (GA-SVM) for modeling daily ET₀ in China using several daily climatic variables including T_max, T_min, wind speed (U₂), relative humidity (RH), and solar radiation (SR). Compared to classical an artificial neural network (ANN) and the SVM models, the scholars demonstrated the superiority of the GA-SVM in predicting ET₀. Jovic et al. [17] proposed a hybrid method called genetic programming (GP) for estimating ET₀ using eight climatic variables. Mattar [20] applied gene expression programming (GEP) for modeling monthly ET₀ in Egypt, using five input variables T_max, T_min, RH, U₂ and Rs. Tao et al. [25] introduced a hybrid method called adaptive neuro-fuzzy inference systems (ANFIS) with a firefly algorithm (FA) (ANFIS-FA) for modeling daily ET₀ at Burkina Faso. Using six input variables namely, T_max, T_min, maximum relative humidity (RH_max), Rs, U₂, and vapor pressure deficit (VP), the authors demonstrated that the FA significantly increased the exactness of the ANFIS method, and that the hybrid ANFIS-FA provided high accuracy with a determination coefficient (R²) nearly equal to 0.97 compared to a R² of 0.91 obtained using standard ANFIS. Using data from India, Adamala [27] compared four models in predicting daily ET₀, using fewer inputs variables: T_max, T_min, and extra-terrestrial radiation (Ra). The applied models were a wavelet neural network (W-ANN), ANN, multi linear regression (MLR), and wavelet linear regression (W-MLR). The authors reported that decomposition of the input variables applying wavelet transform significantly improved the performance of the models with Nash-Sutcliffe efficiency (NSE) equal to 0.82. Using T_max, T_min, RH, U₂, Rs, and sunshine hours (SH), Gavili et al. [28] demonstrated that ANN model was better than GEP and ANFIS for predicting monthly ET₀ in Iran, with a NSE value that reached 0.98 during the testing phase for all tested stations. Khoshravesh et al. [19] compared three regression methods, namely multivariate fractional polynomial (MFP), Bayesian (BR), and robust regressions (RBR) for modeling monthly ET₀ in Iran, using T_max, T_min, mean temperature (T_mean), and Rs. Karbasi [29] built a new Gaussian process regression (GPR) for forecasting daily ET₀ several days in advance and demonstrated that the use of wavelet decomposition significantly increased the abilities of the methods and the RMSE dropped from 0.816 mm to 0.068 mm.

Among several machine learning models explored over the literature, the group method of data handling type neural network (GMDHNN) is an dependent on the Rosenblatt’s perceptron method introduced by Farlow [30]. GMDHNN is successfully applied in diverse engineering applications [31,32,33,34]. Within hydrology and water resources related research, Najafzadeh et al. [35] developed the GMDHNN model for scour depth (SD) of pipelines estimation due to waves variability; the prediction of local SD at bridge abutments in coarse sediments with thinly armored beds was conducted by Najafzadeh et al. [36]; simulation of flow discharge of straight compound channels was reported by Najafzadeh and Zahiri [37]; prediction of significant wave height was established by Shahabi et al. [38]; prediction of turbidity considering daily rainfall and discharge data was determined by Tsai and Yen [39]; an improved modeling of the discharge coefficient for triangular labyrinth lateral weirs was described by Parsaie and Haghiabi [40]; an evaluation of treated water quality in a water treatment plant was carried out by Alitaleshi and Daghbandan [41]; a prediction of turbidity and the free residual aluminum of drinking water was tested by Daghbandan et al. [42]. Based on the reported literature review, only one study reported the implementation of the GMDHNN ET₀ modeling developed by da Silva Carvalho and Delgado [43]. The study conducted based on the calculated FAO56 Penman-Monteith using only previous values and very limited data of daily scale over three years (January 2011 to January 2014), were utilized for the modeling development.

Multivariate adaptive regression splines (MARS) model introduced by Friedman [44], and M5 tree (M5Tree) model established developed by Quinlan [45]. They are another distinguished category of a data driven model, which is mainly used in environmental, hydrology, irrigation, and hydraulic studies. The MARS model is one of the sophisticated AI models, as it has the ability to provide a non-parametric feature that is able to identify the actual relationship between predictors and predicted using splines method for detecting the nonlinearity pattern [46]. The MARS model has been successfully applied in many hydrological applications [47,48,49,50,51,52]. The MARS model was successfully used to predict water pollution by Kisi and Parmar [47], to forecast sediment load by Adnan et al. [48], to model daily streamflow by Yin et al. [49], to predict evaporation by Ghaemi et al., [50], and to predict monthly river flow by Adnan et al. [51].

However, fewer applications related to the ET₀ modeling can be seen in the related literature. For instance, Mehdizadeh et al. [53] compared MARS, SVM, and GEP for modeling monthly ET₀ in Iran, using several climatic variables as inputs: T_max, T_min, T_mean, RH, U₂, VP, Ra, Rs, and Rn. The authors have compared several scenarios, namely temperature-based, radiation-based, mass transfer-based, and meteorological parameters-based scenarios. For the temperature-based scenarios, using only T_max, T_min, and Ra, the research finding approved the potential of MARS model over the SVM and GEP with a R² equal to 0.944 in the validation phase. Mehdizadeh et al. [22] investigated the capacity of MARS and GEP models for estimating daily ET₀ in Iran using four climatic variables: T_mean, RH, U₂, and Rs. The author demonstrated that the MARS model performed the best using all climate variables with a R² nearly equal to 0.99 in the validation phase. Using four climatic variables, namely, T_mean, RH, U₂, and Rs, Kisi [54] compared MARS, M5Tree and least square support vector machines (LSSVM) for modeling monthly ET₀ in Turkey. The authors demonstrated that in some cases, MARS is superior over the two others in terms of performance accuracy. Keshtegar et al., [55] and Keshtegar and Kisi, [56] applied the M5Tree, ANFIS, and ANN for modeling daily ET₀ in Turkey, using T_mean, RH, U₂, and Rs as input variables. Kisi and Kilic [57] compared M5Tree and ANN for modeling daily ET₀ in USA, using T_mean, RH, U₂, and Rs. Rahimikhoob [58] compared M5Tree and ANN for modeling monthly ET₀ in USA, using T_mean, RH, U₂, and Ra, in Iran. The authors reported that both methods produced almost similar estimates with smaller differences.

The majority of the aforementioned studies have been conducted using several input variables. With the exception of the investigation by Mehdizadeh et al. [53], in which the MARS model was applied for modeling ET₀ using only temperature data as inputs, there are limited studies that have applied MARS and M5Tree models for ET₀ utilizing only temperature inputs. Hence, the major objective of the present investigation was to assess the performances of GMDHNN, MARS, and M5Tree models to estimate ET₀ using only temperature and extra-terrestrial radiation and validating the results against the empirical formulations (i.e., HS, CHS and SS). The main motivation of the current study is using specific climate data (temperature) to simulate the ET₀, as this involves highly essential and significant factors influencing ET₀, while recording of such data for long durations is an easy task in developing countries. The other difference of this study compared to previous ones is the use of different data splitting scenarios and the inclusion of periodicity (month number of the year) as an input to the GMDHNN, MARS, and M5Tree models.

2. Materials and Methods

2.1. Case Study

In the present study, monthly maximum and minimum temperatures (T_max and T_min), solar radiation, relative humidity, and wind speed measured at Adana (latitude 37°00′ N, longitude 35°19′ E, altitude 27 m) and Antakya (latitude 36°33′ N, longitude 36°30′ E, altitude 100 m) stations in the Mediterranean Region of Turkey were utilized. The stations operated by the Turkish Meteorological Organization can be observed from Figure 1. The data periods used for the Adana and Antakya are 1968–2015 and 1983–2010, respectively. The statistical parameters of the data employed in the applications are summed up in

Table 1. The statistical parameters of climatic data used in the study.

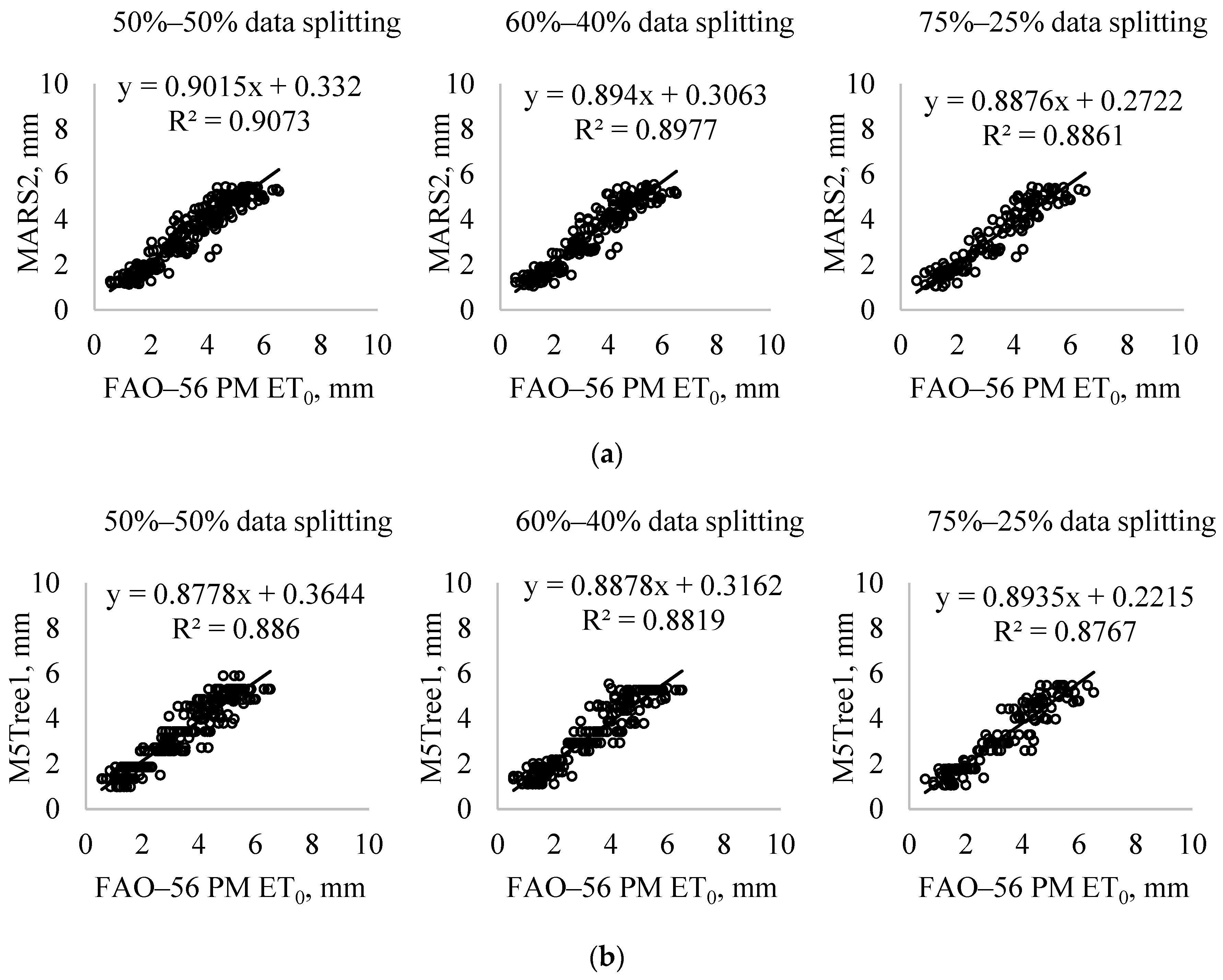
Station	Variable	xmin	xmax	xmean	Sx	Csx	Correlation with ET0
Adana	Tmin (°C)	−3.4	23.4	9.33	7.70	0.08	0.828
	Tmax (°C)	17.0	44.0	31.3	7.02	−0.41	0.850
	Ra (MJ/m2)	15.5	41.7	29.4	9.35	−0.14	0.920
	ET0 (mm)	0.57	6.52	3.32	1.52	0.04	1.000
Antakya	Tmin (°C)	−4.6	24.8	9.18	8.16	0.22	0.860
	Tmax (°C)	14.4	42.6	28.8	7.64	−0.32	0.878
	Ra (MJ/m2)	16.0	41.6	29.5	9.16	−0.11	0.926
	ET0 (mm)	0.28	7.20	3.39	1.86	0.06	1.000

T_min, T_max, R_a, and ET₀ are minimum and maximum temperatures, extraterrestrial radiation, and reference evapotranspiration, respectively. x_min, x_max, x_mean, S_x, and C_sx are minimum, maximum, mean, standard deviation, and skewness, respectively.

. R_a has the highest correlation with ET₀ followed by the T_min and T_max and R_a has a higher correlation with ET₀ in Antakya compared to Adana. It is also visible from Table 1 that ET₀ in Adana is higher than for Antakya.

2.2. Group Method of Data Handling Type Neural Network

GMDHNN is a powerful machine learning tool based upon the principle of termination. In this principle, the system follows the one process through data importing, rearing, hybridizing, choice, and rejection. The GMDH algorithm is divided into two parts: one is the parameter and other is the non-parameter. If the variance is low, then parametric algorithms provide the best results and for high variance, non-parametric algorithms perform better. The GMDHNN model is capable of handling the multiple input variables and provides single output. There are different layers in the GMDHNN model, which have a set of neurons; these neurons are further linked with quadratic polynomial in every layer, which provides the new neurons for the next layer [59,60,61]. The output of the database with multiple input variables and M numbers of observations is defined as below.

$$m_i=f\left(y_{i,1},y_{i,2},y_{i,3},\dots ,y_{i,M}\right) (i=1,2,3,4,\dots ,N)$$

(1)

Here, $\left(y_1,y_2,y_3,y_4,\dots ,y_M\right)$ is the real input of the mapping f and $m_i$ is the real output based upon the real input. For the identification of the problem, $\widehat{f}$ is considered as mapping instead of $f$ to forecast the $\widehat{m}$ (output value) instead of m, and this $\widehat{m}$ is close to m. The provided input $\left(y_1,y_2,y_3,y_4,\dots ,y_M\right)$ is used for the GMDHNN training to attain the output ${\widehat{m}}_i$ as given below.

$${\widehat{m}}_i=\widehat{f}\left(y_{i,1},y_{i,2},y_{i,3},\dots ,y_{i,M}\right) \left(i=1,2,3, \dots , N\right)$$

(2)

The GMDH-NN algorithm is working to minimize the MSE (mean square error) for making the model most effective for prediction. This MSE is calculated as E below to make the error level reach its minimum.

$$\langle E=\left\{{\displaystyle \sum }_{i=1}^N{\left[\widehat{f}\left(y_{i,1},y_{i,2},y_{i,3},\dots ,y_{i,M})-y_i\right)\right]}^2\right\}/N \to \min \rangle$$

(3)

As we discussed above, neurons are connected with the quadratic polynomial, while Kolmogorov-Gabor polynomial is used to conduct relation mapping between input and output variables [53,55,56]. This Kolmogorov-Gabor polynomial can be expressed as below

$$m=d_0+{\displaystyle \sum }_{i=1}^M{d}_i{y}_i+{\displaystyle \sum }_{i=1}^M{\displaystyle \sum }_{j=1}^M{d}_{ij}{y}_i{y}_j+{\displaystyle \sum }_{i=1}^M{\displaystyle \sum }_{j=1}^M{\displaystyle \sum }_{k=1}^M{d}_{ijk}{y}_i{y}_j{y}_k+\dots$$

(4)

To minimize the variation between the actual output ($m$) and estimated output ($\widehat{m}$), a regression model is applied for each pair of input variables $\left(y_i,y_j\right)$.

2.3. Multivariate Adaptive Regression Splines

The Multivariate adaptive regression splines model (MARS) was proposed by Friedman [44] as a new data driven technique, looking for any possible nonlinear and nonparametric relationship which can exist and can be built between a set of inputs and output variables. MARS is used to try to identify and automatically establish the possible explicit regression equation between the regressors and the dependent variables in a stepwise manner; another important advantage of the MARS model is its abilities to provide the part of the contribution of each predictor to the dependent variable, and at the end of the training procedure it provides the final rankings of the regressors individually based on its rank [44]. A wide range of applications of the MARS model can be found in the literature including: estimating heating load in buildings [62,63], predicting centerline segregation in steel cast products [64], predictions of landslide susceptibility [65], estimating fractional snow cover (FSC) from MODIS data [66], and predicting monthly discharge and mean soil temperature [22,62]. Using the MARS model, the space of regressors is divided into several subspaces called knots, each has its own function and splines (segments) which are used to link all these knots, and all the spline are grouped to form a basis function (BF). Hence, globally speaking, the MARS model is based on three major clear and precise components: knots, spline, and BF, and the development of the model is achieved in two phases: forward (building) and backward (pruning) phases. In the forward phase, a high dimensional model is built that contains the chosen knots and their corresponding BF. During the backward phase, the BF that provides fewer contributions to the decreasing of the error is pruned via generalized cross-validation (GCV) [66].

Firstly, MARS starts by building a set of BF with the following equation [44]:

$${{\displaystyle BF}}_m\left(x\right)=\max \left(0,c-x\right) \mathrm{or} {{\displaystyle BF}}_m\left(x\right)=\max \left(0,x-c\right)$$

(5)

where x is one of the regressor variables, c is the threshold value for the regressor x, and the BF is the basis function. Consequently, the MARS model is developed as an ensemble of the BF as follow:

$$Y=f\left(x\right)={{\displaystyle \psi }}_0+{\displaystyle \sum _{m=1}^M{{\displaystyle \psi }}_m}{{\displaystyle BF}}_m\left(x\right).$$

(6)

Y is the response (dependent) variable (ET₀), BF is the basis function, x is a regressor that contributing to the formation of the BF, and ψ_m are unknown coefficients of the mth BF, while M is the total number of the BF [44,66]. The GCV is expressed as follow:

$$GCV\left(M\right)=\frac{\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left({{\displaystyle y}}_i-f\left({{\displaystyle x}}_i\right)\right)}^2}}{{\left(1-\frac{c\left(M\right)}{N}\right)}^2}.$$

(7)

N is the quantity of the pattern, M presents the BF number, y_i is the targeted variable (ET₀), f (x_i) is the predicted value of the pattern i, and c(M) is the penalty factor [67]. The MARS model was implemented utilizing the MatLab toolbox ARESLab [68].

2.4. M5 Model Tree

The M5 model tree (M5Tree), which is an amended version of the original decision tree (DT), was proposed by Quinlan [45]. DT was originally proposed for solving classification problems using a splitting method, for which the available information from the data is extracted via the construction of a tree composed of three kinds of nodes: the internal, the roots, and the leaves nodes [45]. The M5Tree has been used for solving several problems, such as predictions of energy consumption in buildings [69], air quality modeling [70], predicting liquefaction-induced lateral spreading [71], forecasting solar ultraviolet [72], and predicting daily water levels in rivers [73]. The M5Tree is a regression model in which the training data are being apportioned to smaller subsets through the construction of a tree and using a gain ratio criterion, an individual regression model is built for each subset [45]. Once the tree had been constructed, the training process starts and tries to determine the best separation to different subsets with respect to two conditions: (i) the leaves nodes of the tree only contains patterns from one subset or (ii) separation does not occur until any improvement in the gain ratio is observed. For a given n number of nodes leaves corresponding to k breaking points, each subset has its own linear model as follow [73]:

$${\rm Y}=\{\begin{array}{c}{{\displaystyle \lambda }}_{01}+{{\displaystyle \lambda }}_{11}x, if x\le {{\displaystyle {\rm Z}}}_1\\ {{\displaystyle \lambda }}_{02}+{{\displaystyle \lambda }}_{12}x, if x > {{\displaystyle {\rm Z}}}_1\\ \dots ,\\ {{\displaystyle \lambda }}_{0n-1}+{{\displaystyle \lambda }}_{1n-1}x, if x\le {{\displaystyle {\rm Z}}}_k\\ {{\displaystyle \lambda }}_{0n}+{{\displaystyle \lambda }}_{1n}x, if x >{{\displaystyle {\rm Z}}}_k \end{array}$$

(8)

where Y is the calculated ET₀, x is one of the input variables selected for model development (climatic variables), λ₀₁ and λ_1i (i = 1:n) are the parameters of the linear models at n leave, and Z_1:k are the breaking points values. According to Quinlan [45], building an M5Tree model generally takes two major steps: the growth step (create a DT) and the tree pruning step to prune back an overgrown tree. The standard deviation reduction (SDR) statistical metric was used to compute the error at each node as the splitting criterion [74,75]:

$$SDR=sd\left(T\right)-{\displaystyle \sum \frac{\left|{{\displaystyle T}}_i\right|}{\left|T\right|}}sd\left({{\displaystyle T}}_i\right).$$

(9)

T_i indicates the subset of the ith possible test, T represents the examples number reaching the node, and sd is the standard deviation of the observations. The M5Tree is applied utilizing the MATLAB toolbox M5PrimeLab [76].

2.5. Stephens-Stewart Model

Stephens and Stewart’s [77] method is used for pan evaporation estimation. It can be expressed as

$$E_{pan}=R\left(a+b{T}_{mean}\right)$$

(10)

where E_pan is daily pan evaporation (mm/month), R is solar radiation (mm/month) at daily scale, and a and b refer the fitted parameters. In the present study, the SS method given in Equation (9) was used for ET₀ estimation by using extraterrestrial radiation instead of solar radiation data:

$$E{T}_0=Ra\left(a+b{T}_{mean}\right)$$

(11)

where ET₀ denotes the reference evapotranspiration (mm/month) and Ra refers the extraterrestrial radiation (mm/month).

2.6. Hargreaves and Samani Model

Hargreaves and Samani (HS) [78,79] is a temperature-based model and need only fewer input variables: extraterrestrial radiation (Ra) (mm/day), T_max and T_min (°C):

$$E{T}_0=0.0023{{\displaystyle R}}_a\left({{\displaystyle T}}_{mean}+17.8\right) {\left({{\displaystyle T}}_{\max }-{{\displaystyle T}}_{\min }\right)}^{0.5}$$

(12)

where T_max and T_min are the monthly maximum and minimum temperatures (°C), respectively. The calibrated version of HS given in the following equation was also employed in this study:

$$E{T}_{0, calibrated}=a+bE{T}_0$$

(13)

where a and b are fitted parameters.

2.7. Model Development by Heuristic Methods

In the presented study, three abovementioned heuristic methods were implemented for monthly ET₀ estimation. Three different data division scenarios: 50–50%, 60–40%, and 75–25%, were employed in the applications so as to see the effect of training/test size on models’ accuracy. It is well-known that data-driven methods are highly affected by the size of the training data and that more data generally produce a better model. As also mentioned in the introduction section, the studies in the existing literature generally utilize four climatic inputs: air temperatures (T_max, T_min), wind speed (U₂), relative humidity (RH), and solar radiation (SR) in ET₀ estimation. In developing countries, measurement of all these variables is always not possible and therefore models requiring a limited number of inputs are necessary in such cases. As was also reported by a recent review [1], future studies are required for developing new models with limited inputs. Keeping this in the mind, the following two input combinations were considered in this study:

• T_min, T_max, R_a
• T_min, T_max, R_a, α.

It is worth mentioning that the air temperature is easily available in every place and that R_a can be calculated using the Julia date. The developed models are be useful in practical applications because they only need a smaller number of input variables. The periodicity (α, month number of the year) was also considered in the model input to see its influence on models’ exactness if there is any. The flowchart provided in Figure 2 summarizes the model development procedure.

In the applications, GMDHNN, MARS, and M5Tree heuristic methods were employed to estimate monthly ET₀ while only utilizing temperature data as model inputs. Data of two stations, Adana and Antakya, were used for calibration of the methods. First, monthly ET₀ values were calculated by the FAO–56 PM formula using data of minimum and maximum temperatures, relative humidity, solar radiation, and wind speed following the guideline of Allen et al. [7]. Then, the obtained ET₀ data were used for the calibration and test of the selected models. The outcomes of GMDHNN, MARS, and M5Tree methods were compared with the empirical HS, calibrated HS (CHS), and SS regression methods.

3. Application and Results

The models were evaluated with respect to three commonly used statistics: root mean square error (RMSE), mean absolute error (MAE), and Nash-Sutcliffe efficiency (NSE) [80,81,82]. RMSE and MAE varied from 0 to positive infinity. RMSE and MAE outcomes equivalent to 0 indicate a perfect fit. NSE varies from negative infinity to 1 and 1 means that models perfectly catch the observed values. The expressions of the RMSE, MAE, and NSE are:

$$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^N{\left(E{T}_{0,i}-E{T}_{0,iM}\right)}^2}{N}}$$

(14)

$$MAE=\frac{{{\displaystyle \sum }}_{i=1}^N\left|E{T}_{0,i}-E{T}_{0,iM}\right|}{N}$$

(15)

$$NSE=1-\frac{{{\displaystyle \sum }}_{i=1}^N{\left(E{T}_{0,i}-E{T}_{0,iM}\right)}^2}{{{\displaystyle \sum }}_{i=1}^N{\left(E{T}_{0,i}-{\overline{ET}}_0\right)}^2}.$$

(16)

In the equations, N is the quantity of data, ${\overline{ET}}_0$ is average value of the reference evapotranspiration computed by FAO–56 PM, $E{T}_{0,iM}$ is estimated ET₀, and $E{T}_{0,i}$ is computed reference evapotranspiration.

For Adana Station, GMDHNN, MARS, M5Tree, HS, CHS, and SS models are compared in

Table 2. Root mean square error (RMSE), Mean absolute error (MAE), and Nash-Sutcliffe efficiency (NSE) statistics of each model for different data splitting strategies—Adana.

Model	Input	Training			Test
		RMSE (mm)	MAE (mm)	NSE	RMSE (mm)	MAE (mm)	NSE
50% training and 50% test
MARS1	Tmin, Tmax, Ra	0.454	0.363	0.908	0.467	0.359	0.907
MARS2	Tmin, Tmax, Ra, α	0.461	0.356	0.905	0.466	0.357	0.907
M5Tree1	Tmin, Tmax, Ra	0.408	0.301	0.926	0.518	0.406	0.885
M5Tree2	Tmin, Tmax, Ra, α	0.408	0.301	0.926	0.518	0.406	0.885
HS	Tmin, Tmax, Ra	2.021	1.777	−0.82	2.006	1.782	−0.72
CHS	Tmin, Tmax, Ra	0.523	0.407	0.878	0.510	0.383	0.889
SS	Tmin, Tmax, Ra	0.501	0.390	0.888	0.463	0.355	0.909
GMDHNN1	Tmin, Tmax, Ra	0.448	0.353	0.898	0.456	0.347	0.895
GMDHNN2	Tmin, Tmax, Ra, α	0.443	0.347	0.901	0.453	0.343	0.898
60% training and 40% test
MARS1	Tmin, Tmax, Ra	0.435	0.344	0.916	0.510	0.389	0.889
MARS2	Tmin, Tmax, Ra, α	0.447	0.347	0.912	0.492	0.376	0.898
M5Tree1	Tmin, Tmax, Ra	0.402	0.288	0.929	0.529	0.406	0.881
M5Tree2	Tmin, Tmax, Ra, α	0.402	0.288	0.929	0.529	0.406	0.881
HS	Tmin, Tmax, Ra	2.048	1.809	−0.86	1.960	1.734	−0.63
CHS	Tmin, Tmax, Ra	0.509	0.396	0.885	0.527	0.395	0.882
SS	Tmin, Tmax, Ra	0.482	0.376	0.897	0.482	0.368	0.901
GMDHNN1	Tmin, Tmax, Ra	0.428	0.331	0.909	0.480	0.368	0.902
GMDHNN2	Tmin, Tmax, Ra, α	0.424	0.327	0.910	0.478	0.366	0.903
75% training and 25% test
MARS1	Tmin, Tmax, Ra	0.438	0.339	0.916	0.516	0.408	0.884
MARS2	Tmin, Tmax, Ra, α	0.437	0.336	0.917	0.522	0.405	0.882
M5Tree1	Tmin, Tmax, Ra	0.385	0.279	0.935	0.550	0.424	0.869
M5Tree2	Tmin, Tmax, Ra, α	0.385	0.279	0.935	0.550	0.424	0.869
HS	Tmin, Tmax, Ra	2.053	1.821	−0.841	1.894	1.659	−0.556
CHS	Tmin, Tmax, Ra	0.504	0.388	0.889	0.552	0.414	0.868
SS	Tmin, Tmax, Ra	0.479	0.370	0.900	0.491	0.382	0.896
GMDHNN1	Tmin, Tmax, Ra	0.421	0.322	0.914	0.497	0.385	0.881
GMDHNN2	Tmin, Tmax, Ra, α	0.420	0.320	0.915	0.495	0.384	0.883
Average
MARS1	Tmin, Tmax, Ra	0.442	0.349	0.913	0.498	0.385	0.893
MARS2	Tmin, Tmax, Ra, α	0.448	0.346	0.911	0.493	0.379	0.896
M5Tree1	Tmin, Tmax, Ra	0.398	0.289	0.930	0.532	0.412	0.878
M5Tree2	Tmin, Tmax, Ra, α	0.398	0.289	0.930	0.532	0.412	0.878
HS	Tmin, Tmax, Ra	2.041	1.802	−0.840	1.953	1.725	−0.635
CHS	Tmin, Tmax, Ra	0.512	0.397	0.884	0.530	0.397	0.880
SS	Tmin, Tmax, Ra	0.487	0.379	0.895	0.479	0.368	0.902
GMDHNN1	Tmin, Tmax, Ra	0.432	0.335	0.907	0.478	0.367	0.893
GMDHNN2	Tmin, Tmax, Ra, α	0.429	0.331	0.909	0.475	0.364	0.895

T_min, T_max, R_a, and α are minimum and maximum temperatures, extraterrestrial radiation, and periodicity (month number), respectively. RMSE, MAE, and NSE are the root mean square error, mean absolute error, and efficiency coefficient, respectively.

while considering RMSE, MAE, and NSE statistics. In the table, training and testing accuracies can be observed for three different train-test scenarios. In the three implemented heuristic methods, default structures were used and models were calibrated by introducing the training data; in case of the 1st, 2nd, and 3rd scenarios, 50%, 60%, and 75% of the whole data were utilized to obtain optimal parameters of the models. After calibration process, the calculated parameters of the GMDHNN, MARS, and M5Tree models were kept and they were directly used in the testing stage and models were validated by the test data; in case of the 1st, 2nd, and 3rd scenarios, 50%, 40%, and 25% of the whole data were utilized to assess the models’ accuracies based on the three aforementioned statistics (RMSE, MAE, and NSE). GMDHNN2, MARS2, and M5Tree2 models were also developed by adding periodicity component (α) to the GMDHNN1, MARS1, and M5tree1 models so as to see its effect on models’ accuracy in estimation ET₀. It is obvious that there was not any considerable effect of α on models’ exactness in this station. M5Tree models had better fitting in the training stage whereas the GMDHNN and MARS models has a superior performance to the M5Tree in the testing stage. GMDHNN has a better accuracy than the MARS but the difference is not too large. The calibration process considerably increases the HS performance in the estimation of ET₀. Average statistics in Table 2 show that the GMDHNN and SS have almost the same performance and they show a superior performance to the other models with respect to three criteria. The relative differences between the GMDHNN/SS and MARS2 models with respect to average RMSE and MAE are 2.9% and 3%, respectively. Detailed results indicate that a slight difference exists between periodic MARS (MARS2) and SS models in 50–50% and 60–40% train-test scenarios, while the latter performs better than the first in a 75–25% scenario. These results tell us that the use of one data-splitting scenario may mislead modelers during evaluation of the methods’ accuracy. The methods are also compared in Figure 3 with respect to RMSE and NSE in the testing stage. The variation of the criteria (RMSE, NSE) with respect to different splitting scenarios is parallel to each other for all of the applied methods. NSE decreases and RMSE slightly increases from the first splitting scenario (50–50%) to the third scenario (75–25%).

Table 3. RMSE, MAE, and NSE statistics of each model for different data splitting strategies—Antakya.

Model	Input	Training			Test
		RMSE (mm)	MAE (mm)	NSE	RMSE (mm)	MAE (mm)	NSE
50% training and 50% test
MARS1	Tmin, Tmax, Ra	0.383	0.290	0.959	0.635	0.521	0.872
MARS2	Tmin, Tmax, Ra, α	0.369	0.286	0.962	0.566	0.460	0.963
M5Tree1	Tmin, Tmax, Ra	0.341	0.257	0.968	0.639	0.527	0.870
M5Tree2	Tmin, Tmax, Ra, α	0.335	0.256	0.969	0.598	0.489	0.886
HS	Tmin, Tmax, Ra	1.513	1.316	0.367	1.781	1.613	0.065
CHS	Tmin, Tmax, Ra	0.641	0.456	0.886	0.718	0.603	0.848
SS	Tmin, Tmax, Ra	0.438	0.339	0.947	0.678	0.572	0.864
GMDHNN1	Tmin, Tmax, Ra	0.350	0.268	0.963	0.552	0.436	0.912
GMDHNN2	Tmin, Tmax, Ra, α	0.345	0.263	0.965	0.550	0.433	0.913
60% training and 40% test
MARS1	Tmin, Tmax, Ra	0.464	0.359	0.938	0.468	0.370	0.933
MARS2	Tmin, Tmax, Ra, α	0.454	0.345	0.941	0.453	0.373	0.966
M5Tree1	Tmin, Tmax, Ra	0.406	0.305	0.953	0.478	0.380	0.930
M5Tree2	Tmin, Tmax, Ra, α	0.439	0.326	0.945	0.441	0.348	0.941
HS	Tmin, Tmax, Ra	1.612	1.402	0.256	1.722	1.569	0.127
CHS	Tmin, Tmax, Ra	0.676	0.487	0.869	0.647	0.538	0.877
SS	Tmin, Tmax, Ra	0.526	0.400	0.921	0.510	0.436	0.923
GMDHNN1	Tmin, Tmax, Ra	0.441	0.339	0.939	0.426	0.345	0.943
GMDHNN2	Tmin, Tmax, Ra, α	0.430	0.335	0.941	0.424	0.342	0.945
75% training and 25% test
MARS1	Tmin, Tmax, Ra	0.455	0.351	0.941	0.368	0.276	0.957
MARS2	Tmin, Tmax, Ra, α	0.443	0.349	0.944	0.335	0.269	0.971
M5Tree1	Tmin, Tmax, Ra	0.390	0.291	0.957	0.373	0.304	0.963
M5Tree2	Tmin, Tmax, Ra, α	0.406	0.299	0.953	0.367	0.292	0.958
HS	Tmin, Tmax, Ra	1.663	1.463	0.211	1.641	1.489	0.168
CHS	Tmin, Tmax, Ra	0.677	0.497	0.869	0.601	0.481	0.888
SS	Tmin, Tmax, Ra	0.526	0.416	0.621	0.410	0.327	0.648
GMDHNN1	Tmin, Tmax, Ra	0.439	0.347	0.940	0.318	0.248	0.968
GMDHNN2	Tmin, Tmax, Ra, α	0.426	0.337	0.944	0.304	0.247	0.969
Average
MARS1	Tmin, Tmax, Ra	0.434	0.333	0.946	0.490	0.389	0.921
MARS2	Tmin, Tmax, Ra, α	0.422	0.327	0.949	0.451	0.367	0.967
M5Tree1	Tmin, Tmax, Ra	0.379	0.284	0.959	0.497	0.404	0.921
M5Tree2	Tmin, Tmax, Ra, α	0.393	0.294	0.956	0.469	0.376	0.928
HS	Tmin, Tmax, Ra	1.596	1.394	0.278	1.715	1.557	0.120
CHS	Tmin, Tmax, Ra	0.665	0.480	0.875	0.655	0.541	0.871
SS	Tmin, Tmax, Ra	0.497	0.385	0.830	0.533	0.445	0.812
GMDHNN1	Tmin, Tmax, Ra	0.410	0.318	0.947	0.432	0.343	0.941
GMDHNN2	Tmin, Tmax, Ra, α	0.401	0.312	0.950	0.426	0.341	0.942

T_min, T_max, R_a, and α are minimum and maximum temperatures, extraterrestrial radiation, and periodicity (month number), respectively. RMSE, MAE, and NSE are the root mean square error, mean absolute error, and efficiency coefficient, respectively.

reports the training and testing statistics of the employed methods for Antakya Station. Unlike the Adana Station, including the periodicity input considerably improves the accuracy of MARS and M5Tree methods in the testing stage. Similar to for the previous station, here temperature based GMDHNN models also show superior performance to the MARS and M5Tree models in the estimation of ET₀. All heuristic methods outperform the SS method. A considerable improvement is observed for the HS method after calibration: RMSE and MAE are increased from 1.715 mm and 1.557 mm to 0.655 mm and 0.541 mm with respect to average statistics, respectively. The SS model has better accuracy than the HS and CHS models in the estimation of ET₀ using only temperature data as inputs. The relative differences between GMDHNN2 and MARS2/M5Tree/SS models with respect to average RMSE and MAE are 3.7%/10.7%/0.8% and 4%/11.7%/1.1%, respectively. The results of the Antakya Station suggest the use of a periodicity input in model development. The RMSE and NSE values of the applied methods are also compared in Figure 4 for the testing stage. Here the criteria also vary in similar ways for all the methods except for the CHS. Unlike Adana Station, the NSE slightly increases and RMSE decreases from the 50–50% splitting scenario to a 75–25% scenario. Comparison of the two stations (compare Figure 3 and Figure 4 or Table 2 and Table 3) reveals that the models generally provide better estimates for Antakya Station compared to Adana. A higher correlation between the inputs (T_min, T_max, R_a) and output (ET₀) in Antakya compared to Adana may be the reason for this.

Figure 5 illustrates the FAO–56 PM and estimated ET₀ obtained by using six different methods for Adana Station. It is apparent from the scatterplots that the HS considerably overestimates ET₀ while the CHS has less scattered estimates compared to HS. GMDHNN and SS methods have the least scattered estimates among the applied methods and are closely followed by the MARS method. The methods are graphically compared in Figure 6 in estimation of ET₀ of Antakya Station. Here the CHS also considerably improves the HS accuracy. GMDHNN also has the least scattered estimates followed by the MARS in this station.

The monthly mean estimates of the GMDHNN, MARS, M5Tree, HS, CHS, and SS methods are compared in Figure 7. In Adana Station, the GMDHNN2, MARS2, M5Tree1, and SS model results are generally very close to each other while the CHS underestimates the ET₀ of March and May and overestimates those of July and August. The models’ estimates do not considerably change with respect to splitting scenarios. In Antakya Station, however, the models’ accuracy changes for different train-test scenarios. For example, the GMDHNN2, MARS2, M5Tree1, and SS models are less successful in estimation of ET₀ in the case of the 50–50% splitting scenario while the 75–25% train-test scenario provides the best estimates. This also confirms the necessity of considering different splitting scenarios in evaluating the accuracy of the applied methods in the estimation of ET₀. It is apparent that the CHS has the worst estimates while the GMDHNN2 maps the mean monthly ET₀ better than the other models. All the models underestimate ET₀ of Antakya Station in the 50–50% splitting scenario.

4. Conclusions

The ability of new temperature based regression methods were compared with Hargreaves-Samani, calibrated Hargreaves-Samani, and Stephens-Stewart methods in modeling monthly reference evapotranspiration. The applied models only used maximum and minimum temperatures and extraterrestrial radiation inputs that were measured and calculated for two stations in Turkey. Data division scenarios of 50–50%, 60–40%, and 75–25% were applied in the study to evaluate the aforementioned methods. The periodicity component (the month number of the year varying from 1 January to 12 December) was also used as an input to the models so as to examine its effect on models’ performances. Three commonly used criteria: RMSE, MAE, and NSE, were used for comparison of the methods. The results indicated the following conclusions:

In Adana Station, GMDHNN and the SS model performed better than the other models. In Antakya Station, however, the GMDHNN model provided the best accuracy followed by the MARS and M5Tree in modeling monthly reference evapotranspiration.

The calibration procedure considerably increased HS model accuracy. For example, average RMSE and MAE statistics of HS were increased from 1.715 mm and 1.557 mm to 0.655 mm and 0.541 mm for Antakya Station.

The periodicity component increased the accuracy of GMDHNN, MARS, and M5Tree models in Antakya Station only. RMSE decrements of the GMDHNN, MARS, and M5Tree models in the test stage were 1.4%, 8%, and 6%, respectively.

The applications revealed the necessity of using different data division scenarios for better evaluation of the compared models.

Comparison of the models in estimating monthly mean reference evapotranspiration revealed that the GMDHNN model generally had better accuracy compared to other models while the CHS models provided the worst estimates. By implementing the GMDHNN model, the average RMSE of MARS, M5Tree, HS, CHS, and SS models respectively decreased by 3.7–6.4%, 10.7–3.9%, 76–75%, 10–35%, and 0.8–17% when estimating monthly ET₀.

The results of this study recommend the use of the GMDHNN model for the prediction of ET₀ in regions where only the temperature is available while other meteorological data are not available or are missing for a long duration.