Decision Tree and AHP Methods Application for Projects Assessment: A Case Study

Abstract

This research is dedicated to the modelling of decision process occurring during the implementation of construction projects. Recent studies generally do not assess the robustness of the decisions regarding the possible changes during the construction project implementation. However, such an assessment might increase the reliability of the decision-making process. We addressed this gap through a new model that combines the decision-making process modelling with the AHP method and includes the analysis of model stability concerning stakeholders’ behaviour. We used the Analytic Hierarchy Process (AHP) and Decision tree methods to model the decision-making process. The proposed model was validated on a case study of multiple construction projects. The assessment was performed from individual investor’s and independent expert’s perspectives. The criteria for the assessment were selected according to the principles of sustainability. We performed the sensitivity analysis, making it possible to assess the possible changes of the decisions depending on the potential patterns of the decision-makers’ behaviour. The results of the study show that, sometimes, small fluctuations in the project factors affect the project selection indicating the possible lack of the robustness of the project decisions.

1. Introduction

The problem of project selection has attracted significant attention among construction project participants [1]. In many decision-making processes, it has become common practice to take uncertainty into account, while considering it as an important part of sustainability assessment [2]. In this research, two key concepts are considered: the robustness of the decision, which describes how well the decision performs across a wide range of futures, preferences, and worldviews, although it may not be optimal in any particular one [3]; and, the sensitivity of the decisions, which describes how big the changes of input of the model must be in order for decisions to be changed.

The lack of robustness of decisions made in an uncertain project environment raises the risks in decision-making and, accordingly, leads to unreliable solutions [3] negatively affecting the sustainable city development [4]. Additionally, the compromises between the competing goals of different sustainability categories (environmental, social, and economic) have to be found. There is usually a trade-off between the different objective functions that can help the decision-maker to choose a particular solution according to the preference of an organisation [5]. For example, [6] focus on the trade-offs between economic sustainability on one hand, and environmental sustainability and resilience on the other hand. As pointed out by Kamali [7], multi-criteria assessment (MCA) studies generally do not evaluate the robustness of the overall MCA outcome to uncertainty regarding scores and weights; in such studies the sensitivity analysis is usually addressed in terms of sensitivity of the results to the choice of MCA method [8]. However, in the scope of this research, the sensitivity analysis is similar to the one that is widely used in Operations Research theory, which deals with finding out the amount by which the input data can be changed for the output of model to remain almost unchanged.

Construction project is a series of activities to define, design, construct, and put to use construction work [9]. The term ‘construction project’ refers to a high-value, time bound, special construction mission with predetermined performance objectives [10]. Construction projects include new construction, renovation, and demolition for both residential and non-residential projects, as well as public works projects, such as streets, roads, highways, utility plants, bridges, tunnels, and overpasses [11]. Construction projects are intricate, time-consuming undertakings [12]. Construction projects are complex systems involving multiple and mutual components. Thus, construction projects consist of many interacting stakeholders, such as clients, contractors, consultants, and workers with different management objectives and functions that contribute to the whole [13].

A construction project involves the use of different resources (e.g., machinery, materials, manpower, etc.) to produce the final product (e.g., a building, a bridge, a water distribution system, etc.) that serves the targeted users’ needs. The difficulties that are met in construction projects include budget limitations, contractual time constraints, safety and health issues, sustainability ratings, local building codes, the desired level of quality, to name but a few. Consequently, a construction project has multiple objectives, including maximum productivity, minimum cost, minimum duration, specified quality, safety, and sustainability [14].

For most clients, a construction project is necessary for satisfying their business objectives. The client’s objectives may be as complex as the introduction and accommodation of some new technology into a manufacturing facility or the creation of a new corporate headquarters; or, they may be as simple as obtaining the optimum return on resources available for investment in a office building [15].

Building design involves generating several design alternatives and the subjective assessment of each option according to a variety of requirements [16]. The organisational and technological complexities of construction projects, diversity of stakeholders, and their multiple interests result in a variety of risks and complicated decision-making.

This work is a continuation of the research [17] with a brief reiteration of some key points from that research throughout this article. In the mentioned research, primary attention is paid to the investor’s needs, thus it was assumed that the investor cannot be changed, he has a fixed opinion that is applied to solve the optimisation problem using Dynamic programming method to form a decision strategy. However, this implies the limitation of the results to only be considered in the context of a single point of view. In the mentioned paper, the combination of the decision tree and AHP method was proposed, permitting the to enrichment of the stochastic Markov process modelling by a decision tree with a multi-criteria AHP method, applied on the leaves of the tree. Such an enrichment creates the dependency of the decisions in the tree to the possible changes in the evaluations of the projects.

The modelling, as proposed in the previous research, is used in the current research to simulate the possible construction project implementation outcomes, even the selection of the project itself. The projects being assessed are virtual, i.e., the assessment is applied to the projects as the products of simulation in order to fill the values on the tree leaves which is a necessary condition to optimise the investor’s decisions. During the simulation, different projects might be assessed providing an opportunity to include the assessments into the decision tree. As mentioned before, in [17], it is shown how to create the dependency of the decisions in the tree to the possible changes in the evaluations of the projects. In the current research, we analyse this dependency, i.e., we provide the approach to perform a sensitivity analysis. In order to achieve that, we suggest constructing a series of mappings of the rating scale to the monetary values and apply them in order to extract different monetary values for project evaluation from the AHP assessment. In practice, this makes it possible to answer questions, like “what will happen if”, i.e., what will happen if the investor changes, or his priorities shift, etc. The examples of information that might be included into the mappings are:

• The changes of the priorities leading to improved value of the object, e.g., the other burnt house might stimulate the investor to build the current project for himself, or some various reasons might drop the interest of having some property for the investor—he might tend to want to sell it, meaning the values in AHP assessment will shift.
• The investor might face the financial problems leading to drops in the costs to ratings mapping.
• The investor might financially succeed with some other projects, extending his abilities to invest, which would increase the costs to ratings mapping.
• The investor might react to some external factors, changing his priorities, such as financial crisis, any other reasons for the changes of the market prices.

Note that the type of the investor being investigated is domestic individual investor [18]. In the considered case, he is also an owner of the privately owned house to which the project is going to be applied. The investor has the power to choose the project from the all propositions, such choice can be modelled via decision tree and AHP method. This means that the investor is also a developer, he initialises the project, and leads the process of the project implementation.

This article makes the following contributions:

• We provide the approach to assess the decision model in terms of sensitivity to the changes of conditions, more specifically—the mappings of the rating scale to the monetary values, which describe the investor-specific information.
• The application of the proposed techniques to the case study leads to a deeper understanding of how to apply it in a similar way to other types of applications that are required in other researches.
• The proposed methodology contributes to the general analysis of the robustness of decisions, i.e., how sensitive the possible decisions are, depending on the changes of the decision-maker.

By considering all of these elements, the paper aims to contribute to the analysis of the robustness of decisions, specifically, giving the possibility of assessment of how sensitive decisions of construction project stakeholders are depending on the changes of the situation and the decision-maker. To this aim, a new decision-making model for quantitative assessment of solutions was proposed. Applying this model, first, the most common stakeholders in construction project were analysed. Secondly, the criteria were selected according to the principles of sustainability, more specifically—from the main categories of sustainability: social, environmental, and economic. After that, the created decision-making algorithms were applied to the case study. Note that the impact of the presence of sustainability criteria on the decision robustness is out of the scope of the current research.

The remainder of paper is structured as follows. In Section 2 the background of the research is provided. Section 3 describes the methodology of research. Section 4 presents the results of the proposed research methodology applied to the real case. Finally, Section 5 presents and discusses the results coming from the case study. It also provides concluding remarks and proposes future research areas.

2. The Background of the Research

Sustainability in the decision-making process has reached greater influence in the academic field in the last few years [19]. Decision-making in a changing environment was addressed from different viewpoints. Recent researches were focused on the synthesis of sustainability and decision-making using multidisciplinary approaches [20,21,22,23], which suggested treating sustainability as a first-class element in the early stages of business engineering. Researches comprised sustainability taxonomy that allows stakeholders to take environmental matters into consideration when making decisions. Cuadrado et al. [21] used MIVES methodology to determine a global sustainability index of an industrial building based on environmental, economic, and social factors. MacDonald et al. [22] compared the decision-making processes of sustainability-focused multi-stakeholder partnerships, and found that collaborative decision-making has an indirect and positive impact on the implementation of community sustainability plans [23] proposed an integrated approach for sustainability assessment in qualitative and quantitative viewpoints using economic, environmental, and social indices.

A set of policy initiatives [24,25,26,27,28] was issued having the aims to encourage us to make rational and more robust decisions in our projects, lives, and communities. These initiatives advise an organisation to take into consideration social, environmental, legal, cultural, and political heterogeneity, thus assisting organisations in contributing to sustainable development. It means that, at least, organisations have to balance the stakeholders’ needs and make decisions taking possible impacts on society and the environment into account. According to [27], these actions along with improving process sustainability should also help to improve the competitiveness and profitability of businesses.

Sustainability has been addressed as a part of innovative business strategies, requiring rethinking and reshaping of prevailing business systems and behaviours [29,30]. Sustainable business models examine a spectrum of stakeholders’ interests, including environmental and social issues [31]. The concept of corporate sustainability gives the potential to be more embracing in terms of the company benefits, as well as the social and environmental implications for stakeholders [32].

Sustainability has been studied in many sectors, especially in the construction industry due to its significant impact on the environment. Assessing the growing importance of sustainability and project management topics in the current business context, Martens & Carvalho [33] reported the need for research combining both topics. The initiatives, like Green Project Management [28], were committed to stress social, environmental, and economic risks, as well as opportunities in project activities. However, research focusing on sustainability in a project context can still be characterised as emergent and fragmented [34].

Recent studies on a project evaluation and selection suggest different ways to assess the sustainability of solutions; however, the majority are based on methods of a decision theory. For example, Hatefi & Tamošaitienė [35] proposed fuzzy AHP-improved grey relational analysis model to prioritise construction projects that are based on the sustainable development criteria. Kudratova et al. [32] proposed the project selection decision-making model that allows investors to find positive sustainability trade-offs without harming returns on the investment. Decision theory was evolved from the interaction of many disciplines: operational research, economics, mathematics, and statistics. However, the origins of real estate analysis lie in the interaction between the physical, legal, and financial aspects of land and property [36]. Decision-making in the real estate sector mainly focuses on selection between the sale and redevelopment of real estate assets. For example, Carbonara and Stefano [37] analysed the structure of the decision-making process behind the sale or redevelopment of real estate assets. For the assessment of possible actions, they proposed three different indexes: urban values index, use index, and technical-maintenance index.

The increasing interest in sustainability concepts led to the incorporation of the latter at various levels of the decision-making process. For example, the sustainability index for real estate projects was proposed and analysed using multiple criteria decision-making (MCDM) methods [38,39] as well as tested to what extent green buildings could have a higher price and an overall economic performance when comparing to traditional real estate. The sustainable new construction operations need to take into account the environmental sustainability, better living conditions for individuals, and to pursue the highest possible economic value. There are many opportunities in the real estate market to increase the value of a property, e.g., by investing in the projects for the creation or renovation of infrastructure or building structures. The common goal is to renovate the building to improve living or working conditions and create a higher value of the object. Together with policy developments, the perceptions of real estate project stakeholders have an influence on project investor decisions in achieving ambitious goals. When compared to other industries, projects in the construction industry have been facing numerous risks, e.g., if they are not managed properly, they will fail in achieving main goals [40].

Construction projects differ in the budget, duration, variety of works, a number of implementers, and stakeholder [41]. The results of the projects also vary in following ways: some of them can be implemented successfully and others can be terminated with losses. The risks that are associated with the execution of construction projects influence each other. For example, the risks related to construction project delivery time can influence project costs and vice versa [42]. The success or failure of real estate investment decisions depends on the assessment and management of the inherent risk and uncertainty [43]. In some AHP method applications for a real estate investment problem, multi-criteria group decision-making method first uses analytic hierarchy process to construct decision preference matrix, and then it uses the hesitant probabilistic fuzzy linguistic set to model uncertainties.

The risks that are related to decision-making in construction projects were recently studied in many related works [42,44,45,46,47]. For example, Hatefi et al. [44] state that the source of the project risks is the presence of high uncertainty in construction projects. Because of the existence of factors that are associated with uncertainty, the appropriate models for decision-making are necessary. Hatefi & Tamošaitienė [42] applied an integrated fuzzy DEMATEL-fuzzy ANP model to assess the relative importance of risk factors and alternatives, as well as to prioritise construction projects. Ghasemi et al. [45] developed Bayesian network (BN) methodology for modelling and analysing the risks and then applied it to a project portfolio of a construction company. Asadi et al. [46] proposed a three-stage approach that is based on the fuzzy inference system for project risk evaluation. The approach combines different parameters (e.g., the time, cost, quality, contribution rate, resilience, and resistance) to assess the risk index. For sustainable risk analysis and decision-making in the construction sector [47], an alternative approach based on consistent fuzzy preference relation and ANP methodology provided. Multi-criteria decision-making methods are used by individuals and enterprises to achieve effective solutions for many of their problems, since they usually include subjective, intangible, and not easily quantifiable aspects [48]. The research [49] applies Fuzzy multi criteria decision-making methodology, called DEcision-Making Trial and Evaluation Laboratory (DEMATEL) and Analytic Network Process (ANP) method, to investigate the Critical Success Factors (CSFs) of project management. These factors were categorised into five criteria groups: (1) project, (2) project management, (3) organisation, (4) external environment, and (5) sustainability, from which the highest weights were assigned to the sub-criteria of top management and sponsors’ support, stakeholders’ expectations, and end users’ imposed restrictions.

In addition to different measurable risks, the investor’s strategy can be strongly affected by the possible cyclical recurring crises in the real estate market, like the housing crisis, which affected many economies in 2007–2008 [50]. In times of global financial crisis, the decision to invest at a certain point in time and the correct assessment of risks are key issues: investors need to know how to measure risks and identify the relationship between risks appearance and risks incentives demanded, according to their attitude towards risks [51]. To operate in unfavourable business conditions, it is appropriate to gather and analyse more information to make rational decisions. The use of information systems enables to collect necessary data and the coordinate solutions with business partners remotely. This can provide an advantage in carrying out construction project activities in a difficult situation. Because each construction project has specific complexities and uniqueness, it is necessary to take these factors into account while proposing an advanced decision-making tool for project managers [40].

One of the sophisticated tools for improving the decision-making process in construction projects is the decision tree method. The decision tree, as a construction projects risk management tool, can be useful in providing real estate market participants with the necessary information. The information advantage gives agent buyers a greater bargaining power when buying houses for their use at lower prices than other non-agent buyers (for example, agents bought houses at prices that are 2.54 lower than comparable houses that were bought by other buyers) [52].

With the diversification of Internet technology and cloud computing, an increasing number of Internet companies has started to afford users with a variety of remote services. Data analysis and prediction, including risk assessment, image recognition, and spam detection are among the most popular services. The functions that are mentioned above were achieved through machine learning classifiers that have recently attracted considerable attention [53]. Decision trees are among the most popular tools for learning and extracting classification rules from data [54]. When compared with other algorithms, decision trees require less effort for data preparation. The constructed decision tree model is intuitive and easy to explain to technical teams and stakeholders. At the same time, the result of the decision tree may be unstable because a little change in the data may lead to the creation of a completely different tree. A problem can be solved by using an ensemble decision tree [55]. Constructing a decision tree is usually a recursive procedure, where a function is repeatedly optimized and training data are partitioned into the root and internal nodes until a termination condition is met [56]. Usually, the termination condition is the logic disjunction of several stopping predicates that account for different kinds of imposed limitations, for example, on the branch length, on the possible information gain [57].

Analytic Hierarchy Process (AHP) is another tool for improving the decision-making process [58]. AHP is a broadly applied multi-criteria decision-making method for determining the weights of criteria and it priorities of alternatives in a structured manner that is based on pairwise comparison. Because subjective judgements during comparison might be imprecise, the modifications of AHP by combining fuzzy sets with AHP are proposed and referred to as fuzzy AHP or FAHP [59]. It is noteworthy that the AHP method is widely used for construction project assessment, for example, to develop a decision support system that embodies the relative preferences of the owner and architect among multiple key criteria [16], in order to assess the building performance in the field of anti-seismic behaviour [60], to evaluate building material suppliers while taking a large number of criteria that are often subjective and hard to measure into consideration [61].

Changes of decisions raise the uncertainties and can negatively affect the sustainability of the project results, e.g., the changes that were made in the middle of a project can significantly differ from its implementation from the initial plan, as it was pointed out in the above-mentioned articles. In order to analyse the possible shifts in the decisions, the analysis of model robustness must be performed, i.e., it is important to understand how sensitive decisions are to possible changes in project participants’ behaviour. For example, the investor changes his/her priorities or the project can be transferred to/inherited by another investor. The resistance of the decisions during project implementation to the possible changes of the project conditions must be assessed. Thus, there is a lack of studies that provide clear solutions for the accurate assessment of the stability and robustness of the decision model in terms of its sensitivity to changes in conditions, including the change of the investor. Note that the current study is not necessily a source for the improvement over the mentioned works, it is hard to judge the usefulness of the requirement to perform the additional analysis mentioned above. Instead, we analyse the case where it is needed, and the lack of such analysis in other studies creates a gap, which this article intends to fill. It became especially topical in the context of the recent changes in the policy of EU regarding the sustainability of the investments.

Assessing investment against sustainability criteria has only just begun to be included in the debates, and new initiatives are emerging to assess the sustainability of investments, such as the EU classification system for green investments [62]. Sustainable investment decisions are commonly referred to as those that involve sustainability-related considerations [63]. However, until now, the assessment of investment solutions was strictly based on financial indicators, like NPV (Net Present Value), (IRR (Internal Rate of Return), PI (Profitability Index), and similar [64,65]. Lee et al. (2016) [66] used the rate of return, relative return, investment, and relative investment rate for the analysis of investment options. Some of the studies applied qualitative assessment, like SWOT (Strengths, Weaknesses, Opportunities, and Threats) analysis [67]. Seeking to ensure the attractiveness of investments in the future organization addressing the LEED (The Leadership in Energy & Environmental Design), BREEAM (Building Research Establishment Environmental Assessment Method), and similar certification methods for managing the construction projects [68]. However, these methods require a lot of time and effort to evaluate a single alternative and, due to this shortcoming, are rarely applied to the evaluation of multiple alternatives. The recently issued EU Corporate Sustainability Reporting Directive (COM (2021) 189) [69] requires companies to provide information on the sustainability of their business practices in a transparent and comparable way, which will also serve as a reliable guide for investment decisions. Market players should apply the requirements of this Directive and include sustainability criteria in their investment valuation models to contribute to the Green Deal objectives and get a chance to benefit from the financial support mechanisms that are offered by the EU. This study is dedicated to analyse how different conditions (innovations, restrictions) might affect the behaviour of market players (investors). Such an analysis could be applied as a part of methodology for developing the means for supporting the Green Deal objectives. The study of Duong et al. (2021) [70] revealed that there is a positive stock market reaction to incremental sustainability innovation; however, there is a lack of studies that focus on the analysis of the investor behaviour in the context of changes in the market.

To fill this gap, this study develops a new model that combines the decision-making process modelling with AHP method and includes the analysis of model stability in relation to stakeholders’ behaviour. Accordingly, this study assesses possible patterns of project participants’ behaviour, identifying the key aspects of sustainability in a project management context. It also helps to understand the importance from the project investor’s perspective, at the same time taking into account other stakeholders’ needs. The methodology was validated on a case study of eight roofing projects by assessing different options for their implementation. The sensitivity analysis was performed to determine possible scenarios and to investigate the robustness of decision-making processes, i.e., how resistant the decisions are to possible fluctuations of parameters.

3. The Methodology of the Research

In this section, we describe the main methods that were applied to the case study. The current research is based on the work [17], in which we have provided an example of how to apply the methods of a decision tree and AHP to select the best project. In this article, we further develop the topic of a decision tree and AHP methods application by addressing additional problems, such as the parametrisation of investor’s behaviour, sensitivity analysis, and visualisation of results. The sensitivity analysis is especially important, since it permits assessing the possible changes of the investor’s opinion and its impact on selection of the project. The methodology applied in the paper consists of following main steps:

• Identification of the major stakeholders involved in the project execution process.
• Development of a decision tree scheme to select the best project from the planned set of alternatives.
• Creation of the algorithms for the decision tree solution.
• Adaptation of AHP method to assess the investor’s subjective opinion about the various projects, predicting whether the investor would like to sell the completed project or not.
• The parametrisation of the investor’s behaviour with a special mapping of the ratings scale to the monetary values and the sensitivity analysis.
• Analysis of how the different mappings of the rating scale to the monetary values affect the assessment of the projects in the decision tree and visualisation of the obtained results.

The developed methodology was validated on the real case study to demonstrate how algorithms work in real conditions.

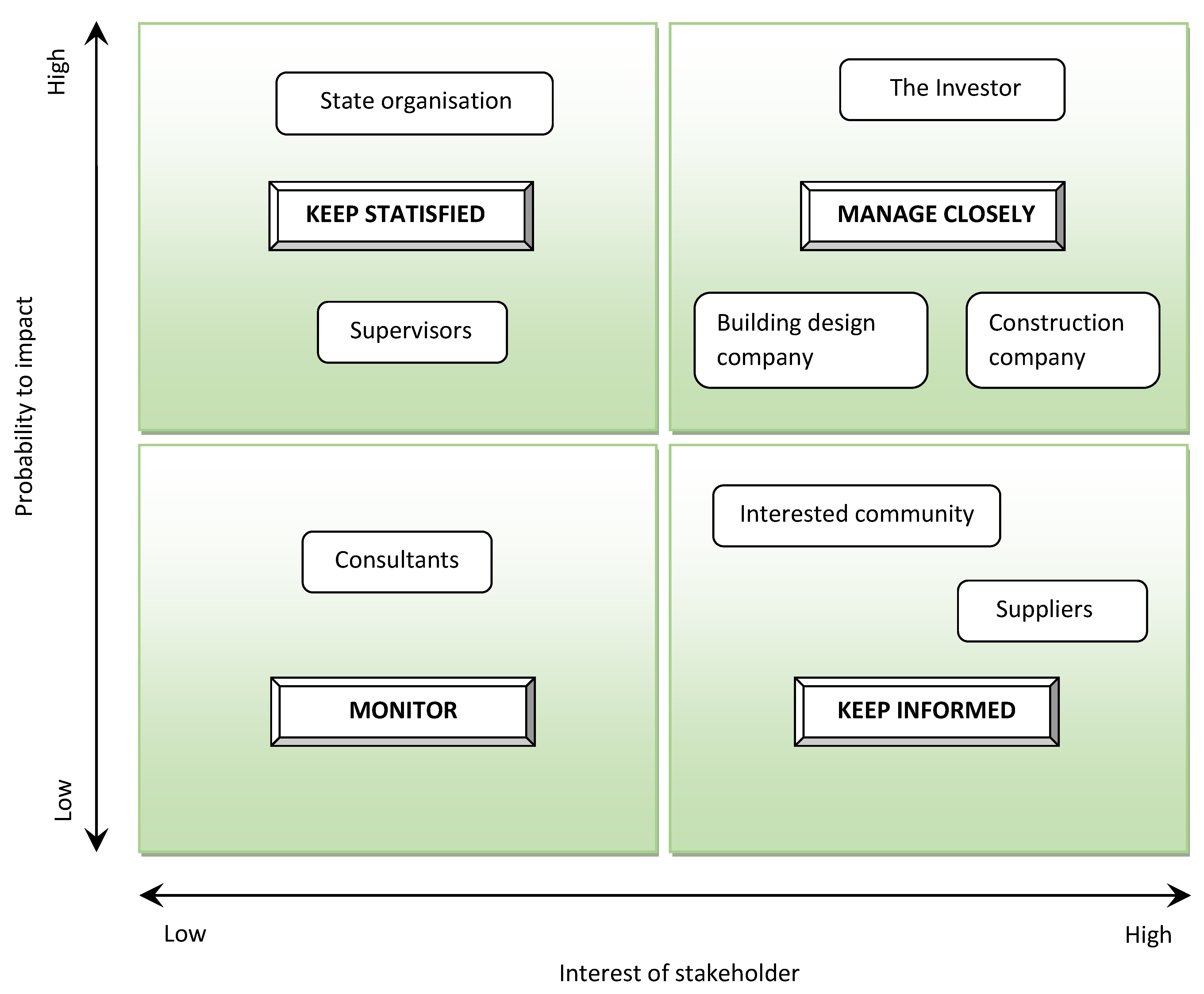
3.1. Identification of Major Stakeholders

The creation of the decision tree starts from the analysis of the participants’ behaviour during the project execution. These participants are identified as stakeholders in the project outcomes.

Local governments, community-based organisations, foundations, neighbourhood and other advocacy groups (for example, Greenpeace organisation), construction companies, investors, commercial banks, tenants and their brokers, ecologists, media and unions—all of these are the city stakeholders and participants of the city development. They should be able to create feasible projects that generate benefits and reduce the risk that is involved in urban development [71].

It is important to consider the factors that are driven by stakeholders in order to manage construction projects. The impact of these factors can lead to the project success or failure. Depending on the directions of the research, various authors indicate the factors, components, and dimensions that need to be evaluated and controlled during project implementation.

In the research [72] that was performed by N. Srinivasan and S. Dhivya, the major factors that were concerned with stakeholder management in construction projects were identified, as follows: stakeholder participation, decision making powers, organisational structure, quality performance, customer related factors, and employee related factors.

S. Demirkesen and B. Ozorhon in article [73] identify integration components and dimensions that are important for successful construction project management. These components are presented, as follows: the development of a project charter, knowledge integration, process integration, staff integration, supply chain integration, and integration of changes. The dimensions of project management performance are presented, as follows: time, cost, quality, safety, and client satisfaction.

Various authors who study stakeholder theory, distinguish various groups of them.

Table 1. Groups of stakeholders that were researched in the sources related to construction projects and sustainability.

Sources	Researched Groups of Stakeholders	Content of the Research
Li et al. (2018) [74]	Buyers, sales personnel, financial institutions, developers, designers and drafting personnel, estimators, project managers/coordinators, regulators, superintendents, inspectors, trades/suppliers, home occupants and warranty staff	Stakeholder’s studies and the social networks of NetZero energy homes
Zhao et al. (2012) [75]	Employees, customers, shareholders, creditors, suppliers and partners, environment and resources agencies, local communities, government, competitors and non-governmental organisations	A corporate social responsibility indicator system for construction enterprises
Freudenreich et al. (2020) [76]	Social stakeholders, financial stakeholders, customers, business partners and employees	Value creation for sustainability
Chu et al. (2020) [77]	Government, developers and residents	Evolutionary game analysis on improving collaboration in sustainable urban regeneration
Vilutiene and Ignatavičius (2018) [78]	Finance institutions, local authorities, building owners, tenants, contractors, technology providers, material suppliers, consultants and facility managers	Key performance indicators for quality monitoring during sustainable renovation
Zheng et al. (2019) [79]	Governments, cost consultants, owners, building information modelling consultants, designers, general contractors and subcontractors	Quantifying and visualising value exchanges in building information modelling projects
Lin et al. (2019) [80]	Internal stakeholders (end users, developers and investors, main contractors, subcontractors, suppliers and employees) and external stakeholders (governments, non-governmental organizations, communities and the public)	Stakeholders’ influence strategies on social responsibility implementation in construction projects
Maceika et al. (2020) [17]	Project owner, state organisations, building design company, interested community, construction company, suppliers, construction business partners, consultants and supervisors	The modelling of roof installation projects using decision trees and the AHP method

presents the stakeholder groups that can influence roof installation projects.

Based on the Table 1, especially with regard to the [17], the major stakeholders that are involved in the roofing project execution process were identified, as follows:

• Investor in a roof installation project.
• State organisations.
• Building design company.
• Interested community.
• Construction company.
• Suppliers.
• Consultants.
• Supervisors.

The interests of the major stakeholders and probability to impact were assessed using the expert method [81]. Figure 1 presents the obtained results of stakeholders’ positioning. The investor was rated as the most interested and able to make the greatest impact on the project, as can be seen from Figure 1.

It is notable to mention that the building process is mainly implemented by a construction company, although with the involvement of building design company, suppliers, consultants, and supervisors. The investor is not directly involved in the building process; however, in the considered case, many key decisions must be made by the investor (more details will be provided later, see Section 4.2).

Therefore, investor’s decisions were examined using both the AHP method and decision tree. However, the influence of other stakeholders was only assessed in the decision tree. Each of the stakeholders influenced the decision making. Each activity involving stakeholders generated revenue or expenses that were expressed in monetary units. The probable additional costs that might be incurred were also assessed with an appropriate probability. Such additional costs might arise if the project needing correction or the project could not be coordinated by interested local community, and state organisations, or construction and supply companies failed. The tree also calculated the probable loss if the project fails completely. It should be noted that the creation of the fragments of the decision tree is a non-trivial task, which is out of our research scope. As an example, the assessment to select supply organisation is needed and that information must be converted into a fragment in the decision tree. For this purpose, some advanced supplier selection techniques might be applied, as shown in [82].

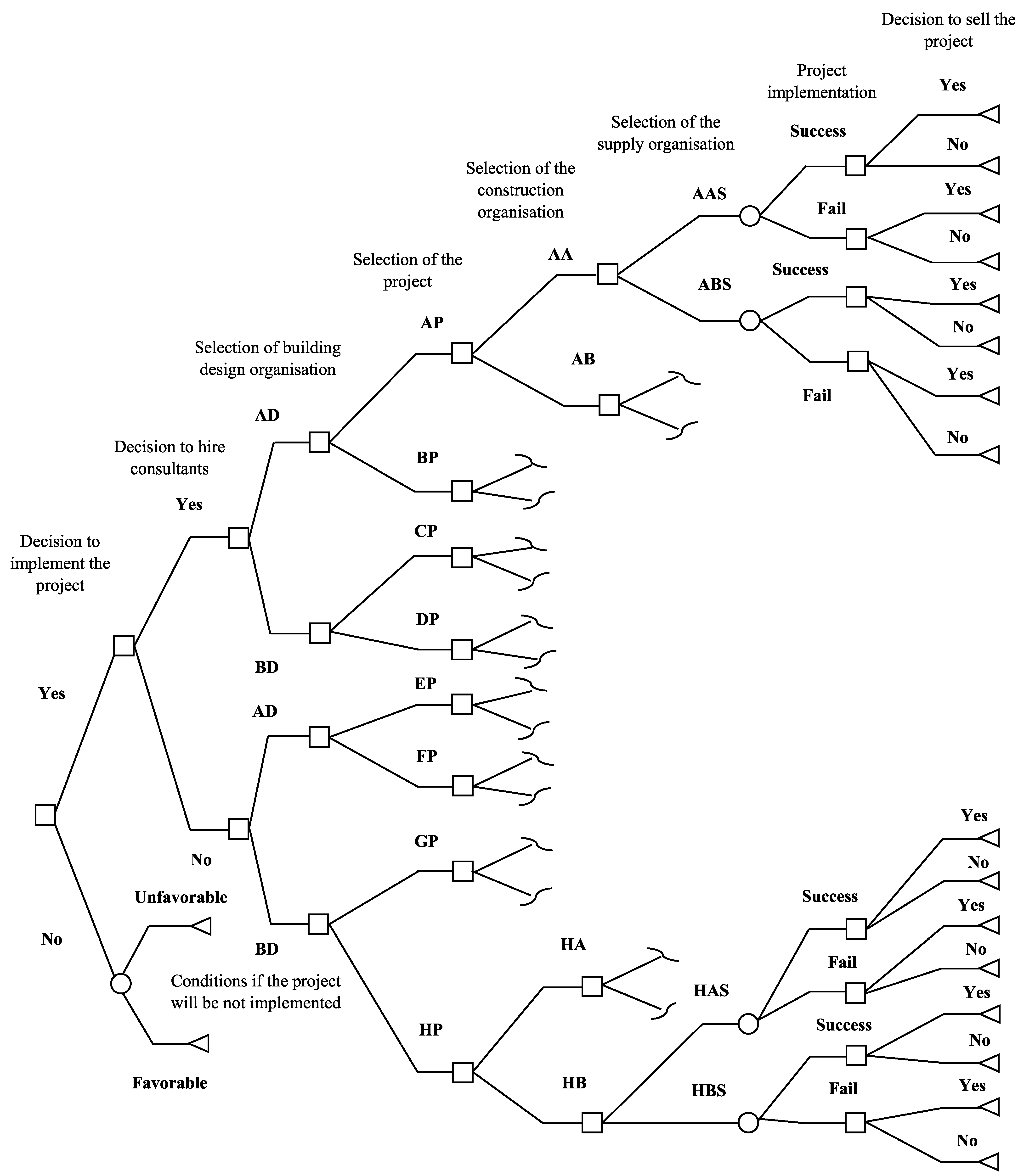
3.2. The Decision Tree

Here, we briefly present the modelling of stochastic process that was introduced in the previous researches. The objective function is to maximize value (profit), which should be received by the investor (the model was developed for a private investor). The decisions were expressed in integer form by $X_{ijk}=0$ or 1, i = 1, 2, 3, ..., g (describes the decision tree level); j = 1, 2, 3, ..., m (describes the branch group in the decision tree level); k = 1, 2, 3, ..., n (describes the branch in the group); $X_{ijk}\ge 0$; ${\displaystyle \sum _{k=1}^n}{\mathrm{X}}_{\mathrm{ijk}}=1$; if $X_{ijk}=1$—alternative ijk is selected; if $X_{ijk}=0$—alternative ijk is not selected; $P_{ijk}$—describes probability of events, $P_{ijk}\ge 0$; ${\displaystyle \sum _{k=1}^n}{\mathrm{P}}_{\mathrm{ijk}}=1$. We also measure the profit/losses $S_{(i-1)jk}$, which can be chosen as a better alternative:

$$S_{(i-1)jk}={\displaystyle \sum _{k=1}^n}{S}_{ijk}{X}_{ijk};$$

(1)

or it can be a probabilistic quantity:

$$S_{(i-1)jk}={\displaystyle \sum _{k=1}^n}{S}_{ijk}{P}_{ijk}.$$

(2)

The mathematical model of the decision tree was constructed based on the algorithms that are presented in [4].

3.3. The Main Steps for the Sensitivity Analysis

To perform the modelling of the investor’s behaviour, we propose applying a special mapping of the ratings scale to the monetary values, describing the influence of the wealthness on the decision of the individual. We show how to integrate that mapping into the model and evaluate the obtained results.

Initially, the model was developed for a single investor. Thus, possible changes in the assessment or parameters were taken into account, which would be the case if the number number of investors will increase. The parametrisation of investor’s behaviour and sensitivity analysis of AHP method were performed in the following steps:

• The investor’s behavior was parameterized based on a subjective opinion regarding the monetary value of the project (more details will be provided later, see Section 4.4).
• Subsequently, by changing the introduced monetary value for the economic criterion, a series of mappings with the rating scale were formed.
• It was calculated how the parameters of the economic criterion would change if we apply different scale mapping multipliers.
• It was analysed how the results (of the decision tree and AHP method application) were changed, depending on the changes in the scale.
• It was analysed how the investor’s behavior would change if we offer him various projects based on the market price.
• The consequences of decisions regarding whether to sell project results or not were investigated. It was taken into account that not only the investor was interested in the results of the project, but there were also other stakeholders affected by the investor’s changing opinion. It is well known that stakeholders were interested in how the starting market price was formed.
• The visualisation of the results of the decision tree for various projects was performed.
• It was described how the possible final result that was obtained in the decision tree might be changed, depending on possible changes in the investor’s opinion.

Note that, in the steps mentioned above, only economic criteria can be seen explicitly. However, the assessment by the AHP method implicitly includes all of the criteria that were discussed in Section 4.3.

3.4. The AHP-Based Project Assessment

The data of the decision tree end nodes on the investor’s subjective opinion when assessing possible options were obtained by applying the AHP method, as already shown in the article [17].

At this stage, we used the AHP method, because we wanted to evaluate the investor’s subjective opinion regarding the value of the project. The AHP method was chosen because it was simple enough to use and it enabled to perform the sensitivity analysis based on [83,84].

The APH method was adapted according to the methodology that was proposed by [58]. Based on this methodology, a comparison matrix was initially created to determine the weights of the criteria of pair-wise $C_{lm}$ elements:

$$\left[\begin{array}{cccc}{C}_{11}& C_{12}& ...& C_{1z}\\ C_{21}& C_{22}& ...& C_{2z}\\ ...& ...& ...& ...\\ C_{z1}& C_{z2}& ...& C_{zz}\end{array}\right];$$

(3)

all elements are positive ($C_{lm}>0$) and reciprocal ($C_{lm}=1/C_{lm},\forall ,m=1,2,\cdots ,z$).

The relative value in comparison to the sum of the columns consisting of z criteria is then found:

$$Y_{lm}=\frac{C_{lm}}{{\displaystyle \sum _{l=1}^z}{C}_{lm}};$$

(4)

where z is the number of criteria.

A normalised matrix is formed for comparison:

$$\left[\begin{array}{cccc}{Y}_{11}& Y_{12}& ...& Y_{1z}\\ Y_{21}& Y_{22}& ...& Y_{2z}\\ ...& ...& ...& ...\\ Y_{z1}& Y_{z2}& ...& Y_{zz}\end{array}\right].$$

(5)

Dividing by the number of criteria gives a weight matrix:

$$W_l=\frac{{\displaystyle \sum _{m=1}^z}{Y}_{lm}}{z};$$

(6)

$$\left[\begin{array}{c}{W}_1\\ W_2\\ ...\\ W_z\end{array}\right],$$

(7)

The consistency vector is calculated according to the formulas:

$$C{\nu }_1=\frac{1}{W_1}\left[C_{11}{W}_1+C_{12}{W}_2+...+C_{1z}{W}_z\right];$$

$$C{\nu }_2=\frac{1}{W_2}\left[C_{21}{W}_1+C_{22}{W}_2+...+C_{2z}{W}_z\right];$$

$$...$$

$$C{\nu }_z=\frac{1}{W_z}\left[C_{z1}{W}_1+C_{z2}{W}_2+...+C_{zz}{W}_z\right].$$

(8)

The Eigen value ${\lambda }_{max}$ is found by:

$${\lambda }_{max}=\frac{1}{z}{\displaystyle \sum _{l=1}^z}C{\nu }_l$$

(9)

then a consistency index (CI) was calculated by formula:

$$CI=\frac{{\lambda }_{max}-z}{z-1};$$

(10)

and consistency ratio (if CR of 0.1 or below, the results are acceptable):

$$CR=\frac{CI}{RI};$$

(11)

where RI is the random index that is determined by [58], for example, in our case the number of criteria is 4, so RI = 0.9.

We determined the criterion of economic logic that we will use in the decision tree. Using the redesigned AHP method, when two possible alternatives—to sell the object or keep it for yourself—are the same (F = 0.5 weighted and normalised points):

$$F={\displaystyle \sum _{m=1}^z}{\displaystyle \frac{W_m{V}_m}{V_m+1}},$$

(12)

where $V_m$ is the rating value of m-th criteria before the normalisation. The rating value of the first criteria:

$$V_1={\displaystyle \frac{a}{1-a}},a=\left(F-{\displaystyle \sum _{m=2}^z}{\displaystyle \frac{W_m{V}_m}{V_m+1}}\right)/W_1,$$

(13)

Subsequently, we calculated the value (the rating is represented by a real value in intervals $[-9,-1]$ and $[1,9]$):

$${\overline{V}}_1\left(V_1\right)=\left\{\begin{array}{cc}-1/V_1,\hfill & \mathrm{when}{V}_1<1\hfill \\ V_1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(14)

If the rating value ${\overline{V}}_1$ exceeds the maximum permissible limit of 9 points or is less than $-9$ points, then this value is specified as equal to 9 or $-9$, depending on the situation. The implementation of this requirement must be done in formula (13) by limiting $a\le 0.9$, because it is the value where the rating 9 is achieved, otherwise there is a possibility for a to obtain the negative values.

Regarding the rest of criteria, we assume that the rating values ${\overline{V}}_i,i=2,\cdots ,z$ are given, according to the fundamental rating scale that is used to evaluate the weights of criteria.

Table 2. The fundamental rating scale for AHP elements assessment (based on [58]).

Rating	Definition	Explanation
9	Extreme importance of the first element	The evidence favouring the first element over the second is of highest possible order of affirmation
8	Very, very strong importance of the first element	Intermediate value between two adjacent judgments when a compromise exists
7	Very strong or demonstrated importance of the first element	The first element is strongly favoured and its dominance is demonstrated in practice
6	Strong plus importance of the first element	Intermediate value between two adjacent judgments when a compromise exists
5	Strong importance of the first element	Experience and judgement strongly favour the first element over the second
4	Moderate plus importance of the first element	Intermediate value between two adjacent judgments when a compromise exists
3	Moderate importance of the first element	Experience and judgement favour a little more the first element over the second
2	Weak importance of the first element	Intermediate value between two adjacent judgments when a compromise exists
1 and −1	Equal importance of the elements	Both elements contribute equally to the objective
−2	Weak importance of the second element	Intermediate value between two adjacent judgments when a compromise exists
−3	Moderate importance of the second element	Experience and judgement favour a little more the second element over the first
−4	Moderate plus importance of the second element	Intermediate value between two adjacent judgments when a compromise exists
−5	Strong importance of the second element	Experience and judgement strongly favour the second element over the first
−6	Strong plus importance of the second element	Intermediate value between two adjacent judgments when a compromise exists
−7	Very strong or demonstrated importance of the second element	The second element is strongly favoured and its dominance is demonstrated in practice
−8	Very, very strong importance of the second element	Intermediate value between two adjacent judgments when a compromise exists
−9	Extreme importance of the second element	The evidence for favouring the second element over the first is of the highest possible order of affirmation

presents these criteria

We used rating scale from 1 to 9 if the first comparable criterion was more important than the second, and from −9 to −1 if vice versa. A higher number on the rating scale means a higher degree of criterion importance. A rating scale from 1 to 9 was used in the standard AHP method. We extended that scale with the usage of negative values −1 to −9 for more convenient assessment of the criteria and interpretation of the obtained data.

Note that, in Formulas (12) and (13), the values $V_i,i=2,\cdots ,z$ are calculated from the inverse function of Formula (14) which is the same function:

$$V_m\left({\overline{V}}_m\right)=\left\{\begin{array}{cc}-1/{\overline{V}}_m,\hfill & \mathrm{when}{\overline{V}}_m<1\hfill \\ {\overline{V}}_m,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(15)

Note that ${\overline{V}}_m<1$ in Formula (15) means integer values from $-9$ to $-1$, however, in Formula (14) $V_1<1$ means real values from interval $[1/9,1)$.

The AHP assessment in the context of this research can be summarised as follows:

• Opinion data is written to Formula (3).
• Weights are calculated by Formulas (4)–(7).
• The consistency ratio (11) is checked to fulfill the AHP method requirements (otherwise the opinion data must be re-evaluated).
• The value ${\overline{V}}_1$ representing the economic logic is calculated using Formula (14). Note that according to formula, this criterion expresses the remaining criteria.
• Depending on the case, the value ${\overline{V}}_1$ is converted to a monetary value, e.g., using the scale and interpolation between scale values. See Section 4.4 for more details about the case which was studied in this research.

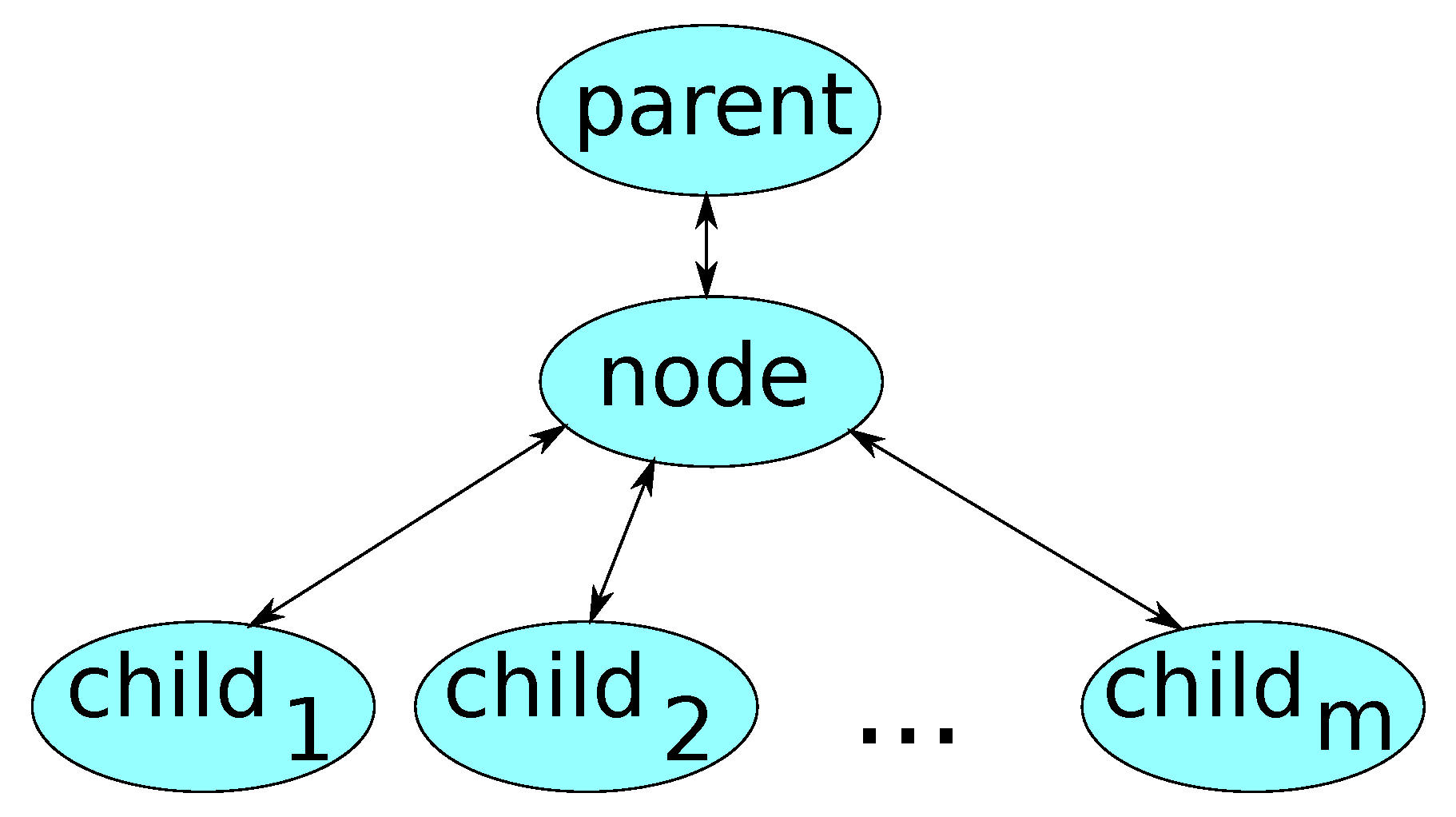
3.5. The Algorithms for a Solution

The basic element of our data structure (a tree) is a node with connections to parent and children nodes (Figure 2).

Algorithm 1 describes a data structure that includes a type of node, which can be equal to 1 if a positive decision was made, and 0 otherwise, a tariff that is used to calculate the costs of consulting, the price of the event and the additional price, the estimate of an event duration, and other data.

Algorithm 1: Data structure

struct {  int type; //type of the node  float p; //probability for this node to be selected by a parentfloat price; //price of the event  float time; //time before the event starts  float ap; //probability of the additional cost and duration  float aprice; //additional price  float atime; //additional time  float tariff; //additional price per day  node* parent; //the pointer to parent node  vector< node* > children; //list of children  float priceTotal; //accumulated price  float timeTotal; //accumulated time  float value; //value of the expected profit of the node  float extime; //expected time of the node  string project; //reference to the project data } node;

The details of the fields are provided in paper [17]. The field $project$ describes a reference to the project data; in practical implementation, it can be a name of the file with the required data. We will also use algorithms from the mentioned work to define the solving procedure, more specifically function $CalcPars$ from Algorithm 1, $CalcValues$ from Algorithm 2. Algorithm 2 presents the general calculation procedure. Here, $ReadTree$ defines the procedure for reading the tree data from the given input that is defined by the variable $data$. $GenerateScales$ returns the list of the possible mappings of rating values to the monetary price values.

Algorithm 2: The general calculation procedure

input: data output: Array of functions F tree = ReadTree(data); mappings = GenerateScales(data); for each scale p in mappings do  ApplyAHP(tree, data, p);  CalcPars(tree);  CalcValues(tree);  $P=\left\{\right\}$;  CollectProjectValues(tree, P);  F.add(P); end

The mapping p can be seen as a function describing the dependency of the monetary price values on rating values, since, later in Algorithm 3, the interpolation procedure is applied. The array P represents the evaluations of all projects in the tree with a given mapping p. Such evaluations are collected in the array functions F, where we assume that method $add$ adds a single point for each function in the array.

Algorithms 3 and 4 both use typical preorder tree traversal to reach the leaves of the tree and apply the necessary operations to them—the AHP method in Algorithm 4 and collection of the project values as a final output in Algorithm 3.

Algorithm 3: Sensitivity analysis procedure

Function$CollectProjectValues(node,P)$  if$node.project!=NULL$then    P[$node.name$] = $node.value$;  end  if $node.children!=NULL$ then   for each node t in $node.children$ do     CollectProjectValues(t);   end  end end

Algorithm 4: The algorithm for the application of AHP to the tree

FunctionApplyAHP($node$,$data$,p)  if$node.project!=NULL$then   evaluate v from AHP parameters from $data$ according to formula (14);   evaluate $node.value$ by interpolating at the point v using mapping p;  end  if $node.children!=NULL$ then   for each node t in $node.children$ do     ApplyAHP(t);   end  end end

4. Case Study: The Modelling of Investor’s Behaviour

4.1. The Description of the Case

In this section, we briefly introduce the case and apply the previously described methodology to that case, more specifically, the general procedure from Algoritm 2 was applied. Algorithms are described by pseudo-code that can be easily converted using any general purpose programming language, like Python, Java, etc., depending on the needs of integrating this logic into existing systems or other reasons for the language preferences. In this research, the algorithms were implemented using C++ solely for the purposes of this research without any support of user interface or any other advanced features for the general user.

The case study was chosen as an empirical research method to demonstrate how algorithms work by applying them to a real-life example, i.e., the type the case study is illustrative in this research. The case study examines a real-life individual building project that was implemented in Vilnius, Lithuania. An individual residential house project with a usable area of 167.84 square meters was chosen as an example. It is very close to typical housing. For comparison: in Lithuania in 2019, the average usable living space in an individual house was 136.2 square meters, while in an apartment it was 57.3 square meters [85]. In the considered case, the old roof was removed and a new one was installed. Thus, this is a reconstruction project involving the installation of roof structures, which is the modelled process in this research. The reconstruction project in the presented case faced problems that are typical when the investor is a person, not a company. For example, it was necessary to adapt the project to meet the investor’s requirements, paying special attention to the professional installation of the roof. The work performance was inspected by hired consultants and supervisors, who identified errors and helped to correct them. The possible alternatives for the roof implementation of this project were examined and presented in the decision tree as eight different projects, which were also evaluated using the AHP method. Groups of stakeholder were also identified, and their influence on project progress and decision-making were taken into account.

The roof installation projects were considered as a separate case of construction projects. The implementation of such projects covers the typical stages of construction projects [86]—feasibility, design, construction, and the beginning of the operation. Note that the selected illustrative case is a separate case of construction projects, which is a part of the real estate. Besides the mentioned case, the proposed model is suitable for a wide range of other projects within the real estate life cycle. Moreover, the methodology can be easily expanded to cover other types of projects, such as R&D projects, which support the return to the previous stages (for example, after testing stage) [87]—for that purpose, the cyclic expansion algorithm can be used [4].

Note that the considered case of roof installation projects does not represent all possible construction projects, and the projects must share these main properties:

• The pool of possible construction solutions must be well-defined in order to define the leaves of the decision tree.
• The investor must have the leading developers role, i.e., he must initialise the project and lead the process of the project implementation. The involvement of additional stakeholders might change the role of the investor making some possible decisions in the tree obsolete, the decision strategy might become trivial from the investor’s point of view, and such modelling might become not useful.

There are no major limitations other than those listed above, for hypothetical possibility to apply the discussed approach to the projects modelling, as long as the process can be described as a Markov process, which is a very general way of process formalisation. Problems to apply the technique may arise because some of the cases might require a lot of information to be defined in order to fill the decision tree by possible events.

4.2. The Application of the Proposed Approach to the Case Study

During the project implementation, there are many decisions to be made by different project participants; however, in the context of the current research, the only the decisions made by investors were considered. Additionally, in this study, we analyse the small scale construction project, which implies the limited set of the decisions for the considered case. The peculiarity of other projects could greatly affect the decisions and their order, potentially creating a more complex graph of dependencies between decisions.

The investor must decide whether or not to carry out the roof reconstruction project, taking into account the potential losses if nothing is done. He also makes decisions regarding whether or not to hire consultants and supervisors. The investor can choose a building design company from options marked with the letters “A” and “B”. The different roof installation projects to be selected are marked with the letters “A”, “B”, “C”, “D”, “E”, “F”, “G”, and “H”. The construction companies are connected to each of the projects according to the planned works, and they are marked “AA”, “AB”, “BA”, “BB”, “CA”, “CB”, “DA”, “DB”, “EA”, “EB”, “FA”, “FB”, “GA”, “GB”, “HA”, and “HB”. The supply companies are connected to the construction site of intended construction companies and they are marked “AAS”, “ABS”, “BAS”, “BBS”, “CAS”, “CBS”, “DAS”, “DBS”, “EAS”, “EBS”, “FAS”, “FBS”, “GAS”, “GBS”, “HAS”, and “HBS” (Figure 3). We provide all decisions in the

Table 3. A description of the investor’s decisions that form the basis of the decision tree.

The Order	Description of the Investor’s Decisions
1	Decision whether to implement the project
2	Decision whether to hire the consultants and supervisor
3	Decisions whether to select the building design company “A” or “B”
	for the branches of the decision tree with or without consulting
4	Decisions whether to select the medium-cost project from a set of projects
	“A”, “C”, “E”, “G” or expensive project from a set of projects “B”, “D”, “F”, “H”
5	Decisions whether to select the construction company “AA” or “AB” for the project “A”;
	“BA” or “BB” for the project “B”; “CA” or “CB” for the project “C”;
	“DA” or “DB” for the project “D”; “EA” or “EB” for the project “E”;
	“FA” or “FB” for the project “F”; “GA” or “GB” for the project “G”;
	“HA” or “HB” for the project “H”
6	Decisions whether to select the supply company “AAS” or “ABS” for construction company “AA”;
	“AAS” or “ABS” for construction company “AB”; “BAS” or “BBS” for construction company “BA”;
	“BAS” or “BBS” for construction company “BB”; “CAS” or “CBS” for construction company “CA”;
	“CAS” or “CBS” for construction company “CB”; “DAS” or “DBS” for construction company “DA”;
	“DAS” or “DBS” for construction company “DB”; “EAS” or “EBS” for construction company “EA”;
	“EAS” or “EBS” for construction company “EB”; “FAS” or “FBS” for construction company “FA”;
	“FAS” or “FBS” for construction company “FB”; “GAS” or “GBS” for construction company “GA”;
	“GAS” or “GBS” for construction company “GB”; “HAS” or “HBS” for construction company “HA”;
	“HAS” or “HBS” for construction company “HB”
7	Decisions whether to sell the object of the project,
	based on the results of applying the AHP method

, where we sort them in the order in which they must be performed.

The decision tree scheme for selecting the best project (Figure 3) presents the chances of failure or success of a project execution, and the decisions that are related to the different stages of the project. Three types of nodes were used:

• Decision nodes which are represented by rectangle shapes.
• Chance nodes represented by circles.
• End nodes represented by triangles.

It is worth mentioning that the decisions are performed based on the values of the nodes in a tree; these values are computed as a probabilistic expectation by Formula (2). This means that the dynamic programming method allows for indirectly including the AHP evaluation into the whole tree, i.e., the criteria to decide are the ones that are used in AHP method.

The AHP output for the tree is represented by a single value; however, this value is not necessarily the actual price of the object—it is the result of the evaluation of all criteria that are included into AHP method. For example, the criteria that are connected to the environment might raise the value in the eyes of the investor, as a result—the values on the leaves change, followed by changes of the solution of the dynamic programming method, which could affect the decision to select the consultants. Next, the actual criteria that are included in the analysis will be discussed.

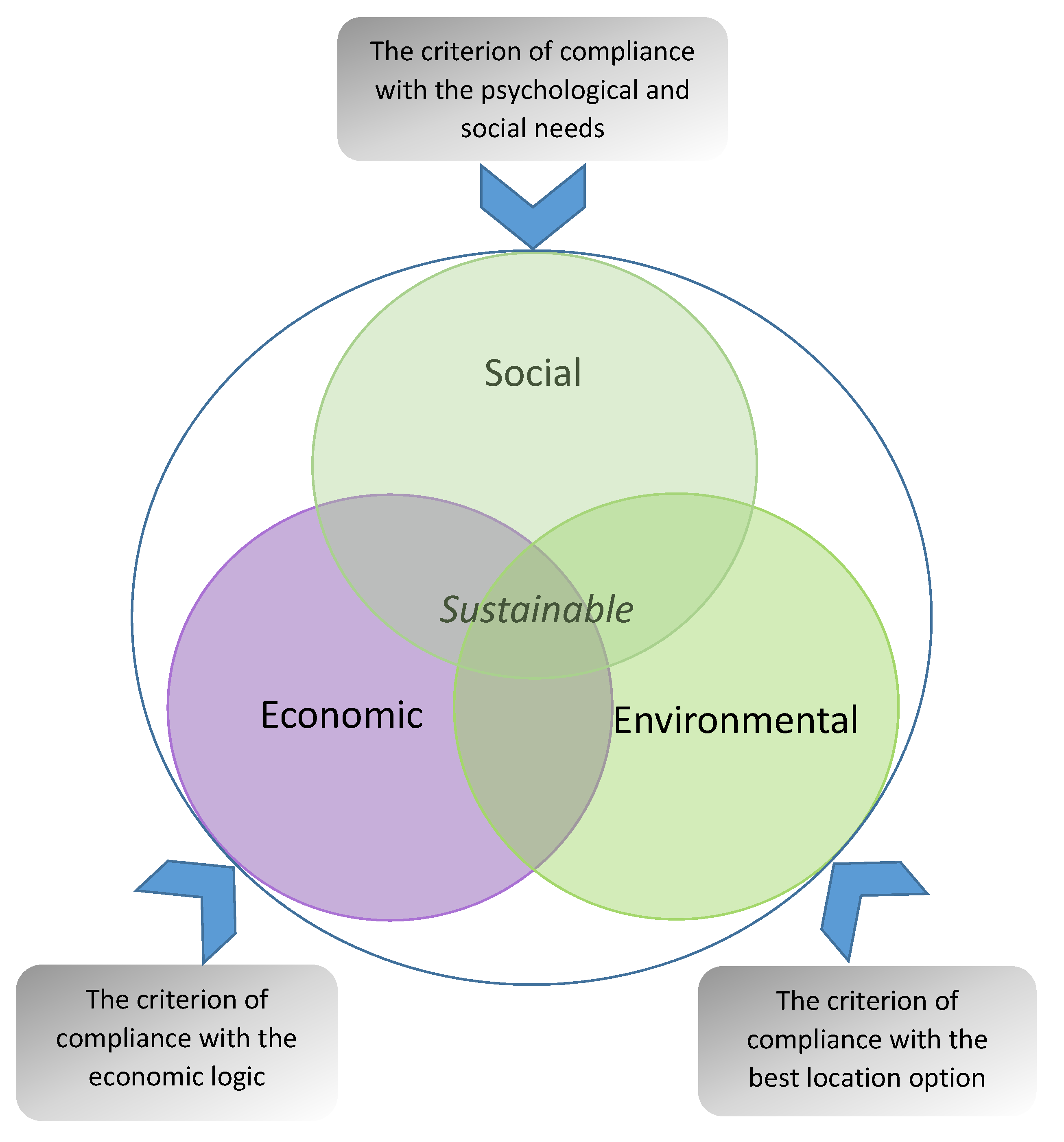
4.3. Criteria

The criteria for AHP method were selected based on the results of the article [17]. The main difference of current research is that one of these criteria (the criterion of compliance with the economic logic) is very special—it varies depending on the scale, and we consider a series of scales in order to perform the sensitivity analysis. Additionally, in this section, we provide deeper insight of the dependence of the criterion of compliance with the economic logic on the rest. These four criteria were selected:

• The criterion of compliance with the psychological and social needs (situation of neighborhood, habitual place, status, lifestyle, appearance, romanticism, and history).
• The criterion of compliance with the economic logic including an assessment of the object price.
• The criterion of compliance with the strategic (political) objectives including an assessment of the investor’s plans—whether the object will be rented, sold, or used for living.
• The criterion of compliance with the best location option—best location option including an assessment of the site quality, accessibility, and amenities of public and private service.

It is notable that the selected criteria fit into the general sustainability categories (see Figure 4): Economic (compliance with the economic logic), Social (compliance with the psychological and social logic), and Environmental (compliance with the best location option) [88].

The selected criteria are weighted using a rating scale from 1 to 9 if the first comparable criterion is more important than the second, and from −9 to −1 if vice versa.

The investor compared the selected criteria according to their importance in choosing the best roof installation project, thus determining the weight of each criterion.

Table 4. Comparison table for weights of the criteria.

Criteria for Comparison	Importance and Intensity
Compliance with the psychological and social needs	−3
vs. Compliance with economic logic
Compliance with the psychological and social needs	−3
vs. Compliance with strategic objectives
Compliance with the psychological and social needs	2
vs. Compliance with best location option
Compliance with economic logic	−1
vs. Compliance with strategic objectives
Compliance with economic logic	5
vs. Compliance with best location option
Compliance with strategic objectives	5
vs. Compliance with best location option

presents this assessment.

The data from Table 4 are entered into the Formulas (3)–(7) according to AHP method. After applying these formulas, the weights of the criteria were compared and normalised;

Table 5. Weights for the criteria.

Criteria	Compliance with the Psychological and Social Needs	Compliance with Economic Logic	Compliance with Strategic Objectives	Compliance with Best Location Option
Weights	0.1376	0.3935	0.3935	0.0754

presents the obtained results. Note that the consistency ratio (11) in that case is equal to $0.001541$.

The criteria for selecting projects were assessed using a rating value from 1 to 9 if the investor wanted to sell the project and from −9 to −1 if the sale was undesirable.

At this point, we assume that the evaluations of all ratings of criteria are known, with the exception of the compliance with the economic logic, i.e., we model a situation when this single parameter could differ, depending on various conditions, and the rest of values are fixed. We derive the single case where that value is such that the decision is on the edge, i.e., the weighted scores for both alternatives are equal, and they are equal to 0.5. Thus, the value of criterion of compliance with the economic logic is calculated from the rest of criteria, assuming that both alternatives whether to sell the object or not have the same weighted scores 0.5. In order to illustrate the dependency of the compliance with the economic logic (the main criteria) on the rest of criteria, we chose the same values for all three of them. Figure 5 presents the result function. The graph shows how the points of compliance with the economic logic criterion decrease as the rest of the criteria rise, i.e., for a better project, the calculated price (estimated according to the economic logic) is worse. It is also worth mentioning that, due to the AHP method restrictions, we have a maximum of assessment, which is nine points. It means that both of the alternatives are not necessarily equal anymore, and it leads to a natural restriction of the proposed approach.

Table 6. THe assessment of the criteria by the investor (decision whether to sell the object).

Criteria	Values of Projects Criteria
	A	B	C	D	E	F	G	H
Compliance with the psychological and social needs	−3	−9	−3	−9	−3	−9	−3	−9
Compliance with strategic objectives	−2	−5	−1	−4	−3	−6	−2	-5
Compliance with best location option	2	2	2	2	2	2	2	2
Compliance with economic logic, points from AHP when both alternatives are equal	2.6	9	1.25	9	4.14	9	2.6	9

presents the investor’s assessment of the compliance of A-H projects criteria with psychological and social needs, strategic objectives and best location. The criterion of compliance with economic logic was calculated on the basis of the assessment of the above criteria using Formulas (12)–(14); it is shown at the bottom of Table 6. Here, it should be noted that, due to the restrictions of the AHP method when the investor evaluates the criteria as more appropriate for alternative do not to sell the project, and the scores are negative below the limits, the values of the economic logic criterion are nine points.

4.4. The Sensitivity Analysis

This section presents the parametrisation of the investor’s behaviour and sensitivity analysis of the AHP method. Sensitivity analysis helps to assess the robustness of the decision. We propose modelling the investor’s behaviour using a special linking of the rating scale to the monetary values, describing the influence of the property on the individual’s decision. We show how to integrate that mapping into the model and evaluate the obtained results.

The model was initially developed for a single investor. Thus, possible changes in the assessment or parameters that will occur if the number of the investors increases are taken into account.

For the sensitivity analysis, we introduce different mappings of the ratings scale to the monetary values of project prices, as presented in

Table 7. The mappings of the scale to monetary values of the project for economic criteria.

Scale	Multiplier of the Scale Mapping and the Corresponding Monetary Values in Euros
	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
9	8000	16,000	24,000	32,000	40,000	48,000	56,000	64,000	72,000	80,000
8	7625	15,250	22,875	30,500	38,125	45,750	53,375	61,000	68,625	76,250
7	7250	14,500	21,750	29,000	36,250	43,500	50,750	58,000	65,250	72,500
6	6875	13,750	20,625	27,500	34,375	41,250	48,125	55,000	61,875	68,750
5	6500	13,000	19,500	26,000	32,500	39,000	45,500	52,000	58,500	65,000
4	6125	12,250	18,375	24,500	30,625	36,750	42,875	49,000	55,125	61,250
3	5750	11,500	17,250	23,000	28,750	34,500	40,250	46,000	51,750	57,500
2	5375	10,750	16,125	21,500	26,875	32,250	37,625	43,000	48,375	53,750
1	5000	10,000	15,000	20,000	25,000	30,000	35,000	40,000	45,000	50,000
−1	5000	10,000	15,000	20,000	25,000	30,000	35,000	40,000	45,000	50,000
−2	4625	9250	13,875	18,500	23,125	27,750	32,375	37,000	41,625	46,250
−3	4250	8500	12,750	17,000	21,250	25,500	29,750	34,000	38,250	42,500
−4	3875	7750	11,625	15,500	19,375	23,250	27,125	31,000	34,875	38,750
−5	3500	7000	10,500	14,000	17,500	21,000	24,500	28,000	31,500	35,000
−6	3125	6250	9375	12,500	15,625	18,750	21,875	25,000	28,125	31,250
−7	2750	5500	8250	11,000	13,750	16,500	19,250	22,000	24,750	27,500
−8	2375	4750	7125	9500	11,875	14,250	16,625	19,000	21,375	23,750
−9	2000	4000	6000	8000	10,000	12,000	14,000	16,000	18,000	20,000

. For the sake of simplicity, we use a single parameter describing the differences between mappings—a multiplier which ranges from 0.2 to 2 with a step of 0.2; the values in the table are proportional to that multiplier. The investor has estimated project prices that correspond to the maximum and minimum ratings when the multiplier is equal to one. The rating scale is the result of the investor’s survey. In our case, the investor agreed that the project intermediate prices will be determined by linear interpolation and assigned to the remaining ratings of the scale.

In

Table 8. Market prices of the investigated roof installation projects to be used in the decision tree.

Criteria	Projects
	A	B	C	D	E	F	G	H
Market price for sale (b)	27,313	42,341	28,468	43,501	16,326	80,231	27,486	41,401

, we present the market prices of projects A–H, which, in the decision tree, are compared with the prices that are determined by the AHP method based on the investor’s subjective opinion. The market prices for the roof projects A–H were determined on the basis of an expert’s assessment, while taking into account statistical indicators and the fact that the roof area of all projects was 63.2 square meters, the geographical location of the building was also identical, and the price varied due to the differences of roof and attic layout, materials, finishing, comfort, and design features. The detailed procedure of market pricing is outside the scope of our study and, therefore, is not presented in this paper.

Figure 6 shows the data that were obtained by solving the decision tree in the presence of various multipliers. Data on the values of projects for the investor were entered into the relevant end nodes of the decision tree. These values are determined by interpolating the monetary values from Table 7 at the points of the scores of the criterion of the economic logic value from Table 6. The market prices of the projects, which are presented in Table 8, were also entered into the relevant end nodes of the decision tree.

As the scale changes, the results obtained in the decision tree for each project change differently, as can be seen from Figure 6. Initially, when the values of the multipliers are small, the main factors influencing the final result are the market price and project implementation costs; a little later, when the multipliers increase, the value for the investor exceeds the market price, and causes a breaking point on the graph. As the multiplier continues to increase, the final result is determined by the investor’s subjective opinion and the cost of the project. Here, it is possible to find points of lines intersection where the monetary value of some different projects is the same. Analysis of the changes in the investor’s subjective opinion is useful in the selection of parameters for scale mapping, in assessment how the final result depends on the chosen scale. The results of this analysis can be used to determine the price of the project and reconcile the stakeholders’ interests. Depending on the investor’s subjective opinion about the value of the project, brokers can make attractive offers to the investor that would lead to the sale of the project outcomes, if there is a corresponding need.

It is worth mentioning that the horizontal parts of the curves represent the cases when the decision to sell the project is made. With the mapping multiplier 1 and lower, the investor decides to select the project F and sell it, as can be seen from Figure 7. However, with higher values the decision not to sell the project is made, the results might differ, depending on value of the mapping multiplier: with values 1.2 and 1.4, A and G projects are selected, both having very similar values (A has approximately 0.7% higher values). This behaviour of changes in decision can be interpreted as:

• Lower values of scale mapping mean a greater tendency to sell the project rather than not to.
• When choosing the project with lower values for sale, the project F is the best option.
• Higher mapping values mean the investor’s bigger tolerance to the higher costs, thus he tends not to sell the project.
• With values 1.2 and 1.4 the investor selects the medium-cost project, but does not sell it.
• As the scale multiplier raise, the investor chooses to invest in expensive project and not to sell it.

4.5. An Example of Case Assessment Made by Independent Expert

Up to this point, decisions were made solely on the basis of the investor’s opinion. In the context of the research, one investor is sufficient for performng the analysis, because it is necessary to analyse his behaviour. In other words, there is no need to aggregate the data of multiple experts’ opinion, as it is useful to do for an estimation of some objects, where multiple opinions give a better and less subjective picture—in the case of the considered situation we want to assess the effect of investor’s subjective opinion. However, in order to estimate the possible changes in the results in the case of the radical changes during the implementation of the project, such as the change of the investor, we had to consider all of the steps affected by the investor. What we assumed up to the point is that the mapping of the scale to the monetary values will change; however, it is obvious that the whole assessment could also change. Here, all possible parts of the model, affected by such changes, will be taken into account, and, for this purpose, to achieve, we will briefly follow all of the necessary steps.

A person with five years of experience in the field of construction marketing was selected as an independent expert. Further, we assume that the expert assesses the situation from the investor’s point of view. Note that we do not want to enrich the results of the assessment of the considered case; instead, we provide an illustration of what needs to be changed if the investor changes. Further, we will provide the following steps that are needed for modification:

• The independent expert compares the criteria for weights determination (analogically to Table 4). All of the criteria are rated as equally important, i.e., by 1 point.
• Using AHP, the weights (Table 5) for criteria are calculated. The weights of the criteria in this case are the same and equal to 0.25.
• Table 6 is re-evaluated by the expert, the results are provided in

  Table 9. Criteria assessment made by the expert (decision whether to sell the object).

  Criteria	Values of the Projects Criteria
  	A	B	C	D	E	F	G	H
  Compliance with psychological and social needs	−2	1	1	1	2	5	3	7
  Compliance with strategic objectives	1	2	2	2	−2	5	2	3
  Compliance with best location option	−2	−2	1	−2	−2	5	1	3
  Compliance with economic logic, points from AHP when both alternatives are equal	5	1	−2	1	2	−9	−9	−9

  .
• The table, analogous to Table 7, is filled according to the new opinion. It is important to note, that every field in it can be evaluated individually, however, it can be simplified as it was done already—the interpolation can be applied to form the base mapping, and the multiplier can produce the rest of mappings. We interpolated between two values to create the base mapping; the results are provided in

  Table 10. The mappings of the scale to monetary values of the project for economic criteria (based on expert’s opinion).

  Scale	Multiplier of the Scale Mapping and the Corresponding Monetary Values in Euros
  	0.2	0.4	0.6	0.8	1	1.2	1.4	1.6	1.8	2
  9	10,200	20,400	30,600	40,800	51,000	61,200	71,400	81,600	91,800	102,000
  8	9793.75	19,587.5	29,381.25	39,175	48,968.75	58,762.5	68,556.25	78,350	88,143.75	97,937.5
  7	9387.5	18,775	28,162.5	37,550	46,937.5	56,325	65,712.5	75,100	84,487.5	93,875
  6	8981.25	17,962.5	26,943.75	35,925	44,906.25	53,887.5	62,868.75	71,850	80,831.25	89,812.5
  5	8575	17,150	25,725	34,300	42,875	51,450	60,025	68,600	77,175	85,750
  4	8168.75	16,337.5	24,506.25	32,675	40,843.75	49,12.5	57,181.25	65,350	73,518.75	81,687.5
  3	7762.5	15,525	23,287.5	31,050	38,812.5	46,575	54,337.5	62,100	69,862.5	77,625
  2	7356.25	14,712.5	22,068.75	29,425	36,781.25	44,137.5	51,493.75	58,850	66,206.25	73,562.5
  1	6950	13,900	20,850	27,800	34,750	41,700	48,650	55,600	62,550	69,500
  −1	6950	13,900	20,850	27,800	34,750	41,700	48,650	55,600	62,550	69,500
  −2	6543.75	13,087.5	19,631.25	26,175	32,718.75	39,262.5	45,806.25	52,350	58,893.75	65,437.5
  −3	6137.5	12,275	18,412.5	24,550	30,687.5	36,825	42,962.5	49,100	55,237.5	61,375
  −4	5731.25	11,462.5	17,193.75	22,925	28,656.25	34,387.5	40,118.75	45,850	51,581.25	57,312.5
  −5	5325	10,650	15,975	21,300	26,625	31,950	37,275	42,600	47,925	53,250
  −6	4918.75	9837.5	14,756.25	19,675	24,593.75	29,512.5	34,431.25	39,350	44,268.75	49,187.5
  −7	4512.5	9025	13,537.5	18,050	22,562.5	27,075	31,587.5	36,100	40,612.5	45,125
  −8	4106.25	8212.5	12,318.75	16,425	20,531.25	24,637.5	28,743.75	32,850	36,956.25	41,062.5
  −9	3700	7400	11,100	14,800	18,500	22,200	25,900	29,600	33,300	37,000

  .
• Based on the achieved results, the new set of curves describing the dependency of profit/loss on the scale mappings are produced; the results are provided in Figure 7.

With the mapping multiplier 0.8 and higher, the expert selects project A, as can be seen from Figure 7. The result shows that the expert’s decision in favour of selecting project A and not selling the project is robust, and it does not change with higher multiplier values. However, with lower multiplier values, the expert decides to select the project F and sell it.

4.6. The Application of the Model to Other Cases

Up to this point, it was focused on the selected case study that was used as a tool to demonstrate the proposed ideas. However, the modelling approach provides a powerful way to deal with a wide range of situations. Here are some key points that the applicator must take into account:

• The process being modelled must be described as a Markov process.
• All possible scenarios in different process states must be evaluated by the probabilities of their occurrence.
• The dependencies between states must form a tree, so, in some cases, some redundant information must be included (i.e., the structure of the tree branch is identical in both cases: either the consultant will be selected or not). However, there is an important feature—the model supports some process costs that occur as additional costs with some probabilities, it can be added directly without the duplication of some branches of a tree.
• The pool of projects must be formed with an appropriate assessment of each of them via AHP method.
• If one would like to an add additional parametrisation of the project, he should consider every set of parameters (e.g., some quality parameters) as a separate project entity and then add it as a leaf to the tree together with the needed branch.
• As was mentioned above, s wide variety of decisions can be added and the proposed algorithms are absolutely compatible with as many decision choices from the single state as needed, i.e., there is no requirement for the tree to be binary.
• The mappings of the scale to the monetary values are decisive for the outcome of the modelling. Thus, these mappings must be carefully thought of before the final sensitivity analysis.

5. Discussion

After studying a joint derivative of the Decision Tree and AHP methods, it was found that a combination of these methods can be used for project assessment. Although data collection and modelling is quite labour-intensive, the development of a model template opens up a wide range of possibilities for project assessment, exploiting the potential of information technology and remote working.

It was found that the rating values for the economic criterion, which were obtained using the AHP method, sometimes exceed the limits that are set by AHP method (i.e., the maximum score according to the considered scale is 9). This happens, for example, in the case when the rest of criteria have the same rating, and when the rating values for the remaining criteria reach −3.1588 points. This situation is typical for expensive projects, when the investor tends not to sell the results of the project, i.e., the economic criterion rating exceeds the maximum value in the rating scale—in such a case, the maximum value will be used.

When modelling the investor’s behavior, it is necessary to examine his opinion in detail, as well as to know the real estimate of the project, which also poses certain difficulties. On the one hand, in order to solve this problem, the examples of known projects that are similar in content and value can be used; on the other hand, many typical projects can be created and their data can be applied to the model.

The methodology that was considered in the article, which combines AHP and decision tree methods, solves the problem of the selection of the most suitable project. As a part of the methodology, it was introduced a sensitivity analysis, which enables taking the investors’ different opinions into account. Such sensitivity analysis shows how sensitive the possible decisions are, depending on changes of the situation (e.g., if the investor changes)—it is dedicated to the analysis of the robustness of decisions.

In this research, different options of medium-cost and expensive roofing projects were examined. The costs of all roof elements and project activities were provided and applied according to the methodology; these values were used in the decision tree. The AHP method was used to estimate the investor’s subjective opinion.

It is notable to mention that the criteria for the AHP method were selected in accordance with the principles of sustainability, more specifically—the main categories of sustainability: social, environmental, and economic. The proposed approach was applied to estimate how one of the parameters (the economic one) reacts to changes of the rest parameters, provided that the assessment by the AHP method is on the edge between two decisions for two alternatives. In this research, we examined variations of mappings, which directly affected the economic criterion. The economic criterion is derived from the rest of criteria, thus the analysis can be extended by additional modification of the rest of criteria, which would greatly expand the analysis; however, from a methodological point of view, the current method does not need any modifications.

The considered case study has the primary typical attributes of building projects, thus we assume that it is sufficient to demonstrate the proposed approach. We believe that this approach can be applied to other cases—it is a topic for future research. Moreover, investor’s and independent expert’s opinions were used to produce a base mapping of the scale to the monetary values. The rest of the scales were derived using a simple multiplier representing different opinions, which was applied to a simple linear interpolation of the monetary values. Thus, the logical addition would be to use different scales without clear dependency between them; however, it is out of scope of this research, as it would not qualitatively improve the results—in this research, the illustrative type of the case study was performed. The set of the decisions and their order were selected from the point of view of the investor. Thus the set of the decisions to form the decisions strategy might look quite limited, because the decisions performed or affected by other stakeholders are included into probabilistic nodes and via additional costs and duration with probabilities.

It is worth mentioning that the AHP method was chosen, since it is widely used and the explicit formula (see Formula (13)) can be derived for the required assessment. Other methods of multi-criteria assessment can also be applied; however, it is not a straightforward task and it needs a separate investigation. The analysed case can be directly described as a Markov process that permits formulating the optimisation problem in order to maximise investor’s profit—it was used to model the investor’s behaviour. The solution of this problem was exact and it was achieved using the dynamic programming method. Thus, as long as the modelled process was the Markov process, and the computations were performed in the reasonable time, there was no reason to analyse any other methods to solve that optimisation problem. The AHP method gives the assessment of the economic criterion for the decision tree method; the usage of the alternative multi-criteria methods could be studied in future work.

In this research, the case covering most of the aspects that must be taken into account when filling the model with data was analysed. The investor is individual and the project is single. Additionally, it was assumed that the projects are well-defined, so the investor can choose one of them that absolutely defined the constructional solutions (unless some risks will trigger, for example, with mistakes, etc.). This means that all quality parameters or any project specific constructional details must be bundled with one of project and used in the model as a separate example. The considered case was a limited by a single project, the decisions were made using the probabilistic expectation values according to dynamic programming method that was defined by Formula (2), which can be altered to estimate the risks in a non-linear way. However, if the investor considers the pool of projects forming a possible portfolio, then the diversification of the investment can lead to a better tolerance to the possible risks, making the mentioned expectation values more suitable for the needs of the investor.

The main stakeholder in this research is the investor; thus, for the reader, it might create the suspicion that this research is dedicated to some sort of a tool for the investor. However, the mentioned sensitivity analysis considers the investor as a part of the model that might be prone to the changes, so the proposed techniques are potentially useful for any stakeholder who want to analyse the possible scenarios and changes. For example, the building design company might be interested to analyse what do investor choose and under which conditions, for example, if the investor tends to choose some specific type of projects, the company might want to prepare more variations for this type of projects.

The conducted research is not oriented to investor’s needs; however, the investor might find the discussed techniques useful for:

• including the possible changes of priorities, financial abilities, etc., into risk assessment routines; and,
• getting recommendations for selection of the consultants and supervisors, companies of building design, construction, and supply, also different roof installation projects.

Summarising, the topic of such analysis of possible changes is important for hypothetical usage, for example, for these stakeholders:

• By investors to include the information into their risk assessment and obtain some recommendations.
• By building design or construction companies to improve their pool of potential projects.
• By government to model how possible restrictions might affect the priorities of investors.
• The representatives of interested community might be interested in predictable successful project implementation as a part of sustainable city development, so the lack of decision robustness might indicate an important information for these stakeholders.

Note that the exact procedure of how to apply the results in the mentioned cases is up for discussion, and it is out of scope of this research.

As it was already mentioned in introduction, the AHP application assumes that the criteria are evaluated by individual; thus, the current approach is limited to dealing with an opinion of a single evaluator. Thus, the reader should not try to apply it to some study where the collective evaluation is needed by the group of experts. This research considers the opposite—taking the bias of the individual investor into account in the case when the type of project implies the assessment by a single person. Certainly, it can be assumed that the evaluation made by that individual is performed with the help (consultations) of some sort experts; however, technically it is not important for the methods in the current research.

In the context of this research, the AHP assessment is dedicated to the decisions on whether to sell the project or not, which directly reflects the opinion of the investor about that project: if in the eyes of the investor the project is not worth the price, then he will tend to sell it. In the case when some of the criteria are very important for the investor, the value of the project will exceed the value of the price—here, the word “value” stands to represent the evaluation of the project or the money (this value might depend on the richness of the investor) that can be earned from it. The fact of the direct comparison between these two values might create the illusion that only the actual object price is included into decision directly; however, the value that comes from the AHP assessment has nothing to do with the actual price of the object—in fact, it is the opposite, it represents all of the remaining criteria and does not include any direct information about the market prices or the prices of materials, etc. In other words, the comparison in the nodes is a comparison between the actual price, which does not depend on the investor’s opinion and the value of the rest criteria that is scaled, so it could be comparable to the value of the price. Thus, all of the criteria are directly included into the decision via AHP method. However, the evaluation of the rest of the decisions is derived from the last decision (to sell or not), so it is up for discussion as to whether the criteria should affect those decisions in the same manner as they do on the decision to sell the object or not. For example, the importance of hiring consultants might be driven by the importance of some criteria to a greater degree that it is in the case of the decision to sell the object. The proposed approach is unable to include a special role for different criteria for intermediate decisions directly, it needs a special analysis to identify the necessity for support of such decisions and the way to implement them—this could lead to the potential improvement of the proposed model; however, it is out of scope of the current research.

6. Conclusions

It was shown that different mappings influence the project assessment differently, leading to changes in the best project selection. It was found that, with a small mapping multiplier, more expensive projects were unprofitable, with the exception of E and F projects.

The effect of the investor’s and the independent expert’s subjective opinion on the selection of the best project was visualised. The obtained results are visually presented in the form of graphs (Figure 6 and Figure 7). The graphs of the dependence of the projects assessment results on the special mapping of the ratings scale helped to understand the situation of the most appropriate project selection. It showed how close the potential projects were to each other in terms of the assessment, which was directly used for the selection of the best project. The visualisation of the obtained results can be useful in forecasting the investor’s behaviour during project development and in negotiations for the sale of project outcomes.

After examining the results of the decisions tree, it was found that more expensive project F was the most attractive with a multiplier of 1. Project F, due to its design features, was rated significantly better from a market perspective than other more expensive projects. With multiplier values from 1.1 to 1.6, the profit value of this project was lower than the values of some other projects; in other cases, project F was more profitable. The medium-cost project E was rated badly by the market—it was not profitable to sell it, although the investor with some multiplier values rated it as the most suitable for him in comparison with other medium-cost projects. The independent expert’s opinion was also evaluated. The expert’s decisions differed from the investor’s opinion—if multipliers were higher than 0.7, then the expert selected project A, but, if the multiplier was less than 0.7, both opinions almost coincided. A small increase in project implementation costs can affect the project selection—this means a possible lack of the robustness of the project decisions may appear.

The analysed methodology can be generalised for application to other project selection problems, not only for implementation of roofing projects. For the application, it is necessary to take the specifics of the projects, the costs of certain types of activities, the probabilities, the possible losses, the factors that affect the system, and the possible patterns of the process participants’ behaviour into account. It is also worth considering the amount of time for project preparation and implementation, because, in some cases, this factor can be extremely important.