A Simulation Model of Construction Projects Executed in Random Conditions with the Overlapping Construction Works

Abstract

Reducing the duration of construction works requires additional organizational measures, such as selecting construction methods that assure a shorter realization time, engaging additional resources, working overtime, or allowing construction works to be performed simultaneously in the same working units. The simultaneous work of crews may affect the quality of works and the efficiency of construction processes. This article presents a simulation model aimed at assessing the impact of the overlap period on the extension of the working time of the crews and the reduction of a repetitive project’s duration in random conditions. The purpose of simulation studies is to provide construction managers with guidelines when deciding on the dates of starting the sequential technological process lines realized by specialized working crews, for sustainable scheduling and organization of construction projects.

1. Introduction

The main purpose of developing the sustainable schedule at the project planning stage is to determine the expected completion date of the project and the duration of individual processes, as well as their cost. On the other hand, the schedule is also the main tool for monitoring and controlling the realization of the planned project. During the execution of the project, smaller or larger discrepancies between the as-planned and actual dates are to be expected. It is a common phenomenon and it is difficult to avoid, especially in the case of long-term projects, which involve multiple resources and consume considerable funds. The reasons for deviations from the plan typically include problems with human resources, changing weather conditions, or the lack of adequate financial reserves. Other factors that may result in differences between the plan and its realization are changes in resource availability, untimely deliveries of material and the equipment failures [1,2,3,4,5,6,7].

The growing requirements for the conservation of natural resources have a major impact on the development of concepts for planning and executing construction projects. Additionally, in a rapidly changing environment, with increasing investor demands for cost, quality and timeliness, and increasing sustainability requirements, project managers need to improve project planning and control tools. Construction projects consume large quantities of resources. Therefore, their appropriate allocation to construction processes ensuring their rational management is one of the main challenges of sustainable construction project management [8,9]. Untimely completion of construction processes can have a negative impact on other parties involved in its implementation, mainly material suppliers, construction machinery owners, and subcontractors [9]. It may lead to improper use of their resources and even losses.

As a result of delays in the realization of works, additional resources may need to be hired to help make up for the lost time. Most often, delays with some works propagate throughout the schedule as subsequent works cannot start unless their predecessors are completed. In such cases, the schedule developed at the planning stage is an appropriate starting point for verification of the assumptions adopted in the plan. A detailed analysis of these assumptions may allow the deadline for the project realization to be met [10,11,12,13].

The necessity to revise the assumptions is most often caused by the need to accelerate the project, by incorrect determination of the realization time of individual processes, or by delays in/speeding up the realization of some tasks. Reconsideration of the assumptions cannot be avoided in the event of changes in the demand for resources and their availability, or when it is necessary to change the adopted technological and organizational solutions [14,15,16,17].

The reduction of the project realization time very often results in additional costs. They mainly result from higher overtime rates, additional charges for subcontractors for express works, or the use of more advanced technology. To effectively accelerate the project, the cost analysis should be based on the processes of the critical path. Increasing the efficiency of non-critical tasks is economically ineffective if the focus is on reducing the project time. Many sources recommended to first accelerate those critical activities whose changes generates the lowest additional costs [18,19,20].

Depending on whether resource analysis is included in the schedule development stage, the deadlines for realization of individual tasks result from the critical path or from the sequence of tasks constituting the critical chain. Critical chain processes have limited availability of one or several resources used during their realization. The critical path and the critical chain overlap if all levels of resource availability allow the work to be realized within the time limits resulting from the time analysis. If the deadline for completing the project after the resource analysis exceeds the directive deadline resulting from the time analysis, there is a need to compress the schedule. Therefore, in the first place, it is necessary to identify the critical chain and resources that limit the efficiency and capacity of the entire chain as well as extend the deadline for the realization of the project [3,21,22].

There are many techniques that can be used to shorten the duration of a project while maintaining its scope. One of them is fast-tracking, which makes it possible to shorten the critical path by planning parallel realization of processes that were previously scheduled in sequence. It is recommended that fast-tracking method be the first of accelerating the project duration, because it does not generate additional costs and can also contribute to reducing the company’s fixed costs. However, starting work before the completion of another stage is associated with a high risk of errors, generating additional resources and work [23,24].

Another schedule compression technique is crashing. This method is based on accelerating the realization of processes by increasing resources (employing additional people, using equipment with higher efficiency). The essence of the effective use of crashing is the maximum reduction of task durations using the minimum amount of additional resources necessary to optimize these processes. Effective implementation of crashing involves the application of this technique to the critical path activities, starting with tasks whose optimization is associated with the lowest cost [19,25,26,27].

Another method that allows for the effective use of time for project realization is the critical chain method. This technique assumes a time reserve (buffer) for the entire project instead of for individual processes. The use of the critical chain method enables the project to be completed in 10–50% less time compared with other techniques [28,29,30].

Short deadlines for the realization of projects imposed by investors who want to benefit from projects as soon as possible, as well as the risk of contractual penalties for failure to meet the deadline, often force general contractors to compress schedules. To help managers analyze the effects of schedule compression measures, the authors put forward a simulation model. It is specifically intended for assessing the impact of the scale of task overlap period on the extension of the working time of the crews and the reduction of the project duration in random conditions. To illustrate the idea, we present an example—simulation tests on a repetitive construction project. The purpose of simulation studies is to provide construction managers with guidelines when deciding on the dates of starting the sequential technological process lines realized by specialized working crews, for sustainable scheduling and organization of construction projects. The model aims to eliminate delays in construction projects while taking into account the degree of resource utilization, which is one of the objectives of sustainable construction project management.

2. Materials and Methods

2.1. Literature Review

There are many terms in the literature that define the overlapping of processes, such as fast-tracking, concurrent engineering, or parallel engineering. Research related to overlapping processes mainly cover two areas: product development and project management [31,32,33,34,35,36,37]. The models developed in these studies informed researchers who implemented them in the construction industry.

Constraints in managing overlapping are caused by, among other things, time-cost trade-offs problems. Meier et al. [38] used a multi-objective evolutionary algorithm to derive Pareto points of the best solutions to time–cost trade-off.

Ballesteros-Pérez [39] proposed a stochastic model that allows for extensive analysis of overlapping activity. This proves that the possibility of reducing a schedule by more than a quarter of its original duration is very unlikely. The relationship between cost and overlap was also defined.

Dehghan et al. [40], having interviewed experts dealing with the mechanism of overlapping tasks, created a model that solves the problem of the compromise of time and cost overlapping in the design phase. The developed model can obtain the optimal degree of overlapping for schedule tasks while maintaining minimal costs.

Hossain and Chua [41] noted the large impact of the accuracy of the design phase information on the reduction of project duration and the number of additional works overlapping with design and construction tasks. As a result of the research, they created a simulation model that determined the project parameters regarding the total duration of the investment and the expected number of reworks.

Pena-Mora and Park [42], observing the dynamic construction process carried out in fast-tracking conditions, developed the dynamic planning methodology (DPM). This method aims to improve the planning and management of fast-tracking construction projects by providing overlapping strategies, hiring control policies, and schedule adjustments that minimize the negative impact of fast-tracking.

Berthaut et al. [43] paid attention to the lack of consideration of resource availability constraints when overlapping tasks in the schedule. Using linear programming, they developed a resource-constrained project scheduling model with different modes of task overlap and the resulting rework. Research results also show a close interaction between limited resources and task overlapping modes.

Simulation models have been used in the planning and testing of complex construction projects for many years. The main advantage of simulation models is the lack of constraints on the structure and complexity of the tested system and the possibility of taking into account the risk conditions, which allows the modelling of real systems with a high degree of complexity and a high proportion of random factors.

Referring to their previous research on the sensitivity and development of processes, Bogus et al. [44] implemented one of the first comprehensive computer algorithms to optimize the overlap of activities in schedules. This algorithm used Monte Carlo simulations to predict different discrete outcomes for each activity to obtain more accurate rework probabilities. The simulation model determined the risk of having to redo the task or part of it. The simulation results provide information about the probability of rework based on different combinations of variations, sensitivities, overlap strategies, and percentage overlap between the process and the upstream and downstream activities.

Wang and Lin [33] created a simulation model in which they analyzed the impact of the tasks sequence and the degree of activities overlap on the duration of the project. However, in their research they did not take into account the constraints related to the availability of resources.

Cho and Eppinger [45], thanks to the use of a simulation model, analyzed the structure of information flow in a project in which cyclical, parallel, and overlapping tasks were repeated. The model also took into account the randomness of the duration of the processes and constraints in the availability of resources. The authors showed that resource constraints can delay the overlap of certain activities and, thus, the completion time of a project. As a result, they obtained an effective tool to evaluate alternative planning and execution strategies.

Srour et al. [46] presented a methodology for using bi-directional information exchange to schedule the design phase in an accelerated manner. As a result, it is possible to generate the shortest (with overlapping) schedule based on the dependencies between different design phases. Apart from task durations, the algorithm also takes into account the exchange of information between them.

Hossain et al. [47] developed a simulation model to determine the total duration of a project with overlapping tasks and the number of rework expected. The results show that the reduction in project duration and the expected number of reworks vary depending on the accuracy of the information from the earlier stages and the sensitivity of the downstream activities. Moreover, unplanned overlap may not necessarily reduce the project duration, but may result in an excessive amount of design and construction work which can be very costly. The proposed optimization method minimizes the expected number of rework while maintaining the project completion date and aids in deciding on an overlay strategy.

The simulation model proposed by Lim et al. [48] uses schedule data and parallel process parameters to calculate the variability of time and cost to realize a project by adjusting the overlap of tasks. The study produces a compressed schedule that allows for a limited budget to be implemented within a specific contract duration.

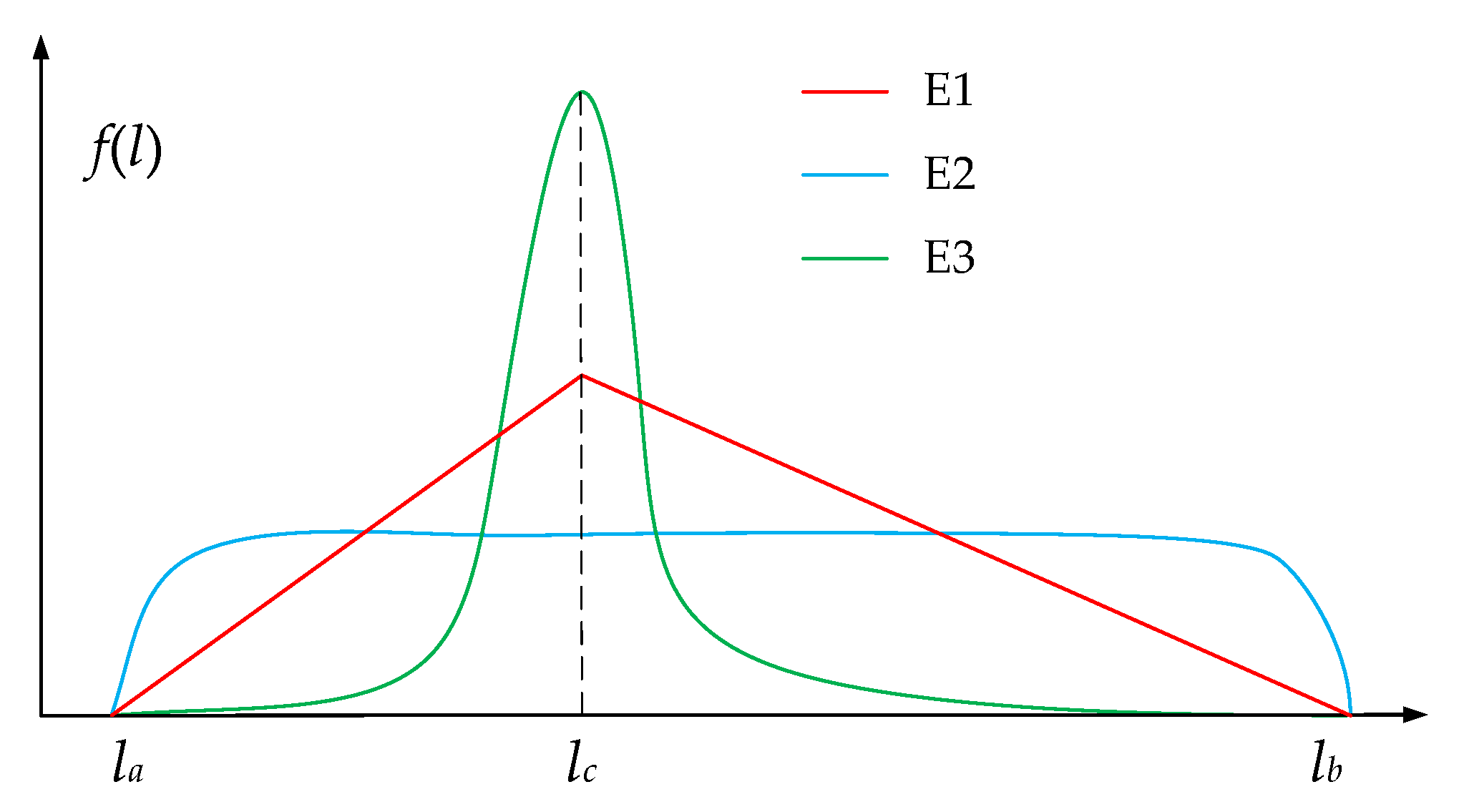
2.2. Simulation Model

Including simultaneous execution of successive technological processes on the same unit in construction schedules requires describing the interaction between activities. It is necessary to determine the probability function of rework occurrence as a function of the time of overlapping activities and to determine the impact on time or cost of simultaneously performed processes. The use of historical data to determine the impact of overlapping on the occurrence of future rework is limited. Such information is not collected, stored, or analyzed by construction managers. Construction projects are unique and are executed under varying conditions (site location, ground conditions, different seasons) which adds to the difficulty of both obtaining such data and applying it to a new construction project. Many works, e.g., [43,45], assume that the relationship between overlap and amount of rework is known. Bogus et al. [44] assume a theoretical relationship between the probability of rework and degree of overlap. The issue of the model parameter estimation problem is very often neglected in the literature.

The proposed method uses estimates, as in the widely accepted PERT method in the construction, of duration distributions using three parameters. Estimates are also made for the conditional distributions of process performance taking into account their simultaneous execution on the same unit. The expert must consider the impact of overlapping activities on process performance. A decrease in productivity can be caused by using the same equipment on the construction site, e.g., limited number of concrete mixers or insufficient capacity of construction cranes. Estimating the parameters of the conditional distributions should not be difficult for an experienced construction manager. The expert can specify the decrease in productivity as a percentage of the base productivity, which further simplifies the method of estimating the parameters of the probability distributions of the duration of construction processes. The model takes into account organizational constraints typical for the construction industry: carrying out works on one work plot by two working brigades at the same time at the most; and, first of all, meeting the precedence constrained by introducing front reserve into the model.

The proposed simulation model allows the user to analyze the repetitive construction project consisting of non-uniform processes (the durations of processes of the same kind may differ from unit to unit) under random conditions. An example of such an undertaking may be the construction of several buildings differing in size (e.g., cubic capacity or usable space) using the same materials and methods in the same construction site, or the construction of a tall building. Let us assume that the project consists of j (j = 1, 2,…, n) units where processes i (i = 1, 2,…, m) are consecutively performed by specialized crews. The start of process i on the unit (j + 1) can take place after the completion of this process on the unit j. Let us assume the labor consumption P_ij associated with processes i in unit j are known; they can be calculated on the basis of standard productivity rates and work quantities.

If the quantity of labor in a unit is considerable (e.g., the unit is the entire story of a multistory building including several apartments), the crew does not need to occupy the entire unit at the same time—e.g., partition walls are made only in one apartment on a given day. This makes it possible to share the unit with a crew performing another process—thus, conducting various processes at the same time. The processes overlapping should, however, take into account technological limitations (e.g., partition walls cannot be bricked and plastered at the same time) and ensure appropriate technological breaks.

It was assumed that, due to the impact of risk factors, the daily output of crews performing the processes are random variables L_i described by arbitrary probability distributions of known type and parameters of the distribution. The type and parameters of the distribution should be determined by experts (construction managers with significant experience). The number of works performed on the unit j by a crew i up to date t is calculated as:

$$P_{ijt}={\displaystyle \sum _{s=1}^{t-1}{P}_{ijs}+{\delta }_{ij1}\cdot l_{ij1}+}{\delta }_{ij2}\cdot l_{ij2}+{\delta }_{ij3}\cdot l_{ij3};\forall i\left(i=1,2,\dots m\right),\forall j\left(i=1,2,\dots n\right),$$

(1)

where:

• δ_ij1 = {0, 1} and takes the value 1 in the event when, within the time limit t on the unit i, only the process j is realized; 0 in other cases;
• δ_ij2 = {0, 1} and takes the value 1 in the event when, within the time limit t on the unit i, the process j and (j + 1) are realized simultaneously; 0 in other cases;
• δ_ij3 = {0, 1} and takes the value 1 in the event when, within the time limit t on the unit i, the process j and (j − 1) are realized simultaneously; 0 in other cases;
• l_ijt1, l_ijt2, l_ijt3—random numbers according to the probability distribution of daily efficiency appropriate for the variant of the process overlap L_i1, L_i2, L_i3 taking into account overlap processes.

This principle is presented in Figure 1. Process 3 is started on subsequent work units with some delay due to the provision of time buffer between process 2 and 3 (no work front) required by technological constraints.

The simultaneous performance of works on the same unit by different crews may lead to a reduction in the daily efficiency of works. Their influence on the preceding crew is usually smaller than on the subsequent crew.

Due to technological limitations, it was assumed that the works’ front reserve R_i(i+1)t on every day t between processes i and (i + 1) on each unit (maximum allowable overlap) must meet the following condition:

$$R_{i(i+1)t}\ge D_{i(i+1)},$$

(2)

where: D_i(i+1)—the minimum reserve amount resulting from technological limitations (model parameter).

Reserve D_i(i+1) on the first unit of the process i simultaneously determines the earliest starting date of S_i(i+1)1 process (i + 1). It is the smallest natural number that meets the condition:

$$S_{(j+1),1}\ge S_{j,1}+D_{i(i+1)},$$

(3)

where: S_j,1—the start date of the process i, and the start date of project (the first process on the first unit) S_1,1 = 0.

For every day t (t = 1, 2,…), the real reserve between processes i and i + 1 in random conditions can be calculated for as:

$$\begin{array}{c}{R}_{i,(i+1),t}\ge \left(1-\frac{P_{ij,t}}{P_{ij,p}}\right)-\left(1-\frac{P_{(i+1)j,t}}{P_{(i+1)j,p}}\right)\\ i=1,\dots ,m-1;j=1,\dots ,n\end{array}$$

(4)

where: P_ij,p, P_(i+1)j,p is the labor-consumption of works i and (i + 1), respectively, to be performed on unit j; and P_ij,t, P_(i+1)j,t is the amount of work of the process i and (i + 1), respectively, realized by the date t on the unit j.

In order to meet the condition (1), the number of works performed by a crew realizing the process (i + 1) being a successor of i on day t may be further decreased—the lack of a work front caused by insufficient involvement of works i prevents the crew from achieving the assumed efficiency (i + 1). Additionally, it was assumed that only two crews could work on one unit.

The principle of the simulation model can be described in the following steps (Figure 2):

• Increase the simulation clock by 1 day: t = t + 1;
• Check if there are processes not yet realized. If yes, move to step 3. If not, move to step 8;
• Find the earliest process possible to realize due to date t according to the sequence relation—remember it as (r, s);
• If there are no processes to be realized by the date t, go to step 1;
• Check if P_rs,t = 0. If yes, remember the starting date for this process;
• Check whether, on the date t, process r on unit s is performed independently or whether it is a subsequent of the (r − 1) process carried out on the date t or a predecessor of (r + 1). Select according to the assumed distributions of the value of the daily amount of works P_rs,t. If process r is a successor to (r − 1) and condition 2 is not unfulfilled, reduce the daily output of that process. Increase the amount of realized works up to day t according to Equation (1). Remember that the process (r, s) was implemented on the date t;
• Check if P_rs,t ≥ P_rs,p. If yes, remember the end date of this process;
• Move to step 2;
• End of the simulation run. Remember the end date of the last process, which is also the end date of the project.

The simulation model was developed using the General-Purpose Simulation System in the GPSS World version 5.2.2 developed by Minuteman Software (http://www.minutemansoftware.com accessed on 20 April 2021).

3. Results

It was assumed that the project consists of five processes, e.g., partition walls, plasters, concrete screeds, floor finish layers and painting, carried out on subsequent working units. The labor consumption of the works is presented in

Table 1. The labor consumption of works in man-hours.

Unit j	Process i
	1	2	3	4	5
1	400	800	900	1200	500
2	500	600	1000	1000	400
3	350	720	800	900	600
4	600	900	750	700	450
5	550	1000	850	900	300

.

Due to the impact of risk factors, the daily efficiency of the crews realizing the process i are random variables described by triangular distributions defined by three parameters: $w_i^a$ (minimum efficiency), $w_i^b$ (maximum efficiency), and $w_i^c$ (most likely efficiency). Random numbers are drawn using predefined generators in the GPSS simulation language. The generator of numbers from the triangular distribution has the form TRIANGULAR (Stream, Min, Max, Mode), where Stream is the number of random numbers generated from the s (0, 1), Min is the smallest and Max is the largest value to be drawn from the distribution, and Mode is the most frequent value of the distribution. To increase the statistical reliability of the results obtained (narrowing the confidence interval for the mean), 100,000 simulation runs were conducted in each simulation experiment for different values of reserve D. Process i (i = 2, 3, 4) can be realized on any day t independently on a unit ($w_i^1$ efficiency distribution), simultaneously with a process (i − 1) preceding it technologically ($w_i^2$ efficiency distribution), with a successor (i + 1) ($w_i^3$ efficiency distribution). The assumed efficiency distribution parameters for processes (model input parameters) are shown in

Table 2. Parameters ($w_i^a$, $w_i^b$, $w_i^c$) distributions of daily efficiency in manhours/working day.

Process i	Simultaneity of Works on Units	$\mathbf{Parameters}\mathbf{of}\mathbf{the}\mathbf{Triangular}\mathbf{Distribution}\left({\mathit{l}}_{\mathit{i}}^{\mathit{a}},{\mathit{l}}_{\mathit{i}}^{\mathit{b}},{\mathit{l}}_{\mathit{i}}^{\mathit{c}}\right)$$\mathbf{for}\mathbf{Distributions}{\mathit{L}}_{\mathit{i}1},{\mathit{L}}_{\mathit{i}2},{\mathit{L}}_{\mathit{i}3}$
1	Only 1	(34, 47, 39)
	Process 1 (predecessor) and 2 (successor) simultaneously	(30, 40, 33)
2	Only 2	(50, 70, 55)
	Process 1 (predecessor) and 2 (successor) simultaneously	(37, 61, 46)
	Process 2 (predecessor) and 3 (successor) simultaneously	(43, 67, 52)
3	Only 3	(88, 118, 94)
	Process 2 (predecessor) and 3 (successor) simultaneously	(65, 98, 77)
	Process 3 (predecessor) and 4 (successor) simultaneously	(75, 107, 88)
4	Only 4	(63, 97, 80)
	Process 3 (predecessor) and 4 (successor) simultaneously	(52, 80, 60)
	Process 4 (predecessor) and 5 (successor) simultaneously	(58, 90, 68)
5	Only 5	(25, 36, 30)
	Process 4 (predecessor) and 5 (successor) simultaneously	(18, 30, 24)

.

The simulation tests were carried out for the reserve value of D_{i(i + 1)} in the range of 0.4 to 1.0, and for the sake of simplification of the analyzed issue, it was assumed D_{i(i + 1)} = const. for every i. As a result, the average project duration time and the average length of employment of working crews realizing subsequent technological processes were calculated. The results are summarized in

Table 3. The dependence of the project duration time and working time of working crews on the time reserve.

Variant m	Reserve D	Project Duration (Days)	Process Duration Ti [Days]
			1	2	3	4	5
1	0.4	107.434	64.617	77.767	72.588	74.931	79.893
2	0.5	108.968	63.759	76.422	70.780	73.889	78.990
3	0.6	111.715	63.441	75.158	68.613	72.014	78.146
4	0.7	114.748	63.124	74.066	67.084	70.380	77.622
5	0.8	117.871	62.868	73.195	65.300	69.026	77.323
6	0.9	121.260	62.537	72.337	64.232	67.529	76.849
7	1.0	124.746	62.268	71.729	63.604	67.091	76.644

.

The influence of the choice of the reserve size D_i(i+1) on the quality of the obtained solution can be assessed using the value of the criterion function, which can be equated with the penalty for extending the average duration of the project beyond the agreed deadline and extending the working time of the working crews:

$$W_w=w_1\cdot (T_m-T_{\min })+{\displaystyle \sum w_{2i}}\cdot (T_{\max i}-T_i),$$

(5)

where: w₁ is the weight (cost) of extending the project duration over the assumed T_min value, w_2i is the weight (cost) of extending the working time of the crew realizing the process j over the assumed T_i value.

The values of T_min and T_maxi can be assumed based on the results of simulation tests—Table 3. In the example, T_min = 107.434, T_max1 = 64.617, T_max2 = 77.767, … days.

The example assumes w_2i = const. regardless of the type of work being carried out (it was assumed that the unit labor cost of the crews is similar).

Three cases were analyzed:

• The duration of the project realization is crucial for the contractor, and they are ready to incur additional costs caused by extending the work of the working crews; hence, w₁ = 0.9 and w₂ = 0.1 (1st set of weights);
• The directive deadline of the project is distant, and the contractor aims to reduce the costs of the crews work; hence, w₁ = 0.1 and w₂ = 0.9 (2nd set of weights);
• Intermediate solution: weights equal to 0.6 and 0.4 (3rd set of weights).

The results are presented in Figure 3.

In the analyzed example, thanks to the introduction of overlapping, it was possible to reduce the average duration of the project by approximately 13.9% from 124.746 to 107.434 days. This effect was achieved by increasing the total average working time of working crews by about 8.3%, from 341.336 to 369.796 days. The analysis of the results for different contractor preferences (different values of weights) may be helpful in choosing the variant of carrying out the works consisting in determining the amount of the time reserve between processes and, consequently, the dates of starting subsequent technological process lines. When striving to shorten the project time as much as possible, one should take into account a significant increase in the value of the criterion function.

The triangular distribution of daily productivity in the example was arbitrarily assumed. In reality, the type of distribution is unknown. In the extreme case, it may assume a quasi-uniform (E2 in Figure 4) or a quasi-delta shape (E3 in Figure 4), which differ in mean and variance from the assumed triangular distribution (E1 in Figure 4). In further simulation studies, the E2 distribution was approximated by a uniform distribution on the interval (l_a, l_b) and the E2 distribution by a constant value that is equal to the mode of the triangular distribution. The results of the sensitivity analysis of the effect of distribution type on the construction project duration are shown in

Table 4. The relationship between the sample project duration (days) and the type of construction processes’ probability distribution (days).

Variant m	Reserve D	Type of Distribution
		E1	E2	E3
1	0.4	107.434	106.543	109.000
2	0.5	108.968	107.965	110.000
3	0.6	111.715	110.791	113.000
4	0.7	114.748	113.709	116.000
5	0.8	117.871	116.789	119.000
6	0.9	121.260	120.189	122.000
7	1.0	124.746	123.590	126.000

.

Assuming a triangular distribution may result in an error of no more than 2.5% in estimating project duration.

4. Discussion and Conclusions

High competition in the construction market requires the contractor to prepare an offer that meets the investor’s expectations as much as possible. One of the key factors of competitive advantage is the realization of construction projects within short time limits. A reduction of the project duration can be achieved by using organizational methods such as overtime work, increasing the number of working crews, or allowing parallel work of working crews on working units. However, the contractor, when preparing the offer, must not neglect the impact of schedule compression measures on the cost of the works. The impact of risk factors, such as weather conditions or workers’ absence, mean that the daily efficiency of working crews is not a deterministic value as well as the duration of construction processes. Currently, there are no analytical solutions for a multipath case with stochastic durations, and the exact compression can only be calculated by computer simulation. Therefore, as a partial conclusion, accelerating the schedule requires at least a minimum consideration of the probabilistic dimension.

The presented simulation model makes it possible to study the influence of the simultaneity of processes on the average duration of a construction project and the working time of working crews with the assumed variability of daily efficiency of working crews. It can be used as a tool to support the work of construction managers and to determine the starting dates of working crews taking into account the random condition of the construction project realization.

Choosing the optimal amount of overlap between successive processes on the basis of the assumed aggregation objective function, which is a compromise between the duration of the entire construction project and the sum of the working crews’ working times, allows for the development of a deterministic schedule of construction works. Depending on the construction manager’s willingness to accept risk, the schedule can be developed based on average values or mode of the distribution L of daily productivity. The daily output can be determined by the condition $1-K=P\left(L\le l\right)$ which means that the planner assumes a probability K that the daily productivity will not be less than l.

The developed schedule allows for the calculation of the planned duration of the project, and conducting simulation studies, by analogy with the random simulation method for the PERT network and allows for the estimation of the probability of its fulfillment.

The direction of further research should be the expansion of the simulator with additional options most often introduced in a fast-track project, e.g., overtime work. At a later stage, simulation studies should be combined with optimization methods. This will enable separately determining the reserve of the work front for each pair of technological process lines (pairs of predecessors and successors). In addition, it will be possible to analyze the impact of the dates of starting the sequences on the continuity of working crews. The presented simulation model can be easily adapted to the analysis of non-repetitive non-uniform construction projects