Effects of Compression Ratio of Bio-Fueled SI Engines on the Thermal Balance and Waste Heat Recovery Potential
Abstract
:1. Introduction
2. Methodology
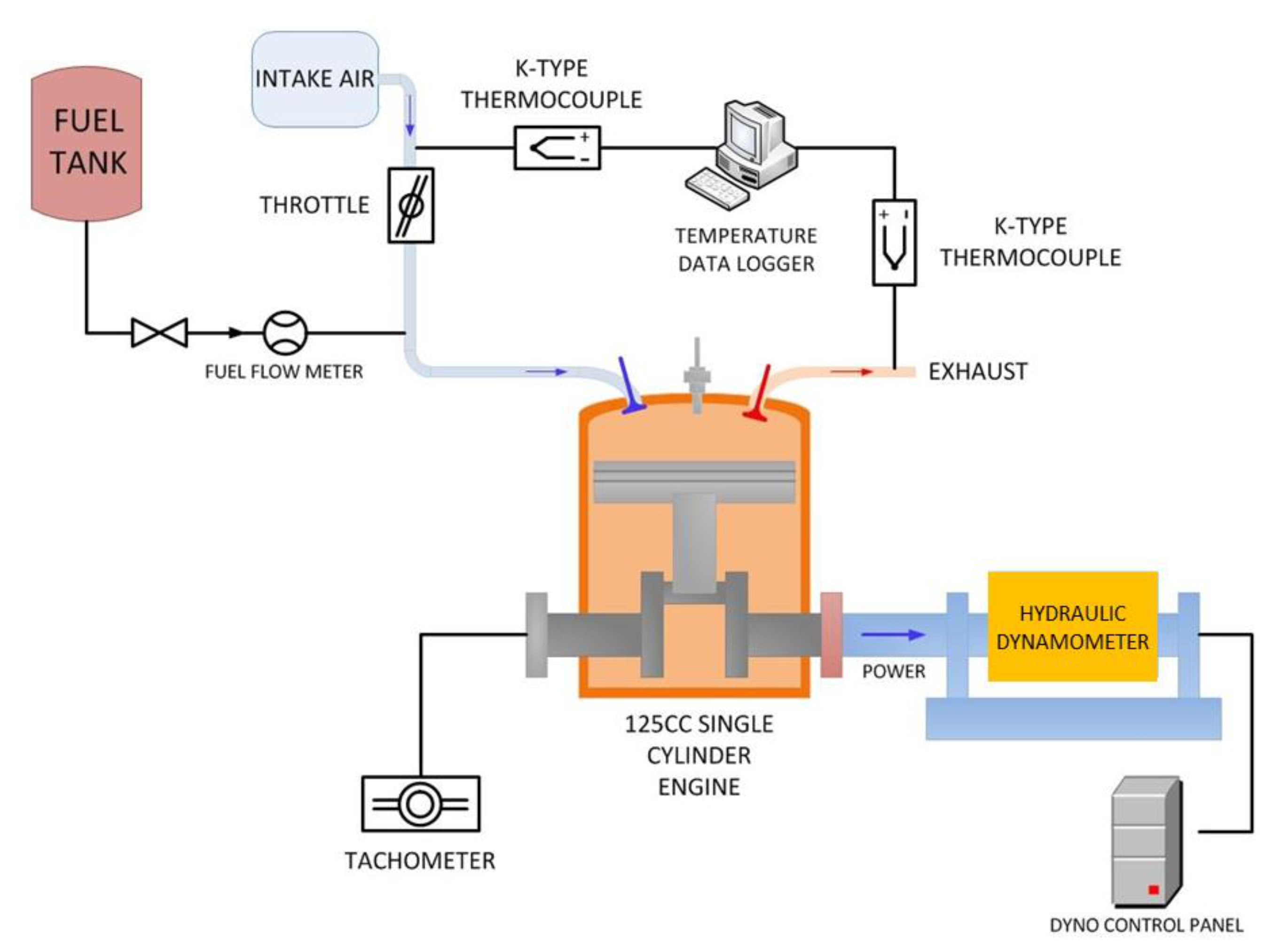
2.1. Experimental Analysis
2.2. Numerical Analysis
2.2.1. Geometry
2.2.2. Combustion
2.2.3. Heat Transfer
2.2.4. Fuel
2.2.5. Engine Energy Balance
3. Results and Discussion
3.1. Validation
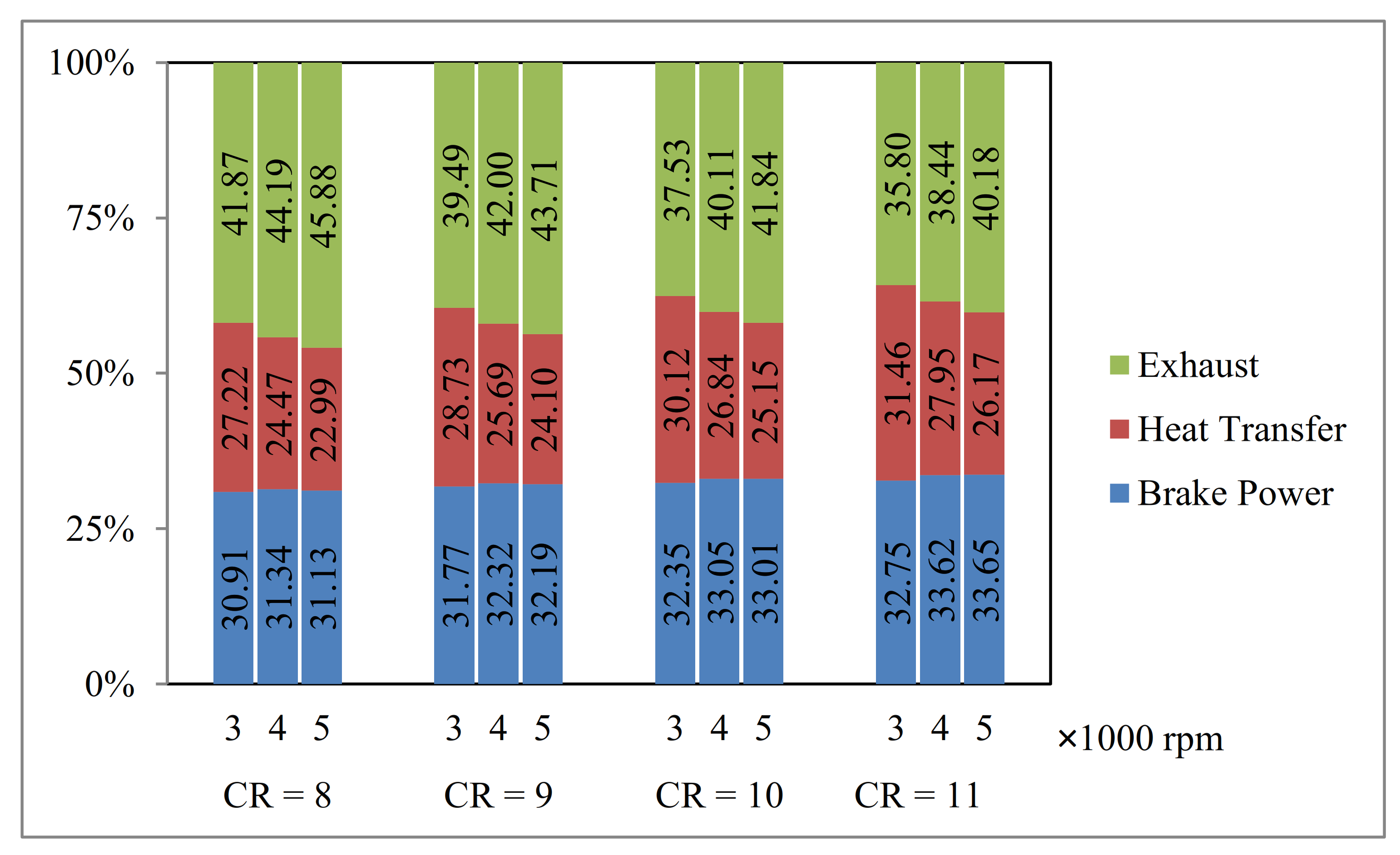
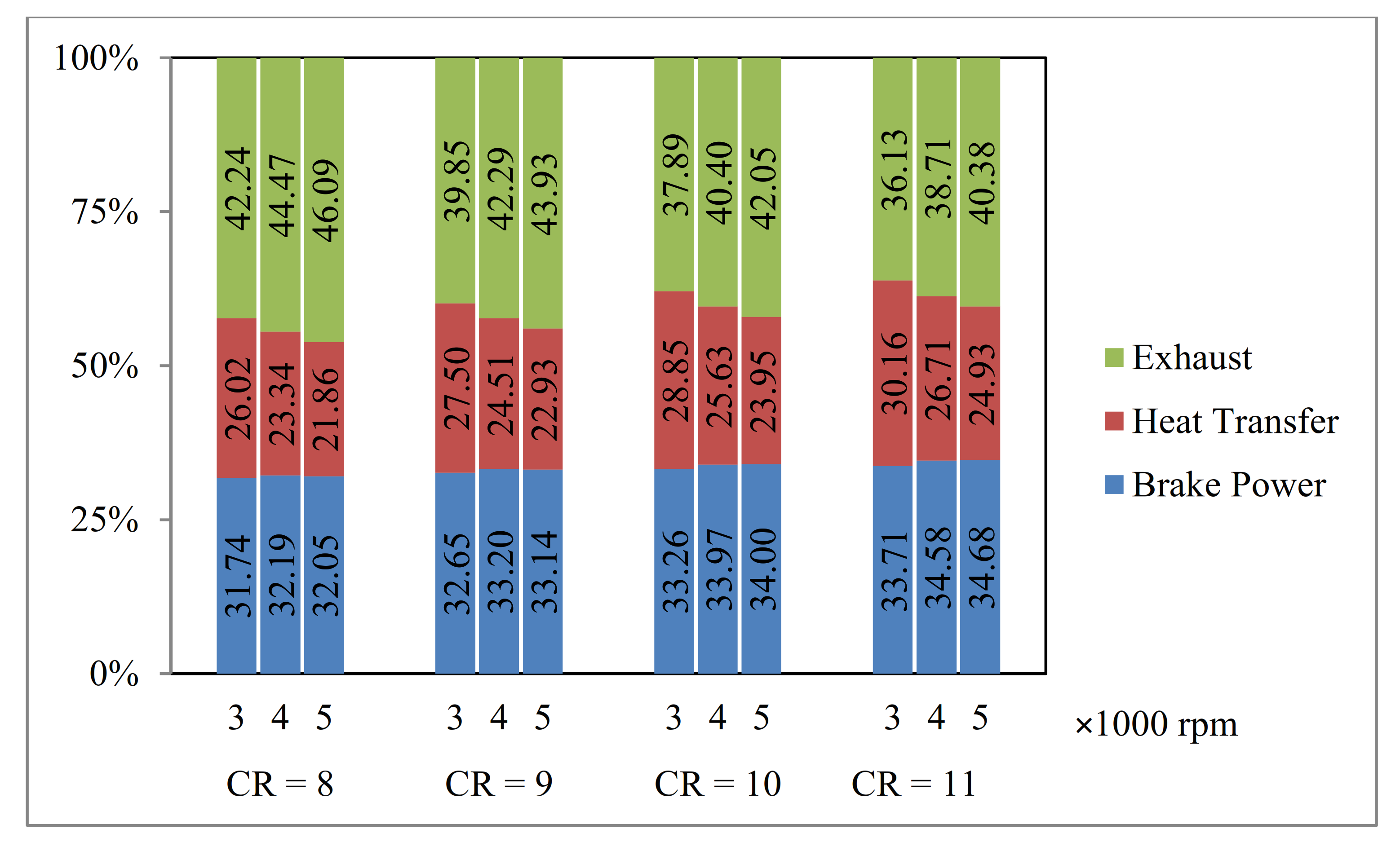
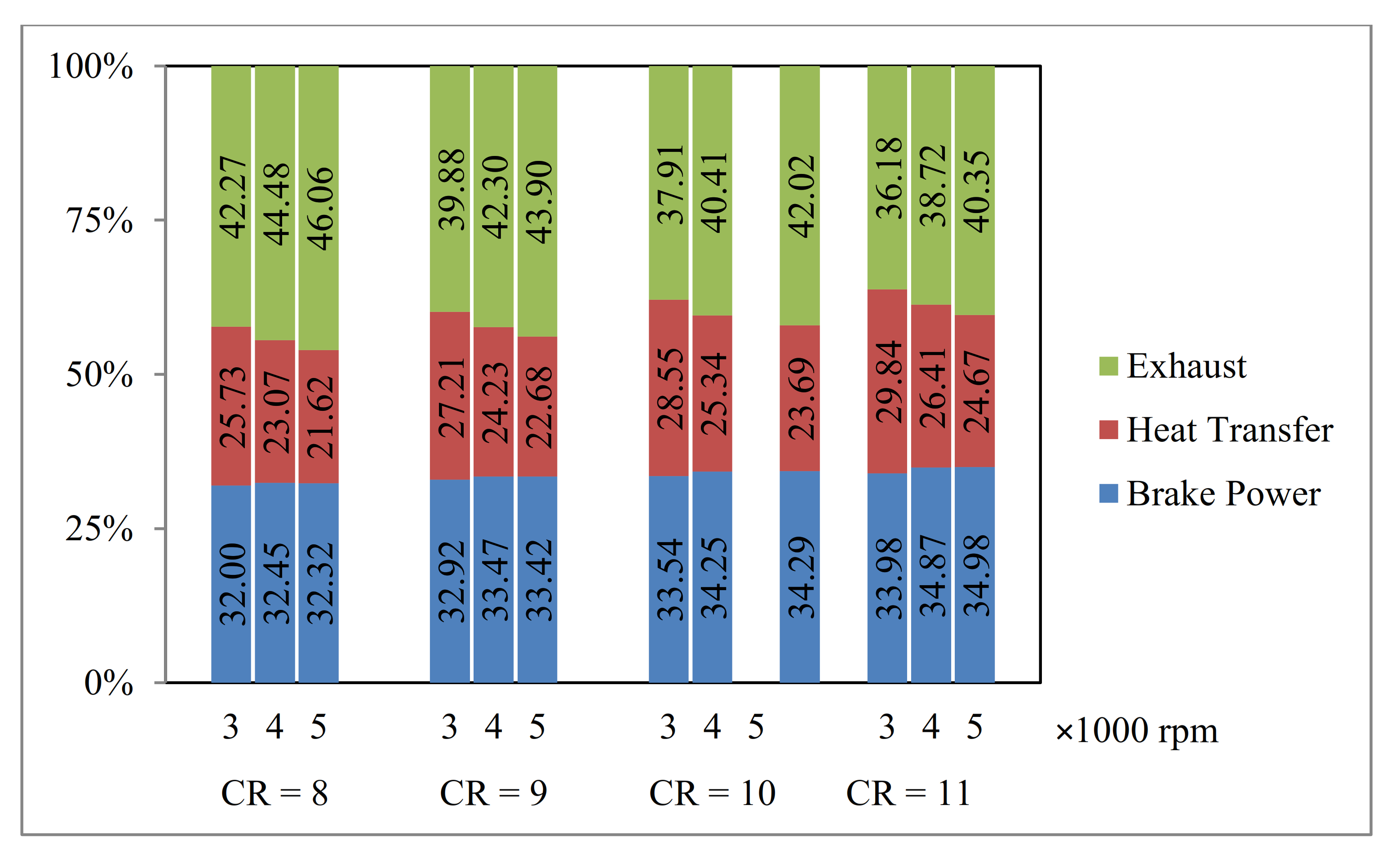
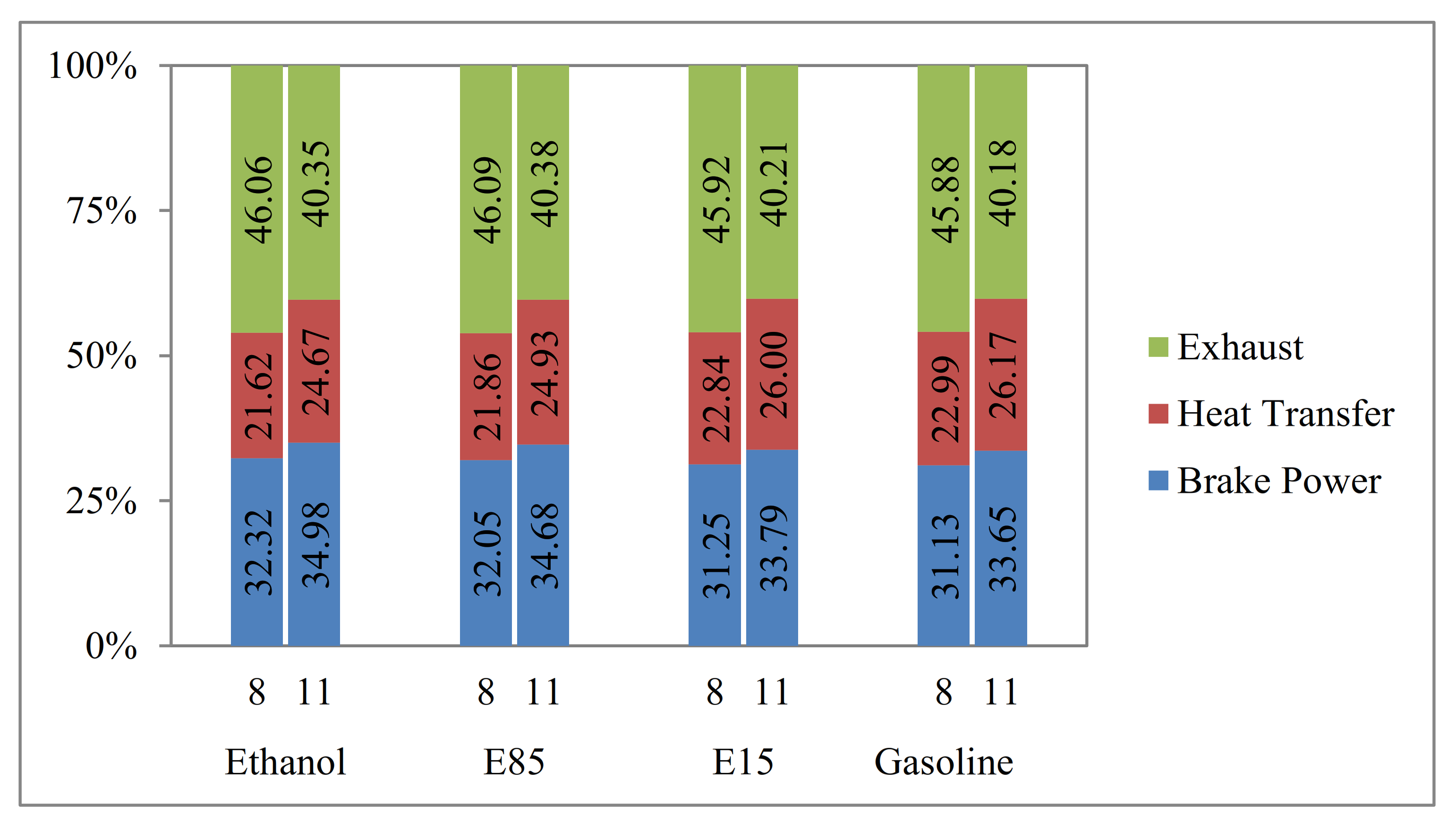
3.2. Energy Balance Investigation
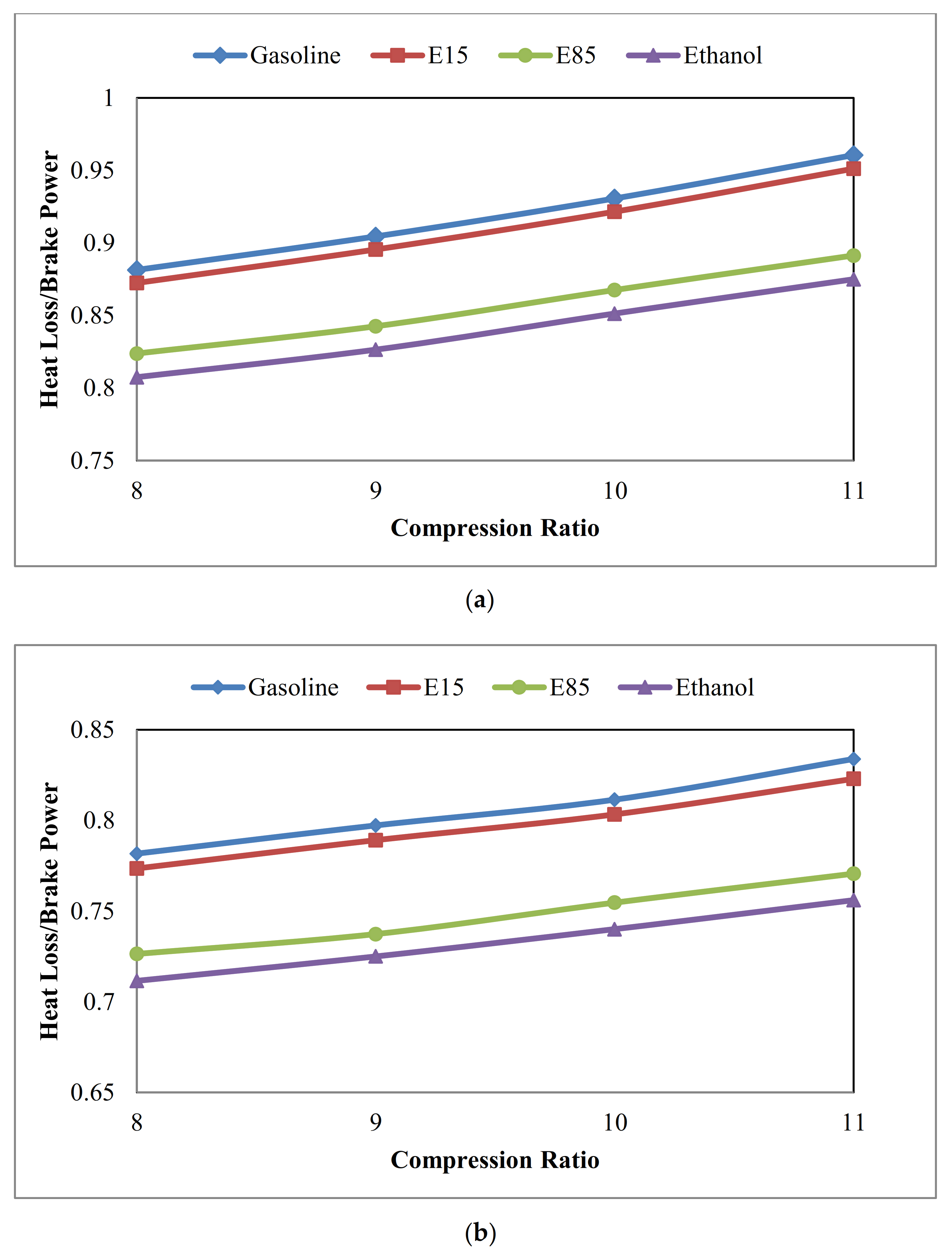
3.3. Heat Loss to Brake Power Ratio ()
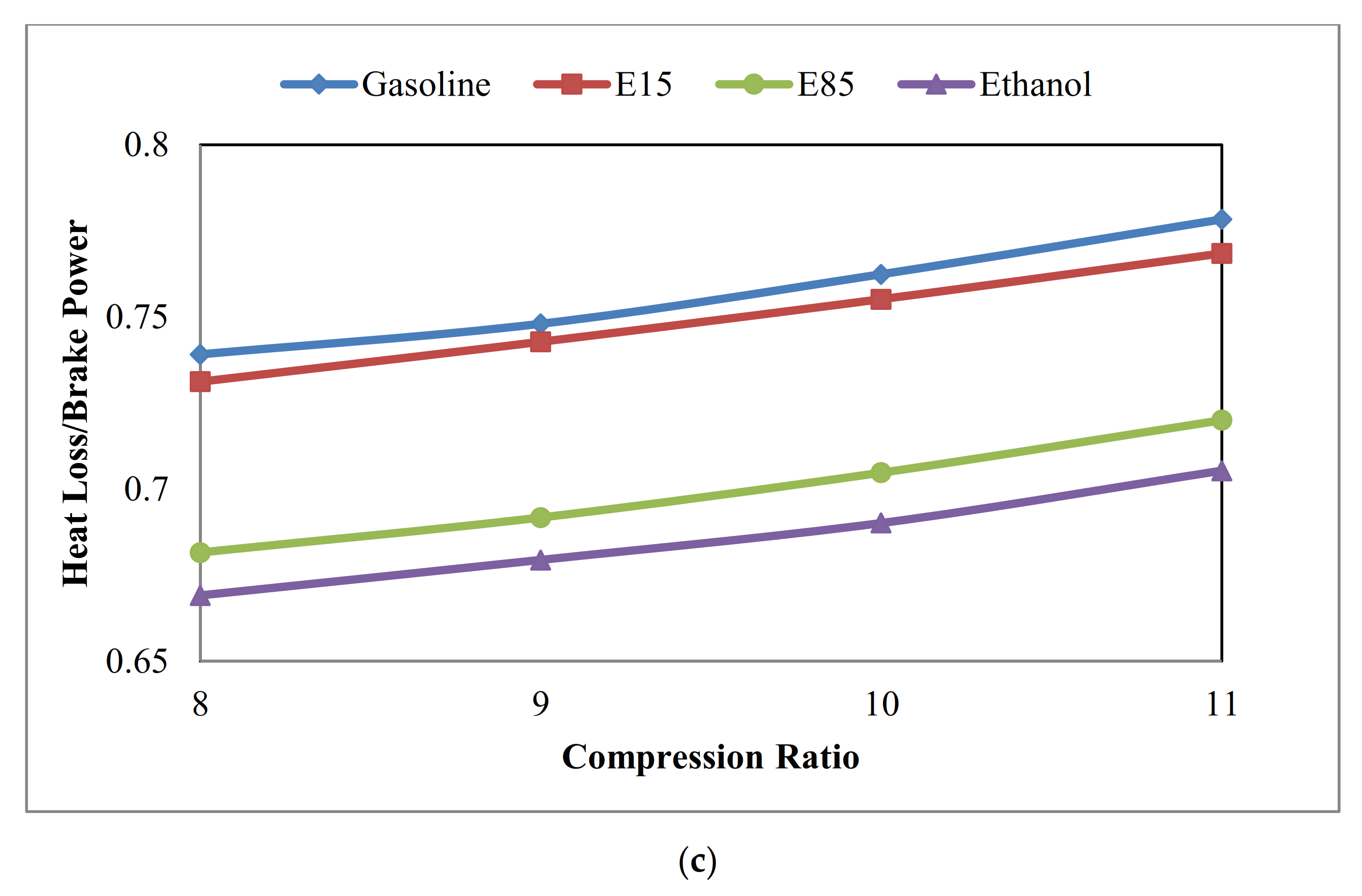
3.4. Exhaust Losses to Heat Losses Ratio ()
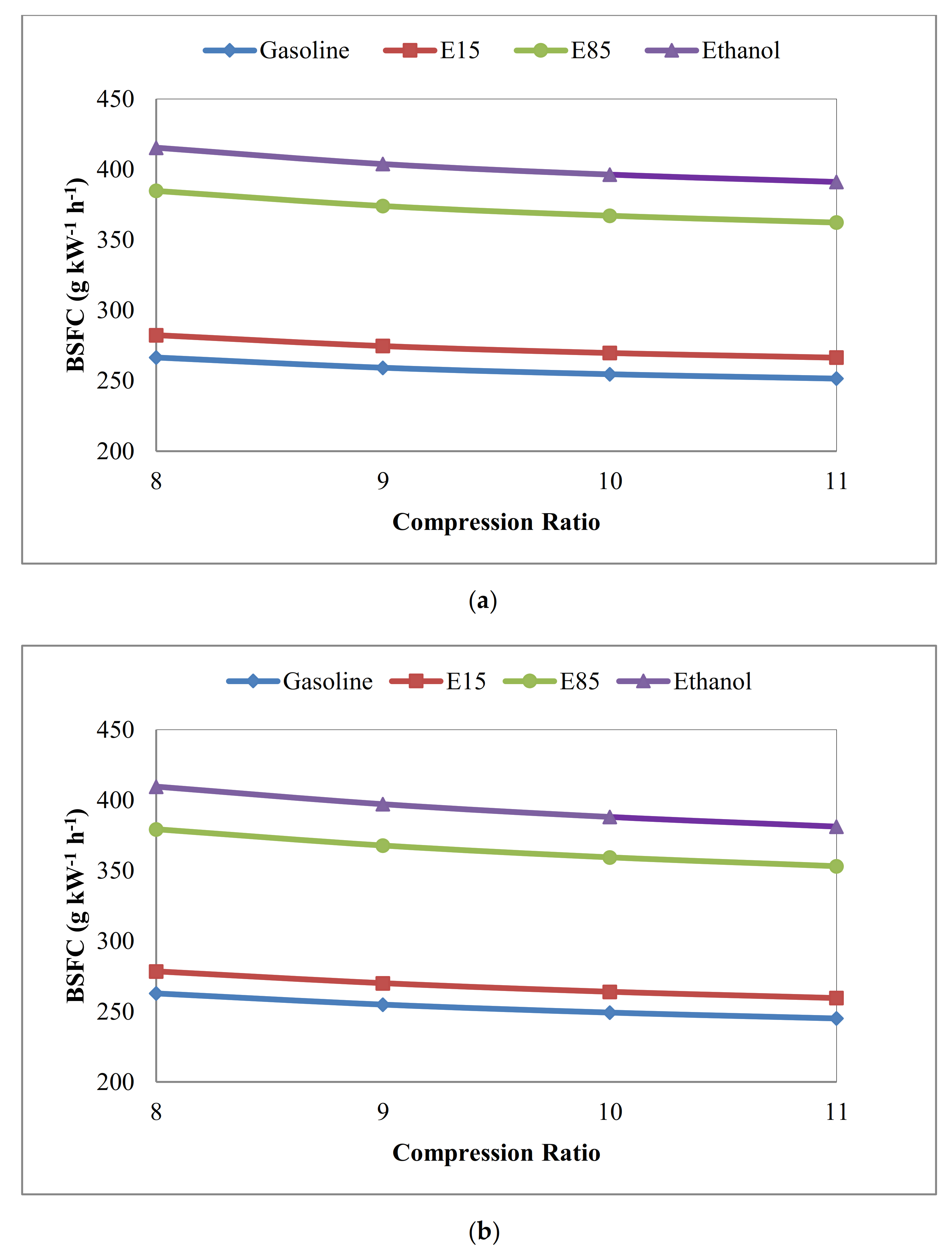
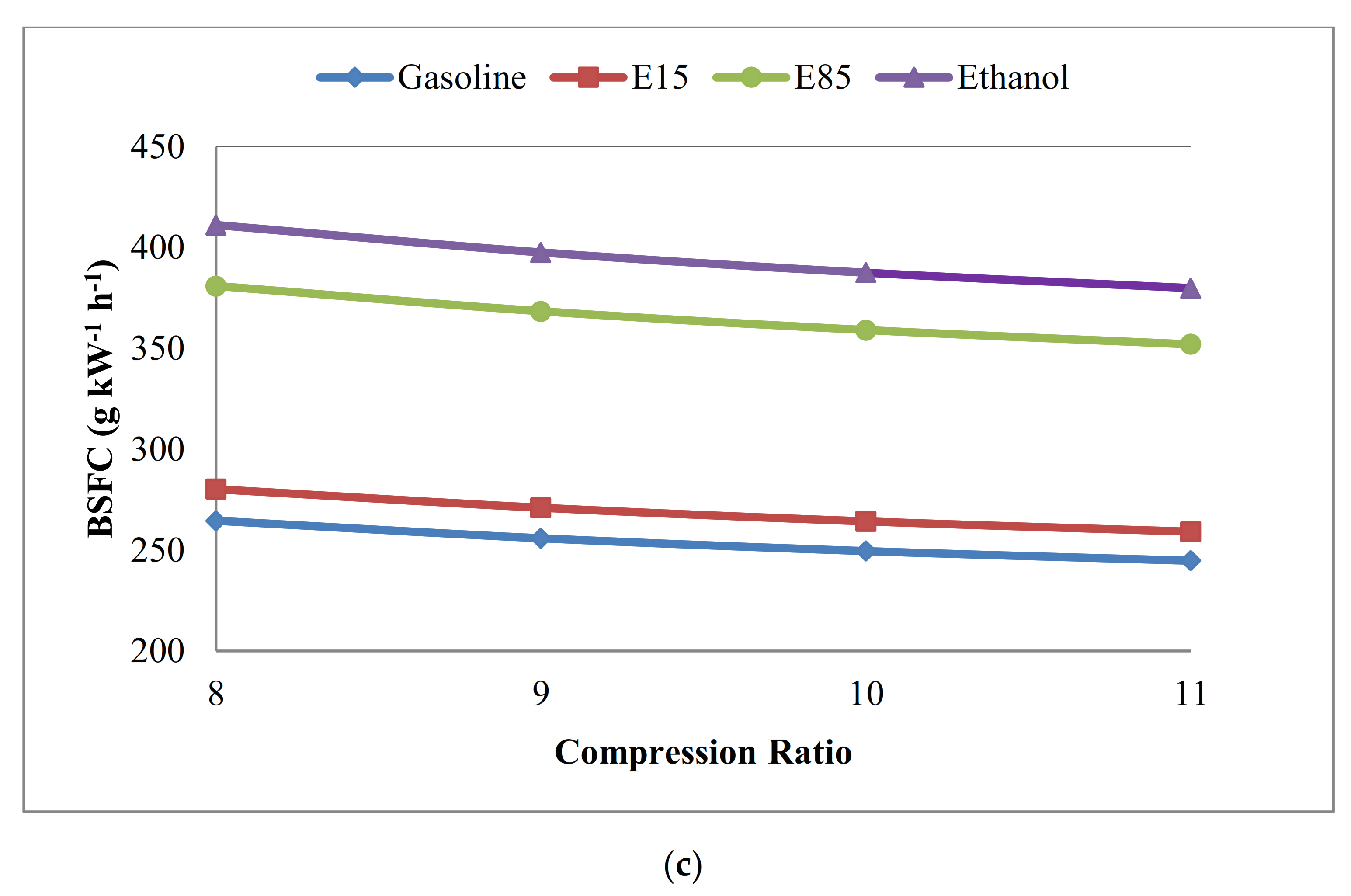
3.5. Brake Specific Fuel Consumption (BSFC)
4. Conclusions
- (1)
- At a constant engine speed, by increasing the compression ratio, the brake power and heat loss increase while the exhaust power decreases.
- (2)
- At engine speeds of 3000 to 5000 rpm, the maximum brake power is produced at 5000 rpm and a compression ratio of 11 by pure ethanol (E100). E85, E15 blends and E00 come next in the consecutive order.
- (3)
- For the range of the engine speeds and compression ratios examined in this study (3000 to 5000 rpm and CR of 8 to 11), the maximum efficiency is 34.98% happening at 5000 rpm and the compression ratio of 11 for E100. The minimum percentage of heat loss is 21.62% at 5000 rpm and the compression ratio of 8 for E100. The minimum percentage of exhaust loss is 35.8% happening at 3000 rpm and the compression ratio of 11 by E00.
- (4)
- As the percentage of heat loss increases by the compression ratio increment, ratio increases and the lowest is found for ethanol.
- (5)
- For all studied fuels, the decreasing compression ratio leads to increasing the ratio. Thus, the less the compression ratio, the more the capability of waste heat recovery.
- (6)
- According to the results, there is a direct relationship between ethanol in fuel content and the ratio. As the percentage of ethanol in fuel increases, the ratio rises. It is found that pure ethanol (100% ethanol) has the highest ratio for all tested compression ratios and engine speeds. E85 (85% ethanol), E15 (15% ethanol) and gasoline (0% ethanol) come next, respectively. Thus, the more the ethanol in the fuel, the more the potential for the waste heat recovery of the IC engine.
- (7)
- E00 (pure gasoline), due to its highest heating value, has the minimum BSFC among all investigated fuels.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Abbreviations
| CR | Compression Ratio |
| Ht/Br | Heat Transfer to Brake Power Ratio |
| Ex/Ht | Exhaust Power to Heat Transfer Ratio |
| E100 | Pure Ethanol |
| E00 | Pure Gasoline |
| E85 | Mixture of 85% Ethanol and 15% Gasoline |
| E15 | Mixture of 15% Ethanol and 85% Gasoline |
| BMEP | Brake Mean Effective Pressure |
| IMEP | Indicated Mean Effective Pressure |
| FMEP | Friction Mean Effective Pressure |
| BSFC | Brake Specific Fuel Consumption |
| Cylinder Pressure, kPa | |
| Crank Angle, degree | |
| Specific Heat Ratio | |
| In-Cylinder Volume, m3 | |
| Cylinder Clearance Volume, m3 | |
| Cylinder Bore, m | |
| Connecting Rod’s Length, m | |
| Crank Radius, m | |
| Distance Between Piston Pin Axis and Crank Axis, m | |
| Adjustable Parameter | |
| Adjustable Parameter | |
| Mass Fraction Burned | |
| Start of Combustion, degree | |
| Total Combustion Duration | |
| Heat Transfer Coefficient, W/m2K | |
| Temperature, K | |
| Average Cylinder Gas Velocity, m/s | |
| Wall Area, m2 | |
| Wall Temperature, K | |
| In-Cylinder Gas Temperature, K | |
| Constant Parameter | |
| Mean Piston Speed, m/s | |
| Constant Parameter | |
| Working-Fluid Temperature, K | |
| Working-Fluid Pressure, kPa | |
| Working-Fluid Volume, m3 | |
| In-Cylinder Maximum Pressure, kPa | |
| Motored Cylinder Pressure, kPa | |
| Engine Speed, rpm | |
| Rate of Energy, kJ | |
| Total Heat Addition, J | |
| Heat Transfer from the Combustion Chamber Wall, J | |
| Fuel Power, kW | |
| Brake Power, kW | |
| Dissipated Power by Exhaust, kW | |
| Dissipated Power by Heat Transfer, kW | |
| Fuel Heating Value, kJ/kg | |
| Combustion Efficiency | |
| Mass Flow Rate of Air, kg/s | |
| Mass Flow Rate of Fuel, kg/s | |
| Exhaust Gases Temperature, | |
| Ambient Temperature, | |
| Average Specific Heat of Exhaust Gases, kJ/kg.K | |
| Displacement Volume, m3 | |
| Number of Cylinders |
References
- Zabihi, N.; Saafi, M. Recent Developments in the Energy Harvesting Systems from Road Infrastructures. Sustainability 2020, 12, 6738. [Google Scholar] [CrossRef]
- Sher, F.; Curnick, O.; Azizan, M. Sustainable Conversion of Renewable Energy Sources. Sustainability 2021, 13, 2940. [Google Scholar] [CrossRef]
- Markiewicz, M.; Muślewski, Ł. The Impact of Powering an Engine with Fuels from Renewable Energy Sources including its Software Modification on a Drive Unit Performance Parameters. Sustainability 2019, 11, 6585. [Google Scholar] [CrossRef] [Green Version]
- Tucki, K.; Mruk, R.; Orynycz, O.; Wasiak, A.; Botwińska, K.; Gola, A. Simulation of the Operation of a Spark Ignition Engine Fueled with Various Biofuels and Its Contribution to Technology Management. Sustainability 2019, 11, 2799. [Google Scholar] [CrossRef] [Green Version]
- Sarabi, M.; Aghdam, E.A. Experimental analysis of in-cylinder combustion characteristics and exhaust gas emissions of gasoline–natural gas dual-fuel combinations in a SI engine. J. Therm. Anal. Calorim. 2019, 139, 3165–3178. [Google Scholar] [CrossRef]
- Miskat, M.; Ahmed, A.; Chowdhury, H.; Chowdhury, T.; Chowdhury, P.; Sait, S.; Park, Y.-K. Assessing the Theoretical Prospects of Bioethanol Production as a Biofuel from Agricultural Residues in Bangladesh: A Review. Sustainability 2020, 12, 8583. [Google Scholar] [CrossRef]
- Lapuerta, M.; Ballesteros, R.; Barba, J. Strategies to Introduce n-Butanol in Gasoline Blends. Sustainability 2017, 9, 589. [Google Scholar] [CrossRef] [Green Version]
- Al-Esawi, N.; Al Qubeissi, M.; Sazhin, S.S.; Whitaker, R. The impacts of the activity coefficient on heating and evaporation of ethanol/gasoline fuel blends. Int. Commun. Heat Mass Transf. 2018, 98, 177–182. [Google Scholar] [CrossRef]
- Shirazi, S.A.; Foust, T.D.; Reardon, K.F. Identification of Promising Alternative Mono-Alcohol Fuel Blend Components for Spark Ignition Engines. Energies 2020, 13, 1955. [Google Scholar] [CrossRef] [Green Version]
- Behrad, R.; Aghdam, E.A.; Ghaebi, H. Experimental study of knocking phenomenon in different gasoline–natural gas combinations with gasoline as the predominant fuel in a SI engine. J. Therm. Anal. Calorim. 2020, 139, 2489–2497. [Google Scholar] [CrossRef]
- Thakur, A.K.; Kaviti, A.K.; Mehra, R.; Mer, K.K.S. Performance analysis of ethanol–gasoline blends on a spark ignition engine: A review. Biofuels 2017, 8, 91–112. [Google Scholar] [CrossRef]
- Jang, J.; Choi, J.; Yi, H.; Park, S. Effects of the Bore to Stroke Ratio on Combustion, Gaseous and Particulate Emissions in a Small Port Fuel Injection Engine Fueled with Ethanol Blended Gasoline. Energies 2020, 13, 321. [Google Scholar] [CrossRef] [Green Version]
- Channappagoudra, M.; Ramesh, K.; Manavendra, G. Comparative study of standard engine and modified engine with different piston bowl geometries operated with B20 fuel blend. Renew. Energy 2019, 133, 216–232. [Google Scholar] [CrossRef]
- Hasan, A.O.; Al-Rawashdeh, H.; Al-Muhtaseb, A.H.; Abu-Jrai, A.; Ahmad, R.; Zeaiter, J. Impact of changing combustion chamber geometry on emissions, and combustion characteristics of a single cylinder SI (spark ignition) engine fueled with ethanol/gasoline blends. Fuel 2018, 231, 197–203. [Google Scholar] [CrossRef]
- Monsalve-Serrano, J.; Belgiorno, G.; Di Blasio, G.; Guzmán-Mendoza, M. 1D Simulation and Experimental Analysis on the Effects of the Injection Parameters in Methane–Diesel Dual-Fuel Combustion. Energies 2020, 13, 3734. [Google Scholar] [CrossRef]
- Babu, D.; Karvembu, R.; Anand, R. Impact of split injection strategy on combustion, performance and emissions characteristics of biodiesel fuelled common rail direct injection assisted diesel engine. Energy 2018, 165, 577–592. [Google Scholar] [CrossRef]
- Ashok, B.; Nanthagopal, K.; Chaturvedi, B.; Sharma, S.; Raj, R.T.K. A comparative assessment on Common Rail Direct Injection (CRDI) engine characteristics using low viscous biofuel blends. Appl. Therm. Eng. 2018, 145, 494–506. [Google Scholar] [CrossRef]
- Feng, D.; Wei, H.; Pan, M.; Zhou, L.; Hua, J. Combustion performance of dual-injection using n-butanol direct-injection and gasoline port fuel-injection in a SI engine. Energy 2018, 160, 573–581. [Google Scholar] [CrossRef]
- Turner, D.; Xu, H.; Cracknell, R.F.; Natarajan, V.; Chen, X. Combustion performance of bio-ethanol at various blend ratios in a gasoline direct injection engine. Fuel 2011, 90, 1999–2006. [Google Scholar] [CrossRef]
- Tornatore, C.; Marchitto, L.; Costagliola, M.A.; Valentino, G. Experimental Comparative Study on Performance and Emissions of E85 Adopting Different Injection Approaches in a Turbocharged PFI SI Engine. Energies 2019, 12, 1555. [Google Scholar] [CrossRef] [Green Version]
- Xu, Z.; Zhu, L.; He, Z.; Li, A.; Shao, Y.; Huang, Z. Performance optimization of in-cylinder thermochemical fuel reforming (TFR) with compression ratio in an SI natural gas engine. Fuel 2017, 203, 162–170. [Google Scholar] [CrossRef]
- Yücesu, H.S.; Topgül, T.; Cinar, C.; Okur, M. Effect of ethanol–gasoline blends on engine performance and exhaust emissions in different compression ratios. Appl. Therm. Eng. 2006, 26, 2272–2278. [Google Scholar] [CrossRef]
- Cooney, C.P.; Yeliana; Worm, J.J.; Naber, J.D. Combustion Characterization in an Internal Combustion Engine with Ethanol−Gasoline Blended Fuels Varying Compression Ratios and Ignition Timing. Energy Fuels 2009, 23, 2319–2324. [Google Scholar] [CrossRef]
- Leone, T.G.; Anderson, J.E.; Davis, R.S.; Iqbal, A.; Reese, R.A.; Shelby, M.H.; Studzinski, W.M. The Effect of Compression Ratio, Fuel Octane Rating, and Ethanol Content on Spark-Ignition Engine Efficiency. Environ. Sci. Technol. 2015, 49, 10778–10789. [Google Scholar] [CrossRef]
- Wittek, K.; Geiger, F.; Andert, J.; Martins, M.; Cogo, V.; Lanzanova, T. Experimental investigation of a variable compression ratio system applied to a gasoline passenger car engine. Energy Convers. Manag. 2019, 183, 753–763. [Google Scholar] [CrossRef]
- Balki, M.K.; Sayin, C. The effect of compression ratio on the performance, emissions and combustion of an SI (spark ignition) engine fueled with pure ethanol, methanol and unleaded gasoline. Energy 2014, 71, 194–201. [Google Scholar] [CrossRef]
- Çelik, M.B.; Özdalyan, B.; Alkan, F. The use of pure methanol as fuel at high compression ratio in a single cylinder gasoline engine. Fuel 2011, 90, 1591–1598. [Google Scholar] [CrossRef]
- Costa, R.C.; Sodré, J.R. Compression ratio effects on an ethanol/gasoline fuelled engine performance. Appl. Therm. Eng. 2011, 31, 278–283. [Google Scholar] [CrossRef]
- Thomas, R.; Sreesankaran, M.; Jaidi, J.; Paul, D.M.; Manjunath, P. Experimental evaluation of the effect of compression ratio on performance and emission of SI engine fuelled with gasoline and n-butanol blend at different loads. Perspect. Sci. 2016, 8, 743–746. [Google Scholar] [CrossRef] [Green Version]
- Luo, Q.-H.; Sun, B.-G. Experiments on the effect of engine speed, load, equivalence ratio, spark timing and coolant temperature on the energy balance of a turbocharged hydrogen engine. Energy Convers. Manag. 2018, 162, 1–12. [Google Scholar] [CrossRef]
- Ma, B.; Yao, A.; Yao, C.; Wang, B.; Gao, J.; Chen, C.; Wu, T. Experimental study on energy balance of different parameters in diesel methanol dual fuel engine. Appl. Therm. Eng. 2019, 159, 113954. [Google Scholar] [CrossRef]
- Shojaeefard, M.; Azarikhah, P.; Qasemian, A. Experimental Investigation of Thermal Balance and Valve Cover Heat Transfer in a Small Internal Combustion Engine. Int. J. Automot. Eng. 2017, 7, 2423–2433. [Google Scholar] [CrossRef]
- da Silva, J.A.; Seifert, V.; de Morais, V.O.; Tsolakis, A.; Herreros, J.; Torres, E. Exergy evaluation and ORC use as an alternative for efficiency improvement in a CI-engine power plant. Sustain. Energy Technol. Assess. 2018, 30, 216–223. [Google Scholar] [CrossRef]
- Saidur, R.; Rezaei, M.; Muzammil, W.K.; Hassan, M.H.; Paria, S.; Hasanuzzaman, M. Technologies to recover exhaust heat from internal combustion engines. Renew. Sustain. Energy Rev. 2012, 16, 5649–5659. [Google Scholar] [CrossRef]
- Heywood, J.B. Internal Combustion Engine Fundamentals; Mcgraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Ferguson, C.R.; Kirkpatrick, A.T. Internal Combustion Engines: Applied Thermosciences, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2016. [Google Scholar]
- Cooney, C.; Worm, J.; Michalek, D.; Naber, J. Wiebe function parameter determination for mass fraction burn calculation in an ethanol-gasoline fuelled SI engine. J. Kones 2008, 15, 567–574. [Google Scholar]
- Choi, W.; Song, H.H. Composition-considered Woschni heat transfer correlation: Findings from the analysis of over-expected engine heat losses in a solid oxide fuel cell–internal combustion engine hybrid system. Energy 2020, 203, 117851. [Google Scholar] [CrossRef]
- De Cuyper, T.; Broekaert, S.; Chana, K.; De Paepe, M.; Verhelst, S. Evaluation of empirical heat transfer models using TFG heat flux sensors. Appl. Therm. Eng. 2017, 118, 561–569. [Google Scholar] [CrossRef] [Green Version]
- Lounici, M.S.; Loubar, K.; Balistrou, M.; Tazerout, M. Investigation on heat transfer evaluation for a more efficient two-zone combustion model in the case of natural gas SI engines. Appl. Therm. Eng. 2011, 31, 319–328. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, A.; Yaghoubi, M. Estimation of instantaneous local heat transfer coefficient in spark-ignition engines. Int. J. Therm. Sci. 2010, 49, 1309–1317. [Google Scholar] [CrossRef]
- Qasemian, A.; Azarikhah, P.; Haqparast, S.J. Derivation of Specific Heat Rejection Correlation in an SI Engine; Experimental and Numerical Study. Int. J. Automot. Eng. 2018, 8, 2679–2691. [Google Scholar]
- Azarikhah, P.; Haghparast, S.J.; Qasemian, A. Investigation on total and instantaneous energy balance of bio-alternative fuels on an SI internal combustion engine. J. Therm. Anal. Calorim. 2019, 137, 1681–1692. [Google Scholar] [CrossRef]
- The National Institute for Occupational Safety and Health (NIOSH) Pocket Guide to Chemical Hazards. Available online: www.cdc.gov (accessed on 14 August 2019).
- Abedin, M.; Masjuki, H.; Kalam, M.; Sanjid, A.; Rahman, S.A.; Masum, B. Energy balance of internal combustion engines using alternative fuels. Renew. Sustain. Energy Rev. 2013, 26, 20–33. [Google Scholar] [CrossRef]
- Ozcan, H.; Söylemez, M. Thermal balance of a LPG fuelled, four stroke SI engine with water addition. Energy Convers. Manag. 2006, 47, 570–581. [Google Scholar] [CrossRef]
- Ajav, E.; Singh, B.; Bhattacharya, T. Thermal balance of a single cylinder diesel engine operating on alternative fuels. Energy Convers. Manag. 2000, 41, 1533–1541. [Google Scholar] [CrossRef]
- Martyr, A.J.; Plint, M.A. Engine Testing: Theory and Practice; Elsevier: Oxford, UK, 2011. [Google Scholar]
- Yun, K.T.; Cho, H.; Luck, R.; Mago, P.J. Modeling of reciprocating internal combustion engines for power generation and heat recovery. Appl. Energy 2013, 102, 327–335. [Google Scholar] [CrossRef]
- Sandoval, D.; Heywood, J.B. An Improved Friction Model for Spark-Ignition Engines. SAE Trans. 2003, 112, 1041–1052. [Google Scholar] [CrossRef] [Green Version]
- Yusri, I.; Mamat, R.; Azmi, W.; Najafi, G.; Sidik, N.; Awad, O.I. Experimental investigation of combustion, emissions and thermal balance of secondary butyl alcohol-gasoline blends in a spark ignition engine. Energy Convers. Manag. 2016, 123, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Sayin, C.; Hosoz, M.; Canakci, M.; Kiliçaslan, I. Energy and exergy analyses of a gasoline engine. Int. J. Energy Res. 2007, 31, 259–273. [Google Scholar] [CrossRef]
- Thakur, A.K.; Kaviti, A.K.; Mehra, R.; Mer, K. Progress in performance analysis of ethanol-gasoline blends on SI engine. Renew. Sustain. Energy Rev. 2017, 69, 324–340. [Google Scholar] [CrossRef]
- Owen, K.; Coley, T. Automotive fuels reference book. In Fuel and Energy Abstracts; Society of Automotive Engineers: Warrendale, PA, USA, 1995; Volume 1, p. 10. [Google Scholar]
- Bayraktar, H. Experimental and theoretical investigation of using gasoline–ethanol blends in spark-ignition engines. Renew. Energy 2005, 30, 1733–1747. [Google Scholar] [CrossRef]
- Najafi, G.; Ghobadian, B.; Tavakoli, T.; Buttsworth, D.; Yusaf, T.; Faizollahnejad, M. Performance and exhaust emissions of a gasoline engine with ethanol blended gasoline fuels using artificial neural network. Appl. Energy 2009, 86, 630–639. [Google Scholar] [CrossRef]
- Di Iorio, S.; Mancaruso, E.; Sementa, P.; Vaglieco, B.M. A comprehensive analysis of the impact of biofuels on the performance and emissions from compression and spark-ignition engines. Int. J. Engine Res. 2015, 16, 680–690. [Google Scholar] [CrossRef]


| Engine Characteristic | |
|---|---|
| Type | SI |
| Volume of Cylinder | 124.1 cm3 |
| Bore Stroke | 56.5 mm 49.5 mm |
| Compression Ratio | 9.1:1 |
| Maximum Power | 7.4 kW @ 8492 rpm |
| Maximum Torque | 9.23 N.m @ 6997 rpm |
| Intake Valve Timing | 5 Degrees bTDC/35 Degrees aBDC |
| Exhaust Valve Timing | 30 Degrees bBDC/5 Degrees aTDC |
| Cooling type | Air-cooled |
| Fuel Properties | Gasoline (E00) | Ethanol (E100) |
|---|---|---|
| Chemical Formula | C8H15 | C2H5OH |
| Lower Heating value (kJ/kg) | 43,000 | 26,950 |
| Higher Heating value (kJ/kg) | 47,300 | 29,710 |
| Flash Point (°C) | −42.7 | 12.8 |
| Ignition Temperature (°C) | 276.7 | 422.8 |
| Specific Gravity | 0.72 | 0.79 |
| Vapor Density | 3 | 1.49 |
| Boiling Point (°C) | 201.7 | 78.3 |
| Upper Explosive Limit | 7.6% | 19% |
| Lower Explosive Limit | 1.4% | 3.3% |
| Rpm | Model | Experiment | Error (%) | |
|---|---|---|---|---|
| Heat Loss/Brake Power | 3000 | 0.75 | 0.695 | 7.91 |
| 4000 | 0.633 | 0.601 | 5.32 | |
| 5000 | 0.578 | 0.529 | 9.43 | |
| Total Fuel Power (kW) | 3000 | 5.9 | 5.937 | 0.62 |
| 4000 | 8.59 | 8.113 | 5.87 | |
| 5000 | 11.138 | 10.245 | 8.71 | |
| Exhaust Power (kW) | 3000 | 2.4 | 2.208 | 8.69 |
| 4000 | 3.7 | 3.451 | 7.21 | |
| 5000 | 5 | 4.68 | 6.83 | |
| Brake Power (kW) | 3000 | 2 | 2.2 | 9.09 |
| 4000 | 3 | 2.9 | 3.44 | |
| 5000 | 3.89 | 3.6 | 8.05 |
| rpm | Total Power (kW) | Brake Power (kW) | Heat Loss (kW) | Exhaust Loss (kW) | |
|---|---|---|---|---|---|
| (a) | 3000 | 6.27 | 1.94 | 1.71 | 2.63 |
| 4000 | 9.05 | 2.84 | 2.22 | 4.00 | |
| 5000 | 11.81 | 3.68 | 2.72 | 5.42 | |
| (b) | 3000 | 6.27 | 1.99 | 1.80 | 2.47 |
| 4000 | 9.02 | 2.91 | 2.32 | 3.79 | |
| 5000 | 11.71 | 3.77 | 2.82 | 5.12 | |
| (c) | 3000 | 6.23 | 2.02 | 1.88 | 2.34 |
| 4000 | 8.99 | 2.97 | 2.41 | 3.61 | |
| 5000 | 11.61 | 3.83 | 2.92 | 4.86 | |
| (d) | 3000 | 6.20 | 2.03 | 1.95 | 2.22 |
| 4000 | 8.96 | 3.01 | 2.51 | 3.45 | |
| 5000 | 11.53 | 3.88 | 3.02 | 4.63 |
| rpm | Total Power (kW) | Brake Power (kW) | Heat Loss (kW) | Exhaust Loss (kW) | |
|---|---|---|---|---|---|
| (a) | 3000 | 6.32 | 1.96 | 1.71 | 2.65 |
| 4000 | 9.12 | 2.87 | 2.22 | 4.03 | |
| 5000 | 11.91 | 3.72 | 2.72 | 5.47 | |
| (b) | 3000 | 6.31 | 2.01 | 1.80 | 2.50 |
| 4000 | 9.08 | 2.94 | 2.32 | 3.82 | |
| 5000 | 11.81 | 3.81 | 2.83 | 5.17 | |
| (c) | 3000 | 6.28 | 2.04 | 1.88 | 2.36 |
| 4000 | 9.05 | 3.00 | 2.41 | 3.63 | |
| 5000 | 11.71 | 3.88 | 2.93 | 4.90 | |
| (d) | 3000 | 6.25 | 2.05 | 1.95 | 2.24 |
| 4000 | 9.03 | 3.05 | 2.51 | 3.47 | |
| 5000 | 11.63 | 3.93 | 3.02 | 4.68 |
| rpm | Total Power (kW) | Brake Power (kW) | Heat Loss (kW) | Exhaust Loss (kW) | |
|---|---|---|---|---|---|
| (a) | 3000 | 6.63 | 2.10 | 1.73 | 2.80 |
| 4000 | 9.54 | 3.07 | 2.23 | 4.24 | |
| 5000 | 12.55 | 4.02 | 2.74 | 5.79 | |
| (b) | 3000 | 6.62 | 2.16 | 1.82 | 2.64 |
| 4000 | 9.50 | 3.16 | 2.33 | 4.02 | |
| 5000 | 12.44 | 4.12 | 2.85 | 5.47 | |
| (c) | 3000 | 6.58 | 2.19 | 1.90 | 2.49 |
| 4000 | 9.47 | 3.22 | 2.43 | 3.83 | |
| 5000 | 12.34 | 4.20 | 2.96 | 5.19 | |
| (d) | 3000 | 6.54 | 2.21 | 1.97 | 2.36 |
| 4000 | 9.45 | 3.27 | 2.52 | 3.66 | |
| 5000 | 12.26 | 4.25 | 3.06 | 4.95 |
| rpm | Total Power (kW) | Brake Power (kW) | Heat Loss (kW) | Exhaust Loss (kW) | |
|---|---|---|---|---|---|
| (a) | 3000 | 6.67 | 2.13 | 1.72 | 2.82 |
| 4000 | 9.61 | 3.12 | 2.22 | 4.28 | |
| 5000 | 12.63 | 4.08 | 2.73 | 5.82 | |
| (b) | 3000 | 6.65 | 2.19 | 1.81 | 2.65 |
| 4000 | 9.57 | 3.20 | 2.32 | 4.05 | |
| 5000 | 12.52 | 4.18 | 2.84 | 5.50 | |
| (c) | 3000 | 6.61 | 2.22 | 1.89 | 2.51 |
| 4000 | 9.54 | 3.27 | 2.42 | 3.85 | |
| 5000 | 12.42 | 4.26 | 2.94 | 5.22 | |
| (d) | 3000 | 6.58 | 2.24 | 1.96 | 2.38 |
| 4000 | 9.51 | 3.32 | 2.51 | 3.68 | |
| 5000 | 12.33 | 4.31 | 3.04 | 4.98 |
| Increase in Variable | Reason | |
|---|---|---|
| Compression Ratio | Increase | Increase of in cylinder gas temperature and convection heat transfer coefficient |
| Engine Speed | Decrease | Shortening the time of a cycle reduces the time and opportunity for heat transfer and on the other hand brake work increases due to the volumetric efficiency increase; so, the brake power increases. |
| Percent of Ethanol | Decrease | The percentage increase in ethanol increases the flame speed and brings the combustion closer to the constant volume combustion. Therefore, the thermal efficiency increases and brake power increases. |
| Increase in Variable | Effect on | Reason |
|---|---|---|
| Compression Ratio | Decrease | Increase of expansion ratio leads to less energy at the end of power stroke |
| Engine Speed | Increase | Shortening the time of a cycle reduces the time and opportunity for heat transfer leads to more energy remaining at the end of power stroke |
| Percent of Ethanol | Increase | Decrease of flame temperature in comparison of gasoline; so, less heat loss occurs and more energy remains at the end of power stroke |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qasemian, A.; Haghparast, S.J.; Azarikhah, P.; Babaie, M. Effects of Compression Ratio of Bio-Fueled SI Engines on the Thermal Balance and Waste Heat Recovery Potential. Sustainability 2021, 13, 5921. https://doi.org/10.3390/su13115921
Qasemian A, Haghparast SJ, Azarikhah P, Babaie M. Effects of Compression Ratio of Bio-Fueled SI Engines on the Thermal Balance and Waste Heat Recovery Potential. Sustainability. 2021; 13(11):5921. https://doi.org/10.3390/su13115921
Chicago/Turabian StyleQasemian, Ali, Sina Jenabi Haghparast, Pouria Azarikhah, and Meisam Babaie. 2021. "Effects of Compression Ratio of Bio-Fueled SI Engines on the Thermal Balance and Waste Heat Recovery Potential" Sustainability 13, no. 11: 5921. https://doi.org/10.3390/su13115921
APA StyleQasemian, A., Haghparast, S. J., Azarikhah, P., & Babaie, M. (2021). Effects of Compression Ratio of Bio-Fueled SI Engines on the Thermal Balance and Waste Heat Recovery Potential. Sustainability, 13(11), 5921. https://doi.org/10.3390/su13115921







