Climatic Issue in an Advanced Numerical Modeling of Concrete Carbonation

Abstract

Damage in reinforced concrete structures is frequently caused by reinforcement corrosion due to carbonation. Although a wide range of literature contributed to the concrete carbonation consisting of experimental investigations and numerical simulations, research work on a complete numerical model for concrete carbonation prediction with integrated climatic variables (e.g., temperature, relative humidity) is still a challenge. The present paper aims to propose an advanced numerical model to simulate the penetration of carbon dioxide and moisture, diffusion of calcium ions, heat transfer, and porosity modification in concrete material using COMSOL Multiphysics software. Three coupled mass conservation equations of calcium, water, and carbon dioxide are solved together with additional equations regarding the heat transfer, variation of porosity, and content of portlandite and other hydrates and calcites. In this study, the actual temporal variabilities of temperature and relative humidity in Toulouse, France, are used as a case study. The predicted results of portlandite profiles and carbonation depth are compared with the experimental data and discussed to identify the effect of climatic variables on the concrete carbonation.

1. Introduction

Invented in the late nineteenth century, reinforced concrete (RC) is today the most widespread building material in the world. Unfortunately, during the service life of existing structures (e.g., buildings, bridges, tunnels), the deterioration of RC elements occurs due to many factors including structural loads, quality of materials, environmental conditions, etc. [1,2]. Furthermore, the impact of climate change (e.g., global warming) on existing RC structures is considerable, since the corrosion deteriorations induce an increase in repair cost. The elevated carbon dioxide (CO₂) levels related to global warming can increase the potential of carbonation-induced corrosion. Reinforcement corrosion is one of the most dominant deterioration mechanisms. It inflicts damages that lead to a decrease in the performance as well as the safety of existing structures [3]. Corrosion attacks can be classified into two sources, which are the carbonation of concrete and the penetration of chloride ions. The carbonation of concrete implies a potential risk in the durability of RC structures if the carbonation depth reaches the steel rebars [4].

Carbon dioxide in gaseous form in the atmosphere penetrates the porous network of concrete. In contact with the pore solution, the CO₂ dissolves and causes a chemical reaction with hydrated cement paste. This reaction transforms the hydration products (e.g., portlandite, calcium silicate hydrates) into calcium carbonate. The carbonation kinetics depend on the concrete mix (e.g., cement type, cement content, water/cement ratio) and exposure conditions (e.g., concrete surface sheltered or not from rain, relative humidity) [5,6,7,8,9]. During carbonation, the pore solution pH of concrete should be below 9.0 for a fully carbonated zone [10]. This process can induce the destabilization of the passive film on the rebar surface. Steel corrosion can then be initiated according to the conditions of humidity and oxygen, which causes disturbances in the mechanical behavior of concrete structures and may lead to cracking [11,12].

The carbonation issue has been intensively investigated for decades, mainly in accelerated conditions (high relative pressure of carbon dioxide) due to its slowness in atmospheric conditions. Although the findings of these investigations have brought significant and valuable knowledge, some aspects of the phenomenon remain comprehensively unelucidated. The kinetics and type of hydrated compounds carbonated are drastically different with respect to the exposure conditions. The constant fluctuation of relative humidity and temperature in outdoor conditions is often reduced to an average effect. The diffusion of calcium ions in the pore solution, from the dissolution site to the reactive site, should be taken into account in the carbonation models [13]. Climate change, the impact of which on concrete structures is expected to increase over the century, ought to be more extensively investigated, in particular the thermo-activation on reactions [14,15]. The present paper addresses these aspects from the numerical viewpoint.

Numerous models have been developed to estimate the carbonation depth of concrete, which are classified by either the approach or the targeted objective. Simplified models were established [16,17,18,19,20,21,22] to provide easy-to-use tools for engineers that estimate the carbonation depth with an acceptable precision using a limited number of input parameters. In general, these models were based on the assumption that the partial pressure of carbon dioxide varies linearly from the exposed surface of the material to the carbonation front. The carbonation depth is thus a square root function of time. Meanwhile, the numerical models of concrete carbonation have been also developed by many researchers [7,9,23,24,25,26,27,28,29]. The numerical models aim to describe the phenomena involved as well as various influencing factors using a more detailed approach than the simplified models. These models are mainly based on solving the mass conservation equations and require implementation in a calculation program.

Among the numerical carbonation models developed in the recent research works, Bary et al.’s model has been the most promising regarding the aspects previously mentioned [26,27]. This model couples the transfer of carbon dioxide in the gaseous phase with the transfers of liquid water and calcium ions in an aqueous solution. The chemical model of hydrate leaching is only governed by the concentration of calcium ions. The approach used makes it possible to take into account the carbonation of all hydrated phases consisting of portlandite, C-S-H, ettringite (AFt or trisulfoaluminate), and monosulfoaluminate (AFm). The mass conservation equations in the model of Bary et al. 2004 [26] have been considered in this study. In addition, specific developments have been achieved to account more realistically for outdoor exposure conditions. The results over a long time of exposure are given through various profiles (hydrated compounds, porosity, saturation degree, calcite, etc.). Results show how the computed carbonation rate is influenced by both the boundary conditions and the usually accepted assumptions.

The present study aims to propose an advanced numerical model to simulate the penetration of carbon dioxide and moisture, diffusion of calcium ions, heat transfer, and porosity modification in conventional concrete. The predictions of portlandite profile and carbonation depth are compared with the experimental data. Then, the proposed model has been applied to two concretes having compressive strengths measured on cylindrical specimens that correspond to C25 and C45 classes according to European standard EC2. Furthermore, the actual temporal variabilities of temperature and relative humidity in Toulouse, France, are used as a case study to identify the effect of climatic variations on concrete carbonation.

2. Numerical Model of Concrete Carbonation

The model proposed by Bary and Sellier 2004 [26] assumes that a volume of concrete is composed of three phases (liquid, solid, and gas), and the chemical reactions of dissolution, solidification, vaporization, and liquefaction occur at the interface between these phases. In this model, the phenomena are considered, such as water permeability of the porous medium, diffusion of CO₂ in the gas phase of the pore solution, migration of calcium ions in the liquid phase, gradual decalcification by the dissolution of hydrated cement paste, formation of calcite by reaction between calcium ions and dissolved CO₂, and variation in porosity due to both decalcification and formation of calcite. The modeling approach proposed is based on the coupling of three equations of mass conservation for water, carbon dioxide, and calcium.

2.1. Mass Conservation Equations

The model is based on three equations of mass conservation that are written for the contents of water, carbon dioxide, and calcium in the concrete medium. These parameters are characterized by the degree of water saturation, the partial pressure of carbon dioxide in the interstitial gas phase, and the concentration of calcium ions in the pore liquid phase [26,27]. The mass conservation equations are shown in detail for each parameter in the next paragraphs.

2.1.1. Mass Conservation of Water

The mass variation of water (liquid phase) in a unit volume during a time interval (dt) is based on the water mass flow (devoted w_l) and the amount of water released (devoted S_l) with the hydrates dissolution, as expressed in Equation (1) with S_r being the saturation degree, ρ_l (kg/m³) being the density of water, and ϕ being the porosity.

$$\frac{\partial {\rho }_l\varphi S_r}{\partial t}=S_l-div[w_l]$$

(1)

The water mass flow w_l is given by Equation (2), with K^ϕ (m²) being the intrinsic permeability of the material, η (kg/m.s) being the dynamic viscosity coefficient of water, k_rl being the relative permeability that depends on the saturation degree S_r of concrete [30], p_cap (Pa) being the capillary pressure, and h_r being the relative humidity.

$$w_l=-\frac{K^{\varphi }{\rho }_l}{\eta }{k}_{rl}{p}_{cap}^{\prime hr}{h}_r^{\prime S_r}grad(S_r)$$

(2)

The water released S_l through the hydrates dissolution is expressed in Equation (3), with k_sl being the coefficient for the influence of the saturation degree on the reaction process [31] (due to the variation of the contact surface between water and hydrates), $M_{H_{2}O}$ (kg/mol) is the molar mass of water, the term n_w refers to the concentration of water involved in the solid phase dissolution by unit volume of material, and its value depends on the calcium concentration C_a (mol/m³) in the pore solution [6,32,33].

$$S_l=-k_{sl}{M}_{H_{2}O}{n}_w\frac{\partial C_a}{\partial t}$$

(3)

Finally, the equation of water mass conservation is expressed as follows:

$${\rho }_l\varphi \frac{\partial S_r}{\partial t}=div\left[\frac{K^{\varphi }{\rho }_l}{\eta }{k}_{rl}{p}_{cap}^{\prime hr}{h}_r^{\prime S_r}grad(S_r)\right]-k_{sl}{M}_{H_{2}O}{n}_w\frac{\partial C_a}{\partial t}-{\rho }_l{S}_r\frac{\partial \varphi }{\partial t}$$

(4)

2.1.2. Mass Conservation of Carbon Dioxide

The mass variation of carbon dioxide in a volume unit during a time interval (dt) depends on the carbon dioxide mass flow (devoted w_c) through the volume and on its consumption by the chemical reaction to form calcite (devoted S_c), as expressed in Equation (5), with ρ_c (kg/m³) being the density of carbon dioxide and ϕ being the porosity.

$$\frac{\partial \varphi (1-S_r){\rho }_c}{\partial t}=-S_c-div\left[w_c\right]$$

(5)

The CO₂ mass flow w_c is expressed in Equation (6) with $D_{C{O}_2}$ (m²/s) being the diffusion coefficient of CO₂ in the air, $f_{\left(\varphi ,S_r\right)}$ being a factor of diffusion resistance, M_c (kg/mol) being the molar mass of carbon dioxide, R (m²·kg/mol·K·s²) being the ideal gas constant, T (K) being the temperature, and p_c being the capillary pressure [26,34].

$$w_c=-f_{\left(\varphi ,S_r\right)}{D}_{C{O}_2}\frac{M_c}{R.T}grad(p_c)$$

(6)

The CO₂ mass precipitated S_C from the pore solution per unit of time to form calcite is given by Equation (7), with n_cal being the molar formation rate of calcite.

$$S_c=M_c\frac{\partial n_{cal}}{\partial t}$$

(7)

Thus, the equation of the mass conservation of carbon dioxide can be rewritten as follows:

$$\varphi (1-S_r)\frac{\partial p_c}{\partial t}=div\left[f_{(\varphi ,S_r)}{D}_{CO2}grad(p_c)\right]-RT\frac{\partial n_{cal}}{\partial t}+\varphi p_c\frac{\partial S_r}{\partial t}-\left(1-S_r\right)p_c\frac{\partial \varphi }{\partial t}$$

(8)

2.1.3. Mass Conservation of Calcium

The variation of calcium concentration C_a in the porous solution is expressed in Equation (9) for a volume unit, with w_a being the flux of calcium ions and S_a being the source term of the production of calcium ions released from the hydrates during the decalcification process [35].

$$\frac{\partial \varphi S_r{C}_a}{\partial t}=S_a-div\left[C_a\frac{w_l}{{\rho }_l}+w_a\right]$$

(9)

The flux of calcium ions through the porous solution the calcium flux derives from the concentration gradient is determined by Equation (10), with $D_{C_a}$ being the effective diffusion coefficient of calcium ions in the pore solution that depends on both the saturation degree and the porosity.

$$w_a=-D_{C_a}grad(C_a)$$

(10)

The calcium ions production S_a is partially offset by calcium consumption through the formation of calcite as expressed in Equation (11), with n_CaS (mol/m³) being the concentration of calcium in the solid phase in a unit volume of a porous material.

$$S_a=-k_{sl}\frac{d{n}_{CaS}}{d{C}_a}\frac{\partial C_a}{\partial t}-\frac{\partial n_{cal}}{\partial t}$$

(11)

Through this mass balance equation, the concentration of calcium ions in the porous solution, as well as the concentration of calcium in the solid phase of the porous material, is calculated depending on the water flow, the calcium ions flow, and the calcite formation and hydrates dissolution rates.

2.2. Additional Equations

In order to assess detailed evolutions in the porous material, the additional equations are also used for the porosity variation, the content of portlandite, other hydrates, and calcite.

2.2.1. Equation of Porosity Variation

The porosity variation is due to a difference in molar volume between the initial products (hydrates) and final products (calcite, vaterite, aragonite) of the carbonation process. The dissolution of one mole of portlandite releases one mole of calcium that precipitates in one mole of calcite. The ratio is somehow different for other hydrates (including C-S-H, aluminates, ettringite, etc.). The difference between the molar volumes of these components induces a decrease in the material porosity. This variation is modeled by Equation (12), in which V_dS (m³/mol) is the volume fraction of dissolved hydrates in a unit volume of the hydrated material, C_a (mol/m³) is the concentration of calcium ion in the aqueous phase, and $V_{CaC{O}_3}$ (37 × 10⁻⁶ m³/mol) is the molar volume of calcite [17].

$$\frac{\partial \varphi }{\partial t}=-k_{sl}\frac{d{V}_{dS}}{d{C}_a}\frac{\partial C_a}{\partial t}-V_{CaC{O}_3}\varphi S_r\frac{\partial n_{cal}}{\partial t}$$

(12)

2.2.2. Equation of Hydrates Dissolution Rate

The hydrates of cement paste are dissolved during the carbonation process, and the kinetic of the solubilization depends on the dissolved carbon dioxide and the saturation degree. Different kinds of kinetics for portlandite and other hydrates have been considered here, due to the high dependency of the global carbonation kinetics on the dissolution of portlandite.

● Portlandite Dissolution Rate

The kinetics of portlandite dissolution is highly important to assess the carbonation degradation, because this hydrate is the most sensitive to any chemical disorder and is responsible for the basic pH of concrete. Therefore, carbonation depth estimation is based on the portlandite dissolution. In this study, a different kinetic is proposed for portlandite and other hydrates, as in Equation (13) proposed by Thiery 2005 [7] and Bary and Mügler 2006 [27].

$$\frac{\partial n_{CH}}{\partial t}=-k_{sl}{k}_H{k}_{CH}{p}_c$$

(13)

where k_H (mol·m⁻³·Pa⁻¹) is Henry’s constant for carbon dioxide [33,35] and k_CH is the kinetic coefficient for portlandite dissolution [7,27], depending on the current volume fraction of portlandite (V_p). This coefficient expresses the formation and growth of a calcite layer around spherical portlandite crystals during the carbonation process. Thus, the kinetic coefficient decreases as the calcite layer grows:

$$k_{CH}=\frac{3V_p}{R_{p0}}\frac{{(1-k_p)}^{2/3}{D}_{CaC{O}_3}}{\lambda +R_{p0}\left[{\left(1+k_p\left(\frac{V_{CaC{O}_3}}{V_{CH}}-1\right)\right)}^{1/3}-{(1-k_p)}^{1/3}\right]}$$

(14)

where V_p (m³/mol) is the current volume fraction of portlandite; R_p0 (m) is the equivalent radius of the initial portlandite crystals; $V_{CH}$ and $V_{CaC{O}_3}$ (m³/mol) are portlandite and calcite molar volumes; λ stands for the equivalent thickness of the calcite layer.

The degradation index k_p (m) is determined following Equation (15):

$$k_p=1-\frac{n_{CH}}{n_{CH,0}}$$

(15)

where: n_CH,0 and n_CH (mol/m³) are the initial and remaining amount of portlandite per unit volume, respectively.

● Other Hydrates Dissolution Rate

All other hydrates are assimilated to C-S-H. The dissolution kinetic is assumed to depend linearly on the carbon dioxide pressure.

$$\frac{\partial n_{CSH}}{\partial t}=-k_{sl}{k}_H{k}_{CSH}{p}_c$$

(16)

where k_CSH is the kinetic coefficient of hydrates dissolution that is calculated for C-S-H, aluminates, and ettringite as Equation (17) [7,27].

$$k_{CSH}={\alpha }_{CSH}\frac{n_{CSH}}{n_{CSH,0}}$$

(17)

where α_CSH is a model’s coefficient; n_CSH,0 and n_CSH (mol/m³) are the initial and current amounts of other hydrates assimilated to C-S-H, respectively.

2.2.3. Equation of Calcite Formation Rate

The molar velocity of calcite formation is expressed by the rate of dissolution of molar portlandite and other hydrates (C-S-H mainly), introducing α_HYD a coefficient of equivalent stoichiometry for calcium in hydrates (but portlandite) and calcite.

$$\frac{\partial n_{cal}}{\partial t}=\left(\frac{\partial n_{CH}}{\partial t}+\frac{\partial n_{CSH}}{\partial t}\frac{1}{{\alpha }_{HYD}}\right)$$

(18)

2.2.4. Carbonation Depth

The carbonation depth is estimated through the amount of remaining portlandite in the material. The damaged area is assimilated to the part of the material where the portlandite concentration is less than 10% of the initial amount for the accelerated carbonation [17,27] and less than 50% for the atmospheric carbonation.

3. Validation of Numerical Model

Two-dimensional simulation is performed using COMSOL Multiphysics software for modeling the carbonation process into a concrete structure of 10 cm length × 10 cm width × 1 cm height, with a regular spacing of 1.0 mm between nodes. The direction of carbonation is estimated according to the two sections 1-1 and 2-2, as shown in Figure 1. The mesh at the corner of the model is illustrated in Figure 2.

The first case is studied for the concrete carbonation under atmospheric conditions. The material is totally saturated and then exposed on one face to the outdoor relative humidity of 65% and temperature of 20 °C. Material is broadly equivalent to the concrete that is made of cement CEM I with a water–cement ratio of 0.42. The input parameters of the model can be found in the study conducted by Bary and Mügler 2006 [27]. The predicted carbonation depth over 230 days using the proposed model is compared to that of the existing models [27,28], which are based on the same equations under constant exposure conditions. Figure 3 presents the evolution of predicted carbonation depth in time by the proposed model and two existing models. The obtained results in Figure 3 show that the carbonation depth predictions are greatly fitting between these models.

The second case is employed to study accelerated carbonation. The comparison between the predicted results and the experimental results from the study of Thiery 2005 [7] illustrated in Figure 4 does not show a good agreement for portlandite profile at 14–day exposure. Nevertheless, it must be kept in mind that predictions should be regarded in the context of possible uncertainties of many input parameters (obtained from the experimental process), which would lead to estimate a confidence interval of outputs in place of a single result. Such an approach is beyond the scope of the present paper.

4. Modeling of Temperature Variation

4.1. Modeling the Effect of Temperature on the Kinetics

The temperature has an influence on the process of water sorption/desorption, the diffusion of ions, the flow of gaseous and liquid phases, and the chemical transformations [36]. Therefore, many parameters and variables of the model vary under temperature variations.

The diffusion coefficient for CO₂ increases with temperature according to a classical Arrhenius law as follows:

$$D_{C{O}_2}(T)=D_{C{O}_2}(T_{ref}).\exp \left(-\frac{Q_D}{R}\left(\frac{1}{T}-\frac{1}{T_{ref}}\right)\right)$$

(19)

where Q_D = 39 kJ/mol is the activation energy for the diffusion process; R is the gas constant; T_ref = 298 K is a reference temperature [5,28].

The chemical stability of portlandite (as well as other hydrates) decreases when the temperature increases, which is modeled by Arrhenius law with a negative activation energy Q_CH to be −40 kJ/mol [31,37,38]:

$$k_{CH}(T)=k_{CH}(T_{ref}).\exp \left(-\frac{Q_{CH}}{R}\left(\frac{1}{T}-\frac{1}{T_{ref}}\right)\right)$$

(20)

The coefficient of Henry’s law describing the equilibrium between the gas and liquid phase of CO₂ is altered according to temperature, with an activation energy Q_H to be 19.95 kJ/mol [39], as follows:

$$k_H(T)=k_H(T_{ref}).\exp \left(-\frac{Q_H}{R}\left(\frac{1}{T}-\frac{1}{T_{ref}}\right)\right)$$

(21)

Water viscosity decreases with increasing temperature [40,41], which corresponds to a negative activation energy Q_η to be −15.7 kJ/mol, as follows:

$$\eta (T)=\eta (T_{ref}).\exp \left(-\frac{Q_{\eta }}{R}\left(\frac{1}{T}-\frac{1}{T_{ref}}\right)\right)$$

(22)

The last point is that the temperature modifies the sorption–desorption isotherms [37,41]. Therefore, we propose to correct the isotherms with an Arrhenius equation where the activation energy Q_s depends on water pressure and temperature according to the functions presented in Van Balen and Van Gemert 1994 [24] and Ishida et al. 2007 [37], inspired by the study by Poyet and Charles 2009 [36] and based on the experimental results presented in Hundt and Kantelberg 1978 [42].

$$S_r(T)=S_r(T_{ref}).\exp \left(-\frac{Q_S}{R}\left(\frac{1}{T}-\frac{1}{T_{ref}}\right)\right)$$

(23)

$$Q_S=a_1+\frac{a_2}{{\left(a_3+\frac{p_l}{P_m(T)}\right)}^2}$$

(24)

$$P_m(T)=a_4+a_5\left(T-T_{ref}\right)$$

(25)

where: the coefficients are a₁ = 427 J/mol; a₂ = 646 J/mol; a₃ = 1.31; a₄ = −52.35 MPa; a₅ = 1.46 MPa/K [14].

4.2. Modeling Heat Transfer in the Material

The environmental conditions (e.g., temperature, relative humidity) vary during the interval of a time step for the numerical simulation of the carbonation process. Due to this variation, the temperature profile in the material varies as well.

The equation of heat transfer in the material by conduction is assumed to be:

$${\rho }_{concrete}.c_{concrete}.\frac{\partial \left(1-\varphi \right).T}{\partial t}=-div\left[{\lambda }_{concrete}.grad(T)\right]$$

(26)

where ρ_concrete = 2300 kg/m³ is the density; c_concrete = 960 J/kg·K is the specific heat; and λ_concrete = 0.92 J/kg·K is the thermal conductivity of concrete.

It is noticed that only conduction has been accounted for in the heat transfer modeling. It is assumed that the concrete surface is not exposed to solar radiation. The effect of air convection in the neighborhood of the concrete surface is limited to a thin layer of concrete and is almost negligible on the long-term concrete carbonation. The effect of a constant outer temperature on concrete carbonation is illustrated in Figure 5 and Figure 6 for C45 concrete and C25 concrete (cf.

Table 1. Characteristics of the tested concretes.

Concrete.		Compressive Strength Class
		C45	C25
Cement composition (%)	Clinker	98.74	96
	SiO2	14.0	20.3
	Al2O3	6.0	5.6
	Fe2O3	4.5	2.3
	CaO	68.0	64.2
	SO3	3.45	3.2
Concrete mix (kg/m3)	C (cement)	340	295
	W (water)	153	200
	G (aggregates)	1850	1781
Main hydrated compounds (mol/m3)	nCH,0	1440	1508
	nCSH,0	1118	866
Porosity ϕ0		0.12	0.155
Intrinsic permeability K0 (m2)		2.1 × 10−22	5 × 10−17
Diffusion coefficient $D_{C{O}_2}$ (m2/s)		3.84 × 10−5	6.2 × 10−5
Hydration degree αHYD		0.56	0.893
Parameter interprets the equivalent thickness of calcite λ (m)		5 × 10−7	5 × 10−7
Initial radius of hydrated products Rp0 (m)		20 × 10−6	20 × 10−6

), respectively. It can be seen that the difference is about half a millimeter after 50 years of exposure when the outer temperature changes from 278 to 298 K.

5. Application of Proposed Numerical Model in the Case Study

A comprehensive finite element modeling of concrete carbonation has been proposed in the previous sections. It encompasses the carbon dioxide transfer in the gaseous phase; the transfer of calcium ions provided by the dissolution of the main hydrated compounds of the cement paste includes interdependent and nonlinear source and sink terms of mass conservation equations, the heat transfer, and the chemical and physical heat activation and accounts for variable boundary conditions. In the present section, its utilization will highlight some still questionable aspects of carbonation modeling.

Although some previous modeling works have integrated non-constant boundary conditions in terms of outer moisture and temperature, very few have investigated in detail the effect of the variability of these conditions on the long-term carbonation rate. Bakker 1993 [18] attempted to assess the influence of wetting–drying cycles in the framework of a simplified approach where carbonation was stopped under wetting. More recently, Thiery et al., 2012 [43] added to Bakker’s model [18], simplified modeling of moisture transfer. Nevertheless, how far accounting for realistic outdoor conditions can change the predicted carbonation rate remained has not been experienced until now.

The calcium ion concentration in the pore solution has been demonstrated to present a significant effect on the carbonation phenomenon. However, it has not been discovered whether the motion of ions plays a significant role in carbonation kinetics. The extended modeling proposed above has enabled addressing such analyses.

5.1. Concrete Material

The concrete cover of existing structures constitutes the main barrier to prevent the initiation corrosion of steel reinforcement by carbonation due to carbon dioxide penetration. The concrete structure considered herein is only the concrete cover, with 1D ingress of carbon dioxide. The amount and type of hydrated compounds of the cement paste, as well as the porosity mainly depending on the concrete mix, are essential parameters influencing the carbonation rate. In this paper, two concretes having compressive strengths corresponding to C25 and C45 classes are studied, respectively. The characteristics of the two concretes are synthesized in Table 1.

5.2. Case Study: Outdoor Environmental Variables in Toulouse, France

Hourly average values of relative humidity and temperature have been computed over the period from 1970 to 2020 using the data recorded by a meteorological station in Toulouse, Southern France, in order to identify the evolution of outdoor environmental conditions. The boundary conditions of the numerical problem that are the outside temperature and the relative humidity are simulated using average values during each time step in the numerical simulation. The shorter this time step is, the more precise the simulation is, but computation time will also increase. Figure 7 and Figure 8 illustrate the chronicle of environmental conditions (temperature, relative humidity) used in the simulation with a temporal discretization ranging from 5 to 90 days that is assumed to be repeated every year.

5.3. Results and Discussion

5.3.1. Effect of Time Granularity on the Carbonation Depth

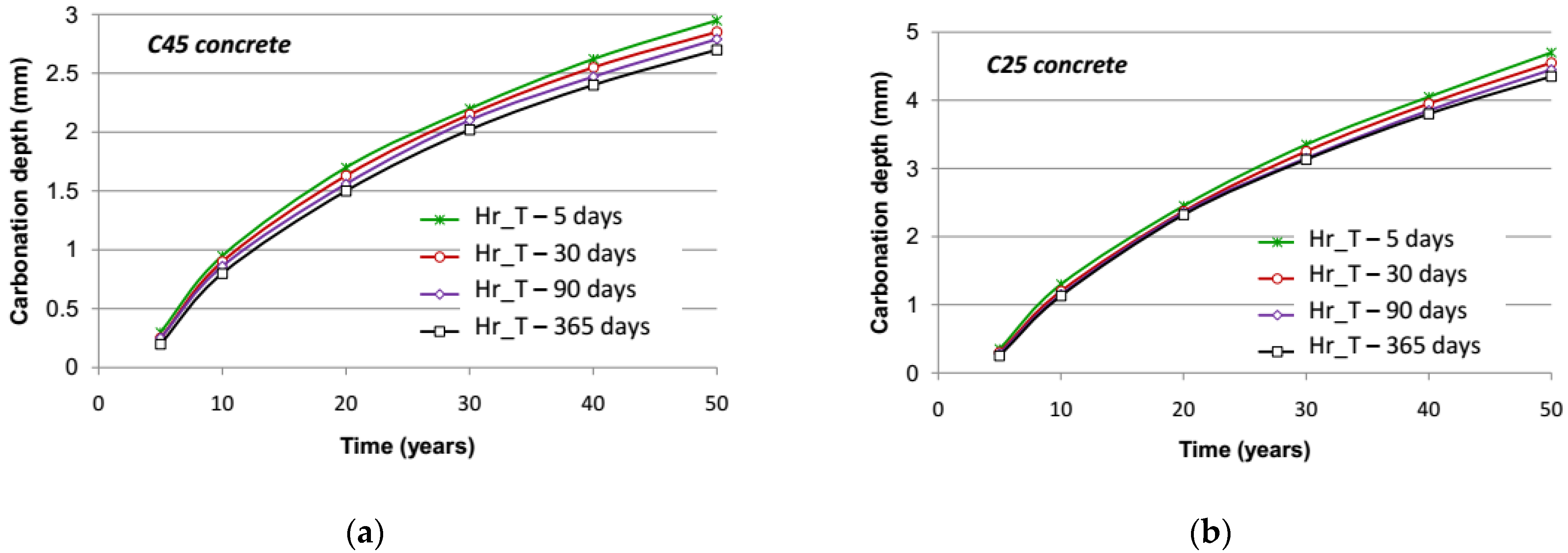
The results of carbonation simulations for C45 concrete and C25 concrete under the different spatial discretization hypotheses are shown in Figure 9, respectively. These results are summarized in

Table 2. Prediction of carbonation depth after 50 years with different time steps.

Time Step	Carbonation Depth Xc (mm)
	C45 Concrete	C25 Concrete
Hr_T–5 days	Xc,C45	Xc,C25
Hr_T–30 days	0.966% Xc,C45	0.968% Xc,C25
Hr_T–90 days	0.946% Xc,C45	0.947% Xc,C25
Hr_T–365 days	0.915% Xc,C45	0.926% Xc,C25

, in which the relative difference of the simulation results appears by taking the carbonation depth at 50 years under the lowest time step as a reference value. It is noted that the impact of an increase in the time step is relatively limited: the difference is about 10% between a time step of five days and 365 days (annual average value) after 50 years of exposure for C45 concrete and C25 concrete.

It is worth noting that the larger the time step is, the lower the carbonation depth becomes. When increasing the time step, the variation of relative humidity taken into account with regard to its average value is reduced. If the average value is fairly elevated (higher than 75%), eliminating low values of relative humidity (slightly less than 65%) by reduction of its extent, which are favorable to carbonation compared to the average value, leads to a decrease in the long-term carbonation rate. When only annual average moisture is accounted for, the resulting carbonation depth is far smaller than that obtained with a 30-day step. Comparing computational run times with respect to the time step, it can be seen that a 30-day step constitutes a good compromise between accuracy and efficiency.

The calculation time for a numerical simulation is a direct function of the time step retained to model the external conditions and of the calculation step of the simulation itself.

Table 3. Calculation time of atmospheric carbonation after 50 years of C25 concrete with different time steps and calculation steps.

Time Step	Criteria	The Calculation Step (Days)
		1	5	10	30	60
Hr-T–5 days	Calculation time (s)	Tcal5d	73% Tcal5d	68% Tcal5d	68% Tcal5d	67% Tcal5d
	Xc (mm)	4.77	4.78	4.77	4.78	4.77
Hr-T–30 days	Calculation time (s)	Tcal30d	47% Tcal30d	38% Tcal30d	35% Tcal30d	33% Tcal30d
	Xc (mm)	4.57	4.57	4.57	4.57	4.57
Hr-T–90 days	Calculation time (s)	Tcal90d	38% Tcal90d	28% Tcal90d	23% Tcal90d	22% Tcal90d
	Xc (mm)	4.39	4.40	4.38	4.40	4.39

and

Table 4. Calculation time of accelerated carbonation after 180 days of concrete C25 with different time steps and calculation steps.

Time Step	Criteria	The Calculation Step (Days)
		0.5	1	3	5	10
Hr-T–3 days	Calculation time (s)	Tcal3d	91% Tcal3d	84% Tcal3d	84% Tcal3d	81% Tcal3d
	Xc (mm)	10.96	11.01	10.95	10.97	10.97
Hr-T–5 days	Calculation time (s)	Tcal5d	84% Tcal5d	81% Tcal5d	81% Tcal5d	81% Tcal5d
	Xc (mm)	10.92	10.92	10.92	10.92	10.93
Hr-T–10 days	Calculation time (s)	Tcal10d	80% Tcal10d	77% Tcal10d	77% Tcal10d	73% Tcal10d
	Xc (mm)	10.88	10.91	10.91	10.90	10.87
Hr-T–30 days	Calculation time (s)	Tcal30d	69% Tcal30d	59% Tcal30d	59% Tcal30d	55% Tcal30d
	Xc (mm)	10.83	10.85	10.84	10.85	10.84

present the lengthening of the duration of the atmospheric carbonation simulations to 50 years and accelerated carbonation to 180 days, respectively, and the estimated depth of carbonation, according to the size of the time step for the description of the climatic chronicles and the step of the numerical simulations. These results on atmospheric and accelerated carbonation show that the calculation step only affects the calculation time and not the depth of carbonation. The obtained results presented above make it possible to consider a step of calculation and discretization of the environmental chronicles of 30 days for atmospheric carbonation and three days for accelerated carbonation.

Due to the fact that both warm temperature and low moisture of the material are favorable factors of concrete carbonation, a matter arises regarding the influence of the season when the concrete surface is first exposed to carbonation on the future of the phenomenon. The carbonation is more favorable in summer under high temperature and low moisture than in winter under favorable moisture. Results reported in Figure 10 and Figure 11 show that a noteworthy difference is visible at first with respect to the season at the onset of exposure and that this difference decreases after several months, yet it remains. It should be noted anyway that this difference is mainly significant for an accelerated process. It can be explained by the global decreasing kinetic of the carbonation process, which allows greater importance to the first months of the degradation. If the onset is in spring, for instance, the first six months of the degradation are under the warmest months of the year; therefore, the degradation is accelerated in comparison to an onset in autumn and six cold first months.

5.3.2. Effect of Heat Transfer on the Carbonation Depth

A temperature gradient always exists between surface and bulk concrete due to the fact that external temperature is not constant. Within the concrete, there is hence a variation of temperature that potentially impacts the carbonation phenomenon, therefore justifying the modeling of the heat transfer. The latter prominently depends on the concrete thermal conductivity, which may strongly vary among various concretes according to the nature of the aggregates and slightly more with respect to the moisture and temperature of the concrete.

In the present section, it is assumed that the thermal conductivity may vary by a ratio of 1 to 1000. Nonetheless, the evolution of the carbonation depth remains almost similar whatever the value of the thermal conductivity, as illustrated in Figure 12. It could then be suggested to consider that the temperature over the cover depth is constant and equal to the external one, if the time step accounted for in the modeling of outdoor conditions is stated at least at 30 days, as proposed in the former section. This conclusion derives from the kinetics of the heat transfer, which are significantly higher than those of the diffusion process.

5.3.3. Effect of Diffusion of Calcium on the Carbonation Depth

The proposed model enables the diffusion of calcium ions in the pore solution to be considered. These ions are in equilibrium with the hydrated products in a sound concrete at a concentration of 22 mol/m³. According to the decalcification process, the solubility of hydrated compounds decreases, and the concentration of calcium ions drops at a value ranging between 0 and 0.4 mol/m³ in the fully carbonated area [30]. The calcium ions are hence prone to migrating from the sound area to the carbonated one. The transfer of these ions depends on the saturation degree and porosity that both affect the diffusion coefficient for calcium. It can be seen in Figure 13 that the effect of the motion of calcium ions is very limited even for a high value of diffusion coefficient under reference conditions. This results from the fact that the gaseous diffusion kinetics of carbon dioxide remain much greater than those of calcium ions in the liquid phase for the outdoor climatic conditions retained in the study.

However, when the concrete surface is exposed to rain for a long time, the saturated concrete extent may reach the sound concrete and subsequently connect the sound region to the carbonated one in a continuously saturated way. In this case, a more significant transfer of calcium ions is expected to occur, because the ingress of carbon dioxide is blocked by the liquid phase, and the formation of calcite is not possible anymore. Extreme situations have been simulated by the change of the yearly average relative humidity in the C25 concrete to 95% and 65% in place of 78%. A porosity of 0.18 is used to increase the transfer of calcium ions. Longer periods with almost complete saturation of concrete cover then appear. Taking into account various diffusion coefficients of calcium ions shows in Figure 14 that the faster the motion of ions, the lower the long-term carbonation rate as well. In this case, indeed, calcite is formed close to the concrete surface because calcium ions are available, even if the region is already carbonated.

6. Conclusions

This study proposed a FE model for modeling concrete carbonation by using a simplified approach that is based on simple numerical models and detailed chemo-physical processes. Each numerical model used aims to assess the initiation corrosion time in reinforced concrete structures when the carbonation front reaches the reinforcing bar. The model was used with acceptable accuracy for atmospheric and accelerated carbonation. It is noted that predictions should be related to the possibility of the uncertainty of several input parameters, which lead to a range of output values instead of a single result. Some tests have been achieved on 2D simulation for atmospheric carbonation under outdoor environmental conditions in Toulouse, France, as a case study.

It appears that for modeling the concrete carbonation process under atmospheric conditions, it is relevant to take into account the variation of the environmental conditions (e.g., temperature, relative humidity) with each time step being 30 days. It is shown that the season for the onset of the degradation has a slight influence on the kinetics of the process during the first year. It has also been discovered that, provided the time step for the numerical simulation is long enough, it is not necessary to model the heat transfer within the material, and the temperature could be considered equal to the external one.

This study also focuses on the process of calcium ion diffusion, whose kinetics are much slower than for the diffusion processes for water and carbon dioxide. Therefore, unless the material is fully saturated all along with the degradation duration, it appears that a local chemical equilibrium hypothesis for calcium can be satisfactorily formulated. Therefore, modeling the carbonation process requires two coupled mass conservation equations for water and carbon dioxide instead of three conservation equations (with calcium ions).