Designing a Multi-Stage Transport System Serving e-Commerce Activity
Abstract
1. Introduction
- Multi-stage transport system with storage which focuses on a warehousing strategy;
- Multi-stage transport system with transshipment which focuses on an immediate freight transfer strategy. Under the transshipment strategy, there is no option to stock products; the strategy requires vehicle changing when freight is unloaded at the warehouse from the incoming vehicle and loaded into the outgoing vehicle without changing the freight’s nature [7].
2. Theoretical Background
2.1. The Design of a Multi-Stage Transport System
2.2. The Selection of Serving Warehouse in the Multi-Stage Transportation System
- From all alternative warehouses, which do not cover geographic territory;
- From the list, left after the previous elimination, in which other alternative warehouses are eliminated, mainly those which total service distance is the highest.
3. The Methodology for Serving e-Commerce Activity
- The retrieval of addresses and coordinates of all locations and the calculation of service distances following two distance metrics;
- The application of the maximal coverage model incorporating mandatory closeness service distance. The model incorporating the analytical linear programming (LP) method is used for the revision of the locational system configuration and the number of warehouses covering the geographical territory identification;
- The review of the impact of returns on the overall service distances important for e-commerce activity through the modelling. For identification of which location requires pick-up, the author uses a pseudorandom number generator (PRNG) applied by the Mersenne Twister algorithm;
- The ranking of alternative warehouses following the sum of service distances evaluation results that are important for the efficiency increase in the multi-stage transport system. Following the ranking rule logic, the enterprise should choose a warehouse to which total distance is the lowest at the priority row.
- The straight-line or arch-based distance metric between two points is called Euclidean distance;
- The path distance metric connecting two locations is called path-based distance.
- where
- herein: —the level of coverage provided by warehouse j to location i; I, i—the set of locations and the index of individual location; J, j—the set of warehouses and the index of specific warehouse location; —the set of potential warehouses; —the shortest distance from location i to warehouse j, S—acceptable service distance, T—maximum service distance, when warehouse facility j is away from location i, as T > S; and —binary variable, 1 if warehouse j is selected, otherwise 0.
- where , .
- herein: —binary variable, 1 if location i is not covered by warehouse j in S distance, otherwise 0, —the set of potential warehouses that could reach location i within the acceptable service distance S ( is lower than ).
4. Empirical Research
4.1. Case Study and Review of Service Distance
- Warehouse1 (Lat 54, 61 and Lon 25, 08),
- Warehouse2 (Lat 56, 88 and Lon 24, 15),
- Warehouse3 (Lat 56, 80 and Lon 23, 94),
- Warehouse4 (Lat 59, 33 and Lon 24, 82).
- The retrieval of the coordinates of all locations and calculation of the distances for the case study;
- The application of the maximal coverage model and the number of warehouses covering the geographical territory identification;
- The review of the impact of returns on the accumulated distances;
- The application of ranking of alternative warehouses following the accumulated distances.
4.2. Results of the Analysis
5. Discussion
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- OECD. OECD’s Elaboration Based on Data from the US Census Bureau, the Office for National Statistics in the United Kingdom and Eurostat. 2020. Available online: https://www.oecd.org/coronavirus/policy-responses/e-commerce-in-the-time-of-covid-19-3a2b78e8/ (accessed on 18 December 2020).
- Janjevic, M.; Winkenbach, M.; Merchán, D. Integrating collection-and-delivery points in the strategic design of urban last-mile e-commerce distribution networks. Transp. Res. Part E Logist. Transp. Rev. 2019, 131, 37–67. [Google Scholar] [CrossRef]
- Dutta, P.; Mishra, A.; Khandelwal, S.; Katthawala, I. A multiobjective optimization model for sustainable reverse logistics in Indian E-commerce market. J. Clean. Prod. 2020, 249, 119348. [Google Scholar] [CrossRef]
- Winkenbach, M.; Kleindorfer, P.R.; Spinler, S. Enabling urban logistics services at La Poste through multi-echelon location-routing. Transp. Sci. 2016, 50, 520–540. [Google Scholar] [CrossRef]
- Cao, F.; Guo, J.; Liang, C. Multi-stage layout optimization for reverse logistics network of rural e-commerce under b2c mode: A case study of e-commerce enterprises on 3c products. In Proceedings of the 2016 IEEE 13th International Conference on e-Business Engineering (ICEBE), Macau, China, 4–6 November 2016; pp. 287–292. [Google Scholar]
- Bertazzi, L.; Maggioni, F. A stochastic multi-stage fixed charge transportation problem: Worst-case analysis of the rolling horizon approach. Eur. J. Oper. Res. 2018, 267, 555–569. [Google Scholar] [CrossRef]
- Gonzalez-Feliu, J. Multi-Stage LTL Transport Systems in Supply Chain Management; Cheung, J., Song, H., Eds.; Logistics: Perspectives, Approaches and Challenges; Nova Science Publishing: New York, NY, USA, 2013; pp. 65–86. [Google Scholar]
- E-Commerce News. On-Line Returns in Europe. 2021. Available online: https://ecommercenews.eu/online-returns-in-europe/ (accessed on 18 April 2021).
- ShippyPro. Ecommerce Reverse Logistics: Facts and Findings. 2021. Available online: https://www.blog.shippypro.com/ecommerce-reverse-logistics/ (accessed on 20 April 2021).
- Guo, J.; Wang, X.; Fan, S.; Gen, M. Forward and reverse logistics network and route planning under the environment of low-carbon emissions: A case study of Shanghai fresh food E-commerce enterprises. Comput. Ind. Eng. 2017, 106, 351–360. [Google Scholar] [CrossRef]
- Wang, S.; Sarker, B.R. Optimal models for a multi-stage supply chain system controlled by kanban under just-in-time philosophy. Eur. J. Oper. Res. 2006, 172, 179–200. [Google Scholar] [CrossRef]
- Manzini, R.; Bindi, F. Strategic design and operational management optimization of a multi stage physical distribution system. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 915–936. [Google Scholar] [CrossRef]
- Closs, D.J.; Cook, R.L. Multi-Stage Transportation Consolidation Analysis Using Dynamic Simulation. Int. J. Phys. Distrib. Mater. Manag. 1987, 47, 777–780. [Google Scholar] [CrossRef]
- Zhao, P.; Batta, R. Analysis of centroid aggregation for the Euclidean distance p-median problem. Eur. J. Oper. Res. 1999, 113, 147–168. [Google Scholar] [CrossRef]
- Elshaikh, A.; Salhi, S.; Brimberg, J.; Mladenović, N.; Callaghan, B.; Nagy, G. An adaptive perturbation-based heuristic: An application to the continuous p-centre problem. Comput. Oper. Res. 2016, 75, 1–11. [Google Scholar] [CrossRef]
- Erkut, E.; Ülküsal, Y.; Yeniçerioğlu, O. A comparison of p-dispersion heuristics. Comput. Oper. Res. 1994, 21, 1103–1113. [Google Scholar] [CrossRef]
- You, M.; Xiao, Y.; Zhang, S.; Yang, P.; Zhou, S. Optimal mathematical programming for the warehouse location problem with Euclidean distance linearization. Comput. Ind. Eng. 2019, 136, 70–79. [Google Scholar] [CrossRef]
- Al-Loughani, I.M. Algorithmic Approaches for Solving the Euclidean Distance Location and Location-Allocation Problems; Virginia Tech: Blacksburg, VA, USA, 1997. [Google Scholar]
- Murray, A.T.; Tong, D. Coverage optimization in continuous space facility siting. Int. J. Geogr. Inf. Sci. 2007, 21, 757–776. [Google Scholar] [CrossRef]
- Weintraub, A.; Epstein, R.; Morales, R.; Seron, J.; Traverso, P. A truck scheduling system improves efficiency in the forest industries. Interfaces 1996, 26, 1–12. [Google Scholar] [CrossRef]
- Park, Y.B. An integrated approach for production and distribution planning in supply chain management. Int. J. Prod. Res. 2005, 43, 1205–1224. [Google Scholar] [CrossRef]
- Goetschalckx, M.; Vidal, C.J.; Dogan, K. Modeling and design of global logistics systems: A review of integrated strategic and tactical models and design algorithms. Eur. J. Oper. Res. 2002, 143, 1–18. [Google Scholar] [CrossRef]
- Lababidi, H.M.S.; Ahmed, M.A.; Alatiqi, I.M.; Al-enzi, A.F. Optimizing the supply chain of a petrochemical company under uncertain operating and economic conditions. Ind. Eng. Chem. Res. 2004, 43, 63–73. [Google Scholar] [CrossRef]
- Chern, C.C.; Hsieh, J.S. A heuristic algorithm for master planning that satisfies multiple objectives. Comput. Oper. Res. 2007, 34, 3491–3513. [Google Scholar] [CrossRef]
- Selim, H.; Am, C.; Ozkarahan, I. Collaborative production–distribution planning in supply chain: A fuzzy goal programming approach. Transp. Res. Part E Logist. Transp. Rev. 2008, 44, 396–419. [Google Scholar] [CrossRef]
- Aliev, R.A.; Fazlollahi, B.; Guirimov, B.G.; Aliev, R.R. Fuzzy-genetic approach to aggregate production–distribution planning in supply chain management. Inf. Sci. 2007, 177, 4241–4255. [Google Scholar] [CrossRef]
- Roghanian, E.; Sadjadi, S.J.; Aryanezhad, M.B. A probabilistic bi-level linear multi-objective programming problem to supply chain planning. Appl. Math. Comput. 2007, 188, 786–800. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, S.H. Production–distribution planning in supply chain considering capacity constraints. Comput. Ind. Eng. 2002, 43, 169–190. [Google Scholar] [CrossRef]
- Lim, S.J.; Jeong, S.J.; Kim, K.S.; Park, M.W. A simulation approach for production–distribution planning with consideration given to replenishment policies. Int. J. Adv. Manuf. Technol. 2006, 27, 593–603. [Google Scholar] [CrossRef]
- Timpe, C.H.; Kallrath, J. Optimal planning in large multi-site production networks. Eur. J. Oper. Res. 2000, 126, 422–435. [Google Scholar] [CrossRef]
- Kallrath, J. Combined strategic and operational planning–An MILP success story in chemical industry. Or Spectr. 2002, 24, 315–341. [Google Scholar] [CrossRef]
- Sakawa, M.; Nishizaki, I.; Uemura, Y. Fuzzy programming and profit and cost allocation for a production and transportation problem. Eur. J. Oper. Res. 2001, 131, 1–15. [Google Scholar] [CrossRef]
- Ryu, J.H.; Dua, V.; Pistikopoulos, E.N. A bilevel programming framework for enterprise-wide process networks under uncertainty. Comput. Chem. Eng. 2004, 28, 1121–1129. [Google Scholar] [CrossRef]
- Oh, H.C.; Karimi, I.A. Global multi-product production–distribution planning with duty drawbacks. AICHE J. 2006, 52, 595–610. [Google Scholar] [CrossRef]
- Chen, C.L.; Wang, B.W.; Lee, W.C. Multi-objective optimization for a multienterprise supply chain network. Ind. Eng. Chem. Res. 2003, 42, 1879–1889. [Google Scholar] [CrossRef]
- Gupta, A.; Maranas, C.D. Managing demand uncertainty in supply chain planning. Comput. Chem. Eng. 2003, 27, 1219–1227. [Google Scholar] [CrossRef]
- Perea-Lopez, E.; Ydstie, B.E.; Grossmann, I.E. A model predictive control strategy for supply chain optimization. Comput. Chem. Eng. 2003, 27, 1201–1218. [Google Scholar] [CrossRef]
- Bilgen, B.; Ozkarahan, I. A mixed-integer linear programming model for bulk grain blending and shipping. Int. J. Prod. Econ. 2007, 107, 555–571. [Google Scholar] [CrossRef]
- Romo, F.; Tomasgard, A.; Hellemo, L.; Fodstad, M.; Eidesen, B.H.; Pedersen, B. Optimising the Norwegian Natural gas production and transport. Interfaces 2009, 39, 46–56. [Google Scholar] [CrossRef]
- Chen, C.L.; Lee, W.C. Multi-objective optimization of multi-echelon supply chain networks with uncertain product demands and prices. Comput. Chem. Eng. 2004, 28, 1131–1144. [Google Scholar] [CrossRef]
- Rizk, N.; Martel, A.; D’amours, S. Multi-item dynamic production–distribution planning in process industries with divergent finishing stages. Comput. Oper. Res. 2006, 33, 3600–3623. [Google Scholar] [CrossRef]
- Meijboom, B.; Obel, B. Tactical coordination in a multi-location and multi-stage operations structure: A model and a pharmaceutical company case. Omega Int. J. Manag. Sci. 2007, 35, 258–273. [Google Scholar] [CrossRef]
- Jung, H.; Jeong, B.; Lee, C.G. An order quantity negotiation model for distributor-driven supply chains. Int. J. Prod. Econ. 2008, 111, 147–158. [Google Scholar] [CrossRef]
- Kim, T.Y.; Dekker, R.; Heij, C. Cross-border electronic commerce: Distance effects and express delivery in European Union markets. Int. J. Electron. Commer. 2017, 21, 184–218. [Google Scholar] [CrossRef]
- Xu, S.X.; Cheng, M.; Huang, G.Q. Efficient intermodal transportation auctions for B2B e-commerce logistics with transaction costs. Transp. Res. Part B Methodol. 2015, 80, 322–337. [Google Scholar] [CrossRef]
- Wang, X.; Xie, J.; Fan, Z.P. B2C cross-border E-commerce logistics mode selection considering product returns. Int. J. Prod. Res. 2020, 1–20. [Google Scholar] [CrossRef]
- Ji, S.; Sun, Q. Low-carbon planning and design in B&R logistics service: A case study of an e-commerce big data platform in China. Sustainability 2017, 9, 2052. [Google Scholar] [CrossRef]
- Allen, J.; Piecyk, M.; Piotrowska, M.; McLeod, F.; Cherrett, T.; Ghali, K.; Nguyenc, T.; Bektasc, T.; Batesd, O.; Fridayd, A.; et al. Understanding the impact of e-commerce on last-mile light goods vehicle activity in urban areas: The case of London. Transp. Res. Part D Transp. Environ. 2018, 61, 325–338. [Google Scholar] [CrossRef]
- Lahyani, R.; Khemakhem, M.; Semet, F. Rich vehicle routing problems: From a taxonomy to a definition. Eur. J. Oper. Res. 2015, 241, 1–14. [Google Scholar] [CrossRef]
- Bergmann, F.M.; Wagner, S.M.; Winkenbach, M. Integrating first-mile pick-up and last-mile delivery on shared vehicle routes for efficient urban e-commerce distribution. Transp. Res. Part B Methodol. 2020, 131, 26–62. [Google Scholar] [CrossRef]
- Shen, Z.; Sessions, J. Log truck scheduling by network programming. For. Prod. J. 1989, 39, 47–50. [Google Scholar] [CrossRef]
- Linnainmaa, S.; Savola, J.; Jokinen, O. EPO: A knowledge based system for wood procurement management. In Proceedings of the 7th Conference on Innovation Applications of Artificial Intelligence, Montreal, QC, Canada, 20–23 August 1995; AAAI Press: Pittsburgh, PA, USA, 1995; pp. 113–117. [Google Scholar]
- McDonald, C.M.; Karimi, I.A. Planning and scheduling of parallel semicontinuous processes. 1. Production planning. Ind. Eng. Chem. Res. 1997, 36, 2691–2700. [Google Scholar] [CrossRef]
- Mendell, B.C.; Haber, J.A.; Sydor, T. Evaluating the potential for shared log truck resources in middle Georgia. South. J. Appl. For. 2006, 30, 86–91. [Google Scholar] [CrossRef]
- Audy, J.F.; El Hachemi, N.; Michel, L.; Rousseau, L.M. Solving a combined routing and scheduling problem in forestry. In Proceedings of the International Conference on Industrial Engineering and Systems Management, Metz, France, 25–27 May 2011; International Institute for Innovation, Industrial Engineering and Enterpreneurship: Hornu, Belgium, 2011; pp. 50–59. [Google Scholar]
- Balakrishnan, A.; Graves, S.C. A composite algorithm for a concave-cost network flow problem. Networks 1989, 19, 175–202. [Google Scholar] [CrossRef]
- Kedia, A.; Kusumastuti, D.; Nicholson, A. Establishing collection and delivery points to encourage the use of active transport: A case study in New Zealand using a consumer-centric approach. Sustainability 2019, 11, 6255. [Google Scholar] [CrossRef]
- Yildiz, A.; Ayyildiz, E.; Gumus, A.T.; Ozkan, C. A Modified Balanced Scorecard Based Hybrid Pythagorean Fuzzy AHP-Topsis Methodology for ATM Site Selection Problem. Int. J. Inf. Technol. Decis. Mak. 2020, 19, 365–384. [Google Scholar] [CrossRef]
- Rahmaniani, R.; Ghaderi, A. A combined facility location and network design problem with multi-type of capacitated links. Appl. Math. Model. 2013, 37, 6400–6414. [Google Scholar] [CrossRef]
- Bronfman, A.; Marianov, V.; Paredes-Belmar, G.; Lüer-Villagra, A. The maxisum and maximin-maxisum HAZMAT routing problems. Transp. Res. Part E Logist. Transp. Rev. 2016, 93, 316–333. [Google Scholar] [CrossRef]
- Klose, A.; Drexl, A. Facility location models for distribution system design. Eur. J. Oper. Res. 2005, 162, 4–29. [Google Scholar] [CrossRef]
- Santiváñez, J.A.; Melachrinoudis, E. Reliable maximin–maxisum locations for maximum service availability on tree networks vulnerable to disruptions. Ann. Oper. Res. 2020, 286, 669–701. [Google Scholar] [CrossRef]
- Zarrinpoor, N. An exploration of evolutionary algorithms for a bi-objective competitive facility location problem in congested systems. Int. J. Supply Oper. Manag. 2018, 5, 266–282. [Google Scholar] [CrossRef]
- Park, Y.; Nielsen, P.; Moon, I. Unmanned aerial vehicle set covering problem considering fixed-radius coverage constraint. Comput. Oper. Res. 2020, 1, 104–136. [Google Scholar] [CrossRef]
- Zhang, B.; Peng, J.; Li, S. Covering location problem of emergency service facilities in an uncertain environment. Appl. Math. Model. 2017, 51, 429–447. [Google Scholar] [CrossRef]
- Heyns, A.M.; van Vuuren, J.H. Multi-Type, Multi-Zone Facility Location. Geogr. Anal. 2018, 50, 3–31. [Google Scholar] [CrossRef]
- Sayah, D.; Irnich, S. A new compact formulation for the discrete p-dispersion problem. Eur. J. Oper. Res. 2017, 256, 62–67. [Google Scholar] [CrossRef]
- Tutunchi, G.K.; Fathi, Y. Effective methods for solving the Bi-criteria p-Center and p-Dispersion problem. Comput. Oper. Res. 2019, 101, 43–54. [Google Scholar] [CrossRef]
- Ko, J.; Gim, T.H.T.; Guensler, R. Locating refuelling stations for alternative fuel vehicles: A review on models and applications. Transp. Rev. 2017, 37, 551–570. [Google Scholar] [CrossRef]
- Daskin, M.S.; Tucker, E.L. The trade-off between the median and range of assigned demand in facility location models. Int. J. Prod. Res. 2018, 56, 97–119. [Google Scholar] [CrossRef]
- Du, B.; Zhou, H.; Leus, R. A two-stage robust model for a reliable p-center facility location problem. Appl. Math. Model. 2020, 77, 99–114. [Google Scholar] [CrossRef]
- Teye, C.; Bell, M.G.; Bliemer, M.C. Entropy maximizing facility location model for port city intermodal terminals. Transp. Res. Part E Logist. Transp. Rev. 2017, 100, 1–16. [Google Scholar] [CrossRef]
- Fernández, E.; Sgalambro, A. On carriers collaboration in hub location problems. Eur. J. Oper. Res. 2020, 283, 476–490. [Google Scholar] [CrossRef]
- Jafari, D.; Pour, M.H. The Single-Allocation Heuristic Hub Location Problem Solving. Ind. Eng. Manag. Syst. 2018, 17, 588–599. [Google Scholar] [CrossRef]
- Mohammadi, M.; Jula, P.; Tavakkoli-Moghaddam, R. Reliable single-allocation hub location problem with disruptions. Transp. Res. Part E Logist. Transp. Rev. 2019, 123, 90–120. [Google Scholar] [CrossRef]
- Roghanian, E.; Haghdoost, M. Mathematical model for P-hub location problem under simultaneous disruption. J. Ind. Syst. Eng. 2018, 12, 83–94. [Google Scholar]
- Lawler, E.L.; Lenstra, J.K.; Rinnooy, K.A.H.G.; Shmoys, D.B. The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization; Wiley: Chichester, UK, 1985. [Google Scholar]
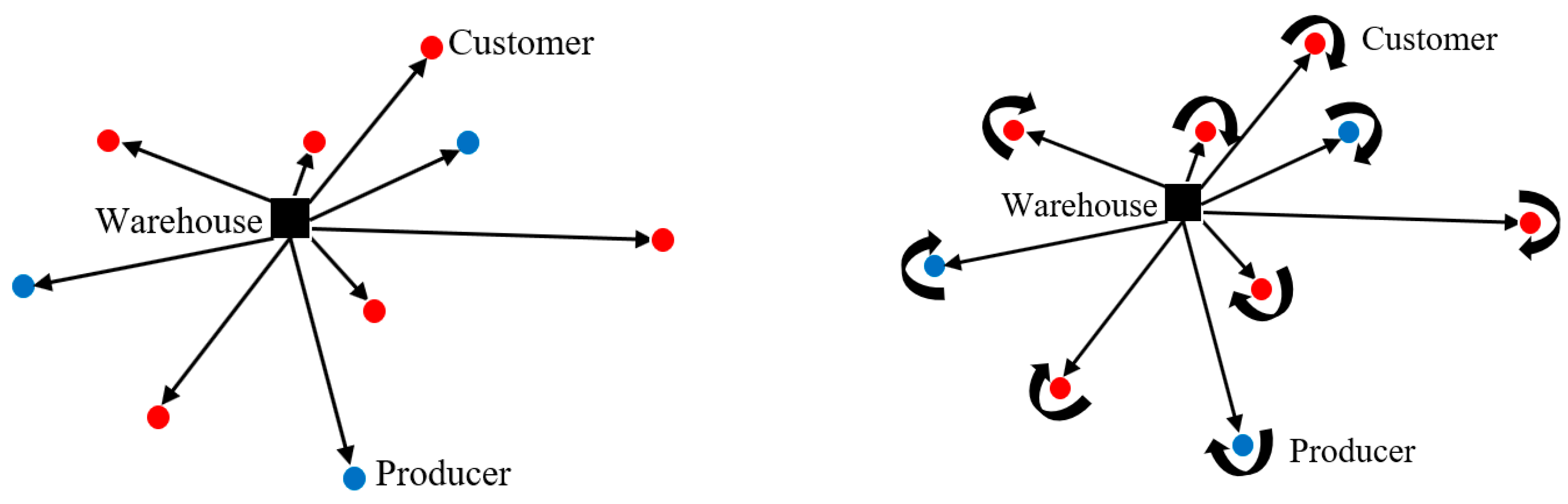

| Components | Lead-Time | Transport Time | Transport Costs | Revenue |
|---|---|---|---|---|
| Authors | [28,29] | [30,31] | [32,33,34] | [35,36,37] |
| [38,39] | [40,41] | [25,26] | [42,43] |
| Model | The Objective of the Model | Unique Focus in the Transport System | Requirements Specifying the Number of Warehouses | Findings Following the Coverage of Demand Points in Defined Response Time | Results Following the Coverage in Defined Service Distance |
|---|---|---|---|---|---|
| Maximum service distance models | |||||
| Maximal covering model | Maximization of the coverage of demand points | Accessibility and efficiency | Yes | No | Yes |
| Set covering model | Identification of the minimum number of warehouses and preferences among physical locations | Availability | No | Yes | Yes |
| P-dispersion model | Maximization of the coverage in case of network extension | Accessibility | No | No | Yes |
| P-centre | Assignment of the closest warehouse to serve demand point by minimizing the distance | Accessibility | Yes | No | Yes |
| Average service distance models | |||||
| Classic p-median model | Minimization of the overall weighted distance between demand points and warehouses | Accessibility | Yes | No | No |
| Fixed charge location model | Assignment of demand points to the serving warehouse by incorporating cost constrains | Efficiency | Yes | No | Yes |
| Basic p-hub location model | Minimization of total costs, which are distance-dependent | Efficiency | Yes | Yes | Yes |
| Maxisum | Maximization of the overall weighted distance between demand points and serving facility | Accessibility | Yes | No | Yes |
| The Structure of the Methodology | The Evaluation of Functionality | The Application of Methods | Usability of Results and Their Validation | The Assessment of Compliance with Sustainable Development |
|---|---|---|---|---|
| I layer (Multi-stage transport system) | It consists of producers, warehouses, and business customers with pick-up (return) and delivery services. | The design of a multi-stage transport system includes the revision of the locational configuration to reach the best possible performance of the system. | Combined pick-up (return) and delivery services involving multiple locations. | Achievements in the development of the transport system required going forward to reach the savings of natural resources. |
| II layer (Delivery service to e-commerce activity) | The revision of the combined delivery and pick-up (return) to increase the motivation of business customers. | Comparative analysis of key service delivery components stimulating e-commerce activity. | The reduction of delivery service price for the business customers. | |
| III layer (Warehouse selection) | The warehouse selection to improve demand coverage and minimize maximum service distance in fulfilment of delivery and pick-up (return) transportation. | The evaluation of service distance required to reach the warehouse facility and the selection among warehouse alternatives. | The formulation of suggestion, allowing a maximal coverage model incorporating mandatory closeness to service distance. | The selection of alternatives which enables the requirements of sustainable development. |
| Locations | j1 (Lat1, Lon1) | j2 (Lat2, Lon2) | … | j4 (Lat4, Lon4) |
|---|---|---|---|---|
| i1 (Lat1, Lon1) | 0 | … | ||
| … | ||||
| in (Latn, Lonn) | … | 0 |
| Components | Warehouse1 (WH1) | Warehouse2 (WH2) | Warehouse3 (WH3) | Warehouse4 (WH4) |
|---|---|---|---|---|
| 1. Euclidean distance (max, ) | 568 km | 366 km | 381 km | 594 km |
| 1.1 to producers (mean) | 107 km | 212 km | 207 km | 446 km |
| 1.2 to business customers (mean) | 214 km | 177 km | 176 km | 361 km |
| 2. Path-based distance (max, ) | 735 km | 444 km | 472 km | 699 km |
| 2.1 to producers (mean) | 129 km | 245 km | 250 km | 520 km |
| 2.2 to business customers (mean) | 256 km | 209 km | 214 km | 429 km |
| Mandatory Closeness Distance (S) | Not Covered Objects | Covered by WH1 | Covered by WH2 | Covered by WH3 | Covered by WH4 |
|---|---|---|---|---|---|
| 1. Euclidean distance ( | |||||
| 300 km | 0% | 3% | 4% | 93% | 1% |
| 250 km | 0% | 16% | 20% | 60% | 4% |
| 200 km | 5% | 55% | 29% | 11% | 0% |
| 2. Path-based distance () | |||||
| 300 km | 0% | 18% | 34% | 48% | 0% |
| 250 km | 6% | 52% | 28% | 14% | 0% |
| 200 km | 11% | 56% | 29% | 3% | 0% |
| The Sum of Service Distances (L) | WH1 | WH2 | WH3 | WH4 | |
|---|---|---|---|---|---|
| 1. The sum of Euclidean distances ( | WH3 | 194,429 km | 188,218 km | 186,443 km | 386,422 km |
| 2. The sum of path-based distances () | WH2 | 231,967 km | 220,083 km | 225,891 km | 454,173 km |
| Comparison with rank: the difference of the sum of Euclidean service distances, % | WH3 | 4% | 1% | 0% | 52% |
| Comparison with rank: the difference of the sum of path-based service distances, % | WH2 | 5% | 0% | 3% | 52% |
| Return Level | 1% | 2% | 3% | 4% | 5% |
| 1. Euclidean distance case | WH3 | WH3 | WH2 | WH2 | WH2 |
| 2. Path-based distance case | WH2 | WH2 | WH2 | WH2 | WH2 |
| Return Level | 6% | 7% | 8% | 9% | 10% |
| 1. Euclidean distance case | WH3 | WH3 | WH2 | WH2 | WH3 |
| 2. Path-based distance case | WH2 | WH2 | WH2 | WH3 | WH2 |
| Return Level | 11% | 12% | 13% | 14% | 15% |
| 1. Euclidean distance case | WH3 | WH2 | WH2 | WH3 | WH2 |
| 2. Path-based distance case | WH2 | WH3 | WH2 | WH2 | WH2 |
| Return level | 16% | 19% | 23% | 24% | 29% |
| 1. Euclidean distance case | WH3 | WH3 | WH3 | WH2 | WH2 |
| 2. Path-based distance case | WH2 | WH2 | WH3 | WH2 | WH2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burinskienė, A. Designing a Multi-Stage Transport System Serving e-Commerce Activity. Sustainability 2021, 13, 6154. https://doi.org/10.3390/su13116154
Burinskienė A. Designing a Multi-Stage Transport System Serving e-Commerce Activity. Sustainability. 2021; 13(11):6154. https://doi.org/10.3390/su13116154
Chicago/Turabian StyleBurinskienė, Aurelija. 2021. "Designing a Multi-Stage Transport System Serving e-Commerce Activity" Sustainability 13, no. 11: 6154. https://doi.org/10.3390/su13116154
APA StyleBurinskienė, A. (2021). Designing a Multi-Stage Transport System Serving e-Commerce Activity. Sustainability, 13(11), 6154. https://doi.org/10.3390/su13116154





