Mathematical Model to Simulate the Transfer of Heavy Metals from Soil to Plant

Abstract

Heavy metals are naturally occurring elements, but their various applications have led to their wide circulation in the environment, raising concerns over their latent effects on the environment and human health. Their toxicity depends on numerous factors, including chemical species, concentration of heavy metal ions, environmental factors, etc. Experimental studies on the single or cumulative effects of heavy metals on plants are complex, time consuming and difficult to conduct. An alternative is mathematical modeling, which can include different factors into an integrated system and can predict plant and environmental behavior under multiple stressors. This paper presents a mathematical model that simulates the dependence of temperature, concentration of Zn in the soil and the subsequent bioaccumulation in lettuce (Lactuca sativa L.); respectively, the reaction of lettuce to Zn contamination. The main results consist of three mathematical models, based on systems of ordinary differential equations and checking their predictions with available experimental data. The models are applied to predict an optimal harvest time of lettuce with low concentration of Zn, in identifying the availability of the analyzed species to phytoremediation operations and the possibility of maneuvering certain control factors to reduce or increase the intensity of the bioaccumulation process.

1. Introduction

Heavy metals are natural components of all environments. However, the intensification of human activities has led to an altered biochemical balance and increased quantities of heavy metals in the air, water and soil. Heavy metals are toxic, abundant and non-biodegradable, they have irreversible characteristics, high persistence, long half-lives and their bioaccumulation capacity facilitates their transfer into the soil–plant–human body system.

A variety of sources contribute to soil contamination with heavy metals: industrial processes, deposition in the atmosphere, emissions from traffic transported by precipitation, agricultural activities such as the long-term use of wastewater (municipal, industrial) in irrigation, use of agrichemicals, application of inorganic fertilizers and animal manure. Thus, contamination of agricultural soil has become a real problem worldwide, to which no valid solution has been found so far [1].

Heavy metal transfer from soil or water to crops, or to any living organism (including the microbial biomass of soils, plants, animals and humans) [2,3,4,5,6,7,8,9] causes many agronomic, environmental and human health problems [10,11,12,13,14,15,16,17,18].

Many research studies have shown that various plant varieties can tolerate and bioaccumulate high concentrations of heavy metals in their tissues [19,20,21,22,23,24,25,26,27,28,29]. Lettuce (Lactuca sativa), a common leafy plant in the human diet, accumulates high concentrations of Zn [19,30,31,32,33,34,35,36], Cu [19,30,35,37,38], Cd, Cr, La, Fe, Ni, Mn, Pb, Ti, Sc and V [19].

The possible effects of Zn bioaccumulation in plants are: reduced germination; low plant height; reduced plant growth; decrease in nutrient content; decrease in carotenoid, sugar, chlorophyll, starch and amino acid content; alteration of chloroplast structure; decrease in photosystem activity; accumulation in leaves; decreased efficiency of photosynthetic energy conversion.

The absorption of heavy metals is influenced by: soil pH and cation exchange capacity, plant species, varieties and degree of development. Heavy metal bioaccumulation and transfer vary between plant species [39,40], plant varieties [41] and different parts of plants [20,42,43]. The transfer of heavy metals from soil to plants involves many physical, chemical and biological processes that occur in the soil, in the soil rhizosphere and in the plant [44]. These processes are difficult to monitor and evaluate without the use of simplified mathematical models, which can describe the bioaccumulation of heavy metals based on fewer experimental data.

Heavy metals bioaccumulation is assimilated to multi-faceted systems, which also influences a series of physiological processes: plant development and lifespan, nutrition, quantity and quality of accumulated biomass, transfer and/or translocation, etc. The new mathematical model presented in this paper introduces the factors of influence that highlight the influence of environmental factors to plant life.

Models can be used to improve the sustainability of experimental studies associated with the functioning of environmental and natural systems, reducing costs, project development time and also providing answers on the bioaccumulation of contaminants in the environment and beyond.

Mathematical modeling has been used intensively in recent years in many fields of science. The rising costs of experimental studies have given researchers an urge to intensify the use of mathematical models, with an aim to achieving a cheaper alternative to further research. This effort has been going on for decades and, not infrequently, has led to desperate attempts to force reality to take the form of theoretical molds, which has led to failures, at least from a certain level of development. The models thus obtained have been used successfully to describe and optimize biological processes such as the growth and development of plants. Mathematical models have also been used to simulate complex processes in the environment, such as bioremediation. Numerical simulation techniques and statistical modeling use very sophisticated tools, capable of providing extremely complex mathematical models, yet these models cannot be used without a minimum of experimental validation. Model complexity involves expensive experiments for the validation and development of the models.

On the other hand, usually, mathematical modeling of biological material (biomathematics) aims to improve or even optimize some processes using the economic parameters as objective functions, thus serving primarily the management of these processes, an activity that could finance at least partially scientific activity. From this perspective, plant cultivation or animal husbandry stop the course of life of biological entities at the optimal age for sacrifice. Nevertheless, for plants and animals, life continues even after this age, but the effects of aging have rarely been researched.

These aspects substantiate our attempt to build a mathematical model of heavy metal bioaccumulation in plants and to apply the model in the elaboration and optimization of phytoremediation techniques. The accumulation of heavy metals in plants (or animals) is a widespread phenomenon in the post-industrial era. Bioremediation, developed by research in biology and in the environment, was one of the solutions of man to curtail the destruction of the environment generated by industrial activities.

Mathematical modeling aims to distinguish the mechanisms involved in heavy metal bioaccumulation and to discover the paths to restrict or optimize the processes of bioaccumulation and bioremediation that plants undertake in the soils. Researchers are looking for methods, techniques or resources to accelerate the absorption efficiency of heavy metals from polluted soils using phytoremediation and the subsequent use of these plants, which, depending on the type of plants and heavy metals that are absorbed, exceeds the maximum absorption efficiency of heavy metals.

Over the last 20 years, mathematical modeling has become a common topic in the studies on the accumulation of heavy metals in plants [1,5,9,45,46,47,48,49,50,51,52].

A sketch of the factors influencing the bioaccumulation of heavy metals in plants is presented in study [53]. Some of those factors are included in the model described in this paper (plant biomass, absorption, metal bioavailability), a model that pursues phytoremediation. Although it refers to the accumulation of heavy metals in the aquatic, terrestrial and human food chain, study [54] highlights several mathematical models of bioaccumulation which are also based on differential equations of population balance, heavy metal concentration, pH, ambient temperature, organic carbon content in the environment, etc. The selective parameters of plants and animals are also highlighted, and they are of great importance in phytoremediation.

Study [55] describes a model for heavy metal bioaccumulation based on two main components: the required equations describe the flow of water and its absorption by crops in the unsaturated area, as well as the transport of heavy metals and their uptake by agricultural crops. Both components of the model are described by algebraic and differential equations with partial derivatives. Soil moisture capacity, hydraulic conductivity, water retention curve, potential transpiration rate, root depth and absorption rate at the top of the roots are among the most important parameters that characterize the phenomenon of the respective model. Another model with two basic components is presented in study [56]: the model of pollutant transport in the water–soil–plant system, and the model of hydrodynamics and water quality. Both components are described by partial differential equations. The first component consists of three equations with partial derivatives given by the balance of chromium content in the liquid and solid phase, and in the plant. In addition to chromium concentrations in the first component, the second component include water depth, water level before the horizontal reference plane, components of external forces, mass density of water, fluid velocity and components of bed shear stress.

A series of studies present the statistical models of heavy metal bioaccumulation. A statistical model combined with algebraic equations is presented in study [57], in which model parameters are the concentrations of heavy metals in water, soil and plant, plant mass, concentrations of heavy metals in leaves and roots and the rates of change of these parameters. Study [58] are gives statistical models in the form of regressions, where model parameters are metal concentrations in the soil, roots, stems, leaves and fruits. Study [59] detailed the development a new stochastic framework that provides the analytical expressions to quantify the distribution of contaminants between leaching and plant uptake, and the phytoremediation duration based on statistical precipitation and soil and vegetation characteristics. Simple expressions are derived for the average duration and efficiency of phytoremediation (the fraction of contaminant that is recovered in plant biomass). The proposed framework can be used to estimate the conditions in which phytoremediation is more effective, and to design phytoremediation projects that maximize contaminant recovery and minimize process duration. Study [59] also gives a comprehensive list of factors that influence the bioaccumulation of heavy metals, many of which become, or should become, parameters in mathematical models used in the simulation of bioaccumulation or phytoremediation, and aim at controlling and optimizing these processes.

The models in this paper aim at the further development of the growth models according to the influencing and bioaccumulation factors shown in studies [47,48,49,60]. Compared to the original model [50,61,62], study [49] introduced the influence of temperature. The method used to develop the original model can also be used to introduce the dependence on light, water availability and genetic factors, which influence the bioaccumulation and plant growth. These important factors for understanding the bioaccumulation process will be introduced as the constructed model is validated experimentally, in stages. All the influential factors of the process were not introduced simultaneously because, from a numerical point of view, this would lead to a difficult control in model calibration, especially in the construction stage. On the other hand, as new influencing factors of the bioaccumulation process are introduced, it is necessary to repeat and amplify expensive experiences, usually multifactorial, for research (construction of functions and influencing operators), but also for model validation.

The basic ideas that our model of heavy metal bioaccumulation states are:

-

the life of a plant (or of any other biological entity) does not end at harvest or sacrifice; hence it must be studied entirely over generations and the optimal choices can be made only after these studies;

-

Newtonian time is a useful parameter for accurately tracking and reporting events in the evolution of biological entities, but there are intrinsic parameters of each entity that indicate in which stages of evolution they are.

The main purpose of this model is to simulate the dependence of temperature, bioaccumulation and the reaction of plants to heavy metal ions in the soil, a factor that depends on the concentration of heavy metals. Taking into account the models presented in this paper, and following the same working method as that in study [47], different mathematical models can be developed, which contain the most important or all the factors involved in the growth, vegetative evolution, aging and death of plants [49]. In this paper, we developed the exposition of the model from [49] and the presented results imply a better understanding of the model and the construction method. Also, the extensive results are useful in the further development of the model, but the validation of models requires a huge experimental effort. The realization of mathematical models focused on plant development in different environmental factors and different cultivation technologies is beneficial in terms of compensating for certain shortcomings of experimental data by calibrating the model according to the known data. In addition, as new experimental data become available, the models can be easily recalibrated. The study of the stability of these methods, of the introduced functions and operators, but also of the numerical methods used to solve the system of differential equations, remains open. This is why, for the start, we chose a model based on differential equations from the balance sheets of the process components. To solve differential (even nonlinear) equations, one benefits more from richer software than from partial differential equations (which are present in some models that use transfer functions).

The creation of a mathematical model is aimed not only at use for simulation and optimization of the phenomenon, but also for planning experiences. The most complete coverage of the set of parameters that describe the phenomenon is a controllable goal with the help of mathematical modeling. Using the method of mathematical modeling, a modern description of heavy metal bioaccumulation in plants (in this case, in lettuce) is also suggested. The systemic description of the phenomenon in the physical and biological world inventories as completely as possible the influencing factors (input, command and control parameters), as well as the output parameters, mostly the qualitative parameters of the process. This was the reason for choosing the dynamic mathematical modeling method. In addition, the belief of some authors was always taken into account that the main parameter for tracking the phenomenon is not time, but one or more parameters intrinsic to the system. Such parameters were constantly sought.

The sustainability of human activities is targeted by this research by experimental techniques that avoid environmental destruction and depletion of resources, but especially by the application of models aimed at forecasting the optimal harvest time so that the concentration of heavy metal in the plant is not dangerous to humans, no matter how insignificant a bioremediation process may seem. Also, forecasts are obtained that establish a harvesting time for the crops used for phytoremediation, so that the return of heavy metals in the soil does not occur by falling on the ground from the aerial parts of the plants.

2. Materials and Methods

The methods used to create the mathematical models are: General Mathematical Model, Zinc bioaccumulation Model, Simulation of temperature influence, Simulation of the effects of heavy metal build-up on the development of lettuce leaves.

2.1. The General Mathematical Model

The mathematical model presented in study [50] resulted from a series of experimental studies in which the authors proved that the bioavailability of metals in plants is not necessarily linked to a low pH. Thus, the model is applicable not only to aluminium (shown in the application) but also to other metals in the soil.

The general reaction on which the transfer of any heavy metal (Me) to the plant is based (how heavy metals ensure their mobility in soils with normal pH levels) is as follows:

$$Me{(OH)}_n+{nH}^{+}\to {Me}^{n+}+{nH}_{2}O$$

(1)

This model starts from the most important parameters that are efficient for the mathematical modeling of the transfer of different heavy metals due to the interaction between soil and plants (

Table 1. Main parameters used in the mathematical model given by the equation system (2).

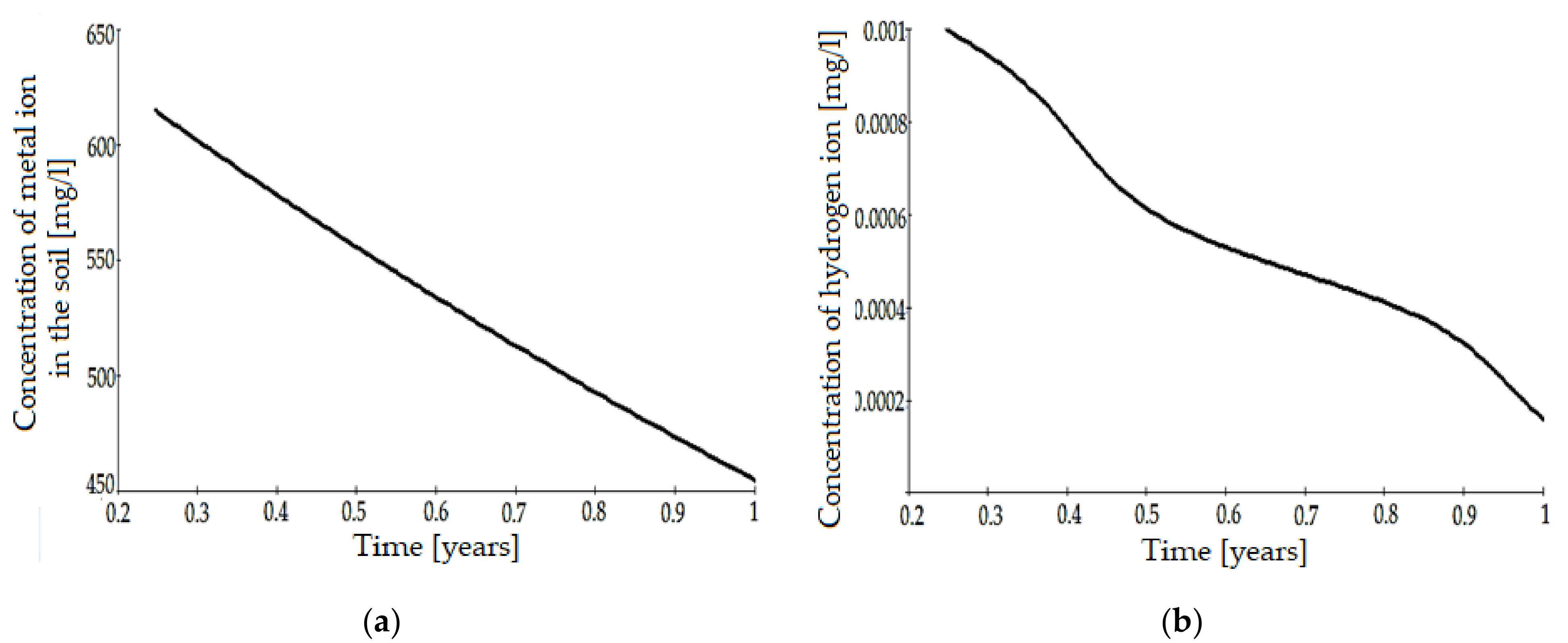
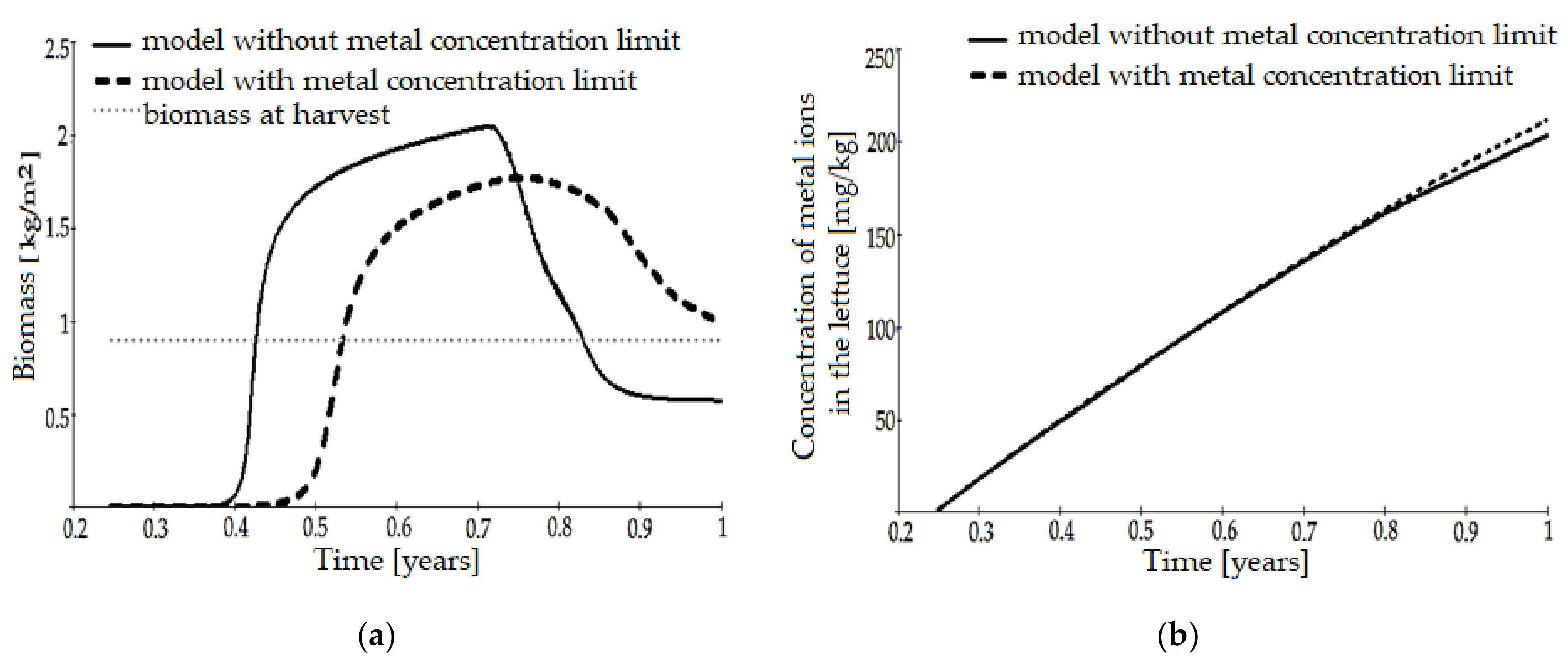
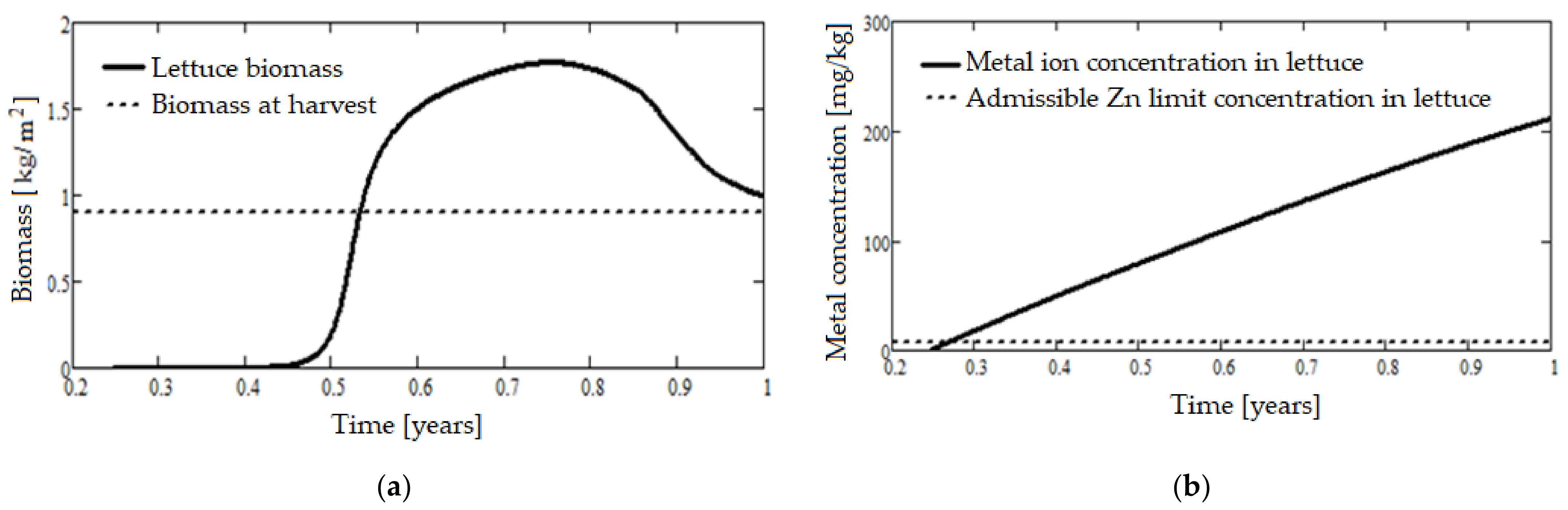
Parameter	Notation	Measurement Unit
Plant biomass	PB(t)	kg·m−2
Concentration of metal ions in the plant	Me(t)	mg·kg−1
Concentration of metal ions in the soil	S(t)	mg·L−1
Concentration of hydrogen ions in the soil	H(t)	mg·L−1
Time	t	years
Flux of protons to the soil during rainfall	W(t)	mg·m−2·year−1
Available water for roots	p(t)	mm
Absorption coefficient	α	L·kg−1·year−1
Leakage coefficient	β	year−1
Reaction coefficient	φ	year−1
Net growth function	h(PB)	year−1
Function of mortality or metabolic inefficiency of trees due to the concentration of metal ions in plant	μ(Me)	year−1
Constant a of the model (positive)	a	year−1
Constant b of the model (positive)	b	kg−1·m2
Constant c of the model (positive)	c	year−1
Constant f of the model (positive)	f	year−1
Constant e of the model (positive) or survival limit value	e	mg·kg−1
Gaussian function	G	-
Bump function	B	-
Temperature influencing factors	${\mathsf{\Theta }}_{\mathrm{h}},{\mathsf{\Theta }}_{\mathsf{\mu }},{\mathsf{\Theta }}_{\mathrm{h}\mathrm{M}\mathrm{e}}$	-
Influencing factors that give the concentration of heavy metals in the plant	Ch, Cµ	-

).

To mathematically model the mobility of aluminium due to soil acidity to the plants, study [50] used a mathematical model initially found in study [61] and adjusted in study [62], which is given by the system of equations:

$$\begin{array}{c}\frac{dPB}{dt}=PB\left(t\right)\left(h\left(PB\right)-\mu \left(Me\right)\right)\hfill \\ \frac{dMe}{dt}=\alpha S-h\left(PM\right)Me\hfill \\ \frac{dS}{dt}=\phi H-\beta S-\frac{\alpha SPB}{p}\hfill \\ \frac{dH}{dt}=\frac{-\phi H}{9}-\beta H+\frac{W}{p}\hfill \end{array}$$

(2)

Net growth of the plant, by hypothesis presented in study [61], is given by the following function:

$$h\left(PB\right)=\frac{a}{1+bPB}$$

(3)

or, according to study [62], it has the form (by hypothesis):

$$h\left(PB\right)=r\left(1-\frac{PB}{k}\right)$$

(4)

As a plus, there are several studies that state that the original model proposed for trees could also be used for non-tree plants, assuming that each plant will interact with the contaminant in the same way as in deterministic models from study [51]. This theory is supported by the postulates of “modular plant architecture” and “plant as a population of modules”, which present plants as modular structures consisting of “relatively independent, repetitive units such as leaves, flowers, buds and branch segments”, which makes it possible for lettuce to be analyzed similarly to a tree [52].

In study [61], the form of metabolic inability or the possible mortality is given by Equation (5):

$$\mu \left(Me\right)=\frac{c-fMe}{e-Me}$$

(5)

Constant e represents the survival limit value:

$$Me\in \left[0,e\right]$$

(6)

However, plants will not last until Me = e, as this would only be possible if the function μ(Me) were cancelled before Me became equal to e, which, according to study [50], shows that the plants would be completely indifferent to a concentration lower than e. Hence, the h and μ functions are describing the growth rate and the mortality rate of plants, respectively.

2.2. Model of Zinc Bioaccumulation Process

The mathematical model given by Equation (2), with monotonous growth and mortality rates expressed by Equation (9), is used to simulate the process of zinc bioaccumulation in lettuce crops (Lactuca sativa L., family Asteraceae). Equation (9) was used to express the growth and mortality rates in the constructed mathematical model because, for the equations given in study [50], the information for obtaining the numerical values of the model constants is little or missing (for example, lettuce).

Data needed for the modelling are vast and cannot be obtained experimentally or from other sources. For this reason, the usual data for the lettuce crop will be further used to calibrate the model. Some data will be used to calculate the constants of the model and other data will be used for the main validation of the mathematical model. In addition, in models (2)–(6), a change is made that controls the growth of biomass by temperature.

This model is the first stage in introducing functions related to the control of plant growth: temperature, lighting, nutrients, pH, etc. The existence of water is already taken into account in the system, and it will be determined later whether or not the model can be upgraded.

To introduce the most important factors that show the influence of temperature in the mathematical models (2)–(6), introduced first is a Gaussian function of real variable, y:

$$G\left(p_1,p_2,p_3,p_4,y\right)=p_1\times exp\left(\frac{-{\left(y-p_2\right)}^2}{2p_3^2}\right)+p_4$$

(7)

where p_i, i = 1,…, 4 are parameters, and the bump function also of a real variable, y:

$$B\left(d,b_1,b_2,c_1,c_2,e_1,e_2,y\right)=\left\{\begin{array}{c}G\left(d-e_1,b_1,c_1,e_{1}y\right),if y<b_1\hfill \\ d,if y\in \left[b_1,b_2\right]\hfill \\ G\left(d-e_2,b_2,c_2,e_{2}y\right),if y>b_2\hfill \end{array}\right.$$

(8)

where d, b₁, b₂, c₁, c₂, e₁ and e₂ are parameters that can define favorable or unfavorable intervals for the process.

The following equation was used to determine the growth and mortality rates:

$$h\left(U\right)=G\left(1,t_0,0.5,0.001,U\right)+0.1,\mu \left(U\right)=9-G\left(1,t_0,0.3,0.0000005,U\right)$$

(9)

where U is a process parameter.

2.3. The Introduction of Temperature Influence in the Original Model

The mathematical model (2) introduces the influence of temperature by replacing the growth and mortality rates given in Equation (9) with factors describing the influence of temperature, shown in system (11). As can be observed, the mathematical model (10) differs from model (2) in terms that show the influence of temperature in the growth Equation (10a) and in the equation that gives the alternation of the concentration of heavy metals in the plant, (10b).

Introduction of the temperature dependence to the bioaccumulation phenomenon on the background of a multiplicative growth model is a hypothesis and is not mandatory. Soil or environmental temperature could be implicitly introduced in the expression of growth rates and mortality rates. In the latter case, it should take longer to investigate the dependence and experimental support would be needed.

$$\frac{dPB}{dt}=PB\left(t\right)(h\left(PB\right){\Theta }_h\left(\theta \left(t\right)\right)-\mu \left(Me\right){\Theta }_{\mu }\left(\theta \left(t\right)\right))$$

(10a)

$$\frac{dMe}{dt}=\alpha S-h\left(PB\right){\Theta }_{hMe}\left(\theta \left(t\right)\right)Me$$

(10b)

$$\frac{dS}{dt}=\phi H-\beta S-\frac{\alpha SPB}{p}$$

(10c)

$$\frac{dH}{dt}=\frac{-\phi H}{9}-\beta H+\frac{W}{p}$$

(10d)

where the factors influencing the temperature are defined as:

$$\begin{array}{c}{\Theta }_h\left(\theta \right)=B\left(1.5,15,25,1,1,0.5,0.5,\theta \right)\hfill \\ {\Theta }_{\mu }\left(\theta \right)=4\times \left(1.5-{\Theta }_h\left(\theta \right)\right)\hfill \\ {\Theta }_{hMe}\left(\theta \right)=B\left(0.005,15,55,10,10,0.001,0.0005,\theta \right),\theta \in \left[-30,60\right]\hfill \end{array}$$

(11)

All numerical values were determined by numerical experiments to achieve experimentally deduced behaviors and intuitive expectations. For reference in the calibration of process parameters, the following were taken into account:

• the temperature favorable to the development of the lettuce crop is between 15–25 °C;
• harvesting is done at an average weight of 0.9 kg·m⁻² or at an average mass of 113 g per lettuce;
• the accumulation of heavy metal in the plant must be monotonous (it does not decrease, because there is no experimental support to reduce the concentration of metal in the plant).

2.4. The Thermal Control Modification of the Model to Simulate the Effects of Heavy Metal Accumulation

An alternative model was created from models (10)–(11), by introducing an influence factor of metal concentration in the plant. To obtain a new model, the growth and mortality rates must be multiplied by a new factor. Hence, the new model is given by Equation (12) of evolution:

$$\begin{array}{c}\frac{dPB}{dt}=PB\left(t\right)\left(h\left(PB\right){\Theta }_h\left(\theta \left(t\right)\right)C_h\left(Me\left(t\right)\right)-\mu \left(Me\right){\Theta }_{\mu }\left(\theta \left(t\right)\right)C_{\mu }\left(Me\left(t\right)\right)\right)\hfill \\ \frac{dMe}{dt}=\alpha S-h\left(PB\right){\Theta }_{hS}\left(\theta \left(t\right)C_h\left(Me\left(t\right)\right)\right)Me\hfill \\ \frac{dS}{dt}=\phi H-\beta S-\frac{\alpha SPB}{p}\hfill \\ \frac{dH}{dt}=\frac{-\phi H}{9}-\beta H+\frac{W}{p}\hfill \end{array}$$

(12)

where factors that show the influence of temperature on heavy metal transfer are defined by:

$$C_h\left(\theta \right)=B\left(1,0,6,0.1,0.1,0.7,0.45,\theta \right),C_{\mu }\left(\theta \right)=B\left(0.006,0,6,0.1,0.1,0.3,0.3,\theta \right)$$

(13)

3. Results

Accumulation of Zinc in Green Lettuce

To verify the mathematical models described in the previous section, the most complex model (12) is applied to the exact data of the lettuce crop presented in study [63]. For the simulation, we considered a lettuce crop with the following characteristics: average mass at harvest is between 0.45–0.9 kg·m⁻²; density: 30,000–80,000 plants per ha; mass of 1000 seeds: 0.9–1.2 g (900 seeds per 1 g); an average of 8 plants per m².

The initial value of biomass was chosen to be PB₀ = 9 mg·m⁻². The concentration of the metal ion in plants (initial) is considered 0 (zero): Me₀ = 0 mg·kg⁻¹; the concentration of the metal ion in the soil (initial) is S₀ = 615 mg·L⁻¹; the concentration of the hydrogen ion in the soil (initial) is H₀ = 0.001 mg·L⁻¹.

Model constants (

Table 2. Results of simulation with temperature control.

Reference Time		Years	Months		Days
Time planting (initial) measured at the beginning of the year (January 1st)		0.2	3		90
The end time (end of year)		1	12		365
Reference Data—the Lettuce Crop
Harvest time (estimated)		0.4	5		156
Production of harvested lettuce (kg·m−2)		0.91
Average mass—one lettuce plant (kg)		0.11
Metal concentration at harvesting in the plant (mg·kg−1)		56.45
Model Constants
α = 0.55	β = 0.44	a = 10		b = 1

) were chosen to achieve the following culture characteristics: extent of 50, up to 60, days for the vegetation stage (from sowing to crop dismemberment by lettuce harvesting). This is a calibration of the model.

Under these conditions, the variations in the parameters of the growth of lettuce crops in a soil contaminated with heavy metal ions are shown in Figures 1–5, which were obtained by the numerical analysis of model (2).

It is observed that, for the whole simulation time, the flow of protons in the soil was maintained as constant during rain events (Figure 1a), having no experimental reasons for known variations. The water accessible to the roots during the simulation varies according to a sinusoidal curve (Figure 1b). The simulation lasts from the end of March until the last day of December, following a much longer lifespan than that of lettuce crops harvested for consumption. The simulation time is more than six times longer than the lifespan before harvest, due to the interest in knowing the storage capacity of heavy metal, the utility in phytoremediation and the desire to highlight interesting effects of the complete life of a plant species subjected to the influence of heavy metals. Last but not least, the aim is to profile an extension of the model to the genetic transmission of information on the concentration of heavy metal and to possible changes in the behavior of future generations of plants, due to the accumulation of heavy metals.

Figure 2a shows the time variation of the zinc accumulation rate in lettuce. It is observed that, as the plant matures, the accumulation rate decreases. Therefore, younger plants accumulate heavy metals faster and more intensely. Over time, metabolic inefficiency increases and metabolic efficiency decreases, as seen in Figure 2b.

Figure 3a shows the variation of the thermal regime during the simulation, through the daily variation curve and through the monthly average variation curve. We remind that lettuce grows optimally in the temperature range of 15–20 °C, information included in the model equations. The variation of soil pH during the simulation is represented graphically in Figure 3b. The range of variation of soil pH is not large and does not change from acid to basic or vice versa.

Figure 4a shows the variation of lettuce biomass over the entire duration of the simulation. The constant value of the biomass at harvest is plotted on the same graph. There is a short lifespan before harvesting. By doing so, information is lost about most of the crop’s lifespan, about the most important events: flowering, reproduction, death. Moreover, the remaining biomass will generate another crop and the starting properties of this new crop are very important to its evolution. The amount of metal remaining in the seeds is unknown at this time. Finally, the concentration of heavy metal in lettuce increases monotonously during the simulation, according to Figure 4b. Other types of behaviors are not excluded, including behavioral changes that cause heavy metal removal.

Figure 5a shows the variation of the concentration of metal ions in the soil and Figure 5b presents the variation of the concentration of hydrogen ions in the soil.

Table 3. Results of simulation with temperature control and bioaccumulation on plant health.

Reference Times		Years	Months		Days
Time, initial (planting): beginning of the year (January 1)		0.2	3		90
Time (end of year)		1	12		365
Reference Data—the Lettuce Crop
Harvest time (estimated)		0.5	6		195
Production of harvested lettuce (kg·m−2)					0.9
Average mass—one lettuce plant (kg)					0.11
Metal concentration: in the plant at harvest (mg·kg−1)					88.77
Model Constants
α = 0.55	β = 0.44	a = 10		b = 1

(which gives the same type of results as Table 2 and Figure 6 contain data and results from the simulation performed using the mathematical model described by the system of ordinary differential Equation (12). The variations during the simulation of lettuce biomass and zinc concentration in lettuce are represented graphically in Figure 6.

The comparative behavior of mathematical models (2) and (12), during the same simulation duration and under the same conditions is represented in Figure 7. The variation of lettuce biomass is given in Figure 7a, and the variation of zinc concentration in lettuce, respectively, is shown in Figure 7b. It is observed that model (12), at the parameters at which it was calibrated, has a lower value of the maximum biomass mass, while model (2) reaches the biomass harvesting value faster. Instead, model (12) accumulates a larger concentration of heavy metal. Overall, taking into account the value of biomass, the difference between the amounts of zinc accumulated is relatively small to the biomass of model (2).

All the results presented correspond to initial zinc loading of the soil, after which external modifications for the introduction or extraction of metal from the plant soil system were not made.

4. Discussion

The proposed mathematical models represent an embryo of the systemic formulation of heavy metal bioaccumulation in plants. The systemic description of the processes include, in addition to the mathematical model that underlies the simulation tool, a list of parameters that influence the process. These parameters are classified in the systemic vision into input, output and, respectively, command and control parameters. Typical input parameters of zinc bioaccumulation in lettuce are: the concentration of zinc ions in the soil, the flow of protons in the soil during rains and water accessible to roots. Command or control functions can be considered absorption, ion exchange, redox reactions, precipitation–dissolution, soil pH, soil temperature and moisture, etc. [64]. Output functions of zinc bioaccumulation in lettuce are plant biomass, concentration of heavy metal in the plant, concentrate, etc. There are also two very important parameters, which characterize the internal properties of the system, formulated by relationships that can be qualified as constitutive relationships: the net growth function and the function of mortality disorders in plant metabolism [50]. The output functions are also quality functions of the process because they measure the performances of the system from certain points of view (obtaining the mass for food purposes or the phytoremediation capacity). A systemic formulation of the process was tried, but not an exhaustive one, which claims to have covered all the parameters required to describe the process.

The model proposed in this study makes it possible to characterize the behavior of the soil–plant interaction with heavy metal pollution, and contributes to establishing threshold values for the toxic effects of heavy metals on plants and eventual plant mortality, to avoid lethal levels of soil contamination. The effects of heavy metals on plant development vary depending on different soil characteristics, the type of plant and the metal [50]. The model makes it possible to directly compare the relative fragility of different environments to the same pollutant. The effects of heavy metals on both plants and crops must be considered in order to establish the risk of these contaminants being transferred to the food chain. The mathematical models presented in the paper have multiple applications, which will be definitively validated.

A first example of using the model is the calculation of the harvest time at which the concentration of heavy metal in the plants is below the permissible limit by standards. Thus, for example on the graph in Figure 4 or Figure 6b, by drawing the horizontal line corresponding to the concentration of heavy metal admissible by standards, the intersection of this line with the graph of increasing the concentration of heavy metal in the plant gives a safe harvest time. Moving to the graphs in Figure 4 or Figure 6a, the corresponding harvesting mass is forecasted, hence the economic effects, etc.

Another application is related to the phytoremediation capacity. It is assumed that if certain parts of the plant (lettuce leaves) remain in contact with the soil, there is a reverse process of returning the heavy metal to the soil. In order to avoid this process, an average biomass limit must be considered, below which such phenomena do not occur. Then the harvesting of the plants used for phytoremediation must be done until the average biomass reaches this critical value. To predict the optimal harvesting moment from this point of view, go to the graphs in Figure 4 or Figure 6a: a horizontal line corresponding to the critical biomass and the optimal time for harvesting is the abscissa of the point of intersection between the horizontal line drawn and the biomass variation graph. For contaminated soil with a higher concentration of heavy metal (4.5%), the accumulation is more intense. Heavy metal accumulation in plants increases from plants grown in the least heavy metal infested soil to plants grown in soil with the highest initial concentration of heavy metal [59,65,66].

Similar curves of evolution over time of the metal concentration in plants are obtained by simulating the passage of pollutants through xylem and phloem in study [65], also using mathematical models based on ordinary differential equations. In study [33], experiments were performed on lettuce, using a soil with a pH between 6.5–7 units, similar to that used in our paper. Zinc values varied between 66.84–137.74 mg/kg, and the highest accumulation occurred in the roots of lettuce plants, compared to leaves that have accumulated less zinc. Also, in study [36], zinc accumulation was 120 mg/kg in lettuce roots and, respectively, 75 mg/kg in lettuce leaves, for a soil load of 620 mg/kg and soil pH of 7.3 units.

In study [67] was tested the accumulation of zinc in lettuce grown on five different sites, in which the plants were watered with wastewater. The results have shown a linear and progressive increase, significantly higher in the case of zinc in lettuce (104.09 mg/kg), compared to the results of our study (an average zinc concentration of 88.77 mg/kg in the whole plant at harvest).

The two applications explained above are graphically represented In Figure 8. We work with an initial Zn concentration in the soil of 615 g/L, the value of the harvest mass of 0.9 kg and the value of 7.9 mg/kg of the permissible limit concentration of zinc in lettuce. The optimal harvesting time, if zinc pollution is not taken into account, results from the intersection of the biomass evolution curve with the horizontal line which represents the optimal mass (from the point of view of food) at harvesting (Figure 8a). The time with the value of 0.5 years is obtained which, taking into account that the lettuce culture begins the evolution at the time of 0.25 years, means a duration of approximately 15 weeks until the harvest.

If it is taken into account that the soil is contaminated at a zinc concentration with the value given above and the admissible limit concentration is imposed in terms of food health, then, first, the harvesting time is determined at which zinc concentration in lettuce is equal to the admissible one. In this case, the abscissa of the intersection point between the evolution curve of the zinc concentration in the plant and the line is read, which represents the admissible concentration limit (Figure 8b). The harvesting time is 0.3 years, and then, on Figure 8a, we find the value of the harvest mass, 0.000014 kg/m², i.e., approximately 2 g per plant. This is a very low value and the crop is practically compromised for consumption. In study [64], the mass of a lettuce plant after 12 weeks of growth in soil contaminated with heavy metals was between 11.04–14.05 g.

Other variation curves of the concentrations of heavy metals, resulting from similar mathematical models, appear in study [68]; however, on a higher time scale. Also, study [50] presents predictions on the absorption of zinc in lettuce, zinc being the most absorbed metal. It has been observed that at different concentrations of zinc in the soil, metabolic problems and plant mortality occur before the end of the vegetation period, which is between 45–50 days [63].

Similar curves of bioaccumulation phenomena are presented in study [66], and similar experimental curves of lettuce mass growth are found in [64]. The similarity is valid only in the time interval limited by the time of harvest. A visual result of model validation by the subsequent experiments that we have conducted is presented in Figure 9, where we used three zinc concentrations for each group of lettuce plants: 1.5%, 3% and 4.5%.

In the group of plants whose soil was infested with solution containing 4.5% zinc, the difference in size of the plants and leaves compared to the other two groups can be easily observed. This confirms, experimentally, the phenomenon or symptom of dwarfism and the comparative graph in Figure 7a.

Study64] shows the growth of lettuce in fertilized and unfertilized soils, both contaminated with heavy metals (zinc, copper and lead) over a period of 12 weeks. After two weeks the plants had grown between 0.7–1 cm and had no leaves. Then, constant watering of the soils with fertilizer solutions based on nitrogen and phosphorus was applied. Starting with week eight, the lettuce plants started to show signs of recovery; the leaves appeared and regained their specific color. The dimensions of the lettuce at the end of the 12 weeks were 15 cm for the plants grown in fertilized soils and 13 cm in unfertilized soils, respectively. The accumulation of zinc was higher in lettuce grown in pots with unfertilized soil than in lettuce grown in fertilized soil.

5. Conclusions

The models and results presented in this paper represent the most advanced form reached after four years of research. During this time, the models were tested by numerical experiments and, in the last two years, by physical experiments. Gradually, the experimental results have validated the phenomenon, completed the systemic picture of the parameters, clarified their influence and corrected or completed the model.

The first applications in forecasts related to the harvest with the imposed limit of accumulated heavy metals or the harvest in the case of phytoremediation with a time limit, are given in this paper.

The fundamental goal of the detailed understanding of plant life, from the initial seed (or seedling) to the final seed, the germs of the next generation of plants, was reached. The following developments of the model are outlined, as new experimental results will appear: mathematical models with several parameters or influencing factors of the process, mathematical models of development over crop generations, when the new crop takes over the data and history of older generations, at least through seed information.

The development program suggested above has a multidisciplinary character, a consequence of the complexity of life and biological processes. The theoretical aspects require great efforts, but the experimental aspects involve extremely heavy tasks. Multifactorial experimental studies, which cannot be avoided although they are extremely expensive, cannot generally be supported by a single research unit.

The sustainability of such theoretical and, especially, experimental activities (anthropic activities that have the quality to be carried out without depleting the available resources and without destroying the environment), can be ensured only by collaborating with the most advanced research units, which can provide high-level techniques and equipment to less advanced research units, where most experiments will take place. Good quality communication must ensure that joint research reports are prepared.

From a theoretical point of view, the models researched in this paper need adjustments, in the sense of finding stable or constitutive internal functions (growth and mortality functions) with several influencing factors, such as to describe the phenomena and immunization against pollutants.

It should be mentioned that, as future research directions, we intend to deepen our research in this field and integrate in our studies some factors such as plant species/cultivar and water, as a central factor of soil-plant exchange processes.