Frequent Discounts and Loss of VAT for the State Budget of the Czech Republic: Scenario Estimations for Milk

Abstract

Frequent price discounts have become one of the features of retail chains in the Czech Republic. Discounts are most often provided for products popular with customers. One of the products that is subject to frequent discounts is milk. Several expert opinions estimate that up to 50% of milk is sold with frequent price discounts. Price pressure on farmers and food producers owing to frequent price promotions is supported by the purchasing power of retailers and, in extreme cases, leads to sub-cost purchasing prices. These facts set up the framework to assess the impact of frequent price discounts on policymaking, including tax administration. One of the effects of selling goods at discounts is lower VAT collection from shops, and thus lower revenue to the state budget. This paper attempts to estimate one of the potential impacts of frequent price discounts, namely the loss of VAT for the state budget due to low retail prices of milk. Theoretical estimation of the effect of frequent price discounts on VAT can help to assess policy that touches on mark-ups in specific markets, such as food. The estimation is based on data obtained from Czech Statistical Office, FADN, and Orbis databases and employs Monte Carlo simulation to capture the stochastic element of retail markups. Sub-cost prices of producers of milk have a more significant negative effect on VAT revenue than prices of other supply chain participants. The theoretical effect on VAT revenue is estimated to be in the range from a negative effect of 14.9 billion CZK to a positive effect of 7.4 billion CZK. Values of zero VAT effect points (mark-ups of producers, dairies, and retailers) are shown, as well as the critical value of price elasticity of demand (−0.1715), at which the effect of frequent price discounts on VAT revenue is zero.

1. Introduction

Retail stores spend considerable resources in order to attract customers, improve the pricing image, and prevent consumers from shopping at competing retailers. In some cases, it is possible to talk about price wars. However, these goals of retailers do not necessarily reflect the interest of manufacturers in maximizing their brand sales and market share targets. As a result of inter-chain price wars, food prices are being pushed down, which significantly affects the profitability of retailers and suppliers [1]. Efforts to gain customers through price reductions are common both during economic downturns [2,3] and during periods of economic boom [4]. During a period of prosperity, price wars can occur owing to higher immediate incomes [4]. This was confirmed by another study [5]. Another entity that is negatively affected by the effects of price wars is the state, in terms of reduced revenues from VAT collection.

A significant portion of the current professional literature is focused on the research of price competition from the point of view of retail chains as initiators. Very few studies focus on the impacts on other stakeholders, such as suppliers and the state, in terms of lower VAT collection from shops and, in connection with this, lower revenue to the state budget by up to the amounts comparable with the deficit (or surplus) of the state budget. The existing body of literature discusses the effects of frequent price discounts on producers and retailers [4,5], while possible effects on state budget via VAT collections are often out of the scope of these studies, albeit the amount of VAT collected by the state is in direct connection to consumer prices (as this tax is usually calculated as a percentage of consumer prices). To the best of our knowledge, underlying economic mechanisms, on micro and macro levels, are relatively new to these discussions, and thus demand deeper investigation. This paper attempts to start the discussion about economic mechanisms connected to frequent price discounts and proposes a new perspective on the topic, namely, the VAT revenue effect of frequent price discounts for state budget.

The aim of the work is to estimate the annual theoretical value of VAT revenue foregone for the state budget of the Czech Republic in the example of year 2018 and show the dependencies between factors influencing frequent price discounts effects on VAT revenues. Estimation is done on the basis of data from the Czech Statistical Office, FADN, and Orbis database using the Monte-Carlo approach to capture a stochastic portion of mark-ups and mathematical analysis of equations, which describe the VAT effect.

While the Czech Republic has been taken as an example to apply the proposed methodology of VAT effect estimation, this methodology can be applied to any country where frequent price discounts are observed. The definition of frequent price discounts is key in this case. As will be shown later in the paper, the share of the products sold within price discounts is one of the symptoms of possible VAT loss or gain for the state budget. A higher than average (in comparison with similar economies) share of such products might indicate a need to perform the assessment of a possible VAT effect of price discounts on state budget VAT revenues. A high or rapidly increasing share of retail chains might serve as another indication of a possible VAT effect of frequent price discounts, as these types of promotional activities are more likely to be used by retail chains [1,2,3]. At the same time, the topic of frequent price discounts is of interest for both developed and developing countries.

The paper is structured as follows. The literature review provides an overview of the current approaches and understanding of the effect of frequent price discounts on producers, retailers, and consumers. The research methodology section provides an overview of methods used to estimate frequent price discount effects on VAT and dependencies between influencing factors. The results section presents estimations of the VAT effect. The discussion section shows limitations and compares our results with the results of other authors working on similar topics. The conclusion section summarizes the findings on the value of the VAT effect and dependencies between influencing factors, and outlines possibilities for further research.

2. Literature Review

The reasons for providing frequent discounts on some products in stores have been discussed in the current literature on price adjustment and price sensitivity. Two effects relate to frequent price discounts: first, they may stimulate trade due to a declining demand curve and, second, they may reduce sales because consumers expect lower prices in the future. There is a non-linear relationship between frequent price discounts and consumer price sensitivity using the real options model, emphasizing that, when the second effect is stronger, increasing price sensitivity reduces price discounts [6]. An Australian industry report showed that 40% of products in Australian supermarkets are sold at promotional prices, an increase of 10% over the last 8 years [7]. Retailers should compete in various dimensions, not only in terms of price, but also, for example, in the diversity of the range [8] and other attributes associated with the sale of goods [9].

In retail, which in the Czech Republic is characterized by strong competition between retail chains [10], competition for customers is largely influenced by price. In such a competitive environment, the usual response to a price reduction by one retailer is a retaliatory reduction in prices by a competing chain, which may be one of the causes of a price war [11,12]. The timing of promotions and items included in these promotions for competing food chains was examined [13]. He found that some products are used as a leading item to protect the market share of a retailer, but for other products, it is in the retailer’s best interest to avoid direct competition and encourage cross-purchases to maintain a promotional pricing strategy. Discussions about whether more manufacturers or retailers benefit from price promotions are still relevant. Promotions are more profitable for manufacturers than for retailers [14]. This may be because the loss of retailers’ revenue from non-promoted items is equal to or greater than their profit from the promoted items.

It is a well-known fact that the Czech customer is extremely price sensitive. Price is a significant factor influencing customers’ purchasing decisions. Volume discounts, loyalty programs, or non-monetary promotions are often less effective than net price reductions [15]. So, price is a really effective marketing tool. The results of a model showed that price promotion is effective with 91% of brands (which make up to 94% of promotions) [16]. In terms of promotional effectiveness, previous research has shown that higher relative prices are associated with higher promotional effectiveness [17,18]. The Czech customer is characterized by persistently high price sensitivity and the purchase of goods at discounts in all categories of goods in the Czech Republic exceeds more than half of all sales of consumer goods [10]. The influence of competition in retail on sales prices was also confirmed by several studies [19,20,21]. Another empirical study also shows that competitor factors are important determinants of retail pricing [22]. In contrast, another study found that the competition factor has little effect on retail pricing [23].

Discounts are most often provided for products popular with customers or products advantageous in terms of retail margin [24]. This is because unsupported products are less able to attract consumers’ attention [25]. Most products offered at discounts are sold at a very low price, often below cost with a negative margin. An item that is promoted and offered at a discount very often is milk. The price of milk is often discounted (even below the cost) in order to entice customers at the supermarket to buy other products, which are more profitable. It is often justified by three factors [26]. On the one hand, milk has an irreplaceable role in the budgets of many families, it spoils very quickly, and is thus bought quite often; further, on the contrary, because of this need to buy, sellers usually do not apply discounts again in a short period of time and customers can only buy it at standard prices.

In the spirit of the existing literature [7,15,24] and based on reliable evidence from OECD, it is possible to state the unique situation around frequent price discounts in the Czech Republic [10]. As already mentioned, milk is one of the basic food products [26], and it is one of the products with most frequent price discounts; therefore, close investigation of frequent price discounts VAT effect in terms of such products is needed.

3. Materials and Methods

The potential effect of frequent price discounts on VAT revenue for the state budget can be estimated as a difference between potential VAT revenue and actual VAT revenue. The scope of the current paper includes the effect on VAT due to frequent price discounts and sub-purchase prices; therefore, the comparison should be done between regulated price discounts and unregulated (or currently observed on the market) price discounts. At the same time, regulation of price discounts relates to price increases, which in turn would lead to a decrease in demand for products. All in all, we estimate the effect on VAT revenue as per the following equation:

$${\mathsf{\Delta }}_{VATi}=c_i{r}_0{q}_{1i}\left(R_{1i}-R_{2i}+E_{di}{R}_{2i}\left(1-\frac{R_{2i}}{R_{1i}}\right)\right)$$

(1)

where ${\mathsf{\Delta }}_{VATi}$ is the difference in VAT revenue from commodity $i$ for the budget in unregulated and regulated situations; $c_i$ is the production cost of the commodity $i$; $r_0$ is the VAT rate for the commodity $i$; $q_{1i}$ is the number of units of product $i$ sold in an unregulated situation on market within frequent price discounts; $E_d$ is the price elasticity of demand for commodity $i$; $R_{1i}$ is the product of markups on each stage of supply chain of commodity $i$ in an unregulated situation on the market; and $R_{2i}$ is the product of markups on each stage of supply chain of commodity $i$ in a regulated situation on the market.

Equation (1), used to estimate the effect of price discounts on VAT revenues for the state budget, is formulated as a difference between VAT due to be paid to the state budget in an unregulated (or actually observable) situation on the market, and counterfactual regulated situation, which means that price discounts are smaller or are not observed, and the number of units sold within price discounts is lower.

The number of units sold in an unregulated situation on the market within frequent price discounts can be estimated from the market size of the product:

$$q_{1i}={\alpha }_i\times Q_i$$

(2)

where $Q_i$ is the market size for the commodity $i$ in respective units and ${\alpha }_i$ is the coefficient, showing how many units of commodity $i$ have been sold within frequent price discounts.

Coefficient ${\alpha }_i$ relates to commodity prices via average price of commodity. In general, the average price of commodity $i$ can be calculated as follows:

$$p_{ai}^{}=\frac{S_i^{}}{Q_i^{}}$$

(3)

where $S_i^{}$ is the total sales of commodity $i$ annually and $Q_i^{}$ is the quantity of commodity $i$ sold annually in units.

$$p_{ai}^{}=\frac{{{\displaystyle \sum }}_{m=1}^{{\alpha }_i{V}_i^{}}{p}_m^{}+{{\displaystyle \sum }}_{n=1}^{{\beta }_i{V}_i^{}}{p}_n^{}}{Q_i^{}}$$

(4)

where $p_m^{}$ is the average price of milk in frequent price discounts; $p_n^{}$ is the price of milk without frequent price discounts; ${\alpha }_i$ is the share of milk sold in frequent price discounts; ${\beta }_i$ is the share of milk sold without frequent price discounts.

$R_{1i}$ and $R_{2i}$ can be further explained by following equations:

$$R_{1i}=r_{11}{r}_{12}{r}_{13}$$

(5)

where $r_{11}$, $r_{12}$, $r_{13}$ are markups, increased by 1, on each stage of the supply chain, in an unregulated situation on the market.

$$R_{2i}=r_{21}{r}_{22}{r}_{23}$$

(6)

where $r_{21}$, $r_{22}$, $r_{23}$ are mark-ups, increased by 1, on each stage of the supply chain, in a regulated situation on the market.

Elasticity of demand for the product can be calculated based on statistical data for several years. In this case, there is a need to set up a few assumptions. Firstly, it assumes no impact on demand except that from prices; secondly, it assumes no impact on prices except that from the demand. In other words, it assumes no exogeneous influence on prices and quantity of demand from any other factor.

Price elasticity of demand $E_d$ can be calculated as follows:

$$E_d=\frac{Q_{d1}-Q_{d0}}{P_1-P_0}\times \frac{P_0}{Q_{d0}}=\frac{\left(Q_{d1}-Q_{d0}\right)/Q_{d0}}{\left(P_1-P_0\right)/P_0}$$

(7)

where $Q_{d0},Q_{d1}$ is the quantity of demand for the previous and current year, respectively; $P_0,P_1$ is price for the previous and current year, respectively.

As data for the consumption for the Czech Republic are difficult to obtain, it is possible to use production volumes reduced by the export volume.

$$Q_{di}=Q_{pi}-X_i$$

(8)

where $Q_{pi}$ is production volume of commodity $i$ and $X_i$ is the export volume of commodity $i$.

Coefficient ${\alpha }_i$ is difficult to determine as it depends on many factors influencing decisions of all retailers on the market to apply price discount to specific commodity $i$. We use a conservative estimation of 25%. As a reference, calculations for the case ${\alpha }_i=50\%$ are shown later in the text.

Mark-ups from the first group ($r_{1i}$) are set up as per the following scenarios:

• $r_{11}<1; r_{12}\ge 1;r_{13}\ge 1;$ this scenario represents the case when farmers sell milk at a price lower than their cost of production.
• $r_{11}\ge 1; r_{12}<1;r_{13}\ge 1;$ this scenario represents the case when industrial producers (i.e., dairies in case of milk) sell the commodity at a price lower than their cost of production, which includes the purchasing cost of commodity from farmers.
• $r_{11}\ge 1; r_{12}\ge 1;r_{13}<1;$ this scenario represents the case when retailers sell the commodity at a price lower than their cost, which includes the purchasing cost of the commodity from industrial producers.
• $r_{11}<1; r_{12}<1;r_{13}\ge 1;$ this scenario represents the case when both farmers and industrial producers sell the commodity at a price lower than their cost of production.
• $r_{11}\ge 1; r_{12}<1;r_{13}<1;$ this scenario represents the case when farmers sell the commodity with margin (mark-up is higher than zero), while industrial producers and retailers sell the commodity at a price lower than their cost.
• $r_{11}<1; r_{12}<1;r_{13}<1;$ this scenario represents the case when all participants of supply chain sell commodity at a price lower than their cost of production.

As a reference point, scenario 0 represents the following case:

$$1<r_{11}\le 1.3; 1<r_{12}\le 1.3;1<r_{13}\le 1.3;$$

(9)

Scenario 0 is used to illustrate the case with no sub-purchase or sub-cost prices. The value of VAT loss calculated in scenario 0 is subtracted from values of VAT loss in each of the scenarios to arrive to the value of VAT loss due to sub-purchase and sub-cost prices.

As mark-ups from the first group ($r_{1i}$) contain a portion of random effect in an unregulated market situation, a Monte Carlo estimation with 1000 repetitions was employed. Within the pre-defined conditions of each of the scenarios, estimation was based on the random values of variables $r_{11}$, $r_{12}$, and $r_{13}$ within the pre-defined mean and standard deviation values. Each scenario estimation contained 27,000 data cases.

Mark-ups from the second group ($r_{2i}$) are set up in accordance with farmers’, producers’, and consumers’ prices obtained from the Czech Statistical Office for the year 2018.

Assumptions of normal distribution of variables $r_{11}$, $r_{12}$, and $r_{13}$ are tested using the classical approach based on the analysis of skewness, kurtosis, mean and median, and Shapiro–Wilk test with the null hypothesis of normal distribution.

Each of the markups in the first group $r_{1i}^{}$ can be estimated from the financial statements of market participants taken as an example for each stage of the supply chain, following the formulae:

$$r_{1i}^{}=\frac{Net Revenue}{Operating Costs}$$

(10)

For variable $r_{11}$, data are obtained from FADN (Farm Accountancy Data Network). Net revenue and operating costs for calculation of $r_{12}$ are obtained from Orbis, the global database of financial information. Enterprises that are active in the dairy processing industry fall under category NACE rev.2 class 10.5. For variable $r_{13}$, data for the 10 biggest retailers in the Czech Republic in 2018 are obtained from publicly available financial statements.

Markups from the second group, $r_{2i}^{}$, can be set as per the data from the Czech Statistical Office as a ratio between prices on different stages of supply chain (all prices are without VAT).

$$r_{21}^{}=\frac{Producer price}{Production cost}$$

(11)

$$r_{22}^{}=\frac{Price of industrial producer}{Purchase price}$$

(12)

$$r_{23}^{}=\frac{Consumer price}{Purchase price}$$

(13)

The approach of setting the markups from the group $r_{2i}^{}$ as per (11), (12), and (13), together with (4), ensures that the theoretical VAT loss is estimated on the lowest level. Possible revisions of VAT loss due to new data on markups can only increase the value of the theoretical VAT loss.

This work attempts to answer the following research question: what are the theoretical values of VAT loss due to frequent price discounts for state budget of the Czech Republic in year 2018? Based on the theoretical values of VAT loss, we attempt to identify possible scenarios where VAT loss is zero or approaches its theoretical minimum. It is important to mention that practical minimization of VAT loss due to frequent price discounts can have externalities that are not included in the current estimation, such as a decrease in food security for specific groups of the population. Instead of proposing specific steps aimed to decrease VAT loss due to frequent price discounts, the work aims to show the scope of the problem and underlying mechanisms driving the increase or decrease of VAT loss.

4. Results

Tests for normal distribution of variables $r_{11}$ and $r_{13}$ have shown that the null hypothesis of normal distribution cannot be rejected (

Table 1. Tests for normal distribution of variables $r_{11}$, $r_{12}$, and $r_{13}$.

Variable	Standard Deviation	Skewness	Kurtosis	Distribution
$r_{11}$	0.2592	0.308	−0.665	Normal
$r_{12}$	0.0307	0.001	−0.334	Log-Normal
$r_{13}$	0.0962	0.105	−0.979	Normal

Source: own calculations.

). Variable $r_{12}$ has shown log-normal distribution. On this basis, it is possible to say that mark-ups of milk producers in the Czech Republic follow normal distribution (variable $r_{11}$), mark-ups of industrial milk processors follow log-normal distribution (variable $r_{12}$), and mark-ups of retailers follow normal distribution (variable $r_{13}$).

Based on the standard deviations calculated for mark-ups, we perform several Monte Carlo simulations with 216,000 repetitions each. Each simulation employs a sequence of values for each of the variables ($r_{11}$, $r_{12}$, and $r_{13}$). Within the simulation, each repetition uses a random value of each variable to calculate the VAT loss. Elasticity of demand $E_{di}$ and share of frequent price discounts in the market (coefficient ${\alpha }_i$) are constant for each simulation. Figure 1 shows the case of ${\alpha }_i=25\%,E_{di}=0.171$.

Elasticity of demand equal to 0.171 is the average of demand elasticities for milk in the Czech Republic in the years 2010–2018 and is given as a reference. Simulation 1 shows that the mean value of VAT loss equals 7464 million CZK. The probability distribution of VAT loss closely follows a normal distribution, which is expected as input variables follow a normal distribution too. However, it is possible to see non-symmetrical tails of the distribution, which will be more evident in figures of further simulations.

As shown in Figure 1, the probability distribution of VAT loss changes its skewness and kurtosis in different scenarios.

Simulations for negative values of price elasticity of demand show that theoretical VAT loss moves into positive values, which means additional VAT revenue for the state budget. Changes in coefficient ${\alpha }_i$ only multiply the theoretical VAT loss, but do not change the form of the distribution. Several scenarios with different values of price elasticity of demand are reported in

Table 2. Results of Monte Carlo estimation. Negative values mean loss of VAT for the state budget.

N	Repetitions	${\mathit{\alpha }}_{\mathit{i}}$	${\mathit{E}}_{\mathit{d}\mathit{i}}$	VAT Loss
				Mean, mln CZK	Standard Deviation, mln CZK	Max, mln CZK	Min, mln CZK	Mode, mln CZK
1	216,000	25%	0.171	−7464	1910	2062	−13,983	−7102
2	216,000	25%	−0.195	−3203	2560	7508	−9374	−4668
3	216,000	25%	−0.788	3700	6159	26,554	−9538	288
4	216,000	50%	0.171	−14,928	3815	3225	−28,999	−15,665
5	216,000	50%	−0.195	−6406	5116	16,277	−18,287	−8789
6	216,000	50%	−0.788	7394	12,317	52,672	−19,700	4828

Source: own calculations.

.

Analysing the results of the Monte Carlo estimation (Table 2), simulations 1–2 and 4–5 show negative mean and mode values of VAT loss. The decrease of price elasticity of demand decreases the VAT loss because sales volumes fall and increase in prices cannot compensate the loss of VAT. Positive values of VAT loss suggest that frequent price discounts have a positive impact on VAT revenue collected by the state. In the case of the positive VAT loss value, higher sales volumes due to lower prices within price discounts not only compensate falling of VAT revenue because of low prices, but also provide additional VAT revenue. This effect can be further noticed in scenarios estimations in

Table 3. Results of Monte-Carlo estimation per scenarios, mln CZK. Negative values mean loss of VAT for the state budget. Standard errors in parenthesis.

${\mathit{\alpha }}_{\mathit{i}},{\mathit{E}}_{\mathit{d}\mathit{i}}$	25%; 0.171	25%; −0.195	25%; −0.788	50%; 0.171	50%; −0.195	50%; −0.788
N	1	2	3	4	5	6
Scenario 0	−4864 (8.5)	491 (10.27)	9200 (23.22)	−9755 (16.99)	980 (20.44)	18,377 (46.16)
Scenario 1	−8663 (9.06)	−548 (9.72)	12621 (28.5)	−17,353 (17.99)	−1040 (19.33)	25,300 (57)
Scenario 2	−5988 (6.43)	−3018 (8.62)	1769 (19.22)	−11,976 (12.84)	−6074 (17.13)	3444 (38.13)
Scenario 3	−6253 (6.74)	−3091 (8.96)	2026 (20)	−12,524 (13.5)	−6181 (17.86)	4077 (40.28)
Scenario 4	−8800 (6.64)	−3794 (8.13)	4327 (23.27)	−17,573 (13.43)	−7560 (16.38)	8677 (46.31)
Scenario 5	−7004 (5.06)	−5684 (7.24)	−3545 (16.3)	−14,003 (10.02)	−11,383 (14.47)	−7111 (32.49)
Scenario 6	−9060 (5.13)	−6177 (6.83)	−1524 (19.64)	−18,133 (10.27)	−12,331 (13.61)	−3010 (39.12)

Source: own calculations.

.

Depending on elasticity values, the lowest values of the effect on VAT are shown by different scenarios. For example, for simulation N1, scenarios 1, 4, and 6 show very similar mean values of the negative effect on VAT. Scenario 1 represents the case when farmers sell milk at sub-cost price. Scenario 4 represents the case when both farmers sell at sub-cost price and industrial producers sell at sub-purchase prices, while scenario 6 shows the case when sub-cost or sub-purchase prices arise on each step of supply chain. Interestingly, estimations show that the magnitude of frequent price discounts effect on VAT (in other words, VAT loss) does not have a strong connection with the number of supply chain steps that apply sub-cost or sub-purchase prices. In other words, if a farmer sells milk at sub-cost prices, VAT loss appears and does not significantly increase if an industrial producer (dairy) or a retailer apply sub-purchase prices at the same time.

This does change, however, when the price elasticity of demand decreases. This is clearly seen in simulations 2 and 3, where increasing sales amounts almost offset VAT loss due to sub-cost prices on the farmer level, but still cause a negative effect on VAT on the level of industrial producer (dairy plant) and retailer (scenarios 2 and 3). Price elasticity of demand plays an important role in determining the value of the effect on VAT and its sign. In simulation 3, the negative effect on VAT appears only in scenarios 5 and 6, which are scenarios with sub-purchase on 2 and 3 steps of the supply chain, respectively.

Table 4. VAT loss due to sub-purchase prices of milk, mln CZK. Negative values mean loss of VAT for state budget. Standard errors in parenthesis.

${\mathit{\alpha }}_{\mathit{i}},{\mathit{E}}_{\mathit{d}\mathit{i}}$	25%; 0.171	25%; −0.195	25%; −0.788	50%; 0.171	50%; −0.195	50%; −0.788
N	1	2	3	4	5	6
Scenario 1	−3799	−1039	3421	−7598	−2020	6923
Scenario 2	−1124	−3509	−7431	−2221	−7054	−14,933
Scenario 3	−1389	−3582	−7174	−2769	−7161	−14,300
Scenario 4	−3936	−4285	−4873	−7818	−8540	−9700
Scenario 5	−2140	−6175	−12,745	−4248	−12,363	−25,488
Scenario 6	−4196	−6668	−10,724	−8378	−13,311	−21,387

Source: own calculations.

reports the values of VAT loss owing to sub-purchase prices, i.e., the situation when consumer prices of milk are lower than the purchasing prices of retailers. Values are calculated by subtracting the values of scenario 0 (Table 3) from every scenario 1–6.

Data on VAT loss per scenarios show that VAT loss exists until the price elasticity of demand reaches a specific value. After some value of $E_{di}$, the VAT loss changes its sign and becomes positive, meaning the VAT loss becomes an additional VAT revenue for the state budget. The source of this change is the decreasing amount of demand, and thus the decreasing sales of the product. Based on the Monte Carlo estimation, the average value of elasticity of demand at which VAT loss is equal to zero is −0.4996. The probability distribution of estimated $E_{di}$ that nullifies VAT loss is shown on Figure 2. Interestingly, the probability distribution has a thick left tail, while the right tail is thinner, and this differs from the probability distributions of VAT loss (for example, in comparison with Figure 1, ${\alpha }_i=25\%,E_{di}=0.171$).

The results of VAT loss estimation by applying the Monte Carlo approach might bring one to the question of what are the values of variables, or zero VAT loss points, which will eliminate the VAT loss? Zero VAT loss is possible in two cases:

$${\alpha }_i=0$$

(14)

$$R_{1i}-R_{2i}+E_{di}{R}_{2i}\left(1-\frac{R_{2i}}{R_{1i}}\right)=0$$

(15)

The case of ${\alpha }_i=0$ is trivial, as it essentially means the absence of frequent price discounts. Equation (15) contains three variables that influence the VAT effect: $E_{di}$, $R_{1i}$, and $R_{2i}$.

In the case of price elasticity of demand, zero VAT effect is possible when the following holds true:

$$E_{di}=\frac{R_{2i}-R_{1i}}{R_{2i}\left(1-\frac{R_{2i}}{R_{1i}}\right)}=\frac{\left(1-\frac{R_{1i}}{R_{2i}}\right)}{\left(1-\frac{R_{2i}}{R_{1i}}\right)}$$

(16)

Similarly, for $R_{1i}$, zero VAT loss is possible when the following holds true:

$$R_{1i}^2-R_{1i}^{}{R}_{2i}^{}+E_{di}^{}{R}_{1i}^{}{R}_{2i}^{}-E_{di}^{}{R}_{2i}^2=0$$

(17)

Assuming $x_{}=R_{1i}^{}$:

$$x_{}^2-x_{}^{}\left(R_{2i}^{}+E_{di}^{}{R}_{2i}^{}\right)-E_{di}^{}{R}_{2i}^2=0$$

(18)

This equation has two possible roots:

$$x_1^{}=\frac{\left(R_{2i}^{}+E_{di}^{}{R}_{2i}^{}\right)-\sqrt{{\left(R_{2i}^{}+E_{di}^{}{R}_{2i}^{}\right)}^2-4\left(-E_{di}^{}{R}_{2i}^2\right)}}{2}$$

(19)

$$x_2^{}=\frac{\left(R_{2i}^{}+E_{di}^{}{R}_{2i}^{}\right)+\sqrt{{\left(R_{2i}^{}+E_{di}^{}{R}_{2i}^{}\right)}^2-4\left(-E_{di}^{}{R}_{2i}^2\right)}}{2}$$

(20)

Values of variable $R_{1i}^{}$ in points specified by (19) and (20) are the points with zero theoretical loss of VAT for the state budget (zero VAT loss points). One or two real roots of quadratic Equation (18) exist when the following holds true:

$${\left(R_{2i}^{}+E_{di}^{}{R}_{2i}^{}\right)}^2-4\left(-E_{di}^{}{R}_{2i}^2\right)\gg 0$$

(21)

Or, after simplification:

$$E_{di}^2+6E_{di}^{}+1\gg 0$$

(22)

Numerical solving shows that two real roots of quadratic equation (18) exist when $E_{di}^{}\in \left(-\infty ;-5.828\right){\displaystyle \cup }\left(-0.1715;+\infty \right)$, while one real root exists at two points: $E_{di}^{}=-5.828$ and $E_{di}^{}=-0.1715$. Interestingly, solutions of inequality (21) are invariant to $R_{2i}^{}$ and $R_{1i}^{}$, i.e., they are the same for any given value of mark-up.

In economic terms, there is only one unique value of total mark-up $R_{1i}^{}$ when price elasticity of demand equals −5.828 or −0.1715. At the same time, the lower value of price elasticity (−5.828) is not likely to appear in the real world, as milk is usually characterized as a food product with inelastic demand, which would essentially mean that a 1% increase in the consumer price of milk decreases demand by 5.828%. Therefore, when price elasticity of demand is higher than −0.1715, there are two possible values of mark-ups $R_{1i}^{}$ that eliminate the VAT loss for the state budget.

The existence of two roots means that, at any given value of elasticity (within the range specified above), there are only two values of mark-ups $R_{1i}^{}$ that eliminate the VAT loss. A lower value of root represents the mark-up at which VAT loss due to lower prices is offset by higher sales volumes, while a higher value of root represents the mark-up at which higher price offset VAT loss due to lower sales volume. Some of the theoretical roots are negative or equal to zero, and thus cannot exist on the market.

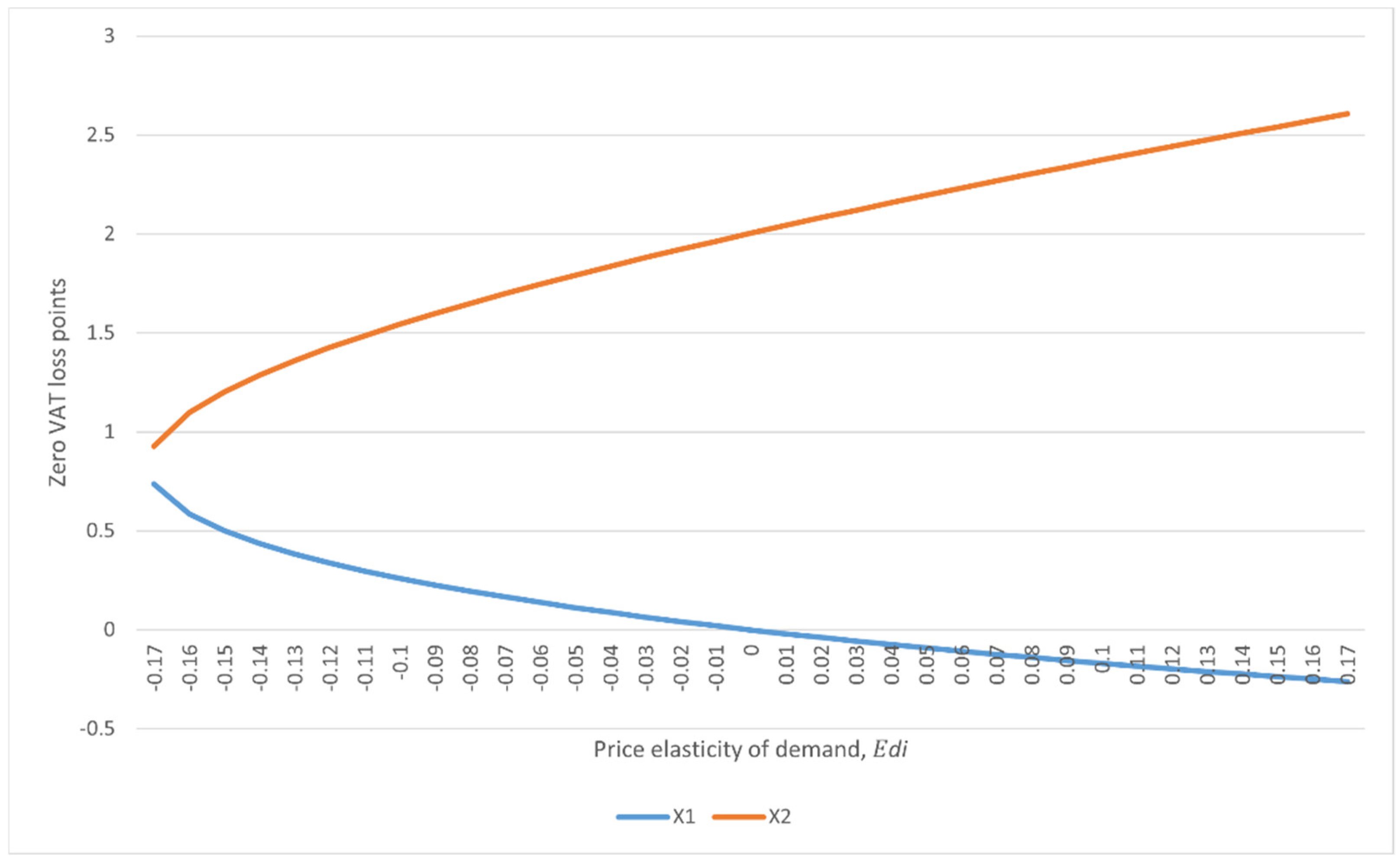
In order to determine all possible zero VAT loss points, we calculated all possible roots of Equation (18) for values of $E_{di}^{}$ between −10 and 10 with step 0.01 and for the case of $R_{2i}=2.004$, which was observed on the Czech market in 2018 (Figure 3). As can be concluded from these results, zero VAT effect points for $R_{1i}^{}$ have non-linear dependence on price elasticity of demand. The values of zero VAT effect points for $E_{di}^{}<-0.17$ are negative, and thus do not make economic sense. Lower zero VAT effect point ($x_1^{}$) takes negative values at point $E_{di}^{}=0$ and higher, thus only the higher root ($x_2^{}$) makes economic sense. The form of the $x_2^{}$ line depends on both $E_{di}^{}$ and $R_{2i}$.

Estimation of zero VAT effect points has its evident limitations, as there are several underlying assumptions, such as the omittance of the cross-price elasticity effect. However, even these estimations can have some value for policy makers. When the price elasticity of demand is defined, it is possible to determine mark-ups at which the negative effect of frequent price discounts can be nullified or minimized. In some situations, frequent price discounts might have a positive impact on VAT revenues for the state budget. At the same time, these possibilities should not be overestimated. Changing demand elasticity has the potential to reverse the positive VAT effect to a negative effect.

The topic of frequent price discounts has received attention in the literature to date; however, many questions have not yet been answered. The current paper contributes to the discussion by estimating the critical value of price elasticity of demand (−0.1715), which has been given relatively little focus in other pieces of research.

As shown in Equation (11), there is a non-linear relationship between price elasticity of demand ($E_{\mathrm{d}i}$) and mark-ups in regulated and unregulated situations on the market ($R_{1i}$ and $R_{2i}$, respectively). These results are generally in line with findings that showed a non-linear relationship between frequent price discounts and consumer price sensitivity using the real options model [7]. The non-linear relationship between price discounts and demand elasticity is especially important in light of the fact that net price reductions are more effective promotional strategies than volume discounts or loyalty programs [15]. Within the assumption of rational behavior of retailers, it is prudent to assume that net price reductions will be used more often by market participants. Policy makers should be aware of the relationships between such price reductions and the effect on VAT revenues for the state budget.

The condition of zero effect on VAT revenues, which was shown in (12) and (13), complements the findings suggesting that retailers often use some items as loss-leaders to keep the market share, while stimulating cross-purchases [13]. Condition (12) can be applied for such loss-leader items. This condition can also be improved by further studies in order to include the effect of cross-price elasticity. At the same time, the findings of the current paper do not show at which stage of supply the biggest loss occurs. As shown by other studies, price promotions might benefit mainly manufacturers [14]. The approach used in the current paper focuses on the final mark-up of the supply chain; therefore, the proposed approach cannot confirm or reject this statement.

5. Conclusions

Under several underlying assumptions, it is possible to estimate the theoretical effect on VAT due to frequent price discounts in the range from the negative effect of 14.9 billion CZK to the positive effect of 7.4 billion CZK.

Scenarios estimations have shown a new side of dependence between the negative effect on VAT and the number of supply chain stages that apply sub-cost or sub-purchase prices. In the scenario when farmers sell at sub-cost prices, the negative effect on VAT does not significantly increase if further stages of the supply chain (dairies and retailers) apply sub-purchase prices. The situation changes when demand becomes more elastic.

Price elasticity of demand has been proven to be one of the main factors determining the negative or positive effect on VAT due to frequent price discounts. As shown, more elastic demand has an offsetting effect on VAT by compensating decreasing VAT from a unit of a product due to an increase in sales volume. The probability distribution of elasticity values, which nullifies the negative effect on the VAT revenue, has properties different from the probability distribution of the VAT loss.

There are cases when the VAT loss can be zero. We have shown numerically that, when the elasticity of demand is higher than −0.1715, there is at least one set of mark-ups $r_{11}$, $r_{12}$, and $r_{13}$ (zero VAT effect points) at which a negative effect of frequent price discounts is offset by a change in sales volume. Frequent price discounts do not have a unidirectional (negative) effect on the VAT revenue, but might also increase the tax revenue. In general terms, this is applicable not only to VAT, but to any other indirect tax on consumption, which has a fixed tax rate.

Theoretical estimation of frequent price discounts VAT effect can help to assess policy that touches on mark-ups in specific markets, such as food. As shown in the scenario estimations, the loss of VAT is more connected with situations when farmers sell at sub-cost prices. When the state budget receives a decreased value of tax revenue, this effectively means subsidization of consumers at the cost of farmers. With the presence of frequent price discounts for specific products on the market (especially for the products with inelastic demand), policy makers should pay attention to the fact that non-regulation of frequent price discounts might have a two-folded effect.

The precision of the estimation of frequent price discounts effect on VAT can be improved by calculating the VAT effect for other years (before and after 2018), as well as by applying more precise values of mark-ups currently observed on the market. Another insight might be gained by estimating the frequent price discounts VAT effect for other basic food products, such as poultry and eggs. In the future, these improvements might shed more light on the problem of whether there is a need for the regulation of frequent price discounts.