Research on Multi-Echelon Inventory Optimization for Fresh Products in Supply Chains
Abstract
:1. Introduction
2. Methodology
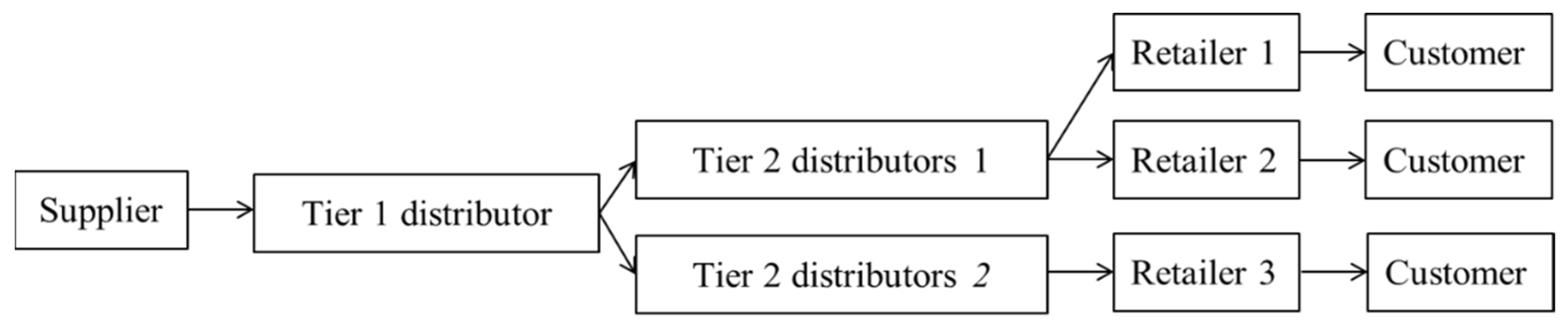
2.1. System Description
2.2. Inventory Cost
2.3. Model Assumptions
- The demand of each node is stable and continuous, that is, the demand of each node to its upper echelon node is .
- It is hypothesized that the fresh products are processed by certain approaches so that the deterioration rate of the fresh products at each node is constant .
- The supply of goods from upper level to lower level is delayed by a unit of time , and the goods are replenished instantly upon arrival.
- Product shortage is not allowed for retailers.
2.4. Notation
2.5. Model Formulation
2.6. Inventory Control Strategy
3. Illustrative Case Study
3.1. Case Description
3.2. Decentralized Strategy
3.3. Centralized Strategy
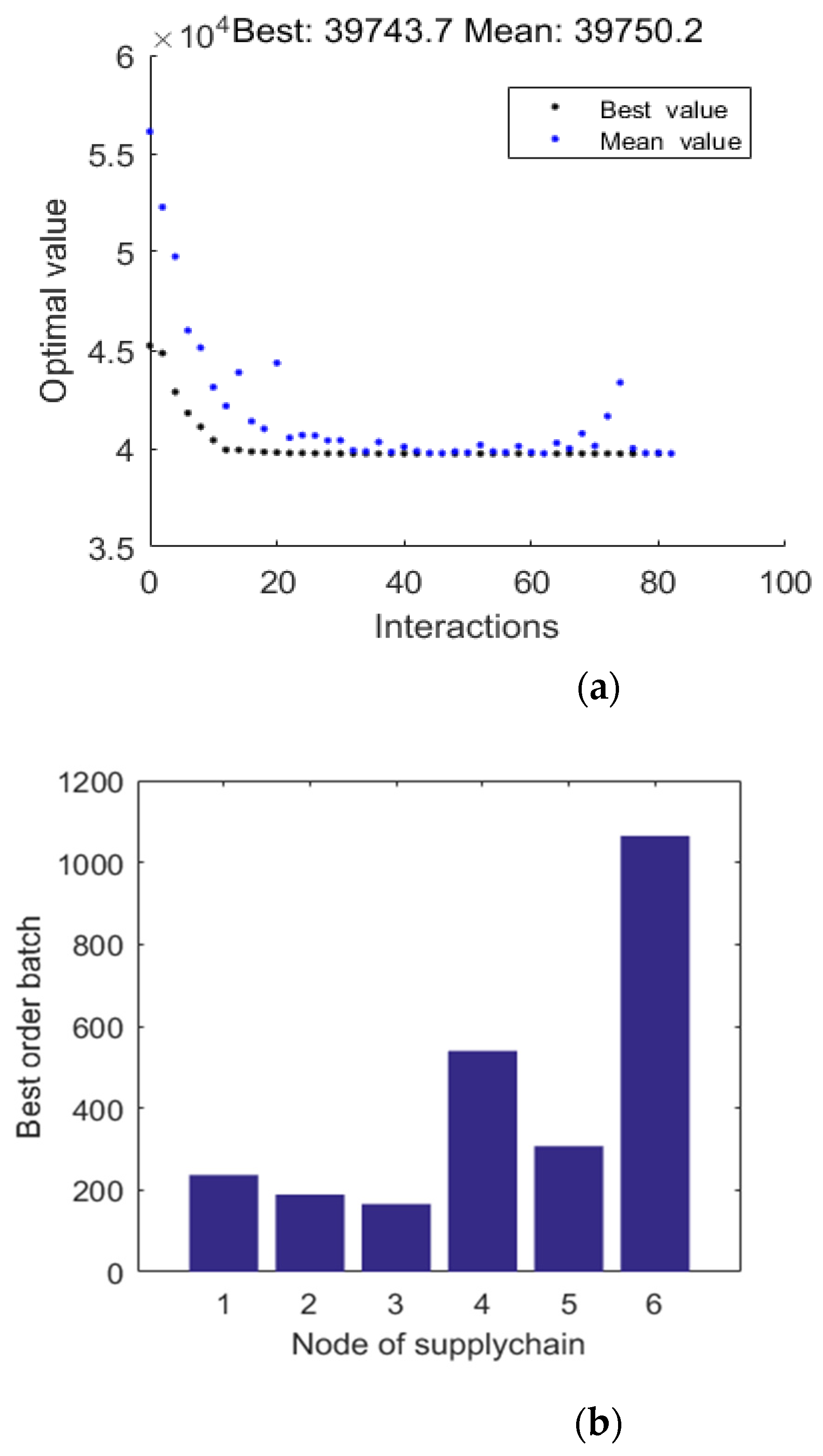
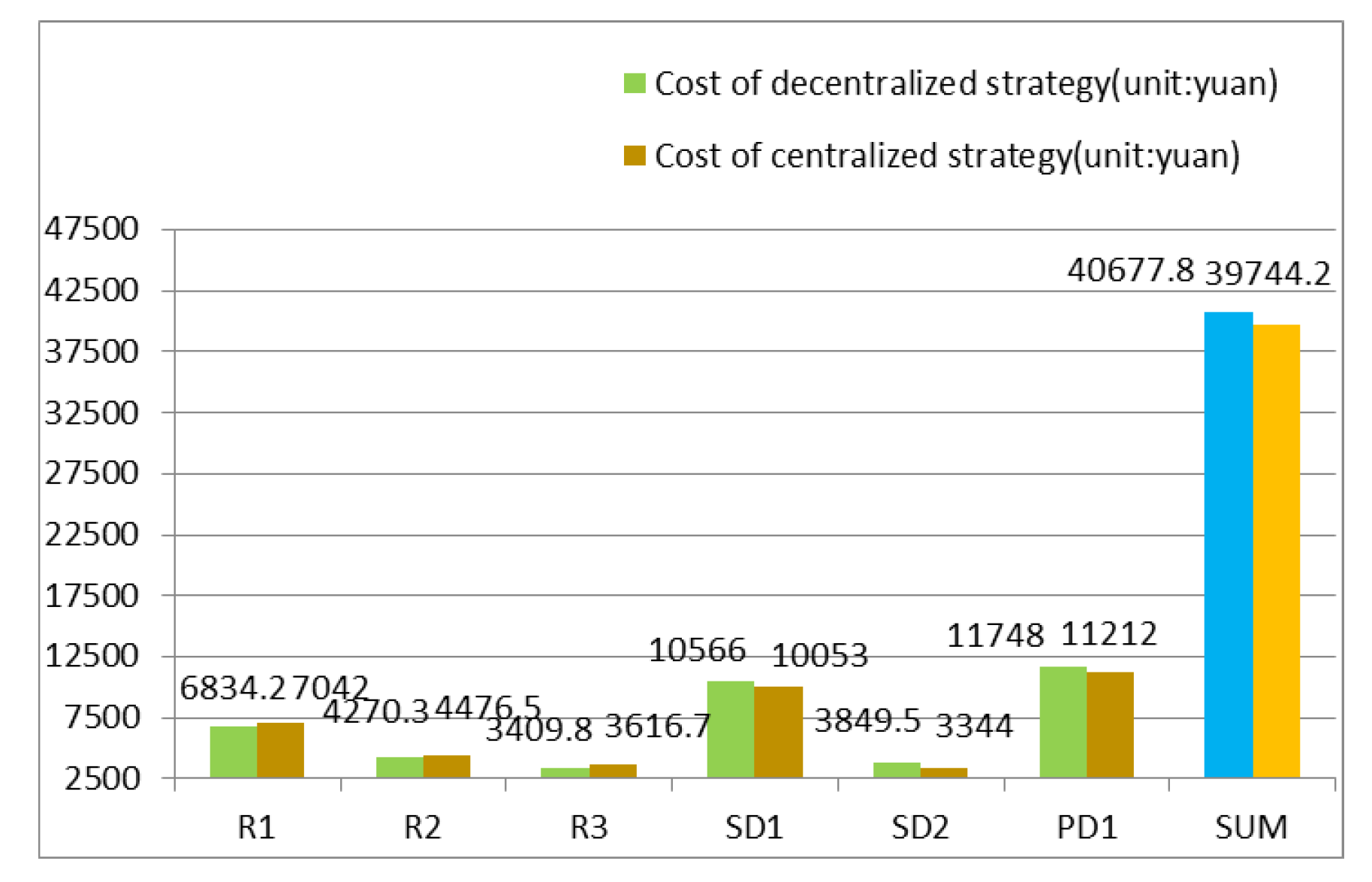
3.4. Results Analysis
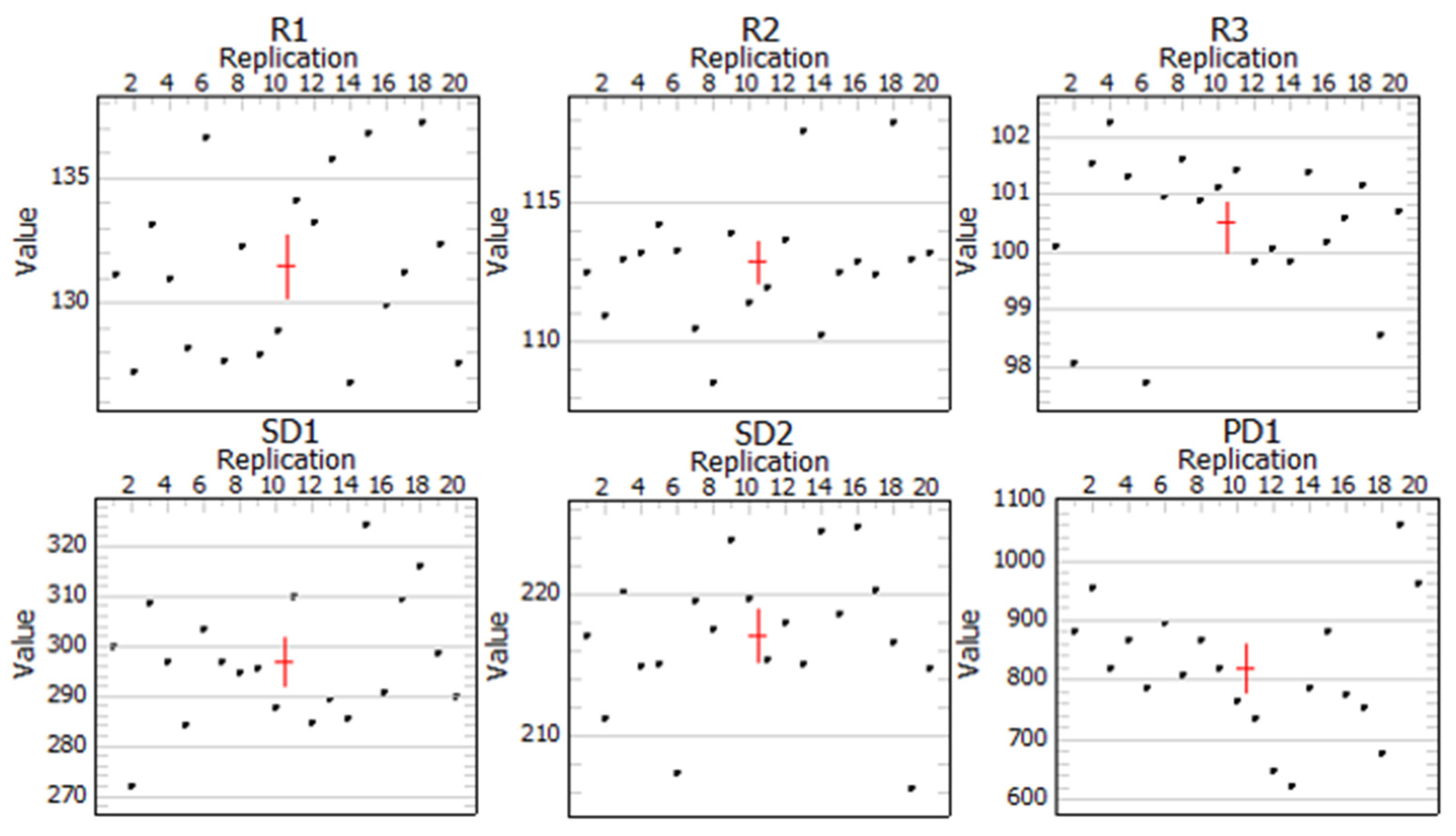
4. Simulation Model Verification
4.1. Simulation Model Establish
4.2. Simulation Results Analysis
5. Conclusions and Further Research
5.1. Conclusions
5.2. Limitations and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Olsson, F. Modelling two-echelon serial inventory systems with perishable items. IMA J. Manag. Math. 2010, 21, 1–17. [Google Scholar] [CrossRef]
- Mo, J.T.; Chen, G.M.; Fan, T.; Mao, H. Optimal ordering policies for perishable multi-item under stock-dependent demand and two-level trade credit. Appl. Math. Model. 2014, 38, 2522–2532. [Google Scholar]
- Kaya, O.; Ghahroodi, S.R. Inventory control and pricing for perishable products under age and price dependent stochastic demand. Math. Methods Oper. Res. 2018, 88, 1–35. [Google Scholar] [CrossRef]
- Rijpkema, W.A.; Roberto, R.; van der Vorst, J.G.A.J. Effective Sourcing Strategies for Perishable Product Supply Chains. Int. J. Phys. Distrib. Logist. Manag. 2014, 44, 494–510. [Google Scholar] [CrossRef] [Green Version]
- Zheng, Q.; Ieromonachou, P.; Fan, T.J.; Zhou, L. Supply chain contracting coordination for fresh products with fresh-keeping effort. Ind. Manag. Data Syst. 2017, 117, 538–559. [Google Scholar] [CrossRef]
- Janssen, L.; Diabat, A.; Sauer, J.; Herrmann, F. A stochastic micro-periodic age-based inventory replenishment policy for perishable goods. Transp. Res. Part E Logist. Transp. Rev. 2018, 118, 445–465. [Google Scholar] [CrossRef]
- Clark, A.J.; Scarf, H. Optimal polices for multi-echelon inventory problem. Manag. Sci. 1960, 6, 475–490. [Google Scholar] [CrossRef]
- Duong, L.N.; Wood, L.C.; Wang, W.Y. Effects of consumer demand, product lifetime, and substitution ratio on perishable inventory management. Sustainability 2018, 10, 1559. [Google Scholar] [CrossRef] [Green Version]
- Hill, R.M. The single-vendor single-buyer integrated production inventory model with a generalized policy. Eur. J. Oper. Res. 1997, 97, 493–499. [Google Scholar] [CrossRef]
- Weng, Z.K. Modeling quantity discounts under general price-sensitive demand function: Optimal policies and relationships. Eur. J. Oper. Res. 1995, 86, 300–314. [Google Scholar] [CrossRef]
- Diks, E.B.; De Kok, A.G. Optimal control of a divergent multi-echelon inventory system. Eur. J. Oper. Res. 1998, 111, 75–97. [Google Scholar] [CrossRef]
- Moinzadeh, K. A multi-echelon inventory system with information exchange. Manag. Sci. 2002, 48, 414–426. [Google Scholar] [CrossRef] [Green Version]
- Giannoccaro, I.; Pontrandolfo, P.; Scozzi, B. A fuzzy echelon approach for inventory management in Supply chains. Eur. J. Oper. Res. 2003, 149, 185–196. [Google Scholar] [CrossRef]
- Chen, J.M.; Chen, T.H. The multi-item replenishment problem in a two-echelon supply chain: The effect of centralization versus decentralization. Comput. Oper. Res. 2005, 32, 3191–3207. [Google Scholar] [CrossRef]
- Wang, Y.C.; Geng, X.X.; Zhang, F. An immune genetic algorithm for multi-echelon inventory cost control of IOT based supply chains. IEEE Access 2018, 6, 8547–8555. [Google Scholar] [CrossRef]
- Presbitero, A.; Krzhizhanovskaya, V.; Mancini, E.; Brands, R.; Sloot, P. Immune system model calibration by genetic algorithm. Proc. Comput. Sci. 2016, 101, 161–171. [Google Scholar] [CrossRef]
- Iida, T. The infinite horizon non-stationary stochastic multi-echelon inventory problem and near-myopic policies. Eur. J. Oper. Res. 2001, 134, 525–539. [Google Scholar] [CrossRef]
- Mandel, A.; Vilms, M. Local supply chain control model with unreliable suppliers. IFAC Pap. Online 2016, 49, 437–442. [Google Scholar] [CrossRef]
- Wang, L.L.; Zhang, T.; Guo, Y. Under the environment of agile supply chain inventory control research. Adv. Mater. Res. 2014, 945–949, 3179–3182. [Google Scholar] [CrossRef]
- Ech-Cheikh, H.; Elhaq, S.L.; Rachid, A.; Douraid, A. Simulating demand uncertainty and inventory control variability of multi-echelon distribution supply chain. Int. J. Appl. Logist. 2014, 5, 12–31. [Google Scholar] [CrossRef]
- Goswami, M.; Daultani, Y.; De, A. Decision modeling and analysis in new product development considering supply chain uncertainties: A multi-functional expert based approach. Expert Syst. Appl. 2021, 166, 114016. [Google Scholar] [CrossRef]
- De, A.; Mogale, D.; Zhang, M.; Pratap, S.; Kumar, S.K.; Huang, G.Q. Multi-period multi-echelon inventory transportation problem considering stakeholders behavioural tendencies. Int. J. Prod. Econ. 2020, 225, 107566. [Google Scholar] [CrossRef]
- Choudhary, A.; De, A.; Ahmed, K.; Shankar, R. An integrated fuzzy intuitionistic sustainability assessment framework for manufacturing supply chain: A study of UK based firms. Ann. Oper. Res. 2021. [Google Scholar] [CrossRef]
- Ray, A.; De, A.; Mondal, S.; Wang, J.W. Selection of best buyback strategy for original equipment manufacturer and independent remanufacturer—Game theoretic approach. Int. J. Prod. Res. 2020, 7, 1–30. [Google Scholar] [CrossRef]
- Pourhejazy, P.; Kwon, O.K. The new generation of operations research methods in supply chain optimization: A review. Sustainability 2016, 8, 1033. [Google Scholar] [CrossRef] [Green Version]
- Schwartz, J.D.; Wang, W.; Rivera, D.E. Simulation-based optimization of process control policies for inventory management in supply chains. Automatica 2006, 42, 1311–1320. [Google Scholar] [CrossRef]
- Chu, Y.; You, F.; Wassick, J.M.; Agarwal, A. Simulation-based optimization framework for multi-echelon inventory systems under uncertainty. Comput. Chem. Eng. 2015, 73, 1–16. [Google Scholar] [CrossRef]
- Attar, A.; Raissi, S.; Khalili-Damghani, K. Simulation-optimization approach for a continuous-review, base-stock inventory model with general compound demands, random lead times, and lost sales. Simul. Transp. Soc. Model. Simul. Int. 2016, 92, 547–564. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, S.H.; Moo, C. Production distribution planning in supply chain using a hybrid approach. Prod. Plan. Control 2002, 13, 35–46. [Google Scholar] [CrossRef]
- Kochel, P.; Nielander, U. Simulation-based optimization of multi-echelon inventory systems. Int. J. Prod. Econ. 2005, 93–94, 505–513. [Google Scholar] [CrossRef]
- Heidary, M.H.; Aghaie, A.; Jalalimanesh, A. A simulation-optimization approach for a multi-period, multi-objective supply chain with demand uncertainty and an option contract. Simul. Transp. Soc. Model. Simul. Int. 2018, 94, 649–662. [Google Scholar] [CrossRef] [Green Version]
- Zhao, W.D.; Wang, D.W. Simulation-based optimization on control strategies of three-echelon inventory in hybrid supply chain with order uncertainty. IEEE Access 2018, 6, 54215–54223. [Google Scholar] [CrossRef]
- Avci, M.G.; Selim, H. A multi-objective simulation-based optimization approach for inventory replenishment problem with premium freights in convergent supply chains. Omega 2018, 80, 153–165. [Google Scholar] [CrossRef]
- Gueller, M.; Uygun, Y.; Noche, B. Simulation-based optimization for a capacitated multi-echelon production-inventory system. J. Simul. 2015, 9, 325–336. [Google Scholar] [CrossRef]
- Thammatadatrakul, P.; Chiadamrong, N. Optimal inventory control policy of a hybrid manufacturing-remanufacturing system using a hybrid simulation optimisation algorithm. J. Simul. 2019, 13, 14–27. [Google Scholar] [CrossRef]
- Xu, G.Y.; Feng, J.H.; Chen, F.L.; Wang, H.; Wang, Z.F. Simulation-based optimization of control policy on multi-echelon inventory system for fresh agricultural products. Int. J. Agric. Biol. Eng. 2019, 12, 184–194. [Google Scholar] [CrossRef] [Green Version]
- Bardzinski, P.J.; Walker, P.; Krol, R. Simulation of random tagged ore fow through the bunker in a belt convering system. Int. J. Simul. Model. 2018, 17, 597–608. [Google Scholar] [CrossRef]
- Jiao, Y.L.; Xing, X.C.; Zhang, P. Multi-objective storage location allocation optimization and simulation analysis of automated warehouse based on multi-population genetic algorithm. Concurr. Eng. Res. Appl. 2018, 26, 367–377. [Google Scholar] [CrossRef]
- Grzybowska, K.; Kovacs, G. The modelling and design process of coordination mechanisms in the supply chain. J. Appl. Log. 2017, 24, 25–38. [Google Scholar] [CrossRef]
- Kierzkowski, A.; Kisiel, T. Simulation model of security control system functioning: A case study of the Wroclaw Airport terminal. J. Air Transp. Manag. 2017, 64, 173–185. [Google Scholar] [CrossRef]




| Symbol | Description |
|---|---|
| CS | Inventory maintaining inventory cost refers to the expenses necessary to maintain inventory, that is, the costs incurred because inventory exists to ensure the continuity of production and supply. |
| CO | Order cost refers to the cost of the purchase order issued by the upstream supplier. |
| CF | Transportation cost refers to the cost of transporting items from the upstream inventory to the downstream inventory, and is proportional to the number of transportation and the single transportation volume. It is mainly determined by the price of a single transportation unit. |
| CP | Purchase cost refers to the cost of purchasing the item itself. |
| CL | Shortage cost refers to the loss caused by insufficient inventory. The cost can be ignored if the shortage is not allowed. |
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| Deterioration rate of ith level, jth node | Stock cycle of ith level, jth node | ||
| Inventory of ith level, jth node at time t | Storage cost per unit time of ith level, jth node | ||
| Demand amount of ith level, jth node | Order cost per unit time of ith level, jth node | ||
| Order quantity of ith level, jth node | Transportation cost per unit time of ith level, jth node | ||
| Inventory quantity of ith level, jth node when the order is placed | Purchase cost per unit time of ith level, jth node | ||
| Storage cost per unit of product per unit of time of ith level, jth node | Total cost of each node of the supply chain in time T | ||
| One-time order cost of ith level, jth node | Number of orders in cycle T of ith level, jth node | ||
| Transportation cost per unit of product per unit of time of ith level, jth node | Supply chain management cycle | ||
| Unit purchasing price of unit product of ith level, jth node | Order lead time of ith level, jth node |
| Node | |||||||
|---|---|---|---|---|---|---|---|
| R1 | 0.04 | 10 | 0.1 | 1 | 1 | 200 | 0.1 |
| R2 | 0.04 | 10 | 0.1 | 1 | 1 | 125 | 0.1 |
| R3 | 0.04 | 10 | 0.1 | 1 | 1 | 100 | 0.1 |
| SD1 | 0.03 | 20 | 0.09 | 0.8 | 1.5 | — | 0.1 |
| SD2 | 0.03 | 20 | 0.09 | 0.8 | 1.5 | — | 0.1 |
| PD1 | 0.02 | 30 | 0.08 | 0.6 | 1.8 | — | 0.1 |
| Node | ||||
|---|---|---|---|---|
| R1 | 289 | 209 | 1.35 | 6834.2 |
| R2 | 230 | 131 | 1.68 | 4270.3 |
| R3 | 206 | 105 | 1.87 | 3409.8 |
| SD1 | 616 | 566 | 1.62 | 10,566 |
| SD2 | 352 | 178 | 2.78 | 3849.5 |
| PD1 | 1077 | 1000 | 1.93 | 11,748 |
| Node | ||||
|---|---|---|---|---|
| R1 | 238 | 210 | 1.12 | 7042.0 |
| R2 | 189 | 131 | 1.40 | 4476.5 |
| R3 | 166 | 105 | 1.53 | 3616.7 |
| SD1 | 561 | 559 | 1.50 | 10,053.0 |
| SD2 | 307 | 175 | 2.50 | 3344.0 |
| PD1 | 1066 | 978 | 1.94 | 11,212.0 |
| Node | Inventory (unit: kg) | Cost (unit: yuan) | ||
|---|---|---|---|---|
| Before Optimization | After Optimization | Before Optimization | After Optimization | |
| R1 | 131.5 | 109.5 | 6974.7 | 7010.2 |
| R2 | 112.9 | 92.3 | 4446.5 | 4438.8 |
| R3 | 100.5 | 80.8 | 3579.6 | 3602.4 |
| SD1 | 297.0 | 280.0 | 9949.8 | 9991.3 |
| SD2 | 217.1 | 197.7 | 3352.2 | 3341.9 |
| PD1 | 820.0 | 698 | 11,360.4 | 11,274.0 |
| Total cost | 39,663.2 | 39,658.5 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Chai, Y.; Ma, L. Research on Multi-Echelon Inventory Optimization for Fresh Products in Supply Chains. Sustainability 2021, 13, 6309. https://doi.org/10.3390/su13116309
Zhang Y, Chai Y, Ma L. Research on Multi-Echelon Inventory Optimization for Fresh Products in Supply Chains. Sustainability. 2021; 13(11):6309. https://doi.org/10.3390/su13116309
Chicago/Turabian StyleZhang, Yingying, Yi Chai, and Le Ma. 2021. "Research on Multi-Echelon Inventory Optimization for Fresh Products in Supply Chains" Sustainability 13, no. 11: 6309. https://doi.org/10.3390/su13116309
APA StyleZhang, Y., Chai, Y., & Ma, L. (2021). Research on Multi-Echelon Inventory Optimization for Fresh Products in Supply Chains. Sustainability, 13(11), 6309. https://doi.org/10.3390/su13116309






