Abstract
In this paper, we describe an interactive web application (deaR-shiny) to measure efficiency and productivity using data envelopment analysis (DEA). deaR-shiny aims to fill the gap that currently exists in the availability of online DEA software offering practitioners and researchers free access to a very wide variety of DEA models (both conventional and fuzzy models). We illustrate how to use the web app by replicating the main results obtained by Carlucci, Cirà and Coccorese in 2018, who investigate the efficiency and economic sustainability of Italian regional airport by using two conventional DEA models, and the results given by Kao and Liu in their papers published in 2000 and 2003, who calculate the efficiency scores of university libraries in Taiwan by using a fuzzy DEA model because they treat missing data as fuzzy numbers.
Keywords:
data envelopment analysis; DEA; fuzzy DEA; R software; efficiency; deaR package; shiny; Malmquist index 1. Introduction
Data Envelopment Analysis (DEA) is a widely used mathematical programming technique for evaluating the relative efficiency of a set of homogeneous DMUs (Decision Making Units) which consume the same inputs (in different quantities) to produce the same outputs (in different quantities).
In the last two decades, there have been remarkable advances in both DEA methodologies and practical applications in many different fields (education, banking and finance, sustainability, arts and humanities, hospitals and healthcare, industrial sectors, agriculture, transportation, etc.). Although there are several bibliographic reviews available—see, for instance [1,2,3,4]—the recent bibliographic compilation by [5] is noteworthy. Emrouznejad and Yang provide a full listing of more than 10,000 DEA-related articles ranging from 1978 to late 2016. Recently, [6] reviewed the literature on DEA applications in the field of sustainability, covering papers published in journals indexed by the Web of Science from 1996 to 2016 (a total of 320 relevant papers were analyzed).
The first original DEA model is known as the CCR model since it was proposed by Charnes, Cooper and Rhodes [7] and assumes that the technology exhibits constant returns to scale (CRS). However, as the assumption of constant returns to scale is not always real, Banker et al. (1984) [8] relax this assumption by including the so-called convexity restriction. Thus, the resulting model, popularly known as the BCC model (or Banker, Charnes and Cooper’s DEA model), allows the efficient frontier to exhibit variable returns to scale (VRS). Both CCR and BCC models can be either input- or output-oriented and provide radial efficiency measures.
Based on these basic DEA models, several extensions have been proposed in the DEA literature. For example, and without being exhaustive, the possibility of considering non-discretionary (or uncontrollable) inputs and/or outputs [9], the presence of categorical or ordinal inputs and/or outputs [10,11], imposing restrictions on the weights of inputs and/or outputs [12,13,14,15,16] or taking into account the presence of undesirable factors [17,18].
Over the years, and at the same time as these variations of the basic radial DEA models were emerging, methodological developments have also led to a wide variety of new DEA models. One of these first new DEA models is the additive model [19], which simultaneously allows input reductions and output increases. A disadvantage of the additive model, which is a non-radial (models that do not preserve the mix within inputs and within outputs in movements toward the frontier [20]) and non-oriented model, is that it identifies inefficient DMUs but does not provide an efficiency score. To solve this problem, other non-radial models were proposed. For example, the Slacks-Based Measure (SBM) of efficiency model introduced by Tone (2001) [21], the Russell measure of efficiency models [22,23,24], the preference structure model [25], the range-adjusted measure of efficiency model [26], etc.
Typically, the efficiency scores obtained by executing a DEA model allow us to classify the DMUs into two groups: efficient DMUs, which define the best practice frontier, and inefficient DMUs. However, it is not possible to rank the DMUs based on their efficiency score in principle. In order to get a ranking of the DMUs (see [27] for a review of methods), super-efficiency models [28,29,30] or cross-efficiency models [31,32] are commonly used models.
On the other hand, if we have panel data and we want to compare the performance of a set of DMUs over time, the most frequently used method is the Malmquist productivity index [33,34,35,36,37,38] and, to a lesser extent, window analysis [39].
So far, the models reviewed have one common feature: they consider that inputs and outputs are precise data. However, what if it is acceptable to assume that the inputs and/or outputs are imprecise data? In these situations, although bootstrapping [40,41,42,43] or stochastic DEA [44,45,46] models have been proposed, fuzzy set theory has prevailed to quantify the imprecise or vague inputs and/or outputs. DEA models with imprecise data are often called Fuzzy DEA models (FDEA). Hatami-Marbini, Emrouznejad and Tavana [47] provide a taxonomy and review of FDEA methods. Zhou and Xu [48] review the research status, method development, real application, and theory trend of the FDEA.
In our opinion, many of the theoretical models referred to in the previous paragraphs are not widely applied because many practitioners and researchers do not have the proper basic tools, that is to say: the software. Therefore, to fill this gap between theory and practice, we developed deaR-shiny, a free web application that allows them to run an amazingly wide variety of DEA models, both traditional and fuzzy, and decompositions of the Malmquist Index.
2. DEA Software: A Brief Review
In parallel to the development of DEA models, some software has also emerged to facilitate their use by practitioners. Barr (2004) [49] provides an overview and compares the features and capabilities of several commercial and non-commercial DEA software:
- Commercial software:
- DEA Solver Pro (http://www.saitech-inc.com/Products/Prod-DSP.asp (accessed on 12 June 2021)). A student free version of this software is included in Cooper, Seiford and Tone (2007) [50].
- Frontier Analyst (https://banxia.com/frontier/ (accessed on 12 June 2021)). It is possible to download a restricted version of the software which allows analyzing up to 12 DMUs.
- OnFront from Economic Measurement and Quality Corporation.
- Warwick DEA (It is currently known as PIM-DEA) (http://www.deasoftware.co.uk (accessed on 12 June 2021)).
- Non-commercial software:
- DEA Excel Solver (https://www.deafrontier.net/deafree.html (accessed on 12 June 2021)). It is an Add-In for Microsoft Excel. There is a DEA Frontier free trial version but the maximum number of DMUs allowed is 20 DMUs and the DEA models are also limited.
- DEAP (https://economics.uq.edu.au/cepa/software (accessed on 12 June 2021)).
- EMS (http://www.holger-scheel.de/ems/ (accessed on 12 June 2021)).
- PIONEER. A DEA software developed by Thomas McLoud and Richard Barr.
More recently, Daraio, Kerstens and Cavalcante [51] conducted a comprehensive review of current software options for productivity and efficiency analysis and carried out a comparative analysis on them. It is worth noting the great diversity of models implemented in MaxDEA (http://www.maxdea.cn (accessed on 12 June 2021)), which is developed with VBA Access. MaxDEA offers two versions to users: (1) MaxDEA Basic, which allows running basic models (CCR, BCC, Slacks Based Model and Cost model) under different orientations (input, output and non-orientation) and returns-to-scale with no limit of DMUs, and (2) MaxDEA Ultra, the commercial version in which a wide variety of models are available (a list of them can be consulted at: http://maxdea.com/Features.htm (accessed on 12 June 2021)). It should also be mentioned that some of the most popular software used by mathematicians, engineers and econometricians—such as GAMS, STATA, SAS or Matlab—have also incorporated modules to estimate efficiency through DEA models (for example: [52,53]). The main drawback we see in all these software options is commercial software and their access is therefore limited for many practitioners.
Regarding non-commercial software, one of the alternatives that has had the greatest growth in recent years is the programming language R (it is a programming language and free software environment for statistical computing) [54]. One of the greatest strengths of the R programming language is in the ease of creating extensions through packages contributed by a constantly growing user community. Currently (as of 2020), there are more than 16,000 user-contributed packages available at CRAN (Comprehensive R Archive Network). Those packages contain applications in almost every scientific field, e.g., Biology, Finance, Data Science, Meteorology, etc. Data Envelopment Analysis is no exception. In recent years the contribution of R packages to estimate efficiency has increased significantly, and a wide variety of DEA models can be applied. One of the first R packages is FEAR [55] and it is the first DEA software that includes functions for running the bootstrap methods proposed in [40]. Other popular R packages (with more than 10,000 downloads from 2019-01-01) are Benchmarking [56], nonparaeff [57], rDEA [58], DJL [59], and deaR [60,61].
All the applications we have referred to so far need to be installed locally on the user’s computer and in many cases require an intermediate knowledge in order to be used effectively and extract their full potential (applications in R, Matlab, Python, etc.).
There are also some commercial and non-commercial web-based DEA solutions. For example:
- Commercial online software:
- DEAOS (https://www.deaos.com (accessed on 12 June 2021)). The DEA models available in DEAOS are: basic radial models (envelopment and multiplier forms), scale efficiency measurement, radial super-efficiency models, radial models with value judgments, Free Disposal Hull (FDH), basic additive models, range directional measurement, variant of radial measure (VRM), cost efficiency models, SBM models and modified SBM models.
- There is a free version (lite version) limited to a maximum of 15 DMUs and 4 indexes (inputs/outputs) in a maximum of 2 projects.
- DEA online (http://www.onlineoutput.com/dea-software/ (accessed on 12 June 2021)). The company offers a demo version with a limited number of inputs/outputs and number of DMUs.
- Non-commercial online software:
- WebDEA (https://sites.google.com/site/dsslabunipi/home (accessed on 12 June 2021)). This application, which currently is not working, includes DEA models under constant and variable returns to scale assumptions as well as their oriented and non-oriented variants. Additionally, weight restrictions can be incorporated into the aforementioned models and post-DEA analysis can be carried out based on cross-efficiency analysis (aggressive and benevolent versions).
- DEA Solver Online (http://www.dea.fernuni-hagen.de (accessed on 12 June 2021)). It is necessary to register on the platform and accept the terms of use. This software (the last update is from 2013) can solve the following models: CCR, BCC, FDH (under VRS), additive (under CRS), Range Adjusted Measure (RAM, under VRS) and Russell measure (under CRS). It is possible to select non-discretionary variables and calculate the radial super-efficiency.
- DEAShiny (https://deaumh.shinyapps.io/DEASHINY/ (accessed on 12 June 2021)) [62]. All the DEA models in this shiny app are based on the “loss distance function” proposed by Pastor, Lovell and Aparicio [63], providing a unified method for computing the scores of a wide family of DEA models. DEAShiny covers the basic models of DEA and extensions including CCR, BCC, Russell measures, Enhanced Russell Graph (or, equivalently, SBM), Directional Distance Functions, Weighted Additive Models, and more, under different returns to scale: variable (VRS), constant (CRS), non-increasing (NIRS) and non-decreasing (NDRS).
deaR-shiny aims to fill the gap that currently exists in the availability of online DEA software and it offers practitioners free access to a wide variety of DEA models and without any requirement of prior registration.
3. deaR-Shiny: A Web App for Data Envelopment Analysis
deaR-shiny is an interactive web application for DEA built with Shiny [64] and shiny dashboard [65], and it serves as a frontend for the functions defined in the deaR package [60] to execute the selected DEA model and to get the results. Anyone can access the web app deaR-shiny in the URL: https://rbensua.shinyapps.io/deaR/ (accessed on 12 June 2021).
All shiny applications, from the simplest to the most complex ones, consist of two components: a user interface (UI) object and a server function. In the case of deaR-shiny:
- the UI contains the R code that controls the design and appearance of the application. That is, what the application will look like: sidebar panels, main or body panels, tabs, colors, etc. For example, as Figure 1 shows, the deaR-shiny’s user interface consists of 5 sidebars: Data, DEA Models, Results, Plots, and About.
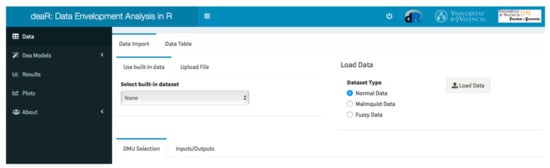 Figure 1. The deaR-shiny window.
Figure 1. The deaR-shiny window. - By default, the application displays the Data body panel, which consists of two main horizontal boxes. The first box is related to the selection of data and has two tabs: Data Import and Data Table. The second box is related to the variable selection: DMUs and inputs/outputs. We will discuss this in more detail in the next section
- the server section contains the necessary instructions to build the application. The relationships between the inputs that are introduced in the UI and the outputs that will be obtained are defined in the server. Thus, in this section we will find the R code for loading data, transforming data, running models or creating plots.
The interactivity of the shiny apps lets the user interact with the data without manipulating the R code, and it is based on reactive programming: any changes made by the user in the interface make the application instantly update itself.
The models that can currently be chosen in deaR-shiny are listed in Table 1. Detailed technical information about the DEA models and built-in datasets available in deaR-shiny can be consulted at: https://rdrr.io/cran/deaR/man/ (accessed on 12 June 2021).

Table 1.
DEA models available in deaR-shiny 1.
Table 2 shows the average computation time of an input-oriented BCC model under different scenarios. Note that deaR-shiny has no limitation on the number of DMUs or inputs/outputs.

Table 2.
Input-oriented BCC model. Average computation time (in seconds) in deaR-shiny 1.
As we said in the introduction section, the increasing number of published articles on DEA applications in sustainability gives an idea of the growing interest of practitioners and researchers in this area. The availability of powerful software, such as deaR-shiny, that allows a wide variety of DEA models to run can help advance sustainability performance analysis research.
Now, we will explain how deaR-shiny works.
The deaR-shiny interface is structured in three parts, which roughly correspond to the logic for performing an efficiency analysis using DEA (see Figure 2): (1) load data, (2) select and run a DEA model, and (3) show the results (numerically and graphically). Each of these parts is discussed below with two case studies. In both cases, there are missing values in the dataset. However, their treatment is different. Thus, in the first case, the DMU with missing values will be omitted from the analysis and a conventional output-oriented DEA model will be applied. In the second case, the missing values will be transformed into triangular fuzzy numbers and, consequently, a fuzz DEA model will be used. Specifically, we are going to reproduce the main results given in Carlucci, Cirà and Coccorese [76] (case study 1), and Kao and Liu [77,78] (case study 2).
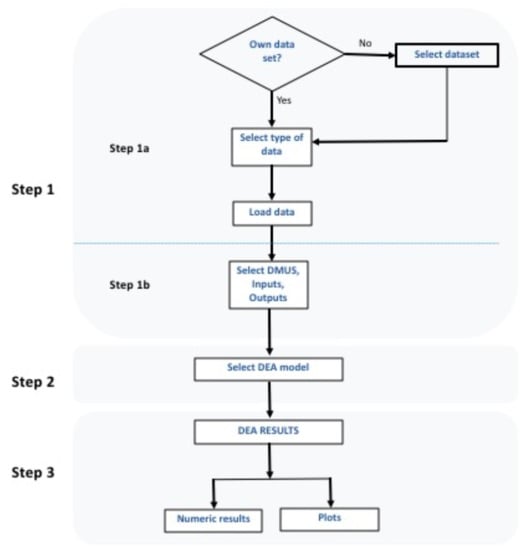
Figure 2.
Steps to perform a DEA analysis.
3.1. Case Study 1. Carlucci, Cirà and Coccorese (2018)
In this case study, we are going to illustrate how to use deaR-shiny by reproducing some of the results given in Carlucci, Cirà and Coccorese (2018) [76]. These authors analyze the impact of several external factors, such as the size of the airport and the presence of low-cost carriers, on the efficiency and environmental sustainability of regional airports in Italy. They estimate the efficiency of 34 airports by means of an output-oriented DEA model (both under constant and variable returns to scale). To do that, they consider six outputs (APM = Passenger movements (number); CAR = Cargo; AAM = Aircraft movements; AR = Revenues from aeronautical activities; HR = Revenues from handling activities; CR = Revenues from commercial activities) and three inputs (LC = Labor costs; IC = Invested capital; OC = Other expenses).
Data used for the DEA analysis are shown in Table 3 and supplied as Supplementary Material with this article in order to reproduce the results. The dataset can also be downloaded from: https://go.uv.es/dearshiny/case_study1 (accessed on 12 June 2021).

Table 3.
Data from Carlucci, Cirà and Coccorese (2018).
Being on the web app (https://rbensua.shinyapps.io/deaR/ (accessed on 12 June 2021)), the first step is to load the data. As Figure 2 shows, this step is done in two phases:
- Step 1 a: Loading data. Firstly, we can upload our own dataset (the app identifies the most common file extensions: txt, csv, tsv, xls, xlsx, sav, dta, xpt, etc.) or load a built-in dataset (deaR-shiny is not only oriented to research but also to teaching, so the application provides 24 built-in datasets from published articles). Once the data file is selected, we have to indicate the type of data we will work with, which depends on the analysis model to be applied. Thus, we will select the Normal Data option if a conventional DEA model is going to be executed, the Malmquist Data option to perform the Malmquist productivity index, or the Fuzzy Data option to run an FDEA model with uncertain data.To reproduce the results given in [76], we need to click on the Upload file tab and then on the button Browse to select the Excel file (case_study1.xlsx). As the option Normal Data is selected by default, we only have to click on the button Load Data to load the dataset. We should see something similar as Figure 3.
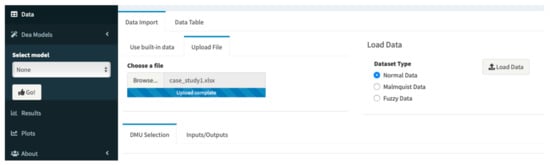 Figure 3. Uploading data from a file.To take a quick glimpse at the uploaded data, we click on the Data table Table In doing this, we can see that Comiso Airport has three missing values.
Figure 3. Uploading data from a file.To take a quick glimpse at the uploaded data, we click on the Data table Table In doing this, we can see that Comiso Airport has three missing values. - Step 1 b: Selecting variables. Once the dataset is loaded, deaR-shiny automatically reads it and identifies the names of the header as the names of the variables. By default, the application considers that the DMUs are in the first column (if it is not, we can select the correct DMU column by pulling down the menu) and the rest of the columns are the inputs/outputs.At this point, all the DMUs are selected for evaluation. Alternatively, we can select the DMUs that will constitute the evaluation reference set (DMU ref) and the DMUs to be evaluated (DMU eval). As Comiso Airport has missing values and we do not know how [76] treated them, we will omit this DMU. Therefore, we deselect Comiso from both DMU eval and DMU ref.In addition, as Figure 4 shows, we also must identify which variables are inputs and which are outputs. This is done in the tab Inputs/Outputs. To measure the efficiency of regional Italian airports, [76] use three inputs (LC, IC, and OC) and six outputs (APM, CAR, AAM, AR, HR, and CR). To select them, we click on the corresponding check box. Note that we could also indicate whether there are uncontrollable, non-discretionary or undesirable inputs/outputs.
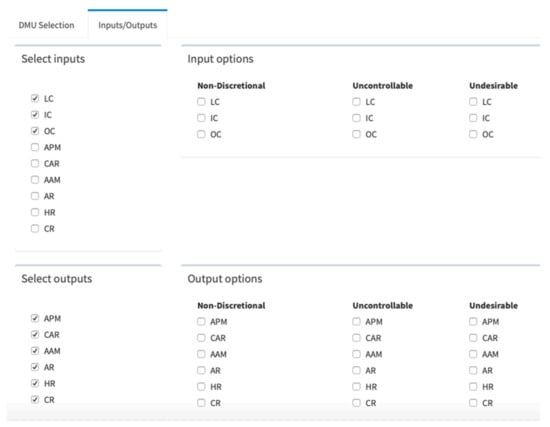 Figure 4. Data: selection of inputs and outputs.
Figure 4. Data: selection of inputs and outputs.
Once we have selected the DMUs to be evaluated and have identified the inputs and outputs, the second step (see Figure 2) is to choose the model that we want to execute (see Figure 5). All DEA models available in deaR-shiny are written in R and are called from the deaR package [60].
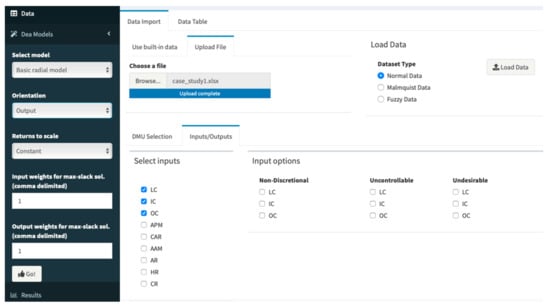
Figure 5.
Data: selection of inputs and Selection of the DEA model.
Carlucci, Cirà and Coccorese [76] run two output-oriented conventional DEA models: the CCR and the BCC DEA models. So, to run the CCR model, we pull down the Select model, which is located on the left-hand column side, and choose the Basic radial model (see Figure 5). New options appear immediately. From the Orientation menu we select the option output, and from the Returns to scale menu the option Constant. If we had selected the option Variable, we would have selected the BCC DEA model.
At this point, we are ready to run the selected model. To do so, we just have to click on the button: Go! Immediately, a dialog box appears with the following message: “Model run finished! Check the Results Tab!”. Note that if deaR-shiny finds some error in the data (for example, negative values or blank cells), the message “Disconnected from server. Reload” will be shown. This message can also be shown if the system detects inactivity.
The main numerical results obtained from the executed model are shown in the Results Table The graphical results are shown in the Plots tab.
The Results tab is structured in two panels:
- In the left panel, the different types of results, organized in tabs, are shown in a table. In general, the numeric results offered by deaR-shiny refer to efficiency scores, slacks, target values, intensities (lambdas) or multipliers, and the reference set for inefficient DMUs. However, the results shown depend on the model executed. For example, if we run the Malmquist index, the results provided by deaR-shiny will be related to total factor productivity change, technical efficiency change (under CRS), pure technical efficiency change (under VRS), scale efficiency change, and technological change.Three action buttons are also provided in the left panel: Copy, Print and Download (to download the results in csv, pdf or excel format).
- In the right panel are some options for saving the results. Thus, we can select the results to be exported as well as give a name and extension format to the file. deaR-shiny gives the name ResultsDEAyear-month-day_hour:minute:second.xlsx by default. To save the results, we click on the button Create Excel file and then on Download excel file.
To get the results of our example, we click on the Results Table Results are shown in Figure 6.
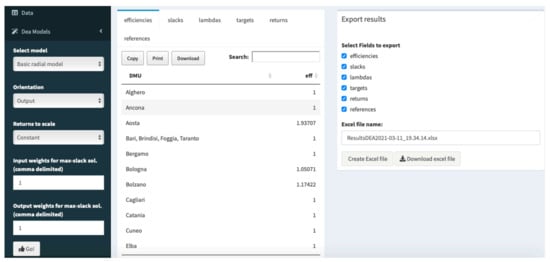
Figure 6.
Getting the results of the selected model (output-oriented CCR DEA model).
Table 4 shows the efficiency scores obtained by the application of the output-oriented DEA model under constant and variable returns to scale. Airports with efficiency scores equal to 1 are efficient while those with scores greater than 1 are inefficient. Under constant-returns-to-scale, 12 out of 33 airports are inefficient: Aosta, Bologna, Bolzano, Florence/Pisa, Olbia, Palermo, Parma, Pescara, Reggio/Calabria, Salerno, Turin, and Verona/Brescia. Under de assumption of variable returns-to-scale only 9 airports are inefficient: Aosta, Bolzano, Palermo, Parma, Pescara, Reggio/Calabria, Salerno, Turin, and Verona/Brescia.

Table 4.
Efficiency scores of the 34 Italian regional airports.
The graphical results also depend on the selected model. As we executed a basic output-oriented CCR DEA model (or alternatively an output-oriented BCC DEA model), the plots obtained are: (1) bar plot of the number of efficient and inefficient DMUs, (2) distribution of the efficiency score of the inefficient DMUs, (3) horizontal bar plot of the number of times that efficient DMUs appear in the peer set of the inefficient DMUs, and (4) the references chart. In this last plot, which is a novelty in the exploitation of DEA results, a network graph in which the green circles represent the efficient DMUs and the red circles the inefficient ones. As it is well known, an inefficient DMU has a reference set that is built with the efficient DMUs with which it is directly compared. These efficient DMUs can be used as the benchmarks of the inefficient one, since they represent the projection point on the efficient frontier in order to eliminate the inefficiency. Efficient DMUs in a reference set can have different weights or intensities (lambdas). Reference sets obtained from the output-oriented CCR model are shown in Table 5.

Table 5.
Reference sets of inefficient airports 1 (output-oriented CCR model).
Thus, the reference plot (see Figure 7) is a graphical depiction of the reference sets of the inefficient DMUs. In this plot, the inefficient DMUs are represented as red nodes in the inner circle, while the efficient DMUs correspond to the green nodes lying in the outer circle. From each inefficient DMU, there is an arrow joining it with each one of the efficient DMUs in its corresponding reference set. Additionally, the size of each efficient DMU (i.e., each green node) is proportional to the sum of the intensities (lambdas) obtained in the different reference sets to which it belongs.
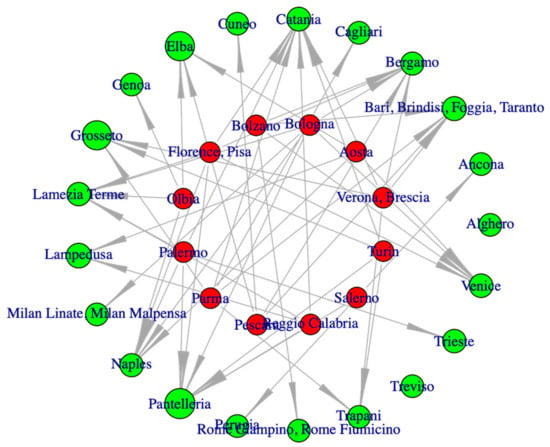
Figure 7.
Plotting the reference sets (output-oriented CCR model). DMUs in green color are efficient and those in red color are inefficient.
3.2. Case Study 2. Kao and Liu (2000, 2003)
In this second case study, we reproduce the results in Kao and Liu [77,78]. In this article, the authors calculate the efficiency scores of the 24 university libraries in Taiwan. To measure the relative efficiency of the libraries, Kao and Liu [77,78] consider one input (Patronage) and five outputs (Collections, Personnel, Expenditures, Buildings, and Services). Specifically, they consider [77] (pp. 151–152)
- Patronage: It is a weighted sum of the standardized scores of faculty, graduate students, undergraduate students, and extension students.
- Collections: Books, serials, microforms, audiovisual works, and database.
- Personnel: Classified staff, unclassified staff, and student assistants.
- Expenditures: Capital expenditure, operating expenditure, and special expenditure.
- Buildings: Area and seats.
- Services: Operating hours, attendance, circulation, communication channels, range of services, amount of services, etc.
However, there are three libraries that are unable to provide all the data. That is, there are missing values in Expenditures and Services. Kao and Liu treat these missing data as imprecise data (fuzzy numbers) that can be represented by a triangular membership function. More specifically, the smallest possible, most possible, and largest possible values of the missing data are set to the minimum, median, and maximum values from the observed data in the corresponding category. Since Kao and Liu have imprecise data, they use a fuzzy DEA model [68] to calculate the fuzzy efficiency scores.
The data used by Kao and Liu [77,78] are available in deaR-shiny. Therefore, to load the data we only need to pull down the menu Select built-in dataset and select Kao_liu_2003. Then we select the option Fuzzy data because we are working with imprecise data, and finally, we click on the button Load Data.
Now, we have to identify which variables are inputs and which are outputs. As mentioned above, Patronage is a crisp (non-fuzzy) input; Collections, Personnel, and Buildings are crisp outputs. Expenditures and Services have some missing observations. So, Kao and Liu [77,78] represent these two outputs by triangular fuzzy numbers, which are described by the triplet . In the Kao_Liu_2003 dataset, dL = beta_3_l and dR = beta_3_u for Expenditures. Similarly, dL = beta_5_l and dR = beta_5_u for Services.
The selection of inputs/outputs variables should be similar to the one shown in Figure 8.
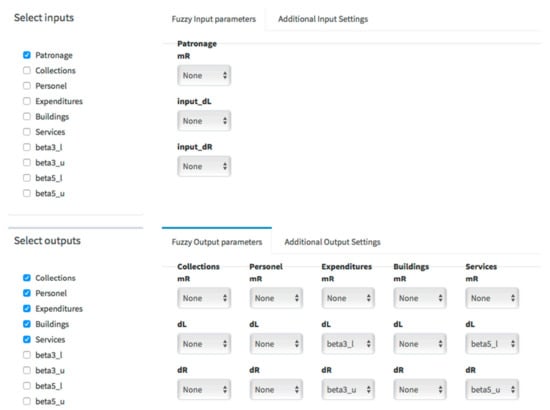
Figure 8.
Data: selection of inputs and outputs with imprecise data.
The relative efficiency scores of the university libraries in Kao and Liu [77,78] are obtained by running an output-oriented fuzzy DEA model under variable returns to scale. Therefore, to replicate these results, we choose Kao–Liu fuzzy model from the DEA models tab and the Basic radial model among the options in the drop-down menu Select crisp DEA model. Finally, we select an output orientation, variable returns to scale for the model, and set the Alpha-Cuts at the value 1 because efficiency scores in [77] are estimated for an alpha-cut at . If we want to get the results in [78], we will set the Alpha-Cuts at the value 11, since in this article the authors give fuzzy efficiency scores expressed by the -cuts at eleven values. Figure 9 shows the different selected options. To run the model, we click on the button Go!
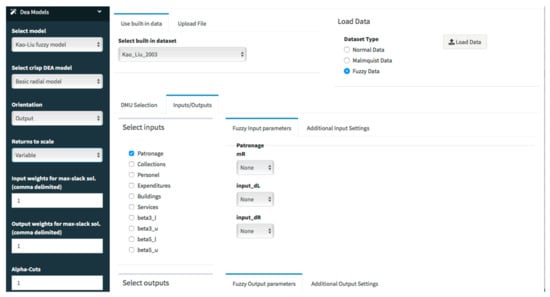
Figure 9.
Selection of Kao and Liu’s output-oriented fuzzy DEA model under variable returns to scale.
Now, to get the results from the fuzzy DEA model, we need to click on the Results Table. deaR-shiny allows us to graphically visualize the fuzzy efficiency scores by means of a dumbbell plot (see Figure 10). The lowest and highest efficiency scores (fuzzy efficiency scores) are shown for each library.
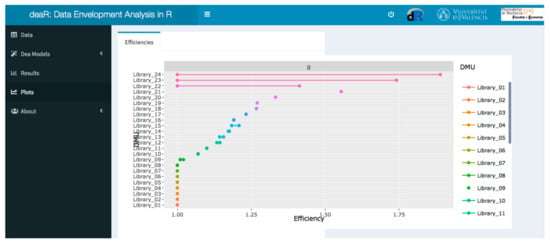
Figure 10.
Plotting the fuzzy efficiency scores.
4. Conclusions
deaR-shiny is an interactive web application used to evaluate efficiency and productivity using Data Envelopment Analysis. deaR-shiny is the result of linking several R packages. On one hand, it uses the shiny and shinydashboard packages, which are R packages for creating reactive web applications. On the other hand, it calls the deaR package to execute the selected DEA model, inheriting the versatility of this package and a large number of different models it integrates. Both practitioners and researchers will find deaR-shiny a very intuitive and user-friendly web application, and at the same time, a very powerful tool for efficiency and productivity analysis. In this paper, we illustrated how to use the web app in two case studies. In the first case study, we have replicated the results given in Carluci, Cirà and Carcasee [76], who use two traditional output-oriented DEA models: CCR model (under constant returns to scales) and BCC model (under variable returns to scale). In the second case study, we reproduced the results obtained by Kao and Liu [77,78], who apply a fuzzy DEA model because they are treating with imprecise data.
We are currently working to extend the capabilities of deaR-shiny by incorporating more models such as network DEA, models treating with negative data, stochastic DEA, or FDEA models. Moreover, we are also trying to improve the graphic results of DEA models.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/su13126774/s1. Data file (Excel file) is supplied as supplementary material with this article. Data can also be download from: https://go.uv.es/dearshiny/case_study1 (accessed on 13 June 2021).
Author Contributions
All the authors contributed equally to this research paper. Conceptualization, R.B., V.C.-S. and V.J.B.; Methodology, R.B., V.C.-S. and V.J.B.; Software, R.B., V.C.-S. and V.J.B.; Writing–original draft, R.B., V.C.-S. and V.J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data used in case study 1 comes from Carlucci, Cirà and Coccorese [76]. Data used in case study 2 comes from Kao and Liu [77,78].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Seiford, L.M. A bibliography for Data Envelopment Analysis (1978–1996). Ann. Oper. Res. 1997, 73, 393–438. [Google Scholar] [CrossRef]
- Tavares, G. A Bibliography of Data Envelopment Analysis (1978–2001); RUTCOR; Rutgers University: New Brunswick, NJ, USA, 2002. [Google Scholar]
- Emrouznejad, A.; Parker, B.R.; Tavares, G. Evaluation of research in efficiency and productivity: A survey and analysis of the first 30 years of scholarly literature in DEA. Socioecon. Plann. Sci. 2008, 42, 151–157. [Google Scholar] [CrossRef]
- Cook, W.D.; Seiford, L.M. Data envelopment analysis (DEA)—Thirty years on. Eur. J. Oper. Res. 2009, 192, 1–17. [Google Scholar] [CrossRef]
- Emrouznejad, A.; Yang, G. A survey and analysis of the first 40 years of scholarly literature in DEA: 1978–2016. Socioecon. Plann. Sci. 2018, 61, 4–8. [Google Scholar] [CrossRef]
- Zhou, H.; Yang, Y.; Chen, Y.; Zhu, J. Data envelopment analysis application in sustainability: The origins, development and future directions. Eur. J. Oper. Res. 2018, 264, 1–16. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manage. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Banker, R.D.; Morey, R.C. Efficiency Analysis for Exogenously Fixed Inputs and Outputs. Oper. Res. 1986, 34, 513–521. [Google Scholar] [CrossRef]
- Banker, R.D.; Morey, R.C. The Use of Categorical Variables in Data Envelopment Analysis. Manag. Sci. 1986, 32, 1613–1627. [Google Scholar] [CrossRef]
- Cook, W.D.; Kress, M.; Seiford, L.M. On the Use of Ordinal Data in Data Envelopment Analysis. J. Oper. Res. Soc. 1993, 44, 133–140. [Google Scholar] [CrossRef]
- Thompson, R.G.; Singleton, F.D.; Thrall, R.M.; Smith, B.A. Comparative Site Evaluations for Locating a High-Energy Physics Lab in Texas. Interfaces 1986, 16, 35–49. [Google Scholar] [CrossRef]
- Thompson, R.G.; Langemeier, L.N.; Lee, C.T.; Lee, E.; Thrall, R.M. The role of multiplier bounds in efficiency analysis with application to Kansas farming. J. Econom. 1990, 46, 93–108. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Wei, Q.L.; Huang, Z.M. Cone ratio data envelopment analysis and multi-objective programming. Int. J. Syst. Sci. 1989, 20, 1099–1118. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Huang, Z.M.; Sun, D.B. Polyhedral Cone-Ratio DEA Models with an illustrative application to large commercial banks. J. Econom. 1990, 46, 73–91. [Google Scholar] [CrossRef]
- Dyson, R.G.; Thanassoulis, E. Reducing Weight Flexibility in Data Envelopment Analysis. J. Oper. Res. Soc. 1988, 39, 563–576. [Google Scholar] [CrossRef]
- Seiford, L.M.; Zhu, J. Modeling undesirable factors in efficiency evaluation. Eur. J. Oper. Res. 2002, 142, 16–20. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Lovell, C.A.K.; Pasurka, C. Multilateral Productivity Comparisons When Some Outputs are Undesirable: A Nonparametric Approach. Rev. Econ. Stat. 1989, 71, 90–98. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Golany, B.; Seiford, L.; Stutz, J. Foundations of data envelopment analysis for Pareto-Koopmans efficient empirical production functions. J. Econom. 1985, 30, 91–107. [Google Scholar] [CrossRef]
- Thanassoulis, E.; Portela, M.C.S.; Despić, O. DEA—The Mathematical Programming Approach to Efficiency Analysis. In The Measurement of Productive Efficiency and Productivity Change; Fried, H.O., Knox Lovell, C.A., Schmidt, S.D., Eds.; Oxford Scholarship: Oxford, UK, 2008; pp. 1–161. ISBN 9780195183528. [Google Scholar]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Fare, R.; Lovell, C. Measuring the technical efficiency of production. J. Econ. Theory 1978, 19, 150–162. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Knox Lovell, C.A. The Measurement of Efficiency and Production; Kluwer-Nijhoff: Boston, MA, USA, 1985; ISBN 9789048158133. [Google Scholar]
- Pastor, J.T.; Ruiz, J.L.; Sirvent, I. An enhanced DEA Russell graph efficiency measure. Eur. J. Oper. Res. 1999, 115, 596–607. [Google Scholar] [CrossRef]
- Zhu, J. Data envelopment analysis with preference structure. J. Oper. Res. Soc. 1996, 47, 136–150. [Google Scholar] [CrossRef]
- Cooper, W.W.; Park, K.S.; Pastor, J.T. RAM: A Range Adjusted Measure of Inefficiency for Use with Additive Models, and Relations to Other Models and Measures in DEA. J. Product. Anal. 1999, 11, 5–42. [Google Scholar] [CrossRef]
- Adler, N.; Friedman, L.; Sinuany-Stern, Z. Review of ranking methods in the data envelopment analysis context. Eur. J. Oper. Res. 2002, 140, 249–265. [Google Scholar] [CrossRef]
- Andersen, P.; Petersen, N.C. A Procedure for Ranking Efficient Units in Data Envelopment Analysis. Manage. Sci. 1993, 39, 1261–1264. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of super-efficiency in data envelopment analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef]
- Du, J.; Liang, L.; Zhu, J. A slacks-based measure of super-efficiency in data envelopment analysis: A comment. Eur. J. Oper. Res. 2010, 204, 694–697. [Google Scholar] [CrossRef]
- Sexton, T.R.; Silkman, R.H.; Hogan, A.J. Data envelopment analysis: Critique and extensions. New Dir. Progr. Eval. 1986, 1986, 73–105. [Google Scholar] [CrossRef]
- Doyle, J.; Green, R. Efficiency and Cross-efficiency in DEA: Derivations, Meanings and Uses. J. Oper. Res. Soc. 1994, 45, 567–578. [Google Scholar] [CrossRef]
- Caves, D.W.; Christensen, L.R.; Diewert, W. The Economic Theory of Index Numbers and the Measurement of Input, Output, and Productivity. Econometrica 1982, 50, 1393–1414. [Google Scholar] [CrossRef]
- Fare, R.; Grosskopf, S.; Norris, M.; Zhang, Z. Productivity Growth, Technical Progress, and Efficiency Change in Industrialized Countries. Am. Econ. Rev. 1994, 84, 66–83. [Google Scholar]
- Ray, S.C.; Desli, E. Productivity Growth, Technical Progress, and Efficiency Change in Industrialized Countries: Comment. Am. Econ. Rev. 1997, 87, 1033–1039. [Google Scholar]
- Grifell-Tatjé, E.; Lovell, C.A.K. A generalized Malmquist productivity index. Top 1999, 7, 81–101. [Google Scholar] [CrossRef]
- Shestalova, V. Sequential Malmquist Indices of Productivity Growth: An Application to OECD Industrial Activities. J. Product. Anal. 2003, 19, 211–226. [Google Scholar] [CrossRef]
- Pastor, J.T.; Lovell, C.A.K. A global Malmquist productivity index. Econ. Lett. 2005, 88, 266–271. [Google Scholar] [CrossRef]
- Charnes, A.; Clark, C.T.; Cooper, W.W.; Golany, B. A developmental study of data envelopment analysis in measuring the efficiency of maintenance units in the U.S. air forces. Ann. Oper. Res. 1984, 2, 95–112. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Sensitivity analysis of efficiency scores: How to bootstrap in nonparametric frontier models. Manage. Sci. 1998, 44, 49–61. [Google Scholar] [CrossRef]
- Löthgren, M. How to Bootstrap DEA Estimators: A Monte Carlo Comparison; SSE/EFI Working Paper Series in Economics and Finance; Stockholm School of Economics: Stockholm, Sweden, 1998. [Google Scholar]
- Löthgren, M.; Tambour, M. Bootstrapping the data envelopment analysis Malmquist productivity index. Appl. Econ. 1999, 31, 417–425. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Statistical Inference in Nonparametric Frontier Models: The State of the Art. J. Product. Anal. 2000, 13, 49–78. [Google Scholar] [CrossRef]
- Cooper, W.W.; Deng, H.; Huang, Z.; Li, S.X. Chance constrained programming approaches to technical efficiencies and inefficiencies in stochastic data envelopment analysis. J. Oper. Res. Soc. 2002, 53, 1347–1356. [Google Scholar] [CrossRef]
- Ray, S.C. Data Envelopment Analysis. Theory and Techniques for Economics and Operations Research; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Olesen, O.B.; Petersen, N.C. Stochastic data envelopment analysis—A review. Eur. J. Oper. Res. 2016, 251, 2–21. [Google Scholar] [CrossRef]
- Hatami-Marbini, A.; Emrouznejad, A.; Tavana, M. A taxonomy and review of the fuzzy data envelopment analysis literature: Two decades in the making. Eur. J. Oper. Res. 2011, 214, 457–472. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, Z. An Overview of the Fuzzy Data Envelopment Analysis Research and Its Successful Applications. Int. J. Fuzzy Syst. 2020, 22, 1037–1055. [Google Scholar] [CrossRef]
- Barr, R.S. DEA software tools and technology. A State-of-the-Art Survey. In Handbook on Data Envelopment Analysis; Cooper, W.W., Seiford, L.M., Zhu, J., Eds.; Springer: Boston, MA, USA, 2004; pp. 539–566. [Google Scholar]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software, 2nd ed.; Springer: Boston, MA, USA, 2007. [Google Scholar]
- Daraio, C.; Kerstens, K.H.J.; Nepomuceno, T.C.C.; Sickles, R. Productivity and Efficiency Analysis Software: An Exploratory Bibliographical Survey of the Options. J. Econ. Surv. 2019, 33, 85–100. [Google Scholar] [CrossRef]
- Ji, Y.; Lee, C. Data envelopment analysis. Stata J. 2010, 10, 267–280. [Google Scholar] [CrossRef]
- Álvarez, I.C.; Barbero, J.; Zofío, J.L. A Data Envelopment Analysis Toolbox for MATLAB. J. Stat. Softw. 2020, 95, 1–49. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021; Available online: https://www.R-project.org/ (accessed on 14 June 2021).
- Wilson, P.W. FEAR: A software package for frontier efficiency analysis with R. Socioecon. Plann. Sci. 2008, 42, 247–254. [Google Scholar] [CrossRef]
- Bogetoft, P.; Otto, L. Benchmarking with DEA, SFA, and R; Springer: New York, NY, USA, 2011; ISBN 978-1-4419-7960-5. [Google Scholar]
- Oh, D.; Suh, D. nonparaeff: Nonparametric Methods for Measuring Efficiency and Productivity. R package version 0.5-5. 2013. Available online: https://CRAN.R-project.org/package=nonparaeff (accessed on 14 June 2021).
- Simm, J.; Besstremyannaya, G. rDEA: Robust Data Envelopment Analysis (DEA) for R. R package version 1.2-6. 2020. Available online: https://CRAN.R-project.org/package=rDEA (accessed on 14 June 2021).
- Lim, D. DJL: Distance Measure Based Judgment and Learning. R package version 3.7. 2020. Available online: https://CRAN.R-project.org/package=DJL (accessed on 14 June 2021).
- Coll-Serrano, V.; Bolós, V.; Benítez Suárez, R. deaR: Conventional and Fuzzy Data Envelopment Analysis. R package version 1.2.3. 2021. Available online: https://CRAN.R-project.org/package=deaR (accessed on 14 June 2021).
- Coll-Serrano, V.; Benítez, R.; Bolós, V. Data Envelopment Analysis with deaR. 2018, pp. 1–48. Available online: https://www.uv.es/deaRshiny/deaR.html (accessed on 14 June 2021).
- Aparicio, J.; Ortiz, L.; Pastor, J.T. Design and implementation of a shiny interactive web application by rstudio for estimating Data Envelopment Analysis efficiency measures. Bol. Estad. e Investig. Oper. 2018, 34, 25–50. [Google Scholar]
- Pastor, J.T.; Lovell, C.A.K.; Aparicio, J. Families of linear efficiency programs based on Debreu’s loss function. J. Product. Anal. 2012, 38, 109–120. [Google Scholar] [CrossRef]
- Chang, W.; Cheng, J.; Allaire, J.; Xie, Y.; MacPherson, J. Shiny: Web Application Framework for R. R package version 1.6.0. 2021. Available online: https://CRAN.R-project.org/package=shiny (accessed on 14 June 2021).
- Chang, W.; Borges Ribeiro, B. shinydashboard: Create Dashboards with “Shiny”. R package version 0.7.1. 2018. Available online: https://CRAN.R-project.org/package=shinydashboard (accessed on 14 June 2021).
- Chambers, R.G.; Chung, Y.; Färe, R. Benefit and Distance Functions. J. Econ. Theory 1996, 70, 407–419. [Google Scholar] [CrossRef]
- Chambers, R.G.; Chung, Y.; Färe, R. Profit, Directional Distance Functions, and Nerlovian Efficiency. J. Optim. Theory Appl. 1998, 98, 351–364. [Google Scholar] [CrossRef]
- Kao, C.; Liu, S.T. Fuzzy efficiency measures in data envelopment analysis. Fuzzy Sets Syst. 2000, 113, 427–437. [Google Scholar] [CrossRef]
- Guo, P.; Tanaka, H. Fuzzy DEA: A perceptual evaluation method. Fuzzy Sets Syst. 2001, 119, 149–160. [Google Scholar] [CrossRef]
- León, T.; Liern, V.; Ruiz, J.L.; Sirvent, I. A fuzzy mathematical programming approach to the assessment of efficiency with DEA models. Fuzzy Sets Syst. 2003, 139, 407–419. [Google Scholar] [CrossRef]
- Sirvent, I.; León, T. Cross-Efficiency in Fuzzy Data Envelopment Analysis (FDEA): Some Proposals. In Performance Measurement with Fuzzy Data Envelopment Analysis. Studies in Fuzziness and Soft Computing; Emrouznejad, A., Tavana, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-642-41371-1. [Google Scholar]
- Coelli, T.J.; Prasada Rao, D.S.; Battesse, G.E. An Introduction to Efficiency and Productivity Analysis; Kluwer Academic Publishers: Boston, MA, USA, 1998. [Google Scholar]
- Deprins, D.; Simar, L.; Tulkens, H. Measuring Labor-Efficiency in Post Offices; CORE Discussion Papers RP; Université catholique de Louvain, Center for Operations Research and Econometrics (CORE): Louvain, Belgium, 1984. [Google Scholar]
- Thrall, R.M. What Is the Economic Meaning of FDH? J. Product. Anal. 1999, 11, 243–250. [Google Scholar] [CrossRef]
- Portela, M.C.A.S.; Thanassoulis, E.; Simpson, G. Negative data in DEA: A directional distance approach applied to bank branches. J. Oper. Res. Soc. 2004, 55, 1111–1121. [Google Scholar] [CrossRef]
- Carlucci, F.; Cirà, A.; Coccorese, P. Measuring and explaining airport efficiency and sustainability: Evidence from Italy. Sustainability 2018, 10, 400. [Google Scholar] [CrossRef]
- Kao, C.; Liu, S.T. A mathematical programming approach to fuzzy efficiency ranking. Int. J. Prod. Econ. 2003, 86, 145–154. [Google Scholar] [CrossRef]
- Kao, C.; Liu, S.-T. Data Envelopment Analysis with Missing Data: An Application to University Libraries in Taiwan. J. Oper. Res. Soc. 2000, 51, 897–905. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).